Kinetics and thermodynamics of the decarboxylation of 1,2-glycerol carbonate to produce glycidol: computational insights†
Donald J.
Darensbourg
* and
Andrew D.
Yeung
Department of Chemistry, Texas A&M University, 3255 TAMU, College Station, TX 77840-3255, USA. E-mail: djdarens@mail.chem.tamu.edu
First published on 5th November 2013
Abstract
The kinetics and thermodynamics of the decarboxylation of 1,2-glycerol carbonate to yield glycidol were studied using “chemically accurate” quantum chemical calculations. Both base- and acid-catalyzed reactions were examined, as were the potential reactions that yield the 3-hydroxyoxetane isomer. Under all conditions, glycidol was the preferred product. While the free energy barrier for the alkoxide form of 1,2-glycerol carbonate to form the epoxide ring is low, the rate-determining step of the overall reaction is the loss of carbon dioxide from the resultant carbonate anion (ca. 21.7 kcal mol−1). Protonation of 1,2-glycerol carbonate is expected to be difficult, but decarboxylation henceforth is exergonic, and the free energy barrier is lower (12.3 kcal mol−1). Calculations also indicate that oligomerization of 1,2-glycerol carbonate (ΔG = 4.9 kcal mol−1), followed by degradation to glycidol, is unlikely on thermodynamic grounds.
Introduction
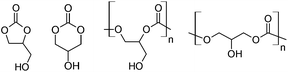
Glycerol carbonates1,2 and polycarbonates3,4 (Fig. 1) may potentially be synthesized from glycerol and carbon dioxide. Both starting materials are themselves inexpensive and renewable carbon sources. Glycerol is a co-product of the transesterification of triglycerides that occurs during biodiesel manufacture,5 and carbon dioxide is produced by various activities, such as the combustion of carbonaceous fuel for the generation of electricity.6 Straightforward routes to glycerol carbonates and polycarbonates and practical applications for them are highly sought. Success in this endeavor will permit the conversion of two waste products into useful chemicals and materials.Although several groups have successfully prepared poly(1,3-glycerol carbonate) and related derivatives,7–9 there have been no successful reports of the ring-opening polymerization of 1,2-glycerol carbonate. Rather, the common method of preparing these poly(1,2-glycerol carbonate) polymers is to copolymerize glycidol with carbon dioxide3,4,10–16 using the well-developed CO2-epoxide chemistry;17 in this case, glycidol serves as a glycerol surrogate, and its free hydroxyl moiety is invariably shielded by an appropriate ether. The benzyl protecting group is a favorite, where easy and complete deprotection by hydrogenation is desired.3,4,7,16
There have been few reports of the successful conversion of 1,2-glycerol carbonate (that can be obtained ultimately from CO2 and glycerol) to glycidol, catalyzed by acids or bases (Scheme 1).18–26 We anticipate that this reaction, an indirect method to obtain glycidol from glycerol for eventual copolymerization with carbon dioxide, will be of increasing interest. As a result, we undertook a computational study that attempts to understand the kinetics and thermodynamics of the base- and acid-catalyzed decarboxylation reactions. Our results are presented herein.
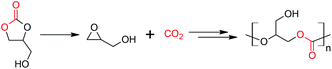 | ||
| Scheme 1 1,2-Glycerol carbonate is decarboxylated to glycidol. After suitable protection, it copolymerizes with CO2, and poly(1,2-glycerol carbonate) is obtained after deprotection.3,4,10–16 In this idealized scheme, glycidol copolymerizes with CO2 that is produced by decarboxylation. | ||
Results and discussion
Prior to an in-depth discussion of both pathways, we note that as a matter of thermodynamics, decomposition of 1,2-glycerol carbonate to glycidol and carbon dioxide causes an increase in entropy. A direct result is that decarboxylation is favored at higher temperature. To illustrate, experimentalists have found elevated temperatures of ca. 200 °C to be appropriate.18,19,21,22,25 Since one of the reaction products is a gas, the use of a vacuum to remove one of the coproducts is helpful too, similarly demonstrated.18,19,25The base- and acid-catalyzed decarboxylation reactions were modeled using the composite CBS-QB3 method27,28 designed to give “chemical accurate” energies (±1 kcal mol−1), modified per Martin et al. by the use of added diffuse functions in the geometry optimization step.29 Solvation models were applied throughout the calculations. We assume that the cationic and anionic reactants are well solvated, such that ion-pairing may be neglected.
Base-catalyzed decarboxylation
The formation of a highly-strained three-membered cyclic ether is difficult, but precedence exists. When deprotonated, poly(cyclopentene carbonate) yields the corresponding epoxide via an intramolecular nucleophilic displacement reaction; an alkyl carbonate is an adequate leaving group for this reaction.30,31 The pendant hydroxy group on glycerol has been implicated in the degradation of poly(1,2-glycerol carbonate) as well.3In the transesterification of dimethyl carbonate with glycerol catalyzed by triethylamine, Ochoa-Gómez et al. observed too, that trace glycidol was produced.23 We agree with their proposed mechanism (Fig. 2(a) and Scheme 2), and studied it with the “chemically accurate” CBS-QB3(+) method.29
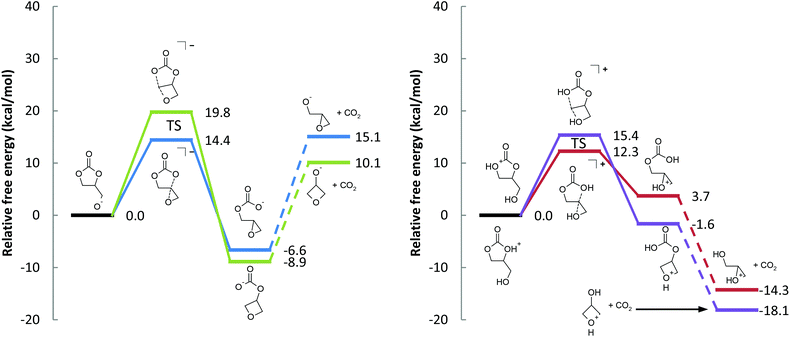 | ||
| Fig. 2 Free energy profiles for the (a) base-catalyzed and the (b) acid-catalyzed decarboxylation reactions (see Schemes 2 and 4). The transition states are also depicted in Fig. 3. | ||
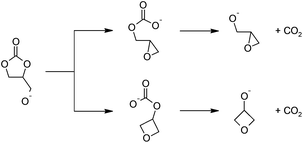 | ||
| Scheme 2 Proposed mechanism for the base-catalyzed decarboxylation reactions leading to (a) glycidol (top) and (b) 3-hydroxyoxetane (bottom) after hydrolysis. | ||
In the proposed mechanism, a strong base deprotonates 1,2-glycerol carbonate's pendant hydroxyl group (not shown), leading to a cyclic carbonate-alkoxide. An intramolecular nucleophilic substitution reaction occurs, ring-opening the five-membered cyclic carbonate, yielding a carbonate anion; the transition states are shown in Fig. 3. The O–C bonds and O–C–O angles for this base-catalyzed example are similar to the corresponding bonds and angles when polymeric alkoxides degrade to epoxides, and require no further comment.30
Parenthetically, we acknowledge an alternate mechanism, in which the chosen base acts as a nucleophile and attacks the carbonate carbon of glycerol carbonate. In an experimental study by Darensbourg and Wei,32 poly(styrene carbonate) was found to depolymerize with a linear decrease in molecular weight, while its polydispersity index remained close to unity. Were random scission of the carbonate linkages preferred, the polymer's molecular weight would drop precipitously. When the terminal hydroxy groups were protected as acetate esters, a higher temperature and a longer reaction time was needed for the polymer to degrade via, presumably, this alternate route. Where terminal hydroxy groups are present, e.g. glycerol carbonate, we expect the base-catalyzed intramolecular reaction route in Scheme 2 to dominate.
The free energy barrier to form the epoxide-carbonate anion is 14.4 kcal mol−1. Forming the oxetane-carbonate anion has a higher free energy barrier at 19.8 kcal mol−1 (Fig. 2(a)), likely due to mutually eclipsed substituents on the oxetane.30 The reaction between an alkoxide and carbon dioxide is fast,33 and the additional barrier is expected to be small, so it should be sufficient to only consider the thermodynamics of the process. Despite the gain of entropy, decarboxylation of the epoxide-carbonate and oxetane-carbonate are endergonic by 21.7 and 19.0 kcal mol−1, respectively, at room temperature. At elevated temperatures, decarboxylation is expected to become easier due to the entropic component of ΔG.
Starting from deprotonated 1,2-glycerol carbonate, glycidol is the favored product due to the kinetics of ring closure. Despite the relatively low barrier for the first reaction, the rate limiting step is loss of CO2. In practice, we expect the reaction to be feasible, especially at high temperatures and low pressures that favor the irreversible loss of CO2. This is exemplified by experimental reports using a strong base (e.g. sodium triphosphate) and reduced pressure to drive the reaction.18
The free energy barriers for the anionic homopolymerization of glycidol was calculated too, the polymeric alkoxide being represented by a methoxide anion. Attack at the methine position has a lower free energy barrier than at the methylene position (Scheme 3, 12.2 vs. 17.0 kcal mol−1, respectively). In the usual case, steric reasons cause attack at the methine position to be less favored.34,35 The ease of the former reaction is due to the pendant hydroxy group hydrogen-bonding with the incoming methoxide nucleophile at the transition state for the reaction (Fig. 4). For completeness, both ring-opening reactions are exergonic by −16.3 and −16.9 kcal mol−1, respectively, giving the reverse reactions (depolymerization of polyglycerol to yield glycidol) high free energy barriers of 28.5 and 33.9 kcal mol−1.
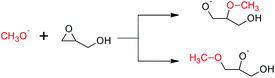 | ||
| Scheme 3 Free energy barriers for the ring-opening polymerization of glycidol. Methine attack (top) has a lower free energy barrier than methylene attack (bottom) (12.2 vs. 17.0 kcal mol−1), because hydrogen bonding stabilizes the former case's transition state (Fig. 4). | ||
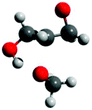 | ||
| Fig. 4 Transition state for methoxide to ring-open glycidol at the methine position. Distances (Å): CH3O–C 2.13; Oepoxide–C 1.88; OH–OCH3 1.58. | ||
These results indicate that if sufficient heat is available for the decarboxylation reaction, there should be sufficient heat for the homopolymerization of glycidol due to its low free energy barrier, as has been observed.36 This should explain why Seki et al. advise that 1,2-glycerol carbonate be dropped into the decarboxylation system, and that the glycidol's residence time in the reactor be reduced by continuous distillation.21
Acid-catalyzed decarboxylation
In 2010, Ferreira et al.37 investigated the acid-catalyzed hydrolysis of epoxides using theoretical methods. Inspired by that work, the acid-catalyzed decarboxylation to give both 1,2- and 1,3-glycerol carbonates were studied. Instead of water, the incoming nucleophile is 1,2-glycerol carbonate's pendant hydroxy group. Similar to Ferreira, a naked proton was used as the prototypical acid; such a simplification may be directly applicable toward heterogeneous catalysts with hydroxyl groups on the surface. This present work may also be helpful in understanding Lewis acid-catalyzed decarboxylation reactions.20–22,25Only the SN2 mechanism is discussed; this mechanism is favored according to Ferreira. The SN1 mechanism (spontaneous ring-opening of protonated cyclic carbonate or cyclic ether) was examined too, but we were similarly unable to locate stable geometries for the resultant primary carbocations, despite using a solvation model.37
The proposed mechanism (Scheme 4) is similar to the base-catalyzed reaction (Scheme 2). Protonated 1,2-glycerol carbonate undergoes nucleophilic substitution by the pendant hydroxy group, leading to a protonated cyclic ether-carbonic acid. At the transition states (Fig. 3), the O–C distances are slightly longer than for the base-catalyzed examples, while the frequencies of the imaginary vibrational mode are lower. The O–C interactions for the protonated species are weaker than for the deprotonated species, as expected. Decarboxylation proceeds thereafter, followed by proton transfer to another 1,2-glycerol carbonate molecule.
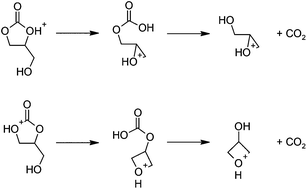 | ||
| Scheme 4 Proposed mechanism for the acid-catalyzed decarboxylation reactions leading to (a) glycidol (top) and (b) 3-hydroxyoxetane (bottom) after hydrolysis. | ||
Ring closure has a relatively small free energy barrier (12.3 and 15.4 kcal mol−1, leading to glycidol and 3-hydroxyoxetane, respectively). Subsequent decarboxylation of the cyclic ether-carbonic acid under acidic conditions is exergonic, paralleling the water, CO2, and carbonic acid system.
To be clear, both protonated 1,2-glycerol carbonate molecules in Scheme 4 are within 1.3 kcal mol−1 (free energy) of each other, so both free energy profiles in Fig. 2(b) can be directly compared. Additionally, the protonated oxetane (b) is 6.6 kcal mol−1 lower in free energy than protonated epoxide (a), in agreement with our understanding of oxetanes as stronger bases than epoxides.38
On the surface, the calculated free energy barriers indicate that the acid-catalyzed reaction is more accessible than the base-catalyzed one; the supposition is that 1,2-glycerol carbonate is as easily protonated as it is deprotonated. The protonated epoxide-carbonic acid is 1.6 kcal mol−1 lower in free energy than the protonated cyclic carbonate-alcohol (Fig. 5), suggesting that their acidities are comparable. The proton affinities of ethylene carbonate and ethylene oxide are close, at 774.2 and 814.2 kJ mol−1 respectively (positive by convention).39 In contrast, the deprotonation of alcohols to yield alkoxides is well understood. The absolute basicity of cyclic carbonates is not addressed in this article, though we would point out that cyclic carbonates do react with electrophiles.40
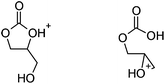 | ||
| Fig. 5 The protonated epoxide-carbonic acid (right) is 1.6 kcal mol−1 lower in free energy than the protonated cyclic carbonate-alcohol (left); refer to the free energy profiles in Fig. 2(b). | ||
To sum up, protonation aside, the free energy barriers for the acid-catalyzed decarboxylation reactions are simply attributed to that of the initial cyclic ether-formation reaction. Glycidol is preferred for both instances, consistent with how 3-hydroxyoxetane is not observed experimentally.41,42 Since both classes have been confirmed by experiments,19–23,25 the current analysis remains quite relevant.
Ring-opening polymerization of 1,2-glycerol carbonate
Early this year, Bañares proposed that the decarboxylation of 1,2-glycerol carbonate proceeded by its oligomerization, followed by some sort of back-biting reaction that yielded glycidol with the loss of carbon dioxide gas.22 In the laboratory, we have not been able to have five-membered cyclic carbonates undergo ring-opening polymerization to yield the polymer, though the six-membered cyclic carbonates do so quite well.43 Subsequent computational work rationalized this observation: the ring-opening polymerization of five-membered cyclic carbonates is endergonic, and the ring-opening polymerization of trimethylene carbonate is exergonic.35We determined the enthalpies and free energies of CO2 and the epoxide or oxetane to react to give the respective polymer vs. cyclic carbonate formation using the CBS-4M method,37,40 similar to our previous report (Table 1).35 In that report, we found that the enthalpies for the 1-mer to 2-mer reactions predicted the average of three iterations within 1 kcal mol−1, so we only examined the 1-mer to 2-mer reaction in the current study.
| Enthalpy | Free energy | |||
|---|---|---|---|---|
| Polymer | Cyclic carbonate | Polymer | Cyclic carbonate | |
| a From CO2 and the corresponding cyclic ether. GC = glycerol carbonate; MeGC = glycerol carbonate, methyl ether. Thermodynamics for all the reactions that we have calculated to date are tabulated in the ESI for the reader's convenience. | ||||
| 1,2-GC | −21.3 | −16.2 | 0.6 | −4.3 |
| 1,2-MeGC | −22.1 | −15.3 | 0.0 | −3.9 |
| 1,3-GC | −22.3 | −9.0 | −0.5 | 1.7 |
| 1,3-MeGC | −20.9 | −8.2 | 0.7 | 2.8 |
Polymer formation is exothermic by ca. 22 kcal mol−1, while formation of the five- and six-membered cyclic carbonates are exothermic by 15 and 9 kcal mol−1 respectively. The ring-opening polymerization of five-membered cyclic carbonates is endergonic, and that of the six-membered analogs is exergonic. Specifically, ring-opening 1,2-glycerol carbonate is endergonic by 4.9 kcal mol−1, and CBS-4M free energies have successfully been used to explain why trimethylene carbonate undergoes ring-opening polymerization, where the isomeric propylene carbonate does not. Glycerol-derived oxetanes do not appear distinct from other aliphatic oxetanes,35 and that the necessity of ether protecting groups is unrelated to the thermodynamics of the overall reaction.
The study of glycerol-derived polycarbonates and cyclic carbonates affords us with the unique opportunity to more-fairly compare the enthalpies of the 1,2- and 1,3-glycerol polycarbonates, as well as the isomeric propylene and trimethylene carbonates (Table 2). From these two examples, five-membered cyclic carbonates appear lower in enthalpy than the six-membered cyclic carbonates, although the reasons for it are not obvious. We speculate that the carbonate O–C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–O angles for the five-membered cyclic carbonate are closer to that of unstrained dimethyl carbonate, than for the six-membered cyclic carbonates. Other metric data are tabulated in the ESI.†
O)–O angles for the five-membered cyclic carbonate are closer to that of unstrained dimethyl carbonate, than for the six-membered cyclic carbonates. Other metric data are tabulated in the ESI.†
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–O angles for cyclic carbonates
O)–O angles for cyclic carbonates
| DMC | GC | PC/TMC | |
|---|---|---|---|
DMC = dimethyl carbonate; GC = glycerol carbonate; PC = propylene carbonate; TMC = trimethylene carbonate. *![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Defined as Enthalpy(1,2-carbonate) − Enthalpy(1,3-carbonate). Defined as Enthalpy(1,2-carbonate) − Enthalpy(1,3-carbonate). |
|||
| 1,2-Carbonate (5-membered ring) | 110.0 | 108.8 | 108.8 |
| 1,3-Carbonate (6-membered ring) | 116.0 | 116.6 | |
| Enthalpy difference* (kcal mol−1) | N.A. | −7.3 | −9.0 |
Concluding remarks
Although it is not possible to prepare poly(1,2-glycerol carbonate) directly by the ring-opening polymerization,44 it can be done indirectly, by decarboxylation of 1,2-glycerol carbonate to prepare glycidol for subsequent copolymerization with CO2. The proposed degradation of 1,2-glycerol carbonate via oligomerization followed by back-biting appears to be unfavorable according to thermodynamic arguments (ΔG = 4.9 kcal mol−1 for ring-opening 1,2-glycerol carbonate).The free energy profiles of the base- and acid-catalyzed routes have been studied. The base-catalyzed reaction has a modest free energy barrier for ring formation, but decarboxylation is the rate-determining step (ΔG‡ ≈ 21.7 kcal mol−1); this reaction has been demonstrated for 1,2-glycerol carbonate,18,23 and for related systems,31 including under reduced pressure. For the base-catalyzed reaction, anionic homopolymerization of the glycidol formed is a concern, such that continuous removal of the glycidol product by distillation is recommended.21
Ease of protonating 1,2-glycerol carbonate notwithstanding, the acid-catalyzed reaction has a lower free energy barrier for decarboxylation, and the rate-determining step for the acid-catalyzed reaction is ring formation (ΔG‡ = 12.3 kcal mol−1). It is unclear how easily 1,2-glycerol carbonate may be protonated, but the successful use of zeolites (that contain both Brønsted and Lewis acidic sites) to produce glycidol supports this mechanism.21,22
Computational methods
All calculations were performed using the Gaussian 09 suite.45 All local minima and saddle points were verified by their calculated vibrational frequencies (zero and one imaginary frequencies respectively. The saddle points found were confirmed to be the correct ones by visualizing the imaginary vibrational modes with AGUI46 and Avogadro.47 No attempts were made to locate global energy minima of the structures studied.Consistent with previous work,30,35 free energy barriers were obtained using CBS-QB3(+) calculations:29 B3LYP48–50/6-311+G(2d,d,p)51–53 reference geometries and frequencies were read-in, and the CBS-QB327,28 calculation proceeded directly to the third step (CCSD(T)/6-31+G(d′)) using the CBS-QB3(StartMP2) keyword in Gaussian 09. The scale factor for the zero-point energies was not changed from the 0.99 pre-defined by CBS-QB3. The Integral Equation Formalism Polarization Continuum Model (IEFPCM) calculation with radii and non-electrostatic terms for Truhlar and coworkers’ SMD solvation model54 was used with tetrahydrofuran as the prototypical solvent. Also consistent with our previous work,35 enthalpies of polymerization were obtained by the CBS-4M method in the gas phase.27,55
Competing interest
The authors declare no competing financial interests.Acknowledgements
We thank the National Science Foundation (CHE1057743) and the Robert A. Welch Foundation (A-0923) for financial support for this work. The authors acknowledge the Laboratory for Molecular Simulation and the Supercomputing Facility at Texas A&M University for providing computing resources.References
- M. O. Sonnati, S. Amigoni, E. P. Taffin de Givenchy, T. Darmanin, O. Choulet and F. Guittard, Green Chem., 2013, 15, 283 RSC.
- J. R. Ochoa-Gómez, O. Gómez-Jiménez-Aberasturi, C. Ramírez-López and M. Belsué, Org. Process Res. Dev., 2012, 16, 389 CrossRef.
- H. Zhang and M. W. Grinstaff, J. Am. Chem. Soc., 2013, 135, 6806 CrossRef CAS PubMed.
- J. Geschwind and H. Frey, Macromolecules, 2013, 46, 3280 CrossRef CAS.
- R. Christoph, B. Schmidt, U. Steinberner, W. Dilla and R. Karinen, in Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH Verlag GmbH & Co. KGaA, 2006 Search PubMed.
- M. Aresta, in Utilization of Greenhouse Gases, American Chemical Society, 2003, vol. 852, pp. 2–39 Search PubMed.
- W. C. Ray III and M. W. Grinstaff, Macromolecules, 2003, 36, 3557 CrossRef.
- P. G. Parzuchowski, M. Jaroch, M. Tryznowski and G. Rokicki, Macromolecules, 2008, 41, 3859 CrossRef CAS.
- J. Simon, J. V. Olsson, H. Kim, I. F. Tenney and R. M. Waymouth, Macromolecules, 2012, 45, 9275 CrossRef CAS.
- J. Hilf and H. Frey, Macromol. Rapid Commun., 2013, 34, 1395 CrossRef CAS PubMed.
- J. Łukaszczyk, K. Jaszcz, W. Kuran and T. Listoś, Macromol. Biosci., 2001, 1, 282 CrossRef.
- Q. Zhou, L. Gu, Y. Gao, Y. Qin, X. Wang and F. Wang, J. Polym. Sci., Part A: Polym. Chem., 2013, 51, 1893 CrossRef CAS.
- N.-Y. Mun, K.-H. Kim, D.-W. Park, Y. Choe and I. Kim, Korean J. Chem. Eng., 2005, 22, 556 CrossRef CAS.
- W.-M. Ren, M.-W. Liang, Y.-C. Xu and X.-B. Lu, Polym. Chem., 2013, 4, 4425 RSC.
- J. Geschwind and H. Frey, Macromol. Rapid Commun., 2013, 34, 150 CrossRef CAS PubMed.
- H. Frey, J. Hilf and A. Phillips, Polym. Chem., 2013 10.1039/c3py00977g.
- For comprehensive reviews in this area, see: (a) D. J. Darensbourg and M. W. Holtcamp, Coord. Chem. Rev., 1996, 153, 155 CrossRef CAS; (b) G. W. Coates and D. R. Moore, Angew. Chem., Int. Ed., 2004, 43, 6618 CrossRef CAS PubMed; (c) H. Sugimoto and S. Inoue, J. Polym. Sci., Part A: Polym. Chem., 2004, 42, 5561 CrossRef CAS; (d) D. J. Darensbourg, R. M. Mackiewicz, A. L. Phelps and D. R. Billodeaux, Acc. Chem. Res., 2004, 37, 836 CrossRef CAS PubMed; (e) M. H. Chisholm and Z. Zhou, J. Mater. Chem., 2004, 14, 3081 RSC; (f) D. J. Darensbourg, Chem. Rev., 2007, 107, 2388 CrossRef CAS PubMed; (g) S. Klaus, M. W. Lehnmeier, C. E. Anderson and B. Rieger, Coord. Chem. Rev., 2011, 255, 1460 CrossRef CAS PubMed; (h) M. R. Kember, A. Buchard and C. K. Williams, Chem. Commun., 2011, 47, 141 RSC; (i) X.-B. Lu and D. J. Darensbourg, Chem. Soc. Rev., 2012, 41, 1462 RSC; (j) D. J. Darensbourg and S. J. Wilson, Green Chem., 2012, 14, 2665 RSC; (k) X.-B. Lu, W.-M. Ren and G.-P. Wu, Acc. Chem. Res., 2012, 45, 1721 CrossRef CAS PubMed.
- J. D. Malkemus, V. A. Currier and J. B. Bell Jr., Method for preparing glycidol, US Pat, 2,856,413, 1958 Search PubMed.
- J.-W. Yoo, Z. Mouloungui and A. Gaset, Method for producing an epoxide, in particular of glycidol, and installation for implementation, US Pat, 6316641 B1, 2001 Search PubMed.
- A. Dibenedetto, A. Angelini, M. Aresta, J. Ethiraj, C. Fragale and F. Nocito, Tetrahedron, 2011, 67, 1308 CrossRef CAS PubMed.
- Y. Seki, T. Sasa, H. Takeuchi, M. Uno and M. Namba, Process for producing glycidol, US Pat, 7868192 B1, 2011 Search PubMed.
- C. L. Bolívar-Diaz, V. Calvino-Casilda, F. Rubio-Marcos, J. F. Fernández and M. A. Bañares, Appl. Catal., B, 2013, 129, 575 CrossRef PubMed.
- J. R. Ochoa-Gómez, O. Gómez-Jiménez-Aberasturi, C. Ramírez-López and B. Maestro-Madurga, Green Chem., 2012, 14, 3368 RSC.
- K. Gumlich, R. Merten and J. H. Teles, Process for preparing glycidyl esters, US Pat, 8236974 B2, 2012 Search PubMed.
- J. S. Choi, F. S. H. Simanjuntaka, J. Y. Oh, K. I. Lee, S. D. Lee, M. Cheong, H. S. Kim and H. Lee, J. Catal., 2013, 297, 248 CrossRef CAS PubMed.
- G. Parameswaram, M. Srinivas, B. Hari Babu, P. S. Sai Prasad and N. Lingaiah, Catal. Sci. Technol., 2013 10.1039/c3cy00532a.
- J. A. Montgomery, M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 1999, 110, 2822 CrossRef CAS.
- J. A. Montgomery, M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 2000, 112, 6532 CrossRef CAS.
- S. Parthiban, G. de Oliveira and J. M. L. Martin, J. Phys. Chem. A, 2001, 105, 895 CrossRef CAS.
- D. J. Darensbourg, A. D. Yeung and S.-H. Wei, Green Chem., 2013, 15, 1578 RSC.
- D. J. Darensbourg, S.-H. Wei, A. D. Yeung and W. C. Ellis, Macromolecules, 2013, 46, 5850 CrossRef CAS.
- D. J. Darensbourg and S.-H. Wei, Macromolecules, 2012, 45, 5916 CrossRef CAS.
- B. O. Heston, O. C. Dermer and J. A. Woodside, Proc. Okla. Acad. Sci., 1942, 23, 67 Search PubMed.
- S. M. Bachrach, Computational Organic Chemistry, John Wiley & Sons, Inc., 2006 Search PubMed.
- D. J. Darensbourg and A. D. Yeung, Macromolecules, 2013, 46, 83 CrossRef CAS.
- K. Iaych, S. Dumarçay, E. Fredon, C. Gérardin, A. Lemor and P. Gérardin, J. Appl. Polym. Sci., 2011, 120, 2354 CrossRef CAS.
- R. C. D. Muniz Filho, S. A. A. de Sousa, F. da Silva Pereira and M. M. C. Ferreira, J. Phys. Chem. A, 2010, 114, 5187 CrossRef CAS PubMed.
- D. J. Darensbourg and W.-C. Chung, Polyhedron, 2013, 58, 139 CrossRef CAS PubMed.
- E. P. Hunter and S. G. Lias, in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg, MD Search PubMed.
- T. Ariga, T. Takata and T. Endo, Macromolecules, 1997, 30, 737 CrossRef CAS.
- G. Rokicki, P. Rakoczy, P. Parzuchowski and M. Sobiecki, Green Chem., 2005, 7, 529 RSC.
- K. M. Tomczyk, P. A. Guńka, P. G. Parzuchowski, J. Zachara and G. Rokicki, Green Chem., 2012, 14, 1749 RSC.
- D. J. Darensbourg and A. I. Moncada, Macromolecules, 2009, 42, 4063 CrossRef CAS.
- G. Rokicki, Prog. Polym. Sci., 2000, 25, 259 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- Ampac GUI 9, Semichem, Inc., 2008 Search PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Chem. Inf. Model., 2012, 4, 17 CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef CAS PubMed.
- G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193 CrossRef CAS.
- G. A. Petersson and M. A. Al-Laham, J. Chem. Phys., 1991, 94, 6081 CrossRef CAS.
- G. A. Petersson, T. G. Tensfeldt and J. A. Montgomery, J. Chem. Phys., 1991, 94, 6091 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378 CAS.
- J. W. Ochterski, G. A. Petersson and J. A. Montgomery, J. Chem. Phys., 1996, 104, 2598 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Metric parameters for carbonates; thermodynamics of polymer vs. cyclic carbonate formation. See DOI: 10.1039/c3gc41643g |
| This journal is © The Royal Society of Chemistry 2014 |