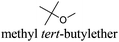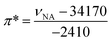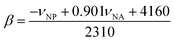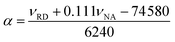Eco-friendly solvents and amphiphilic catalytic polyoxometalate nanoparticles: a winning combination for olefin epoxidation
Adrien
Mouret
,
Loïc
Leclercq
,
Andrea
Mühlbauer
and
Véronique
Nardello-Rataj
*
Université Lille Nord de France, Université Lille 1, ENSCL, EA 4478, Chimie Moléculaire et Formulation, F-59655 Villeneuve d'Ascq Cedex, France. E-mail: veronique.rataj@univ-lille1.fr; Tel: +33 (0)320 336 369
First published on 25th October 2013
Abstract
Eighteen eco-friendly solvents were examined to carry out the epoxidation of olefins with the amphiphilic catalytic dodecyltrimethylammonium polyoxometalate nanoparticles [C12]3[PW12O40] in comparison with [H]3[PW12O40] and [Na]3[PW12O40]. Surprisingly, the screening of solvents with cyclooctene has revealed that the [C12]3[PW12O40] catalyst is much more active with initial turn-over frequencies, TOF0, increasing up to a factor of 10. Moreover, the reaction occurs at competitive rates in four relevant solvents, i.e. cyclopentyl methyl ether, 2-methyl tetrahydrofuran, methyl acetate and glycerol triacetate, for which TOF0 values are higher than 260 h−1. The recyclability of the systems is demonstrated and the scope of substrates has been successfully extended to cyclohexene, 1-octene, limonene, 3-carene, α-pinene, β-pinene and neryl acetate with good epoxide selectivity. The catalytic performances in the “green” solvent are assigned to the formation of stable [C12]3[PW12O40] nanoparticle dispersions which have been characterized by transmission electron microscopy and dynamic and multiple light scattering experiments. Finally, the Kamlet–Taft parameters were measured in order to correlate the physicochemical properties of the solvents and the catalytic activity.
Introduction
In the context of “green” chemistry, developed by Anastas and Warner,1 the use of solvents should be made unnecessary whenever possible. However, most organic reactions require a solvent and then hazardous solvents must be substituted by innocuous ones with better solubilizing properties and a higher biodegradability, the key points to obtain “green” processes. In addition, chemical wastes generated by stoichiometric processes are a serious issue for industries. Therefore, catalytic reagents (as selective as possible) become more and more obvious. In this context, catalytic oxidation processes play a central role in the chemicals industry.2 Indeed, the formation of organic intermediates from petroleum and natural gas is used to obtain an amazing variety of products that include many kinds of plastics, synthetic fibers, elastomers, surface coatings, drugs, solvents, detergents, insecticides, herbicides, explosives, and countless specialty chemicals. One of the most “green” oxidizing reactants is hydrogen peroxide, H2O2, because it is quite cheap, readily available, easy to handle, and gives water as the only co-product.3 On the other hand, polyoxometalates (POMs), which consist of three or more transition metal oxyanions linked together by sharing oxygen atoms to form a large closed 3-D framework, have received a great deal of attention as homogeneous and heterogeneous catalysts for a wide variety of oxidation reactions.4 Alkene epoxidation is one of the basic reactions in industrial organic synthesis because epoxides are key intermediates for the manufacture of a wide variety of valuable products.5 In the last three decades, some elegant epoxidation reactions have been performed with POMs.6 For instance, Ishii and co-workers have developed a process using [H]3[PW12O40] and H2O2 to epoxidize various alkenes.7 The epoxidation mechanism based on the [PW12O40]3− catalyst is presented in Fig. 1.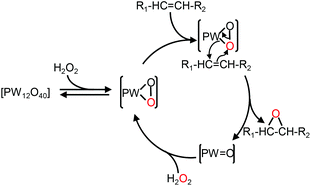 | ||
| Fig. 1 Mechanism of olefin epoxidation with the [PW12O40] catalyst.8 | ||
However, most hydrogen peroxide-based epoxidation reactions catalyzed by [H]3[PW12O40] are performed in biphasic systems using chlorinated (e.g. methylene chloride, chloroform) or hazardous solvents (e.g. acetonitrile, a very inflammable liquid with a flash point of 12.8 °C).9 As pointed out by Hill et al.: “the use of chlorocarbons largely defeats the significant environmental and economic advantages of using H2O2as the oxidant”.10 In 2003, Noyori et al. developed the epoxidation of olefins under organic solvent- and halide-free conditions.11 This smart catalytic system seems to be ideal because it is economically, technically, and environmentally satisfying. However, the reaction is performed at high temperature (90 °C) in the presence of a surfactant (quaternary ammonium hydrogenosulfate) and phosphonic acid in order to create in situ the Venturello catalyst. In recent years, balanced catalytic surfactants, combining an amphiphilic quaternary ammonium cation and a catalytic counteranion, such as MoO42− or WO42−, have been designed to obtain very efficient two- and three-phase microemulsion systems for the catalytic oxidation (i.e. dark singlet oxygenation, epoxidation, sulfide oxidation) of various substrates.12 More recently, based on the same concept, catalytic amphiphilic POM nanoparticles resulting from the electrostatic coupling of [PW12O40]3− anions and alkyltrimethyl ammonium cations have been shown to stabilize the so-called Pickering emulsions.13 This new amphiphilic catalyst gives pH-neutral conditions (pH ≈ 6.5) preventing epoxide hydrolysis.12 This catalyst works at 65 °C with competitive reaction rates.13 However, the drawback of this method is the aromatic solvents used to generate the Pickering emulsion.13 In order to obtain a more sustainable catalytic process, the use of these amphiphilic nanoparticles has been investigated for the epoxidation of olefins in eighteen eco-friendly solvents with the aim to find relevant alternatives to the aromatic, chlorinated and other hazardous solvents which are commonly used to perform reactions with POM catalysts (Table 1). The reaction media as well as the catalytic nanoparticle behavior in the “green” solvents have been characterized by transmission electron microscopy (TEM) and dynamic and multiple light scattering experiments. Finally, the Kamlet–Taft parameters were measured in order to correlate the physicochemical properties of the solvents with their catalytic activity.
Results and discussion
Choice of solvents and their physicochemical characteristics
“Green” solvents are used to minimize the environmental impact resulting from the use of solvents during chemical processes. Eighteen “green” or “sustainable” solvents, with a good EHS (Environment, Health and Safety) profile and preferably obtained from the biomass feedstock, have been selected through the review of the technical, commercial and scientific literature (Table 1). In particular, the choice of the “green” solvents was dictated by the freezing (F.p. < 0 °C) and the boiling (B.p. > 50 °C) points and also by the toxicity index, Itox, according to Hodge and Sterner between 4 and 6 (4: slightly toxic, 6: relatively harmless). This information is reported in Table 1 as well as the emission of volatile organic compounds (VOCs) according to the European Directive 1999/13/CE. Also, if existing, the risk phrase associated with a flammability hazard (R10: flammable, R11: highly flammable) is indicated. Another criterion for the selection of solvents was their miscibility with aqueous H2O2 solution because it is used as an oxidizing agent in the proposed olefin epoxidation (see below). The “bio-solvents”, i.e. solvents produced from renewable resources, are labeled as green in Table 1. For comparison, two conventional and widely used solvents (chloroform and acetonitrile) have also been reported and investigated for POM-based catalyses (see below).4 It is noteworthy that the solvents in Table 1 have been classified according to their initial turnover frequency (TOF0) observed in the catalytic cyclooctene epoxidation (see below).In a chemical process, the use of a solvent is dictated by its basicity/acidity, its polarity and its protic or aprotic nature. In order to estimate the physicochemical properties of solvents, one classical approach consists of determining the Kamlet–Taft plot.15,16 Indeed, solvents are identified by three descriptors: α (a measure of the “proticity” or H-bond donating ability), β (an expression of their basicity or H-bond accepting ability) and π* (a measure of their polarity and polarizability). Classically, a 2D chart is plotted with π* on the x-axis and β on the y-axis (Fig. 2).
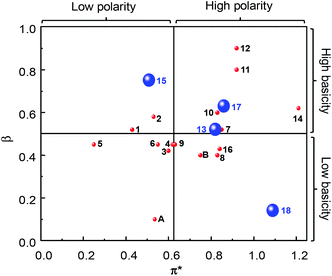 | ||
| Fig. 2 Kamlet–Taft plot of solvents (1–19, A and B) as a function of their π* (polarity and polarizability), β (basicity or H-bond accepting ability) and α (“proticity” or H-bond donating ability) values (blue large sphere: α > 0.5; red small sphere: α < 0.5). Data were obtained from ref. 15 and 16 or experimentally determined for 1, 4, 7, 14, 16, and 17. | ||
In Fig. 2, the sphere size represents the protic (α > 0.5: small sphere) or the aprotic nature of the solvent (α < 0.5: large sphere). The data values were obtained from the literature or experimentally determined (see Table 2). Although the investigated solvents cover a large part of the Kamlet–Taft plot, we can distinguish different groups. The first one is composed of solvents 1–10, 13, 16 and B. For these solvents, the β values are between 0.4 and 0.6 (i.e. all of them possess the same basicity or H-bond accepting ability) but π* varies between 0.25 for 5 and 0.84 for 16 (i.e. between these two solvents we have an increase of the polarity and the polarizability). The π* parameter follows the relative polarity values extracted from the literature: 0.12 (5), 0.18 (2), 0.22 (6), 0.25 (3) and 0.46 (B) vs. 0.25 (5), 0.53 (2), 0.55 (6), 0.60 (3) and 0.75 (B) for π*.17 Moreover, it is noteworthy that for all the solvents in this group, α is lower than 0.19 except for EtLac 13 (α = 0.69) due to the presence of one hydroxyl functional group. The second group is composed of water 18 and chloroform A for which β is very low (0.14 and 0.10, respectively) due to their weak basicity. However, these two solvents are very different from the viewpoint of α and π*. In fact, α and π* parameters are very high for 18 compared to A due to the high polarity, polarisability and the large ability of water to form H-bonds. The third family is composed of solvents 14, 15 and 17, for which the β values are between 0.6 and 0.8 but with various α and π* depending on the structure and the presence of OH functions. The fourth and last family is composed of solvents 11 and 12, for which the three Kamlet–Taft parameters are very close due to the similarity of the two structures.
| Solvent | α | β | π* |
|---|---|---|---|
| a Our experimental data (see the Experimental section). b Taken from ref. 15. c Taken from ref. 16. | |||
| 1 | 0 | 0.52 (0.53)b | 0.43 (0.42)b |
| 2 | 0 | 0.58 | 0.53 |
| 3 | 0 | 0.42 | 0.60 |
| 4 | 0 | 0.45 | 0.62 (0.63)b |
| 5 | 0 | 0.45 | 0.25 |
| 6 | 0 | 0.45 | 0.55 |
| 7 | 0 | 0.52 | 0.85 |
| 8 | 0 | 0.40 | 0.83 |
| 9 | 0 | 0.45 | 0.63 |
| 10 | 0 | 0.60 | 0.83 |
| 11 | 0 | 0.80 | 0.92 |
| 12 | 0 | 0.90 | 0.92 |
| 13 | 0.69 | 0.52 | 0.82 |
| 14 | 0 | 0.62 | 1.21 |
| 15 | 0.83 | 0.75 | 0.51 |
| 16 | 0 | 0.43 | 0.84 |
| 17 | 0.59 | 0.63 | 0.86 |
| 18 | 1.17 | 0.14 | 1.09 |
| A | 0.20 | 0.10 | 0.53 |
| B | 0.19 | 0.40 | 0.75 |
Catalytic epoxidation of cyclooctene in the selected solvents
Cyclooctene was first chosen as a model substrate. This choice was dictated by its easy and selective conversion into the corresponding epoxide. In order to evaluate the performances of the [C12]3[PW12O40] amphiphilic catalyst (neutral conditions), the reactions were also performed with the classical [H]3[PW12O40] catalyst (acidic conditions) and its sodium salt ([Na]3[PW12O40], neutral conditions) under the same concentration and temperature conditions. The reactions were conducted at 65 °C in the presence of only 1 equivalent of H2O2 relative to the substrate until its complete conversion was reached (>95%). The results in terms of the initial turn-over frequency (TOF0) and reaction time as a function of the solvent are reported in Table 3 and in Fig. 3.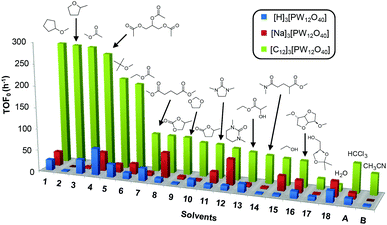 | ||
| Fig. 3 Initial turn-over frequency (TOF0) observed for the epoxidation of cyclooctene in various eco-friendly solvents (1–18) in comparison with two classical solvents (A and B). | ||
| Solvent | [H]3[PW12O40] | [Na]3[PW12O40] | [C12]3[PW12O40] | |||
|---|---|---|---|---|---|---|
| TOF0 (h−1) | Δt (h) | TOF0 (h−1) | Δt (h) | TOF0 (h−1) | Δt (h) | |
| a Reaction conditions: [X]3[PW12O40] nanoparticles = 15 μmol (X = C12, Na or H), solvent = 3 mL, olefin = 1.5 mmol, H2O2 = 1.5 mmol, 65 °C, conversion > 95%, epoxide > 99%. b Time at which a plateau is reached (conversion obtained at this time). | ||||||
| 1 | 24.8 | 3 | 33.2 | 3 | 283.2 | 0.6 |
| 2 | 2.4 | 30 | 0 | 0 | 281.2 | 0.7 |
| 3 | 33.2 | 5.5 (62)b | 3.9 | 60 | 279.2 | 0.8 |
| 4 | 66.4 | 1 (66)b | 43.7 | 5 | 266 | 0.8 |
| 5 | 30.4 | 4 | 19.1 | 14 | 211.2 | 0.8 |
| 6 | 14.4 | 3 (48)b | 24.3 | 6 | 201.6 | 1 |
| 7 | 29.1 | 1 (32)b | 8.2 | 30 | 88.4 | 3 |
| 8 | 10.3 | 1 (11)b | 58.5 | 3 | 87.3 | 3 |
| 9 | 2.9 | 100 | 6.5 | 50 | 87.2 | 3 |
| 10 | 16.3 | 10 | 3.2 | 50 | 79 | 4 |
| 11 | 9.2 | 3 (44)b | 26.4 | 1 (71)b | 78.4 | 1 (73)b |
| 12 | 10.8 | 3 (43)b | 59.8 | 1 (67)b | 72.9 | 1 (70)b |
| 13 | 19.4 | 8 | 6.7 | 60 | 68.4 | 1.5 |
| 14 | 2.3 | 30 | 3.2 | 40 | 64.7 | 6 |
| 15 | 4.1 | 30 | 34.2 | 4 | 61.7 | 3 |
| 16 | 16.1 | 7 | 28.4 | 5 | 60.4 | 3 |
| 17 | 8.9 | 1 (9)b | 2.2 | 50 | 24.3 | 6 |
| 18 | 10.9 | 12 | 13.9 | 12 | 7.3 | 15 |
| A | 14 | 10 | 13.5 | 12 | 67.5 | 2 (81)b |
| B | 2.8 | 50 | 0 | 0 | 48.4 | 5 |
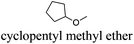
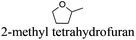
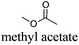
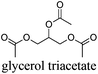
As indicated in Table 3, both reference experiments with [H]3[PW12O40] and [Na]3[PW12O40] gave similar results with relatively low catalytic activity in almost all solvents (1–18). The initial turn-over frequency (TOF0) does not exceed ≈30 h−1 for [H]3[PW12O40] except for solvent 4 (66.4 h−1), whereas for [Na]3[PW12O40], the best TOF0 values are obtained for solvents 4, 8 and 12 with TOF0 equal to 43.7, 58.5 and 59.8 h−1 respectively. On the other hand, apparent good reaction times would be obtained in GTA 4, DMG 7, PC 8 and Solketal 17 but the reaction reaches a plateau, limiting the final conversion to 66, 32, 11 and 9% respectively. Moreover, in chloroform (A) and acetonitrile (B), both the acidic and sodic forms of the catalyst are inefficient. It is noteworthy that [H]3[PW12O40] and [Na]3[PW12O40] catalysts give biphasic media with chloroform in the presence of H2O2 whereas with acetonitrile, they lead to a homogeneous medium. Surprisingly, the catalytic activity is better in chloroform than in acetonitrile. We suppose that the nature of the intermediates (i.e. the active species formed by [PW12O40]3− decomposition) depends on the solvent properties. Indeed, as described by Rhodes et al., the decomposition of [H]3[PW12O40] is reduced in an ethanol–water mixture or an acetone solution compared to pure water.18 As clearly shown by the TOF0 reported in Fig. 3, the cyclooctene epoxidation in the “green” solvents is remarkably more efficient with the [C12]3[PW12O40] amphiphilic catalyst than with [H]3[PW12O40] or [Na]3[PW12O40] (except in water 18). The four best solvents exhibiting TOF0 up to ten times higher can be highlighted: cyclopentyl methyl ether (CPME 1), 2-methyl tetrahydrofuran (2-MeTHF 2), methyl acetate (AcOMe 3) and glycerol triacetate (GTA 4). In all the “green” solvents 1–17, the [C12]3[PW12O40] nanoparticles give a fine and stable dispersion leading to a homogeneous mixture upon hydrogen peroxide addition for solvents 2, 3, 8–14 and 16 whereas with solvents 1, 4–7, 15 and 17, the solid nanoparticles remain dispersed in the solvents. As the reaction media are different for the four most active solvents, we can assume that the catalytic activity is not directly correlated to the nature of the medium but dictated by the dispersion stability as well as the solvation and the formation of the peroxo-catalytic species.
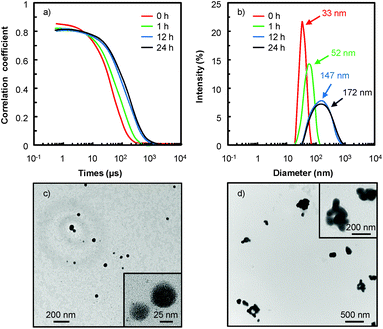
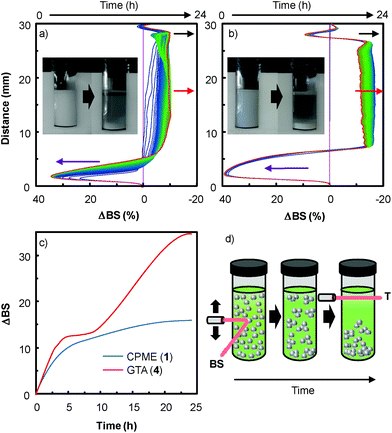
As an example, in water 18, the [C12]3[PW12O40] nanoparticles tend to aggregate as indicated by the evolution of the correlograms over time (Fig. 4). At short time delays, the correlation is high because the particles do not have a chance to move. In contrast, as the time delays become longer, the correlation decays exponentially, meaning that, after a long time period has elapsed, there is no correlation between the scattered intensity of the initial and final states. As this exponential decay is related to the motion of the particles, specifically to the diffusion coefficient itself correlated to the particle size, it is clear that the particle size increases as a function of time. Indeed, the [C12]3[PW12O40] nanoparticles aggregate: at low time (≤1 h), the correlogram is typical of a sample containing small particles (52 ± 3 nm) but for a time range ≥ 1 h, the correlation functions indicate the presence of large aggregates (i.e. the signal decays more slowly and the aggregate size is estimated to be between 147 ± 7 and 172 ± 9 nm). It is noteworthy that the correlograms highlight a progressive aggregation, which is also confirmed by TEM (see Fig. 4c and d), followed by a precipitation of the aggregated nanoparticles. From a catalytic point of view, the low activity observed in water 18 is clearly due to this gradual aggregation of the [C12]3[PW12O40] nanoparticles.
In order to extend the dispersion stability effect to other solvents, we also performed multiple light scattering experiments with solvents 1 and 4 (Fig. 5). These two solvents were investigated because dispersion is observed both with and without H2O2 (see above).
As the backscattering intensity is directly proportional to the volume fraction of the dispersed phase, local changes in concentration (e.g. creaming and sedimentation) and global changes in size (e.g. flocculation and coalescence) can be detected. The evolution in time of the backscattering at mid-height of the tube (red arrow) indicates an increase in size whereas the decrease at the sample top (black arrow) and the increase of the backscattering at the sample bottom (purple arrow) are characteristic of the formation of clarification and sedimentation processes. This evolution is clearly characteristic of an aggregation process of the nanoparticles leading to sedimentation and clarification (see above and the macroscopic views in Fig. 5). As depicted in Fig. 5c, the stability kinetic profiles reveal that the [C12]3[PW12O40] nanoparticle dispersion is more stable in CPME 1 than in GTA 4.
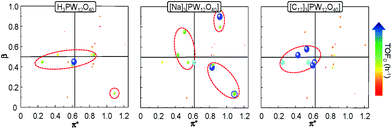
In order to get a better insight into the solvent effect on the catalytic epoxidation of cyclooctene, we have plotted the TOF0 as a function of the α, β and π* Kamlet–Taft parameters. Indeed, a 2D chart is plotted with π* on the x-axis and β on the y-axis. It is noteworthy that the sphere size represents the TOF0 and if α > 0.5, the sphere is surrounded by a blue circle (Fig. 6).
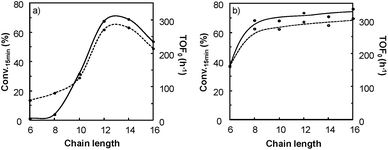
It is clear that the best catalytic activity is obtained for solvents with similar Kamlet–Taft parameters. Indeed, for [H]3[PW12O40], the highest reaction activity is achieved in the solvents with intermediate basicity and low and intermediate polarity. However, water is also a good solvent for the epoxidation reaction but unfortunately it does not afford the solubilization of hydrophobic substrates. For [Na]3[PW12O40], the best catalytic activity is obtained for three solvent families: (i) solvents with intermediate polarity and intermediate or high basicity, (ii) highly polar solvents with a low basicity, and (iii) highly polar solvents with a high basicity. In contrast, for [C12]3[PW12O40], the best activity is obtained for aprotic solvents with low or intermediate polarity and a clear intermediate basicity. This observation confirms that a relationship exists between the solvent properties and the catalytic activity for [C12]3[PW12O40]. The discussion below focuses on the two best solvents, i.e. CPME 1 and 2-MeTHF 2. For these two solvents, the effect of the alkyltrimethyl ammonium cation chain length, abbreviated as [Cn] (with C6 to C16 alkyl groups), has been investigated. Fig. 7 shows the cyclooctene conversion at 15 min and the TOF0. In the case of CPME 1, the results show that the catalytic performance is strongly affected by the ammonium cation chain length. Optimal performances are obtained with [C12] and [C14] chain lengths. In contrast, in the case of 2-MeTHF 2, the highest reaction activity is achieved for a large range of ammonium alkyl chain lengths (between C8 and C16).
A direct correlation between the solvent properties and their efficiency can be easily established. Indeed, 1 is more apolar than 2 (see the Kamlet–Taft plot in Fig. 2). Therefore, 2-MeTHF is able to dissolve more easily the [Cx]3[PW12O40] and the peroxotungstate catalysts (i.e. the Venturello species) whereas CPME leads to whitish dispersions due to the partial insolubility of the [Cx]3[PW12O40] and the peroxotungstate catalysts. In this last case, the activity follows the same behavior as that previously observed in the case of catalytic Pickering emulsions: i.e. the hydrophobicity/lipophilicity balance of the [Cx]3[PW12O40] nanoparticles has an effect on the stability and on the nature of the solid dispersion (Fig. 8).13
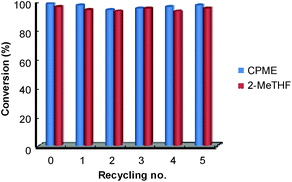
Finally, for these two solvents, the recycling of the [C12]3[PW12O40] nanoparticles was studied (Fig. 9). Thus, at the end of the reaction, the [C12]3[PW12O40] nanoparticles were easily separated from the solvent by centrifugation. In the case of 2-MeTHF (2), the nanoparticles become soluble in the presence of H2O2 but re-precipitate at the reaction end (i.e. when all H2O2 has been consumed). It is noteworthy that Raman and 31P NMR MAS spectra obtained for the precipitate recovered after reaction are similar to those of the initial [C12]3[PW12O40] nanoparticles. (Fig. 10). On the other hand, the 31P NMR and FTIR analyses reveal the absence of phosphorus derivatives in the residual solution.
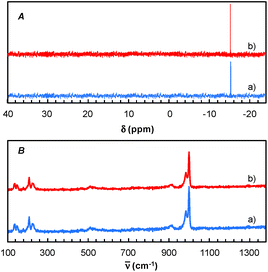 | ||
| Fig. 10 31P NMR MAS (A) and Raman spectra (B) of [C12]3[PW12O40] nanoparticles: before (a) and after reaction (b). | ||
Hence, in both solvents, the epoxide could be readily isolated by removing the solvent whereas the catalytic nanoparticles were charged again with a fresh batch of solvent containing cycloctene and H2O2. The activity (conversion and TOF0) and selectivity of the recovered catalyst were quasi the same after at least five consecutive recyclings (see Fig. 9).
Catalytic epoxidation of various olefins in CPME 1 and 2-MeTHF 2
In order to extend the scope of the eco-friendly oxidizing catalytic system, the epoxidation of cyclohexene, 1-octene, limonene, 3-carene, α-pinene, β-pinene and neryl acetate was performed in CPME 1 and 2-MeTHF 2. The results are reported in Table 4. The reactivity of cyclohexene is lower than that of cyclooctene (TOF0 ≈ 40 versus 280 h−1) and a complete conversion is obtained within 3.5 h with 1 equiv. of H2O2 relative to the substrate. The lower activity of cyclohexene compared to that of cyclooctene has already been described in the literature.19 It is noteworthy that the TOF0 is superior to that of biphasic reactions performed with PTC and reported in the literature.20 For instance, Maksimchuk et al. have reported a TOF0 of 24.6 h−1 for the homogeneous epoxidation of cyclohexene in acetonitrile with the [H]3[PW12O40] catalyst.20 The epoxide selectivity observed in CPME and 2-MeTHF is also superior to that of Maksimchuk et al. (95 versus 78%).20 Moreover, for the homogeneous epoxidation, the catalyst and products cannot be separated easily and the reaction requires 2 equiv. of H2O2 per substrate. In contrast, in the “green” solvents, only 1 equiv. of H2O2 is required for a complete conversion.| Substrate | Solvent | H2O2 (equiv.) | Δtb (h) | Sel. (%) | TOF0 (h−1) |
|---|---|---|---|---|---|
| a Reaction conditions: [C12]3[PW12O40] nanoparticles = 15 μmol, solvent = 3 mL, olefin = 1.5 mmol, H2O2 = 1.5 mmol, 65 °C. b Time required to obtain a conversion ≥ 95%. c [C12][H2PO4] = 30 μmol. d Time at which a plateau is reached (conversion obtained at this time). e Limonene 1,2-epoxide. f Neryl acetate 2,3-epoxide. | |||||
|
1 | 1 | 0.6 | 99 | 283.2 |
| 2 | 0.7 | 99 | 281.2 | ||
|
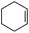
1 | 1 | 3.5 | 95 | 38.4 |
| 2 | 95 | 42.2 | |||

|
1 | 1 | 24 (53)d | 71 | 4.2 |
| 1 × 2 | 24 (84)d | 48 | 4.1 | ||
| 2 | 1 | 24 (62)d | 73 | 3.1 | |
| 1 × 2 | 24 (87)d | 52 | 3.1 | ||
|
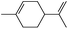
1 | 1.5 | 3 (81)d | 41e | 81 |
| 0.5 × 3 | 3.5 | 65e | 53 | ||
| 2 | 1.5 | 3 (85)d | 46e | 85 | |
| 0.5 × 3 | 3 | 73e | 61 | ||
|
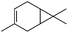
1 | 1.5 | 3 (82)d | 54 | 66.2 |
| 0.5 × 3 | 3 | 68 | 56.2 | ||
| 2 | 1.5 | 3 (79)d | 49 | 57.7 | |
| 0.5 × 3 | 3 | 72 | 49.7 | ||
|
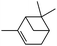
1 | 2 | 3 (58)d | 32 | 39.2 |
| 0.5 × 4 | 4 | 49 | 23.5 | ||
| 2 | 2 | 3 (51)d | 34 | 37.4 | |
| 0.5 × 4 | 4 | 51 | 30.0 | ||
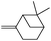
|
1 | 2 | 3 (60)d | 31 | 45.4 |
| 0.5 × 4 | 4.5 | 43 | 35.4 | ||
| 2 | 2 | 3 (63)d | 29 | 40.1 | |
| 0.5 × 4 | 4 | 45 | 32.3 | ||
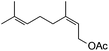
|
1 | 1 | 1 (60)d | 87f | 59.7 |
| 2 | 1 | 43f | 89.5 | ||
| 2 | 1 | 1 (62)d | 91f | 63.3 | |
| 2 | 1 | 59f | 86.3 | ||
For 1-octene, the conversion reaches 53% in CPME and 62% in 2-MeTHF after 24 h with 1 equiv. of H2O2 and in the presence of [C12][H2PO4] (used to improve catalyst performance through interactions with the polyoxotungstate).13 Moreover, the TOF0 and the epoxide selectivity are around 3.5 h−1 and 70%, respectively, which is relatively high compared with the literature data. Indeed, when [H]3[PW12O40] is dissolved in acetonitrile (i.e. homogeneous conditions), a TOF0 of 7.8 h−1 with an epoxide selectivity of 56% has been reported in the literature.20 It is noteworthy that with 1 equiv., the reaction reaches a plateau from which the conversion reaches a limiting value that does not change appreciably even if the reaction time is further increased. However, if H2O2 is added in several batches, the conversion increases up to 84 and 87% in CPME and 2-MeTHF, respectively. However, the epoxide selectivity decreases in favor of the corresponding diol (48 and 52%, in CPME and 2-MeTHF, respectively). It is noteworthy that with 2 equiv. of H2O2 in one batch the epoxide selectivity decreases more strongly (around 30%).
Next, we investigated some terpenes (limonene, 3-carene, α-pinene, β-pinene and neryl acetate). For these five less reactive and frailer substrates, the reaction needs more than 1 equiv. to give a satisfactory conversion. Moreover, as depicted in Table 4, we have reported the effect of H2O2 addition in one or several batch(es). For limonene, 3-carene, α-pinene and β-pinene, the sequential addition of H2O2 gives better epoxide selectivities. The TOF0 is in the following order: limonene < 3-carene < neryl acetate < β-pinene < α-pinene (between 20 and 80 h−1). The reactivity for terpenes could be dictated by their structures.21 It is noteworthy that Maksimchuk et al. have reported similar results for α-pinene (TOF0 = 25.8 h−1).20 On the other hand, Sato et al. under the conditions of Noyori (see below) have performed the epoxidation of α-pinene; the reported conversion and selectivity are 91 and 95%, respectively.22 However, the main drawback of this reaction is the use of phosphonic acid. The TOF0 values observed for limonene and 3-carene are ≥53 h−1 depending on the “green” solvents (see Table 4) whereas the TOF0 reported for a homogeneous system are clearly lower (27.6 and 34.2 h−1, respectively).19 Sakaguchi et al. have reported a conversion of 94% in 1.5 h and a very good selectivity (97%) for the epoxidation of limonene.23 The same authors have also reported that neryl acetate can be epoxidized in 5 h with a quantitative conversion and a selectivity of 86%. However, this system uses peroxotungstophosphate coupled with quaternary ammonium in a chloroform solution. It is noteworthy that an interesting methodology has been developed by Yamazaki.24 The author reports on the epoxidation of 3-carene, α- and β-pinene in the presence of the methyltrioxorhenium(VII) catalyst. The reactions have been performed without an organic solvent and the conversions are quantitative. However, the principal drawback of this solvent-free system is the use of toxic 3-methylpyrrazole and/or 1-methyimidazole as reaction additive(s). Finally, Alsters et al. have described the quantitative epoxidation of 3-carene with H2O2/Na12[WZn3(ZnW9O34)2]/quaternary ammonium.25 This catalytic system gives a very active reaction medium due to the formation of a stable emulsion that can be easily separated into an aqueous and an organic phase at full conversion. The principal drawback of this methodology is the use of toluene.
Conclusions
Eighteen eco-friendly solvents were examined to carry out the epoxidation of olefins with hydrogen peroxide and the amphiphilic catalytic polyoxometalate nanoparticles made of [C12]3[PW12O40] in comparison with the commonly used [H]3[PW12O40] and [Na]3[PW12O40]. Among them, cyclopentyl methyl ether and 2-methyl tetrahydrofuran are particularly efficient for the epoxidation of various olefins (cyclooctene, cyclohexene, 1-octene, limonene, 3-carene, α-pinene, β-pinene and neryl acetate) leading to competitive rates, good yields and high selectivity. The screening of these solvents using cyclooctene as a model has revealed that the [C12]3[PW12O40] catalyst is much more active than [H]3[PW12O40] and [Na]3[PW12O40] with initial turn-over frequencies, TOF0, increasing up to a factor of 10. Moreover, the reaction occurs at competitive rates with four “green” solvents (TOF0 > 260 h−1 for CPME, 2-MeTHF, AcOMe and GTA). Such catalytic systems combine the advantages of biphasic catalysis and of heterogeneous catalysis as they allow an easy separation of products and catalysts, without their drawbacks (e.g. high reaction time, catalyst leaching). Moreover, this catalytic system, based on eco-friendly solvents, allows for the recovery of the catalyst and product(s) in two distinct phases (solid and liquid) and the catalyst can be readily recycled. Due to the current interest in new “green” catalytic processes, further developments of such catalytic systems made of amphiphilic polyoxometalate nanoparticles, hydrogen peroxide and eco-friendly solvents are expected for other catalytic processes such as alcohol and sulfide oxidation, olefin cleavage, etc.Experimental
Materials and methods
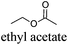
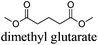
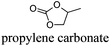
CDCl3 and DMSO-d6 were purchased from Euriso-top. Hydrogen peroxide was used as a 50 wt% solution in water. Heteropolyacid [H]3[PW12O40] was purchased from Aldrich. The compound purity was confirmed by 31P NMR exhibiting a single peak at −13.6 ppm in D2O. Dimethylisosorbide, a generous gift from Roquette, was distilled as other solvents. The compound purity was confirmed by 1H, 13C NMR and GC. Methyl 5-(dimethylamino)-2-methyl-5-oxopentanoate, also known as Polarclean, was provided by Rhodia. Ethyl lactate, propylene carbonate, 1,3-dimethyl-3,4,5,6-tetrahydro-2(1H)-pyrimidinone, cyclopentyl methyl ether, 2-methyl tetrahydrofuran, γ-valerolactone, 1,3-dimethylimidazolidin-2-one, ethylene glycol, methyltertbutyl ether and glycerol triacetate were purchased from Sigma-Aldrich, and methyl acetate and dioxane were purchased from Acros and Prolabo. All solvents have a purity of 99% or more. Distilled deionized water was used in all experiments. The 4-nitroanisole, 4-nitrophenol and Reichardt's dyes for the determination of Kamlet–Taft parameters were purchased from Acros or Aldrich. The GC analyses were performed on an Agilent Technologies 6890N Network GC system (HP-1: 30 m × 0.32 mm). The 1H, 13C and 31P NMR spectra were recorded using an Advance 300 Brucker spectrometer, at 300.13, 75.49 and 121.49 MHz respectively. Chemical shifts are given in ppm (δ) and were measured relative to residual solvent, for 1H and 13C, and to an external reference (H3PO4) for 31P{1H} NMR. The UV-visible spectra have been recorded on a Cary 50 Probe (Varian) spectrophotometer.Synthesis of tri(n-alkyltrimethylammonium)-12-tungsto-phosphate
Alkyltrimethylammonium bromide [Cn][Br] (19.5 mmol) was dissolved in water (100 mL). The aqueous solution of [Cn][Br] was eluted on a hydroxide ion exchange resin to obtain an aqueous solution of [Cn][OH]. Aqueous solution of [H]3[PW12O40] (6.5 mmol) was added dropwise to the aqueous [Cn][OH] solution until pH 7 at 25 °C under dry argon and vigorous magnetic stirring (1500 rpm). The colorless precipitate of tri(n-alkyltrimethyl-ammonium)dodecatungstophosphate ([Cn]3[PW12O40]) almost immediately formed was washed with water and lyophilized. For all synthesized salts, no melting point was observed between 20 and 260 °C.Catalytic oxidation procedure
Catalytic experiments were carried out in sealed glass under vigorous stirring (1000 rpm) at 65 ± 1 °C. Each reaction was carried out in 3 mL of solvent, with 15 μmol of catalyst. The reaction started with the addition of 1.5 mmol of olefin and 1.5 mmol of H2O2. The reactions were followed by GC and the products were identified and quantified by 1H and 13C NMR.Kamlet–Taft parameters26
In 1 cm path-length cells, a small crystal of the solvatochromic probe was dissolved. The reference cell contained only the solvent. A high-resolution, UV-visible spectrophotometer was used to determine the peak maximum of the electronic transition in each of the solvents at room temperature. The absorbance values of the solvatochromic probe in solution were adjusted between 0.2 and 1.0 absorbance units. At equilibrium, the spectrum of the solvatochromic probe in solution was measured at a resolution of 0.05 nm per data point. Five spectra for each probe were taken successively and the average of electronic transition maximums of the dissolved solvatochromic probe was reported. The cells were cleaned between each measurement with ethanol, then water, and then were rinsed with the next solvent. This measurement procedure was repeated for each of the three solvatochromic probes. The π* value of the solvent (i.e. the measure of the polarity and the polarizability) was calculated using the measured frequency maximum (cm−1) for the electronic transition of dissolved 4-nitroanisole, using the following equation:The measured frequency maximum of 4-nitroanisole (νNA) and 4-nitrophenol (νNP) was used to calculate β (measure of the basicity or H-bond accepting ability) using the following equation:
Lastly, the peak maxima of Reichardt's dye (νRD) and 4-nitroanisole (νNA) were used to calculate α (measure of the “proticity” or H-bond donating ability) from the following equation:
Dynamic light scattering (DLS)
Particle-size measurements were also performed using a Zetasizer Nano ZS (Malvern). Light-scattering cells of 10 mm were used. All measurements were performed at 173°. An automatic process was performed with a 10-runs method for each sample. The particle size and its attendant software provided first the time-correlation function of the scattered intensity. The decrease of this correlation function with displacement time can be used to extract information about the diffusion coefficient of a particle or droplet in solution. The measured diffusion coefficient can be used to calculate a hydrodynamic radius of the droplet using the Stokes–Einstein equation. The data are first analyzed by cumulative analysis to obtain an average diffusion coefficient and subsequently by CONTIN analysis in order to obtain information about the entire distribution of the particle size.Transmission electron microscopy (TEM)
The nanoparticles were examined using a FEI Tecnai G2-20 twin transmission electron microscope with the “Centre Commun de Microscopie” (Université Lille 1 facility). Two drops of water containing the nanoparticles were then deposited on a carbon–copper grid.Dispersion stability analysis
The stability of the [C12]3[PW12O40] nanoparticle dispersions was analyzed with the Turbiscan Lab Expert (Formulaction). The dispersions were placed in cylindrical glass tubes and subjected to Turbiscan Lab® Expert stability analysis. The analysis of stability was carried out as a variation of backscattering (ΔBS) profiles. Measurements were carried out using a pulsed near infrared LED at a wavelength of 880 nm for 24 h. Two different synchronous optical sensors received the light transmitted through and backscattered by samples at an angle of 180° and 45° with respect to the incident radiation, respectively. The two sensors scanned the entire height (≈ 30 mm) of the dispersion (12 mL) for 24 h. Experimental data were correlated in percentage to the light flux of two reference standards constituted by a polystyrene latex suspension (absence of transmission and maximum backscattering) and a silicon oil (maximum transmission and absence of backscattering). The stability kinetics were obtained from Easysoft (Formulaction).Acknowledgements
We are most grateful to ANR Catasurf (project ANR-10-CD2I-01) for financial support and Ahmed Addad for performing TEM experiments with the Université Lille 1 facility (Centre Commun de Microscopie).References
- (a) P. T. Anastas and J. C. Warner, Green Chemistry: Theory and Practice, Oxford University Press, New York, 1998, p. 30 Search PubMed; (b) P. T. Anastas and J. B. Zimmerman, Environ. Sci. Technol., 2003, 37, 94A CrossRef.
- F. Cavani, G. Centi, S. Perathoner and F. Trifirò, Sustainable inductrial chemistry, Wiley-VCH, Weinheim, 2009, p. 167 Search PubMed.
- C. W. Jones, Applications of Hydrogen Peroxide and Derivatives, Clean Technology Monographs, Royal Society, 1999 RSC; Y. Deng, Z. Ma, K. Wang and J. Chen, Green Chem., 1999, 1, 275 RSC.
- C. Venturello and R. D'Aloisio, J. Org. Chem., 1988, 53, 1553 CrossRef CAS; C. L. Hill and C. M. Prosser-McCartha, Coord. Chem. Rev., 1995, 143, 407 CrossRef; T. Okuhara, N. Mizuno and M. Misono, Adv. Catal., 1996, 41, 113 CrossRef; B. Notari, Adv. Catal., 1996, 41, 253 CrossRef; R. Neumann, Prog. Inorg. Chem., 1998, 37, 317 CrossRef; T. Sakamoto and C. Pac, Tetrahedron Lett., 2000, 41, 10009 CrossRef; R. G. Finke, in Polyoxometalate Chemistry, ed. M. T. Pope and A. Müller, Kluwer Academic Publisher, Netherlands, 2001. pp. 363–390 CrossRef PubMed; I. V. Kozhevnikov, Catalysis by Polyoxometalates, Wiley, Chichester, 2002 CrossRef PubMed; M. Klawonn, M. K. Tse, S. Bhor, C. Döbler and M. Beller, J. Mol. Catal. A: Chem., 2004, 218, 13 CrossRef PubMed; N. Mizuno, K. Yamaguchi and K. Kamata, Coord. Chem. Rev., 2005, 249, 1944 CrossRef PubMed; Y. Ding, B. Ma, D. Tong, H. Hua and W. Zhao, Aust. J. Chem., 2009, 62, 739 CrossRef; K. Kamata, K. Yonehara, Y. Nakagawa, K. Uehara and N. Mizuno, Nat. Chem., 2010, 2, 478 CrossRef PubMed.
- R. A. Sheldon and M. C. A. van Vliet, in Fine Chemicals through Heterogeneous Catalysis, ed. R. A. Sheldon and H. van Bekkum, Wiley, Weinheim, 2001, pp. 473–490 Search PubMed; F. Cavani and A. M. Gaffney, in Sustainable Industrial Processes, ed. F. Cavani, G. Centi, S. Perathoner and F. Trifirò, Wiley-VCH, Weinheim, 2009 Search PubMed; K. Bauer, D. Garbe and H. Surburg, Common Fragrance and Flavor Materials, Wiley-VCH, New York, Weinheim, 1997 Search PubMed.
- R. Neumann and A. M. Khenkin, J. Org. Chem., 1994, 59, 7577 CrossRef CAS; A. Lambert, P. Plucinski and I. V. Kozhevnikov, Chem. Commun., 2003, 714 RSC; A. Haimov, H. Cohen and R. Neumann, J. Am. Chem. Soc., 2004, 126, 11762 CrossRef PubMed; S. Zhang, G. Zhao, S. Gao, Z. Xi and J. Xu, J. Mol. Catal. A: Chem., 2008, 289, 22 CrossRef PubMed; J. Gao, Y. Zhang, G. Jia, Z. Jiang, S. Wang, H. Lu, B. Song and C. Li, Chem. Commun., 2008, 332 RSC; Q. Wang, X. Zhang, L. Wang and Z. Mi, J. Mol. Catal. A: Chem., 2009, 309, 89 CrossRef PubMed; J. Xue, A. Wang, H. Yin, J. Wang, D. Zhang, W. Chen, L. Yu and T. Jiang, J. Ind. Eng. Chem., 2010, 16, 288 CrossRef PubMed; G. Grigoropoulou, J. H. Clark and J. A. Elings, Green Chem., 2003, 5, 1 RSC.
- C. Venturello, E. Alneri and M. Ricci, J. Org. Chem., 1983, 48, 3831 CrossRef CAS; C. Venturello, R. D'Aloisio, J. C. J. Bart and M. Ricci, J. Mol. Catal., 1985, 32, 107 CrossRef; Y. Ishii, K. Yamawaki, T. Yoshida and M. Ogawa, J. Org. Chem., 1988, 53, 5549 CrossRef.
- Y. Ishii, K. Yamawaki, T. Ura, H. Yamada, T. Yoshida and M. Ogawa, J. Org. Chem., 1988, 53, 3587 CrossRef CAS; Metal oxide catalysis, ed. S. D. Jackson and J. S. J. Hargreaves, Viley-VCH, Weinheim, vol. 1, 2009, pp. 575–578 Search PubMed.
- Y. Sasson and R. Neumann, Handbook of Phase Transfer Catalysis, Blackie Academic & Professional, New York, 1997 CrossRef CAS PubMed; S. G. Casuscelli, M. E. Crivello, C. F. Perez, G. Ghione, E. R. Herrero, L. R. Pizzio, P. G. Vazquez, C. V. Caceres and M. N. Blanco, Appl. Catal., A, 2004, 274, 115 CrossRef CAS PubMed; Y. Ding, Q. Gao, G. Li, H. Zhang, J. Wang, L. Yan and J. Suo, J. Mol. Catal. A: Chem., 2004, 218, 161 CrossRef PubMed; R. Tayebee, Asian J. Chem., 2008, 20, 8 Search PubMed.
- D. C. Duncan, R. C. Chambers, E. Hecht and C. L. Hill, J. Am. Chem. Soc., 1995, 117, 681 CrossRef CAS.
- R. Noyori, M. Aoki and K. Sato, Chem. Commun., 2003, 1977 RSC.
- V. Nardello-Rataj, L. Caron, C. Borde and J.-M. Aubry, J. Am. Chem. Soc., 2008, 130, 14914 CrossRef CAS PubMed; M. Fressancourt-Collinet, B. Hong, L. Leclercq, P. L. Alsters, J.-M. Aubry and V. Nardello-Rataj, Adv. Synth. Catal., 2013, 355, 409 Search PubMed.
- L. Leclercq, A. Mouret, A. Proust, V. Schmitt, P. Bauduin, J.-M. Aubry and V. Nardello-Rataj, Chem.–Eur. J., 2012, 18, 14352 CrossRef CAS PubMed; L. Leclercq, R. Company, A. Mühlbauer, A. Mouret, J.-M. Aubry and V. Nardello-Rataj, ChemSusChem, 2013, 6, 1533 CrossRef PubMed.
- L. Moity, M. Durand, A. Benazzouz, C. Pierlot, V. Molinier and J.-M. Aubry, Green Chem., 2012, 14, 1132 RSC.
- P. G. Jessop, D. A. Jessop, D. Fu and L. Pam, Green Chem., 2012, 14, 1245 RSC.
- K. Hofmann, K. Schreiter, A. Seifert, T. Rüffer, H. Lang and S. Spange, New J. Chem., 2008, 32, 2180 RSC.
- C. Reichardt, Solvents and Solvent Effects in Organic Chemistry, Wiley-VCH Publishers, 3rd edn, 2003 Search PubMed.
- Z. Zhu, R. Tain and C. Rhodes, Can. J. Chem., 2003, 81, 1044 CrossRef CAS.
- T. Yamase, E. Ishikawa, Y. Asai and S. Kanai, J. Mol. Catal. A: Chem., 1996, 114, 237 CrossRef CAS; N. M. Gresley, W. P. Griffith, A. C. Laemmel, H. I. S. Nogueira and B. C. Parkin, J. Mol. Catal. A: Chem., 1997, 117, 185 CrossRef.
- N. V. Maksimchuk, K. A. Kovalenko, S. S. Arzumanov, Y. A. Chesalov, M. S. Melgunov, A. G. Stepanov, V. P. Fedin and O. A. Kholdeeva, Inorg. Chem., 2010, 49, 2920 CrossRef CAS PubMed.
- J. M. de Se Silva, F. S. Vinhado, D. Mandelli, U. Schuchardt and R. Rinaldi, J. Mol. Catal. A: Chem., 2006, 252, 186 CrossRef PubMed.
- Y. Kon, H. Hachiya, Y. Ono, T. Matsumoto and K. Sato, Synthesis, 2011, 1092 CAS.
- S. Sakaguchi, Y. Nishiyama and Y. Ishii, J. Org. Chem., 1996, 61, 5307 CrossRef CAS.
- S. Yamazaki, Org. Biomol. Chem., 2010, 8, 2377 CAS.
- P. T. Witte, P. L. Alsters, W. Jary, R. Müllner, P. Pöchlauer, D. Sloboda-Rozner and R. Neumann, Org. Process Res. Dev., 2004, 8, 524 CrossRef CAS.
- A. F. Lagalante, C. Wood, A. M. Clarke and T. J. Bruno, J. Solution Chem., 1998, 27, 887 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2014 |