Analytical factors to be considered for the application of enriched strontium spikes to monitor biological systems†
Johanna
Irrgeher
,
Andreas
Zitek
,
Magdalena
Cervicek
and
Thomas
Prohaska
*
University of Natural Resources and Life Sciences Vienna, Department of Chemistry, Division of Analytical Chemistry, VIRIS Laboratory, Konrad-Lorenz-Straße 24, 3430 Tulln, Austria. E-mail: thomas.prohaska@boku.ac.at
First published on 23rd September 2013
Abstract
A full metrological protocol for data processing during isotope pattern deconvolution of an enriched Sr isotope double spike as an intrinsic marker in a biological system is described for the first time. The study is based on data gained during a transgenerational marking study, where the transfer of a Sr isotope double spike (84Sr and 86Sr) from female spawners of the common carp (Cyprinus carpio L.) to the centre of the otoliths of their offspring was studied by (LA)-MC-ICPMS. Special emphasis is made on evaluating different data processing strategies, whereat the following analytical key parameters are considered: the blank (Kr, Sr and Rb), variation of the natural Sr isotopic composition in the sample, mass bias, interferences (Rb) and total combined uncertainty. Compared to other systems, which have been used for spiking and subsequent deconvolution (e.g. Ba), isotope pattern deconvolution (IPD) of Sr (double) spikes using multiple linear regression analysis is limited by the number of degrees of freedom available (as a result of the number of natural isotopes). Therefore single parameters have to be evaluated comprehensively in order to develop a proper strategy for isotope pattern deconvolution along with uncertainty calculations. The developed correction strategies allow for isotope pattern deconvolution of a Sr double spike to sample batches marked at low spike amounts using enriched 86Sr/84Sr double spikes of relative differences of the 86Sr/84Sr ratio of >15%, with respect to the total combined uncertainties entailed. Furthermore, Sr isotope double spikes were successfully calculated in samples with natural Rb/Sr molar fraction ratios of up to ½, which bears great potential for applications of enriched Sr isotope tracers in biological systems that are being studied using LA-MC-ICPMS. Finally, recommendations for data evaluation of the enriched Sr isotope tracers in biological samples are given.
Introduction
Using enriched isotopic spikes has become a major technique for studying biological and ecological processes. The intentional transfer of enriched stable isotope tracers into biological systems hereby aims at artificially inducing a significant change in the natural isotopic composition of an element and allows for studying the fate and fluxes of metals, trace elements and species in an organism or provides an intrinsic marker or tag for particular biological samples.Due to the shoreless potential of the methodology, the number of publications dealing with applications of isotope (double) spikes as tracers to address research questions in ‘real world systems’ is constantly increasing. The first comprehensive and detailed review about the advantageous use of enriched stable isotopes over radioisotopes as tracers in biological systems as well as a survey of published applications of the methodology were outlined in detail by Stürup and co-authors.1 Only recently, Urgast and Feldmann gave a general perspective on the capabilities of laser ablation-(multiple collector)-inductively coupled plasma mass spectrometry (LA-(MC)-ICPMS) for imaging of biological samples carrying an introduced stable isotope tracer, including a short discussion on the beneficial characteristics as well as the limitations of the method.2
Regression based isotope pattern deconvolution analysis as a simplified alternative evaluation strategy to double spike isotope dilution calculations was first suggested by Hintelmann,3 Stürup4 and Meija et al.5 Details about the basic mathematical considerations behind multiple linear regression models being used for evaluating isotope data can be found elsewhere.5–7 The outstanding advantage of this mathematical tool lies in the possibility of deducing the individual contribution of each input source (referred to as molar fraction) to a blend of the natural isotope source and the introduced isotopically enriched tracer, thus allowing for the deconvolution of interconverting analytes.8
Since 2007, isotope pattern deconvolution involving enriched isotopes in biological entities has been successfully applied e.g., for 57Fe in cucumber plants,1074Se and 77Se in lactating rats11 and 77Se in human serum,12135Ba and 137Ba in fish tissues,13,14 and 67Zn and 70Zn in rat brain thin sections.15,16 The methodology has also been picked up for forensic and environmental applications such as the authentication of explosives tagged with a dual isotope spike of tin (117Sn and 119Sn)17 or the analyses of platinum (194Pt) in environmental samples.18
However, although Sr offers unique characteristics (non-toxicity, quick metabolic uptake and bio-storage in different tissues) for being successfully used for spiking biological systems19 – especially in the case of Ca-rich matrices – only a few studies using isotopically enriched Sr isotope tracers exist so far.20,21 A transgenerational marking experiment with a typical salmonid freshwater fish species (brown trout Salmo trutta f.f. L) was conducted successfully using a 84Sr single spike.21 Even though Sr isotope ratio analysis has become a key technique in many fields of science, a large number of corrections, either related to mass bias or interferences,22 have to be addressed and also taken into account when isotope pattern deconvolution is used for Sr isotopes. This is nonetheless a prerequisite to guarantee the metrological quality of Sr isotope ratio data and thus still represents a persisting analytical challenge.
The objective of this manuscript is to evaluate and summarize the analytical aspects for Sr isotope pattern deconvolution and to report on the crucial factors to be considered when performing isotope pattern deconvolution of a low level of multiple enriched stable Sr isotope double spikes used as tracers in a biological system. The work is based on experiments, where a 84Sr/86Sr double spike was applied to female spawners of a typical cyprinid freshwater fish species, carp Cyprinus carpio, L., for transgenerational marking.
Experimental
Reagents and materials
| 84Sr | 86Sr | 87Sr | 88Sr | |
|---|---|---|---|---|
| 84SrCO3-product | 76.4000 ± 1.100 | 4.6400 | 1.9600 | 17.0000 |
| 86SrCO3-product | <0.0020 | 96.3000 ± 0.300 | 1.0200 | 2.6800 |
| Natural Sr | 0.56 ± 0.01 | 9.86 ± 0.01 | 7.00 ± 0.01 | 82.58 ± 0.01 |
The SrCO3 powders were separately dissolved in reagent grade type I water (18 MΩ cm; TKA Wasseraufbereitungssysteme GmbH “Part of Thermo Fischer Scientific”, Niederelbert, Germany), which had been further purified by sub-boiling distillation (Milestone-MLS GmbH, Leutkirch, Germany) and acidified with ca. 150 μL sub-boiled HCl (37%, Merck KGaA, Darmstadt, Germany) for dissolution. The solutions were initially adjusted to pH 7.5–8 using a 10 mol L−1 NaOH solution prepared from suprapure (≤99.99%) sodium hydroxide monohydrate pellets (Merck KGaA, Darmstadt, Germany) and sub-boiled H2O and filled up to 4.53 g (86SrCO3-product) and 4.17 g (84SrCO3-product) total weight, respectively. Subsequently, a mixture of the two solutions was prepared and diluted with sub-boiled water in order to obtain the approximate target molar ratio of xsp1/xsp2 (compare Table 4). It has to be noted that the final ratio might differ significantly from the target value when preparing low-level double spikes since e.g. background levels of natural Sr in the used chemicals cannot be taken into account ab initio. Details about tracer solution preparation are given in ESI 1.†
The double spike solution was adjusted to isotonic conditions (between 128 and 133 mmol L−1 dissolved salts) using sodium chloride (suprapure; Merck KGaA, Darmstadt, Germany) prior to injection into the abdominal cavity of a female spawner of carp (according to Zitek et al. 2013 (ref. 21)) with a length of 800 mm and a weight of 9.1 kg. The final mass fraction of the total Sr in the solution was 4.97 mg g−1 and the total Sr administered to the fish accounted for 2.9 mg Sr per kg of fish.
| Operating parameters | |
|---|---|
| RF power/W | 1300 |
| Cool gas flow rate/L min−1 | 13 |
| Auxiliary gas flow rate/L min−1 | 1 |
| Cones | Ni |
| Sample uptake rate/μL min−1 | 130 |
| Wash time/s | 120 |
| Mass analyzer pressure/mbar | 1.73 × 10−8 |
| Detection system | Faraday cups |
| Axial m/z | 88 |
| Mass separation | 0.5 |
| Nebulizer | PFA |
| DSN nebulizer pressure/psi | ∼35 |
| DSN hot gas flow/L min−1 | ∼0.3 |
| DSN membrane gas flow/L min−1 | ∼3.3 |
| DSN spray chamber temperature/°C | ∼114 |
| DSN membrane temperature/°C | ∼117 |
| Acquisition parameters | |
| Integration time/s | 0.2 |
| Instrument sensitivity/V (μg g−1)−1 | ∼100 |
| Resolution (m/z)/Δ(m/z) | 300 (low resolution) |
Measurement blanks were taken on-peak for solutions of 2% HNO3 (w/w) or laser gas prior to measurement of samples during solution-based or laser ablation analysis, respectively. Solutions of NIST SRM 987 (National Institute of Standards and Technology, Gaithersburg, USA) with a natural Sr isotopic composition were measured periodically throughout sessions of solution-based as well as laser ablation analyses for quality control and external mass bias determination. Solutions of NIST SRM 984 (National Institute of Standards and Technology, Gaithersburg, USA) RbCl with a natural Rb isotopic composition were prepared in 2% HNO3 (w/w) for experiments to validate different strategies applied for Rb interference correction.
Laser ablation analysis was performed by ablating one cross-sectional line scan across the otolith through the core region. Laser ablation parameters are given in Table 3. Data evaluation was accomplished point by point. The precision of one measurement is given for repeatability conditions (see Table 7).
| Ablation mode | Line scan |
|---|---|
| Wavelength/nm | 193 |
| Energy/% | 95 |
| Spot size/μm−1 | 75 |
| Repetition rate/Hz | 20 |
| Scan speed/μm s−1 | 2 |
| Irradiance/GW cm−2 | 2.3 |
| Fluence J cm−2 | 12 |
| He carrier gas L−1 min−1 | 0.9 |
On-peak baseline correction was done for both solution-based and laser ablation analyses by subtracting stable blank signals recorded for nitric acid solutions or the gas blank prior to sample analyses. Rb interference correction was accomplished by external correction via isotopic abundances after mass bias correction (‘peak stripping’) or within the multiple linear regression model. The mass bias correction model by Russell24 was used throughout this study:
 | (1) |
The procedure for calculating the molar amount ratio of xsp1/xsp2 in the otoliths is based on the work of García Alonso and co-workers.13,14,18
The procedure of IPD is given in detail for deconvolving a Sr isotope pattern in an analytical sample of a supposed blend of natural Sr and two enriched Sr isotope spikes in case that blank, Rb interference and mass bias correction are accomplished prior to matrix deconvolution. According to eqn (2), the total molar amount of strontium Ns in a natural sample intentionally spiked with two enriched stable Sr isotopes is made up of the sum of the molar amount of natural Sr (Nnat), enriched Sr from spike 1 (Nsp1) and enriched Sr from spike 2 (Nsp2), resulting in the following mass balance:
| Ns = Nnat + Nsp1 + Nsp2 | (2) |
Eqn (2) can be adapted for each single isotope i of an element (eqn (3)):
| Nis = Ninat + Nisp1 + Nisp2 | (3) |
Eqn (4) additionally takes into account the isotopic abundances:
| Ns × Ais = Nnat × Ainat + Nsp1 × Aisp1 + Nsp2 × Aisp2 | (4) |
All isotope ratios Ricorr are measured and corrected for mass bias. The corresponding corrected isotope abundances Ais are calculated as follows using eqn (5):
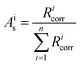 | (5) |
The molar fraction of natural Sr (xnat), spike 1 (xsp1) and spike 2 (xsp2) can be calculated using eqn (6) (given in the example of xnat):
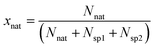 | (6) |
Therefore, the molar amount of the individual contributors to the isotopic composition in the blend can be calculated by deconvolution of the measured isotope abundances and considering all input parameters from natural Sr as well as spike sources following a system of equations resulting in a matrix model (eqn (7)):
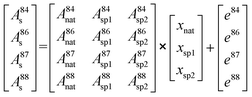 | (7) |
As there are more parameters (isotopic abundances) than unknowns (molar amounts) in the equation system in case all corrections are accomplished prior to deconvolution, an error vector is included. This remaining degree of freedom can be further used for either mass bias or Rb interference correction within the multiple linear regression model. The system of equations is finally solved by using the LINEST array function of Microsoft® Excel by setting the regression intercept to zero. The final result gives the molar fraction of each input parameter (i.e. from natural Sr, from the 84SrCO3-product and from 86SrCO3-product), from which the molar fraction ratio of the double spike (xsp1/xsp2) is calculated.
Metrological processing and results
Determination of the isotopic composition of the enriched strontium solutions
The isotopic composition of the enriched strontium isotope tracer solution was calculated by isotope pattern deconvolution (IPD). IPD was chosen since levels of natural Sr (and Rb) were expected to significantly contribute to the overall Sr isotopic composition after blending solutions of isotope enriched products and adjusting the resulting double spike solution to isotonic conditions using NaOH and NaCl. Even though the reagents used were of suprapure quality, the levels of Sr and Rb stated in the product specifications e.g. for NaCl (i.e. <0.1 ppm (Sr) and <0.5 ppm (Rb)) were considered to be significant. Subsequent IPD showed a molar contribution of natural Sr of 0.65% to the spike solution, which corresponds to 30 μg g−1. The same tracer solution contained 2.5 μg g−1 Rb. This shows that any sources of (natural) impurities or impurities in the tracer material itself have to be taken into account in tracer studies, especially when specific measures (e.g. chemical adjustment of the solutions) to transfer the tracer material into a suitable vector for introduction into the biological system are required.3,5 The resulting molar fraction ratios in the spike solutions are given with their expanded standard uncertainties (considering the blank and measurement repeatability) in Table 4. It is evident that the final value deviates significantly from the assumed target value underlining the necessity of deconvolving the double spike solution.| x sp1/xsp2 | u c (k = 2) | |
|---|---|---|
| Target value | 5.00 | Not applicable |
| Measured value | 3.06 | 0.03 |
Determination of the isotopic composition of spiked biological samples (otoliths)
Nonetheless, IPD of the pure measurement blank can be used to estimate the molar distribution of predefined blank contributors in the blank. This is performed by using the natural isotopic abundances of the assumed and prior defined blank contributors (in our case: Sr, Rb, Kr) and leads to their molar distribution in the blank. IPD showed that the blank contributions to the measured Sr masses (84, 86, 87 and 88) comprised approx. 70% of Rb, 25% of Kr and 5% of Sr (all given as relative molar amount × 100).
Alternatively one might either use a baseline level of natural isotopic composition derived from the unspiked control samples or from areas within the analysed sample, where the isotopic composition is expected to be natural.
Therefore a comparison of (1) the IUPAC representative Sr isotopic composition23 and (2) natural Sr isotopic composition of the same fish otolith sample (calculated as mean measured isotope abundances from the un-spiked rim area of the otolith) was performed (see Table 5 for isotopic abundances of fish otolith rim areas compared to the IUPAC representative isotopic composition).
| Isotope abundance | 84Sr | 86Sr | 87Sr | 88Sr |
|---|---|---|---|---|
| Natural Sr | 0.0056 ± 0.0001 | 0.0986 ± 0.0001 | 0.0700 ± 0.0001 | 0.8258 ± 0.0001 |
| Otolith baseline mean (n = 14; 2 SD) | 0.0057 ± 0.0001 | 0.0988 ± 0.0003 | 0.0699 ± 0.0001 | 0.8257 ± 0.0004 |
| x sp1/xsp2 | u c (k = 1) | |||
| Composition of double spike solution | 3.06 | 0.03 | ||
| (1) Otolith core using IUPAC values as the baseline level | 3.03 | 0.24 | ||
| (2) Otolith core using otolith control as the baseline level | 3.29 | 0.29 | ||
Results show no significant difference between the mean values obtained from the two evaluation strategies (see Table 5) with respect to the total combined uncertainties. Uncertainty calculations were done including (1) the natural variation (given as a range) of the Sr isotopic composition according to the IUPAC23 and (2) the repeatability of the measurement of the natural Sr isotope abundances in the baseline of an otolith sample.
Rb correction via peak stripping. Rb correction was performed via ‘peak stripping’ and assuming the same mass fractionation for Sr and Rb (fSr = fRb, whereby fSr was experimentally determined using solutions of NIST SRM 987). Rubidium correction was performed by deducing the 87Rb contribution at m/z 87 calculated via the recorded blank corrected signal of 85Rb at m/z 85. This approach for Rb interference correction has been widely applied in the field.25,26 The blank and interference corrected isotope ratios were subsequently corrected for mass bias and evaluated by isotope pattern deconvolution following eqn (7).
Rb correction within the multiple linear regression model (IPD). The strategy of interference correction is based on e.g. Rodríguez-Castrillón and Huelga-Suarez, who accounted for the contribution of interferences in the multiple linear regression model.12,13 In the case of Rb correction during Sr isotopic analysis, this would result in eqn (8):
 | (8) |
Robustness and comparison of different strategies for Rb interference correction. Results of xsp1/xsp2 molar fraction ratios obtained from the two Rb interference correction strategies can be found later in the summary and Table 7 shows that the obtained molar fraction ratios in otolith samples do not differ significantly, since they overlap within uncertainties. Therefore both correction approaches are considered as valid for this case study. However, it should be noted that the samples investigated show Rb/Sr ratios of <0.1–0.3% (expressed as the relative Rb/Sr intensity ratio). Since Rb correction within the IPD showed slightly lower total combined uncertainties compared to Rb correction via ‘peak-stripping’, correction for Rb within the multiple linear regression model is preferred in this case study.
The robustness of the two evaluation approaches for samples with significantly higher molar fractions of Rb was tested on data obtained from blend solutions of natural Sr (NIST SRM 987), and natural Rb (NIST SRM 984) at a Rb/Sr molar fraction ratio of up to ½ added to aliquots of the double spike solution. The double spike solution was freshly prepared and therefore a slight deviation from the double spike composition, which was administered to the fish (compare Table 4), is given. Table 6 shows that xsp1/xsp2 molar fraction ratios of the spike solution overlap within uncertainties, when Rb interference correction is performed within the IPD. The classic Rb interference correction (i.e. peak-stripping prior to IPD) leads to significant offsets (<15%) of the xsp1/xsp2 molar fraction ratios deconvolved from the blend.
| Sample | Evaluation strategy | x sp1/xsp2 | u c (k = 2) |
|---|---|---|---|
| Double spike (true composition) | 2.89 | 0.03 | |
| Srnat + Rbnat + double spike | (1) Rb (IPD) | 2.91 | 0.03 |
| Srnat + Rbnat + double spike | (2) Rb (peak stripping) | 2.33 | 0.03 |
| Evaluation 1 | Evaluation 2 | Evaluation 3 | ||||
|---|---|---|---|---|---|---|
| Mass bias | External (SSB) | External (SSB) | IPD | |||
| Rb interference | IPD | Peak stripping | Peak stripping | |||
| x sp1/xsp2 | SD | x sp1/xsp2 | SD | x sp1/xsp2 | SD | |
| S 4-1 | 3.42 | 0.12 | 3.43 | 0.13 | 3.40 | 0.15 |
| S 4-2 | 2.87 | 0.08 | 2.87 | 0.19 | 2.56 | 0.10 |
| S 4-3 | 2.87 | 0.13 | 2.88 | 0.12 | 2.98 | 0.13 |
| S 4-4 | 2.95 | 0.11 | 2.95 | 0.09 | 3.05 | 0.09 |
| S 4-5 | 3.03 | 0.22 | 3.06 | 0.09 | 3.26 | 0.07 |
| S 4-6 | 3.34 | 0.09 | 3.29 | 0.08 | 3.36 | 0.10 |
| S 4-7 | 3.04 | 0.10 | 3.07 | 0.10 | 3.15 | 0.11 |
| S 4-8 | 3.13 | 0.14 | 3.07 | 0.30 | 3.22 | 0.53 |
| S 4-9 | 3.06 | 0.07 | 3.04 | 0.12 | 3.18 | 0.11 |
| S 4-10 | 2.95 | 0.08 | 2.94 | 0.12 | 3.08 | 0.13 |
| S 4-11 | 2.98 | 0.06 | 2.97 | 0.09 | 3.16 | 0.20 |
| S 4-12 | 3.02 | 0.06 | 3.02 | 0.08 | 3.04 | 0.12 |
| S 4-13 | 3.14 | 0.17 | 3.11 | 0.15 | 3.23 | 0.16 |
| S 4-14 | 2.83 | 0.12 | 2.78 | 0.19 | 2.93 | 0.19 |
| Mean | 3.04 | 3.03 | 3.12 | |||
| Reproducibility | 0.17 | 0.17 | 0.21 | |||
| RSD/% (k = 1) | 5.6 | 5.5 | 6.7 | |||
| u c,rel/% (k = 1) | 6.9 | 7.7 | 8.0 | |||
External mass bias correction using sample standard bracketing (SSB). External mass bias correction was performed using a sample standard bracketing procedure by measuring solutions of the natural abundance certified reference material NIST SRM 987 throughout the measurement sequence. Mass bias factors for all individual Sr isotope ratios (i.e.84Sr/88Sr, 87Sr/88Sr and 86Sr/88Sr) were calculated using the Russell's law24 for mass bias correction, averaged for a measurement sequence and subsequently applied for correction of solution-based and laser ablation data.
During LA analyses, the obtained mass bias factors were f(Sr-86/Sr-88) = −1.62 ± 0.01, f(Sr-84/Sr-88) = −1.68 ± 0.01 and f(Sr-87/Sr-88) = −1.66 ± 0.01 for the sample batch (1 SD, n = 14).
Mass bias correction within the multiple linear regression model (IPD). Since the model used for isotope pattern deconvolution allows for one additional parameter to be treated within the multiple linear regression model, mass bias can be corrected by minimizing the regression sum of squared residuals. As a consequence, the measurement of bracketing standards is not required. According to Huelga-Suarez and co-workers13,14 the optimum mass bias correction factor was determined using the SOLVER analysis tool application provided by Microsoft® Excel. One mass bias factor was determined and applied to all Sr isotope ratios (i.e.84Sr/88Sr, 87Sr/88Sr and 86Sr/88Sr) using the Russell law. The optimum mass bias factor obtained was −1.53 ± 0.07 (1 SD, n = 14) for the sample batch.
Comparison of experimentally and mathematically determined mass bias factors. The correction factors of external mass bias correction (using SSB) and internal correction (by finding the optimum mass bias correction factor fitting into the regression model) do not differ significantly, since values overlap within uncertainties.
In contrast to Rodriguez-Castrillón et al.7 we did not observe significant differences in the obtained uncertainties.
| Evaluation strategy | Parameters and relative contributions/% | ||||||
|---|---|---|---|---|---|---|---|
| Blank | Repeatability | Reproducibility | Mass bias | Rb correction | u c,rel (k = 1)/% | ||
| Evaluation 1 | IPD Rb | 29.6 | 32.7 | 13.6 | 10.5 | 13.6 | 6.9 |
| Evaluation 2 | External mb (SSB) | 38.4 | 16.2 | 15.5 | 13.7 | 16.2 | 7.7 |
| Evaluation 3 | IPD mb | 41.0 | 13.4 | 24.7 | 7.6 | 13.4 | 8.0 |
Summary and recommendations
A method for the isotope pattern deconvolution (IPD) of an enriched Sr double spike used as a distinctive tracer in a biological system was successfully developed, which was found to be inevitable as the Sr isotopic system stands in contrast to most isotopic systems used for tracer studies so far, which contained more measurable isotopes than unknowns (i.e., added enriched isotopes).7,12,28 As a consequence, the application of a Sr isotope double spike leaves the analyst with only one degree of freedom in the regression based model that can be used for either mass bias or Rb correction within the IPD. Furthermore, the IPD approach allows for deconvolution of the isotope pattern in a spiked sample without knowing the quantity of the enriched isotope tracer being incorporated into the natural sample matrix as well as the degree of impurities and species-interconversion (from sample preparation); all these aspects are crucial to consider when natural systems are studied. Biological systems underlie complex processes such as metabolism, adsorption/desorption, and oxidation/reduction. As a consequence, the quantities of tracer that finally end up in a tagged sample are unknown and thus classic evaluation approaches such as the isotope dilution mass spectrometry (IDMS) equation9 are not applicable because of the unknown amount of tracer finally present in the sample.3 The additional advantage is that the tracer-to-tracer ratio introduced through the spike solution can be calculated using the same procedure independent of any additional sources of impurities of natural Sr (and Rb). Thus neither the blank concentration nor the isotopic composition of the natural contaminant has to be determined separately.In summary, major aspects for a successful deconvolution of Sr isotope spikes from biological matrices described are:
1. Blank correction.
2. Consideration of the significance of the natural variation of the Sr isotope abundances in the sample.
3. Mass bias correction.
4. Rb interference correction with respect to the molar fraction of Rb in the sample.
5. Calculation of the total combined uncertainties for validation.
In this study, blank correction was done on-peak prior to sample analyses due to the presence of Kr, Sr and Rb in the blank. The possible significance of the natural variation of the Sr isotope abundances was considered insignificant with respect to the total combined uncertainties of the measurement.
Different correction strategies for Rb interference and mass bias were evaluated, with similar uncertainties for the different evaluation strategies applied. These approaches towards ‘virtual’ correction of data for biases (e.g. Rb and mass bias) can be considered as promising alternatives supplementary to existing protocols based on experimental corrections since uncertainties do not differ significantly. In any case, both interference and mass bias correction cannot be done in the least square fitting and thus leaves the analyst with the decision about how to proceed with data evaluation.
In the case of Rb interference corrections, both correction strategies applied were considered as valid for this case study, since natural Rb/Sr molar fraction ratios in the samples investigated were <0.3%. Experiments using standard solutions with Rb/Sr molar fraction ratios of up to ½ showed that Rb interference correction within the IPD leads to no significant deviations from measurements of solutions at lower Rb/Sr molar fraction ratios (i.e. <0.3%) for the double spike applied, whereby Rb correction via peak-stripping and subsequent IPD showed a deviation of >15% in the xsp1/xsp2 molar fraction ratio. Thus, Rb correction within the IPD bears the potential of deducing accurate Sr tracer ratios also from samples with a considerable Rb content.
The total combined uncertainties achieved for deconvolved xsp1/xsp2 molar fraction ratios obtained by LA-MC-ICPMS evaluated using different strategies applied show that double spikes with relative differences of the enriched isotope tracers of >15% can be distinguished with significance at such low spike amounts administered.
In conclusion, external blank correction and external mass bias correction are recommended. The natural baseline Sr isotope abundances used for IPD have to be chosen according to the significance of the natural variation of the Sr isotope abundances in the investigated sample compared to the representative isotopic composition according to the IUPAC and under consideration of the total combined uncertainties entailed.
Rb correction should be accomplished within the multiple linear regression model, especially in the case of Rb-rich matrices and low Sr content along with low Sr spike amounts. This is of particular advantage for laser ablation analysis where matrix separation cannot be achieved. Furthermore, this data evaluation strategy showed the lowest total combined uncertainties. Nonetheless, a full validation of analytical protocols is required when new biological systems are studied. With respect to the combined uncertainties achieved, when multiple double spikes are applied that should be distinguishable by LA-ICPMS analysis, a relative difference of >15% between double spikes should be considered.
Acknowledgements
J. Irrgeher is grateful to the Austrian Academy of Sciences for the DOC-fFORTE-fellowship. The Austrian Science Fund FWF is highly acknowledged for financial support of the work (projects FWF 267N11; FWF P21404B17). We thank J.I. García Alonso for providing supplementary electronic data on isotope pattern deconvolution and fruitful discussions, and B. Spangl (University of Natural Resources and Life Sciences Vienna, Institute of Applied Statistics and Computing) and J. Probst for their support with mathematical considerations. Two anonymous reviewers are acknowledged for their valuable comments on the first draft of this manuscript.References
- S. Stürup, H. R. Hansen and B. Gammelgaard, Anal. Bioanal. Chem., 2008, 390, 541–554 CrossRef PubMed.
- D. S. Urgast and J. Feldmann, J. Anal. At. Spectrom., 2013, 28, 1367–1371 RSC.
- H. Hintelmann and R. Evans, Fresenius' J. Anal. Chem., 1997, 358, 378–385 CrossRef CAS.
- S. Stürup, C. Chen, J. Jukosky and C. Folt, Int. J. Mass Spectrom., 2005, 242, 225–231 CrossRef PubMed.
- J. Meija, L. Yang, J. A. Caruso and Z. Mester, J. Anal. At. Spectrom., 2006, 21, 1294–1297 RSC.
- J. Meija, Anal. Bioanal. Chem., 2006, 385, 486–499 CrossRef CAS PubMed.
- J. A. Rodriguez-Castrillón, M. Moldovan, J. Ruiz Encinar and J. I. García Alonso, J. Anal. At. Spectrom., 2008, 23, 318–324 RSC.
- L. Ouerdane, Z. Mester and J. Meija, Anal. Chem., 2009, 81, 5075–5079 CrossRef CAS PubMed.
- J. Vogl and W. Pritzkow, MAPAN-Journal of Metrology Society of India, 2010, 25, 135–164, DOI:10.1007/s12647-010-0017-7.
- J. Rodriguez-Castrillon, M. Moldovan, J. I. García Alonso, J. J. Lucena, M. L. Garcia-Tomas and L. Hernandez-Apaolaza, Anal. Bioanal. Chem., 2008, 390, 579–590 CrossRef CAS PubMed.
- H. González Iglesias, M. L. Fernández Sánchez, J. I. García Alonso and A. Sanz-Medel, Anal. Bioanal. Chem., 2007, 389, 707–713 CrossRef PubMed.
- J. A. Rodríguez-Castrillón, L. H. Reyes, J. M. Marchante-Gayon, M. Moldovan and J. I. García Alonso, J. Anal. At. Spectrom., 2008, 23, 579–582 RSC.
- G. Huelga-Suarez, B. Fernández, M. Moldovan and J. I. G. Alonso, Anal. Bioanal. Chem., 2012, 1–9 Search PubMed.
- G. Huelga-Suarez, M. Moldovan, A. Garcia-Valiente, E. Garcia-Vazquez and J. I. G. Alonso, Anal. Chem., 2012, 84, 127–133 CrossRef CAS PubMed.
- D. S. Urgast, S. Hill, I. S. Kwun, J. H. Beattie, H. Goenaga-Infante and J. Feldmann, Metallomics, 2012, 4, 1057–1063 RSC.
- D. S. Urgast, O. Ou, M. J. Gordon, A. Raab, G. F. Nixon, I. S. Kwun, J. H. Beattie and J. Feldmann, Anal. Bioanal. Chem., 2012, 402, 287–297 CrossRef CAS PubMed.
- I. Carames-Pasaron, J. A. Rodríguez-Castrillón, M. Moldovan and J. I. García Alonso, Anal. Chem., 2012, 84, 121–126 CrossRef CAS PubMed.
- J. A. Rodriguez-Castrillon, M. Moldovan and J. I. García Alonso, Anal. Bioanal. Chem., 2009, 394, 351–362 CrossRef CAS PubMed.
- R. C. Capo, B. W. Stewart and O. A. Chadwick, Geoderma, 1998, 82, 197–225 CrossRef CAS.
- K. T. Smith and G. W. Whitledge, Fish Manag. Ecol., 2011, 18, 168–175 CrossRef.
- A. Zitek, J. Irrgeher, M. Kletzl, T. Weismann and T. Prohaska, Fish Manag. Ecol., 2013, 20, 654, DOI:10.1111/fme.12018.
- P. Z. Vroon, B. Van Der Wagt, J. M. Koornneef and G. R. Davies, Anal. Bioanal. Chem., 2008, 390, 465–476 CrossRef CAS PubMed.
- M. Berglund and M. E. Wieser, Pure Appl. Chem., 2011, 83, 397–410 CrossRef CAS.
- W. A. Russell, D. A. Papanastassiou and T. A. Tombrello, Geochim. Cosmochim. Acta, 1978, 42, 1075–1090 CrossRef CAS.
- S. Ehrlich, I. Gavrielia, L. B. Dorb and L. Halicz, J. Anal. At. Spectrom., 2001, 16, 1389–1392, 10.1039/b107996b.
- J. Irrgeher, T. Prohaska, R. E. Sturgeon, Z. Mester and L. Yang, Anal. Methods, 2013, 5, 1687–1694 RSC.
- EURACHEM-CITAC, 2012.
- J. Meija and Z. Mester, Anal. Chim. Acta, 2008, 607, 115–125 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3ja50212k |
| This journal is © The Royal Society of Chemistry 2014 |
