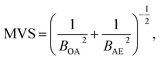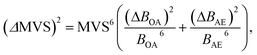Determination of lithium in lithium-ionic conductors by laser-enhanced ionization spectrometry with laser ablation

Abstract

Laser-enhanced ionisation (LEI) with laser ablation (LA) into a methane–air flame was used for lithium determination in ferrites. Since there is a lack of certified reference materials matrix-matched to ferrites powders, a set of spinel samples were synthesised by means of aerosol spray pyrolysis (ASP) or by annealing the mixture of Li and Fe(III) nitrates. Characterisation by X-ray diffraction showed that the annealed ceramics contained two phases, such as either α-LiFe₅O₈ and Fe₂O₃ or α-LiFeO₂ and Fe₂O₃, while ASP ferrites consisted mainly of α-LiFe₅O₈. Total lithium content in samples was certified by conventional flame photometry after dissolution. We explained the strong matrix effects on the LA-LEI signal by the discrepancy of surface microstructure (and hardness) due to the difference in the conditions of sample preparation. The optoacoustic signal and emission line of Fe I at 382 nm were recorded simultaneously with the LA-LEI signal in order to compensate for matrix effects. We suggest that the microstructure (ceramics or pellets from spherical microparticles) influences both mass removal (proportional to OA signal) and plasma temperature (proportional to AE signal). Correlation plots between OA and AE signals deviated strongly from sample to sample, which was the basis for the application of a multivariate correction procedure to reduce strong matrix effects. 3D correlation plots (LEI vs. OA + AE) for each sample were built to obtain a new analytical signal, which represented the slope of the correlation line to the plane of the OA + AE signals. This normalised signal was free from matrix effects within a concentration range of 0.6–7.5 Li%. The proposed approach allows the use of ferrites synthesised by the various techniques as reference materials in order to build a unified calibration curve.

---

1. Introduction

The development of new lithium-ionic conductors is a vigorously advancing field of contemporary chemistry.¹ LiFe₅O₈ is an example of a mixed inverse spinel with the structure Fe(Li_0.5Fe_1.5)O₄. It has been proposed as a cathode material in secondary batteries and as a low-cost substitute for microwave garnets owing to its ferromagnetic properties.² Several techniques are widely used to synthesize these materials. Conventional high temperature annealing for the production of ceramics often leads to phase transitions through electrochemically inactive phases such as LiFeO₂.³ Another method for its synthesis is an aerosol spray pyrolysis (ASP) which allows the creation of spherical particles with controllable sizes.⁴ The stock solution of Fe(III) and Li nitrates is introduced into the horizontal quartz reactor by an ultrasonic nebulizer. The precursors obtained are trapped in a preheated microporous glass filter. Sodium chloride or sodium citrate have been suggested as additives to a stock solution in order to reduce the volatility of lithium nitrates and to produce smaller nanoparticles (10–20 nm).⁵ Nanosized LiFe₅O₈ is a promising cathode material in rechargeable Li-ion batteries. However, the lithium content in the synthesised specimen strongly depends on decomposition conditions (e.g. oven temperature, flow rate of gas, etc.) because of the evaporation of Li atoms from the droplet surface. As a result, strongly heterogeneous ferrites might be obtained with unpredictable conductivity and magnetic properties. X-ray diffraction is a method for the structural characterization of such samples. However, X-ray methods of analysis are appropriate only for the indirect determination of lithium content through precipitation with other elements.⁶ Because of a relatively high Li-content (0.1–10%), direct spectrochemical analysis (for example, laser-induced breakdown spectrometry – LIBS) is generally limited by both strong self-absorption of resonance lithium lines⁷ and narrow linear dynamic range. Nonetheless, ultrafast depth profiling of Li-ionic electrode by means of LIBS with non-resonance Li I line at 413.3 nm was recently demonstrated by Zorba et al.⁸ Therefore, the pivotal task of optimizing the conditions for the synthesis of ASP synthesized ferrite is the accurate and fast control of the lithium contained in the sample. Another challenge for direct analysis of ferrites is a lack of powdered certified reference materials with different lithium contents. Therefore, preliminary synthesis by means of an ASP technique and/or sintering technique is required to prepare such reference samples.

Laser-enhanced ionisation (LEI) spectrometry allows the determination of low alkali metal contents in the presence of strongly interfering components.⁹ It is based on resonant excitation of atoms in a flame or plasma by means of laser radiation passed through the atomizer. An electric field applied to an electrode in the flame accelerates ions produced by collisions between the excited atoms and other particles in the reservoir. The selection of the pumping scheme, the energy of the exciting tunable laser and the spatial arrangement between a laser beam and electrode enable the achievement of an extremely low limit of detection down to 30 fg ml⁻¹.¹⁰ At the same time, the linear dynamic range for lithium determination reaches 7 or more orders of magnitude with the use of this two-step excitation scheme.¹¹ Another advantage of lithium determination by LEI is the negligible influence of sodium on the analytical results. For example, Zorov et al.¹² have demonstrated that sodium strongly interfered with the Li signal only above the mass ratio 10 000 : 1. Thus, LEI spectrometry is a powerful analytical tool for the determination of both traces and matrix elements.¹³ Despite the fact that Gravel et al.¹⁴ have tried to convert LEI into a multielement technique with an additional tunable laser source, LEI spectrometry still remains a single-element technique.

The use of laser ablation (LA) for the elemental analysis of solids can provide many advantages such as the elimination of any reagents, the reduction of sample pre-treatment, and shorter analysis times. Therefore, this microsampling technique is widely used in modern analytical techniques, such as laser-induced breakdown spectrometry,¹⁵ optical emission or mass-spectrometry with inductively-coupled plasma and LA.¹⁶ Analysis with LA requires reference samples which should be matrix-matched with the analyzed one. The matrix effects and the related phenomena observed in LA hyphenated techniques are discussed in detail elsewhere.¹⁷ Among the physical and chemical properties of a sample, the effects of grain size,¹⁸ hardness,¹⁹ microstructure,²⁰ and surface finishes²¹ on the analytical signal seem to be the most valuable properties which should be considered responsible for the matrix effects caused by the difference in the production techniques of ferrites. One way to reduce these matrix effects is by using femtosecond LA.²² Unfortunately, the high cost of fs-lasers limits their analytical applications.

Another way is through the use of an internal standard. However, the applicability of internal standardization to the reduction of these difficulties seems to be questionable for a number of conventional single-element spectroscopic techniques, such as LEI, laser-induced fluorescence (LIF) or various absorption techniques. Therefore, the use of certain signals (as a kind of internal standard), the nature of which differs from an analytical one, presents an interest. These methods use the simultaneous measurement of the analytical signal and some additional signal (reference signal) during the same laser pulse. For example, the proportionality between acoustic signal and ablated mass allowed the compensation for matrix-matched changes of the total amount of ablated material.²³ The Mie-scattering of light on plasma microparticles permits to estimate a loss of ablated mass due to aggregation at the measurement time.²⁴ Other signals can be adapted to real-time plasma diagnostics. Total emission within the spectral window, background emission, and specific emission lines are examples of reference signals usually applied in emission techniques to compensate for shot-to-shot variations of plasma temperature.²⁵ Bredice et al.²⁶ have shown that total RC circuit current correlated with plasma electron density. The main advantage of such approaches is a reduction of matrix effects and an improvement in the figures-of-merit, especially the pulse-to-pulse repeatability. Nevertheless, a reasonable criterion to select reference signals for normalisation purposes is necessary in LA hyphenated techniques.²⁷ Thus, the use of reference signals as internal standards in LA-LEI or LA-LIF is of interest for the analytical employment of these techniques.

Moreover, the use of available reference samples synthesized by annealing ferrite powder having a slightly different microstructure (similar to ceramics) and mechanical properties to build a calibration curve is a challenge to perform LA-LEI analytical measurements. Thus, the LEI analysis of various lithium ferrites with laser sampling into a flame is the main goal of this work. For this purpose, the optimization of experimental set-up and detection conditions is required to operate with several reference signals (optoacoustic, emission from matrix and ion probe current) and to realize the multivariate correction for LA-LEI thoroughly described for aluminium alloys analysis.²⁸

2. Experimental

2.1. Experimental set-up

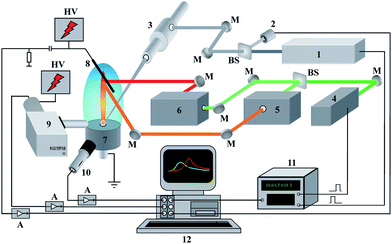
The experimental set-up is shown in Fig. 1. It consists of a laboratory-built LEI spectrometer equipped with a device for the laser ablation of a sample into a flame. The radiation of a Q-switched Nd³⁺:YAG ablation laser (1) operating at 5 Hz, λ = 1064 nm and τ_pulse = 9 ns was focused by a microscope (3) onto the surface of the solid sample. The range of available values of energy for the ablation laser was from 3 mJ per pulse to 80 mJ per pulse. The stability of the laser energy was monitored by the laser energy meter (2). The objective focal length of the microscope was 52 mm. The laser beam incidence angle onto the sample surface was fixed at 45° in order to avoid damage to the focusing optics by hot exhaust gases from a flame. The irradiation spot on the sample surface appeared as an ellipse 0.35 × 0.60 mm² in size. Thus, the maximal laser irradiance on the sample was approximately equal to 4 × 10⁹ W cm⁻². The samples were placed into a specially designed burner head (7). The interaction of laser radiation with a sample results in the formation of a laser plume, which expands into a methane–air flame. Atoms from the laser-produced plasma reach the detection zone of the flame where the radiation of two different dye lasers (5, 6) resonantly excite the analyte atoms. The second harmonic of the Q-switched Nd³⁺:YAlO₃ laser (7) with λ = 540 nm, τ_pulse = 9 ns and 54 ± 5 mJ per pulse synchronously pumped these tunable dye lasers. Rhodamine 640 (Exciton Inc., USA) with λ = 610.31 nm and 130 μJ per pulse and Oxazine 700 (VNIIOPIK, Russia) with λ = 670.8 nm and 200 μJ per pulse were used as laser dyes to excite lithium atoms. An iridium wire cathode in the flame detected the lithium ions generated. A stabilized negative potential, provided by a high-voltage power supply, was applied to the cathode (8). A grounded burner head served as an anode. The optical emission from a ∼100 μm central region of the laser plume was collected by a monochromator equipped with a time-gated PMT (9). A capacitive microphone (10) placed at a distance of 10 cm from the ablated target recorded the acoustic signal. An avalanche photodiode (11) and a square wave generator (12) were used to synchronize the ablation and pump lasers. The controlled changes in laser energy were performed by a set of neutral gray glass filters to obtain correlation between analytical and reference signals. All signal channels after amplification were addressed by the multichannel ADC unit (ADLink™) and recorded by a laboratory-built LabVIEW™ virtual instrument, the features of which are described in detail elsewhere.²⁹ To avoid aliasing related with Nyquist frequency, a sampling ADC unit rate was chosen at 10 MHz per channel because the signals observed had temporal evolution with a minimal duration of 5 μs. It should be noted that another feature for LEI analysis of aqueous solutions without laser sampling was also available.

Fig. 1 Experimental set-up: 1 – ablation laser, 2 – laser energy meter, 3 – microscope, 4 – pump laser, 5, 6 – dye lasers, 7 – burner head, 8 – cathode, 9 – monochromator with PMT, 10 – microphone, 11 – delay generator, 12 – computer, A – amplifiers, BS – beam splitters, HV – high voltage supply modules, M – mirrors.

2.2. Samples

Non-annealed lithium ferrites were synthesized by means of an ASP technique described in detail elsewhere.⁴ Here, the procedure will be briefly presented. All reagents used were analytical grade. To prepare the stock solution of Fe(NO₃)₃ and Li₂CO₃, 2.0 g of pure metallic iron were diluted into 30 ml of 30% nitric acid at low heat. The solution containing 0.25 g of lithium carbonate was added into the mixture after a visual dissolution of the metal. To reduce the volatility of nitrates from drops into a spray, NaCl solution was added into the stock solution so that the mole fraction of Li/Na was equal to a factor of 1 : 5, i.e. a mass fraction of Li/Na ∼ 1 : 16. From the stock solution, an ultrasonic nebulizer equipped with a polymer membrane produced a spray which was transferred with air into an oven pre-heated up to 1000 °C. The oxide powder deposited upon a microporous glass filter (with a porosity of 0.16) as a form of dust was pressed into a circular pellet (diameter of 5 mm) with a small amount of pure polyvinyl alcohol used as a thickening agent. For the synthesis of the annealed ferrite of LiFe₅O₈, the mixture of stoichiometric quantities of Fe₂O₃ and Li₂CO₃ (5 : 1) was ground by a planetary mill under a stratum of petroleum ether. The finely-dispersed powder pressed into the form of circular pellets was annealed in the oven in accordance with the following program: initially for 24 hours at 500 °C, and then for 6 hours at 950 °C. To prepare the ferrite sample containing a high concentration of lithium, another ferrite sample of LiFeO₂ was synthesized by annealing the mixture of stoichiometric quantities of Fe₂O₃ and Li₂CO₃ (1 : 1) at 900 °C for 20 hours. The diameter of the pellets was equal to 5 mm.

The Li content in the synthesised ferrites was determined by means of two independent methods: by flame atomic emission spectrometry (flame photometry) and flame LEI. All reagents used for Li determination were of analytical grade. For this purpose, a pellet of ferrite was ground in an agate mortar into a dispersible fine powder. After weighing, 0.1 g of ferrite powder was placed into a Teflon cup to digest with a mixture of 5 ml of 37% HCl and 5 ml of deionised water while heating. Then the liquid was evaporated in a temperature range of 80–85 °C until the formation of wet salts. The procedure of digestion by the mixture of hydrochloric acid and deionised water during the heating process was repeated twice to avoid the formation of the insoluble oxychloride of iron(III). The residue was further diluted by deionized water in a volumetric flask until 100 ml was reached. The content of Li was determined by the method of standard additions. To prepare these solutions 0.05 g Li₂CO₃ was treated with a mixture of 1 ml of 37% HCl and 5 ml deionized water placed into a Teflon cup. An atomic absorption/emission flame spectrophotometer S-302 (KZAP, Ukraine) equipped with PMT was employed to perform the flame photometry measurement. The resonant emission line of Li I at 670.8 nm was used as the analytical line. To verify the accuracy, another flame analytical technique, LEI, was applied to the determination of Li content in a set of solutions. The principle of flame LEI spectrometry and the arrangement of the home-made LEI set-up are described in detail above. The two-step scheme for Li atom excitation in a flame, including the transition from ground state to a first excited state (λ = 670.8 nm) and the transition from the first state to the second excited state (λ = 610.4 nm), was chosen in accordance with the enhancement of sensitivity.³⁰ The energy of the pumping laser was set at 54 ± 5 mJ per pulse. For both analytical methods the measurements were treated as a set of at least 5 replicate series. The comparison results of flame photometry analysis with those obtained by flame LEI are represented in Table 1. Analytical results from both methods agree within the statistical error of the measurement.

Table 1 Content of Li (% wt) in the ferrite samples used

Ferrite samples description	Flame photometry, % wt Li^b	Flame LEI, % wt Li^b
a ASP – aerosol spray pyrolysis technique. b Confidence intervals calculated for P = 0.99 and N = 5.
LiFeO2, annealed ceramic	7.4 ± 0.2	7.7 ± 0.3
LiFe5O8, annealed ceramic	1.68 ± 0.07	1.6 ± 0.1
LiFe5O8, ASP^a pellet, pyrolysis at 750 °C	1.59 ± 0.05	1.6 ± 0.1
LiFe5O8, ASP^a pellet, pyrolysis at 850 °C	0.79 ± 0.03	0.76 ± 0.05
LiFe5O8, ASP^a pellet, pyrolysis at 950 °C	0.69 ± 0.03	0.71 ± 0.02

---

To characterize the synthesized ferrites, their X-ray powder diffraction patterns were obtained by means of diffractometer STADI P (STOE, Germany). As may be observed in Fig. 2a, an annealed sample of LiFe₅O₈ consists of a mixture of two phases: α-LiFe₅O₈ and 1–2% of α-Fe₂O₃, while the main components of the non-annealed samples of LiFe₅O₈ were α-LiFe₅O₈ and sodium chloride, NaCl, regardless of the temperature of pyrolysis (Fig. 2b). Note that the annealed sample of LiFeO₂ consisted of two phases: α-LiFeO₂ and α-Fe₂O₃, similar to the annealed ferrite of LiFe₅O₈. This was caused by both the decomposition of ferrite and the incomplete reaction between Fe₂O₃ and Li₂CO₃. Because of differences between the methods of synthesis of LiFe₅O₈, the annealed sample and ferrites synthesized by the ASP technique had a different microstructure and properties. Therefore, a variety of spherical microparticles, ranging in size from 0.1–1 μm, usually form a bulk sample due to the rapid evaporation of water from a droplet of aerosol produced in the ASP technique.^31,32 In contrast to ASP, long annealing results in the sintering of ferrite microparticles with the formation of a rigidly related spatial structure similar to ceramics.¹ Therefore, the Mohs hardness of the most ceramic ferrites is equal to ∼5–7,¹ while the hardness of pressed powder consisting of particles with a diameter of ∼0.5–2 μm may be estimated as 1–2 units¹ on the Mohs hardness scale. The properties of laser plasma will strongly differ between the samples, due to the difference in hardness. For example, the excitation temperatures of microplasma on the surface of annealed ceramics were more than 10 times higher than those calculated for the non-annealed sample.¹⁹ It should be noted that LiFe₅O₈ ferrites have a spinel structure and, hence, those compounds have magnetic properties in contrast to LiFeO₂ ferrites.

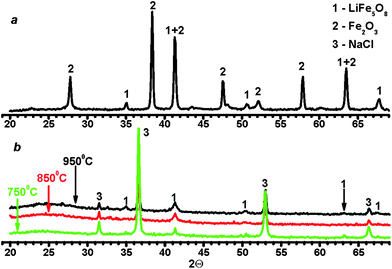Fig. 2 X-ray diffraction patterns of annealed ferrite LiFe₅O₈ (a) and ferrite LiFe₅O₈ prepared by ASP technique (b) at different temperatures in an oven.

3. Results and discussion

3.1. Expansion of laser vapor into a flame

Since an incident beam was directed at an angle of 45° with respect to the sample surface, laser-induced vapor including atoms, ions and droplets deviated from the normal to the surface. Moreover, the flame front propagated from the burner head deflects a plume motion from its original direction. The deflection of the direction of the ablated particles motion from perpendicularity requires the determination of the best spatial layout for the electrode with respect to the laser plasma. To find this position, the LEI signal of Li was studied as a function of the detection point in a flame. The distance between the cathode and the burner head was fixed at 10 mm. As one may expect, the maximal LEI signals shift towards the direction of ablation beam both for ASP ferrites and for ceramic samples. Thus, the cathode in LEI ferrites analysis should be displaced to a distance of ∼3 mm from the ablation point in order to maximize the analytical signal.

The propagation of the laser-induced atomic cloud leads to its “spreading”, i.e. a frontal part of the cloud containing the maximal number of analyte atoms and a long tail of the cloud are formed.³⁰ Since the delay time between ablation and excitation pulses corresponded to illumination by the dye laser part of the atomic cloud, the best temporal conditions for the analysis of lithium ferrites were achieved by variation of the LEI signal vs. delay time. With shorter delays (from 0 to ∼400 μs) the excitation pulses of dye lasers came into the detection volume before analyte atoms. Then the LEI signal dramatically increased up to its maximal value in the frontal part of the plume followed the slow decay of Li analytical signals in a lengthy tail of an atomic cloud produced by laser ablation. The average velocity taken as a ratio of distance between the cathode and the burner to the arrival time of LEI maximum was equal to ∼19 m s⁻¹ for ceramic ablation, while the lithium atoms produced by ablation of ASP ferrites moved twice as slowly, i.e. virtually corresponding to the velocity of the flame level.³³ Optimal values of the delay time were 550 and 800 μs for ceramic ferrites and ASP ferrites, respectively.

3.2. Sample homogeneity

Laser-induced craters on a surface were examined by the use of a contact Step Height Measuring Instrument “Talystep” (Taylor Hobson Ltd, UK). The crater profiles obtained after processing the surface of ceramic ferrite of LiFe₅O₈ by 1, 10 and 50 consecutive laser pulses are shown in Fig. 3. Unfortunately, ASP ferrites could not be explored by means of a profilometer because the crater depths exceeded the 10 μm that were equal to the upper limit of available heights. Strong rims after 50 pulses were observed around the crater on the ceramic surface (trace 3 in Fig. 3) because of the displacement of melts by the plasma. The crater diameter for ceramics evaporation is approximately equal to 350 μm (Fig. 3). In order to estimate average depth, its values were summed along a profile from one rim to the other; then the result was divided by the crater width. As a result, the depth was equal to ∼3 μm after 50 pulses, i.e. depth per pulse was about 60 nm. The latter value is comparable with the value (∼80 nm) which was earlier obtained by Kanicky et al.³⁴ for the ablation of ZrTiN ceramic coatings by 100 pulses. In spite of the considerable roughness (estimated as a maximal deviation in height relative to the bottom line) of the crater bottom, caused by the complex shape of the transverse modal structure of the ablation laser, reaching almost 1 μm, the averaged depth per pulse may be used as an approximate measure of ablation rate for the depth profiling of ceramic ferrites. It should be noted that the ablation rate for depth profiling of ASP ferrites could not be estimated, but in any case the value was larger than 60 nm per pulse due to a greater depth crater.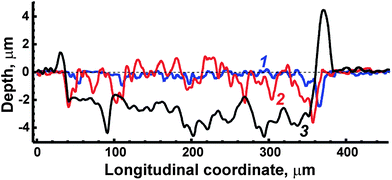

Fig. 3 Crater profiles measured after treatment of ceramic ferrite by 1 (trace 1), 10 (trace 2) and 50 (trace 3) ablation pulses. The dotted line marks the initial level of the surface.

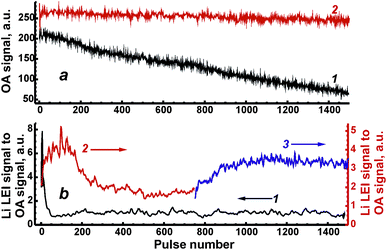
To estimate the relative pulse-to-pulse variations of ablated masses, the drift of optoacoustic (OA) signal measured by the microphone was studied for both types of samples (Fig. 4a) because of the proportionality of the signal to ablated mass. The OA signal was taken as an integral value along the acoustic waveform that was described in detail elsewhere.²⁷ Energy per pulse was fixed at 80 mJ. A fourfold decrease in the OA signal for the ablation of ASP ferrite after 1500 pulses (curve 1 in Fig. 4a) implies that the diminishing ablated mass should be taken into consideration in the depth profiling of these samples. The main reason for the decrease was probably the significantly deepened crater in relatively soft ASP ferrites. Unlike these ferrites, the values of OA signals from ceramics ablation (curve 2 in Fig. 4a) varied around an almost constant value during 1500 pulses.

Fig. 4 Pulse-to-pulse drift of OA signal (a) and ratio of Li LEI signal to OA signal (b). Trace 1 in both figures (left axis) corresponds to the ablation of the ASP pellet. Traces 2 and 3 belong to the case of ceramic ablation before and after polishing, respectively.

Shot-to-shot drifts of the Li LEI signal normalised to the OA signal from Fig. 4a (both signals were measured for each pulse simultaneously to compensate for variations in the mass) are presented in Fig. 4b in order to check the homogeneity of the synthesized ferrite samples. The operating conditions were the same as described above; delay times were 550 μs and 800 μs for ceramic and ASP ferrites respectively, energy was 80 mJ per pulse. The sharp drop observed in the analytical signal during the first 50 laser shots caused by the ablation of ASP ferrites (curve 1 in Fig. 4b) was probably due to the intense enrichment of the vapor by lithium at the time of the crater formation and the melting of spherical microparticles. Unlike the first part of the drift curve, the lithium signal remains constant within the 100–1500 pulse range. It should be noted that other samples of ASP ferrite have demonstrated a similar behavior. The dependencies of the Li LEI signal normalised to the OA signal on the pulse number obtained with ablation of ceramic ferrites significantly differ in two cases of surface treatment: on a fresh surface of the sample (curve 2 in Fig. 4b) and after its polishing (curve 3 in Fig. 4b). The ceramic pellet remaining after laser processing a fresh surface of the sample was polished by an abrasive cloth so that a very small spot originating from the previous crater (i.e. its bottom) could be used to ablate the sample on the same spot. An increase in the Li LEI signal following a drop and a plateau may be observed after treatment of the fresh surface of the sample by the initial 600 laser pulses. Since the crater formation occurs within a 10–50 shot range (Fig. 3), the main reason for such behavior of the drift curve of the analytical signal is probably the heterogeneous distribution of lithium in subsurface layers to a depth of 12 μm (∼0.06 μm per pulse × 200 pulses). The diffusion of lithium atoms from deep layers into subsurface layers and the evaporation of volatile lithium from a surface at annealing are the most reasonable mechanisms resulting from the heterogeneity of ceramic pellets. An area depleted by lithium is stretched for ∼0.06 μm per pulse × 500 pulse = 30 μm under Li-enriched subsurface layers. The fact that the shot-to-shot drift curve obtained after sample polishing continues a trend in the initial curve may be an indirect confirmation of our suggestions. Thus, to obtain accurate analytical results in further work, the upper layers of this ASP ferrite sample must be removed by 50 “cleaning” pulses, while ceramic samples may only be polished by an abrasive cloth.

3.3. Matrix effects

To consider matrix effects, the dependencies of the LEI Li signal on lithium content obtained at different ablation energies were compared. Five successive measurements (20 pulses at each measurement) for each sample were performed. Linear approximation parameters of these curves by means of the equation LEI = a + bw_Li, where LEI – LEI signal intensity, a – intercept, b – slope and w_Li – lithium content (%wt) determined by flame photometry analysis (Table 1), are given in Table 2. Unfortunately, these parameters were insufficient for reliable quantitative analysis (R² < 0.99) for each value of laser energy. Nevertheless, the energy range of 50–60 mJ per pulse was optimal, while there are no significant calibration dependencies below 40 mJ per pulse (b ≈ 0, R² ≈ 0).

Table 2 Parameters of calibration approximation by a function of LEI = a + bw_Li at different laser energies

Laser energy, mJ per pulse	a	b	R ^2
80	1 ± 1	0.7 ± 0.3	0.545
70	0.7 ± 0.8	0.6 ± 0.2	0.671
60	0.2 ± 0.2	0.35 ± 0.06	0.921
50	0.10 ± 0.08	0.20 ± 0.02	0.936
40	0.3 ± 0.2	0.02 ± 0.04	0.050
30	0.5 ± 0.4	−0.1 ± 0.1	0.068
20	0.2 ± 0.2	−0.02 ± 0.05	0.067

---

Such a response may be explained by the fact that the microstructure of ASP ferrites is quite different from that of ceramics. It is well known that softer and looser materials (such as powders) are less effectively ablated at the same laser irradiance value than solid ceramic materials. As a result, LEI signals were maximal for ceramic ablation, while an analytical signal was lower for the ablation of ASP ferrites. Sodium in ASP ferrites can certainly suppress the ionization signal of lithium. This mechanism for Li LEI signal decrease seems doubtful under our conditions since Na content was 16 times greater than Li content and the first ionization potentials of these elements differ by a value of ∼0.2 eV (methane–air flame temperature is about 0.1 eV).¹² Therefore, we suggest that a main reason for Li signal decrease was microstructural differences. Note that the selection of ablation energy as a conventional method for optimization of analysis with LA was unsuitable for this study. Thus, the manifested matrix effects caused by the considerable difference between the microstructures of ferrites did not allow the use of a unified calibration curve for these samples. It is, therefore, necessary to continue searching for other approaches that do reduce the matrix effects.

3.4. Correlation approaches

We previously²⁸ developed two correlation approaches in the case of aluminium alloys analysis to compensate for the strong matrix interferences. It is assumed that there is a relationship between individual physical signals describing specific properties of laser plasma. A concept of such signals, called “reference signals” in opposition to analytical signals, was discussed in detail in recent review.²⁷ This dependence is usually observed within the range of variations of external conditions, e.g. laser energy. Indeed, ablated mass is well known to be directly proportional to laser energy for absorbing plasmas.²³ Therefore, ablation parameters (such as mass, temperature, etc.) may vary according to different levels of laser energy. The first approach is based on a univariate correlation between the analytical and the reference signals; the multivariate correlation with the use of several reference signals is a second approach.

In the present work, OA signal, the emission (AE) from matrix elements, i.e. iron line Fe I at 382 nm, and non-selective ionisation signal (NSI) were chosen as the reference signals. All of these signals grew monotonically with increasing energy (Fig. 5). Fluctuations of the AE signal of Fe I at λ = 382 nm will obviously be determined by random changes in ablated mass, plasma temperature and/or electron density. Since the plasma produced from ceramics is hotter than that from ASP ferrites,¹⁹ iron emission was stronger and, moreover, the threshold value of energy for AE signal formation was less than in the case of ASP ferrite (curve 1 in Fig. 5a and b). Fluctuations of OA signals were caused by changes in ablated mass and flame opacity. A nonselective ionization signal occurred because electrons and ions in plasma had been accelerated in an applied electric field. Therefore, NSI has to be proportional to plasma electron density.²⁶ However, NSI was negligible for the ablation of powdery material (curve 3 in Fig. 5b). A similar phenomenon was explained by a slightly volatile and ionizing matrix when the pressed pellets of lithium vanadate were ablated into a flame.³⁵ Relatively low plasma temperature for ASP may indicate that looser microstructure of non-annealed ferrites prevents the propagation of the heat wave from the plasma inside the bulk sample and leads to lower thermal ionisation of species in the laser plume. Thus, the NSI signal was not used in further investigations for the correction of matrix effects.

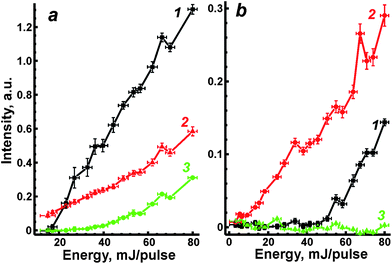Fig. 5 Emission of Fe I at 382 nm (1), OA signal (2) and non-selective ionization (3) as functions of laser energy for ablation of ceramic (a) and ASP (b) ferrites.

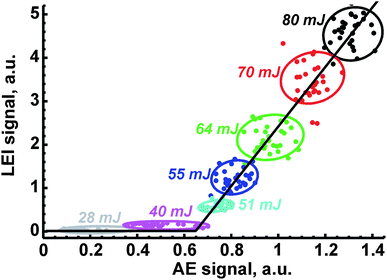
3.5. Univariate correction

Because of the dependencies of LEI, OA and AE signals on laser energy, the correlation inside each pair of them will be observed. An example of such correlation is depicted in Fig. 6. Each point corresponds to a pair of signals measured simultaneously during the same pulse. The variety of points is due to a controlled change in the ablation energy by means of a set of neutral filters; note that the energy was decreasing from 80 mJ per pulse to 5 mJ per pulse, when an ablation point to carry out the measurement at certain energy was new. For the sake of convenience, only partial data (for several energies) were provided in the figure. Points inside an oval which belonged to the given energy do not show any significant correlation, similar to the observation made by Gornushkin et al.³⁶ However, dependence over a wide range of energies has a linear shape with a clear threshold. Indeed there was no LEI signal below 40 mJ per pulse (see Table 2), while reference signals at significant levels were recorded. Moreover, thresholds at which OA and AE signals are at least three times larger than noise differ significantly. Thus, these values in the case of ceramics were 4–5 mJ per pulse and 10 mJ per pulse for OA and AE signals, respectively, while a tenfold difference was observed in the ablation of ASP ferrites (4 mJ for OA signal vs. 40 mJ for AE signal). Because of these differences in the threshold values, the dependence of signal S₁ on signal S₂ was approximated as S₁ = A + BS₂, where A was an intercept and B was the slope of the line.

Fig. 6 Correlation between LEI signal of Li and emission of Fe I at 382 nm observed for the ceramic sample LiFe₅O₈. Points obtained at specific laser energy are bound by colour ovals near to which energy is given.

The coefficients of linear correlation between signals are compared in Table 3. The relationship between LEI signal and reference signal was plotted within the range of 40–80 mJ per pulse, while the OA signal was plotted against AE signal within the range of 5–80 mJ per pulse. Thus, each of the reference signals provides some orthogonality to the LEI signal. It allows the simultaneous use of these signals. Recently, we suggested the use of a coefficient B as a normalised analytical signal similar to the internal standard.²⁷ To examine such a possibility, the variations of B from sample to sample are compared in Table 3. Li content in ferrites can be retrieved from Table 1. One may see that the parameter B (LEI vs. OA or AE) cannot reduce the microstructure effects on calibration while it worked earlier in the case of aluminium alloys. Moreover, the unexpected changes by a factor of two or three of the B parameter obtained as a slope of correlation line between OA and AE signals are obvious (see last column in Table 3). We explain the observed difference by the difference between emission signals obtained at ASP ferrites and ceramics (compare curves 1 in Fig. 5a and b). As a result, the parameter B for pairs of LEI + OA or LEI + AE may be overrated or underrated. To compensate for sample to sample changes of B we suggest taking into account the slope of correlation between OA and emission as well as the difference in thresholds for correlation plot.

Table 3 Parameters of linear correlation of the signal pairs used in the work

Samples	N	B
		S 1 = LEI; S2 = OA	S 1 = LEI; S2 = AE	S 1 = OA; S2 = AE
LiFeO2, ceramics	240	25 ± 3 (R^2 = 0.630)	12 ± 1 (R^2 = 0.734)	0.46 ± 0.05 (R^2 = 0.876)
LiFe5O8, ceramics	240	13 ± 1.5 (R^2 = 0.741)	6.7 ± 0.6 (R^2 = 0.895)	0.35 ± 0.02 (R^2 = 0.918)
LiFe5O8, ASP at t = 750 °C	180	6.7 ± 0.6 (R^2 = 0.848)	2.9 ± 0.3 (R^2 = 0.845)	1.39 ± 0.25 (R^2 = 0.637)
LiFe5O8, ASP at t = 850 °C	180	1.9 ± 0.3 (R^2 = 0.631)	1.4 ± 0.2 (R^2 = 0.734)	0.72 ± 0.05 (R^2 = 0.876)
LiFe5O8, ASP at t = 950 °C	180	3.3 ± 0.6 (R^2 = 0.741)	1.1 ± 0.4 (R^2 = 0.895)	0.62 ± 0.06 (R^2 = 0.918)

---

3.6. Multivariate correction

To reduce the strong matrix effects caused by the microstructure of ferrites, we decided to use a multivariate correlation approach applied to correct matrix variations of aluminium aviation alloys.²⁸ The approach utilized a 3D correlation plot, where the Z axis corresponded to analytical LEI signal, the Y axis corresponded to the reference acoustic signal and the X axis corresponded to the reference emission signal. Considerable multicollinearity between reference signals (see Table 3) resulted in the points in 3D space being scattered near a curve instead of a plane. Because there is a strong linear correlation between each of the three pairs of signals (LEI + AE, LEI + OA and OA + AE), it seems reasonable to approximate the correlation between these three signals by a straight line in 3D space. It should be noted that the views of the 3D plot in the XY, XZ and YZ planes are 2D correlation plots, as shown e.g. in Fig. 6. Therefore, the parameters of the 3D plot should be related to those for 2D plots. The relationship between the slope of a straight line in 3D space to the XY plane and parameters B of 2D plots may be specified by the equation:
where B_OA and B_AE are the B parameters for the pairs LEI + OA and LEI + AE respectively. Recently we have demonstrated²³ that the main advantage of MVS was the exclusion of the variations of correlation between the reference signals as well as the difference in the threshold values for correlation plots. Thus, a slope of the 3D correlation plot may be a new analytical signal normalised according to two reference signals. For the calculation of errors, we deduced an equation from error propagation law:
where symbols with Δ represent the errors of each mentioned value. The linear calibration curve for lithium determination in ferrites by means of MVS shown in Fig. 7 allows the reduction of matrix effects caused by the ferrite microstructure.

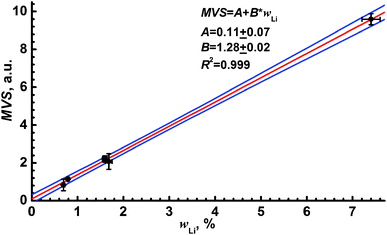Fig. 7 Multivariate signal as a function of Li content in ferrites. Blue lines indicate a confidence interval for P = 0.95. The parameters of linear calibration (red line) are given in the legend.

Despite the advantages of the proposed approach to reduce matrix effects, one may note several limitations. Firstly, the resonance line of iron (a main component of lithium ferrite) as an emission signal obviously limits the range of samples in which lithium may be determined over lithium ferrites by a unified calibration curve. For example, if one takes the mixed spinels such as Li_3xMnFe_2−xO₄ or some other non-iron lithium spinel, e.g. Li₄Ti₅O₁₂ or LiMn₂O₄, the emission line of iron will either be out of self-absorption or absent. Other reference samples and emission lines will be needed to analyse such samples with certainty. Secondly, a large number of analytical measurements is required to build the 3D correlation plots, which results in some increase of analysis time. Nevertheless, the use of two reference signals allowed us to construct a calibration model, where all the experimental points were within the confidence band (P = 0.95). It was impossible with the use of the raw LEI signal or one-dimensional normalisation, since the experimental points were divided into two groups related to annealed and non-annealed ferrites.

4. Conclusion

Two sets of lithium ferrites were prepared by means of the ASP technique and by sintering the mixture of Li and Fe(III) nitrates in order to obtain reference materials. Strong matrix effects on the LA-LEI signal were observed for a wide range of laser energies (5–80 mJ per pulse). The effects were related to the different methods of ferrite synthesis which resulted in changes in the surface microstructure and hardness. To diminish such effects we compared univariate and multivariate correlation techniques with the use of reference signals, such as the OA signal and emission line Fe I at 382 nm. The normalisation of the LEI signal on the single reference signal (either OA or AE) did not allow for a linear calibration curve for lithium determination. The main reason appears to be changes in the slope of the correlation line OA vs. AE from the ASP sample to annealed ferrites. Since the strong colinearity between OA and AE signals was discovered, multivariate correlation between signals may produce the normalised signal (MVS). In conclusion, the MVS approach allows the use of ferrites synthesised by various techniques as reference materials to build a unified calibration curve.

Acknowledgements

We thank Dr. Alexander A. Gorbatenko for his contribution to the development of normalisation techniques in LEI analysis with laser sampling. We also thank Prof. Catherine Le Gouis for help in preparing the manuscript and Dr. Roman B. Vasiliev for obtaining the profiles of craters of ferrite samples

References

1. A. Goldman, Modern Ferrite Technology, Springer, New York, 2006, 438 p.
2. F. O. Ernst, H. K. Kammler, A. Roessler, S. E. Pratsinis, W. J. Stark, J. Ufheil and P. Novák, Mater. Chem. Phys., 2007, 101(2–3), 372–378.
3. Y. T. Lee, C. S. Yoon, Y. S. Lee and Y. K. Sun, J. Power Sources, 2004, 134(1), 88–94.
4. D. J. Kim and K. K. Koo, Cryst. Growth Des., 2009, 9(2), 1153–1157.
5. S. Dey, A. Roy, D. Das and J. Ghose, J. Magn. Magn. Mater., 2004, 270(1–2), 224–229.
6. B. Zawisza, J. Anal. At. Spectrom., 2010, 25(1), 34–39.
7. V. N. Lednev, A. V. Yakovlev, T. A. Labutin, A. M. Popov and N. B. Zorov, J. Anal. Chem., 2007, 62(12), 1151–1155.
8. V. Zorba, J. Syzdek, X. Mao, R. E. Russo and R. Kostecki, Appl. Phys. Lett., 2012, 100(23), 234101.
9. D. Boudreau and J.-F. Gravel, TrAC, Trends Anal. Chem., 2001, 20(1), 20–27.
10. J. P. Temirov, O. I. Matveev, B. W. Smith and J. D. Winefordner, Appl. Spectrosc., 2003, 57(7), 729–732.
11. N. V. Chekalin, A. G. Marunkov, V. I. Pavlutskaya and S. V. Bachin, Spectrochim. Acta, Part B, 1991, 46(5), 551–558.
12. N. B. Zorov, Y. Y. Kuzyakov, O. I. Matveev and V. I. Chaplygin, J. Anal. Chem. USSR, 1980, 35(9), 1108–1112.
13. D. J. Butcher, Appl. Spectrosc. Rev., 2007, 42(6), 543–562.
14. J.-F. Y. Gravel, M. L. Viger, P. Nobert and D. Boudreau, Appl. Spectrosc., 2004, 58(6), 727–733.
15. D. W. Hahn and N. Omenetto, Appl. Spectrosc., 2012, 66(4), 347–419.
16. R. E. Russo, T. W. Suen, A. A. Bol'shakov, J. Yoo, O. Sorkhabi, X. Mao, J. Gonzalez, D. Oropeza and V. Zorba, J. Anal. At. Spectrom., 2011, 26(8), 1596–1603.
17. L. Moenke-Blankenburg, Laser Microanalysis, John Wiley & Sons, New York, 1989, 286 p.
18. E. Cerrai and R. Trucco, Energ. Nucl., 1968, 15(9), 581–585.
19. T. A. Labutin, A. M. Popov, V. N. Lednev and N. B. Zorov, Spectrochim. Acta, Part B, 2009, 64(10), 938–949.
20. S. Yao, J. Lu, K. Chen, S. Pan, J. Li and M. Dong, Appl. Surf. Sci., 2011, 257(7), 3103–3110.
21. I. Lopez-Quintas, V. Piñon, M. P. Mateo and G. Nicolas, Appl. Surf. Sci., 2012, 258(23), 9432–9436.
22. Q. Z. Bian, J. Koch, H. Lindner, H. Berndt, R. Hergenroder and K. Niemax, J. Anal. At. Spectrom., 2005, 20(8), 736–740.
23. C. Chaleard, P. Mauchien, N. Andre, J. Uebbing, J. L. Lacour and C. Geertsen, J. Anal. At. Spectrom., 1997, 12(2), 183–188.
24. S. A. Baker, B. W. Smith and J. D. Winefordner, Appl. Spectrosc., 1998, 52(1), 154–160.
25. U. Panne, C. Haisch, M. Clara and R. Niessner, Spectrochim. Acta, Part B, 1998, 53(14), 1957–1968.
26. F. Bredice, H. Sobral, M. Villagran-Muniz, H. O. Di Rocco, G. Cristoforetti, S. Legnaioli, V. Palleschi, A. Salvetti and E. Tognoni, Spectrochim. Acta, Part B, 2007, 62(8), 836–840.
27. N. B. Zorov, A. A. Gorbatenko, T. A. Labutin and A. M. Popov, Spectrochim. Acta, Part B, 2010, 65(8), 642–657.
28. A. M. Popov, T. A. Labutin, D. N. Sychev, A. A. Gorbatenko and N. B. Zorov, Spectrochim. Acta, Part B, 2007, 62(3), 211–216.
29. A. M. Popov and T. A. Labutin, Meas. Tech., 2011, 54(2), 213–218.
30. G. C. Turk, in Laser-Enhanced Ionization Spectrometry, ed. J. T. Travis and G. C. Turk, Wiley, New York, 1996, pp. 161–208.
31. V. Verma, V. Pandey, S. Singh, R. P. Aloysius, S. Annapoorni and R. K. Kotanala, Physica B, 2009, 404(16), 2309–2314.
32. N. G. Jović, A. S. Masadeh, A. S. Kremenović, B. V. Antić, J. L. Blanuša, N. D. Cvjetičanin, G. F. Goya, M. V. Antisari and E. S. Božin, J. Phys. Chem. C, 2009, 113(48), 20559–20567.
33. P. K. Schenck, J. C. Travis, G. C. Turk and T. C. O'Haver, Appl. Spectrosc., 1982, 36(2), 168–171.
34. V. Kanicky, J. Musil and J.-M. Mermet, Appl. Spectrosc., 1997, 51(7), 1037–1041.
35. A. A. Gorbatenko, N. B. Zorov and T. A. Labutin, J. Anal. Chem., 2003, 58(4), 343–346.
36. I. B. Gornushkin, B. W. Smith, G. E. Potts, N. Omenetto and J. D. Winefordner, Anal. Chem., 1999, 71(23), 5447–5449.

---