Novel features of multiferroic and magnetoelectric ferrites and chromites exhibiting magnetically driven ferroelectricity

Abstract

A few oxides such as YMnO₃, TbMnO₃, YMn₂O₅ and BiFeO₃ constituted the small family of well-characterized multiferroics until recently, but this area of research has been enlarged significantly due to the advent of a novel class of oxides exhibiting interesting multiferroic and magnetoelectric properties arising from magnetically induced ferroelectricity. Interestingly, these materials are simple transition metal oxides, most of them possessing the perovskite structure. In this review article, we present the significant features of multiferroic and magnetoelectric ferrites and chromites which owe their ferroelectricity to magnetic interactions. Some of the important systems discussed are BiFeO₃ whose properties are affected by magnetic and electric fields, rare-earth orthoferrites LnFeO₃ (Ln = Dy, Gd and Sm) and rare-earth orthochromites LnCrO₃, where exchange-striction plays a significant role. Perovskite oxides of the type Y(A_1−xB_x)O₃ (A, B = Fe, Cr, Mn) exhibit multiferroic properties, although the existence of these properties in YFeO₃ and YCrO₃ is in doubt. Such oxides with a non-magnetic rare-earth cation at the A site and two transition metal ions in the B-site permit tuning the transition temperatures by varying the B site ions and their relative proportions or the Ln ion. Multiferroic properties of simple ferrites such as Al(Ga)FeO₃ where cation disorder appears to play a role are also discussed. Problems and challenges in this area of research are indicated.

---

Rana Saha

Rana Saha obtained his B.Sc. degree in chemistry from the University of Calcutta and M.S. degree in materials science from JNCASR. Currently he is carrying out his Ph.D. studies on multiferroics at JNCASR.

A. Sundaresan

A. Sundaresan obtained his Ph.D. degree from Indian Institute of Technology Bombay, and did post-doctoral work in Tsukuba, Caen and Grenoble before joining JNCASR. He is a professor at JNCASR where he works on oxide materials and magnetism. He is the recipient of the bronze medals of the Materials and Chemical Research Societies of India.

C. N. R. Rao

C. N. R. Rao is National Research Professor and Linus Pauling Research Professor at Jawaharlal Nehru Centre for Advanced Scientific Research (JNCASR) and Honorary Professor at the Indian Institute of Science. His main interests are in the chemistry of materials. He is an honorary fellow of RSC and a member of many of the major academies including the Royal Society and the U. S. National Academy of Sciences. He is the recipient of the Royal Medal of the Royal Society of London, Dan David Prize and Erneslo Illy Trieste Science Prize for materials research and the August Wilhelm von Hoffmann medal of the German Chemical Society.

---

Introduction

Although ferroelectricity and magnetism require contradicting characteristics in a material, several multiferroics have indeed been reported in the last few years.^1–4 Multiferroic properties can arise from the operation of different mechanisms. In YMnO₃, electric polarization arises due to polyhedral tilting, in LnMn₂O₅, ferroelectricity arises from the magnetostriction induced by collinear spins in the frustrated magnetic structure.^2,3 In BiFeO₃, the role of the 6s² lone pair of Bi³⁺ ion has been invoked.⁵ Ferroelectricity induced by oxygen octahedral rotation has been predicted in some perovskite oxides.^6–11 Occurrence of ferroelectric polarization has been demonstrated experimentally and theoretically in metal organic frameworks (MOF) and organic crystals as well.^12–15 Based on first-principles calculations, a new proper ferroelectric state has been predicted in PbNiO₃.¹⁶ The most intriguing aspect of multiferroics that has emerged in the last few years relates to electric polarization that results from magnetism which is traditionally considered to be incompatible with ferroelectricity.^3,17 In this review article, we will examine magnetism-driven ferroelectricity in ferrites and chromites, some of which are magnetoelectric. Magnetoelectric materials are those where there is coupling between magnetic and electric order parameters, wherein electric polarization can be controlled by magnetic fields and magnetization by electric fields.¹⁸ All multiferroics are not necessarily magnetoelectric.

We shall concentrate our attention on selected oxide materials which exhibit magnetic ordering and ferroelectricity, important examples of such materials being rare-earth orthoferrites, LnFeO₃ (Ln = rare earth). It may be recalled that multiferroic properties of TbMnO₃, due to the cycloidal magnetic structure which breaks the inversion centre, triggered much interest in such spin-driven polarization phenomena.¹⁹ Besides the orthoferrites, we shall examine the evolution of ferroelectric polarization in rare-earth orthochromites, LnCrO₃. We then present the case of two simple oxides, AlFeO₃ and GaFeO₃, where there is cationic disorder. Another aspect of interest is the possibility of tuning ferroelectric and magnetic ordering temperatures in perovskite oxides containing two transition metal ions in the B-site. We shall briefly touch on the challenges in this area.

BiFeO₃

We shall first examine the well-studied multiferroic and magnetoelectric properties of BiFeO₃ (BFO). It crystallizes in the rhombohedrally distorted perovskite structure (R3c), with relatively high ferroelectric (T_C ∼ 1103 K) and antiferromagnetic (T_N ∼ 643 K) transition temperatures.^20,21 The magnetic structure of BFO is such that the Fe moments couple antiferromagnetically (G-type) in the pseudocubic [111]_c direction which is equivalent to the hexagonal [001]_h direction, leading to an incommensurately modulated cycloidal spiral spin structure with a long wavelength of 620 ± 20 Å along the hexagonal [110]_h direction.^22,23 This cycloidal spin structure is destroyed by magnetic fields resulting in a homogenous spin order which allows linear magnetoelectric coupling.²⁴ Along the [111]_c direction, the Bi³⁺ and Fe³⁺ cations in BFO are displaced from their centrosymmetric positions resulting in spontaneous polarization in this direction.²⁵ The value of spontaneous polarization in the bulk sample is, however, small (∼6 μC cm⁻²). In epitaxial thin films and single crystals, the polarization is higher (∼100 μC cm⁻²),^26,27 with the films showing a considerable magnetoelectric effect (Fig. 1).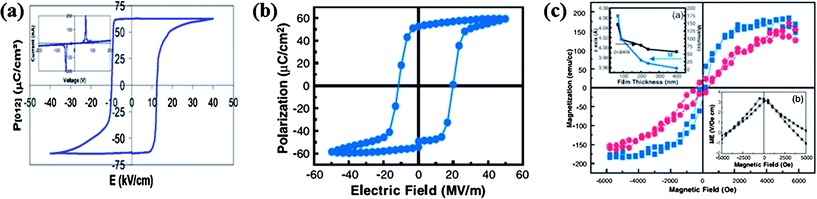

Fig. 1 Ferroelectric hysteresis loops of BiFeO₃ at room temperature for (a) the single crystal, (b) epitaxial thin film and (c) magnetic hysteresis loop of epitaxial BiFeO₃ at room temperature (in-plane loop is in blue and out-of-plane loop is in red) along with the thickness dependence of saturation magnetization (top inset) and magnetoelectric measurements (bottom inset). (reproduced with permission from ref. 26, copyright 2003, by the AAAS; from ref. 27, copyright 2007, by the American Institute of Physics).

Quite recently exchange bias in BFO has been manipulated by electric fields, suggesting possible applications in spintronics, memory devices and sensors.²⁸ With this purpose, epitaxial heterostructures of antiferromagnetic BFO and ferromagnetic La_0.7Sr_0.3MnO₃ (LSMO) have been constructed, which exhibit induced ferromagnetism in the Fe sublattice at the interface due to the interplay between the electronic orbital reconstruction and its coupling to the spin degrees of freedom.²⁹ The moment induced by interfacial coupling together with the antiferromagnetically coupled interfacial and the second Mn layers give rise to the exchange bias (EB)²⁹ on cooling in a magnetic field through a blocking temperature (T_B; ∼100–120 K). The effect of the ferroelectric polarization on the exchange bias has been examined below T_B to maximize the exchange bias by constructing a multiferroic field effect device employing BFO (200–600 nm)/LSMO (3–10 nm)/STO heterostructures.^30,31 Reversible switching of exchange bias between two states with the same (unipolar modulation)³⁰ and opposite polarity (bipolar modulation)³¹ at 5.5 K without the presence of any magnetic field or field cooling has been observed. The mechanism of bipolar modulation of exchange bias is explained on the basis of a model which considers coupled antiferromagnetic–ferroelectric order in BFO along with the modulation of interfacial exchange interactions due to the displacement of Fe³⁺ ions in BFO relative to the Mn^3+/4+ ions in LSMO.³¹

Apart from the electrical control of magnetization in BFO thin films, modification of the cycloidal magnetic structure, exchange bias and GMR by epitaxial strain has been investigated.³² Thus, Sando et al.³² have shown that both compressive and tensile strains induced by the substrate can destroy the cycloidal modulation of Fe spins along the [11̄0] direction, thereby stabilizing the pseudo-collinear antiferromagnetism. On stretching the film, a net in-plane magnetization develops along the [11̄0] direction, while a progressive reorientation of the spins from in-plane to out-of-plane occurs as the film is subjected to a compressive strain as shown in Fig. 2.³³ Sando et al. have also demonstrated that epitaxial strain-induced spin reorientation from in-plane to out-of-plane can be used to tune the exchange bias. Reversible switching between two exchange bias states in the LSMO–BFO heterostructure with opposite exchange bias polarities upon ferroelectric poling of BFO indicates strong coupling of polarization with the magnetization at the interface. Furthermore, strain engineering can play an important role in controlling the magnetization and exchange bias of the BFO film and heterostructures thereby improving the magnetoelectric coupling.

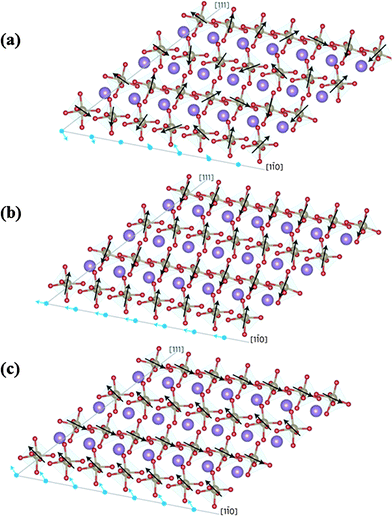Fig. 2 Schematic representation of magnetic moments of BiFeO₃ along crystallographic [11̄0 ] and [111] directions for (a) zero strain inducing zero net moment, (b) a tensile strain inducing a net in-plane magnetic moment and (c) a compressive strain inducing a net out-of-plane magnetic moment. The purple, brown and red colours indicate Bi, Fe and O atoms respectively. The black arrows indicate the magnetic moments of Fe; blue arrows indicate the net magnetic moments produced by rows of iron atoms along [111] (reproduced with permission from ref. 33, copyright 2013, by the Nature Publishing Group).

Rare-earth orthoferrites

Rare-earth orthoferrites of the type LnFeO₃ (Ln = Gd, Dy, Sm) crystallizing in the orthorhombically distorted perovskite structure (Pbnm) exhibit three types of G-type antiferromagnetic spin structures in the Fe sites, Γ₄ (G_xA_yF_z), Γ₂ (F_xC_yG_z) and Γ₁ (A_xG_yC_z),³⁴ where G_x, A_y, F_z correspond to the components of Fe spins along crystallographic a, b and c directions respectively (Fig. 3). Among Fe–Fe, Ln–Fe and Ln–Ln exchange interactions,³⁵ Fe–Fe ordering is the strongest leading to canted antiferromagnetic ordering of the Fe sublattice at 650–700 K.³⁶ The comparatively weak Ln–Fe interactions cause the Ln sublattice to polarize in the exchange field of weakly ferromagnetic Fe moments. The anisotropic nature of the Ln and Fe moments gives rise to two magnetic phase transitions with temperature: (a) spin reorientation where the direction of antiferromagnetic component (G-type) changes its direction from one crystallographic axis to another and (b) temperature induced magnetization reversal below a compensation point where the rare-earth moment and the weak ferromagnetic moment of Fe sublattice are antiferromagnetically coupled. At low temperatures (<10 K), Ln–Ln interactions lead to antiferromagnetic ordering of rare-earth ions. Orthoferrites with a non-magnetic Ln ion shows only the Γ₄ spin structure at all temperatures.³⁶ The above spin structures correspond to nonpolar magnetic point symmetries Γ₄ (m′m′m), Γ₂ (mm′m′) and Γ₁ (mmm), which do not support spontaneous electric polarization.³⁷ Based on symmetry analysis of magnetoelectric interactions in the orthoferrites (and orthochromites), spontaneous polarization or magnetic field induced ferroelectricity is predicted to arise at the antiferromagnetic ordering temperature of the rare-earth ion.³⁸ Indeed experimentally the occurrence of spontaneous polarization was realized at the Néel temperature of Gd³⁺ ions of GdFeO₃ while in DyFeO₃ ferroelectricity was discovered at the T_N of Dy³⁺ ions in the presence of a magnetic field.^39,40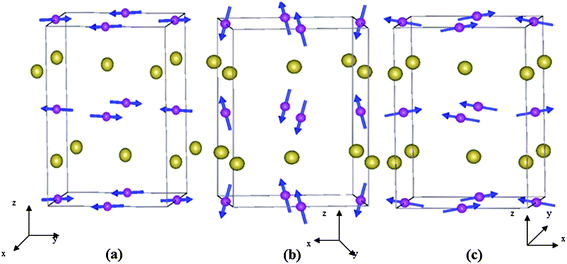

Fig. 3 Different types of G-type AFM spins in (a) Γ₁ (A_xG_yC_z), (b) Γ₂ (F_xC_yG_z) and (c) Γ₄ (G_xA_yF_z) configurations for rare-earth orthoferrites and orthochromites with Pbnm symmetry. Fe and Ln are indicated by spheres with and without spins respectively (reproduced with permission from ref. 62, copyright 2012, by the American Physical Society).

GdFeO₃ (Pbnm)⁴¹ exhibits weak ferromagnetism and spontaneous ferroelectric polarization (0.12 μC cm⁻², at 2 K) below the T_N of Gd³⁺ ions in the absence of a magnetic field unlike DyFeO₃.³⁹ In contrast to Dy³⁺, Gd³⁺ is less anisotropic⁴² and the ground state magnetic spin configuration is Γ₄, with the Fe spins ordering antiferromagnetically at 661 K³⁹ along with weak ferromagnetism due to Dzyaloshinskii–Moriya (DM) interaction.^43,44 The Gd moments undergo antiferromagnetic ordering with the spin configuration G_xA_y (Γ₅) below 2.5 K. The magnetic point group of GdFeO₃ below the ordering temperature of Gd ion is m′m′2 which allows spontaneous polarization along the crystallographic c axis. The dielectric constant measured at 1 kHz shows a peak at the onset of ferroelectric polarization, coinciding with the magnetic ordering temperature of the Gd ions (Fig. 4). The occurrence of a dielectric anomaly at the Curie temperature (T_C = 2.5 K) and the presence of weak ferromagnetism indicate that GdFeO₃ is multiferroic. Accordingly, we see from Fig. 4 that with increasing magnetic field along the a axis, concomitantly the dielectric peak shifts towards low temperatures and the ferroelectric polarization is suppressed.

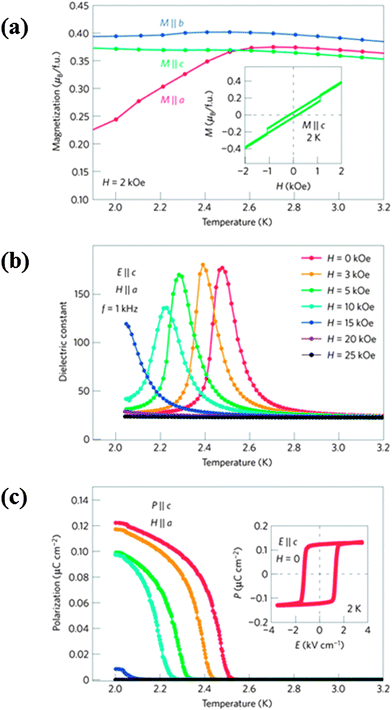Fig. 4 Variation of (a) magnetization at H = 2 kOe and (b) dielectric constant at f = 1 kHz, (c) electric polarization along the c direction for several H ‖ a as a function of temperature in a single crystal of GdFeO₃. Insets in (a) and (c) show ferromagnetic and ferroelectric hysteresis loops respectively at 2 K (reproduced with permission from ref. 39, copyright 2009, by the Nature Publishing Group).

The origin of ferroelectricity and the effect of magnetic field on polarization can be understood from the magnetic structure of GdFeO₃, where the dominant spin configurations for the Fe and Gd sites are of G type (Fig. 5a). The ground state magnetic configurations of the Fe and Gd sublattice are represented by Γ₄ (G_xA_yF_z) and Γ₅ (G_xA_y) respectively as shown in Fig. 5b. In this G type configuration, exchange-striction from the eight nearest neighbour Fe ions on the Gd ions in a cubic cell would be cancelled out (Fig. 5a). On ordering the Gd ions, the total cancellation is lost and therefore exchange-striction force acting on the Gd ions results in displacement along the c direction from the mirror plane giving rise to polarization. On application of a magnetic field (5 < H < 20 kOe) along the a direction the magnetic structure changes to Γ₂ (F_xC_yG_z) and Γ₇ (G_z) for the Fe and Gd sites respectively (Fig. 5c) resulting in the suppression of polarization. Further application of a magnetic field (H > 20 kOe) along the a direction causes the spin structure of Fe (Γ₂) to be retained but the Gd moment goes from G_z to F_x, thereby removing the exchange-striction force from surrounding Fe spins and the disappearance of the polar state as shown in Fig. 5d. However on application of a magnetic field along the c direction, the Fe sublattice retain the Γ₄ spin structure but the Gd spins change from G_xA_y (Γ₅) to F_z as shown in Fig. 5e. Exchange-striction force on the Gd ion therefore disappears, resulting in a non-ferroelectric state. The magnetoelectric nature of GdFeO₃ can be understood on the basis of composite domain wall clamping of the domain walls for magnetization and polarization.³⁹

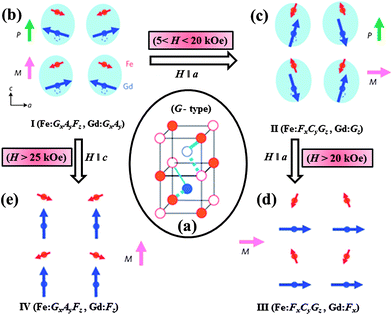Fig. 5 Schematic representation of magnetic structures of GdFeO₃ below the magnetic ordering of Gd³⁺ ions in Pbnm symmetry: (a) exchange striction mechanism with the G-type magnetic structure, (b–e) spin configurations (I–IV) of Fe and Gd ions with varying magnetic field (+ and − symbols indicate the relative spin direction of each ion and blue solid (dotted) lines indicate attractive (repulsive) forces respectively) (modified with permission from ref. 39, copyright 2009, by the Nature Publishing Group).

In the case of DyFeO₃, below the Néel temperature (T_N = 645 K) of Fe³⁺ ions, the spin configuration is Γ₄ which allows the presence of weak ferromagnetism due to DM interaction along the c direction. On lowering the temperature, the Fe sublattice changes the direction of the antiferromagnetic spin component (G-type) from a to b axis resulting in the Γ₁ magnetic structure at 37 K.⁴⁵ Application of an external magnetic field along the c axis rotates the antiferromagnetic spin component from b to a (Γ₁ to Γ₄) and a field along the a axis changes the direction from b to c (Γ₁ to Γ₂).⁴⁶ Further cooling leads to antiferromagnetic ordering of the Dy moments in the Γ₅ (G_xA_y) configuration with the nonpolar magnetic point symmetry (m′m′m′) at 4 K. The point symmetries of Γ₁ and Γ₅ correspond to m_x, m_y and m_z symmetry, giving rise to nonpolar magnetic point group 222 which does not favour spontaneous ferroelectric polarization at the ground state in the absence of a magnetic field. On application of a magnetic field (30 kOe) along the crystallographic c direction, ferroelectric polarization (≥0.2 μC cm⁻²) is realized along the c direction at the magnetic ordering temperature (T_N = 4 K) of the Dy ions after magnetoelectric poling with E = 2 kV cm⁻¹.⁴⁰ The occurrence of ferroelectricity at T_N of Dy and its appearance on application of a magnetic field indicates the combined role of Dy and Fe spin structures. The magnetic structure of DyFeO₃ (Fig. 6) consists of alternate layers of Fe and Dy moments in layered antiferromagnetic fashion.⁴⁰ On application of a sufficiently high magnetic field, the Γ₁ configuration of the Fe sublattice changes to the Γ₄ configuration with weak ferromagnetism along the c direction. The Fe and Dy sublattices, now with Γ₄ and Γ₅ configurations respectively, break the m_z symmetry and adopt the polar point group m′m′2 which allows the spontaneous polarization along the c direction. From Fig. 6, we see that the Fe spins remain parallel to one of the nearest Dy spins and antiparallel to other nearest Dy moments, thereby driving the cooperative displacement of the Dy layers to the Fe layers with opposite spins leading to the generation of polarization along the c direction. Density functional theoretical calculations show that coupling between Dy and Fe spins is mediated by Dy-d and O-2p hybridization.⁴⁷ The existence of a polar state and weak ferromagnetism in the presence of a magnetic field makes DyFeO₃ a magnetoelectric multiferroic material at low temperatures (4 K).

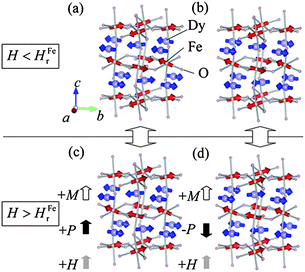Fig. 6 Schematic representation of magnetic structures of DyFeO₃ below the magnetic ordering of Dy³⁺ ion in Pbnm symmetry (a and b) for linear magnetoelectric phase when H < H_r; (c and d) for multiferroic phase when H > H_r (reproduced with permission from ref. 40, copyright 2008, by the American Physical Society).

The presence of electric polarization in the weakly ferromagnetic state of DyFeO₃ was reported in a polycrystalline sample,⁴⁸ wherein ferroelectricity disappears below the spin-reorientation temperature (T_SR = 50 K), accompanied by a change in the magnetic structure from Γ₄ to Γ₁. Temperature dependent magnetization data are shown in Fig. 7a. Results of recent investigations on single crystals by Somnath Ghara are, however, at variance with the results on the polycrystalline material.⁴⁸ Switchable electric polarization has been observed along the [100] direction (Fig. 7b) when poling was carried out across the spin-reorientation transition from 70 to 10 K, and measured while warming. Further investigations on single crystalline DyFeO₃ are clearly necessary to fully understand this ferrite.

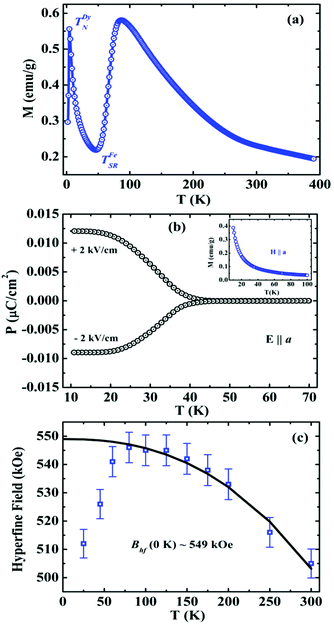Fig. 7 Temperature variation of (a) field-cooled (FC) magnetization in the presence of H = 100 Oe for polycrystalline DyFeO₃, (b) electric polarization (E ‖ a) along with field-cooled (FC) magnetization at 100 Oe (inset) for single crystalline DyFeO₃ (obtained from L. Herve, Vincent Caignaert and Antoine Maignan) and (c) hyperfine field (B_hf) in the range 25–300 K for polycrystalline DyFeO₃ (modified with permission from ref. 48, copyright 2013, by the Institute of Physics).

The importance of the local field induced on Dy ions by the weak ferromagnetic moment of the Fe sublattice in the Γ₄ structure is revealed by the zero-field ⁵⁷Fe Mössbauer spectra of DyFeO₃.⁴⁸ The temperature dependent hyperfine field (B_hf) deviates from the mean field like behaviour as shown in Fig. 7c. The reduction in B_hf at 80 K cannot be accounted as due to a change in the magnetic structure from Γ₄ to Γ₁, thereby indicating the decoupling of the Dy and Fe moments. A similar change in magnetic structure occurs in YFe_0.85Mn_0.15O₃, but without a change in B_hf below the spin-reorientation temperature.⁴⁹ The relatively high value of B_hf in the weak ferromagnetic state (Γ₄) of DyFeO₃ suggests that the iron nucleus experiences a local field that results from the combined effect of Fe and Dy neighbours. When the weak ferromagnetism of the Fe sublattice disappears, the local field at the Dy ions also goes to zero. This study suggests the importance of weak ferromagnetism in the evolution of the polar state in centrosymmetric DyFeO₃. In the light of the recent results obtained from single crystals of DyFeO₃ it is important to reinvestigate whether the magnetic Ln ion and/or weak ferromagnetism play any decisive role in the ferroelectricity of rare-earth orthoferrites.

While the exchange-striction mechanism explains the appearance of ferroelectricity below the Gd(Dy) ordering temperature, it was surprising to note that single crystalline SmFeO₃ (Pbnm) exhibits ferroelectric polarization at the magnetic ordering temperature (670 K) of the Fe spins.⁵⁰ Similar to LnFeO₃ (Ln = Gd and Dy), below the Néel temperatures of Fe³⁺ ions (670 K) the magnetic structure of Fe sublattices of SmFeO₃ is represented by the Γ₄ configuration which shows weak ferromagnetic moment along the c axis. On lowering the temperature, the G-type component shows spin-reorientation from a to c at 480 K (T_SR), with a small canting along the a direction as represented by Γ₂.⁵¹ Pyroelectric current measurements show the evolution of spontaneous polarization only along the b direction at 670 K indicating the origin to be spin-driven. The origin of ferroelectricity in this material has been attributed to inverse DM interaction⁵² involving two non-collinear Fe spin pairs. DFT calculations reveal that spin–orbit coupling is essential to develop this finite polarization and that exchange-striction has no role in the polarization. It has since been pointed out that the neither the Γ₄ nor the Γ₂ magnetic structure is compatible with the observed ferroelectric polarization.³⁷ From group theoretical analysis, it is shown that both the magnetic structures actually correspond to a nonpolar magnetic point symmetry of the Fe sites (m′m′m for Γ₄; mm′m′ for Γ₂).⁴² The magnetic ions (Fe³⁺) located at the inversion centre cannot therefore break the inversion symmetry to generate macroscopic polarization. The origin of the polar state in SmFeO₃ is also explained on the basis of the exchange-striction mechanism between neighbouring Fe spins⁵³ which can lower the symmetry of the material.⁵⁴ In spite of these developments, the role of the rare-earth element in rare-earth orthoferrites with a magnetic Ln ion is not entirely clear.

AlFeO₃ and GaFeO₃

It has been shown recently that AlFeO₃ and GaFeO₃,⁵⁵ crystallizing in the non-centrosymmetric space group Pna2₁, exhibit interesting magnetoelectric properties⁵⁶ due to cationic disorder. Al_1−xGa_xFeO₃ contains four different cation sites namely Fe1, Fe2, Al1 (Ga1) and Al2 (Ga2) where Al1 (Ga1) is present in the tetrahedral environment of oxygen and the other three are present in the octahedral environment of oxygen.⁵⁷ Neutron diffraction data reveal the presence of considerable disorder among the cations.⁵⁸ The tetrahedral site is regular in geometry but the octahedral sites are highly distorted due to the mixed occupancy of the cations having different ionic radii. Because of the unequal distribution of Fe³⁺ ions at the four different sites, it shows ferrimagnetism with a collinear arrangement of spins and a T_N in the 200–250 K range.⁵⁹ These ferrites exhibit spontaneous electric polarization in the vicinity of around 100 K as obtained from pyroelectric current measurements (Fig. 8). The polarization value (±0.3 μC cm⁻², at T = 10 K for E = ±2 kV cm⁻¹) from pyroelectric measurements in the case of GaFeO₃ is comparable to that in other magnetically induced ferroelectric oxides. The temperature variation of lattice parameters shows the occurrence of broad minima in the vicinity of the pyroelectric peak at 100 K.⁵⁸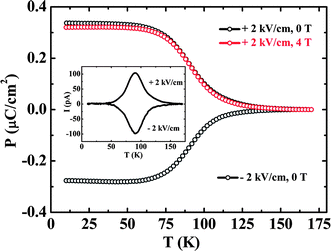

Fig. 8 Temperature variation of ferroelectric polarization for polycrystalline GaFeO₃. Inset shows the variation of pyroelectric current as a function of temperature with a peak maximum (T_P) around 100 K (modified with permission from ref. 60, copyright 2012, by Elsevier).

The origin of the ferroelectric polar state in Al(Ga)FeO₃ is considered to arise from the intrinsic anti-site disorder in the crystal structure.⁶⁰ In the absence of any cationic disorder the ground state magnetic configuration of GaFeO₃ is antiferromagnetic because Fe spins at Fe1 and Fe2 sites are opposite in direction but equal in magnitude resulting in cancellation of their magnetic moments as shown in Fig. 9a. Another important point to note is that the interaction between Fe ions at Fe1 sites (or Fe at Fe2 sites) is ferromagnetic in nature but the interaction of Fe ions between neighbouring Fe1 and Fe2 sites is antiferromagnetic in nature resulting in a considerable amount of magnetic frustration. It is known that in TbMnO₃, nearest neighbour FM and next nearest neighbour AFM interactions frustrate the magnetic structure, resulting in different magnetic structures with the lowering of magnetic symmetry, thereby favouring spontaneous polarization.² In GaFeO₃ one of the symmetry operations of Pna2₁, (x̄, ȳ, z + 1/2) transforms a pair of Fe1 sites to the other of Fe1 sites. As the magnetic moments of Fe at all the Fe1 sites are equal and opposite to those at Fe2 sites, the magnetic structure preserves C_2z rotational symmetry. Thus, it has the planar inversion symmetry in the xy plane and cannot give rise to polarization in the x and y directions. On introduction of anti-site disorder between the Fe and Ga sites, the magnetic moment of the Fe ions at the four Fe1 sites (this holds for Fe2 sites too) no longer remains equal (Fig. 9b) and breaks the spatial inversion symmetry in the ab plane, allowing spontaneous polarization. The switchability of the polarization is explained based on spin–phonon coupling observed in anomalies in their Raman spectra.⁶¹ The unequal size of the magnetic moment which develops on ordering of the magnetic ions distorts the crystal structure locally and the resultant non-centrosymmetric structural distortions due to spin–phonon coupling which is switchable with respect to the direction of the electric field generating polarization in the x and y directions. It is noteworthy that unlike LnFeO₃ with magnetic Ln ions, GaFeO₃ contains only one magnetic ion (Fe³⁺) but intrinsic disorder makes the two octahedral sites magnetically non-equivalent. The origin of ferroelectricity is therefore associated only with the magnetic Fe³⁺ ions (non-centrosymmetric structural distortion coupled with spin–phonon coupling at the onset of ferrimagnetic ordering).

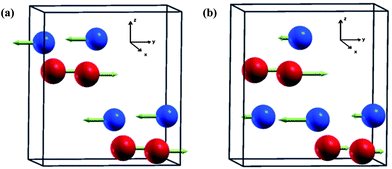Fig. 9 Schematic representation of the magnetic structure of GaFeO₃ (a) without anti-site defect (ordered cationic state) which do not support ferroelectric polarization and (b) with anti-site defect (disordered cationic state) which breaks inversion symmetry in the ab plane allowing ferroelectric polarization. (Red and blue colours indicate the Fe1 and Fe2 sites respectively) (reproduced with permission from ref. 60, copyright 2012, by Elsevier).

Rare-earth orthochromites

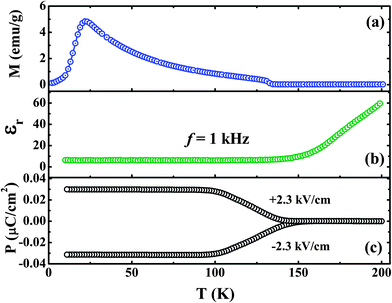
Evolution of ferroelectricity in rare-earth orthochromites, LnCrO₃ which are isostructural with LnFeO₃, has been reported. Ferroelectricity appears below the antiferromagnetic ordering temperature of the Cr ions with the sublattice remaining weakly ferromagnetic.⁶² The magnetic structure of the orthochromites is represented by G-type configurations namely Γ₁, Γ₂ and Γ₄.³⁴ In the case of magnetic rare-earth ions, the high temperature magnetic phase of LnCrO₃ is Γ₄ or Γ₂ depending on the Ln ion, but with lowering temperature it undergoes transformation to another spin configuration namely Γ₂ or Γ₁ due to anisotropic interaction between magnetic Ln and the canted moment of the Cr ion resulting in spin reorientation.⁴² LnCrO₃ with the non-magnetic Ln ground state remains weakly ferromagnetic (Γ₄) and does not show spin-reorientation due to the absence of magnetic interaction between Ln and Cr. On the other hand, the spin-reorientation is induced in YCrO₃ and YFeO₃ by applying a magnetic field along the a direction.^63,64 Polycrystalline SmCrO₃ undergoes antiferromagnetic ordering at 197 K with the evolution of weak ferromagnetism (Γ₄) followed by a change in the Cr spin configuration from Γ₄ to Γ₂ below 40 K, while the Gd, Tb and Tm orthochromites show canted antiferromagnetic ordering at 167, 157 and 127 K respectively but no spin-reorientation phenomena down to 15 K.⁶² Below the magnetic ordering temperature of Gd³⁺ ion, the Cr³⁺ and the Gd³⁺ spins in GdCrO₃ show the occurrence of F_xC_yG_z (Γ₂) and F_xG_z configurations respectively.⁴² ErCrO₃ undergoes magnetic ordering at 133 K with the evolution of weak ferromagnetism which disappears below T_SR (22 K).⁶⁵ The orthochromites are found to exhibit ferroelectric polarization which coincides with the magnetic ordering temperature of the Cr sublattice indicating the origin to be magnetism driven. Polycrystalline SmCrO₃ shows spontaneous polarization with an anomaly at the onset of canted antiferromagnetic ordering and at the spin-reorientation temperature of Cr spins as shown in Fig. 10.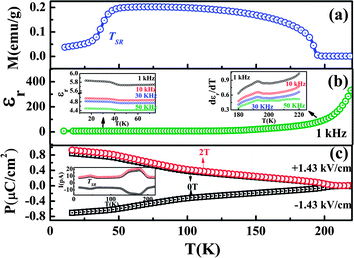

Fig. 10 Variation of (a) field-cooled (FC) magnetization at H = 100 Oe, (b) dielectric constant at f = 1 kHz and (c) electric polarization as a function of temperature in polycrystalline SmCrO₃. Insets in (b) show the frequency dependence of the dielectric constant and the first derivative of dielectric constant at T_SR and T_N; inset of (c) shows the temperature dependence of pyroelectric current (modified with permission from ref. 62, copyright 2012, by the American Physical Society).

In polycrystalline ErCrO₃, the polar state emerges along with the canted antiferromagnetic structure (Fig. 11). Polycrystalline ErCrO₃ has been reported to show the presence of dielectric anomalies at both T_N and T_SR, indicating its magnetoelectric nature. Recent investigations, however, reveal the appearance of electric polarization at T_N which persists down to low temperatures, even below T_SR.⁶⁶ Ferroelectric polarization in GdCrO₃ evolves with the onset of canted antiferromagnetic ordering. Polarization in this chromite is shown to be tuneable by an applied magnetic field in the case of GdCrO₃.

Fig. 11 Variation of (a) field-cooled (FC) magnetization at H = 100 Oe showing a spin reorientation from Γ₄ to Γ₁ at 22 K, (b) dielectric constant at f = 1 kHz and (c) electric polarization as a function of temperature in polycrystalline ErCrO₃ (modified with permission from ref. 62, copyright 2012, by the American Physical Society).

Curious cases of YCrO₃ and YFeO₃

YCrO₃ and YFeO₃ with a non-magnetic rare-earth ion at the A site crystallize in the orthorhombic perovskite structure with the Pbnm space group.⁶⁷ YCrO₃ is a canted antiferromagnet (G-type) with the magnetic ordering temperature of 140 K.⁶⁸ At all temperatures, YCrO₃ possesses the Γ₄ magnetic structure which is not compatible with ferroelectric polarization because of the non-polar magnetic point symmetry. The presence of diamagnetic Y³⁺ ion at the A site of the perovskite structure rules out the magnetic exchange striction between Cr³⁺ and Y³⁺ indicating the absence of a polar state at the magnetic ordering temperature of Cr³⁺ ion even though weak ferromagnetism exists below the Néel temperature. Surprisingly, YCrO₃ is reported to exhibit a ferroelectric state at high temperatures (473 K), accompanied by a leaky hysteresis loop at 300 K.⁶⁸ It also shows a dielectric anomaly at 473 K which is higher than the magnetic ordering temperature of YCrO₃. The frequency-dependent peak maximum of the dielectric phase transition indicates the relaxor nature of the dielectric relaxation. In a centrosymmetric material such as TbMnO₃, only a special kind of magnetic structure (spiral or cycloidal) breaks the inversion symmetry leading to ferroelectric polarization.^19,69 The polar state in centrosymmetric YCrO₃ at a temperature higher than the magnetic ordering temperature can not be associated with magnetic interactions. First principles calculations favour a non-centrosymmetric monoclinic P2₁ space group over the centrosymmetric Pbnm structure.⁶⁸ Analysis of the pair distribution functions (PDF) based on neutron diffraction data confirms the presence of local non-centrosymmetry characterized with a Cr off-centring displacement of the order of 0.01 Å along the z direction which is temperature independent.⁷⁰ Short-range (1–6 Å) neutron diffraction data can be fitted with a non-centrosymmetric P2₁ space group in the low-temperature ferroelectric phase, while in the high-temperature paraelectric region the data are best fitted with a centrosymmetric structure. The PDF data over the range of 1–22 Å can also be fitted with the centrosymmetric structure. Therefore the origin of the polar state has been considered to be local non-centrosymmetry though globally the structure is centrosymmetric. A recent study of polycrystalline films of YCrO₃ grown on single crystalline Rh substrates shows the presence of ferroelectricity with a maximum polarization of 9 μC cm⁻² at 300 K and weak ferromagnetism below 150 K.⁷¹ The nature and origin of ferroelectricity in YCrO₃ are far from being clear. It is noteworthy that LuCrO₃ is also suggested to show ferroelectric polarization at T_N (Fig. 12) similar to ErCrO₃.⁶⁶ Further study of LuCrO₃, however, seems necessary.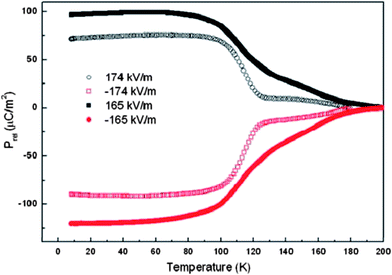

Fig. 12 Temperature variation of the ferroelectric polarization for polycrystalline LuCrO₃ (solid symbols) and ErCrO₃ (open symbols) (reproduced with permission from ref. 66, copyright 2013, by the American Chemical Society).

YFeO₃ with a high magnetic ordering temperature (655 K) appears to exhibit ferroelectricity at 420 K.⁷² The spin configuration of the Fe sublattice of YFeO₃ is Γ₄ which supports the presence of weak ferromagnetism along the crystallographic c direction. Temperature dependent permittivity data as well as dielectric loss data show a peak feature at 420 K at all frequencies suggesting the occurrence of a ferroelectric to paraelectric phase transition. Although the ferroelectric ordering temperature is lower (or it does not coincide with magnetic ordering of the Fe sublattice) than the magnetic ordering temperature, the polar state is suggested to be magnetic in origin following Lee et al.⁵⁰ Cheng et al.⁷³ have shown that a single crystal of YFeO₃ shows magnetocapacitance and relaxor like dielectric behaviour which is attributed to the combined action of Maxwell–Wagner space charge effect and magnetoresistance, indicating the origin to be extrinsic.⁷³ The occurrence and origin of ferroelectricity in YFeO₃ is debatable and needs further investigation.

Solid solutions of YCrO₃ and YFeO₃, YCr_1−xFe_xO₃ with the space group (Pbnm), however, show occurrence of ferroelectricity and magnetoelectric effect at the magnetic ordering temperature of the transition metal ions.⁷⁴ In YCr_1−xFe_xO₃, the Fe³⁺ and Cr³⁺ ions are randomly distributed at the 4b crystallographic site leading to Fe–Fe, Cr–Cr and Cr–Fe superexchange interactions. YCr_0.5Fe_0.5O₃ undergoes antiferromagnetic ordering at 260 K where Fe and Cr moments are coupled antiferromagnetically followed by temperature induced magnetization reversal with a compensation temperature of 248 K.⁷⁵ Unlike YFeO₃ and YCrO₃, the spin configuration of YCr_0.5Fe_0.5O₃ is represented by a magnetic structure which is in between Γ₂ and Γ₄ where spin reorientation is incomplete, magnetic moments are pointing in between a and c axes below the Néel temperature. With lowering temperature, magnetic moments start moving from the a axis, but do not reach the c axis down to 2 K resulting in an incomplete spin-reorientation phenomenon. A complete spin reorientation to the c axis would give rise to a Γ₂ spin configuration. Pyroelectric current measurements show the occurrence of spontaneous polarization at the magnetic ordering temperature (T_N = 260 K) as shown in Fig. 13. YCr_0.5Fe_0.5O₃ shows the presence of a dielectric anomaly at T_N indicating the magnetodielectric nature of this material. The magnetoelectric effect of this material was confirmed by studying the effect of magnetic fields on the pyroelectric current. Tunable ferroelectric transition temperatures in YCr_1−xFe_xO₃ with varying proportions of Fe³⁺ and Cr³⁺ ions at the B site of the perovskite are demonstrated in Fig. 13. The effect of disordered cations of non-equivalent spins in inducing ferroelectricity is understood based on a spin-current model found in canted antiferromagnetic oxide.^52,69 According to this model, when there is only one transition metal ion at the 4b site of the Pbnm structure, the local polarization induced by inverse DM interaction would be cancelled out due to the alternating nature of the spin pairs (Fig. 14a). Upon introducing another transition metal ion of non-equivalent spin at the 4b site, two plausible situations can arise: (a) an ordered distribution of cations of non-equivalent spins giving rise to local polarization following inverse DM interaction which gets cancelled due to a change in the direction of the induced local polarization (Fig. 14b);⁶⁹ (b) A disordered arrangement of cations of non-equivalent spins generating a net polarization because the oxygen displacement need not be equivalent (Fig. 14c). Significant polarization is observed for x ∼ 0.5, because it leads to less cluster formation of Fe–Fe and Cr–Cr resulting in cancellation of the ferroelectric polarization due to alternate spin pairs. Though this model explains the origin of ferroelectric polarization, microscopic insights would be helpful to understand the phenomena properly. Replacing Y³⁺ with another non-magnetic rare earth also generates ferroelectric polarization at the magnetic ordering temperature of Cr–Fe interactions, indicating that the origin of polarization is associated only with the disordered transition metal ions of non-equivalent spins at the 4b sites of the Pbnm structure. Replacing the transition metal ions at the B site (e.g. YCr_1−xMn_xO₃) retains the weak ferromagnetism and ferroelectricity at the magnetic ordering temperature. This behaviour enables tuning of the ferroelectric transition temperature by varying the A and B site cations. It is, however, curious that YFe_1−xMn_xO₃ exhibits magnetodielectric effects at both spin-reorientation and Néel temperatures (T_SR < T_N) and ferroelectricity at even lower temperatures.⁷⁶

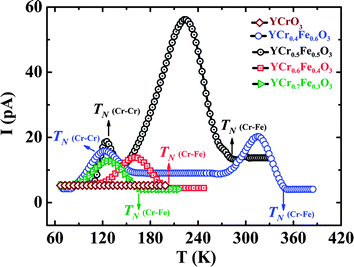Fig. 13 Variation of onset of pyroelectric current with composition of YCr_1−xFe_xO₃ (x = 0.3, 0.4, 0.5, 0.6) demonstrating the occurrence of polarization at T_N (modified with permission from ref. 74, copyright 2012, by the American Chemical Society).

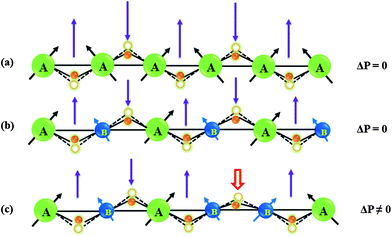Fig. 14 Schematic representation of the origin of ferroelectric polarization in a canted AFM system for (a) an invariant B-site cation, (b) an ordered and (c) a disordered arrangement of two cations of non-equivalent spins at the B-site (modified with permission from ref. 74, copyright 2012, by the American Chemical Society).

Problems and challenges

Traditionally ferroelectricity in a material is established by recording the P–E hysteresis loop using the Sawyer–Tower circuit. This method has been seriously questioned since most materials seem to show hysteresis loops even if they are leaky.⁷⁷ Clearly, one should employ other methods to establish intrinsic ferroelectricity. Most of the transition metal oxides, for example ferrites, show leaky hysteresis loops. Pyroelectric current measurements after electric poling⁷⁸ have been employed to characterize the polar state, but this method is also not free of artifacts due to space-charge effects induced by poling bias, which can be one of the causes of reversal behaviour of the depolarization current in non-ferroelectric materials.⁷⁹ Thus measurement of ferroelectric polarization in a material having residual conductivity remains problematic. The PUND (Positive-Up-Negative-Down) or DWM (Double-Wave Method)⁸⁰ method has been used by several workers recently to extract information of the intrinsic ferroelectric polarization from the non-hysteretic and leakage part.^50,81,82 Practitioners continue to face serious difficulty in establishing the intrinsic ferroelectricity in a material.

Research on multiferroics is often carried out on polycrystalline materials where leakage problems are severe. It would be most useful to carry out measurements on single crystals and good epitaxial thin films. In terms of materials, it will be of great value if one can discover a material which is ferromagnetic and magnetoelectric at room temperature. Tuning the spin and charge ordering as well as orbital degrees of freedom at the interface of thin film heterostructures would be of great interest.^29,30 Controlling interface magnetism using electric fields would be interesting as shown by a recent work on thin film heterostructure of BiFeO₃–LSMO.³¹ It seems that electric field control of magnetism can provide better insight on the magnetoelectric coupling. Fully understanding the role of interfaces in films deposited on substrates requires further investigations.

Concluding remarks

In the preceding sections, we have shown how ferrites and chromites exhibit interesting multiferroic and magnetoelectric properties arising from magnetically induced ferroelectricity. Thus, in thin films of BiFeO₃ magnetoelectric coupling and the exchange bias can be tuned by epitaxial strain.³² It must be noted that in TbMnO₃ ferroelectricity arises from the non-collinear cycloidal spin structure which breaks the spatial inversion symmetry to induce polarization.¹⁹ In rare-earth orthoferrites and orthochromites with a magnetic rare-earth ion, exchange striction between the magnetic rare-earth and Fe³⁺ (Cr³⁺) ions is suggested to cause electric polarization.^40,48 Interestingly, in the simple ferrimagnetic ferrites, Al(Ga)FeO₃, cation disorder driven non-equivalence of the octahedral Fe³⁺ ions alone appears to be sufficient to give rise to ferroelectricity.⁶⁰ The multiferroic nature of ferrites such as LuFe₂O₄ has been reported⁸³ but some doubt has been expressed about this observation.⁸⁴ There is some interest in examining properties of Fe₃O₄ in view of the recent findings related to its structure.⁸⁵ Ferroelectric features reported in orthorhombic YCrO₃ and YFeO₃ are not fully understood. In this context, ferroelectricity in epitaxially constrained hexagonal LuFeO₃ becomes noteworthy.⁸⁶ Another noteworthy observation which needs proper understanding is that of ferroelectricity at the magnetic ordering temperature of Ln(Fe,Cr)O₃ containing two magnetic transition metal ions at the B-site, allowing the tuning of the ordering temperature by varying the Ln ion at the A-site or the composition at the B-site.⁷⁴ Clearly there is a need for further investigations to fully understand the multiferroic and magnetoelectric properties of many of the ferrites and chromites. Problems and challenges in the area of multiferroic and magnetoelectric oxides were mentioned in the previous section of this article but what is worthy of note is that the subject itself is of great interest.

Acknowledgements

We would like to thank L. Herve, Vincent Caignaert and Antoine Maignan for helping and providing the facilities to grow the single crystals of DyFeO₃.

References

1. N. A. Hill, J. Phys. Chem. B, 2000, 104, 6694.
2. S.-W. Cheong and M. Mostovoy, Nat. Mater., 2007, 6, 13.
3. C. N. R. Rao and C. R. Serrao, J. Mater. Chem., 2007, 17, 4931.
4. N. A. Spaldin, S.-W. Cheong and R. Ramesh, Phys. Today, 2010, 63, 38.
5. R. Seshadri and N. A. Hill, Chem. Mater., 2001, 13, 2892.
6. J. M. Rondinelli and C. J. Fennie, Adv. Mater., 2012, 24, 1961.
7. A. T. Mulder, N. A. Benedek, J. M. Rondinelli and C. J. Fennie, Adv. Funct. Mater., 2013 DOI:10.1002/adfm.201300210.
8. T. Fukushima, A. Stroppa, S. Picozzi and J. M. Perez-Mato, Phys. Chem. Chem. Phys., 2011, 13, 12186.
9. N. A. Benedek and C. J. Fennie, Phys. Rev. Lett., 2011, 106, 107204.
10. P. Ghosez and J.-M. Triscone, Nat. Mater., 2011, 10, 269.
11. G. Gou and J. M. Rondinelli, 2013, arXiv:1304.4911.
12. A. Stroppa, P. Jain, P. Barone, M. Marsman, J. M. Perez-Mato, A. K. Cheetham, H. W. Kroto and S. Picozzi, Angew. Chem., Int. Ed., 2011, 50, 5847.
13. A. Stroppa, D. Di Sante, S. Horiuchi, Y. Tokura, D. Vanderbilt and S. Picozzi, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 014101.
14. G. Giovannetti, S. Kumar, J.-P. Pouget and M. Capone, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 205146.
15. D.-W. Fu, H.-L. Cai, Y. Liu, Q. Ye, W. Zhang, Y. Zhang, X.-Y. Chen, G. Giovannetti, M. Capone, J. Li and R.-G. Xiong, Science, 2013, 339, 425.
16. X. F. Hao, A. Stroppa, S. Picozzi, A. Filippetti and C. Franchini, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 014116.
17. C. N. R. Rao, A. Sundaresan and R. Saha, J. Phys. Chem. Lett., 2012, 3, 2237.
18. W. Eerenstein, N. D. Mathur and J. F. Scott, Nature, 2006, 442, 759.
19. T. Kimura, T. Goto, H. Shintani, K. Ishizaka, T. Arima and Y. Tokura, Nature, 2003, 426, 55.
20. Y. N. Venevtsev, G. Zhdanov and S. Solov'ev, Sov. Phys. Crystallogr., 1960, 4, 538.
21. G. Smolenskii, V. Isupov, A. Agranovskaya and N. Krainik, Sov. Phys. Solid State, 1961, 2, 2651.
22. I. Sosnowskat, T. Peterlin-Neumaier and E. Steichele, J. Phys. C: Solid State Phys., 1982, 15, 4835.
23. I. Sosnowska, M. Loewenhaupt, W. I. F. David and R. M. Ibberson, Phys. B, 1992, 180–181, 117.
24. B. Ruette, S. Zvyagin, A. P. Pyatakov, A. Bush, J. F. Li, V. I. Belotelov, A. K. Zvezdin and D. Viehland, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 064114.
25. C. Ederer and N. A. Spaldin, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 060401.
26. J. Wang, J. B. Neaton, H. Zheng, V. Nagarajan, S. B. Ogale, B. Liu, D. Viehland, V. Vaithyanathan, D. G. Schlom, U. V. Waghmare, N. A. Spaldin, K. M. Rabe, M. Wuttig and R. Ramesh, Science, 2003, 299, 1719.
27. D. Lebeugle, D. Colson, A. Forget and M. Viret, Appl. Phys. Lett., 2007, 91, 022907.
28. J. F. Scott, J. Mater. Chem., 2012, 22, 4567.
29. P. Yu, J. S. Lee, S. Okamoto, M. D. Rossell, M. Huijben, C. H. Yang, Q. He, J. X. Zhang, S. Y. Yang, M. J. Lee, Q. M. Ramasse, R. Erni, Y. H. Chu, D. A. Arena, C. C. Kao, L. W. Martin and R. Ramesh, Phys. Rev. Lett., 2010, 105, 027201.
30. S. M. Wu, S. A. Cybart, P. Yu, M. D. Rossell, J. X. Zhang, R. Ramesh and R. C. Dynes, Nat. Mater., 2010, 9, 756.
31. S. M. Wu, S. A. Cybart, D. Yi, J. M. Parker, R. Ramesh and R. C. Dynes, Phys. Rev. Lett., 2013, 110, 067202.
32. D. Sando, A. Agbelele, D. Rahmedov, J. Liu, P. Rovillain, C. Toulouse, I. C. Infante, A. P. Pyatakov, S. Fusil, E. Jacquet, C. Carrétéro, C. Deranlot, S. Lisenkov, D. Wang, J. M. Le Breton, M. Cazayous, A. Sacuto, J. Juraszek, A. K. Zvezdin, L. Bellaiche, B. Dkhil, A. Barthélémy and M. Bibes, Nat. Mater., 2013, 12, 641.
33. A. M. Mulders, Nat. Phys., 2013, 9, 398.
34. E. F. Bertaut, in Magnetism III, ed. G. T. Rado and H. Suhl, Academic, New York, 1968, p. 149.
35. T. Yamaguchi, J. Phys. Chem. Solids, 1974, 35, 479.
36. R. L. White, J. Appl. Phys., 1969, 40, 1061.
37. R. D. Johnson, N. Terada and P. G. Radaelli, Phys. Rev. Lett., 2012, 108, 219701.
38. A. K. Zvezdin and A. A. Mukhin, JETP Lett., 2009, 88, 505.
39. Y. Tokunaga, N. Furukawa, H. Sakai, Y. Taguchi, T.-h. Arima and Y. Tokura, Nat. Mater., 2009, 8, 558.
40. Y. Tokunaga, S. Iguchi, T. Arima and Y. Tokura, Phys. Rev. Lett., 2008, 101, 097205.
41. S. Geller, J. Chem. Phys., 1956, 24, 1236.
42. T. Yamaguchi and K. Tsushima, Phys. Rev. B: Solid State, 1973, 8, 5187.
43. I. Dzyaloshinsky, J. Phys. Chem. Solids, 1958, 4, 241.
44. T. Moriya, Phys. Rev., 1960, 120, 91.
45. G. Gorodetsky, B. Sharon and S. Shtrikman, J. Appl. Phys., 1968, 39, 1371.
46. L. A. Prelorendjo, C. E. Johnson, M. F. Thomas and B. M. Wanklyn, J. Phys. C: Solid State Phys., 1980, 13, 2567.
47. A. Stroppa, M. Marsman, G. Kresse and S. Picozzi, New J. Phys., 2010, 12, 093026.
48. B. Rajeswaran, D. Sanyal, M. Chakrabarti, Y. Sundarayya, A. Sundaresan and C. N. R. Rao, Europhys. Lett., 2013, 101, 17001.
49. Y. Sundarayya, P. Mandal, A. Sundaresan and C. N. R. Rao, J. Phys.: Condens. Matter, 2011, 23, 436001.
50. J.-H. Lee, Y. K. Jeong, J. H. Park, M.-A. Oak, H. M. Jang, J. Y. Son and J. F. Scott, Phys. Rev. Lett., 2011, 107, 117201.
51. G. Gorodetsky and L. M. Levinson, Solid State Commun., 1969, 7, 67.
52. H. Katsura, N. Nagaosa and A. V. Balatsky, Phys. Rev. Lett., 2005, 95, 057205.
53. J.-H. Lee, Y. K. Jeong, J. H. Park, M.-A. Oak, H. M. Jang, J. Y. Son and J. F. Scott, Phys. Rev. Lett., 2012, 108, 219702.
54. S. Goshen, D. Mukamel, H. Shaked and S. Shtrikman, Phys. Rev. B: Solid State, 1970, 2, 4679.
55. J. P. Remeika, J. Appl. Phys., 1960, 31, S263.
56. T. Arima, D. Higashiyama, Y. Kaneko, J. P. He, T. Goto, S. Miyasaka, T. Kimura, K. Oikawa, T. Kamiyama, R. Kumai and Y. Tokura, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 064426.
57. A. Shireen, R. Saha, P. Mandal, A. Sundaresan and C. N. R. Rao, J. Mater. Chem., 2011, 21, 57.
58. R. Saha, A. Shireen, A. K. Bera, S. N. Shirodkar, Y. Sundarayya, N. Kalarikkal, S. M. Yusuf, U. V. Waghmare, A. Sundaresan and C. N. R. Rao, J. Solid State Chem., 2011, 184, 494.
59. R. Saha, A. Shireen, S. N. Shirodkar, U. V. Waghmare, A. Sundaresan and C. N. R. Rao, J. Solid State Chem., 2011, 184, 2353.
60. R. Saha, A. Shireen, S. N. Shirodkar, U. V. Waghmare, A. Sundaresan and C. N. R. Rao, Solid State Commun., 2012, 152, 1964.
61. P. Kumar, A. Bera, D. V. S. Muthu, S. N. Shirodkar, R. Saha, A. Shireen, A. Sundaresan, U. V. Waghmare, A. K. Sood and C. N. R. Rao, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 134449.
62. B. Rajeswaran, D. I. Khomskii, A. K. Zvezdin, C. N. R. Rao and A. Sundaresan, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 214409.
63. I. S. Jacobs, H. F. Burne and L. M. Levinson, J. Appl. Phys., 1971, 42, 1631.
64. G. W. Durbin, C. E. Johnson and M. F. Thomas, J. Phys. C: Solid State Phys., 1975, 8, 3051.
65. Y. Su, J. Zhang, B. Li, B. Kang, Q. Yu, C. Jing and S. Cao, Ceram. Int., 2012, 38, S421.
66. K. R. S. P. Meher, C. Martin, V. Caignaert, F. Damay and A. Maignan, Chem. Mater., 2013 DOI:10.1021/cm4020546.
67. S. Geller and E. A. Wood, Acta Crystallogr., 1956, 9, 563.
68. C. R. Serrao, A. K. Kundu, S. B. Krupanidhi, U. V. Waghmare and C. N. R. Rao, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 220101.
69. T. Kimura, Annu. Rev. Mater. Res., 2007, 37, 387.
70. K. Ramesha, A. Llobet, Th. Proffen, C. R. Serrao and C. N. R. Rao, J. Phys.: Condens. Matter, 2007, 19, 102202.
71. J. D. Seo and J. Y. Son, J. Cryst. Growth, 2013, 375, 53.
72. M. Shang, C. Zhang, T. Zhang, L. Yuan, L. Ge, H. Yuan and S. Feng, Appl. Phys. Lett., 2013, 102, 062903.
73. Z. X. Cheng, H. Shen, J. Y. Xu, P. Liu, S. J. Zhang, J. L. Wang, X. L. Wang and S. X. Dou, J. Appl. Phys., 2012, 111, 034103.
74. B. Rajeswaran, P. Mandal, R. Saha, E. Suard, A. Sundaresan and C. N. R. Rao, Chem. Mater., 2012, 24, 3591.
75. N. Dasari, P. Mandal, A. Sundaresan and N. S. Vidhyadhiraja, Europhys. Lett., 2012, 99, 17008.
76. P. Mandal, V. S. Bhadram, Y. Sundarayya, C. Narayana, A. Sundaresan and C. N. R. Rao, Phys. Rev. Lett., 2011, 107, 137202.
77. J. F. Scott, J. Phys.: Condens. Matter, 2008, 20, 021001.
78. I. Lubomirsky and O. Stafsudd, Rev. Sci. Instrum., 2012, 83, 051101.
79. M. Maglione and M. A. Subramanian, Appl. Phys. Lett., 2008, 93, 032902.
80. M. Fukunaga and Y. Noda, Jpn. J. Appl. Phys., 2008, 77, 064706.
81. S. Horiuchi, Y. Tokunaga, G. Giovannetti, S. Picozzi, H. Itoh, R. Shimano, R. Kumai and Y. Tokura, Nature, 2010, 463, 789.
82. S. M. Feng, Y. S. Chai, J. L. Zhu, N. Manivannan, Y. S. Oh, L. J. Wang, Y. S. Yang, C. Q. Jin and K. H. Kim, New J. Phys., 2010, 12, 073006.
83. N. Ikeda, H. Ohsumi, K. Ohwada, K. Ishii, T. Inami, K. Kakurai, Y. Murakami, K. Yoshii, S. Mori, Y. Horibe and H. Kito, Nature, 2005, 436, 1136.
84. M. Angst, Phys. Status Solidi RRL, 2013, 7, 383.
85. M. S. Senn, J. P. Wright and J. P. Attfield, Nature, 2011, 481, 173.
86. Y. K. Jeong, J.-H. Lee, S.-J. Ahn and H. M. Jang, Chem. Mater., 2012, 24, 2426.

---