Phase transformations in nanograin materials under high pressure and plastic shear: nanoscale mechanisms

Abstract

There are two main challenges in the discovery of new high pressure phases (HPPs) and transforming this discovery into technologies: finding conditions to synthesize new HPPs and finding ways to reduce the phase transformation (PT) pressure to an economically reasonable level. Based on the results of pressure–shear experiments in the rotational diamond anvil cell (RDAC), superposition of plastic shear on high pressure is a promising way to resolve these problems. However, physical mechanisms behind these phenomena are not yet understood. Here, we elucidate generic mechanisms of coupled nucleation and evolution of dislocation and HPP structures in the nanograin material under pressure and shear utilizing the developed advanced phase field approach (PFA). Dislocations are generated at the grain boundaries and are densely piled up near them, creating a strong concentrator of the stress tensor. Averaged shear stress is essentially larger in the nanograin material due to grain boundary strengthening. This leads to the increase in the local thermodynamic driving force for PT, which allows one to significantly reduce the applied pressure. For all cases, the applied pressure is 3–20 times lower than the PT pressure and 2–12.5 times smaller than the phase equilibrium pressure. Interaction between nuclei leads sometimes to their coalescence and growth of the HPP away from stress concentrators. Plasticity plays a dual role: in addition to creating stress concentrators, it may relax stresses at other concentrators, thus competing with PT. Some ways to optimize the loading parameters have been found that lead to methods for controlling PT. Since such a local stress tensor with high shear stress component cannot be created without plastic deformations, this may lead to new transformation paths and phases, which are hidden during pressure induced PTs.

---

There are two main challenges in the discovery of new HPPs and transforming this discovery into technologies: finding conditions to synthesize new HPPs and finding ways to reduce the PT pressure to an economically reasonable level. Various new HPPs with unique properties have recently been discovered experimentally: new superhard phases of carbon,^1,2 BC₅,³ B-BN,⁴ and BC₂N,^5,6 supposedly highly energetic phases of polymeric nitrogen,⁷ CO₂,⁸ and ionic boron.⁹ Many others have been predicted theoretically^10–14 but have not yet been synthesized, because of kinetic barriers or because the proper transformation path could not be realized under quasi-hydrostatic pressure and known phases appeared instead. PT pressure for most of these phases is too high for technological realization. Based on the results of pressure–shear experiments in rotational Bridgman anvils,¹⁵ rotational diamond anvil cell (RDAC),^16–24 high pressure torsion,^25–30 and ball milling^31–33 superposition of plastic shear on high pressure can in principle resolve these problems. Indeed, we recently obtained a new high-density amorphous phase of SiC under a pressure of 30 GPa and large shear,¹⁶ which was not obtained under hydrostatic pressure up to 130 GPa. Phase IV of fullerene C₆₀ (which is believed to be harder than diamond) was first revealed under pressure and shear in the RDAC^17,18 and then reproduced under high pressure and temperature. Highly energetic polymeric phases of nitrogen and sodium azide^19,20 and superhard phase of single wall carbon nanotube²¹ were obtained under pressure and shear in the RDAC. Also, plastic shear reduces the PT pressure by a factor of 2 to 10 for some PTs^{18,22–25,29} – e.g., in Si and Ge,²³ rhombohedral BN to superhard cubic BN,¹⁸ Zr and Zr–Ni alloys,^25,29 and disordered nanocrystalline hexagonal BN to wurtzitic BN.²⁴

Despite the fundamental and applied importance and various intriguing phenomena, our understanding of the mechanisms and theoretical description is in its infancy. Macroscopic continuum thermodynamics fails to describe the significant reduction in PT pressure. Indeed, let the PT occur when the mechanical part of the thermodynamic driving force W (transformation work) reaches a critical value k – i.e., W = −pε_0t + τγ_t = k, where p and τ are the pressure and shear stress, ε_0t < 0 and γ_t are the volumetric and shear transformation strains. Let γ_t = −2ε_0t = 0.2, PT pressure under hydrostatic conditions be p = 15 GPa, with shear strength being limited by the macroscopic yield strength in shear-say τ = 1 GPa. Then, under hydrostatic conditions, W = k = 15 × 0.1 = 1.5; with shear, X_m = (p + 2) × 0.1 = 1.5 – i.e., p = 13; and the reduction in PT pressure is only 13%. Even the fundamental difference between the plastic strain-induced PTs under high pressure and pressure-induced PTs had not been recognized before the appearance of our paper.²² Pressure-induced PTs initiate at pre-existing defects, while strain-induced PTs occur by nucleation at new defects generated during plastic flow, which produce stronger stress concentration. Strain-induced PTs require completely different thermodynamic and kinetic description as well as experimental characterization. A simple three-scale theory for strain-induced PTs in the RDAC was developed in ref. 22, followed by more detailed theoretical and computational treatment for the micro- and macroscales.^34–36 However, the main physical mechanisms of strain-induced PTs, which explain the above phenomena, are still lacking. The only analytical model²² uses numerous strong assumptions and is not applicable, especially for nanograin materials. Barrierless nucleation at defects, even in large-grain materials, is always a nanoscale phenomenon.²² Large plastic deformations under pressure lead to nanograin materials.^25–30 That is why our focus is on nanoscale mechanisms in nanograin materials. Most publications report the significant dislocation activity in nanograin materials.^25–30 In others^37,38 reversible dislocation activity is observed, in which dislocation density after large deformation and unloading practically does not change. In many cases^26,27,37,38 the role of grain boundaries is underscored as source and sink of defects and as an additional plasticity mechanism due to grain boundary sliding. In this paper, we treat dislocational plasticity, in which dislocations nucleate at grain boundaries due to stress concentration near them. While we do not resolve the structure and width of grain boundaries, reversible dislocation activity is observed, unless dislocations are pinned. Also, grain rotations are included in some examples in the simplest way.

Here, we study a coupled nucleation and evolution of dislocations and HPPs in the nanograin material under simple shear and pressure using the developed coupled PFA to martensitic PT and dislocation evolution³⁹ and the corresponding finite element method (FEM) of simulations. This theory combines the most advanced PFA for dislocations⁴⁰ and PT⁴¹ with additional coupling terms.³⁹ Since drastic reduction in PT pressure under plastic shear is observed for various classes of materials with different atomic bonding, crystal lattices and slip systems, and this is the first PFA study on the subject, we will develop the simplest generic model to reveal general features of a broad class of materials.

Main results are summarized at the end of the paper.

Results and discussion

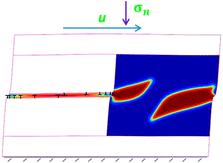
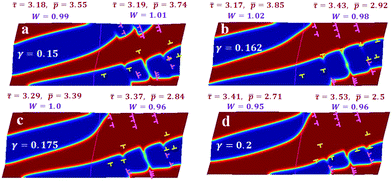
The total system of equations and material parameters is presented in ref. 39 and 42. Typical width of the phase interface is 1 nm; characteristic time for PT and dislocation evolution in the PFA is in a picosecond range; typical shear stresses and pressures of interest are in a GPa range. That is why all size, stress, and time parameters are normalized by 1 nm, 1 GPa, and 1 ps, respectively. Some of the parameters are: ε_t0 = −0.1 and γ_t = 0.2; phase equilibrium pressure p_e = 10, and critical pressure for the instability of the low pressure phase (LPP) is p_cl = 20. The FEM approach and the code COMSOL with the embedded remeshing procedure have been utilized. All results are shown in the deformed configuration. A rectangular sample is considered with the size of 50 × 30, which includes the following regions (Fig. 1): (a) two grains of the size of 25 × 20 each, in which dislocations and/or PT are studied; (b) two regions of the size of 50 × 5 located at the top and bottom of the sample, where only the mechanical problem is solved; these regions model elastic accommodation of the grains that surround two grains with PT and plasticity. For the mechanical problem, periodic conditions for displacements are prescribed for lateral sides; the bottom horizontal side is fixed; the upper side is subjected to normal homogenous stress σ_n in the deformed state and homogeneous horizontal displacement u (which will be given in terms of prescribed macroscopic shear γ = u/h, with the height of grains h = 20). To obtain first generic results, 2D plane strain problems and straight edge dislocations are treated. This is equivalent to the infinite size of a sample or clamping a sample in the out-of-plane direction; no activities in the out-of-plane direction occur and size in the out-of-plane direction is irrelevant. Note that for the simulations corresponding to nucleation on the single dislocation pile up, our numerical solution is in good correspondence with the analytical results²² in terms of length and aspect ratio of nucleus vs. the number of dislocations in the pile up, which confirms validity of the model for the simplest scenario. It was found that under hydrostatic loading, the lowest pressure at which the nucleus appears is p_h = 15.75;⁴² thus, k = −p_hε_t0 = 1.575.

Fig. 1 Schematics of a sample under compression and shear with a stationary nanostructure at p̄ = 1.2 and γ = 0.15. Dislocations in the left grain cause transformation from the low (blue) to the high (red) pressure phases.

1. PT in the left grain and plasticity in the right grain were not included, and the single horizontal slip system was active in the left grain. A sample under vertical stress σ_n = 3.05 was considered, which results in an initial pressure averaged over the sample (or each grain) of 2.0. Note that because of chosen normal transformation strains ε_t^x = ε_t^y,⁴² averaged pressure p = −0.5(σ_x + σ_y) rather than σ_n produced transformation work and should be used for the characterization of PT. Dislocations of opposite signs nucleated from both grain boundaries one after another and moved toward each other. They formed steps at both boundaries corresponding to 3|b| (b is the Burgers vector) and next dislocations densely pile-up at the boundaries (Fig. 1). For γ = 0.2, 7 positive and negative dislocations represent a stationary solution, resulting in average shear stress [small tau, Greek, macron] = 5.86 and [small tau, Greek, macron] = 8.77 in the left and right grains, respectively, and [small tau, Greek, macron] = 7.31 over the sample. These pile-ups create strong concentration of the stress tensor near their tips. Two HPP nuclei appear barrierlessly at the steps and grow, initially like two independent plates, and later they start to interact through the stress field (Fig. 2). For γ = 0.15 the stationary nanostructure still represents two separated HPP regions (Fig. 1), with a concentration c = 0.19 with respect to the grain area in the undeformed state. Increasing γ to 0.2 leads to a morphological transition, the coalescence of two HPP regions, and a significant c increment to c = 0.51 (Fig. 2). Note that the pressure averaged over the grain p̄ is reduced during PT to 1.69 in the left grain, 0.06 in the right grain (where PT occurs), and 0.81 over the both grains, due to volume reduction during PT; [small tau, Greek, macron] is reduced to 4.75 and 5 in the left and right grains, respectively, and 4.9 over the both grains. Since in the experiment PT pressure is measured after PT at the place where PT occurred, we will report p̄ and [small tau, Greek, macron] after PT in the transformed grain as well. Based on averaged stresses, transformation work was W = 1.0 in the right grain – i.e., it is lower than k by a factor of 1.575. Thus, for the nanograin sample, it is possible to reduce the PT pressure by more than an order of magnitude and below GPa, and to cause significant PT in a grain at relatively small applied shear strain. The small distance between stress concentrators leads to a coalescence of nuclei with significant transformation progress. However, [small tau, Greek, macron] is significantly larger than p̄, which makes such a process impractical for technical applications from the point of view of anvil strength;⁴³ instead, it should be p̄ ≥ [small tau, Greek, macron].

Fig. 2 Nucleation and growth of the high pressure phase until the stationary nanostructure at γ = 0.2 and with p̄ varying from 2 (before PT) to a stationary value of 0.8 (averaged over both grains) and with p̄ = 0.06 in the transformed grain.

2. As a next step, we included dislocation activity along two slip systems with a 60° angle between them in the right grain, which competes with the PT. For p̄ = 1.2, γ = 0.2, [small tau, Greek, macron] = 4, and L_ξ = 0.1L_η (L_ξ and L_η are the kinetic coefficients in Ginzburg–Landau equations for dislocations and PT⁴²), PT occurs faster than dislocation evolution in the right grain, and the initial stage of PT is almost the same as without plasticity, including coalescence. However, after one dislocation appeared in the upper slip system and 3 dislocations in the lower one, reverse PT starts. Dislocations relax shear stress and HPP becomes narrower and splits into two regions with the stationary concentration c = 0.166 (Fig. 3). While the evolution of HPP depends on the ratio L_ξ/L_η, the stationary phase and the dislocation structure are practically the same for L_ξ/L_η in the range 0.1–80.

Fig. 3 Simultaneous nucleation and evolution of HPPs and dislocations until the stationary nanostructure at γ = 0.2, and p̄ varied from 2 (before PT) to a stationary value of 1.2.

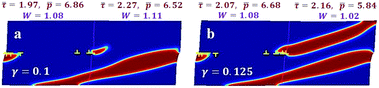
3. For a problem similar to that shown in Fig. 1, the pressure was increased, and shear was reduced (Fig. 4). For γ = 0.1, three dislocations of each sign appeared in the left grain, which generated the HPP band passing through both grains. Averaged shear stress was reduced to 1.97 and 2.27 but the pressure was increased to 6.86 and 6.52, which gave transformation work of 1.08 and 1.11, in the left and right grains, respectively. When γ was increased to 0.125, the forth dislocations appeared in the left grain and the second HPP band appeared in the right grain, leading to reduced p̄ = 5.84, [small tau, Greek, macron] = 2.16, W = 1.02, and c = 0.436.

Fig. 4 Stationary distribution of HPPs and dislocations under compression and shear for γ = 0.1 (a) and γ = 0.125 (b). The line above the plot shows parameters averaged over each grain. Dislocations are allowed in the left grain only and are pinned before PT starts.

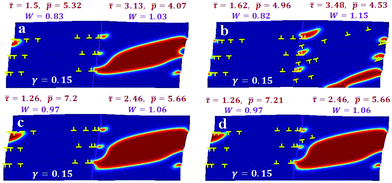
4. Next, we allowed three horizontal slip systems in the left grain and (in some cases) three slip systems inclined under 15° in the right grain (Fig. 5). In all cases, the left grain contains a very small amount of HPP, because slip systems are parallel to the applied shear. For γ = 0.15 with no slip in the right grain, the concentration of HPP reached 0.347 at p̄ = 4.07, [small tau, Greek, macron] = 3.13, and W = 1.03 (Fig. 5a). When a slip is allowed in the right grain, the concentration of HPP reduced to 0.126 in it at increased p̄ = 4.53, [small tau, Greek, macron] = 3.48, and W = 1.15 (Fig. 5b). However, at slightly higher p̄ = 5.66, but lower [small tau, Greek, macron] = 2.46, and W = 1.06, allowing plasticity in the right grain produced just two dislocations of opposite signs; it changed c from 0.126 to 0.439, and did not change p̄, but it created lower [small tau, Greek, macron], and W (Fig. 5c and d). Thus, optimal pressure and shear promote PT instead of plasticity.

Fig. 5 Stationary distribution of HPPs and dislocations under compression and shear for γ = 0.15. (a) Three dislocation systems are allowed in the left grain only and are pinned before PT starts. (b) In addition, in the right grain three dislocation systems inclined under 15° are included, which leads to the suppression of HPPs. (c and d) The same as in (a) and (b) but at higher pressure and lower shear stress. Even when plasticity in the right grain is allowed, just two dislocations appear, and PT to HPP is not suppressed.

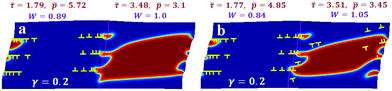
5. One more example of optimized parameters is shown in Fig. 6. For γ = 0.2 and no slip in the right grain, the concentration of HPP reached 0.55 at p̄ = 3.1, [small tau, Greek, macron] = 3.48, and W = 1.0 (Fig. 5a). When a significant slip occurred in the right grain as well, PT to HPP was only slightly suppressed (c = 0.45), and p̄ and [small tau, Greek, macron] grew slightly.

Fig. 6 Stationary distribution of HPPs and dislocations for γ = 0.2. (a) Three dislocation systems are allowed in the left grain only and are pinned before PT starts. (b) In addition, in the right grain three dislocation systems inclined under 15° are included, but this does not lead to severe suppression of HPPs as in Fig. 5b.

6. To study the effect of switching between slip systems – e.g., due to rotation of the grains (which is not included in the model) – the problem described in Fig. 7 was solved. As it is seen in Fig. 7, stresses in the left grain are relaxed due to the PT and the growth of HPPs, and new dislocations in the right grain, in combination with pre-existing dislocations, produce a large HPP zone, which grows with increased shear. In particular, for γ = 0.2 in the left grain, c = 0.629, p̄ = 2.71, [small tau, Greek, macron] = 3.41, and W = 0.95; in the right grain c = 0.761, p̄ = 2.5, [small tau, Greek, macron] = 3.53, and W = 0.96. Thus, using grain rotation and slip on alternative systems, one can reach a high concentration of the HPP at low pressure and comparable shear stress.

Fig. 7 Stationary distribution of HPPs and dislocations under growing shear. The HPP and dislocation solutions in Fig. 5b in each grain are rotated separately by 90° clockwise and applied as initial conditions. The same normal stress distribution and shear strain γ = 0.15 are applied as in Fig. 5b. Three dislocation systems in the left grain disappeared due to normality of the rotated slip plane and the applied shear. In the right grain, three rotated dislocation systems were kept unchanged (designated in magenta). In addition, three new dislocation systems inclined under 15° were introduced.

Conclusion

To summarize, an advanced PFA for PT and dislocation evolution was used for the study of the nanoscale mechanisms of strain-induced PTs in nanograin materials under pressure and shear. Obtained results completely changed our understanding of strain-induced PTs. For nanograin materials, much less dislocations are generated by grain boundaries (i.e., stress concentration is smaller), but much higher averaged shear stress can be sustained, in comparison with the large-grain material. If plasticity in the transforming grain is suppressed, a quite high concentration of HPP c = 0.5 can be obtained at pressure averaged over both grains p̄ = 0.8 (p[small tau, Greek, macron] = 0.06 in the transformed grain) – i.e., at pressure 20 times below the PT pressure and 12.5 times below the p_e, both under hydrostatic conditions. However, [small tau, Greek, macron] = 4.9 is larger than p̄, which makes such a process impractical for technical applications from the point of view of anvil strength.⁴³ At the same time, such a shear-dominated stress tensor may lead to achieving new transformation paths and phases that were hidden during pressure-induced PTs. A more optimal combination of p̄ = 3.1 and [small tau, Greek, macron] = 3.48 also produces quite large c = 0.55. Such an unexpectedly large extent of transformation occurs because the small distance between the stress concentrators leads to the coalescence of nuclei and morphological transition. An increase in shear strain leads to the growth of nuclei. When plasticity is allowed along with PTs it suppresses PT in most cases. In other words, dislocations play a dual role: in addition to creating stress concentrators, they may relax stresses at other concentrators, thus competing with PT. However, some cases were found in which quite intense plasticity slightly reduced the transformed region (Fig. 6 with γ = 0.2, p̄ = 3.45, and [small tau, Greek, macron] = 3.51) or did not affect the HPP region at all (Fig. 5 with γ = 0.15, p̄ = 5.66, and [small tau, Greek, macron] = 2.46) because PT wins the competition over dislocation generation. Also, by using grain rotation and slip on alternative systems, one can reach a high concentration of the HPP at low pressure and comparable shear stress. Note that transformation work based on averaged p̄ and [small tau, Greek, macron] is in the range 0.96–1.11 < k = 1.575, which also confirms contributions from stress concentrators. In most cases, dislocations are localized near grain boundaries and phase interfaces rather than in the middle of the grains, which corresponds to some experiments.^27,30 Also, both coherent interfaces (Fig. 4–7) and interfaces with nearby dislocations (semicoherent interfaces, Fig. 3 and 7) are observed, like in experiments reported in ref. 27 and 30. Note that if dislocations are not pinned, they slide back and disappear after the release of shear, like in some experiments.^37,38 Problems with arresting of dislocations and phase interfaces will be considered in future.

Our results suggest some parameters and methods for controlling strain-induced PTs. They should be combined with a search for new phases and pressure shear loading at the atomistic scale,^10–14 development of strain-controlled kinetics at the microscale,^22,34 and a study of the behavior of a sample in the RDAC at the macroscale^35,36 in order to discover and utilize the multiscale features of strain-induced PTs. In addition to the search for new high pressure phases and reduction in transformation pressure, phase transformations under pressure and shear occur in shear bands in geophysics (especially, during the initiation of earthquakes), penetration of projectiles in materials, and shear ignition of energetic materials. Strain-induced transformations under high pressure also take place in various technological applications, e.g. cutting and polishing of Ge, Si, silicon and boron carbides, and transformations during friction. Still, in all cases nucleation starts at the nanoscale.

Acknowledgements

Support of DARPA, ARO, NSF, and ISU is gratefully acknowledged.

References

1. L. Wang, B. Liu, H. Li, W. Yang, Y. Ding, S. Sinogeikin, Y. Meng, Z. Liu, X.-C. Zeng and W. L. Mao, Science, 2012, 337, 825–828.
2. W. L. Mao, H. K. Mao, P. J. Eng, T. P. Trainor, M. Newville, C.-C. Kao, D. L. Heinz, J. Shu, Y. Meg and R. J. Hemley, Science, 2003, 302, 425–427.
3. V. L. Solozhenko, O. O. Kurakevych, D. Andrault, Y. Le Godec and M. Mezouar, Phys. Rev. Lett., 2009, 102, 015506.
4. V. L. Solozhenko and O. O. Kurakevych, J. Solid State Chem., 2009, 182, 1359–1364.
5. V. L. Solozhenko, D. Andrault, G. Fiquet, M. Mezouar and D. Rubie, Appl. Phys. Lett., 2001, 78, 1385–1387.
6. Y. Zhao, D. W. He, L. L. Daemen, T. D. Shen, R. B. Schwarz, Y. Zhu, D. L. Bish, J. Huang, J. Zhang and G. Shen, et al. , J. Mater. Res., 2002, 17, 3139–3145.
7. M. I. Eremets, A. G. Gavriliuk, I. A. Trojan, D. A. Dzivenko and R. Boehler, Nat. Mater., 2004, 3, 558–560.
8. A. Sengupta, M. Kim and C.-S. Yoo, J. Solid State Chem., 2012, 116, 2061–2067.
9. A. R. Oganov, J. Chen, C. Gatti, Y. Ma, Y. Ma, C. W. Glass, Z. Liu, T. Yu, O. O. Kurakevych and V. L. Solozhenko, Nature, 2009, 457, 863–867.
10. R. Zhou and X.-C. Zeng, J. Am. Chem. Soc., 2012, 134, 7530–7538.
11. S. E. Boulfelfel, A. R. Oganov and S. Leoni, Sci. Rep., 2012, 2, 471.
12. Q. Zhu, A. R. Oganov, M. A. Salvado, P. Pertierra and A. O. Lyakhov, Phys. Rev. B., 2011, 83, 193410.
13. C.-S. Zha, Z. Liu and R. J. Hemley, Phys. Rev. Lett., 2012, 108, 146402.
14. H. Xiao, Q. An, W. A. Goddard, W.-G. Liu and S. V. Zybin, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 5321–5325.
15. P. W. Bridgman, Phys. Rev., 1935, 48, 825–847.
16. V. I. Levitas, Y. Ma, E. Selvi, J. Wu and J. A. Patten, Phys. Rev. B., 2012, 85, 054114.
17. V. D. Blank, M. Popov, S. Buga, V. Davydov, V. N. Denisov, A. N. Ivlev, B. N. Marvin, V. Agafonov, R. Ceolin and H. Szwarc, et al. , Phys. Lett. A, 1994, 188, 281–286.
18. N. V. Novikov, S. B. Polotnyak, L. K. Shvedov and V. I. Levitas, J. Superhard Mater., 1999, 3, 39–51.
19. M. I. Eremets, M. Yu. Popov, I. A. Trojan, V. N. Denisov, R. Boehler and R. J. Hemley, J. Chem. Phys., 2004, 120, 10618–10623.
20. M. Popov, Phys. Lett. A, 2005, 334, 317–325.
21. M. Popov, M. Kyotania and Y. Kogaa, Diamond Relat. Mater., 2003, 12, 833–839.
22. V. I. Levitas, Phys. Rev. B., 2004, 70, 184118.
23. M. M. Alexandrova, V. D. Blank and S. G. Buga, Solid State Phys., 1993, 35, 1308–1317.
24. C. Ji, V. I. Levitas, H. Zhu, J. Chaudhuri, A. Marathe and Y. Ma, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 19108–19112.
25. M. T. Perez-Prado and A. P. Zhilyaev, Phys. Rev. Lett., 2009, 102, 175504.
26. R. Z. Valiev, R. K. Islamgaliev and I. V. Alexandrov, Prog. Mater. Sci., 2000, 45, 103–189.
27. A. P. Zhilyaev and T. G. Langdon, Prog. Mater. Sci., 2008, 53, 893–979.
28. B. Srinivasarao, A. P. Zhilyaev and M. T. Perez-Prado, Scr. Mater., 2011, 65, 241–244.
29. A. P. Zhilyaev, I. Sabirov, G. Gonzalez-Doncel, J. Molina-Aldareguia, B. Srinivasarao and M. T. Perez-Prado, Mater. Sci. Eng., A, 2011, 528, 3496–3505.
30. K. Edalati, S. Toh, Y. Ikomaa and Z. Horita, Scr. Mater., 2011, 65, 974–977.
31. V. V. Boldyrev, Russ. Chem. Rev., 2006, 75, 177–189.
32. F. Delogu, Scr. Mater., 2012, 67, 340–343.
33. C. Suryanarayana, Rev. Adv. Mater. Sci., 2008, 18, 203–211.
34. V. I. Levitas and O. M. Zarechnyy, J. Phys. Chem. B, 2006, 110, 16035–16046.
35. V. I. Levitas and O. M. Zarechnyy, Phys. Rev. B., 2010, 82, 174123.
36. V. I. Levitas and O. M. Zarechnyy, Phys. Rev. B., 2010, 82, 174124.
37. Z. Budrovic, H. V. Swygenhoven, P. M. Derlet, S. V. Petegem and B. Schmitt, Science, 2004, 304, 273–276.
38. X. Yu, J. Zhang, L. Wang, Z. Ding, C. Jin and Y. Zhao, Acta Mater., 2011, 59, 3384–3389.
39. V. I. Levitas and M. Javanbakht, Appl. Phys. Lett., 2013, 102, 251904.
40. V. I. Levitas and M. Javanbakht, Phys. Rev. B. Rapid Communications, 2012, 86, 140101.
41. V. I. Levitas, V. A. Levin, K. M. Zingerman and E. I. Freiman, Phys. Rev. Lett., 2009, 103, 025702.
42. ESI.†.
43. N. V. Novikov, V. I. Levitas, S. B. Polotnyak and M. M. Potyomkin, High Pressure Res., 1991, 8, 507–509.

---

Footnote

† Electronic supplementary information (ESI) available: A PFA to interaction of PTs and dislocation evolution is developed and material properties are described. See DOI: 10.1039/c3nr05044k

---