[NH2NH3][M(HCOO)3] (M = Mn2+, Zn2+, Co2+ and Mg2+): structural phase transitions, prominent dielectric anomalies and negative thermal expansion, and magnetic ordering†
Sa
Chen
,
Ran
Shang
,
Ke-Li
Hu
,
Zhe-Ming
Wang
* and
Song
Gao
*
Beijing National Laboratory for Molecular Sciences, State Key Laboratory of Rare Earth Materials Chemistry and Applications, College of Chemistry and Molecular Engineering, Peking University, Beijing 100871, PR China. E-mail: zmw@pku.edu.cn; gaosong@pku.edu.cn; Fax: +86-10-62751708
First published on 20th December 2013
Abstract
We report here a new class of ammonium metal–formate frameworks of [NH2NH3][M(HCOO)3] (M = Mn2+, Zn2+, Co2+ and Mg2+) incorporating hydrazinium as the cationic template and component. The perovskite Mn and Zn members possess anionic 412·63 metal–formate frameworks with cubic cavities occupied by the NH2NH3+ cations, while the Co and Mg members have chiral 49·66 metal–formate frameworks, with chiral hexagonal channels accommodating NH2NH3+ cations. On heating, the Mn and Zn members undergo phase transitions around 350 K. The structures change from low temperature (LT) polar phases in Pna21 to high temperature (HT) non-polar phases in Pnma, due to the thermally activated librational movement of the NH2 end of the NH2NH3+ in the cavity and significant framework regulation. The Co and Mg members in LT belong to non-polar P212121, are probably antiferroelectric, and they show phase transitions at 380 K (Co) and 348 K (Mg), and the structures change to polar HT phases in P63, triggered by the order–disorder transition of the cation from one unique orientation in LT to three of trigonally-disorder state in HT. Accompanying the phase transitions, which are ferro- to para-electric for Mn and Zn members while antiferro- to ferro-electric for Co and Mg, prominent anisotropic thermal expansions including negative ones, and dielectric anomalies, are observed. The spontaneous polarization values are estimated at 3.58 (Mn, 110 K), 3.48 (Zn, 110 K), 2.61 (Co, 405 K) and 3.44 (Mg, 400 K) μC cm−2, respectively, based on the positive and negative charge separations in the polar structures. The structure–property relevance is established based on the order–disorder transitions of NH2NH3+ and the conformity and adaptability of the metal–formate frameworks to match such order–disorder alternations. The Mn and Co members show spin-canted antiferromagnetic long-range-ordering, with Néel temperatures of 7.9 K and 13.9 K, respectively. Therefore, the two members show coexistence of electric and magnetic orderings in the low temperature region, and they are possible molecule-based multiferroics.
Introduction
In pursuit of new devices and advanced materials, it is more and more desirable to combine or integrate different properties and functionalities within one single phase material. The renaissance of multiferroics in the last decade represents such trend.1,2 Multiferroics are of great importance for both fundamental science and the potential applications in new devices based on the mutual controls of magnetic and electric fields. The materials of metal–organic frameworks, MOFs, have received considerable attention for multi-functional materials.3–7 These materials, by combining inorganic and organic components, can not only possess new and interesting properties or functionalities,4 originating from their organic–inorganic hybrid character,3 but also afford possible coexistence and/or synergism of multiple functionalities within one material. Indeed, multi-functionalities such as conductivity and magnetism,5 magnetic and optical properties,6 porosity and magnetism,7 have been all realized in MOF materials, by incorporating suitable inorganic and organic building blocks and structural features within MOFs. More recently, several MOFs showing coexistence of magnetic and electric orderings or multiferroics have emerged,8 however, these MOF-/molecule-based multiferroics are still very limited compared to the much more well developed pure inorganic ones.1,2 On the other hand, it has been now realized that MOFs themselves could display a rich variety of physical properties and critical phenomena or phase transitions.9 In addition to the magnetic10 and electric11,12 transitions, the unusual mechanical properties of negative thermal expansion (NTE)13–16 and the related framework dynamics,17 negative linear compressibility (NLC),18 pressure or temperature induced amorphization19 and so on have aroused great interest from both a fundamental and a practical point of view, as have those for conventional materials such as oxides.9 These properties are all very closely linked to the structural modifications and/or structural transitions, therefore are possibly also linked one to another. The close link between anisotropic thermal expansion (ATE), including NTE, and the ferro- to para-electric transition is well known for classical ferroelectrics such as BaTiO3 (BTO) and potassium dihydrogen phosphate (KDP) in which the underlying mechanism is order–disorder transitions of cationic components.20Along these lines, we and other authors have studied the ammonium metal–formate frameworks (hereafter abbr. AMFFs) systematically.21 AMFFs are promising MOFs for magnetic and/or electric orderings and phase transitions because of the following observations. (i) The formate HCOO−, the smallest and simplest carboxylate, can adopt various bridging modes such as syn–syn, anti–anti, syn–syn/anti, all short bridges, to link metal ions, and it has small stereo effects. These are all beneficial properties for the formation of MOFs, and for the significant magnetic coupling between magnetic metal sites. (ii) Formate is a good hydrogen-bonding acceptor (hereafter HB = hydrogen-bonding/bond), and the ammonium ions are good HB donors. The combination of such components could produce HB systems required for ferro-/antiferro-electric properties in molecule-based materials, such as those in traditional KDP and TGS,20 and recently organic ones.22 (iii) The metal–formate frameworks have shown malleability and adaptability to conform to the ammonium ions employed, not only the different framework structure types depending on the size, shape, charge etc. of the ammonium ions, but also the framework flexibility and modulation to the order/disorder status of the cations. For AMFFs, many interesting results and developments have been recently reported.21,22–34 The [NH4][M(HCOO)3]23 and [(CH3)2NH2][M(HCOO)3]24–26 series (M = 3d magnetic metal), known as MOF-based multiferroics, display coexistence or synergism of magnetic and electric orderings. Giant dielectric anomalies and relaxor behaviors have been observed for [(CH2)3NH2][M(HCOO)3].27 In several lanthanide metal systems, magnetic relaxation behaviors and structural transitions have been observed.28 [C(NH2)3][Cu/Cr(HCOO)3] have been suggested by DFT calculations to show possible magnetoelectric effect, but this is still awaiting experimental confirmation.29 NTE and NLC have been observed for [NH4][M(HCOO)3]23 and [CH3NH3][Mn(HCOO)3].24a Para- to antiferro-electric transitions of unusual structural alternations together with Néel N-type ferrimagnetism have been observed in mixed-valence [(CH3)2NH2][FeIIIFeII(HCOO)6].30 It has been noted that the order–disorder transitions of ammonium cations could occur in most of these AMFFs,22–34 as observed in many other systems including ammonium components.35–38
To build upon these interesting results and to continue our studies21,23–25,27,28,29a,33,34 on AMFFs, in this work we use the hydrazinium, NH2NH3+, as the cationic component and template to construct a new AMFF class of [NH2NH3][M(HCOO)3], in which the four compounds are named as 1Mn, 2Zn, 3Co and 4Mg for M = Mn2+, Zn2+, Co2+ and Mg2+, respectively. The NH2NH3+ has an intermediate size, larger than NH4+ and HONH3+ ions23,33 but smaller than CH3NH3+ and other larger mono-ammonium ions,24–27,29–32 and it is a good HB donor and possible acceptor. The middle size of hydrazinium resulted in two typical AMFF structures within the series, one is the perovskites (1Mn and 2Zn) and the other the chiral frameworks (3Co and 4Mg). The materials all displayed interesting structural phase transitions with critical temperatures (TC values) close to or above 350 K, comparable to inorganic BTO, accompanied by significant dielectric anomalies and ATE/NTE due to the order–disorder transitions of hydrazinium and the framework modulations. The materials were characterized by thermal analyses, variable temperature (VT) single crystal X-ray diffraction (SXRD) and powder X-ray diffraction (PXRD), and dielectric measurements. The magnetic 1Mn and 3Co showed long-range-ordering (LRO) of spin-canted antiferromagnetism (AF) in the low temperature region.
Experimental section
Synthesis
All chemicals were commercially available, reagent grade, and used without further purification. Cautionary note: perchlorate compounds are potentially explosive. They should be prepared in small quantities and handled with care.The four compounds were synthesized by mild solution methods. Typically, 1Mn was prepared as follows. 5.0 ml of methanol solution containing formic acid 3.94 g (80 mmol) and an aqueous solution of 85% hydrazine 0.35 g (6.0 mmol) were mixed with 5.0 ml of methanol solution containing Mn(ClO4)2·6H2O 0.36 g (1.0 mmol). The mixed solution was kept undisturbed. After two days, the block-shaped colorless crystals of X-ray quality were collected, washed with ethanol and air-dried. The yield is 86% based on Mn(ClO4)2·6H2O. 2Zn, 3Co and 4Mg were obtained similarly with yields of 80%, 96% and 90% for 2Zn, 3Co and 4Mg, respectively. Anal. (%) 1Mn, calcd for C3H8MnN2O6: C, 16.15; H, 3.61; N, 12.56; found: C, 16.15; H, 3.52; N, 12.53; 2Zn, calcd for C3H8ZnN2O6: C, 15.43; H, 3.45; N, 12.00; found: C, 15.48; H, 3.34; N, 11.89; 3Co, calcd for C3H8CoN2O6: C, 15.87; H, 3.55; N, 12.34; found: C, 15.99; H, 3.51; N, 12.21; 4Mg, calcd for C3H8MgN2O6: C, 18.73; H, 4.19; N, 14.56; found: C, 18.68; H, 4.16; N, 14.61. The crystals of 1Mn and 2Zn are nearly rectangular blocks or thick plates, while the crystals of 3Co and 4Mg are hexagonal blocks or pyramids (Fig. S1†).
X-ray crystallography and physical measurements
The SXRD intensity data for the single crystals of the four compounds at low temperatures (LT) were collected on a Nonius Kappa CCD diffractometer (CCD-1),39 and data at high temperatures (HT) on an Agilent Technology SuperNova Dual Atlas CCD diffractometer (CCD-2),40 using monochromated Mo Kα radiation (λ = 0.71073 Å) and equipped temperature control systems. Crystals showed reversible phase transitions and all kept good crystallinity, though single crystals of 3Co and 4Mg became twinned from HT back to LT. All structures were solved by direct method and refined by full-matrix least-squares on F2 using SHELX program.41 The H atoms were located from the difference Fourier synthesis, but constrained according to the ideal geometries in refinements. For 3Co and 4Mg, the HT structures were solved in space groups P63 and P6322. However, the structures refined in P63 resulted in significantly lower R factors (for 3Co, R1 = 0.016 in P63 while 0.021 in P6322) and better models for the trigonally disordered hydrazinium with rational molecular geometry. The crystallographic data are briefly summarized in Table 1 while the details are reported in Table S1,† and the selected molecular geometries are listed in Table S2† (1Mn and 2Zn) and Table S3† (3Co and 4Mg). CCDC-958452 to 958467 contain the supplementary crystallographic data for this paper.| 1Mn, formula = C3H8MnN2O6, fw = 223.05 | ||||
|---|---|---|---|---|
| T (K) | 110 | 200 | 290 | 400 |
| Crystal system | Orthorhombic | Orthorhombic | Orthorhombic | Orthorhombic |
| Space group | Pna21 | Pna21 | Pna21 | Pnma |
| a (Å) | 8.9319(3) | 8.9503(3) | 8.9448(3) | 8.8505(3) |
| b (Å) | 7.8190(2) | 7.8214(2) | 7.8403(3) | 11.8785(4) |
| c (Å) | 11.6928(5) | 11.7189(5) | 11.7669(5) | 7.9240(3) |
| α (°) | 90 | 90 | 90 | 90 |
| β (°) | 90 | 90 | 90 | 90 |
| γ (°) | 90 | 90 | 90 | 90 |
| V (Å3) | 816.61(5) | 820.37(5) | 825.21(5) | 833.06(5) |
| Z, Dc (g cm−3) | 4, 1.814 | 4, 1.806 | 4, 1.795 | 4, 1.778 |
| μ (Mo Kα) (mm−1), F(000) | 1.613, 452 | 1.606, 452 | 1.597, 452 | 1.581, 452 |
| No. total/uniq./obs. reflns. | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 236/2093/1540 236/2093/1540 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 362/2101/1439 362/2101/1439 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 111/2113/1378 111/2113/1378 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 844/1077/873 844/1077/873 |
| R 1, wR2 (for I ≥ 2σ(I)) | 0.0248, 0.0435 | 0.0243, 0.0408 | 0.0259, 0.0426 | 0.0297, 0.0779 |
| GOF | 0.912 | 0.885 | 0.885 | 1.226 |
| 2Zn, formula = C3H8ZnN2O6, fw = 233.48 | ||||
|---|---|---|---|---|
| T (K) | 110 | 200 | 290 | 375 |
| Crystal system | Orthorhombic | Orthorhombic | Orthorhombic | Orthorhombic |
| Space group | Pna21 | Pna21 | Pna21 | Pnma |
| a (Å) | 8.6640(3) | 8.6806(3) | 8.6748(3) | 8.5958(3) |
| b (Å) | 7.7157(2) | 7.7235(3) | 7.7488(3) | 11.6442(5) |
| c (Å) | 11.4824(4) | 11.5056(3) | 11.5478(4) | 7.8468(3) |
| α (°) | 90 | 90 | 90 | 90 |
| β (°) | 90 | 90 | 90 | 90 |
| γ (°) | 90 | 90 | 90 | 90 |
| V (Å3) | 767.58(4) | 771.39(4) | 776.23(5) | 785.40(5) |
| Z, Dc (g cm−3) | 4, 2.020 | 4, 2.010 | 4, 1.998 | 4, 1.975 |
| μ (Mo Kα) (mm−1), F(000) | 3.196, 472 | 3.181, 472 | 3.161, 472 | 3.124, 472 |
| No. total/uniq./obs. reflns. | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 003/1944/1427 003/1944/1427 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 258/1965/1369 258/1965/1369 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 396/1988/1329 396/1988/1329 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 343/1024/756 343/1024/756 |
| R 1, wR2 (for I ≥ 2σ(I)) | 0.0230, 0.0426 | 0.0227, 0.0402 | 0.0233, 0.0395 | 0.0294, 0.0727 |
| GOF | 0.931 | 0.942 | 0.892 | 1.154 |
| 3Co, formula = C3H8CoN2O6, fw = 227.04 | ||||
|---|---|---|---|---|
| T (K) | 110 | 200 | 290 | 405 |
| Crystal system | Orthorhombic | Orthorhombic | Orthorhombic | Hexagonal |
| Space group | P212121 | P212121 | P212121 | P63 |
| a (Å) | 7.9435(2) | 7.9415(2) | 7.9341(3) | 7.9157(3) |
| b (Å) | 13.8339(4) | 13.8460(5) | 13.8697(7) | 7.9157(3) |
| c (Å) | 7.3016(2) | 7.3103(2) | 7.3361(3) | 7.4836(3) |
| α (°) | 90 | 90 | 90 | 90 |
| β (°) | 90 | 90 | 90 | 90 |
| γ (°) | 90 | 90 | 90 | 120.00 |
| V (Å3) | 802.37(4) | 803.83(4) | 807.29(6) | 406.09(3) |
| Z, Dc (g cm−3) | 4, 1.880 | 4, 1.876 | 4, 1.868 | 2, 1.857 |
| μ (Mo Kα) (mm−1), F(000) | 2.136, 460 | 2.132, 460 | 2.123, 460 | 2.110, 230 |
| No. total/uniq./obs. reflns. | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 158/2071/1771 158/2071/1771 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 313/2074/1711 313/2074/1711 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 202/2077/1607 202/2077/1607 |
6226/672/648 |
| R 1, wR2 (for I ≥ 2σ(I)) | 0.0244, 0.0458 | 0.0263, 0.0490 | 0.0279, 0.0497 | 0.0157, 0.0422 |
| GOF | 0.988 | 0.965 | 0.955 | 1.118 |
| 4Mg, formula = C3H8MgN2O6, fw = 192.42 | ||||
|---|---|---|---|---|
| T (K) | 110 | 200 | 292 | 400 |
| Crystal system | Orthorhombic | Orthorhombic | Orthorhombic | Hexagonal |
| Space group | P212121 | P212121 | P212121 | P63 |
| a (Å) | 7.8999(2) | 7.8928(2) | 7.8888(2) | 7.8798(3) |
| b (Å) | 13.7505(4) | 13.7693(4) | 13.7799(4) | 7.8798(3) |
| c (Å) | 7.3829(2) | 7.4007(2) | 7.4295(2) | 7.5682(4) |
| α (°) | 90 | 90 | 90 | 90 |
| β (°) | 90 | 90 | 90 | 90 |
| γ (°) | 90 | 90 | 90 | 120.00 |
| V (Å3) | 801.99(4) | 804.30(4) | 807.64(4) | 406.96(3) |
| Z, Dc (g cm−3) | 4, 1.594 | 4, 1.589 | 4, 1.583 | 2, 1.570 |
| μ (Mo Kα) (mm−1), F(000) | 0.219, 400 | 0.218, 400 | 0.217, 400 | 0.216, 200 |
| No. total/uniq./obs. reflns. | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 126/1993/1864 126/1993/1864 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 119/1993/1827 119/1993/1827 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 178/1996/1756 178/1996/1756 |
6712/678/654 |
| R 1, wR2 (for I ≥ 2σ(I)) | 0.0249, 0.0652 | 0.0283, 0.0747 | 0.0307, 0.0808 | 0.0260, 0.0698 |
| GOF | 1.141 | 1.099 | 1.052 | 1.117 |
PXRD data were collected in the range of 5° < 2θ < 60° at room temperature (RT) for the bulk samples and the pressed tablet samples on a Rigaku Dmax 2000 diffractometer, and VT PXRD patterns for the pressed tablet samples were collected on CCD-2, using Cu Kα radiation.
Elemental analysis of C/H/N was performed on an Elementar Vario MICRO CUBE analyzer. FTIR spectra in the range of 4000 to 600 cm−1 were recorded for pure samples on a NICOLET iN10 MX spectrometer. Thermal analyses were performed on a TA SDT Q600 simultaneous DSC-TGA instrument at the rate of 5 °C min−1 in air flow. The DSC measurements were performed on a TA Q100 DSC analyzer at the rate of 5 °C min−1 in N2 flow and cycled two or three times.
The temperature-dependent ac (alternate current) dielectric permittivity measurements were carried out on a TH2828 Precision LCR meter under 20 frequencies from 100 Hz to 1 MHz and an applied voltage of 1.0 V, at a temperature sweeping rate of ca. 1 K min−1 in dried N2 flow. Samples were ground and pressed into tablets under a pressure of ca. 2 GPa. The phase purity of the pressed tablets and the absence of pressure-induced phase transitions were confirmed by PXRD (Fig. S2†). The capacitors were made by painting the two faces of the tablet pieces with silver conducting paste and copper or golden wires as the electrodes. These capacitors were kept vacuum-dried over silica gel for more than two weeks and finally coated by a very thin layer of AB glue or vaseline before the dielectric measurements, in order to avoid the influence of moisture. The area and thickness of the capacitors were measured under a microscope with a Phenix CCD eye and the software.
Magnetic measurements for 1Mn and 3Co were performed on a Quantum Design MPMSXL5 SQUID system with polycrystalline samples tightly packed and sealed in a capsule. Diamagnetic corrections were estimated using Pascal constants (−91 × 10−6 and −89 × 10−6 cm3 mol−1 for 1Mn and 3Co, respectively)42 and background correction by experimental measurement on sample holders.
Results and discussion
Synthesis, IR spectra, thermal properties, and structural phase transitions
The four AMFF materials were prepared under ambient conditions by employing suitable metal perchlorate salts, hydrazine (85% aqueous solution) and formic acid in methanol (see above). This mild solution chemistry method has proved to be very successful, general, convenient and performed easily in the preparation of various AMFFs in the last few years by us,21,23,24,27–29,33,34 though sometimes solvothermal methods were employed.25,26,30,32 The PXRD patterns (Fig. S2†) confirmed the phase purity of the products, so the small water component of the commercial aqueous hydrazine (85%) did not produce impurities of metal–formate dihydrate in the products, as frequently encountered.21 Similar observations were reported for the preparation of the mixed metal perovskites [CH3NH3][MnxZn1−x(HCOO)3],24b niccolite [CH3NH2CH2CH2NH2CH3][Zn2(HCOO)6],34b and the perovskite series of [C(NH2)3][M(HCOO)3].29a Another interesting observation for the present series is that 1Mn and 2Zn possess the most popular perovskite AMFF structures among several [AmineH][M(HCOO)3] series for mono ammonium ions24–27,29,31,32 where AmineH+ = CH3NH3+, (CH3)2NH2+, CH3CH2NH3+, (CH2)3NH2+, C(NH2)3+ and (NH2)2CH+, while 3Co and 4Mg belong to the chiral structures of the type [NH4][M(HCOO)3]23 and the recently reported [HONH3][M(HCOO)3]33 series. Given the fact that the four compounds have the same constituents except the different metal ions, and usually within one AMFF series the Mn, Fe, Co, Ni, Zn and Mg members are isostructural,21 this observation is quite unexpected. For each metal ion we could expect the existence of two phases or polymorphs. Indeed, we have found that for the Fe member the product is a mixture of two such phases.43 We are still trying to obtain the two Fe phases in pure form so that they will be reported in the future, as well as to prepare the perovskite phases of 3Co and 4Mg and the chiral phases of 1Mn and 2Zn. Finally, attempts to prepare the Ni and Cu members within this series were not successful, probably due to the very low solubility of the Ni member21 and the easy reduction of Cu2+ by hydrazine.The IR spectra of the four compounds are quite similar but still show some slight differences (Fig. S3†), given the fact that the structures belong to two types. The IR absorption bands and their assignments are given in Table S4,† and they are characteristic of NH2NH3+ and HCOO−.33,44
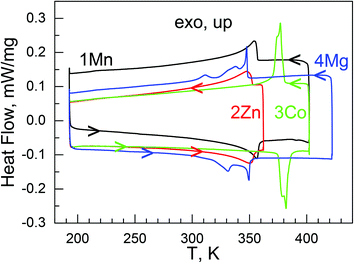
The combined TGA-DSC runs up to 800 °C are shown in Fig. S4.† These materials basically showed two weight loss procedures on their TGA traces. The first endothermic one occurred around 130, 110, 160 and 180 °C (decomposition temperatures Td = 400, 380, 430 and 450 K, Table 2) for 1Mn, 2Zn, 3Co and 4Mg, respectively, and the weight losses were 33.4 (1Mn), 33.3 (2Zn), 33.8 (3Co) and 40.5% (4Mg), corresponding to the departure of one NH2NH2·HCOOH per formula with calculated weight losses of 33.5 (1Mn), 33.4 (2Zn), 34.4 (3Co) and 40.6% (4Mg), respectively, although for 1Mn, 2Zn and 3Co this procedure might include two sub-steps. The energy acquirements were 120 kJ mol−1. After the first decomposition, 1Mn and 3Co further decomposed around 300 °C with high exothermic peaks and energy releases of 540 (1Mn) and 690 (3Co) kJ mol−1. 2Zn further decomposed in two steps, one weak endothermic (3 kJ mol−1) around 400 °C and one strong exothermic (290 kJ mol−1) around 580 °C. The pyrolysis of 4Mg occurred at ca. 420 °C with an energy release of 57 kJ mol−1. The final residues were 35.7, 31.7, 33.8 and 20.8% for 1Mn, 2Zn, 3Co and 4Mg, respectively, in agreement with the calculated values of 35.4, 33.0, 34.9 and 20.9% based on Mn2O3, ZnO, CoO and MgO. The thermal stabilities of the present series are similar to other mono-ammonium metal–formate series23–25,33 except for the most stable [C(NH2)3][M(HCOO)3] structures.29a It should be noted that the four materials showed small but perceivable endothermic peaks around 84, 79, 108 and 77 °C (357, 352, 381 and 350 K) for 1Mn, 2Zn, 3Co and 4Mg, respectively, before their first decomposition in the DSC plots (Fig. S4b,† inset), and these indicated the occurrence of phase transitions.
| Compound | 1Mn | 2Zn | 3Co | 4Mg |
|---|---|---|---|---|
| a The first turning points from room temperature in ε′ vs. T plots. b Spontaneous polarization. | ||||
| Thermal properties and phase transitions (up = heating, down = cooling, and av = averaged) | ||||
| T C (K), by DSC peaks | 357up, 353down | 350up, 349down | 382up, 377down | 349up, 348down |
| 355av | 350av | 380av | 348av | |
| ΔH (kJ mol−1), by DSC | 3.9 | 3.4 | 3.1 | 2.6 |
| ΔS (J mol−1 K−1), N, by DSC, | 10.8, 3.7 | 9.7, 3.2 | 8.2, 2.7 | 7.5, 2.5 |
| T C (K), by TGA-DSC | 357up | 352up | 381up | 350up |
| T d (K), by TGA-DSC | 400 | 380 | 430 | 450 |
| T C range (K), by VT PXRD | 350–360up | 350–360up | 380–390up | 340–350up |
| T d (K), by VT PXRD | 400 | 360 | 410 | 440 |
| Dielectric properties (from ε′ data at 1 MHz) | ||||
| ε′290 K | 7.1 | 8.4 | 8.4 | 8.1 |
T
turn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a (K), and ε′ value at turning point in ε′ a (K), and ε′ value at turning point in ε′ |
353, 10.4 | 342, 12.2 | 378, 12.6 | 336, 9.9 |
| T peak or Tsh, K, and ε′ value at peak or shoulder point in ε′ | 364peak, 28.0 | 362sh, 25.4 | 405sh, 32.1 | 343sh, 11.2 |
| 375sh, 24.1 | ||||
| T dε′/dT peak (K) at dε′/dT peak | 362 | 357 | 390 | 340, 364, 415 |
| C and T0 (K) | HT: 3.2 × 102, 353 | LT: 3.3 × 102, 372 | LT: 3.3 × 102, 405 | I: 3.4 × 103, 508 |
| LT: 1.4 × 102, 368 | II: 5.4 × 102, 393 | |||
| Transition type, LT to HT | Ferro to para | Ferro to para | Antiferro to ferro | Antiferro to ferro |
| E a (eV), τ0 (s), for relaxation | 1.03, 1.45 × 10−17 | |||
Estimated PS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b (μC cm−2) b (μC cm−2) |
3.58 | 3.48 | 2.61 | 3.44 |
| Aizu notation | mmmFmm2 | mmmFmm2 | ||
These phase transitions were further confirmed by the more accurate DSC measurements (Fig. 1, Fig. S5,†Table 2). In the DSC traces endo/exothermic peaks were clearly observed at 357/353 K (1Mn), 350/349 K (2Zn), 382/377 K (3Co) and 349/347 K (4Mg, the highest peak positions), respectively, on heating/cooling, showing thermal hysteresis of few Kelvin. The TC values could be defined to be the averaged values, 355 K (1Mn), 350 K (2Zn), 380 K (3Co), and 348 K (4Mg). 1Mn and 2Zn displayed single, cycle-independent peaks with a somewhat extending tail on the low temperature side. 3Co possessed narrow and more prominent peaks, showing a shoulder in the first cycle. In the second cycle, the shoulder disappeared on heating but restored on the followed cooling. 4Mg behaved in a quite complicated manner, with two, even three thermic peaks in the range of 330 to 350 K, indicating a probably multi-step phase transition. The ΔH values (in kJ mol−1) for the phase transitions were estimated at 3.9 ± 0.2 (1Mn), 3.4 ± 0.1 (2Zn), 3.1 ± 0.1 (3Co), 2.6 ± 0.1 (4Mg), and the ΔS (ΔS = ΔH/TC)45 values were estimated at 10.8 to 7.5 J mol−1 K−1 for the phase transitions. From the Boltzmann equation, ΔS = R ln(N), R being the gas constant and N the ratio of the numbers of respective distinguishable states of different phases, N values of 3.7 to 2.5 could be calculated (Table 2). These values are roughly agreeable with 2 or 3 discrete states for the disordered NH2NH3+ cation in the HT phases but 1 for the ordered NH2NH3+ cation in the LT phases (see below). It is noted that the materials of the present series have high TC values, all close to the typical ferroelectric oxide BTO,20 comparing with the previously reported AMFF series showing structural phase transitions, [(CH3)2NH2][M(HCOO)3],26,31 [NH4][M(HCOO)3]23 and [(CH2)3NH2][M(HCOO)3],27 with TC values below room temperature.
The VT PXRD patterns for the four compounds are shown in Fig. S6.† On heating, the phase transitions were evidenced by the changes, highlighted by stars in the patterns occurring around the individual TC values, including the merging of some diffraction peaks, disappearance of some weak peaks, and relative intensity changes of some peaks, from LT to HT, corresponding to the elevation in structure symmetry. The experimental patterns matched the simulated ones based on the single crystal structures of different phases, confirming the phase transitions, and the TC values determined by VT PXRD are within 350–360 K (1Mn and 2Zn), 380–390 K (3Co), and 340–350 K (4Mg) (Table 2). The VT PXRD patterns could also provide the thermal stability for the powders of the materials, up to the Td values, ca. 410 K (1Mn), 360 K (2Zn), 410 K (3Co), and 440 K (4Mg). These data agree with the thermal analyses. It is worth mentioning that the powder samples of 2Zn to 3Co decomposed shortly after their phase transition, but the single crystals showed better thermal stability. For example, we have successfully collected intensity data for a single crystal of 2Zn at 375 K, 15 K higher than the Td = 360 K observed for powder.
Crystal structures and the relevant negative thermal expansion
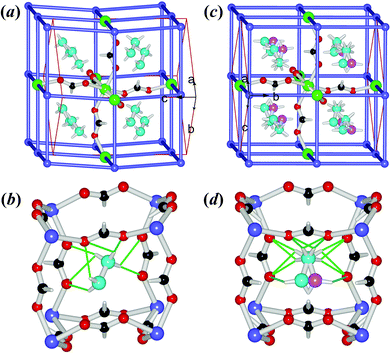
The crystal structures of the ordered LT phase and the disordered HT phase were determined (Table 1, Table S1†) by SXRD. 1Mn and 2Zn are perovskites (Fig. 2), as are those of [AmineH][M(HCOO)3] for mono-ammonium ions with 2–4 non-H atoms,24–27,29,31,32 while 3Co and 4Mg possess the chiral metal–formate networks (Fig. 3) as do those of [NH4][M(HCOO)3],23 K[M(HCOO)3]46 and the very recently reported [HONH3][M(HCOO)3] series.33 They all displayed significant ATE/NTE accompanying the phase transition.The isostructural perovskites 1Mn and 2Zn possess the anionic NaCl-frameworks of [M(HCOO)3−] with the cubic cavities occupied by the NH2NH3+ cations (Fig. 2). Their LT phases belong to the polar orthorhombic space group Pna21. In the structures, each octahedral metal ion connects to six neighboring metal ions in an octahedral spatial arrangement, through six anti–anti formates, thus forming a metal–formate framework with a topology of 412·63 (Fig. 2a and 2b). At RT (Table S2†), the M–O distances are 2.178(2)–2.196(2) Å for 1Mn, and 2.099(2)–2.115(2) Å for 2Zn, respectively, and the cis- O–M–O angles are 86.37(7)–94.43(9)°, and the trans- O–M–O angles are 176.10(8)–179.08(8)°. The framework grid or cavity has M–OCHO–M edges of 5.908–5.951 and 5.791–5.817 Å for 1Mn and 2Zn, respectively. These data are comparable with other known perovskite AMFFs,24–27,29,31 and the decrease in the lattice dimensions and interatomic distances of M–O and M⋯M from 1Mn to 2Zn is in good agreement with the metal ionic radii.47 The grid is somewhat slanted, with the M–OCHO–M grid edges running along the c axis and the two diagonal directions of the ab plane. The cavity volumes are 44.4 (1Mn) and 40.1 (2Zn) Å3, calculated by PLATON (Fig. S7†).48 These allow accommodation of the NH2NH3+ cation with its vdW volume of 44 Å3 estimated by PCModel 9.1.49 In the cavity, the NH2NH3+ cation has its long axis nearly lying on the longest body-diagonal of the cavity, and forms several N–H⋯O HBs to the anionic framework. Each N–H donor of the NH3+ site of the cation forms one short (strong) and one long (weak) N–H⋯O HBs with the two O atoms from one formate, and the HB geometries are: for 1Mn, N⋯O distances 2.876(3)–2.926(4)/2.990(4)–3.110(3) Å, N–H⋯O angles 164.9–173.4/114.5–121.7°; for 2Zn, 2.878(4)–2.944(4)/2.970(4)–3.088(4) Å and 165.3–171.0/117.4–122.5°. Instead, each N–H donor of the NH2 site forms only one long, weak N–H⋯OHCOO HB with N⋯O distances 3.034(4)–3.125(4) Å and N–H⋯OHCOO angles 133.0–139.8°. Therefore, the neutral NH2 site is loosely bonded comparing to the positive NH3+ site. The NH2 end is also inclined to one side of the cavity, leaving the other side empty but available for forming alternative HBs. This asymmetry is very different from the mirror symmetric HBs and cation–cavity relationship in the very closely related [CH3NH3][M(HCOO)3] perovskites24 showing no phase transitions above 180 K. The loosely bonded NH2 end and its asymmetric environment provide the possibility of movement at this end upon warming, as observed in the HT phases. In the framework the metal arrays along the c direction are slightly wavy, and all NH2NH3+ cations have their NH3+ sites aslant towards the −c direction. These are compatible with the polar space group Pna21 and the lack of mirror in the c direction. On cooling down to 110 K the LT structures remain unchanged, with small decreases in cell dimensions and bond distances (Fig. S8a,† Table S2†). Therefore the LT structures are polar, and the polarization should be along the c axis. Indeed, if the planes of the metal atoms, perpendicular to the c axis, are considered as the average, symmetric planes for the distribution of the negative charges of the framework, all NH2NH3+ cations have their positive NH3+ ends showing unequal out-of-plane distances from the two such planes on both sides of the NH3+ end, resulting in shifts, 0.457 Å for 1Mn and 0.417 Å for 2Zn, calculated from the 110 K structures, towards the −c direction with respect to the anionic framework. Assuming that the NH3+ ends are the positive point charges located at the N atoms,23a,b,50 these shifts generate dipoles, 4 per unit cell and parallel to each other, and the spontaneous polarization could be estimated at 3.58 (1Mn) and 3.48 (2Zn) μC cm−2 at 110 K (Table 2), which is typical for molecular ferroelectrics,11,20 along the −c direction.
The structures of the HT phases of 1Mn at 400 K and 2Zn at 375 K, all above the phase transition temperatures (Table 2), are centrosymmetric, in the space group Pnma, by addition of the mirror along the b direction of the HT lattices, i.e. the c direction of the LT lattices, as the relationship between the LT and HT conventional cells for both crystals is aHT ≈ aLT, bHT ≈ cLT and cHT ≈ −bLT. In the HT structures (Fig. 2c and 2d), while the metal–formate frameworks remain unchanged in their topology, the differences in interatomic distances of M–O and M⋯M become smaller (Table S2†), and the wavy metal arrays in the LT structures are now straight. The most remarkable change in the structures is that the NH2NH3+ cation shows two orientations in the HT phases, with its NH2 end splitting into two positions on the two sides of the mirror along the b direction. In fact this disorder, or the librational movement of the NH2 end, introduces the mirror symmetry and thus the centro-symmetry for the HT phase. The NH2NH3+ cation now behaves as a pendulum, a property reminiscent of pendulum-type molecular ferroelectrics.35 Its NH3+ site is anchored by six N–H⋯OHCOO HBs (N⋯O 2.928(3)–3.107(3) Å, N–H⋯OHCOO 117–169°), but the NH2 end can vibrate. However, the NH2NH3+ pendulum does not simply vibrate forward and back. At HT, the vibration locus of the NH2 end across the mirror plane is, in fact, an arc (or a flat V-shape), as shown by the two mirror-symmetric elongated thermal ellipsoids, with the locus plane approximately perpendicular to the N–N bond (Fig. S9a†). The temperature evolution of the N ellipsoids from LT to HT also revealed that the gradually enhanced thermally agitated movements, perpendicular to the N–N bond for the NH2 end, but approximately along the N–N bond for the NH3+, finally led to the librational motion and the caused HB alternations. The two NH2 sites are separated 0.74–0.75 Å, so the vibration amplitude of the NH2 end is 0.37 Å, which corresponds to the distance between NH2 and the mirror plane. The two materials showed ATE behavior during the transition (Fig. S8a,†Table 3). The b and c axes (in LT cell setting) expand ca. 0.1 Å or 1% from 290 K to ca. 400 K, but the a axis contracts ca. 0.1 Å or 1%, resulting in NTE along the a direction. In fact the contraction of a axis might start from a lower temperature of 200 K. The coefficients of the thermal expansion (CTE, or α), negative or positive, are around 100 × 10−6 K−1, estimated by currently available data, and these are classified as “colossal”.15b This behavior could be explained by the librational movement of NH2NH3+ in the c direction with its long molecular axis lying approximately along the a direction, and the conformation adaptability of the metal–formate frameworks. The N–N distances are shortened ca. 0.03 Å from LT to HT, reflecting such librational motion. NTE has been observed in many classes of framework materials,13–16 such as oxides and zeolites14 (e.g., ZrW2O8 and AlPOs), cyanides15 (e.g., Zn(CN)2 and Ag3[Co(CN)6]), and MOFs16 (e.g., MOF-5 and HKUST-1), and the mechanism is thought to consist mainly of the transverse rigid unit modes or the transverse vibration of the linkages.13 The cavity volumes increase quite significantly, 52.8 (1Mn) and 45.2 (2Zn) Å3, compared to 44.4 (1Mn) and 40.1 (2Zn) Å3 of the LT phases at RT (Fig. S7†). The framework cavity becomes more regular (Fig. 2d vs. 2b). From these observations, we suggest that upon heating the expansion of the framework and the change in cavity shape and size and HBs allows first the vibration of the loosely HB-bonded NH2 end of the NH2NH3+ pendulum, then the contraction of the framework along the a direction but still an expansion along b and c, to fit such librational motion. This indicates a double potential well with a small energy barrier for the NH2NH3+ pendulum at HT. While in LT, this vibration is frozen. The fact that the LT phases have a polar space group Pna21 but the HT phases belong to the non-polar, centro-symmetric space group Pnma is of interest for ferroelectricity because such change, from Pnma to Pna21, implies the ferroelectric phase transitions on cooling, for 1Mn and 2Zn, with the Aizu notation mmmFmm2.51 The higher N values of 3.7 (1Mn) and 3.2 (2Zn) by DSC studies indicate that the framework changes, from somewhat wavy one at LT to more regular straight one at HT, together with small twists in the orientation of formate bridges, should have the extra contribution to the N values. This is because the order–disorder transition of the cation, two discrete states in HT structures but one in LT, solely gives the ratio of states, N = 2.
| Compound | 1Mn | 2Zn | ||||
|---|---|---|---|---|---|---|
| T range (K) | 110–200 | 200–290 | 290–400 | 110–200 | 200–290 | 290–375 |
| α a | 23 | −7 | −96 | 21 | −7 | −108 |
| α b | 3 | 27 | 97 | 11 | 36 | 148 |
| α c | 25 | 45 | 86 | 22 | 41 | 98 |
| α V | 51 | 65 | 86 | 55 | 69 | 138 |
| Compound | 3Co | 4Mg | ||||
|---|---|---|---|---|---|---|
| a The values were calculated through the equation αl = Δl/(ΔT × lav) using the data at the two neighbor temperatures. For 1Mn and 2Zn, the cell settings of the HT phases were chosen as the same as the LT phases. For 3Co and 4Mg, a and c axes are the same for LT and HT phases, but for the b axis two settings, orthorhombic (bO) for LT and hexagonal (bH) for HT, were included. The accuracies were estimated at a few 10−6 K−1 in most cases. | ||||||
| T range (K) | 110–200 | 200–290 | 290–405 | 110–200 | 200–290 | 290–400 |
| α a | −3 | −10 | −20 | −10 | −6 | −11 |
| α bO | 10 | 19 | −100 | 15 | 9 | −89 |
| α bH | 7 | 12 | −81 | 9 | 5 | −69 |
| α c | 13 | 39 | 173 | 27 | 43 | 171 |
| α V | 20 | 48 | 56 | 32 | 46 | 72 |
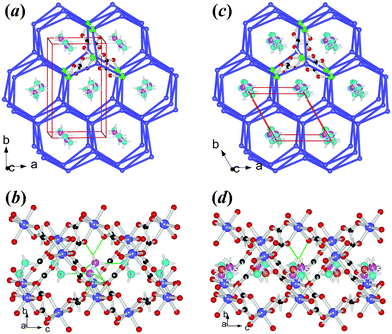
3Co and 4Mg are isostructural (Table 1, S1c, S1d†), possessing a chiral metal–formate framework of 49·66 topology (Fig. 3), with hexagonal channels occupied by the NH2NH3+ cations. As mentioned above, the occurrence of two different metal–formate frameworks within the present series is quite unusual. One possible reason is the size of NH2NH3+, with its vdW volume of 44 Å3, between the relevant ammonium ions,49 25 Å3 of NH4+ and 38 Å3 of HONH3+ for 49·66 frameworks, and 53 Å3 of CH3NH3+ or above of other larger mono-ammonium ions for 412·63 ones. The LT structures of 3Co and 4Mg belong to chiral orthorhombic space group P212121, same as our recently published [HONH3][M(HCOO)3] series,33 and possess quite similar lattice dimensions too (noting that in the present case the c axes are equivalent to the b axes in the [HONH3][M(HCOO)3] series). However, no phase transitions have been detected for the [HONH3][M(HCOO)3] series. Similarly, in 3Co and 4Mg, each octahedral metal node is connected to six neighbors via the anti–anti formate linkages, making up the centered trigonal prism within the frameworks (Fig. 3a). The MO6 octahedron has M–O distances of 2.054(1)–2.122(2) Å, cis- O–M–O angles of 80.62(7)–96.01(7)°, and trans- O–M–O angles of 171.35(7)–176.14(5)° (Table S3,† at RT), similar to the reported data for other relevant Co or Mg AMFF compounds.23,33 The frameworks possess slightly compressed hexagonal channels running along the c direction. In the channel (Fig. 3b) the NH2NH3+ cations are arranged side by side but aslant with respect to the c direction, showing a tilting angle of 65° between the molecular axes and the c direction, and the adjacent cations are oriented up and down. This is significantly different from the [HONH3][M(HCOO)3] series, in which the head to tail arranged HONH3+ cations in the channel have tilting angles of 21°. The shorter c axes of 3Co and 4Mg than the equivalent b axes of the [HONH3][M(HCOO)3] series are compatible with this difference. Two N–H donors of the NH3+ end form four N–H⋯O HBs to the metal–formate framework with N⋯O = 2.824(2)–2.945(2) Å, N–H⋯O angles 118.6–165.8°; and the left N–H donor points to the long electron pair of the NH2 end of the adjacent cation, with N⋯N = 3.058–3.084 Å, and N–H⋯N angles of 172.9–176.4°. Whether this N–H⋯N interaction is a HB or a pseudo HB33,52 merits further investigation. The NH2 end forms N–H⋯O HBs to the framework, with N⋯O = 2.946(2)–3.379(2) Å, and N–H⋯O angles of 101–146°, indicating weaker HB strengths compared to the NH3+ site. The strengths of cation–framework HBs involved in 3Co and 4Mg are weaker than those observed in the [HONH3][M(HCOO)3] series, in which a strong O–H⋯O HB between HONH3+ and the framework probably prohibits the structural phase transition. In the framework the formato-bridged M⋯M distances are 5.820–5.988 Å (Table S3†), larger than those of the perovskites (Table S2†) and the void spaces that the frameworks provide for each NH2NH3+ are 49.7 (3Co) and 53.2 (4Mg) Å3. Surprisingly, these void spaces are larger than those found in 1Mn and 2Zn (Fig. S7†), and the framework is expanded. In fact, in the present series, the perovskite frameworks are denser than the chiral frameworks when considering the cell volumes, all per 4 formula of [NH2NH3][M(HCOO)3], and packing coefficients,53 807.3 (3Co) and 807.6 (4Mg) vs. 776.2 (2Zn) Å3 and 0.710 (3Co) and 0.705 (4Mg) vs. 0.745 (2Zn), considering that the three divalent metal ions have very close radii.47 This is quite unexpected because in our previous work we have observed that the chiral 49·66 frameworks should be denser than perovskite frameworks.21,33 The framework expansion of the chiral 49·66 frameworks vs. the perovskites within the series is due to the significant enlargement of the M–O–C angles of 3Co and 4Mg, 121.4(2)–131.9(1)°, compared with 1Mn and 2Zn, 118.2(2)–123.4(2)°, the change in these angles indicating again the breathing nature of the framework.24,54 The LT structures remained unchanged down to 110 K, showing a small decrease in b, c, V of the cell dimensions but a slight increase in a, thus NTE in the a direction (Table 3, Fig. S8b†), and a very slight decrease in the interatomic distances (Table S3†). The LT structures in P212121 belong to the non-polar D2 point group. However, the polarization properties merit to be discussed here. In fact, in one channel shown in Fig. 3b of the LT phase, the cations are tilting up and down, and their NH3+ ends shift slightly to +c and the NH2 ends to −c with respect to the framework. This could result in a net, small dipole in the channel along the c direction, and the channels arranged along the a axis include the cations in the same tilting arrangement. Thus, these channels together with the cations forming a layer have the same polarization direction. However, the channels packing along the b direction contain NH2NH3+ cations in different tilting directions, related by the 21 axis, thus resulting in anti-parallel arranged dipoles. Therefore, 3Co and 4Mg are antiferroelectrics20 in LT.
After their phase transitions (Table 2), the two materials are still isostructural (Table 1, S1c, S1d,†Fig. 3c and 3d). The structures at 405 K for 3Co and 400 K for 4Mg revealed that the two materials underwent several remarkable changes from LT to HT in their symmetry, lattice, and orientations of the NH2NH3+ cations in the framework channel, though the framework topology remained unchanged. The space group changed from non-polar orthorhombic P212121 (LT) to polar hexagonal P63 (HT), and the HT unit cells doubly reduced compared to the LT ones, with a relationship of aHT ≈ aLT, bHT ≈ (bLT − aLT)/2 and cHT ≈ cLT, then VHT ≈ VLT/2. In fact, if the primitive LT cell is added a C-center, the resultant C-centered lattice has a primitive cell with the following dimensions: for 3Co, a = 7.9341, bH = 7.9893, c = 7.3361 Å, α = β = 90°, γ = 119.77°, and V = 403.7 Å3 and for 4Mg, a = 7.8888, bH = 7.9391, c = 7.4295 Å, α = β = 90°, γ = 119.79°; and V = 403.8 Å3. These data are metrically very close to the hexagonal HT cells. Therefore, the HT cell is derived by the addition of C-centers upon the primitive orthorhombic LT cell, together with a/b shrinking but c expanding (Fig. S8b,†Table 3). The α values are close to −100 × 10−6 K−1 in the b direction, and 170 × 10−6 K−1 for the c directions. These data are all quite large.11 The frameworks become regularly hexagonal, and expand slightly, with fewer unique molecular geometries, by minor framework modulation. The void spaces for each NH2NH3+ are 51.0 (3Co) and 54.5 (4Mg) Å3, only 1.3 Å3 larger than those in LT phases, quite different from the perovskites 1Mn and 2Zn showing more enlargements (Fig. S7†). The NH2NH3+ cation becomes trigonally disordered, with triplet orientations related by the 63 axis, and the molecular axis of NH2NH3+ is more inclined to the c direction with a tilting angle of 52°, compatible with the ATE in cell dimensions (a/b shrinking and c expanding) from LT to HT. After the phase transition the motion of the cation increased more significantly, as indicated by the more enlarged thermal ellipsoids, and the thermal ellipsoids of the O atoms of formate became more disk-like, indicating the coupling of the framework with the disordered state of NH2NH3+ (Fig. S9b†). Again, it seems that the order–disorder transition of NH2NH3+ and the conformity or flexibility of the metal–formate frameworks to fit such transition contribute to the ATE. Such anisotropic changes in cell dimensions are a reversal of the behaviour observed for the [NH4][M(HCOO)3]23a,b series, where a/b expanded and c shrank, with the same framework topology but different librational motion or disordered state of the cation. In fact, in [NH4][M(HCOO)3] the NH4+ cation oscillates along the c direction. Fewer and weaker HBs are observed for each orientation of NH2NH3+ as we countered 3 rational N–H⋯O HBs for the NH3+ end with longer N⋯O distances and probably only one for the NH2 end, and the N–H⋯N contacts between two adjacent cations are not favorable because the N–H groups are more or less oriented towards one another. Now in the polar HT structures the NH3+ ends of all cations shift toward +c, and the shifts are 0.331 and 0.437 Å for 3Co and 4Mg respectively, as calculated by the HT structures. In the same way as we did for [NH4][M(HCOO)3],23a,b by these shifts we calculated polarization values of 2.61 and 3.44 μC cm−2 for 3Co and 4Mg respectively in their HT phases (Table 2). Therefore, from the above structural information, the phase transitions for the two materials from LT to HT are probably antiferro- to ferroelectric. Since the framework has minor changes during the transition, the N values of 2.7 (3Co) and 2.5 (4Mg) could be considered solely as the results of three discrete states of the trigonally disordered cation in the HT structures vs. one state of ordered cation in the LT phases, with a ratio of N = 3.
The structure investigation revealed that phase transitions occurring in the present materials are all order–disorder like, triggered by the thermally activated motions of the NH2NH3+ cation and the accompanied framework modulations. Upon heating, for the perovskites of 1Mn and 2Zn the framework expansion and change are significant, but for the chiral 3Co and 4Mg the framework alterations are small. The significant ATE including NTE for these materials is due to the librational motion of NH2NH3+ and the conformity and adaptability of the metal–formate frameworks to match such motion. This coupling between the cations and anionic frameworks probably provides a new mechanism for NTE of MOFs, because the guests or cations usually dampen NTE,17 but this does not seem to be the case for the present AMFFs. We also think that the middle size of NH2NH3+ and its characteristics in forming HBs have resulted in such interesting series with two typical AMFF structures.
Dielectric properties and their relevance to structure transitions
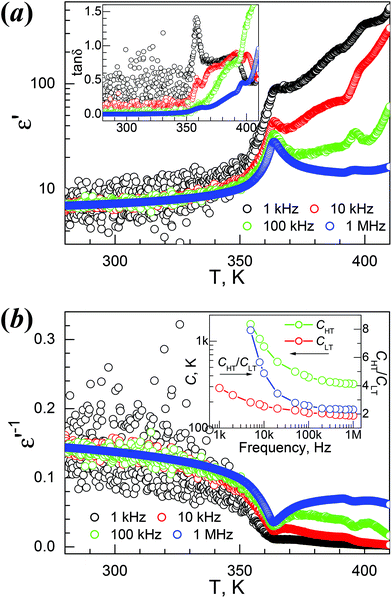
The temperature-dependent dielectric permittivity (dielectric constant ε′ and loss tanδ) of the four materials were investigated. The Td values of 1Mn and 4Mg are ca. 50 K and 90 K higher than their TC values, whereas Td values for 2Zn and 3Co are ca. 20 K higher than their TC values (Table 2). Therefore, the dielectric responses and anomalies of the 1Mn and 4Mg corresponding to the phase transitions could be studied with fair reliability, and we focused on these two materials. For 2Zn and 3Co the thermal decomposition is quite close to the phase transition, so their dielectric properties are briefly discussed.The ε′/tanδ vs. T traces of 1Mn at 1, 10, 100 and 1000 kHz are shown in Fig. 4a. On heating, the ε′ value at 1 MHz increased slowly from 7.0 around 280 K to 10.4 at the turning point of 353 K (Table 2), which is close to the TC, then it rose to the quite sharp maximum of 28.0 around 364 K, and went down on further heating, first quickly then slowly, to 14.3 around 390 K. After that the trace showed a small peak around 395 K, then started to rise, and above 410 K it went up more rapidly due to thermal decomposition of the sample. The tanδ data (Fig. 4a, inset) showed the related step around 365 K and the rise around 390 K then the enhancement above 400 K. When the frequency (f) was lowered, the ε′ peak values around 364 K increased to 33, 42, 71 and 260 for 100, 10, 1 and 0.1 kHz. The reciprocal permittivity 1/ε′ vs. T plots (Fig. 4b) showed a V-shape around 364 K, allowing the application of the Curie–Weiss laws ε′ = C/(T − T0) for the HT side and ε′ = C/(T0 − T) for the LT side, affording the C/T0 data in K at 1 MHz, 3.2 × 102/353 and 1.4 × 102/368, and the CHT/CLT ratio 2.3. The C values are typical for molecular ferroelectrics undergoing disorder–order transitions of HB systems,11,12,20 and the T0 data are close to the TC. These data remained nearly unchanged for f values above 100 kHz (Fig. 4b, inset), and the CHT/CLT ratios of 2.3 to 2.6 indicated the possible second order ferro- to para-electric phase transition according to the Devonshire theory.20b Below 100 kHz, the C values and CHT/CLT ratios increased, but the T0 data changed a little. The prominent dielectric anomaly around 364 K is clearly related to the phase transition at 355 K, triggered by the order–disorder transition of the NH2NH3+ cation, as discussed before. In the HT para-electric state, the NH2NH3+ cation has its NH2 end quickly vibrating between two mirror-related positions. When the temperature is lowered, this librational movement is frozen and the material undergoes a para- to ferro-electric phase transition, leading to the polar LT phase.
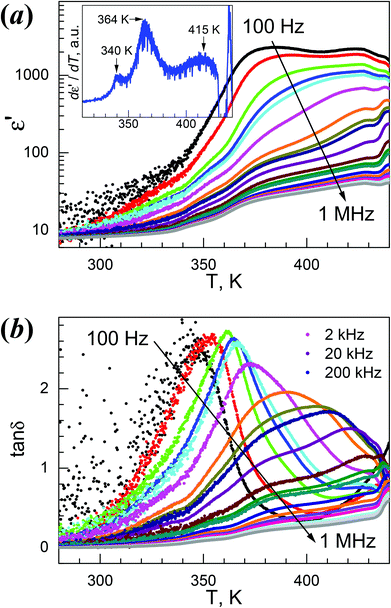
4Mg displayed strong frequency dispersion and quite complicated behavior in its dielectric responses and anomalies (Fig. 5, Fig. S10,†Table 2). At 1 MHz, the ε′ vs. T trace, starting from 7.9 at 280 K, gradually increased to show a first rise step in 335–355 K (ε′ = 10–14), then a second rise step from 355 to 375 K (ε′ = 14–24), then continuously went up to a maximum of 40.3 around 430 K. After a shallow minimum of 38.6 around 435 K, the trace rose again, probably caused by thermal decomposition (Fig. 5a). The derivative dε′/dT plot (Fig. 5a, inset) displayed three maxima at 340, 364 and 415 K, indicating the three increase steps in ε′. The tanδ vs. T trace at 1 MHz (Fig. 5b) possesses very similar stepwise characteristics. These data revealed complicated two or three steps phase transitions, as observed in the DSC study. For lower f values, the rise in ε′ shifted to lower temperatures, the ε′ values increased greatly, and the rise step around 370 K in fact became a broad peak with an ε′ value of up to 2.3 × 103 for 100 Hz. Below 1 kHz, the ε′ values are high above 370 K. The 1/ε′ vs. T plots (Fig. S10a†) are stepwise, and basically include two straight segments in 390–420 K (I) and 350–370 K (II). The data at 1 MHz within these two segments fitted by the Curie–Weiss law ε′ = C/(T0 − T) resulted in the C/T0 in K, 3.4 × 103/508 and 5.4 × 102/393 for segments I and II, respectively (Table 2). These C values are rational,11,12,20 and the T0 values are higher than TC. Strong frequency dependence is clearly observed for the tanδ data shown in Fig. 5b and Fig. S10b.† At 100 Hz, a peak in the tanδ vs. T plot was observed at 346 K. With increasing f values, the peak temperatures shifted higher, and became asymmetric by the emergence of two shoulders, a small one on the left and a large one on the right. The right shoulder developed to broad peaks approaching 430 K for f values higher than 2 kHz, and at the same time the original high peaks observed for lower f values were gradually suppressed into low shoulders. All these results revealed the relaxor-like behavior of 4Mg,23b,26a,55,56 and there are seemingly two dielectric relaxation processes, one around 360 K at low f values and the other around 420 K at high f values. In the isothermal tanδ vs. f traces from 336 K to 436 K in 4 K spaces (Fig. S10b†), the frequency dependence is significant, but the two relaxation processes are not easy to distinguish. However, the log–log plots showed the power law tanδ ∼ fn for low and high frequency sides of the peak positions, and typically, for the data of a temperature of 380 K, the exponents were n = 0.65 and −0.41 for both sides. These represent Jonscher's universal relaxation law for dielectrics,57 relating to the local transition in the orientation of the NH2NH3+ cation and the spread or relaxation in the lattice of the initial transition. The dielectric relaxation observed around 360 K at low f values obeyed the Arrhenius law for the τ = (2πf)−1vs. TP (temperature at peak position) data below 2 kHz where TP is located in the ε′′ vs. T data, with a pre-exponential factor τ0 = 1.45 × 10−17 s and an activation energy Ea/kB = 1.19 × 104 K ∼ 1.03 eV (Fig. S10b,† inset). However, the relaxation processes around 420 K and at high f values could not be parameterized because of the broad shoulder or peaks and the temperature very close to Td.
 | ||
| Fig. 5 Temperature-dependent traces of the dielectric permittivities on heating for 4Mg: (a) ε′ vs. T, and inset dε′/dT plot at 1 MHz, (b) tanδ vs. T. | ||
The dielectric response of 4Mg could be understood based on the VT structures discussed before. In the LT phase, the cations are completely ordered in the lattice and the LT phase is antiferroelectric, thus the material displayed low dielectric response. On heating, the weak strengths of cation-framework HBs and somewhat large void framework space allow the cation to become trigonally disordered. The HT structure is polar, with all NH3+ ends of the cations shifting to the +c direction. The polar character and the disorder of the NH2NH3+ cation in the HT structure satisfied the requirements for relaxor ferroelectrics,56 therefore resulting in the observed dielectric responses of high ε′ values in low f values and strong frequency dispersion. The activation energy for the cation's movement between different orientations is Ea ∼ 1.03 eV, as revealed by Arrhenius fitting for the frequency dependence around 360 K. This fairly high activation energy might be related to the antiferro- to ferroelectric phase transition and the observed two or three steps involved. VT structures with fine temperature intervals will be of help to reveal the details. 4Mg might experience another phase transition above 420 K because of the observation of the peaks in both ε′′ vs. T and tanδ vs. T traces, and this might be ferro- to para-electric, though no further information could be obtained due to sample decomposition.
2Zn and 3Co showed the relevant dielectric anomaly shoulders around their TC values, as shown in Fig. S11† (2Zn) and Fig. S12† (3Co). Since their TC values are close to the Td values, the dielectric anomalies were superimposed by the further enhanced dielectric responses due to the decomposition subsequently occurred. However, some information could still be retrieved from the data below TC, e.g. the rational C/T0 values in K, 3.3 × 102/372 and 3.3 × 102/405 at 1 MHz, for 2Zn and 3Co respectively. These data are listed in Table 2.
Therefore, the dielectric responses and phase transitions of the four present AMFF materials are clearly related to the order–disorder transition of the NH2NH3+ cations within the structures, and their basic relevance has been established. The very prominent dielectric anomalies indicate that the LT phases of 1Mn and 2Zn, and the HT phases of 3Co and 4Mg, being all polar, are probably ferroelectric, though further experimental investigation such as electric hysteresis measurements will be needed when large crystals are available.
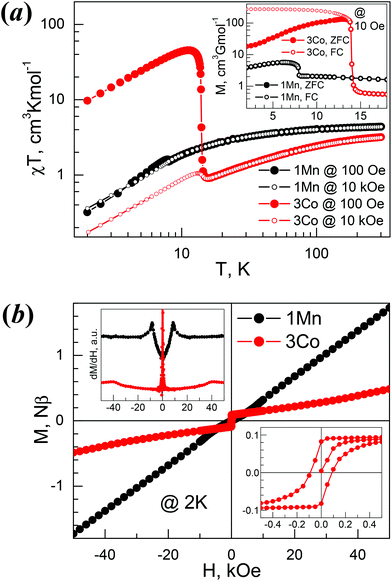
Magnetic properties of 1Mn and 3Co
The temperature evolutions of the direct current (dc) susceptibilities of 1Mn and 3Co (plots of χT vs. T, Fig. 6a) indicate that the two materials mainly displayed spin-canted AF characters. The χT values at 300 K, 4.39 (1Mn) and 3.19 (3Co) cm3 K mol−1, are expected for the two divalent octahedral metal ions.58 On cooling from 300 K to ca. 50 K the χT values decreased slowly. Below 50 K the values of χT decreased quickly to reach the minima, then rose to the maxima and then fell again upon further cooling (Table 4). This suggested the occurrence of spontaneous magnetization or magnetic LRO within the materials. The rise for 3Co was much steeper, with a high maximum of 45.4 cm3 K mol−1, similar to [HONH3][Co(HCOO)3].33 The high temperature susceptibility data obey the Curie–Weiss law well (Fig. S13a†) with Curie constants (C) and Weiss temperatures (Θ) in cm3 K mol−1 and K respectively: 4.57/−13.2 (1Mn), 3.80/−56.8 (3Co). The Landé g-factors derived from the C values are 2.04 (1Mn) and 2.58 (3Co), typical for isotropic Mn2+ and anisotropic Co2+.58 These data are comparable to related metal members in other AMFF series,21 and the significant negative Θ values indicate AF exchange interactions between metal ions, via anti–anti formato bridges. Under an applied field of 10 kOe, in high temperature regions the χT traces were almost identical to the traces under a 100 Oe field, while in low temperature regions the rises after the minima were suppressed for 1Mn, but still observed for 3Co. These observations characterized the two materials as weak ferromagnets.| Compound | 1Mn | 3Co |
|---|---|---|
| a Curie constants. b Weiss constants. c Minimum and maximum χT values and the related temperatures. d Critical temperatures based on ZFC/FC measurements. e Temperatures at peak positions in ac measurements at zero dc field, the first line for in-phase ac response and the second line for out-of-phase response. f Coercive fields. g Remnant magnetizations. h Canting angles, see text. i Fields for spin flop from peak or first turn positions in dM/dH. j Estimated from J/kB = 3Θ/[2zS(S + 1)]. k g Factors derived from Curie constants. | ||
| C /cm3 K mol−1 | 4.57 (4.53) | 3.80 (3.73) |
| Θ /K | −13.2 (−12.8) | −56.8 (−55.8) |
| (χT)300 K/cm3 K mol−1 | 4.39 (4.36) | 3.19 (3.19) |
| (χT)minc/cm3 K mol−1, Tmin/K | 1.50, 8.0 | 0.90, 15.5 |
| (χT)maxc/cm3 K mol−1, Tmax/K | 1.61, 7.8 | 45.4, 11.5 |
| (χT)2 K/cm3 K mol−1 | 0.32 (0.36) | 9.70 (1.88) |
| T N /K | 7.9 | 13.9 |
| T p /K | 8.0 | 13.8–13.9 |
| 13.5–13.8 | ||
| H C /kOe (at 2 K) | <0.01 | 0.09 |
| M R /Nβ (at 2 K) | <0.001 | 0.082 |
| M 50 kOe/Nβ (at 2 K) | 1.73 | 0.49 |
| α /° | <0.001 | 1.10 |
| H SP /kOe (at 2 K) | 8.50 | >40 |
| J /kB (K) | −0.38 | −3.8 |
| g Factor | 2.04 (2.04) | 2.85 (2.82) |
The magnetism in the low temperature region for 1Mn and 3Co were further investigated by zero-field and field cooled measurements (ZFC/FC, Fig. 6a, inset), isothermal magnetizations (Fig. 6b), and ac susceptibility measurements (Fig. S13b†). The bifurcations in ZFC/FC traces, though not very significant for 1Mn, indicated the 3D spin-canted AF LRO for the two materials at Néel temperatures (TN) of 7.9 K and 13.9 K for 1Mn and 3Co, respectively, determined by the negative peak positions on the dFC/dT data (not given here). For 1Mn, the spontaneous magnetization was less than 6 cm3 G mol−1, while 3Co showed a large spontaneous magnetization of ca. 250 cm3 G mol−1, in agreement with the large χT values at low temperatures. Known AMFFs with large spontaneous magnetizations include 3Co, chiral [HONH3][Co(HCOO)3],33 perovskite [C(NH2)3][Co(HCOO)3]29a and niccolite [CH3NH2CH2CH2NH2CH3][Fe2(HCOO)6].34 At 2.0 K (Fig. 6b), 1Mn showed nearly no hysteresis (remnant magnetization MR < 0.001Nβ and HC < 10 Oe) but small kinks around 8 kOe (Fig. 6b, top-left inset). In higher fields the magnetization increases linearly and reaches ca. 1.7Nβ at 50 kOe, being one third of the saturation value of 5Nβ for Mn2+ (S = 5/2 and g = 2.00). For 3Co (Fig. 6b, bottom-right inset), a hysteresis was observed, with MR and HC being 0.082Nβ and 90 Oe. In the high field region the magnetizations showed a slow increase with a slight turning up around 40 kOe, and the magnetizations were 0.49Nβ at 50 kOe. Spin-flop transitions (AF-SP)59 occurred at 2 K for 1Mn and 3Co, and the fields for spin-flop (HSP), estimated by peak position of dM/dH, were 8.5 kOe for 1Mn and 40 kOe for 3Co. From the MR values the canting angle could be estimated at less than 0.001° for 1Mn and 1.1° for 3Co, respectively,59 assuming the existence of two AF interacted sub-lattices in the materials. In ac susceptibilities (Fig. S13b†), 1Mn displayed frequency-independent peaks in its in-phase (χ′) responses at 8.0 K, close to the TN = 7.9 K by dc measurement, while the out-of-phase (χ′′) responses were in the noise level. 3Co showed slight frequency-dependent χ′ and χ′′ peaks around 13.8 K, with a small ϕ = (ΔTP/TP)/Δ(log f)60 ∼ 0.004, where TP is the peak temperature of χ′ and f the ac frequency. This relaxation behaviour, similar to that encountered for some Co-AMFFs,29a,33 could be due to domain-wall movement,61 or chirality-related ac responses62 as 3Co is chiral. The M⋯M magnetic couplings through the anti–anti formato bridge within the two solids could be estimated by using the molecular field result, J/kB = 3Θ/[2zS(S + 1)], and were −0.38 (1Mn) and −3.8 K (3Co) for z = 6 and S = 5/2 and 3/2 for 1Mn and 3Co, respectively, and they are comparable to those found in AMFFs.21 The spin-canted AF is due to the occurrence of Dzyaloshinsky–Moriya or the antisymmetric interaction63 resulting from the non-centrosymmetric bridges of anti–anti HCOO linking magnetic sites, as observed for many AMFFs.21
Finally, we emphasize that 1Mn and 3Co showed both electric and magnetic LRO in low temperature regions, and this makes the magnetic members of the present series of great interest for the research on MOF/molecule-based multiferroics which were only recognized very recently,9,23,26,29,30 and probably adds a new family of AMFF multiferroic materials.
Conclusion
In conclusion, we have successfully synthesized and characterized a new class of AMFFs of [NH2NH3][M(HCOO)3] (M = divalent Mn, Zn, Co and Mg) by employing hydrazinium as the cationic template and component. The series has two typical AMFF structures. The Mn and Zn members are perovskites, with anionic 412·63 metal–formate frameworks and the cubic cavities occupied by the NH2NH3+ cations. They undergo structural transitions around 350 K, in which the structures change from LT polar phases in Pna21 to HT non-polar phases in Pnma, due to the occurrence of the librational movement of the NH2 end of the NH2NH3+ cation in the cavity and related significant framework regulation and expansion. The Co and Mg members possess chiral 49·66 metal–formate frameworks with chiral hexagonal channels accommodating NH2NH3+ cations. The LT phases in non-polar P212121 are probably antiferroelectric. They display phase transitions at 380 K (Co) and 348 K (Mg) and change to a polar HT phase in P63 because of the occurrence of trigonal disorder in the cation. Accompanied by these transitions the materials show prominent anisotropic/negative thermal expansion and dielectric anomalies, and their structural relevance is established. From LT to HT, the phase transitions of Mn and Zn members are ferro- to para-electric, while for the Co and Mg members the transitions are probably antiferro- to ferro-electric. The spontaneous polarization for the polar structures was estimated at 3.58 (Mn, 110 K), 3.48 (Zn, 110 K), 2.61 (Co, 405 K) and 3.44 (Mg, 400 K) μC cm−2. The two magnetic Mn and Co members also show long-range-ordering of spin-canted antiferromagnetism, with Néel temperatures of 7.9 K and 13.9 K, respectively. Therefore, they constitute new molecule-based multiferroics. It is also expected that the present series will produce more than ten new AMFFs showing interesting phase transitions occurring at high temperatures even comparable to the ferroelectric oxides, and the relevant NTE, electric, magnetic and possible multiferroic properties if the two polymorphs for all divalent metal ions from Mn to Zn plus Mg were obtained. The series will probably become a new prototypical class of MOF-based multiferroics, and much further research is required. This research is in progress.Acknowledgements
This work was supported by the NSFC (grants 21171010, 21290170, 21290171), and the National Basic Research Program of China (grant 2009CB929403).References
- (a) N. A. Spaldin and M. Fiebig, Science, 2005, 309, 391 CrossRef CAS PubMed; (b) N. A. Spaldin, S.-W. Cheong and R. Ramesh, Phys. Today, 2010, 63, 38 CrossRef PubMed; (c) W. Eerenstein, N. D. Mathur and J. F. Scott, Nature, 2006, 442, 759 CrossRef CAS PubMed; (d) K. F. Wang, J.-M. Liu and Z. F. Ren, Adv. Phys., 2009, 58, 321 CrossRef CAS; (e) M. Mostovoy, Nat. Mater., 2010, 9, 188 CAS.
- (a) S. Dong and J.-M. Liu, Mod. Phys. Lett. B, 2012, 26, 1230004 CrossRef; (b) A. Loidl, H. von Loehneysen and G. M. Kalvius, J. Phys.: Condens. Matter, 2008, 20, 430301 CrossRef; (c) A. R. Akbashev and A. R. Kaul, Russ. Chem. Rev., 2011, 80, 1159 CrossRef CAS PubMed; (d) D. Khomskii, Physics, 2009, 2, 20 CrossRef.
- (a) A. K. Cheetham and C. N. Rao, Science, 2007, 318, 58 CrossRef CAS PubMed; (b) C. N. Rao, A. K. Cheetham and A. Thirumurugan, J. Phys.: Condens. Matter, 2008, 20, 083202 CrossRef.
- For recent reviews, (a) H.-C. Zhou, J. R. Long and O. M. Yaghi, ed., Thematic issue on metal-organic frameworks, Chem. Rev., 2012, 112, 673; (b) J. R. Long and O. M. Yaghi, ed., Special issue on metal-organic frameworks, Chem. Soc. Rev., 2009, 38, 1213 Search PubMed; (c) C. Janiak and J. K. Vieth, New J. Chem., 2010, 34, 2366 RSC.
- E. Coronado, J. R. Galán-Mascarós, C. J. Gómez-García and V. Laukhin, Nature, 2003, 2, 190 CrossRef PubMed.
- (a) O. Sato, J. Tao and Y.-Z. Zhang, Angew. Chem., Int. Ed., 2007, 46, 2152 CrossRef CAS PubMed; (b) C. Train, M. Gruselle and M. Verdaguer, Chem. Soc. Rev., 2011, 40, 3297 RSC.
- P. Dechambenoit and J. R. Long, Chem. Soc. Rev., 2011, 40, 3249 RSC.
- (a) R. Ramesh, Nature, 2009, 461, 1218 CrossRef CAS PubMed; (b) S.-i. Ohkoshi, H. Tokoro, T. Matsuda, H. Takahashi, H. Irie and K. Hashimoto, Angew. Chem., Int. Ed., 2007, 46, 3238 CrossRef CAS PubMed; (c) E. Pardo, C. Train, H. Liu, L.-M. Chamoreau, B. Dkhil, K. Boubekeur, F. Lloret, K. Nakatani, H. Tokoro, S.-i. Ohkoshi and M. Verdaguer, Angew. Chem., Int. Ed., 2012, 51, 8356 CrossRef CAS PubMed; (d) H. B. Cui, Z. M. Wang, K. Takahashi, Y. Okano, H. Kobayashi and A. Kobayashi, J. Am. Chem. Soc., 2006, 128, 15074 CrossRef CAS PubMed.
- I. E. Collings, A. B. Cairns, A. L. Thompson, J. E. Parker, C. C. Tang, M. G. Tucker, J. Catafesta, C. Levelut, J. Haines, V. Dmitriev, P. Pattison and A. L. Goodwin, J. Am. Chem. Soc., 2013, 135, 7610 CrossRef CAS PubMed.
- (a) D.-F. Weng, Z.-M. Wang and S. Gao, Chem. Soc. Rev., 2011, 40, 3157 RSC; (b) E. Coronado and K. R. Dunbar, ed., Special issue for the Forum on Molecular Magnetism: The Role of Inorganic Chemistry, Inorg. Chem., 2009, 48, 3293 Search PubMed; (c) J. S. Miller and D. Gatteschi, ed., Molecule-based magnets themed issue, Chem. Soc. Rev., 2011, 40, 3065 Search PubMed; (d) C. Rovira and J. Veciana, ed., Special issue on crystal engineering in molecular magnetism, CrystEngComm, 2009, 11, 2031 Search PubMed.
- (a) T. Hang, W. Zhang, H.-Y. Ye and R.-G. Xiong, Chem. Soc. Rev., 2011, 40, 3577 RSC; (b) W. Zhang and R.-G. Xiong, Chem. Rev., 2012, 112, 1163 CrossRef CAS PubMed.
- (a) W. Zhang, Y. Cai, R. G. Xiong, H. Yoshikawa and K. Awaga, Angew. Chem., Int. Ed., 2010, 49, 6608 CrossRef CAS PubMed; (b) W. Zhang, H.-Y. Ye, R. Graf, H. W. Spiess, Y.-F. Yao, R.-Q. Zhu and R.-G. Xiong, J. Am. Chem. Soc., 2013, 135, 5230 CrossRef CAS PubMed.
- (a) J. S. O. Evan, J. Chem. Soc., Dalton Trans., 1999, 3317 RSC; (b) W. Miller, C. W. Smith, D. S. Mackenzie and K. E. Evans, J. Mater. Sci., 2009, 44, 5441 CrossRef CAS; (c) K. Takenaka, Sci. Technol. Adv. Mater., 2012, 13, 013001 CrossRef; (d) C. Lind, Materials, 2012, 5, 1125 CrossRef CAS.
- (a) T. A. Mary, J. S. O. Evans, T. Vogt and A. W. Sleight, Science, 1996, 272, 90 CAS; (b) G. Ernst, C. Broholm, G. R. Kowach and A. P. Ramirez, Nature, 1998, 396, 147 CrossRef CAS PubMed; (c) J. S. O. Evans, T. A. Mary, T. Vogt, M. A. Subramanian and A. W. Sleight, Chem. Mater., 1996, 8, 2809 CrossRef CAS; (d) P. Lightfoot, D. A. Woodcock, M. J. Maple, L. A. Villaescusa and P. A. Wright, J. Mater. Chem., 2001, 11, 212 RSC; (e) M. P. Attfield and A. W. Sleight, Chem. Mater., 1998, 10, 2013 CrossRef CAS.
- (a) K. W. Chapman, P. J. Chupas and C. J. Kepert, J. Am. Chem. Soc., 2005, 127, 15630 CrossRef CAS PubMed; (b) A. L. Goodwin, M. Calleja, M. J. Conterio, M. T. Dove, J. S. O. Evans, D. A. Keen, L. Peters and M. G. Tucker, Science, 2008, 319, 794 CrossRef CAS PubMed.
- (a) N. Lock, Y. Wu, M. Christensen, L. J. Cameron, V. K. Peterson, A. J. Bridgeman, C. J. Kepert and B. B. Iversen, J. Phys. Chem. C, 2010, 114, 16181 CrossRef CAS; (b) Y. Wu, A. Kobayashi, G. J. Halder, V. K. Peterson, K. W. Chapman, N. Lock, P. D. Southon and C. J. Kepert, Angew. Chem., Int. Ed., 2008, 47, 8929 CrossRef CAS PubMed; (c) V. K. Peterson, G. J. Kearley, Y. Wu, A. J. Ramirez-Cuesta, E. Kemner and C. J. Kepert, Angew. Chem., Int. Ed., 2010, 49, 585 CrossRef CAS PubMed.
- (a) Y.-S. Wei, K.-J. Chen, P.-Q. Liao, B.-Y. Zhu, R.-B. Lin, H.-L. Zhou, B.-Y. Wang, W. Xue, J.-P. Zhang and X.-M. Chen, Chem. Sci., 2013, 4, 1539 RSC; (b) I. Grobler, V. J. Smith, P. M. Bhatt, S. A. Herbert and L. J. Barbour, J. Am. Chem. Soc., 2013, 135, 6411 CrossRef CAS PubMed; (c) A. L. Goodwin, K. W. Chapman and C. J. Kepert, J. Am. Chem. Soc., 2005, 127, 17980 CrossRef CAS PubMed; (d) N. Lock, M. Christensen, C. J. Kepert and B. B. Iversen, Chem. Commun., 2013, 49, 789 RSC; (e) A. E. Phillips, A. L. Goodwin, G. J. Halder, P. D. Southon and C. J. Kepert, Angew. Chem., Int. Ed., 2008, 47, 1396 CrossRef CAS PubMed; (f) A. E. Phillips, G. J. Halder, K. W. Chapman, A. L. Goodwin and C. J. Kepert, J. Am. Chem. Soc., 2010, 132, 10 CrossRef CAS PubMed.
- (a) R. H. Baughman, S. Stafström, C. Cui and S. O. Dantas, Science, 1998, 279, 1522 CrossRef CAS; (b) A. B. Cairns, J. Catafesta, C. Levelut, J. Rouquette, A. van der Lee, L. Peters, A. L. Thompson, V. Dmitriev, J. Haines and A. L. Goodwin, Nat. Mater., 2013, 12, 212 CrossRef CAS PubMed; (c) A. B. Cairns, A. Thompson, L. M. G. Tucker, J. Haines and A. L. Goodwin, J. Am. Chem. Soc., 2012, 134, 445 CrossRef PubMed.
- (a) G. N. Greaves, F. Meneau, A. Sapelkin, L. M. Colyer, I. A. Gwynn, S. Wade and G. Sankar, Nat. Mater., 2003, 2, 622 CrossRef CAS PubMed; (b) Y. H. Hu and L. Zhang, Phys. Rev. B: Condens. Matter, 2010, 81, 174103 CrossRef; (c) K. W. Chapman, G. J. Halder and P. J. Chupas, J. Am. Chem. Soc., 2009, 131, 17546 CrossRef CAS PubMed; (d) T. D. Bennett, A. L. Goodwin, M. T. Dove, D. A. Keen, M. G. Tucker, E. R. Barney, A. K. Soper, E. G. Bithell, J.-C. Tan and A. K. Cheetham, Phys. Rev. Lett., 2010, 104, 115503 CrossRef.
- (a) F. Jona and G. Shirane, Ferroelectric crystals, Pergamon Press, New York, 1962 Search PubMed; (b) M. E. Lines and A. M. Glass, Principles and Applications of Ferroelectrics and Related Materials, Clarendon Press, Oxford, 1977 Search PubMed; (c) T. Mitsui, I. Tatsuzaki and E. Nakamura, An Introduction to the Physics of Ferroelectrics, Gordon and Breach Science Publishers, New York, 1976 Search PubMed.
- (a) Z. M. Wang, K. L. Hu, S. Gao and H. Kobayashi, Adv. Mater., 2010, 22, 1526 CrossRef CAS PubMed; (b) X.-Y. Wang, Z.-M. Wang and S. Gao, Chem. Commun., 2008, 281 RSC.
- (a) S. Horiuchi, Y. Tokunaga, G. Giovannetti, S. Picozzi, H. Itoh, R. Shimano, R. Kumai and Y. Tokura, Nature, 2010, 463, 789 CrossRef CAS PubMed; (b) S. Horiuchi, R. Kumaia and Y. Tokura, Chem. Commun., 2007, 2321 RSC.
- (a) G.-C. Xu, X.-M. Ma, L. Zhang, Z.-M. Wang and S. Gao, J. Am. Chem. Soc., 2010, 132, 9588 CrossRef CAS PubMed; (b) G.-C. Xu, W. Zhang, X.-M. Ma, Y.-H. Chen, L. Zhang, H.-L. Cai, Z.-M. Wang, R.-G. Xiong and S. Gao, J. Am. Chem. Soc., 2011, 133, 14948 CrossRef CAS PubMed; (c) W. Li, M. R. Probert, M. Kosa, T. D. Bennett, A. Thirumurugan, R. P. Burwood, M. Parinello, J. A. K. Howard and A. K. Cheetham, J. Am. Chem. Soc., 2012, 134, 11940 CrossRef CAS PubMed; (d) Z. M. Wang, B. Zhang, K. Inoue, H. Fujiwara, T. Otsuka, H. Kobayashi and M. Kurmoo, Inorg. Chem., 2007, 46, 437 CrossRef CAS PubMed.
- (a) Z. M. Wang, B. Zhang, T. Otsuka, K. Inoue, H. Kobayashi and M. Kurmoo, Dalton Trans., 2004, 2209 RSC; (b) R. Shang, X. Sun, Z.-M. Wang and S. Gao, Chem.–Asian J., 2012, 7, 1697 CrossRef CAS PubMed.
- X. Y. Wang, L. Gan, S. W. Zhang and S. Gao, Inorg. Chem., 2004, 43, 4615 CrossRef CAS PubMed.
- (a) D.-W. Fu, W. Zhang, H.-L. Cai, Y. Zhang, J.-Z. Ge, R.-G. Xiong, S. D. Huang and T. Nakamura, Angew. Chem., Int. Ed., 2011, 50, 11947 CrossRef CAS PubMed; (b) P. Jain, V. Ramachandran, R. J. Clark, H. D. Zhou, B. H. Toby, N. S. Dalal, H. W. Kroto and A. K. Cheetham, J. Am. Chem. Soc., 2009, 131, 13625 CrossRef CAS PubMed; (c) M. Sánchez-Andújar, S. Presedo, S. Yáñez-Vilar, S. Castro-García, J. Shamir and M. A. Señarís-Rodríguez, Inorg. Chem., 2010, 49, 1510 CrossRef PubMed; (d) Z. Wang, P. Jain, K.-Y. Choi, J. van Tol, A. K. Cheetham, H. W. Kroto, H.-J. Koo, H. Zhou, J. Hwang, E. S. Choi, M.-H. Whangbo and N. S. Dalal, Phys. Rev. B: Condens. Matter, 2013, 87, 224406 CrossRef; (e) R. I. Thomson, P. Jain, A. K. Cheetham and M. A. Carpenter, Phys. Rev. B: Condens. Matter, 2012, 86, 214304 CrossRef; (f) W. Wang, L.-Q. Yan, J.-Z. Cong, Y.-L. Zhao, F. Wang, S.-P. Shen, T. Zou, D. Zhang, S.-G. Wang, X.-F. Han and Y. Sun, Sci. Rep., 2013, 3, 2024, DOI:10.1038/srep02024.
- (a) B. Zhou, Y. Imai, A. Kobayashi, Z.-M. Wang and H. Kobayashi, Angew. Chem., Int. Ed., 2010, 50, 11441 CrossRef PubMed; (b) Y. Imai, B. Zhou, Y. Ito, A. Kobayashi, Z.-M. Wang and H. Kobayashi, Chem.–Asian J., 2012, 7, 2786 CrossRef CAS PubMed.
- M. Y. Li, B. Liu, B. W. Wang, Z. M. Wang, S. Gao and M. Kurmoo, Dalton Trans., 2011, 40, 6038 RSC.
- (a) K.-L. Hu, M. Kurmoo, Z.-M. Wang and S. Gao, Chem.–Eur. J., 2009, 15, 12050 CrossRef CAS PubMed; (b) A. Stroppa, P. Jain, P. Barone, M. Marsman, J. M. Perez-Mato, A. K. Cheetham, H. W. Kroto and S. Picozzi, Angew. Chem., Int. Ed., 2011, 50, 5847 CrossRef CAS PubMed; (c) A. Stroppa, P. Barone, P. Jain, J. M. Perez-Mato and S. Picozzi, Adv. Mater., 2013, 25, 2284 CrossRef CAS PubMed.
- (a) L. Cañadillas-Delgado, O. Fabelo, J. A. Rodríguez-Velamazán, M. Lemée-Cailleau, S. A. Mason, E. Pardo, F. Lloret, J. Zhao, X. Bu, V. Simonet, C. V. Colin and J. Rodríguez-Carvajal, J. Am. Chem. Soc., 2012, 134, 19772 CrossRef PubMed; (b) K. S. Hagen, S. G. Naik, B. H. Huynh, A. Masello and G. Christou, J. Am. Chem. Soc., 2009, 131, 7516 CrossRef CAS PubMed; (c) J.-P. Zhao, B.-W. Hu, F. Lloret, J. Tao, Q. Yang, X.-F. Zhang and X.-H. Bu, Inorg. Chem., 2010, 49, 10390 CrossRef CAS PubMed.
- (a) P. Jain, N. S. Dalal, B. H. Toby, H. W. Kroto and A. K. Cheetham, J. Am. Chem. Soc., 2008, 130, 10450 CrossRef CAS PubMed; (b) T. Asaji and K. Ashitomi, J. Phys. Chem. C, 2013, 117, 10185 CrossRef CAS; (c) T. Besara, P. Jain, N. S. Dalal, P. L. Kuhns, A. P. Reyes, H. W. Kroto and A. K. Cheetham, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6828 CrossRef.
- (a) B. Pato-Doldán, M. Sánchez-Andújar, L. C. Gómez-Aguirre, S. Yáñez-Vilar, J. López-Beceiro, C. Gracia-Fernández, A. A. Haghighirad, F. Ritter, S. Castro-García and M. A. Señarís-Rodríguez, Phys. Chem. Chem. Phys., 2012, 14, 8498 RSC; (b) A. Rossin, A. Ienco, F. Costantino, T. Montini, B. D. Credico, M. Caporali, L. Gonsalvi, P. Fornasiero and M. Peruzzini, Cryst. Growth Des., 2008, 8, 3302 CrossRef CAS; (c) A. Rossin, M. R. Chierotti, G. Giambastiani, R. Gobettob and M. Peruzzini, CrystEngComm, 2012, 14, 4454 RSC.
- B. Liu, R. Shang, K.-L. Hu, Z.-M. Wang and S. Gao, Inorg. Chem., 2012, 51, 13363 CrossRef CAS PubMed.
- (a) M.-Y. Li, M. Kurmoo, Z. M. Wang and S. Gao, Chem.–Asian J., 2011, 6, 3084 CrossRef CAS PubMed; (b) Z. M. Wang, X. Y. Zhang, S. R. Batten, M. Kurmoo and S. Gao, Inorg. Chem., 2007, 46, 8439 CrossRef CAS PubMed.
- D.-W. Fu, W. Zhang, H.-L. Cai, Y. Zhang, J.-Z. Ge, R.-G. Xiong and S. D. Huang, J. Am. Chem. Soc., 2011, 133, 12780 CrossRef CAS PubMed.
- (a) W. Zhang, H.-Y. Ye, H.-L. Cai, J.-Z. Ge, R.-G. Xiong and S. D. Huang, J. Am. Chem. Soc., 2010, 132, 7300 CrossRef CAS PubMed; (b) D. W. Fu, H. L. Cai, Y. M. Liu, Q. Ye, W. Zhang, Y. Zhang, X. Y. Chen, G. Giovannetti, M. Capone, J. Y. Li and R. G. Xiong, Science, 2013, 339, 425 CrossRef CAS PubMed; (c) H. L. Cai, Y. Zhang, D. W. Fu, W. Zhang, T. Liu, H. Yoshikawa, K. Awaga and R. G. Xiong, J. Am. Chem. Soc., 2012, 134, 18487 CrossRef CAS PubMed.
- G. Bator, R. Jakubas and L. Sobczyk, in Crystal Engineering: From molecules and crystals to materials, ed. D. Braga, F. Grepioni and A. G. Orpen, Kluwer Acad. Pub., Dordrecht, 1999, pp. 459–468 Search PubMed.
- A. B. Cairns and A. L. Goodwin, Chem. Soc. Rev., 2013, 42, 4881 RSC.
- (a) B. V. Nonius, Collect software, Delft, The Netherlands, 1998 Search PubMed; (b) B. V. Nonius, HKL2000 and maXus softwares, University of Glasgow, Scotland, UK, Delft, The Netherlands and MacScience Co. Ltd, Yokohama, Japan, 2000 Search PubMed.
- CrysAlisPro software, Agilent Technologies UK Ltd, Oxford, UK, 2012 Search PubMed.
- G. M. Sheldrick, SHELX-97, Program for Crystal Structure Determination, University of Göttingen, Germany, 1997 Search PubMed.
- L. N. Mulay and E. A. Boudreaux, Theory and Applications of Molecular Diamagnetism, John Wiley & Sons Inc., New York, 1976 Search PubMed.
- The Fe products of different batches contained crystals of the two Fe polymorphs, the rectangular pale yellow crystals and the pale blue hexagonal column or bipyramidal crystals. The rectangular crystals have cell dimensions at 290 K as follows: a = 8.7938(3), b = 7.7675(2), c = 11.6312(4) Å, α = β = γ = 90°, V = 794.48(4) Å3, and the structure was determined. The hexagonal crystals always showed as twinned and we are still trying to determine the structure. However its PXRD (data not given) was very close to that of 3Co, confirming the existence of the phase.
- (a) D. H. Williams and I. Fleming, Spectroscopic Method in Organic Chemistry, McGraw-Hill Book Co, Beijing, China, 5th edn, 1998 Search PubMed; (b) K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds, Wiley, New York, 1986 Search PubMed; (c) D. Stoilova and V. Koleva, J. Mol. Struct., 2000, 553, 131 CrossRef CAS; (d) D. Stoilova and V. Koleva, J. Mol. Struct., 2001, 560, 15 CrossRef CAS.
- M. A. White, in Crystal Engineering: The Design and Application of Functional Solids, ed. K. R. Seddon and M. Zaworotko, Kluwer Acad. Pub., Dordrecht, 1999, p. 279 Search PubMed.
- Z.-M. Duan, Z.-M. Wang and S. Gao, Dalton Trans., 2011, 40, 4465 RSC.
- F. A. Cotton, G. C. Wilkinson, A. Murillo and M. Bochmann, Advanced Inorganic Chemistry, Wiley, New York, 6th edn, 1999, p. 1304 Search PubMed.
- A. L. Spek, PLATON, A Multipurpose Crystallographic Tool, Utrecht University, Utrecht, The Netherlands, 2001 Search PubMed.
- This was calculated using PCMODEL Version 9.1, see http://www.serenasoft.com.
- Y. Zhang, W. Zhang, S. H. Li, Q. Ye, H. L. Cai, F. Deng, R. G. Xiong and S. P. D. Huang, J. Am. Chem. Soc., 2012, 134, 11044 CrossRef CAS PubMed.
- K. Aizu, Phys. Rev., 1966, 146, 423 CrossRef CAS.
- D. Braga, F. Grepionia and J. J. Novoab, Chem. Commun., 1998, 1595 Search PubMed.
- A. I. Kitaigorodsky, Molecular Crystals and Molecules, Academic Press, New York, 1973, p. 18 Search PubMed.
- B. Liu, H.-B. Zheng, Z.-M. Wang and S. Gao, CrystEngComm, 2011, 13, 5285 RSC.
- (a) M. Szafrański, A. Katrusiak and G. J. McIntyre, Cryst. Growth Des., 2010, 10, 4334 CrossRef; (b) M. Szafrański and A. Katrusiak, J. Phys. Chem. B, 2008, 112, 6779 CrossRef PubMed.
- (a) G. A. Samara, J. Phys.: Condens. Matter, 2003, 15, R367 CrossRef CAS; (b) A. A. Bokov and Z.-G. Ye, J. Mater. Sci., 2006, 41, 31 CrossRef CAS PubMed; (c) W. J. Kleemann, Mater. Sci., 2006, 41, 129 CrossRef CAS.
- A. K. Jonscher, Dielectric Relaxation in Solids, Chelsea Dielectrics Press, London, 1983 Search PubMed.
- A. T. Casey and S. Mitra, in Theory and Application of Molecular Paramagnetism, ed. L. N. Mulay and E. A. Boudreaux, Wiley, New York, 1976, pp. 183–243 Search PubMed.
- R. L. Carlin, Magnetochemistry, Springer-Verlag, Berlin, Heidelberg, 1986, pp. 148–154 Search PubMed.
- J. A. Mydosh, Spin Glass: an Experimental Introduction, Taylor & Francis, London-Washington, DC, 1993 Search PubMed.
- M. Balanda, in Relaxation Phenomena: Liquid Crystals, Magnetic Systems, Polymers, High-TC Superconductors, Metallic Glass, ed. W. Haase and S. Wróbel, Springer-Verlag, Berlin, Heidelberg, 2003, pp. 97–99 Search PubMed.
- (a) M. Mito, K. Iriguchi, H. Deguchi, J. Kishine, K. Kikuchi, H. Ohsumi, Y. Yoshida and K. Inoue, Phys. Rev. B: Condens. Matter, 2009, 79, 012406 CrossRef; (b) M. Mito, K. Iriguchi, H. Deguchi, J. Kishine, Y. Yoshida and K. Inoue, J. Appl. Phys., 2012, 111, 103914 CrossRef PubMed.
- (a) I. Dzyaloshinsky, J. Phys. Chem. Solids, 1958, 4, 241 CrossRef CAS; (b) T. Moriya, Phys. Rev., 1960, 120, 91 CrossRef CAS; (c) T. Moriya, in Magnetism, ed. G. T. Rado and H. Suhl, Academic Press, New York, 1963, vol. 1, pp. 85–124 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Tables S1 to S4, Fig. S1 to S13, CIF files. CCDC 958452–958467. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c3qi00034f |
| This journal is © the Partner Organisations 2014 |