Experimental, DFT and quantum Monte Carlo studies of a series of peptide-based metal–organic frameworks: synthesis, structures and properties

Abstract

A series of bio-analogous peptide-based metal–organic frameworks (Mn(1), Fe(2), Co(3), Cu(4), Ag(5) and Pb(6)) based on one cyclic dipeptide (2,5-piperazinedione-1,4-diacetic acid, H₂PODC) were obtained and the relationships between properties (luminescence and magnetism) and structure was investigated. Crystal structure analysis shows that (1) 1–3 feature a three-dimensional isomorphic framework; (2) 4 shows one two-dimensional plane structure; (3) 5 shows a three-dimensional framework with one alternate Ag–Ag chain (d_Ag–Ag = 2.7918 and 2.9346 Å); (4) 6 indicates a three-dimensional structure with one dimensional 7.0 × 7.0 Ų channel. Combination of magnetic measures and quantum Monte Carlo (QMC) studies reveals that 1 has anti-ferromagnetic properties with a J of −0.5 cm⁻¹ and 4 exhibits ferromagnetic properties with a J of 2.23 cm⁻¹, while both 2 and 3 show ferrimagnetic properties. Spin polarized density functional theory (DFT) calculations uncover that antiferromagnetism of 1 is attributed to the coupling of paramagnetic Mn(II) ions by −/−/+ spin nets of linking carboxylate, while in 4 ferromagnetic superexchange of Cu(II) ions is derived from the spin polarization effect through the carboxylate bridge in the +/+/+ spin nets of linking carboxylates. Furthermore, DFT calculation results show that two absorption peaks of 5 should be attributed to the transitions of the valence band (VB)→ the second empty band and VB→ the conduction band (CB), and one emission peak is the result of the CB→VB transition, where the electrons transfer from the Ag–Ag metal bond to localized 4d orbitals of Ag atoms.

---

Introduction

In the last two decades, metal–organic frameworks (MOFs) or coordination polymers are of contemporary interest, not merely due to their aesthetically interesting structures¹ by the amalgamation of chemistry and geometry, but mainly due to their potential applications in adsorption,² separation,³ catalysis,⁴ luminescence,⁵ magnetism⁶ and nonlinear optics.⁷ The design philosophy of the second building unit (SBU)⁸ provides a large promotion to the assembly of MOFs, where the linkers involve polycarboxylic acids (e.g. aromatic carboxylic acids and fatty acids),⁹ imidazole¹⁰ and N–O mixed ligands.¹¹ Arguably most notable in this context is the research on bio-analogous MOFs from biologically derived molecules (e.g. amino acids and nucleobases¹²). That may be attributed to two aspects: (1) potential application of the next generation biomimetic porous materials; (2) investigation of the interaction between biological groups and trace metal ions. Peptides, as well-known biological molecules, always play an important role in molecular biology as antibodies and protein tags. Moreover, unique functional groups (e.g. carboxylate and amino groups) and the flexibility of peptides endow them with an adaptable-porous linker of MOFs. Since the pioneering work of Taubert et al.¹³ the studies concerning the synthesis and properties of peptide-based MOFs have begun to emerge.¹⁴ For instance, Rosseinsky et al. have reported two peptide-based adaptable porous materials: [Zn(Gly-Ala)2]^14a and [Zn(Gly-Thr)2].^14b However, owing to the congenital friability of the peptide bond, design and synthesis of peptide-based MOFs are still challenging.

Moreover, accurate design of materials relies on the information regarding connection between the structure and the properties. Therefore, investigations of the structure-to-function relationship have been an important and challenging topic in the field of MOFs. In this regard, experimental views alone are insufficient to produce the profound comprehension. Currently, combination of theoretical calculations and experimental studies has become an effective tool. Various theoretical simulation methods, including DFT,¹⁵ Monte Carlo (MC),¹⁶ and molecular dynamics (MD),¹⁷ have been widely applied to forecast or explain the interesting experimental phenomena of MOFs. However, to the best of our knowledge, the corresponding studies regarding the structure-to-function relationship of peptide-based MOFs have never been reported.

In this article, we report the synthesis and structure of a series of new peptide-based MOFs, and focus on their magnetic and luminescence properties. Furthermore, via QMC and DFT calculations, we investigated the magnetism–structure and luminescence–structure relationships.

Results and discussion

Crystal structure description

Compound 1, [Mn(PODC)(H₂O)₂], crystallized in the P2(1)/c space group of the monoclinic system. Single-crystal X-ray diffraction analysis reveals that the asymmetric unit contains a half Mn(II) ion, a half PODC²⁻ ligand and one aqua ligand. As shown in Fig. 1(a), the coordination environment of the Mn(II) ion can be viewed as a distorted octahedron, featuring the contributions by four carboxylate oxygen atoms from PODC²⁻ ligands and two aqua ligands. The coordination mode of PODC²⁻ is shown in Fig. S3(a).† The corresponding bond lengths of Mn–O are 2.1407–2.2122 Å, consistent with the previous results.¹⁸ Inspecting the whole structure of 1, it is observed that through the syn–anti carboxylate bridges, each Mn(II) ion connects with the adjacent ones so as to form a two-dimensional {Mn(COO)_n} plane structure (see Fig. 1(b)), where the distance of Mn⋯Mn and the torsion angle of Mn–O–C–O–Mn are 6.102 Å and 119.48°, respectively. Furthermore, the 2D {Mn(COO)_n} plane bridges with the adjacent ones via PODC²⁻ ligands, leading to a three-dimensional framework, as shown in Fig. 1(c). The short Schläfli vertex notation of the net can be represented as {6⁵·8}, as indicated by the TOPOS software.¹⁹

Fig. 1 (a) ORTEP plot showing the coordination environment of Mn(II) ions; the two-dimensional structure of 1 viewed along the a axis (b) and the topology sketch map of 1 (c).

Moreover, both 2 and 3 exhibit three-dimensional frameworks with 1. The bond lengths of Fe(II)–O and Co(II)–O are 2.0689(11)–2.1501(13) and 2.0739(10)–2.1095(12) Å, respectively. Additionally, the distance of Fe⋯Fe and Co⋯Co is 6.028 and 6.025 Å, respectively. Generally, these bond distances are slightly smaller than that of 1.

In contrast to compounds 1–3, crystal structure analysis reveals that compound 4 displays a two-dimensional plane structure with the space group C2/c. As is clear from Fig. 2(a), the asymmetric unit of 4 consists of a half Cu(II) ion, a half PODC²⁻ ligand and one aqua ligand. Like 1–3, the coordination configuration of the Cu(II) ion can be described as a distorted octahedron, featuring the coordination by four carboxylate oxygen atoms from PODC²⁻ ligands and two aqua ligands. The resulting bond lengths of Cu–O are 1.9501(14)–1.9573(15) Å, within the expected range reported for Cu(II)-based compounds.²⁰ The PODC²⁻ ligand exhibits the same coordination mode as that of 1. Via syn–anti carboxylate bridges, each Cu(II) ion connects with neighboring ones, resulting in 1D {Cu(COO)}_n chains. Furthermore, each chain is linked to the adjacent ones by PODC²⁻ ligands so as to generate the 4⁴-net 2D plane structure, as shown in Fig. 2(b). The 3D supramolecular architecture can be seen as 2D layers linked by a weak interaction force, e.g. van der Waals force.

Fig. 2 (a) ORTEP plot showing the coordination environment of Cu(II) ions; (b) two-dimensional topology sketch map of compound 4 viewed along the a axis.

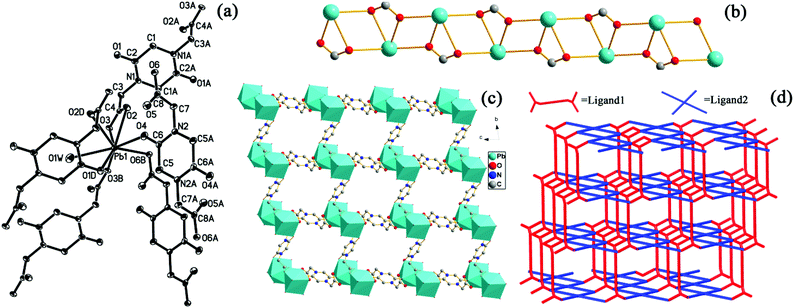
Compound 5 crystallized in the monoclinic system with the P2(1)/n space group. Analysis of the single-crystal diffraction data indicates that the asymmetric unit of 5 contains one Ag(I) ion and a half PODC²⁻ ligand. As shown in Fig. 3(a), the Ag(I) ion is a quad-coordinated tetrahedron with two carboxylate O atoms and two carbonyl O atoms from four PODC²⁻ ligands. The corresponding bond lengths of the Ag–O bond are 2.184(4)–2.8003(39) Å, in agreement with those of quad-coordinated Ag(I).²¹ Interestingly, the PODC²⁻ ligand exhibits a different coordination mode from those of 1–4, where both carboxylate and carbonyl oxygen atoms participate in coordinating to Ag(I) ions, as shown in Fig. S3(b).† Each Ag(I) ion connects with another Ag(I) ion via two carbonyl oxygen atoms and one μ²:η¹,η²-carboxylate to generate a {Ag₂} unit, as shown in Fig. 3(b). Along the a axis, connection of two adjacent ones through two μ²:η¹,η²-carboxylates results in a 1D {AgO(COO)}_n chain, which further forms a 3D structure by the use of two opposite carboxylates and carbonyls of the PODC²⁻ ligand, as shown in Fig. 3(c and d). The short Schläfli vertex notation of the net can be described as {4¹⁴·6}²{4⁴⁴·6²²}, as calculated by the TOPOS software.¹⁹ It must be mentioned that two different Ag–Ag metal bonds (d_Ag–Ag = 2.7918 and 2.9346 Å) appear in 5.

Fig. 3 (a) ORTEP plot showing the coordination environment of Ag(I) ions in 5; (b) {AgO(COO)}_n chain along the a axis; the three-dimensional supramolecule architecture polyhedron (c) view and topology sketch map (d) of compound 5 along the a axis.

The single-crystal X-ray diffraction analysis shows that compound 6 crystallized in triclinic symmetry with the space group P1̄. In the asymmetric unit, there is one crystallographically independent Pb(II) ion, one PODC²⁻ ligand, one aqua ligand and four guest water molecules. As shown in Fig. 4(a), the coordination environment of the Pb(II) ion features the contributions of six carboxylate oxygen atoms, one carbonyl oxygen and one aqua ligand. The corresponding bond lengths of Pb–O are 2.479(2)–2.9557(45) Å, comparable to those in previously reported compounds.²² In 6, the PODC²⁻ ligand exhibits two different coordination modes (see Fig. S3(c and d)†). The 3D structure of 6 can be described as follows: (1) through the carboxylates, each Pb(II) ion connects with the adjacent ones along the a axis to form the 1D {Pb(COO)}_n chain, as shown in Fig. 4(b); (2) each chain further links each other along b and c axes by the use of two opposite carboxylates and carbonyl of the PODC²⁻ ligand, as depicted in Fig. 4(c) and (d). The topology symbol is {4⁴·6²}{4⁶·6⁴}²{4⁸·6⁶·8}, as indicated by the TOPOS software.¹⁹ Notably, the channel of 7.0 × 7.0 Ų size along the a axis was observed in 6, as displayed in the space filing view of Fig. S4.† Three guest water molecules in one unit-cell are enveloped in the channels. Interestingly, they display different dissociative temperatures (see Fig. S5†). Additionally, the pore volume calculated through the PLATON program is approximately 250.4 ų per unit cell volume (32.5%).

Fig. 4 (a) ORTEP plot showing the coordination environment of Pb(II) ions in 6; (b) {Pb(COO)}_n chain along the a axis; the three-dimensional supramolecule architecture polyhedron (c) and the topology sketch map (d) of compound 6 along the a axis.

Magnetism–structure relation: magnetic properties, QMC simulation and DFT calculation

The magnetic properties of 1–3 are investigated through variable-temperature susceptibility measurements in the temperature range of 2.0 to 300 K with an applied magnetic field of 1000 Oe. As shown in Fig. 5, the χ_mT value at room temperature (300 K) is 4.28 cm³ mol⁻¹ K for 1, consistent with the value of 4.38 cm³ mol⁻¹ K for one independent Mn(II) ion (g = 2.0). However, the χ_mT value at 300 K is 7.77 for 2 and 3.08 cm³ mol⁻¹ K for 3, which are larger than those of one independent Fe(II) or Co(II) ion (g = 2.0) expected by the Curie law.²³ That may be due to contribution of the orbital magnetic moment.²⁴ As the temperature decreases, the value of χ_mT of 1 decreases slowly and reaches a value of 0.43 cm³ mol⁻¹ K at 2 K. As shown in Fig. S6,† the data of χ_m⁻¹vs. T over the temperature range of 100–300 K fit well with the Curie–Weiss law²³ with the Weiss constant C = 4.39 cm³ mol⁻¹ K and the Curie constant θ = −7.89 K, which reveals overall very weak anti-ferromagnetic properties. However, upon lowering the temperature, the value of χ_mT of 2 and 3 decreases slowly and reaches a value of 2.66 cm³ mol⁻¹ K for 2 and 2.07 cm³ mol⁻¹ K for 3 at about 6 K. Subsequently, both of them increase abruptly and reach the maximum of 4.15 cm³ mol⁻¹ K for 2 and 6.09 cm³ mol⁻¹ K for 3 at 2 K. Generally, it is observed that both 2 and 3 exhibit ferrimagnetic behavior. Likewise, the fitting for χ_m⁻¹vs. T over the temperature range of 100–300 K (see Fig. S6†) also gives the best parameters: C = 8.90 cm³ mol⁻¹ K and θ = −160.22 K for 2; C = 3.16 cm³ mol⁻¹ K and θ = −8.07 K for 3, which exhibits that they feature anti-ferromagnetic properties at high temperatures.

Fig. 5 Experiment plot of χ_mT vs. T of 1 (black ○, 2 (red □), 3 (blue ◊); QMC fitting line (solid line) of 1.

In order to identify the magnetic exchange interactions of 1, the fitting to the plot of χ_MT vs. T with the given model was performed. As shown in Fig. S8(a) and (b),† magnetic coupling of 1 can be attributed to the interaction between two Mn(II) ions. However, due to periodic characteristics, the fitting based on the well-known irreducible tensor operator method is impossible. Based on the Hamilton operator as shown in Fig. S8(c),† therefore, we herein applied our QMC fitting program (see ESI†), which invokes the LOOP module of the ALPS project.²⁵ The coupling parameter J is utilized to describe the role of the syn–anti carboxylate bridge between two adjacent Mn(II) ions. The weak interaction (zJ) constant,²⁶ which has the capability of describing the interaction of the hydrogen bonds between two 2D layer frameworks, was also taken into account. According to the principle of the least reliability factor R (see Fig. S8(d)†), the best parameters obtained are J = −0.5 cm⁻¹, zJ = −0.10 cm⁻¹, g = 1.99 and R = 8.1 × 10⁻⁵, where R is calculated from ∑[(χ_MT)_obs − (χ_MT)_calcd]²/∑[(χ_MT)_obs]². The small value (−0.50 cm⁻¹) of J reveals a weak antiferromagnetic propagation pathway of the syn–anti carboxylate bridge. The zJ value of −0.10 cm⁻¹ also displays a weak antiferromagnetic coupling between two layers, owing to the effect of the weak-interaction (e.g. hydrogen bond). However, many attempts to simulate the magnetic susceptibility for 2 and 3 with the help of our fitting program failed. Because six-coordinate Fe(II)/Co(II) ions usually present considerable first-order orbital momentum,²⁴ the Hamiltonian operator must be supplemented by the orbitally dependent exchange interactions and spin–orbit coupling effects.

For the exploration of the magnetic exchange mechanism, DFT calculation of 1 based on the GGA + U algorithm was conducted with the help of the VASP²⁷ program. An effective Hubbard U_eff of 6.01 eV for Mn(II) was determined by the linear response method of the PWSCF program²⁸ (see ESI†). Based on optimised geometry with or without the U_eff, the total DOS (TDOS) and PDOS of linking carboxylate (such as O2, C4 O3 atoms) and Mn(II) ions under the U_eff of 0.0 eV and 6.01 eV were calculated, as shown in Fig. 6. In nature, the magnetic properties are controlled by the DOS near the Fermi level. A glance at the DOS shows that the distinct areas between spin-up and spin-down are distributed in the vicinity of the Fermi level. TDOS, 3d PDOS of Mn(II) and 2p PDOS of the linking carboxylate are split clearly, resulting in an ordered spin distribution by the exchange interaction. Combining DOS and spin magnetic moment (see Table 1), it is found that magnetic properties of 1 originated from Mn(II) ions and the linking carboxylate. Obviously, anti-ferromagnetic coupling of 1 is derived from 3d electrons of the Mn(II) ion propagating by four −/−/+ spin nets of O2–C4–O3. In addition, stronger correlation of Mn(II) ions can effectively affect the electronic structure and magnetic properties of 1. There are three aspects as follows: (1) for Mn(II) and bridging atoms, the spin up (black) PDOS peaks at the Fermi level play a dominant role under the U_eff of 0.0 eV, while the spin-down (red) PDOS peaks under the U_eff of 6.01 eV are higher than spin-up PDOS peaks. (2) With the value of U_eff increasing, the absolute spin magnetic moments of Mn(II) ions enhance (4.72 and −4.720μ_B for 6.01 eV, 1.063 and −1.067μ_B for 0.00 eV), where the absolute spin magnetic moments of Mn(II) (4.72μ_B) are very approximate to the experimental value (4.94μ_B) at room temperature. (3) The obtained band gap at the U_eff of 6.01 eV is larger than for the U_eff of 0.00 eV. Generally, magnetic properties of 1 can be attributed to the coupling of paramagnetic Mn(II) ions by −/−/+ spin nets of O2–C4–O3.

Fig. 6 PDOS of 1 under the U_eff of 0.0 eV (a) and 6.01 eV (b) in spin-up (black) and spin-down (red) with the Fermi level (blue line).

Table 1 Theoretical spin magnetic moments (μ_B) of 1

U eff/eV	0.00	6.01
Mn1	1.063	4.720
Mn2	−1.067	−4.720
O2	−0.019	−0.008
C4	−0.004	−0.003
O3	0.009	0.008

---

Likewise, magnetic properties of 4 were also measured. The obtained plot of χ_MT vs. T is presented in Fig. 7. The χ_MT value at room temperature is 0.40 cm³ mol⁻¹ K, which is in line with the value of 0.375 cm³ mol⁻¹ K of a single Cu(II) ion following Curie's law. Before 50 K, the χ_MT value almost remains invariable. Afterward, as the temperature decreases, the χ_MT value rapidly increases and reaches a maximum of 0.87 cm³ mol⁻¹ K at 2 K. Therefore, it is found that 4 exhibits ferromagnetic properties. Furthermore, following the Curie–Weiss law,²³ the fitting for χ_m⁻¹vs. T over the temperature range of 100–300 K generates the parameters with C = 0.39 cm³ mol⁻¹ K and θ = 3.82 K, as shown in Fig. S7.† The positive Curie temperature validates the ferromagnetic properties of 4. Similarly, QMC fitting was performed (see ESI†). In the fitting process, the parameter J was represented as the coupling interaction between two Cu(II) ions (see Fig. 7(b) and (c)), and the zJ parameter was invoked to describe the weak interaction between metal-bound chains, e.g. van der Waals force. The resulting best parameters are J = 2.23 cm⁻¹, zJ = −0.41 cm⁻¹, g = 2.06 and R = 3.23 × 10⁻⁴. The 2.23 cm⁻¹ value of the coupling parameter reveals that 4 has weak ferromagnetic properties. Negative zJ (−0.41 cm⁻¹) suggests the existence of a weak antiferromagnetic interaction between {Cu(COO)}_n chains.

Fig. 7 Experiment plot (black ○) and QMC fitting line (solid line) of χ_mT vs. T in 4 (a); the sketch of Cu²⁺ distribution (b) and Hamilton operator (c) of 4.

The magnetic propagating mechanism was further identified by DFT calculations. By using the linear response method, the U_eff of Cu(II) in 4 is found to be 1.68 eV (see ESI†). It is evident from Fig. 8 and Table 2 that the effective Hubbard U_eff cannot effectively affect the characteristics of DOS and the absolute value of spin magnetic moments, except the change of the spin direction. To examine the PDOS in the vicinity of Fermi level is very helpful to understand magnetic coupling mechanism of 4. According to PDOS distribution in the U_eff of 1.68 eV, it is observed that the main origin of magnetic properties in 4 is provided by Cu(II) ions. However, linking carboxylate atoms also contribute spin magnetic moments, see Table 2. Furthermore, we can see that PDOS of d electrons of Cu(II) ions and p electrons of linking carboxylate (e.g. O2, C4 and O3) have similar peaks, which suggests that these orbitals take part in hybridization. The phenomena play a pivotal role in the indirect propagation between Cu(II) ions of two units, implying that linking carboxylate atoms serve as superexchange pathways. Therefore, ferromagnetic exchanges of two Cu(II) ions come from the spin polarization effect through the carboxylate bridge in the +/+/+ spin nets of O2–C4–O3.

Fig. 8 PDOS of 4 under the U_eff of 0.0 eV (a) and 1.68 eV (b) in spin-up (black) and spin-down (red) with the Fermi level (blue line).

Table 2 Theoretical spin magnetic moments (μ_B) of 4

U eff/eV	0.00	1.68
Cu1	−0.596	0.601
Cu2	−0.596	0.601
O2	−0.002	0.002
C4	−0.009	0.009
O3	−0.072	0.071

---

Luminescence–structure relation: UV-vis absorption, luminescence spectra and DFT calculation

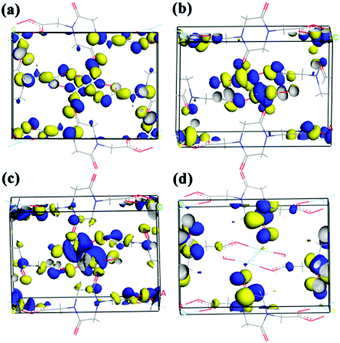
Solid UV-vis absorption and fluorescence emission spectra of compound 5 were also measured at room temperature. As shown in Fig. 9(a) and (b), two absorption peaks appear at 250 and 375 nm, respectively, while one emission peak at 390 nm was found under the excitation at 250 nm. Previous experimental studies advocated the possible emission mechanisms of Ag(I)-based complexes.²⁹ However, this detailed theoretical study is very rare. In order to identify the corresponding mechanism, DFT calculations were carried out. The U_eff value of 6.52 eV obtained by the linear response method (see ESI†) was employed to describe the strongly correlated interaction of 4d electrons of Ag. Electronic properties (band structure and PDOS) were also examined for relaxed geometry. According to the energy difference between two bands (see Fig. 9(c)), it can be concluded that two absorption peaks (250 and 375 nm) can be attributed to transitions of VB→the second empty bands (theoretical value: 302 nm) and VB→CB (theoretical value: 381 nm). In comparison with experimental absorption peaks (250 nm), we found that the first transition (VB→the second empty bands) plays a dominant role in the UV spectra. Furthermore, an inspection of DOS shows that VB mainly involves the 2p state of carboxylate oxygen and 4d states of Ag, while CB is occupied by the 2p state of carboxylate oxygen and 5s states of Ag. On the other hand, frontier orbital analysis results are presented in Fig. 10. The highest occupied molecular orbital (HOMO) and HOMO−2 are concentrated on d_x²–y² orbitals of Ag atoms and localized dangling p orbitals of oxygen atoms. The lowest unoccupied molecular orbital (LUMO) is contributed by the Ag–Ag metal bond (involves 5s orbitals) and dangling p orbitals of oxygen atoms, whereas LUMO+2 is equally distributed on the π* C=O bond and localized dangling p orbitals of nitrogen atoms from four PODC²⁻ ligands. Therefore, it is found that UV light absorption would mainly induce the electron transfer from 4d states to 5s states of Ag. The wavelength of absorption peaks obtained theoretically are smaller than those of experimental measure (see Fig. S12†), owing to an overall overestimated fault of the DFT method. But the whole trends of main absorption peaks are in good agreement with experimental values.

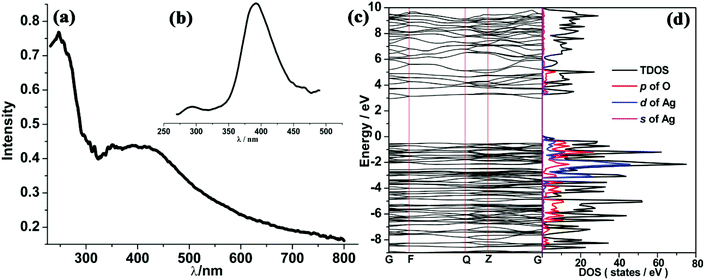Fig. 9 UV (a), fluorescence spectra (b), band structure (c) and PDOS (d) of 5 with the U_eff of 6.52 eV (Fermi level is set to 0.0 eV).

Fig. 10 HOMO−2 (a), HOMO (b), LUMO (c) and LUMO+2 (d) of compound 5.

For solid state materials, it is difficult to faultlessly explain the detailed mechanism of emission by the DFT method. However, via the electronic structure, we can still find that under the exposure to excited light, a majority of electrons readily transfer to the region of the second empty band, and successively rebound to CB without any emission, and lastly return to CB with the specific emission of 390 nm. In nature, the observed emission peak can be attributed to the electron transfer from the Ag–Ag metal bond (features 5s type orbitals) to localized 4d orbitals of Ag atoms.

Conclusion

In summary, the synthesis and properties of six peptide-based MOFs (Mn(1), Fe(2), Co(3), Cu(4), Ag(5) and Pb(6)) based on H₂PODC have been discussed. Via experimental measures and theoretical calculation, we demonstrated the magnetism–structure and luminescence–structure relationships. Therefore, our studies are beneficial for the effective synthetic strategy of peptide-based MOFs and provide some help to understand the relationships between properties and structures.

Acknowledgements

This work was supported by the 973 project (2013CB733501) and the National Natural Science Foundation of China (21101137, 21136001, 21176221, 21306169 and 91334013).

Notes and references

1. (a) G. B. Gardne, D. Venkataraman, J. S. Moore and S. Lee, Nature, 1995, 374, 792; (b) S. S. Y. Chui, S. M. F. Lo, J. P. H. Charmant, A. G. Orpen and I. D. Williams, Science, 1999, 283, 1148; (c) N. L. Rosi, J. Eckert, M. Eddaoudi, D. T. Vodak, J. Kim and O. M. Yaghi, Science, 2003, 300, 1127; (d) G. Férey, C. Mellot-Draznieks, C. Serre, F. Millange, J. Dutour, S. Surblé and I. Margiolaki, Science, 2005, 2040; (e) X.-J. Kong, L.-S. Long, Z. Zheng, R.-B. Huang and L.-S. Zheng, Acc. Chem. Res., 2010, 43, 201; (f) X.-J. Kong, Y.-P. Ren, L.-S. Long, Z. Zheng, R.-B. Huang and L.-S. Zheng, J. Am. Chem. Soc., 2007, 129, 7016; (g) X.-J. Kong, Y. Wu, L.-S. Long, L.-S. Zheng and Z. Zheng, J. Am. Chem. Soc., 2009, 131, 6918; (h) D. Zhao, D. J. Timmons, D. Yuan and H.-C. Zhou, Acc. Chem. Res., 2011, 44, 123; (i) J. Y. Zou, W. Shi, H. L. Gao, J. Z. Cui and P. Cheng, Inorg. Chem. Front., 2014, 1, 242.
2. (a) R. Matsuda, R. Kitaura, S. Kitagawa, Y. Kubota, R. V. Belosludov, T. C. Kobayashi, H. Sakamoto, H. Chiba, M. Takata, Y. Kawazoe and Y. Mita, Nature, 2005, 436, 238; (b) H. Furukawa, N. Ko, Y. B. Go, N. Aratani, S. B. Choi, E. Choi, A. Ö. Yazaydin, R. Q. Snurr, M. O'Keeffe, J. Kim and O. M. Yaghi, Science, 2010, 329, 424; (c) S. H. Yang, X. Lin, W. Lewis, M. Suyetin, E. Bichoutskaia, P. J. Parker, C. C. Tang, D. R. Allan, P. J. Rizkallah, P. Hubberstey, N. R. Champness, K. M. Thomas, A. J. Blake and M. Schröder, Nat. Mater., 2012, 11, 710.
3. (a) J. B. Lin, J. P. Zhang and X. M. Chen, J. Am. Chem. Soc., 2010, 132, 6654; (b) E. D. Bloch, W. L. Queen, R. Krishna, J. M. Zadrozny, C. M. Brown and J. R. Long, Science, 2012, 335, 1606.
4. (a) J. Y. Lee, O. K. Farha, J. Roberts, K. A. Scheidt, S. T. Nguyen and J. Y. Hupp, Chem. Soc. Rev., 2009, 38, 1450; (b) M. Yoon, R. Srirambalaji and K. Kim, Chem. Rev., 2012, 112, 1196.
5. (a) M. D. Allendorf, C. A. Bauer, R. K. Bhakta and R. J. T. Houk, Chem. Soc. Rev., 2009, 38, 1330; (b) Y. J. Cui, Y. F. Yue, G. D. Qian and B. L. Chen, Chem. Rev., 2012, 112, 1126.
6. M. Kurmoo, Chem. Soc. Rev., 2009, 38, 1353.
7. C. Wang, T. Zhang and W. B. Lin, Chem. Rev., 2012, 112, 1084.
8. M. Eddaoudi, D. B. Moler, H. L. Li, B. L. Chen, T. M. Reineke, M. O'keeffe and O. M. Yaghi, Acc. Chem. Res., 2001, 34, 319.
9. (a) M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O'Keeffe and O. M. Yaghi, Science, 2002, 295, 469; (b) C. A. Bauer, T. V. Timofeeva, T. B. Settersten, B. D. Patterson, V. H. Liu, B. A. Simmons and M. D. Allendorf, J. Am. Chem. Soc., 2007, 129, 7136.
10. K. S. Park, A. Ni, A. P. Côté, J. Y. Choi, R. Huang, F. J. Uribe-Romo, H. K. Chae, M. O'Keeffe and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10186.
11. (a) B. F. Abrahams, M. J. Grannas, T. A. Hudson and R. Robson, Angew. Chem., Int. Ed., 2010, 49, 1087; (b) S. C. Sahoo, T. Kundu and R. Banerjee, J. Am. Chem. Soc., 2011, 133, 17950; (c) B. Zhou, A. Kobayashi, H. B. Cui, L. S. Long, H. Fujimori and H. Kobayashi, J. Am. Chem. Soc., 2011, 133, 5736.
12. (a) R. Vaidhyanathan, D. Bradshaw, J.-N. Rebilly, J. P. Barrio, J. A. Gould, N. G. Berry and M. J. Rosseinsky, Angew. Chem., Int. Ed., 2006, 45, 6495; (b) J. Perez Barrio, J.-N. Rebilly, B. Carter, D. Bradshaw, J. Bacsa, A. Ganin, H. Park, A. Trewin, R. Vaidhyanathan, A. Cooper, J. E. Warren and M. J. Rosseinsky, Chem. – Eur. J., 2008, 14, 4521; (c) J. An, S. J. Geib and N. L. Rosi, J. Am. Chem. Soc., 2009, 131, 8376; (d) J. An, O. K. Farha, J. T. Hupp, E. Pohl, J. I. Yeh and N. L. Rosi, Nat. Commun., 2012, 3, 604.
13. A. Mantion, L. Massüger, P. Rabu, C. Palivan, L. B. McCusker and A. Taubert, J. Am. Chem. Soc., 2008, 130, 2517.
14. (a) J. Rabone, Y. F. Yue, S. Y. Chong, K. C. Stylianou, J. Bacsa, D. Bradshaw, G. R. Darling, N. G. Berry, Y. Z. Khimyak, A. Y. Ganin, P. Wiper, J. B. Claridge and M. J. Rosseinsky, Science, 2010, 329, 1053; (b) C. Martí-Gastaldo, J. E. Warren, K. C. Stylianou, N. L. O. Flack and M. J. Rosseinsky, Angew. Chem., Int. Ed., 2012, 51, 11044; (c) H. Y. Lee, J. W. Kampf, K. S. Park and E. N. G. Marsh, Cryst. Growth Des., 2008, 8, 296; (d) L. Lang, R. Yu, W. B. Yang, X. Y. Wu and C. Z. Lu, Cryst. Growth Des., 2012, 12, 3304; (e) W. L. Chen, W. X. Chen, G. L. Zhuang, J. Zheng, L. Tan, X. Zhong and J. G. Wang, CrystEngComm, 2013, 15, 5545; (f) X. J. Kong, G. L. Zhuang, Y. P. Ren, L. S. Long, R. B. Huang and L. S. Zheng, Dalton Trans., 2009, 1707; (g) G. L. Zhuang, X. J. Kong, L. S. Long, R. B. Huang and L. S. Zheng, CrystEngComm, 2010, 12, 2691.
15. (a) T. Sagara, J. Klassen and E. Ganz, J. Chem. Phys., 2004, 121, 12543; (b) Q. Y. Yang and C. L. Zhong, J. Phys. Chem. B, 2006, 110, 655; (c) F. Salles, A. Ghoufi, G. Maurin, R. G. Bell, C. Mellot-Draznieks and G. Ferey, Angew. Chem., Int. Ed., 2008, 47, 8487; (d) T. Mueller and G. Ceder, J. Phys. Chem. B, 2005, 109, 17974; (e) K. Sillar, A. Hofmaan and J. Sauer, J. Am. Chem. Soc., 2009, 131, 4143; (f) L. Grajciar, O. Bludsky and P. Nachtigall, J. Phys. Chem. Lett., 2010, 1, 3354.
16. (a) K. Zhang, L. L. Zhang and J. W. Jiang, J. Phys. Chem. C, 2013, 117, 25628; (b) H. Frost, T. Duren and R. Q. Snurr, J. Phys. Chem. B, 2006, 110, 9565; (c) V. D. Berg, W. C. Annemieke and C. O. Arean, Chem. Commun., 2008, 668; (d) S. Han and W. A. Goddard, J. Am. Chem. Soc., 2007, 129, 8422; (e) Y. L. Xiao, Q. Y. Yang, D. H. Liu and C. L. Zhong, CrystEngComm, 2013, 15, 9588; (f) A. Comotti, A. Fraccarollo, S. Bracco, M. Beretta, G. Distefano, M. Cossi, L. Marchese, C. Riccardi and P. Sozzani, CrystEngComm, 2013, 15, 1503.
17. (a) K. S. Walton, A. R. Millward, D. Dubbeldam, H. Frost, J. J. Low, O. M. Yaghi and R. Q. Snurr, J. Am. Chem. Soc., 2008, 130, 406; (b) A. Vishnyakov, P. Ravikvitch, A. V. Neimark, M. Bulow and Q. M. Wang, Nano Lett., 2003, 3, 713; (c) Q. T. Ma, Q. Y. Yang, A. Ghoufi, G. Ferey, C. L. Zhong and G. Maurin, Dalton Trans., 2012, 41, 3915; (d) A. Malkick, S. Saha, P. Pachfule, S. Roy and R. Banerjee, Inorg. Chem., 2011, 50, 1392; (e) K. Zhang, Y. F. Chen, A. Nalaparau and J. W. Jiang, CrystEngComm, 2013, 15, 10358.
18. C. B. Ma, C. N. Chen and Q. T. Liu, CrystEngComm, 2005, 7, 650.
19. V. A. Blatov, IUCr CompComm Newsletter, 2006, 7, 4.
20. W. X. Chen, S. T. Wu, L. S. Long, R. B. Huang and L. S. Zheng, Cryst. Growth Des., 2007, 7, 1171.
21. L. Brammer, M. D. Burgard, M. D. Eddleston, C. S. Rodger, N. P. Rath and H. Adams, CrystEngComm, 2002, 4, 239.
22. J. X. Yuan, M. L. Hu and A. Morsali, Inorg. Chem. Commun., 2006, 9, 277.
23. K. Charles, Introduction to solid state physics, 7th edn, 1996.
24. (a) J. M. Herrera, A. Bleuzen, Y. Dromzée, M. Julve, F. Lloret and M. Verdaguer, Inorg. Chem., 2003, 42, 7052; (b) D. Maspoch, N. Domingo, D. Ruiz-Molina, K. Wurst, J. M. Hernández, G. Vaughan, C. Rovira, F. Lloret, J. Tejada and J. Veciana, Chem. Commun., 2005, 5035.
25. B. Bauer, L. D. Carr, H. G. Evertz and A. Feiguin, J. Stat. Mech., 2011, P05001.
26. C. Mennerich, H. H. Klauss and M. Broekelmann, Phys. Rev. B: Condens. Matter, 2006, 73, 174415.
27. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter, 1993, 48, 13115.
28. (a) M. Cococcioni and S. de Gironcoli, Phys. Rev. B: Condens. Matter, 2005, 71, 035105; (b) P. Giannozzi, S. Baroni, N. Bonini, M. Calandra and R. Car, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502.
29. (a) C. M. Che and S. W. Lai, Coord. Chem. Rev., 2005, 249, 1296; (b) T. Ren, C. Lin, P. Amalberti, D. Macikenas, J. D. Protasiewicz, J. Clayton Baum and T. L. Gibson, Inorg. Chem. Commun., 1998, 1, 23; (c) J. H. Yang, S. L. Zheng, X. L. Yu and X. M. Chen, Cryst. Growth Des., 2004, 4, 831.

---

Footnote

† Electronic supplementary information (ESI) available: Synthesis and structural information of 1–6; DFT and QMC computation details; TG, XRD and IR plots; the UV-vis theoretical curve. See DOI: 10.1039/c4qi00043a

---