Computation of standard equilibrium acidity of C–H acids in ionic media: shedding light on predicting changes of chemical behavior by switching solvent system from molecular to ionic†
Xiao-Song
Xue
a,
Chen
Yang
a,
Xin
Li
a and
Jin-Pei
Cheng
*ab
aState Key Laboratory of Elemento-organic Chemistry, Collaborative Innovation Center of Chemical Science and Engineering (Tianjin), and College of Chemistry, Nankai University, Tianjin, 300071, China
bCenter of Basic Molecular Science, Department of Chemistry, Tsinghua University, Beijing, 100083, China. E-mail: chengjp@most.cn; chengjp@nankai.edu.cn
First published on 29th January 2014
Abstract
An SMD implicit–explicit approach was developed that allows reproduction of experimental pKa values of various carbon acids in ionic liquids with a mean unsigned error of 1.28 pK units, which is comparable in magnitude to those authentic pKa calculations in conventional molecular solvents. This model may be used for predicting more pKa values in RTILs and may also offer clues for studying other thermodynamic quantities.
Introduction
Room-temperature Ionic liquids (RTILs) have attracted ever-increasing attention in recent years as promising new solvent systems for syntheses1 and many other applications such as biomass conversion,2 CO2 capture3 and fuel cells.4 Consequently, fundamental understanding of the changes in chemical behavior caused by ILs is much in demand. Though great efforts have been made in the past toward achieving relevant quantitative information, until now the focus has been mostly on the physical properties and solvent characteristics of ILs.5 How a chemical parameter, e.g. pKa, BDE, etc., varies as the solvent composition is switched from molecules to ions remains generally a mystery for both experimental and computational chemists due to its multifaceted complexity.The knowledge of equilibrium acidity is fundamentally important in chemistry and biology.6 In fact, a variety of structure–reactivity relationships, including the Brønsted relationship and Hammett equation that laid the foundation of modern physical organic theories, are based on pKa studies. It is known that the dissociation equilibrium of a Brønsted acid depends strongly on the nature of the medium, and the acidity value in a solvent relative to the intrinsic gas-phase acidity should then reflect the effect of solvation in that system.7 Accurate pKa values in a particular solvent can provide important information for designing novel materials or reactions. Thus, it is reasonable to expect that a sound knowledge of the acidic scales in RTILs should be of great value in understanding the interesting chemistry found in ILs as well as their amazing solvent effects. Unfortunately, besides the well known scales in the gas phase and in conventional molecular solvents,8–11 there were basically no absolute equilibrium acidity values, however, measured in pure RTIL in the absence of molecular additives until now.12
In the past two decades or so, enormous efforts have been made to develop theoretical protocols to calculate pKa values to complement experiments.13–15 Among various solvation models applied,14,15 the continuum solvation models16 are viewed as the most popular due to their high efficiency and simplicity. Moreover, they can provide accurate treatment for the strong long-range electrostatic forces that in many cases dominate the solvation.16a Although tremendous progress has been made in computing pKa in classical molecular solvents,14,15 it is still unknown whether these strategies could be equally well applied to calculate pKa values in ionic media that are fundamentally different in nature.17 As the number of RTILs is large with quite diverse behavior of solvation,18 modelling of the solvent cannot be expected to be simple. Therefore, it would be wise to start with a “standard” situation to develop the modelling where standard bond parameters such as absolute pKa have been precisely determined by experiment in pure ILs of minimized specific ion-pair interaction.19
We have previously accumulated experience in experimental20 and theoretical21 determination of fundamental bond energetics in the conventional molecular solvents. To this end, we have recently established the first standard pKa scales of carbon acids in pure RTILs of minimized ion interaction.19 With these experimental pKa's in hand, we are now in a promising situation to develop and at the same time to examine the computational strategy of predicting pKa values in ionic media. At about the same time, Truhlar and co-workers have extended their SMD universal solvation model22,23 (which was claimed to be applicable to any solute in any solvent provided the key descriptors are known) to some ILs.24 Herein we wish to report our finding that a rational choice of theory in combination with a modified SMD model would allow prediction of this fundamental thermodynamic property in RTILs with quite high accuracy.
Results and discussion
Since all the solvent descriptors for [Bmim][NTf2] are readily available,24 the experimental pKa's of a series of carbon acids in [Bmim][NTf2]19 were used to test the performance of different theoretical models. On the basis of Truhlar and co-workers’ pioneering work,24 the pKa's in ionic liquid solvent were evaluated firstly by performing pure SMD calculations.A straightforward way to evaluate pKa is to compute the total change in free energy associated with the solution-phase acid dissociation process (eqn (1)). However, problems arise when treating the solvated proton whose chemical structure is often unknown and theoretically difficult to model. Moreover, the number of charged species is not conserved across the reaction and, since the associated uncertainties in their solvation energies are much larger, it can potentially lead to pKa predictions with very large errors.14a,b
| HA(solv) → H(solv)+ + A(solv)+ | (1) |
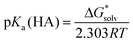 | (2) |
Thus, we opted to focus on the free energy change of the proton-exchange reaction (eqn (3)). The pKa of a given unknown acid HA in eqn (1) can thus be obtained through eqn (4), where “Ref” denotes the reference acid whose pKa is known experimentally and G*ex(solv) is the free energy change for the proton-exchange reaction. As the absolute intrinsic pKa value of 4-nitrophenyl-malononitrile in ionic liquid was directly determined in our previous work,19 it was chosen as the reference acid in the present study. The experimental and calculated pKa values using the pure SMD method (cover a range of about 13 pK units) are given in Table 1.
| HA(solv) + Ref(solv)− → HRef(solv) + A(solv)+ | (3) |
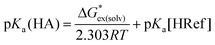 | (4) |
| Acida | pKa (calc.)d | pKa (calc.)e | pKa (calc.)f | pKa (calc.)g | pKa (calc.)h | pKa (calc.)i | pKa (calc.)j | pKa (calc.)k | pKa (exp.) |
|---|---|---|---|---|---|---|---|---|---|
| a Fl, fluorene. b MSE is the mean signed error. c MUE is the mean unsigned error. d Calculated by SMD/M06-2x/6-31+G(d,p)//M06-2x/6-31+G(d,p). e Calculated by SMD/B3LYP/6-31+G(d,p)//M06-2x/6-31+G(d,p). f Calculated by SMD/M05-2x/cc-pVTZ//M06-2x/6-31+G(d,p). g Calculated by SMD/M06-2x/6-31+G(d,p). h Calculated by SMD/M06-2x/6-311++G(d,p). i Calculated by SMD/M06-2x/cc-pVTZ//M06-2x/6-31+G(d,p). j Calculated by SMD/M06-2x/6-311++G(2df,2p)//M06-2x/6-31+G(d,p). k Calculated by SMD/M06-2x/cc-pVTZ//M06-2x/6-31+G(d,p) and a [Bmim] cation is considered explicitly around the conjugate anionic bases. | |||||||||
| 9-EtSO2Fl | 23.98 | 26.94 | 24.47 | 24.98 | 25.04 | 23.68 | 23.96 | 22.27 | 20.3 |
| PhSO2CH2CN | 22.93 | 25.57 | 22.43 | 23.25 | 23.20 | 22.18 | 22.20 | 20.00 | 19.1 |
| PhSO2CH2SO2Ph | 23.58 | 27.24 | 23.51 | 24.02 | 22.72 | 23.34 | 23.66 | 19.96 | 18.8 |
| CH2(CN)2 | 20.37 | 21.61 | 20.28 | 20.44 | 20.09 | 20.23 | 20.12 | 19.90 | 18.9 |
| 9-COOMeFl | 21.07 | 24.09 | 21.63 | 21.59 | 21.42 | 20.91 | 21.33 | 19.77 | 18.3 |
| PhCOCH2CN | 20.88 | 22.84 | 21.03 | 21.65 | 21.56 | 21.24 | 21.05 | 19.24 | 17.0 |
| 9-CNFl | 18.77 | 21.36 | 18.94 | 19.22 | 19.07 | 18.28 | 18.58 | 17.56 | 16.7 |
| p-ClPhCOCH2CN | 19.93 | 21.82 | 20.12 | 20.25 | 19.95 | 20.34 | 20.17 | 18.65 | 16.4 |
| p-OMePhCH(CN)2 | 15.84 | 17.26 | 15.90 | 16.50 | 16.22 | 15.83 | 15.90 | 15.32 | 13.7 |
| 9-CF3SO2Fl | 15.36 | 18.14 | 14.47 | 16.27 | 16.52 | 15.17 | 15.34 | 14.87 | 12.7 |
| PhCH(CN)2 | 13.17 | 14.51 | 13.08 | 13.56 | 13.38 | 12.88 | 12.97 | 12.92 | 12.5 |
| p-ClPhCH(CN)2 | 11.66 | 12.91 | 11.63 | 12.86 | 12.84 | 11.42 | 11.52 | 10.69 | 11.5 |
| p-CF3PhCH(CN)2 | 10.30 | 11.29 | 10.17 | 10.84 | 10.01 | 10.16 | 10.29 | 10.02 | 10.1 |
| p-CNPhCH(CN)2 | 9.07 | 10.10 | 8.70 | 9.53 | 9.43 | 8.60 | 8.79 | 7.88 | 8.8 |
| MSEb | 2.29 | 4.35 | 2.25 | 2.87 | 2.62 | 2.10 | 2.22 | 1.02 | |
| MUEc | 2.29 | 4.35 | 2.27 | 2.87 | 2.63 | 2.14 | 2.22 | 1.28 | |
As can be seen from Table 1, the pure SMD calculations led to reproduction of the experimental values with relatively large errors (entries 2 to 8). The SMD/M06-2x/6-31+G(d,p)//M06-2x/6-31+G(d,p) method predicted pKa values of a series of carbon acids with a MUE of 2.29 pKa units (entry 2). The use of the popular density functional B3LYP led to the largest MUE of 4.35 pK units (entry 3). The performance of the M05-2x functional was found to be similar to that of the M06-2x functional (entry 4). Similar to previous observations,15d the use of solution optimized geometry did not influence the resulting pKa values significantly (entry 5). Moreover, the SMD/M06-2x/6-311++G(d,p) method gave a MUE of 2.63 pKa units (entry 6), revealing that the level of theory of the geometry does not have a substantial effect on the accuracy of the calculation. The enlargement of the basis set (entries 7 and 8), using the SMD/M06-2x/cc-pVTZ//M06-2x/6-31+G(d,p), and SMD/M06-2x/6-311++G(2df,2p)//M06-2x/6-31+G(d,p) methods, led to a small increase in the accuracy of calculation. Among them, the SMD/M06-2x/cc-pVTZ//M06-2x/6-31+G(d,p) method (entry 7) gives the best result, but still has a MUE as high as 2.14 pKa units.
A careful comparison of the calculated results with experimental data showed that the calculated pKa's are generally larger than the corresponding experimental values (i.e. less acidic). Since Truhlar and coworkers demonstrated good performance of the SMD model for neutral species in ILs,24 an important source of error for pKa calculations may arise from the description of the solvation stabilization of the conjugate bases (carbanions).
A number of studies demonstrated that a pure implicit method alone is inadequate for accounting for the strong interaction between the ionic species and solvent in the first layer, and that better results may be obtained by including one or more solvent molecules in the explicit subsystem.25 Recently, such a strategy was shown to improve the accuracy of pKa prediction.14a–d,15d,26 In light of the aforementioned work, it is anticipated that addition of one or more explicit cations of the IL to the conjugate anionic bases would remedy the deficiency of the pure implicit method and thus improve the accuracy of calculation. Since previous experiment has demonstrated the non-coordinating features of the [NTf2] anion,27 for reasons of computational costs we included only one [Bmim] cation instead of an ion pair or a larger set of solvent ions.28,29 This approach was named as a proton exchange scheme based on the implicit–explicit model (PEIE), and its merits for pKa calculations have been highlighted by Ho and Coote in their recent review papers.14a,b
As clearly observed, adding a single explicit ionic liquid cation to the conjugate anionic bases largely improved the agreement of the calculated pKa values with experiment as we expected (Table 1, entry 9). The MUE is reduced from 2.14 pKa units for the pure SMD model (Table 1, entry 7) to 1.28 pKa units for the current implicit–explicit model (Table 1, entry 9), which is comparable in magnitude to those from typical pKa calculations in molecular media. Moreover, the plots of linear regression of the calculated pKa against experimental values yielded a regression equation with a slope of 1.179 (R2 = 0.963) for the SMD implicit–explicit model, showing a considerable improvement compared to the pure SMD model (slope of 1.332 and R2 = 0.952, see Fig. 1). The unsatisfactory performance of a pure SMD model for predicting pKa in RTIL is believed to be mainly due to its deficiency in describing strong interactions between the carbanion and the IL cation. On the other hand, this problem could be better addressed by adding a single explicit IL cation in solvating the carbanion.30 Preliminary application of the SMD implicit–explicit model for pKa prediction in other RTILs suggested that this approach be generally applicable.31 Thus, our results showed that the implicit–explicit model can be applied to ionic liquid media.
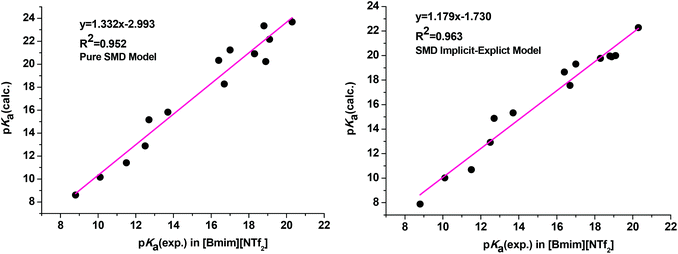 | ||
| Fig. 1 Correlation between experimental and calculated pKa values obtained from the pure SMD calculation (left) and the SMD implicit–explicit model (right). | ||
Conclusions
In summary, an SMD implicit–explicit solvation model was developed in this work that can reproduce experimental pKa values of a variety of carbon acids in ILs with an accuracy that is comparable to authentic pKa calculations in conventional molecular solvents. This is encouraging, because reliable calculation of fundamental thermodynamic properties relating to bond reorganization in chemical transformations in ionic liquid is highly desirable for understanding their amazing chemistry. It is believed that the SMD implicit–explicit solvation model here developed should be a promising approach for studying equilibrium acidities in other ionic media as well, and can provide useful hints for developing computational strategies to study other important thermodynamics, kinetics and mechanisms of chemical transformations in ILs,1,32 and should eventually contribute to a better understanding of the so-called “ionic liquid effects”.33Computational methods
Geometry optimizations were conducted with the M06-2x/6-31+G(d,p) method.34 The nature of the stationary points was confirmed by frequency calculations at the same level of theory. For molecules that have more than one possible conformation, the conformation with the lowest free energy was singled out and used in the ensuing calculations. The solvation free energies of all species in IL were evaluated by performing pure SMD calculation with the gas-phase optimized geometries.24 Solvent descriptors for [Bmim][NTf2] in SMD calculation include dielectric constant (ε = 11.25), refractive index (n = 1.4225), macroscopic surface tension (γ = 56.13), Abraham's hydrogen bond acidity (∑αH2 = 0.259) and basicity (∑βH2 = 0.238), the fraction of non-hydrogen atoms that are aromatic carbon atoms (ϕ = 0.1304), and the fraction of non-hydrogen atoms that are electronegative halogen atoms (ψ = 0.2609). All calculations were performed in Gaussian 09.35Acknowledgements
We are grateful to the National Basic Research Program (no. 2012CB821600), the Natural Science Foundation (grant nos. 21390400, 21172112, and 21172118), the State Key Laboratory on Elemento-organic Chemistry, the Program for New Century Excellent Talents in University (NCET-12-0279), and the Collaborative Innovation Center of Chemical Science and Engineering (Tianjin) for financial support. We thank Drs Hui Deng and Ao Yu for helpful discussions and Mr Jialu Jin for some computational work.Notes and references
- J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508 CrossRef CAS PubMed.
- (a) M. E. Zakrzewska, E. Bogel-Lukasik and R. Bogel-Lukasik, Chem. Rev., 2011, 111, 397 CrossRef CAS PubMed . For selected recent examples: ; (b) F. X. Zeng, H. F. Liu, L. Deng, B. Liao, H. Pang and Q. X. Guo, ChemSusChem, 2013, 6, 60 CrossRef PubMed; (c) A. M. da Costa Lopes, K. G. Joao, D. F. Rubik, E. Bogel-Lukasik, L. C. Duarte, J. Andreaus and R. Bogel-Lukasik, Bioresour. Technol., 2013, 142, 198 CrossRef CAS PubMed.
- (a) X. P. Zhang, X. C. Zhang, H. F. Dong, Z. J. Zhao, S. J. Zhang and Y. Huang, Energy Environ. Sci., 2012, 5, 6668 RSC; (b) Z. Z. Yang, L. N. He, J. Gao, A. H. Liu and B. Yu, Energy Environ. Sci., 2012, 5, 6602 RSC.
- M. Armand, F. Endres, D. R. MacFarlane, H. Ohno and B. Scrosati, Nat. Mater., 2009, 8, 621 CrossRef CAS PubMed.
- (a) J. F. Wishart and W. Castner Edward Jr., J. Phys. Chem. B, 2007, 111, 4639 CrossRef CAS; (b) F. Endres, Phys. Chem. Chem. Phys., 2010, 12, 1648 RSC.
- R. P. Bell, The Proton in Chemistry, Cornell University Press, Ithaca, 2nd edn, 1973 Search PubMed.
- R. W. Taft and F. G. Bordwell, Acc. Chem. Res., 1988, 21, 463 CrossRef CAS.
- E. P. Serjeant and B. Dempsey, Ionisation Constants of Organic Acids in Aqueous Solution, Pergamon Press, New York, 1979 Search PubMed.
- F. G. Bordwell, Acc. Chem. Soc., 1988, 21, 456 CrossRef CAS.
- (a) A. Streitwieser, J. H. Hammons, E. Ciuffarin and J. I. Brauman, J. Am. Chem. Soc., 1967, 89, 59 CrossRef CAS; (b) D. A. Bors, M. J. Kaufman and A. Streitwieser, J. Am. Chem. Soc., 1985, 107, 6975 CrossRef CAS; (c) A. Streitwieser, J. Org. Chem., 2009, 74, 4433 CrossRef CAS PubMed; (d) A. Streitwieser, A. Facchetti, L. F. Xie, X. Y. Zhang and E. C. Wu, J. Org. Chem., 2012, 77, 985 CrossRef CAS PubMed; (e) A. Streitwieser, Y. H. Leong, E. C. Wu and X. Y. Zhang, J. Org. Chem., 2013, 78, 1971 CrossRef CAS PubMed.
- To name a few, see: (a) J. F. Coetzee and I. M. Kolthoff, J. Am. Chem. Soc., 1957, 79, 6110 CrossRef CAS; (b) E. M. Arnett and J. J. Burke, J. Am. Chem. Soc., 1966, 88, 2340 CrossRef CAS; (c) C. D. Ritchie and G. H. Megerle, J. Am. Chem. Soc., 1967, 89, 1447 CrossRef CAS; (d) A. Kütt, T. Rodima, J. Saame, E. Raamat, V. Mäemets, I. Kaljurand, I. A. Koppel, R. Y. Garlyauskayte, Y. L. Yagupolskii, L. M. Yagupolskii, E. Bernhardt, H. Willner and I. Leito, J. Org. Chem., 2011, 76, 391 CrossRef PubMed.
- For measurements of relative acidities in ILs in the presence of molecular additives, see: (a) C. Thomazeau, H. Olivier-Bourbigou, L. Magna, S. Luts and B. Gilbert, J. Am. Chem. Soc., 2003, 125, 5264 CrossRef CAS PubMed; (b) I. B. Malham, P. Letellier and M. Turmine, Talanta, 2008, 77, 48 CrossRef PubMed; (c) G. Angelini, P. D. Maria, C. Chiappe, A. Fontana, M. Pierini and G. Siani, J. Org. Chem., 2010, 75, 3912 CrossRef CAS PubMed; (d) F. D'Anna, S. Marullo, P. Vitale and R. Noto, J. Org. Chem., 2010, 75, 4828 CrossRef PubMed; (e) K. Johnson, R. M. Pagni and J. E. Bartmess, Monatsh. Chem., 2007, 138, 1077 CrossRef CAS; (f) S. K. Shukla and A. Kumar, J. Phys. Chem. B, 2013, 117, 2456 CrossRef CAS PubMed . For measurements of absolute pKb of N-centered bases in ILs: ; (g) R. Barhdadi, M. Troupel, C. Comminges, M. Laurent and A. P. Doherty, J. Phys. Chem. B, 2012, 116, 277 CrossRef CAS PubMed; (h) D. Millan, M. Rojas, P. Pavez, M. Isaacs, C. Diaz and J. G. Santos, New J. Chem., 2013, 37, 3281 RSC; (i) K. Fujii, K. Hashimoto, T. Sakai, Y. Umebayashi and M. Shibayama, Chem. Lett., 2013, 42, 1250 CrossRef CAS.
- For recent examples of calculating the gas phase acidities, see: (a) M. M. Meyer and S. R. Kass, J. Phys. Chem. A, 2010, 114, 4086 CrossRef CAS PubMed; (b) M. Liu, N. T. Tran, A. K. Franz and J. K. Lee, J. Org. Chem., 2011, 76, 7186 CrossRef CAS PubMed; (c) D. Himmel, S. K. Goll, I. Leito and I. Krossing, Chem.–Eur. J., 2012, 18, 9333 CrossRef CAS PubMed.
- For recent reviews on calculating aqueous pKa constants, see: (a) J. M. Ho and M. L. Coote, Theor. Chem. Acc., 2010, 125, 3 CrossRef CAS; (b) J. M. Ho and M. L. Coote, WIREs Comput. Mol. Sci., 2011, 1, 649 CrossRef CAS . For recent examples, see: ; (c) C. C. R. Sutton, G. V. Franks and G. da Silva, J. Phys. Chem. B, 2012, 116, 11999 CrossRef CAS PubMed; (d) S. M. Zhang, J. Comput. Chem., 2012, 33, 517 CrossRef CAS PubMed; (e) Y. L. Chen, N. L. Doltsinis, R. C. Hider and D. J. Barlow, J. Phys. Chem. Lett., 2012, 3, 2980 CrossRef CAS PubMed; (f) J. A. Keith and E. A. Carter, J. Chem. Theory Comput., 2012, 8, 3187 CrossRef CAS; (g) N. Uddin, T. H. Choi and C. H. Choi, J. Phys. Chem. B, 2013, 117, 6269 CrossRef CAS PubMed.
- For selected examples of calculating pKa values in organic solvents, see: (a) Y. Fu, L. Liu, R. C. Li, R. Liu and Q. X. Guo, J. Am. Chem. Soc., 2004, 126, 814 CrossRef CAS PubMed; (b) J. N. Li, L. Liu, Y. Fu and Q. X. Guo, Tetrahedron, 2006, 62, 4453 CrossRef CAS; (c) Y. Fu, H. J. Wang, S. S. Chong, Q. X. Guo and L. Liu, J. Org. Chem., 2009, 74, 810 CrossRef CAS PubMed; (d) F. Z. Ding, J. M. Smith and H. B. Wang, J. Org. Chem., 2009, 74, 2679 CrossRef CAS PubMed; (e) A. Trummal, A. Rummel, E. Lippmaa, I. Koppel and I. A. Koppel, J. Phys. Chem. A, 2011, 115, 6641 CrossRef CAS PubMed; (f) E. Raamat, K. Kaupmees, G. Ovsjannikov, A. Trummal, A. Kutt, J. Saame, I. Koppel, I. Kaljurand, L. Lipping, T. Rodima, V. Pihl, I. A. Koppel and I. Leito, J. Phys. Org. Chem., 2013, 26, 162 CrossRef CAS.
- (a) C. J. Cramer and D. G. Truhlar, Chem. Rev., 1999, 99, 2161 CrossRef CAS PubMed; (b) J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999 CrossRef CAS PubMed.
- C. Chiappe and C. S. Pomelli, Phys. Chem. Chem. Phys., 2013, 15, 412 RSC.
- (a) R. D. Rogers and K. R. Seddon, Science, 2003, 302, 792 CrossRef PubMed; (b) R. D. Rogers, Nature, 2007, 447, 917 CrossRef CAS PubMed; (c) H. Weingäertner, Angew. Chem., Int. Ed., 2008, 47, 654 CrossRef PubMed.
- H. Deng, X. Li, Y. Chu, J. Q. He and J.-P. Cheng, J. Org. Chem., 2012, 77, 7291 CrossRef CAS PubMed.
- For examples, see: (a) J.-P. Cheng, M. Xian, K. Wang, X. Q. Zhu, Z. Yin and P. G. Wang, J. Am. Chem. Soc., 1998, 120, 10266 CrossRef CAS; (b) J.-P. Cheng, B. Liu, Y. Zhao, Z. Wen and Y. Sun, J. Am. Chem. Soc., 2000, 122, 9987 CrossRef CAS; (c) X. Q. Zhu, Q. Li, W. F. Hao and J.-P. Cheng, J. Am. Chem. Soc., 2002, 124, 9887 CrossRef CAS PubMed; (d) Y. Chu, H. Deng and J.-P. Cheng, J. Org. Chem., 2007, 72, 7790 CrossRef CAS PubMed; (e) X. Q. Zhu, M. T. Zhang, A. Yu, C. H. Wang and J.-P. Cheng, J. Am. Chem. Soc., 2008, 130, 2501 CrossRef CAS PubMed; (f) X. Li, H. Deng, B. Zhang, J. Y. Li, L. Zhang, S. Z. Luo and J.-P. Cheng, Chem.–Eur. J., 2010, 16, 450 CrossRef CAS PubMed.
- For examples, see: (a) A. Yu, Y. H. Liu, Z. C. Li and J. P. Cheng, J. Phys. Chem. A, 2007, 111, 9978 CrossRef CAS PubMed; (b) X. Q. Zhu, C. H. Wang, H. Liang and J. P. Cheng, J. Org. Chem., 2007, 72, 945 CrossRef CAS PubMed; (c) C. Yang, X.-S. Xue, J.-L. Jin, X. Li and J.-P. Cheng, J. Org. Chem., 2013, 78, 7076 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378 CrossRef CAS PubMed.
- C. J. Cramer and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 760 CrossRef CAS PubMed.
- V. S. Bernales, A. V. Marenich, R. Contreras, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2012, 116, 9122 CrossRef CAS PubMed.
- J. R. Pliego and J. M. Riveros, J. Phys. Chem. A, 2001, 105, 7241 CrossRef CAS . and references cited herein.
- For selected representative examples, see: (a) J. R. Pliego and J. M. Riveros, J. Phys. Chem. A, 2002, 106, 7434 CrossRef CAS; (b) Z. J. Cao, M. H. Lin, Q. N. Zhang and Y. R. Mo, J. Phys. Chem. A, 2004, 108, 4277 CrossRef CAS; (c) C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 2493 CrossRef CAS PubMed; (d) A. V. Marenich, W. D. Ding, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. Lett., 2012, 3, 1437 CrossRef CAS PubMed; (e) J. Ali-Torres, L. Rodriguez-Santiago and M. Sodupe, Phys. Chem. Chem. Phys., 2011, 13, 7852 RSC; (f) A. Mariana Rebollar-Zepeda, T. Campos-Hernandez, M. Teresa Ramirez-Silva, A. Rojas-Hernandez and A. Galano, J. Chem. Theory Comput., 2011, 7, 2528 CrossRef; (g) A. M. Rebollar-Zepeda and A. Galano, Int. J. Quantum Chem., 2012, 112, 3449 CrossRef CAS; (h) I. D. Cunningham, K. Bhaila and D. C. Povey, Comput. Theor. Chem., 2013, 1019, 55 CrossRef CAS; (i) R. A. Abramson and K. K. Baldridge, J. Chem. Theory Comput., 2013, 9, 1027 CrossRef CAS; (j) M. Gupta, E. F. da Silva and H. F. Svendsen, J. Chem. Theory Comput., 2013, 9, 5021 CrossRef CAS.
- R. Bini, O. Bortolini, C. Chiappe, D. Pieraccini and T. Siciliano, J. Phys. Chem. B, 2007, 111, 598 CrossRef CAS PubMed.
- R. Bini, C. Chiappe, V. L. Mestre, C. S. Pomelli and T. Welton, Theor. Chem. Acc., 2009, 123, 347 CrossRef CAS.
- For conformational studies of these complexes formed from a [Bmim] cation and the conjugate anionic bases please see Fig. S1–S15†.
- As suggested by one reviewer, we calculated the pKa of CH2(CN)2 by adding two explicit [Bmim] cations to the conjugate anionic base of CH2(CN)2. The pKa of CH2(CN)2 predicted by taking two explicit [Bmim] cations is 19.5, which is quite close to the pKa of 19.9 calculated for the same acid by using one explicit [Bmim] cation. This suggests that adding one more explicit [Bmim] cation to the conjugate anionic base provides some but not substantial improvement to the accuracy of the calculation. Overall, the unsatisfactory performance of a pure SMD model for predicting pKa in IL could be well addressed by adding a single explicit IL cation in solvating the carbanion.
- The predicted pKa's of CH2(CN)2, 9-CNFl and PhCH(CN)2 in [Bmim][Otf] are 17.4, 15.0 and 10.6, which are in good agreement with the corresponding experimental values of 16.3, 13.8 and 9.8, respectively.
- C. D. Hubbard, P. Illner and R. van Eldik, Chem. Soc. Rev., 2011, 40, 272 RSC.
- Q. H. Zhang, S. G. Zhang and Y. Q. Deng, Green Chem., 2011, 13, 2619 RSC.
- Y. Zhao and D. G. Truhlar, Chem. Acc. Res., 2008, 41, 157 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09 (Revision B.01), Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1 to S15, and optimized geometries and energies of all computed species. See DOI: 10.1039/c3qo00070b |
| This journal is © the Partner Organisations 2014 |
