Linear and nonlinear optical properties for AA and AB stacking of carbon nitride polymorph (C3N4)
A. H. Reshakab,
Saleem Ayaz Khan*a and
S. Auluckc
aNew Technologies – Research Center, University of West Bohemia, Univerzitni 8, 306 14 Pilsen, Czech republic. E-mail: maalidph@yahoo.co.uk; sayaz_usb@yahoo.com; Tel: +420 777 729 583
bCenter of Excellence Geopolymer and Green Technology, School of Material Engineering, University Malaysia Perlis, 01007 Kangar, Perlis, Malaysia
cCouncil of Scientific and Industrial Research – National Physical Laboratory, Dr. K S, Krishnan Marg, New Delhi 110012, India
First published on 17th February 2014
Abstract
The linear and nonlinear optical susceptibilities of AA and AB stacking of the carbon nitride polymorph were calculated using the all electron full potential linear augmented plane wave method based on density functional theory. The complex part of the dielectric function is calculated using the recently modified Becke and Johnson (mBJ) approximation which gives a better optical gap in comparison to the Ceperley–Alder (CA) local density approximation, the Perdew–Burke–Ernzerhof generalized gradient approximation, and the Engel–Vosko generalized gradient approximation. The complex dielectric function and other optical constants like refractive index, absorption coefficient, reflectivity and energy loss function are calculated and discussed in detail. The calculated uniaxial anisotropy (−1.06 and −1.04) gives a maximum value of birefringence (−0.89 and −0.87) which increases the suitability of both AA and AB stacking for a large second harmonic generation. The calculated second order susceptibility tensor components |χ(2)333(ω)| at the static limit are 19.4 pm V−1 and 59.6 pm V−1 for AA and AB stacking which increases to 34.2 pm V−1 and 106.7 pm V−1 at λ = 1064 nm. The first hyperpolarizability β333(ω) for AA and AB stacking C3N4 for the dominant component |χ(2)333(ω)| at the static limit are calculated to be (1.6 × 10−30 esu and 9.6 × 10−30 esu) respectively.
1. Introduction
The carbon nitride polymorph (C3N4), which comprises covalent bonds, has recently received much interest as a promising material in various applications, for instance as a photocatalyst, fuel cell electrode, light emitting apparatus and chemical sensor. In the past, Liu and Cohen1 have predicted that β-C3N4 has compressibility comparable to that of diamond. The search for the distinct structure of C3N4 has a long history. Teter and Hemley2 studied five types of C3N4, including α-C3N4, β-C3N4, cubic-C3N4, pseudocubic-C3N4 and graphitic C3N4. Their computed results forecast that α-C3N4 and graphitic allotropes are energetically highly favored compared to β-C3N4. Since then, much effort has been made for the synthesis of C3N4. All sorts of methods have been utilized. These include vapor deposition, laser ablation and high pressure high-temperature procedures.3–5 Due to the chemical inertness of C3N4, organizing dense C3N4 phases with large crystalline dimensions for explicit characterization is intricate. The g-C3N4 preparation has been described.6–19 A hypothetical material, C3N4 may have rather smaller bulk modulus than that of diamond as proposed by first-principles calculations.20,21 These outcomes have inspired theoretical calculations22–26 and experimental efforts to synthesize and distinguish this compound.27–38 From the synthesis of amorphous C–N films,30,32,36 small crystallites have been discovered in some of these films.31,33–35 C3N4 is a chemically stable compound having a good thermal hardness and astonishing optical characteristics that make it suitable as a photocatalyst under visible light. The pursuit of C3N4 has potential for introducing new materials with band gap in the 2.6–3.0 eV range for energy, solar, and LED materials. However, it is important to note the recent advances in the fields of InGaN and AlInN alloy have been widely implemented in solar cells,39,40 thermoelectricity,41,42 and LEDs.43–47Wang et al.48 showed that in comparison with other oxides, g-C3N4 (having band gap of 2.7 eV) is metal free photocatalyst which can absorb more visible light and produce hydrogen from water. Tahir et al.49 synthesized the tubular g-C3N4 and investigated the electrochemical properties which suggest it to be a good contestant for a supercapacitor and photocatalyst used for cleaning environment and energy storage purpose. Recently Wang et al.50 synthesized the nanotube g-C3N4 material and demonstrated the intense fluorescence with a photoluminescent, reflecting the applications as a blue light fluorescence material. This material also demonstrates the fabulous visible-light photocatalytic activity, suggesting the high usefulness of g-C3N4 nanotubes for gas storage, photocatalysis and light-emitting devices.50
From above we notice that there is dearth of theoretical calculations for these materials. There exists a theoretical work based on the pseudopotential method which deals only with valence electrons. Moreover the LDA-CA and GGA-PBE are also not much promising due to their band gap underestimation. It is well-known that the linear and nonlinear optical properties are very sensitive the band gap. Thus calculating the linear and nonlinear optical susceptibilities demands a very accurate energy gap value which should be very close to the experimental value. In our previous work51 we have calculated the electronic band structure, effective mass and valence electron charge density of AA and AB stacking of C3N4. Therefore as a natural extension we think it would be interesting to calculate the linear and nonlinear optical properties of AA and AB stacking of C3N4 using an all electron full potential linear augmented plane wave (FPLAPW) method which has proven to be the most precise technique within DFT to calculate the electronic structure of solids.52,53 In order to explore the effect of different exchange correlation potentials we have performed calculations for four type of exchange and correlation potentials. Thus, based on our previous experiences with this approach, we expect to get more accurate results as compared to the pseudopotential method.
2. Crystal structure and computational details
The crystal structure of AA and AB stacking of C3N4 polymorphs is stable in hexagonal symmetry having space group P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2. The crystallographic data of C3N4 polymorphs are taken from Teter and Hemley.2 The crystal structure of AA and AB stacking are shown in Fig. 1(a) and (b). We have employed the full potential linear augmented plane wave (FPLAPW) within Wien2k package.54 Four schemes namely Ceperley–Alder (CA) local density approximation (LDA-CA),55 Perdew–Burke–Ernzerhof generalized gradient approximation (PBE-GGA),56 Engel–Vosko generalized gradient approximation (EV-GGA)57 and a recent modified Becke and Johnson (mBJ) scheme58 were used for the self-consistent calculations. The convergence parameters (RMTKmax) that used to control size of the basis set for present calculation is set to be 7.0. The expression RMT represent muffin-tin (MT) sphere radius and Kmax symbolize the magnitude of largest K vector in plane wave expansion. The selected muffin-tin (MT) sphere radii for C and N is 1.24 atomic units (a.u.) in both AA and AB stacking of C3N4 polymorphs. The wave function inside the MT sphere was expended up to lmax = 10 whereas the Fourier expansion of the charge density was expanded up to Gmax = 12 (a.u.)−1. The cutoff energy was selected as 6.0 Ryd. The convergence of self consistent calculations was done when the difference in total energy of the crystal did not exceed 10−5 Ryd for succeeding steps. The self consistent calculations were obtained for both cases by 308 k points in irreducible Brillouin zone (IBZ).
m2. The crystallographic data of C3N4 polymorphs are taken from Teter and Hemley.2 The crystal structure of AA and AB stacking are shown in Fig. 1(a) and (b). We have employed the full potential linear augmented plane wave (FPLAPW) within Wien2k package.54 Four schemes namely Ceperley–Alder (CA) local density approximation (LDA-CA),55 Perdew–Burke–Ernzerhof generalized gradient approximation (PBE-GGA),56 Engel–Vosko generalized gradient approximation (EV-GGA)57 and a recent modified Becke and Johnson (mBJ) scheme58 were used for the self-consistent calculations. The convergence parameters (RMTKmax) that used to control size of the basis set for present calculation is set to be 7.0. The expression RMT represent muffin-tin (MT) sphere radius and Kmax symbolize the magnitude of largest K vector in plane wave expansion. The selected muffin-tin (MT) sphere radii for C and N is 1.24 atomic units (a.u.) in both AA and AB stacking of C3N4 polymorphs. The wave function inside the MT sphere was expended up to lmax = 10 whereas the Fourier expansion of the charge density was expanded up to Gmax = 12 (a.u.)−1. The cutoff energy was selected as 6.0 Ryd. The convergence of self consistent calculations was done when the difference in total energy of the crystal did not exceed 10−5 Ryd for succeeding steps. The self consistent calculations were obtained for both cases by 308 k points in irreducible Brillouin zone (IBZ).
3. Result and discussions
3.1. Linear optical properties
The complex dielectric function ε(ω) of the material is linked to the energy band structure. The overall band behavior of a solid can be explained by optical spectroscopy analysis of ε(ω).59 The complex dielectric function ε(ω) = ε1(ω) + iε2(ω) is the keynote factor for calculating the optical properties of the materials.60 The dispersion of dielectric function contains intra- and inter-band transitions. The intra-band transitions are present only in metals. In semiconductors only the inter-band transitions are present. Further the inter-band transitions are divided into direct and indirect band transitions. The contribution of the phonons associated from lattice vibration in indirect inter-band transition are ignored because of small the contribution and only direct band to band transition of electron are taken into account. The correct energy eigenvalues and electron wave functions are necessary to calculate the dispersion of dielectric function ε(ω). These are natural output of the band structure calculation. The crystal structure symmetry (hexagonal) of AA and AB stacking of C3N4 contains two non-zero principal diagonal dielectric tensor components εxx(ω) = εyy(ω) and εzz(ω) along a, b and c crystallographic axis. These are required to complete the explanation of the linear optical properties. These components can be calculated using the expression taken from ref. 61;
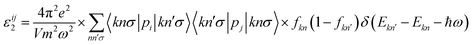 | (1) |
The structures in the optical response are caused by the electric-dipole transitions between the valence and the conduction bands. In order to identify these structures we need to look at the magnitude of the optical matrix elements. The observed structures would correspond to those transitions that have large optical matrix elements. The calculated absorptive and dispersive part of AA and AB stacking of C3N4 by LDA, GGA-PBE, EVGGA and mBJ, are shown in Fig. 2(a)–(d). This elucidates that mBJ approach shows a better optical gap compared to LDA, GGA and EVGGA. According to our previous experience with mBJ62–67 we find that mBJ brings the energy gap closer to the experimental one therefore we preferred mBJ scheme for calculations of the linear and nonlinear optical properties as they are very sensitive to the band gap. Fig. 2(e) and (f) shows the imaginary part of optical dielectric tensor components for AA and AB stacking of C3N4. The calculated ε2(ω) for AA stacking shows a high transparency optical gap up to 2.59 eV while for AB stacking the transparency region increases to 2.99 eV. The first peak in both cases represents transition of electron from valence band maximum to conduction band minimum. Similarly the rest of the peaks represents transitions of electrons from lower occupied bands to upper unoccupied bands. There is a considerable anisotropy between εxx2(ω) and εzz2(ω) for whole energy range of AA and AB stacking of C3N4. The real part of the optical dielectric tensor components is linked to the electric polarizability of the material which can be calculated from imaginary part using Kramers–Kronig relation;68
 | (2) |
Fig. 2(g) and (h) represents the real part of dielectric tensor components for AA- and AB-stacking. The calculated uniaxial anisotropy δε = [(εzz0 − εxx0)/εtot0] presented in Table 1, indicates considerable anisotropy69 between the spectral components of the dielectric function of AA and AB stacking. Table 1 also elucidates the other optical parameters of AA and AB stacking of C3N4 in comparison with diamond, β-C3N4, α-C3N4, γ-C3N4 and pc-C3N4. Fig. 2(i) and (j) shows the calculated refractive index n(ω) of AA and AB stacking. The refractive index is also related to the electric polarizability of the material. The static value of refractive index for two non-zero tensor components of AA and AB stacking are directly linked to n(0) by the relation 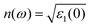 , as shown in Table 1. The most responsible component which increases the refractive index of C3N4 is nxx(ω) while nzz(ω) shows a negligible role in both stacking cases. When the energy of electromagnetic (EM) waves is increased the nxx(ω) also increases and achieves a maximum value at 4.9 and 4.8 eV for AA and AB stacking, respectively. Further increasing the energy cause sharp decrease in nxx(ω). The nxx(ω) curve crosses the unity at 5.5 eV. This shows the high luminescent nature of AA stacking as compared AB stacking.
, as shown in Table 1. The most responsible component which increases the refractive index of C3N4 is nxx(ω) while nzz(ω) shows a negligible role in both stacking cases. When the energy of electromagnetic (EM) waves is increased the nxx(ω) also increases and achieves a maximum value at 4.9 and 4.8 eV for AA and AB stacking, respectively. Further increasing the energy cause sharp decrease in nxx(ω). The nxx(ω) curve crosses the unity at 5.5 eV. This shows the high luminescent nature of AA stacking as compared AB stacking.
| Graphitic-C3N4 (AA stacking) | Graphitic-C3N4 (AB stacking) | Diamond | β-C3N4 | α-C3N4 | γ-C3N4 | pc-C3N4 | |
|---|---|---|---|---|---|---|---|
| a Present work.b Theoretical work ref. 26.c Experimental work ref. 37.d Experimental work ref. 38.e Experimental work ref. 77.f Experimental work ref. 78.g Theoretical work ref. 2.h Experimental work ref. 79. | |||||||
| Space group | P6![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) m m |
P6![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) m m |
Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
P63/m | P31c | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
P4![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) m m |
| Volume (Å3) | 73.8a | 147.1a | 44.2b | 85.49b | 170.63b | 307.91b | 40.52b |
| Eg (eV) | 2.59a | 2.99a | 5.72b, 5.47c | 3.825b | 4.672b | 1.445b | 2.843b |
| εxx1(0) | 3.86a | 3.85a | 5.70c | 4.533b | 4.288b | 6.275b | 5.190b |
| εzz1(0) | 1.15a | 1.18a | 5.79b | 4.755b | 4.296b | ||
| nxx(0) | 1.95a | 1.96a | 2.417d | 2.129b | 2.071b | 2.505b | 2.278b |
| nzz(0) | 1.06a | 1.09a | 2.417d | 2.181b | 2.072b | 2.505b | |
| Δn(0) | −0.89a | −0.87a | |||||
| δε | −1.06a | −1.04a | |||||
| Density (g cm−3) | 2.0215a | 2.0201a | 3.51e | 3.57f | 3.585g | 2.620a,h | 3.811g |
The absorption coefficient of the two dielectric tensor components shows a considerable anisotropy between the two components Ixx(ω) and Izz(ω) for both AA and AB stacking. For both, Ixx(ω) shows dominancy while Izz(ω) exhibits a minor role. In AA stacking of C3N4, the first peak of Ixx(ω) shows maximum absorption of about 175 × 104 cm−1 around 5.4 eV, while in AB-stacking the first peak of Ixx(ω) shifts to 5.2 eV with a smaller value of absorption coefficient (167 × 104 cm−1) as shown in Fig. 2(k) and (l). The two components of the reflectivity Rxx(ω) and Rzz(ω) also shows considerable anisotropy. Rxx(ω) plays a leading role with maximum reflection of 62% (AA stacking) and 56% (AB stacking) around 5.5 eV whereas Rzz(ω) shows a negligible role except in the higher energy range (13.5 eV) as shown in Fig. 2(m) and (n).
The energy loss spectrum is related to the energy loss of a fast moving electron in the crystal. Fig. 2(o) and (p) elucidates considerable anisotropy between Lxx(ω) and Lzz(ω) in AA and AB stacking of C3N4. In the energy range between 2.59 eV and 5.0 eV for AA stacking and from 2.99 eV to 4.60 eV in AB stacking, Lzz(ω) is the dominant component. As one moves to higher energy range Lxx(ω) becomes dominant in both stacking by showing maximum value of energy loss spectrum around 9.5 eV.
The calculated birefringence Δn(ω) of AA and AB stacking of C3N4 polymorph are shown in Fig. 2(q) and (r). Birefringence is given by the relation
| Δn = ne − no |
3.2. Nonlinear optical properties
The present compounds have only one independent dominant tensor components χ(2)333(−2ω; ω; ω). The number in the subscript represents the three polarization directions along x, y and z direction. The first order response only deals with inter-band transitions and involves the square matrix elements giving positive values for ε2(ω). The second harmonic generation (SHG) involves 2ω resonance in accumulation with 1ω resonance which are furthermore separated into inter-band χ(2)inter(−2ω; ω; ω), intra-band χ(2)intra(−2ω; ω; ω) term along with modulation of intra-band on inter-band term χ(2)mod(−2ω; ω; ω). The expressions of the complex second-order nonlinear optical susceptibility tensors are given in the ref. 71–75.Since the nonlinear optical properties are very sensitive to the band gap of the material as compared to linear optical properties therefore, we have selected to show the results obtained by mBJ scheme because it produces better band splitting and hence gives a band gap value close to the experimental one. The importance of the static values of dielectric tensor components of optical susceptibilities cannot be ignored because it is used to calculate the relative frequency of SHG efficiency.75 The real and imaginary part of second order optical susceptibilities χ(2)333 of both AA and AB stacking of C3N4 are shown in Fig. 3(a) and (b). The maximum peak value of Reχ(2)333 and Imχ(2)333 for AA stacking are 300 pm V−1 and 110 pm V−1 which are located at 3.1 eV and 3.5 eV. In AB stacking both peaks shift to 2.8 eV and 3.25 eV with increasing the peak heights to be 610 pm V−1 and 215 pm V−1 for both Reχ(2)333 and Imχ(2)333.
Fig. 3(c) and (d) shows the intra- and inter-band contribution of ω and 2ω resonance for AA and AB stacking of C3N4, respectively. One can see that ω resonance is smaller than 2ω resonance in both cases. The maximum peaks of inter- and intra-band of 2ω resonance in AA stacking are located at 2.9 eV which illuminates value of 13 × 10−7 esu and −22.5 × 10−7 esu. For AB stacking these peaks are situated at 2.7 eV with maximum value of 27.5 × 10−7 esu and −49.0 × 10−7 esu for inter- and intra-band contribution of 2ω respectively. Similarly when one moves from AA stacking to AB staking, both contributions (inter- and intra-) of 1ω resonance shifts to lower energy with increasing value of Imχ(2)333. It is also clear that Imχ(2)333 shows a zero value below half the band gap (Eg/2). The 2ω resonance starts to contribute at energy > Eg/2, while ω resonance begins to contribute at energies above Eg. The clear vision of the ω and 2ω resonance can be seen in Fig. 3(e) and (f). The upper panel of Fig. 3(e) and (f) show the calculated value of |χ(2)333(ω)| for the dominant tensor component. The value of |χ(2)333(ω)| at the static limit |χ(2)333(0)| is 19.4 pm V−1 for AA stacking and 59.6 pm V−1 for AB stacking. At λ= 1064 nm the |χ(2)333(ω)| value increased to be 34.2 pm V−1 for AA stacking and 106.7 pm V−1 for AB stacking.
To analyze the features of the calculated absolute value of the dominant component |χ(2)333(ω)| it would be worthwhile helpful to compare |χ(2)333(ω)| (Fig. 3(e) and (f) – upper panel) with the absorptive part of the corresponding dielectric function ε2(ω) as a function of both ω/2 and ω (Fig. 3(e) and (f) – lower panel). The 2ω resonance is responsible for spectral structure formation in the energy range from 1.29 eV to 2.59 eV (1.50 eV to 2.99 eV) for AA stacking (AB stacking). The subsequent structure ranges from 2.59 eV to 6.80 eV (2.99 eV to 6.80 eV) for AA stacking (AB stacking) is fashioned by the combined effect of ω and 2ω resonance and the rest of the structure is formed by only ω resonance. The calculated values of second order susceptibility for AA and AB stacking of C3N4 are listed in Table 2 in comparison to the experimental and theoretical results of ZnS, GaN and GaAs.
We also have calculated the first hyperpolarizability βijk vector component along dipole moment direction using the static value of |χ(2)333(ω)| and the calculated density for AA stacking and AB stacking (Table 1), using the expression given in ref. 76. The calculated values of β333(ω) are 1.6 × 10−30 esu and 9.6 × 10−30 esu for AA and AB stacking of C3N4, respectively.
4. Conclusions
We have calculated the linear and nonlinear optical properties of AA and AB stacking of carbon nitride polymorph using all electron full potential linear augmented plane wave method based on DFT within the frame work of Wien2k code. The exchange correlation energy was solved using four schemes namely Ceperley–Alder (CA) local density approximation, Perdew–Burke–Ernzerhof generalized gradient approximation, Engel–Vosko generalized gradient approximation and recent modified Becke and Johnson (mBJ) approximation. We have calculated and discussed in detail the complex dielectric function and the other optical constants such as refractive index, absorption coefficient, reflectivity and energy loss function. The uniaxial anisotropy (δε) was calculated to be −1.06 for AA stacking and −1.04 AB stacking which ensures higher value of birefringence. The value of birefringence at the static limit Δn(0) is −0.89 for AA stacking and −0.87 for AB stacking. The values of δε and Δn(0) predict that both AA and AB stacking posses large second harmonic generation. The second order susceptibility tensor components |χ(2)333(ω)| for AA-stacking (AB-stacking) were calculated at static limit and at λ= 1064 nm, these are 19.4 pm V−1 and 34.2 pm V−1 (59.6 pm V−1 and 106.7 pm V−1). In additional we have calculated the first hyperpolarizability β333(ω) using the static value of |χ(2)333(ω)|. These are 1.6 × 10−30 esu and 9.6 × 10−30 esu for AA and AB stacking of C3N4, respectively.Acknowledgements
The result was developed within the CENTEM project, reg. no. CZ.1.05/2.1.00/03.0088, co-funded by the ERDF as part of the Ministry of Education, Youth and Sports OP RDI programme. SA would like to thank CSIR-NPL for financial assistance.References
- A. Y. Liu and M. L. Cohen, Science, 1989, 245, 841–842 CAS
.
- D. M. Teter and R. J. Hemley, Science, 1996, 271, 53–55 CAS
.
- D. W. He, F. X. Zhang, X. Y. Zhang, Z. C. Qin, M. Zhang and R. P. Liu, et al., J. Mater. Res., 1998, 13, 3458–3462 CrossRef CAS
.
- Z. Zhang, H. Guo, G. Zhong, F. Yu, Q. Xiong and X. Fan, Thin Solid Films, 1999, 346, 96–99 CrossRef CAS
.
- Y. Peng, T. Ishigaki and S. Horiuchi, Appl. Phys. Lett., 1998, 73, 3671–3673 CrossRef CAS PubMed
.
- V. N. Khabshesku, J. L. Zimmerman and J. L. Margrave, Chem. Mater., 2000, 12, 3264–3270 CrossRef
.
- M. J. Bojdys, J. O. Muller, M. Antonietti and A. Thomas, Chem.–Eur. J., 2008, 14, 8177–8182 CrossRef CAS PubMed
.
- A. Thomas, A. Fischer, F. Goettmann, M. Antonietti, J. O. Muller and R. Schlogl, et al., J. Mater. Chem., 2008, 18, 4893–4908 RSC
.
- X. Li, J. Zhang, L. Shen, Y. Ma, W. Lei and Q. Cui, et al., Appl. Phys. A: Mater. Sci. Process., 2009, 94, 387–392 CrossRef CAS
.
- D. R. Miller, J. R. Holst and E. G. Gillan, Inorg. Chem., 2007, 46, 2767–2774 CrossRef CAS PubMed
.
- H. Montigaud, B. Tanguy, G. Demazeau, I. Alves and S. Courjault, J. Mater. Sci., 2000, 35, 2547–2552 CrossRef CAS
.
- S. M. Lyth, Y. Nabe, S. Moriya, S. Kuroki, M. A. Kakimoto and J. I. Ozaki, et al., J. Phys. Chem. C, 2009, 113, 20148–20151 CAS
.
- C. Li, X. G. Yang, B. J. Yang, Y. Yan and Y. T. Qian, Mater. Chem. Phys., 2007, 103, 427–432 CrossRef CAS PubMed
.
- K. Gibson, J. Glaser, E. Milke, M. Marzini, S. Tragl and M. Binnewies, et al., Mater. Chem. Phys., 2008, 112, 52–56 CrossRef CAS PubMed
.
- J. L. Zimmerman, R. Williams, V. N. Khabshesku and J. L. Margrave, Nano Lett., 2001, 1, 731–734 CrossRef CAS
.
- H. A. Ma, X. P. Jia, L. X. Chen, P. W. Zhu, W. L. Guo and X. B. Guo, et al., J. Phys.: Condens. Matter, 2002, 14, 11269 CrossRef CAS
.
- G. Goglio, D. Andrault, S. Courjault and G. Demazeau, High Pressure Res., 2002, 22, 535–537 CrossRef
.
- J. Kouvetakis, M. Todd, B. Wilkens, A. Bandari and N. Cave, Chem. Mater., 1994, 6, 811–814 CrossRef CAS
.
- E. G. Gillan, Chem. Mater., 2000, 12, 3906–3912 CrossRef CAS
.
- A. Y. Liu and M. L. Cohen, Science, 1989, 245, 841 CAS
.
- A. Y. Liu and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 10727 CrossRef CAS
.
- J. L. Corkill and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 17622 CrossRef CAS
.
- H. Yao and W. Y. Ching, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 11231 CrossRef CAS
.
- J. Ortega and O. F. Sankey, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 2624 CrossRef CAS
.
- Y. Guo and W. A. Goddard, Chem. Phys. Lett., 1995, 237, 72 CrossRef CAS
.
- J. Hu, Appl. Phys. Lett., 1995, 89, 261117 CrossRef PubMed
.
- T. Sekine, H. Kanda, Y. Bando, M. Yokohama and K. Hojou, J. Mater. Sci. Lett., 1990, 9, 1376 CrossRef CAS
.
- L. Maya, D. R. Cole and E. W. Hagaman, J. Am. Ceram. Soc., 1991, 74, 1686 CrossRef CAS
.
- J. J. Cuomo, P. A. Leary, D. Yu, W. Reuter and M. Frisch, J. Vac. Sci. Technol., 1976, 16, 299 CrossRef
.
- H. X. Han and B. J. Feldman, Solid State Commun., 1988, 65, 921 CrossRef CAS
.
- C. Niu, Y. Z. Liu and C. M. Lieber, Science, 1993, 261, 334 CAS
.
- D. Marton, K. J. Boyd, A. H. Al-Bayati, S. S. Todorov and J. W. Rablais, Phys. Rev. Lett., 1994, 73, 118 CrossRef CAS
.
- K. M. Yu, M. L. Cohen, E. E. Haller, W. L. Hansen, A. Y. Lu and I. C. Wu, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 5034 CrossRef CAS
.
- J. P. Riviere, D. Texier, J. Delafond, M. Jaouen, E. L. Mathe and J. Chaumont, Mater. Lett., 1995, 22, 115 CrossRef CAS
.
- Z. M. Ren, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 5274 CrossRef CAS
.
- Y. Yang, K. A. Nelson and F. Adibi, J. Mater. Res., 1995, 10, 41 CrossRef CAS
.
- M. H. V. Huynh, M. A. Hiskey, J. G. Archuleta and E. L. Roemer, Angew. Chem., Int. Ed., 2004, 43, 5658 CrossRef CAS PubMed
; 2005, 44, 737.
- H. R. Phillip and E. A. Taft, Phys. Rev., 1964, 136, A1445 CrossRef
.
- E. C. Young, F. Wu, A. E. Romanov, D. A. Haeger, S. Nakamura, S. P. Denbaars, D. A. Cohen and J. S. Speck, Appl. Phys. Lett., 2012, 101, 5 CrossRef PubMed
.
- C. J. Neufeld, N. G. Toledo1, S. C. Cruz, M. Iza, S. P. DenBaars and U. K. Mishra, Appl. Phys. Lett., 2008, 93, 143502 CrossRef PubMed
.
- J. Zhang, H. Tong, G. Liu, J. A. Herbsommer, G. S. Huang and N. Tansu, J. Appl. Phys., 2011, 109, 053706 CrossRef PubMed
.
- J. Zhang, S. Kutlu, G. Liu and N. Tansu, J. Appl. Phys., 2011, 110, 043710 CrossRef PubMed
.
- D. Feezell, et al., J. Disp. Technol., 2013, 9, 190–198 CrossRef CAS
.
- H. Zhao, G. Liu, J. Zhang, J. D. Poplawsky, V. Dierolf and N. Tansu, Opt. Express, 2011, 19, A991–A1007 CrossRef CAS PubMed
.
- R. A. Arif, H. Zhao and N. Tansu, Appl. Phys. Lett., 2008, 92, 011104 CrossRef PubMed
.
- H. Zhaol, R. A. Arif and N. Tansu, J. Appl. Phys., 2008, 104, 043104 CrossRef PubMed
.
- K. T. Delaney, P. Rinke and C. G. Van de Walle, Appl. Phys. Lett., 2009, 94, 191109 CrossRef PubMed
.
- X. C. Wang, K. Maeda, A. Thomas, K. Takanabe, G. Xin, J. M. Carlsson, K. Domen and M. Antonietti, Nat. Mater., 2009, 8, 76 CrossRef CAS PubMed
.
- M. Tahir, C. Cao, F. K. Butt, F. Idrees, N. Mahmood, I. Aslam, Z. Ali, M. Tanvir, M. Rizwan and T. Mahmood, J. Mater. Chem. A, 2013, 1, 13949 CAS
.
- S. Wang, C. Li, T. Wang, P. Zhang, A. Li and J. Gong, J. Mater. Chem. A, 2014, 2, 2885 CAS
.
- A. H. Reshak, S. A. Khan and S. Auluck, RSC Adv., 2014, 4, 6957–6964 RSC
.
- S. Gao, Comput. Phys. Commun., 2003, 153, 190–198 CrossRef CAS
.
- K. Schwarz, J. Solid State Chem., 2003, 176, 319–328 CrossRef CAS
.
- P. Balaha, K. Shewartz, G. K. H. Madsen, D. Kvsnicka and J. Luitz, WIEN2K, an Augmented plane wave +local orbitals program for calculating crystals properties, Karlheinz Schewartz, Techn. Universitat, Wien, Austria, 2001, ISBN 3-9501031-1-2 Search PubMed
.
- D. M. Ceperley and B. I. Alder, Phys. Rev. Lett., 1980, 45, 566 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS
.
- E. Engel and S. H. Vosko, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 13164 CrossRef CAS
.
- F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102, 226401 CrossRef
.
- S. A. Khan and A. H. Reshak, Int. J. Electrochem. Sci., 2013, 8, 9459–9473 CAS
.
- A. H. Reshak and S. A. Khan, Comput. Mater. Sci., 2013, 78, 91–97 CrossRef CAS PubMed
.
- A. Delin, P. Ravindran, O. Eriksson and J. M. Wills, Int. J. Quantum Chem., 1998, 69, 349–358 CrossRef CAS
.
- A. H. Reshak, X. Chen, S. Auluck and H. Kamarudin, Mater. Chem. Phys., 2012, 137, 346–352 CrossRef CAS PubMed
.
- A. H. Reshak, X. Chen, S. Auluck and H. Kamarudin, J. Appl. Phys., 2012, 112, 053526 CrossRef PubMed
.
- A. H. Reshak, I. V. Kityk, O. V. Parasiuk, A. O. Fedorchuk, Z. A. Alahmed, N. AlZayed, H. Kamarudin and S. Auluck, J. Mater. Sci., 2013, 48, 1342–1350 CrossRef CAS
.
- A. H. Reshak, I. V. Kityk, O. V. Parasyuk, H. Kamarudin and S. Auluck, J. Phys. Chem. B, 2013, 117, 2545–2553 CrossRef CAS PubMed
.
- M. Benkraouda and N. Amrane, J Alloys Compd., 2013, 546, 151–156 CrossRef CAS PubMed
.
- S. Guo and B. Liu, J. Magn. Magn. Mater., 2012, 324, 2410–2415 CrossRef CAS PubMed
.
- H. Tributsch, Z. Naturforsch., 1977, 32, 972 Search PubMed
.
- A. H. Reshak, X. Chen, S. Auluck and I. V. Kityk, J. Chem. Phys., 2008, 129, 204111 CrossRef CAS PubMed
.
- A. H. Reshak, S. Auluck and I. V. Kityk, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 245120 CrossRef
.
- S. Sharma, J. K. Dewhurst and C. Ambrosch-Draxl, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 165332 CrossRef
.
- A. H. Reshak, Ph.D. thesis, Indian Institute of Technology-Rookee, India, 2005
.
- A. H. Reshak, J. Chem. Phys., 2006, 125, 014708 CrossRef PubMed
.
- A. H. Reshak, J. Chem. Phys., 2006, 124, 014707 CrossRef PubMed
.
- A. H. Reshak, H. Kamarudin and S. Auluck, J. Mater. Sci., 2013, 48, 1955–1965 CrossRef CAS
.
- R. W. Boyd, Nonlinear Optics, Academic Press is an imprint of Elsevier, ISBN: 978-0-12-369470-6, third edition, 2008 Search PubMed.
- J. W. Zou, K. Reichelt, K. Schmidt and B. Dischler, J. Appl. Phys., 1989, 65, 3914–3918 CrossRef CAS PubMed
.
- J. Hu, P. Yang and C. M. Lieber, Phys. Rev. B., 1998, 57(6), R3185–R3188 CrossRef CAS
.
- L. C. Ming, P. Zinin, Y. Meng, X. R. Liu, S. M. Hong and Y. Xie, J. Appl. Phys., 2006, 99, 033520 CrossRef PubMed
.
- D. T. F. Marple, J. Appl. Phys., 1964, 35, 539 CrossRef CAS PubMed
.
- J. L. P. Hughes, Y. Wang and J. E. Sipe, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55(20), 13630 CrossRef CAS
.
- B. F. Levine and C. G. Bethea, Appl. Phys. Lett., 1972, 20, 272 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2014 |



