DFT study on the effects of defect and metal-doping on the decomposition of H₂S on the α-Fe₂O₃(0001) surface

Abstract

The adsorption and decomposition mechanisms of H₂S on different α-Fe₂O₃(0001) surfaces, including Fe-vacancy, O-vacancy, sulfurized and Cu-, Zn- and Co-doped surfaces, have been studied systematically using periodic density functional calculations. The results show that the Fe-vacancy surface exhibits an excellent catalytic activity towards the decomposition of H₂S, which is favorable for the desulfurization. Both O-vacancy and sulfurized surfaces have negative effects on the desulfurization. The doping of Cu, Zn and Co on the α-Fe₂O₃(0001) surface is beneficial to enhance the desulfurization performance of the hematite sorbent, of which Zn addition is a comparatively good candidate taking desulfurization efficiency and economic factors into account.

---

1. Introduction

Coal-derived gaseous products inevitably contain sulfur-containing compounds, in which the content of H₂S is the highest.^1,2 It is necessary to reduce H₂S to a low level due to its negative effects on the environment and chemical processing.^3–6

α-Fe₂O₃ is a widely used desulfurization sorbent to remove H₂S experimentally due to its low cost and high resistance to corrosion.^7–11 The decomposition processes of H₂S into S/H/H are key steps during the desulfurization. Therefore, the adsorption and dissociation of H₂S on the ZnO,¹² TiO₂,¹³ CeO₂ (ref. 14) and Cu₂O¹⁵ surfaces have been studied extensively, while a few researches have been reported for the adsorption and dissociation of H₂S on the α-Fe₂O₃ surface,^16,17 especially for the defective surfaces. The defects on the surface can behave quite different from other surface sites in the surface structures, electronic structures and local atomic coordination, thus may play an important role in catalyzing heterogeneous reactions on the various surfaces.^15,18,19 A few works^20,21 have reported that there are defects on the hematite surface, especially for the point defects. However, surface point-defect species are experimentally difficult to study because of their low concentration and generally non-periodic nature.²² The theoretical studies can provide valuable insight into some features being not easily attainable through experiment. The adsorption and dissociation of H₂O on defective α-Fe₂O₃(0001) surfaces have been investigated using the density functional theory method, which shows that the Fe-adatom and Fe-vacancy surfaces are more reactive for H₂O than the perfect and O-vacancy surfaces.²² What's more, the O vacancy on the TiO₂(110) surface is important for the adsorption behavior of atom S.²³ Our aim in this study is to investigate the effect of Fe-vacancy and O-vacancy on the decomposition of H₂S. In addition, the surface of desulfurizer is sulfurized during the desulfurization. However, the dissociation behavior of H₂S on the sulfurized surface of desulfurizer is not clear.

Doping a small amount of other suitable metals is an effective method to overcome sulfur poison or improve the reactivity of materials. The adsorption of H₂S on the pure Pd, Cu-doped and Nb-doped Pd surfaces has been investigated, and the result shows that there is a strong interaction between H atom in H₂S and the Nb-doped Pd surface, rather than the S-surface interaction. In addition, the binding strength of H₂S on the Nb-doped Pd surface is higher than that on the pure Pd surface. Therefore, doping Pd with Nb can improve the anti-sulfur poisoning property.²⁴ Co- or Ni-doped α-Fe₂O₃ surfaces were shown the most thermodynamically favored reaction pathway for water oxidation.²⁵ What's more, by replacing some of the metal centers of MgO(100) with Ni atoms, the binding energy of sulfur species is enhanced through new electronic states associated with the Ni 3d levels and located above the occupied O 2p + Mg 3s bands.²⁶ The adsorption of CO₂ on the different NiM bimetals on MgO(100) and the perfect surfaces have been compared.²⁷ Moreover, the effects of Ti, Zr, and Hf doping on CO adsorption on the CeO₂(110) surface have been studied, and the adsorption of CO is much stronger on the doped surface than that on the undoped surface.²⁸ Therefore, several first-row transition metals (Cu, Zn and Co) are considered for atom substitutions because their ionic radius are similar to that of Fe atom and which will give rise to different stable oxidation states for their different numbers of 3d electrons.

In this study, we are to investigate the decomposition processes of H₂S on the different modified α-Fe₂O₃(0001) surfaces, including Fe-vacancy, O-vacancy, sulfurized, and Cu-, Zn- and Co-doped α-Fe₂O₃(0001) surfaces by using the density functional theory (DFT) method, and the effects of different surface on the decomposition of H₂S will be obtained. In addition, the suitable modified method will be provided to improve the desulfurization efficiency of α-Fe₂O₃.

2. Computational methods and models

2.1 Calculation methods

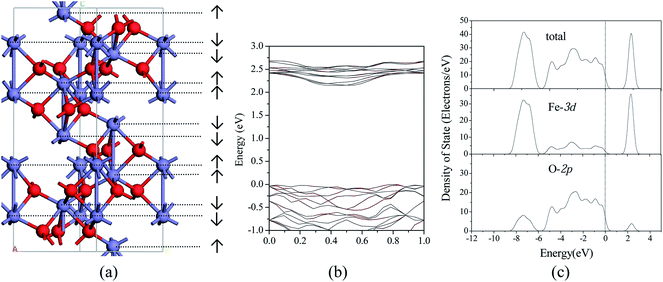
We used the CASTEP program package for all calculations.²⁹ The generalized gradient approximation (GGA)³⁰ with the Perdew–Burke–Ernzerhof (PBE) exchange correlation functional³¹ was employed. The electronic wave functions were expanded in a plane wave basis set, and the ionic core was described by ultrasoft pseudopotentials. Brillouin-zone integration was performed using 2 × 2 × 1 (ref. 32) for Monkhorst–Pack grid with 0.07 Å⁻¹ spacing for the surface structures and a larger gird point of 4 × 4 × 2 with 0.03 Å⁻¹ mesh for the calculation of density of states (DOS) and partial density of states (PDOS). A cutoff energy of 450 eV was used to obtain accurate energies for all systems. A Fermi smearing of 0.1 eV was utilized to speed up convergence. The convergence criteria were set to medium quality with the tolerance for SCF, energy, maximum force, and maximum displacement of 2.0 × 10⁻⁶ eV per atom, 2.0 × 10⁻⁵ eV per atom, 0.05 eV Å⁻¹ and 2.0 × 10⁻³ Å, respectively. Changing the maximum force tolerance to 0.02 eV Å⁻¹ had a negligible effect on the lattice parameters of α-Fe₂O₃, and there were little differences of 0.1 and 2.8 kJ mol⁻¹ in adsorption energy for H₂S on the Fe-vacancy surface with molecular and dissociative modes under the two force tolerances. In addition, the parameters have been widely used to study the electronic structure of metal modified α-Fe₂O₃(0001) surface,³³ the carburization of the Fe₃O₄(111) surface³⁴ and the interaction mechanism of H₂S on the γ-Fe₂O₃(001) surface.³⁵

DFT-GGA level of the theory has provided meaningful structural and energetic properties of α-Fe₂O₃,^33,36 as well as the reaction mechanisms on the α-Fe₂O₃ surfaces.³⁷ However, it is well-established that the addition to the standard density functional of a Hubbard U term acting on the Fe 3d orbitals allows for an accurate description of the electronic structure. The GGA + U method with U = 5 eV was applied for Fe atom to take into account of the strong on-site Coulomb interaction of Fe_3d states in α-Fe₂O₃.^38–40 The energy band, DOS and PDOS of bulk α-Fe₂O₃ and surfaces were calculated. For the α-Fe₂O₃, previous study has reported that GGA + U shows that an on-site Coulomb interaction of U = 5 eV leads to an accurate description of the electronic, and magnetic properties.⁴¹ In order to analyze the influence of Hubbard U on the results, adsorption energies of H₂S and SH on the perfect Fe₂O₃ with GGA and GGA + U are calculated. It shows that adsorption energies are 40.7 and 182.7 kJ mol⁻¹ by GGA + U, which are lower than that of GGA (71.0 and 255.2 kJ mol⁻¹).¹⁶ The results imply that the absolute values of adsorption energies are different with GGA and GGA + U, however, there are the same change trends. Therefore, there is no influence on the results about the effects of defect and metal-doping on the decomposition of H₂S on the α-Fe₂O₃(0001) surface.

2.2 Surface models

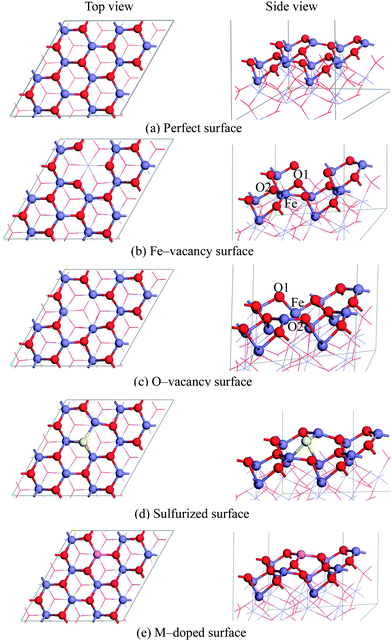
We considered four magnetic configurations for Fe atoms since there are four Fe atoms in a rhombohedral unit cell of Fe₂O₃, such as (+ + + +), (+ − + −), (+ − − +) and (+ + − −), where + and − designated up- and down-spin directions with respect to the z-axis. The total energy of antiferromagnetic arrangement (+ − − +) is the lowest, and the structure of which is the most stable, which have been found in our previous work¹⁶ and are consistent with the other theoretical work.^33,42,43 Fig. 1(a) shows the hexagonal crystal structure of antiferromagnetic α-Fe₂O₃, and the spin arrangements are also shown. Meanwhile, electronic band structure, total and PDOS of α-Fe₂O₃ are calculated, which are shown in Fig. 1(b) and (c). The calculated energy gap of 2.15 eV is in better accordance with the indirect optical gap of 1.9–2.2 eV (ref. 44 and 45) than the previous result of 0.75 eV.⁴³ Between −8.5 to −6.0 and −6.0 to 0.0 eV, 3d states of Fe strongly overlap with the 2p states of O, and the Fe 3d states are hybridized again with O 2p states between 2.0–3.0 eV. It is consistent with the previous results.⁴⁶ Both the top of valence band and the conduction band of α-Fe₂O₃ are mainly contributed by O 2p and Fe 3d, respectively.

Fig. 1 The structure and electronic properties of α-Fe₂O₃. (a) The hexagonal crystal structure of antiferromagnetic α-Fe₂O₃ and the spin arrangements; (b) calculated electronic band structure; (c) total and PDOS analysis of antiferromagnetic α-Fe₂O₃.

The α-Fe₂O₃(0001) surface is one of the predominant growth surfaces, which has three different chemically distinct (clean) terminations: a single iron-layer (Fe–O3–Fe–…), a double iron-layer (Fe–Fe–O3–…), and an oxygen-layer (O3–Fe–Fe–…). The most stable reduced surface termination is Fe–O3–Fe–… indicated by experimental and theoretical work.^47–50 Consequently, the single iron-layer terminated nine atomic layer slab model of the perfect α-Fe₂O₃(0001) surface is built based on the optimized α-Fe₂O₃ bulk structure, as shown in Fig. 2(a). The surface with hydroxyls is not considered since it can only be existed when the clean α-Fe₂O₃(0001) surface is exposed to water vapor at high pressure.^47,51 In addition, the content of water is negligible during the remove of H₂S in high-temperature coal gas in this study. A p(2 × 2) super-cell was large enough to neglect the lateral adsorbate interaction according to the previous calculations,^22,36,52 and a vacuum space of 12 Å was introduced to prevent interaction between the slabs for all the surfaces. In all calculations, bottom three layers of the slab were fixed at their bulk-like position, whereas the remaining atoms in the top six layers, as well as the adsorbed species were allowed to relax.

Fig. 2 The optimized structures of different α-Fe₂O₃(0001) surfaces, top and side views. (a) Perfect surface; (b) Fe-vacancy surface; (c) O-vacancy surface; (d) sulfurized surface; (e) M-doped surface. Purple, red, yellow and pink balls are represented Fe, O and S and the substituted metal atoms, respectively.

Vacancies were created by removing a Fe or O atom from the α-Fe₂O₃(0001) surface. The sulfurized surface was obtained by replacing one of twelve O atoms on the surface according to our previous calculation result.¹⁶ Doping effects of transition metals on surface chemistry were tested by direct atom substitution. The Cu-, Zn- and Co-doping models were constructed by replacing one of the outermost layer Fe atoms since the substitution of the outermost layer Fe is the easiest, and the magnetic moments of the substituting atoms were set as the substituted Fe atom.

The four modified surface models are also presented in Fig. 2, such as Fe-vacancy surface, O-vacancy surface, sulfurized surface, M-doped surface. The defect concentrations of Fe-vacancy and M-doped surfaces are both 25%. In sulfurized surface and O-vacancy surface models, the O vacancy and S substitute are introduced with the concentration of 8.3%.

The adsorption energy is regarded as a measure of the strength of adsorbate–substrate adsorption. The adsorption energy is defined as follows:

E_ads = E_A + E_B − E_A/B (1)

where E_A/B is the total energy of the substrate together with the adsorbate in its equilibrium state, E_A is the total energy of the free adsorbate, and E_B is the total energy of the bare substrate. By this definition, a positive E_ads value corresponded to an exothermic adsorption, and the more positive the E_ads is, the stronger the adsorption is.

The co-adsorption energy is defined as follows:

E_co-ads = E_A + E_B + E_slab − E_(A+B)/slab (2)

where E_A, E_B, E_slab and E_(A+B+C)/slab are the energies for the free A, B, the slab with a p(2 × 2) super-cell and the co-adsorbed (A + B)/slab systems, respectively.

Moreover, the transition states (TS) were searched by means of complete LST/QST methods for reactions.⁵³ The reaction energy (ΔE) and the activation energy (E_a) are defined as follows:

ΔE = E_(P) − E_(R) (3)

E_a = E_(TS) − E_(R) (4)

where E_(P) is the energy of the product in each reaction, E_(R) is the energy of the reactant in each reaction, and E_(TS) is the energy of the transition state in each elementary reaction.

3. Results and discussion

3.1 Decomposition of H₂S on the perfect surface

On the perfect α-Fe₂O₃(0001) surface, H₂S is parallel to the surface and adsorbs at the Fe top site. Then, two dehydrogenation processes, H₂S → SH + H and SH → S + H occur, which has been shown in our previous work.¹⁶ H atom is dissociated to its adjacent surface O atom in both two dehydrogenation steps with the energy barriers of 72.0 and 130.4 kJ mol⁻¹ on a p(2 × 2) super-cell of α-Fe₂O₃(0001) surface, respectively. The relative energies are shown in Fig. 3 with the black line. As to the different coverage, there is a little difference between the energy barrier of the dissociation of H₂S on the p(2 × 2) surface and that on the p(2 × 1) surface.¹⁶

Fig. 3 The dissociation profiles for the H₂S dissociation on the defective and doped α-Fe₂O₃(0001) surface, black, pink, purple, blue, red and green lines are H₂S dissociation on the α-Fe₂O₃(0001) perfect, sulfurized, Fe-vacancy and Cu, Zn, Co-doped surfaces, respectively.

The effect of defects and the doping on the desulfurization sorbent will be evaluated by comparing their decomposition processes with that on the perfect α-Fe₂O₃(0001) surface.

3.2 Decomposition of H₂S on the Fe-vacancy surface

The optimized Fe-vacancy surface is shown in Fig. 2(b), in which the removal of one surface Fe atom results in the three surrounding O atoms exhibiting a much larger contraction in the z-direction than other O atoms at the same layer. The Fe-vacancy formation energy with respect to a free Fe atom and the perfect α-Fe₂O₃(0001) surface is 744.0 kJ mol⁻¹, which is calculated as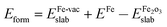 . This value is comparable to the previous study,²² and the E_form of Fe-vacancy is 764.2 kJ mol⁻¹. It can be concluded that the Fe-vacancy can be formed on the α-Fe₂O₃(0001) surface.

In addition, the Fe-vacancy formation energy with respect to the chemical potential of every element has been calculated as

ΔE_f = E(N_Fe, N_O) − N_Feμ_Fe − N_Oμ_O + q∈_f (ref. 54) (5)

where E(N_Fe, N_O) is the total energy of a system containing the vacancy; N_Fe and N_O are the atom numbers; μ_Fe is the calculated elemental energy based on the cubic-Fe and μ_O is the energy of pure O₂ gas (per oxygen atom); q is the charge of the defect, and the neutral system is set in this study. The calculated formation energy is −5692.4 kJ mol⁻¹, which implies that the Fe vacancy surface can be formed.

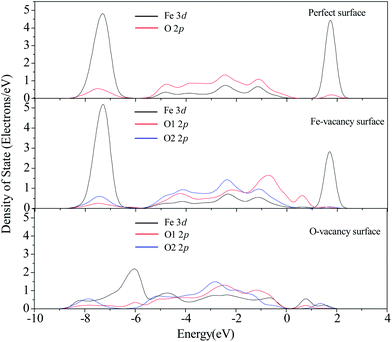
The calculated PDOS of Fe and O atoms on the perfect and Fe-vacancy surfaces are shown in Fig. 4. O1 is surrounding the Fe-vacancy and O2 is far from the Fe-vacancy. The valence band states of O1 2p move strongly upward, which corresponds to its low electron occupation, while the PDOS of O2 is almost unchanged compared with O atom on the perfect surface. The contribution of neighboring surface Fe 3d to conduction band slightly weakens, and to valence band slightly strengthens compared with the perfect surface. The Mulliken charge of the 2-coordinated O1 is −0.52e, which is smaller than that of other 3-coordinated O atoms connected to Fe in electronegativity. It leads to a good electron acceptor and highly reactive to H and other electron donors, which is in good agreement with the results of Yin et al.²²

Fig. 4 PDOS for Fe and O atoms on the perfect, Fe-vacancy and O-vacancy α-Fe₂O₃(0001) surfaces.

The adsorption of H₂S on the Fe-vacancy surface is calculated, there exists two adsorption modes. One is the molecular adsorption, the most stable molecular adsorption configuration is Fe(V)–H₂S(a) displayed in Fig. 5(a) with an adsorption energy of 81.7 kJ mol⁻¹. The other is dissociation mode due to the high reactivity of O atoms surrounding the Fe-vacancy with H atom of H₂S molecule. The dissociated adsorption configuration Fe(V)–H₂S(b) is shown in Fig. 5(b) with an adsorption energy of 177.6 kJ mol⁻¹, which is more exothermic than molecular adsorption mode, predicting that dissociative adsorption is the primary adsorption form for H₂S on the Fe-vacancy surface.

Fig. 5 The optimized structures of H₂S and its dissociation species adsorption on the Fe-vacancy surface as well as transition states of dissociation.

The co-adsorption configuration of S/H/H on the Fe-vacancy surface is constructed, and its optimized structure is shown in Fig. 5(c), denoted as Fe(V)–S/H/H, which is the finally stable configuration of the dissociation of H₂S on the Fe-vacancy surface.

The dissociation profile for H₂S on the Fe-vacancy surface is presented in Fig. 3 (the purple line). H₂S is dissociatively adsorbed on the Fe-vacancy surface without a tight transition state, which implies the surface accelerates the decomposition of H₂S into SH/H. The Fe-vacancy surface also increases the reactivity for H₂O dissociation.²² Then, Fe(V)–H₂S(b) is decomposed into Fe(V)–S/H/H via transition states Fe(V)–TS2 (see Fig. 5(d)) by overcoming an energy barrier of 89.7 kJ mol⁻¹.

3.3 Decomposition of H₂S on the O-vacancy surface

As shown in Fig. 2(c), it is clearly observed that the surface Fe atom formerly bonded with the lost O atom collapses and moves into the bulk, and the surface structure shows a strong relaxation for the optimized O-vacancy surface. Our calculations show that the formation energy (with respect to the total energy of an oxygen atom) of O-vacancy is 531.5 kJ mol⁻¹, which is higher than the formation energy of a surface O-vacancy on the O-termination surface with 402.4 kJ mol⁻¹.²² At the same time, the O-vacancy formation energy with respect to the chemical potential has also been calculated according to eqn (5). The formation energy is −5536.7 kJ mol⁻¹, which also shows that the O-vacancy surface can be formed. The PDOS of the collapsed Fe atom shows that the sharp in conduction band nearly disappears and the strength of sharp in valence band becomes weaker than that on the perfect surface, which implies that the activation of Fe may vanish. While the PDOS of neighboring O1 and the second neighboring O2 atoms of the collapsed Fe atom show little modification compared with that on the perfect surface. According to the previous experiments and calculations, sulfur species mainly interact with the metal centers of the oxide surface.^55–57 Therefore, we speculate that the collapses of Fe atom may have an adverse effect on the adsorption of H₂S. Then, our study validates the assumption. When H₂S is initially placed at the top of O-vacancy sites, it goes far away from the surface. Because the adsorption of H₂S on the surface is the first step of desulfurization, the process of desulfurization on the O-vacancy surface is difficult to happen. Based on the above analysis, it is concluded that the surface with O-vacancy has an adverse effect on the process of desulfurization. Pretreatment of the desulfurization sorbent under oxygen atmosphere may repair the O-vacancy of the α-Fe₂O₃(0001) surface. The different conclusions have been obtained that H₂S is dissociatively adsorbed on the O-vacancy ZnO(101̄0) surface, and a little difference in activation energy for the dissociation of H₂S on the perfect and O-vacancy ZnO(101̄0) surface.⁵⁸ The oxygen vacancy on the Cu₂O(111) surface also exhibits a strong chemical reactivity toward the dissociation of H₂S.¹⁵ However, the dissociated S atom is easier to deposit on the O-vacancy ZnO(101̄0) surface, which is unfavorable to the desulfurization of H₂S. Thus pretreatment of the desulfurization sorbent under oxygen atmosphere may repair the O-vacancy of the α-Fe₂O₃(0001) surface, as well as the O-vacancy ZnO(101̄0) surface.

3.4 Decomposition of H₂S on the sulfurized surface

In order to check on the influence of the sulfurized surface on the desulfurization, the dissociation of H₂S on the sulfurized α-Fe₂O₃(0001) surface is investigated. The optimized sulfurized surface is shown in Fig. 2(d).

Just as the adsorption of H₂S on the perfect α-Fe₂O₃(0001) surface, both H₂S perpendicular and tilting to the sulfurized surfaces convert to the structure of H₂S nearly parallel to the surface, which is shown in Fig. 6(a). Then, this structure is regarded as the initial state for the study of the dissociation of H₂S on the sulfurized surface. In addition, the co-adsorption structures of S–SH/H and S–S/H/H are shown in Fig. 6(c) and (e), which are also similar to that on the perfect α-Fe₂O₃(0001) surface.

Fig. 6 The reactant, intermediate and transition state structures for the dissociation of H₂S on the sulfurized surface.

For the dissociation of H₂S on the sulfurized surface, two dissociation steps are undergone, which is the same as that on the perfect α-Fe₂O₃ surface. The dissociation profile of H₂S on the sulfurized surface is also presented in Fig. 3 using the pink line. Firstly, with the breakage of one S–H bond in H₂S, the intermediate “S–SH/H” is formed via transition state “S–TS1” by overcoming an energy barrier of 243.1 kJ mol⁻¹, while a lower energy barrier of 42.0 kJ mol⁻¹ is needed on the sulfurized Cu₂O(111) surface.¹⁵ Comparing with the perfect α-Fe₂O₃(0001) surface, the energy barrier on the sulfurized surface is far larger. The different conclusions have been obtained on the Cu₂O(111) surface in our previous work,¹⁵ the energy barrier of this step on the sulfurized surface is less than that on the perfect surface, which shows that the sulfurized Cu₂O(111) surface is favorable to the dissociation of H₂S. In this step, the distance between S and H atoms is elongated to 3.669 Å and the distance of H and surface O atom decreases to 0.987 Å. Then, the second dissociation step happens corresponding to the decomposition of S–SH/H into S–S/H/H through transition state “S–TS2” by overcoming an energy barrier of 83.2 kJ mol⁻¹. This step is endothermic by 30.2 kJ mol⁻¹.

3.5 Decomposition of H₂S on the M-doped surface

Doping effects on the surface chemistry are tested by direct cation substitution. On the Cu-, Zn- and Co-doped α-Fe₂O₃(0001) surface, H₂S is still parallel to the surface and interacts with the surface metal atoms through S atom. Herein, we mainly research the interaction of H₂S with the doped metal atoms.

For the Cu-doped α-Fe₂O₃ surface, the Mulliken charge of Cu is 0.810e, which is smaller than that of Fe atom on the perfect surface with 1.090e. The formation energy of O-vacancy by deleting an O atom binding with Cu is 529.4 kJ mol⁻¹, which is similar to that on the perfect surface. It implies that the Cu-doped α-Fe₂O₃ surface is stable although Cu with lower valent than Fe, which is not agreement with the results that Cu doping facilitates O vacancy formation on the CeO₂(111) surface.⁵⁹ On the doped surface, H₂S firstly dissociates into SH/H via a transition state “Cu-doped TS1” shown in Fig. 7(d). An energy barrier of 51.6 kJ mol⁻¹ is overcome with an exothermicity of 46.2 kJ mol⁻¹, which is shown in Fig. 3 with the blue line. This barrier is smaller than that on the perfect α-Fe₂O₃(0001) surface. And then, the second dissociation step happens with the decomposition of Cu-doped SH/H into “Cu-doped S/H/H” via the transition state “Cu-doped TS2” by overcoming an energy barrier of 45.4 kJ mol⁻¹.

Fig. 7 The reactant, intermediate and transition state structures in the dissociation of H₂S on the Cu-doped surface.

In the case of the Zn-doped α-Fe₂O₃ surface, higher formation energy of O-vacancy with 544.7 kJ mol⁻¹ than that on the perfect surface suggests that the Zn-doped α-Fe₂O₃ surface is also stable. The Mulliken charge of Zn is 0.960e, and which of three O atoms binding with Zn are 0.750, 0.740 and 0.700e. It implies that the charge is shared between Zn and O. Si-doped hematite by a Si⁴⁺ insteading of a Fe atom also shows that charge can transfer and is shared between neighboring atoms.²⁵ Similar to the dissociation process of H₂S on the Cu-doped surface, H₂S firstly dissociates into SH/H, and then dissociates into S/H/H. The corresponding reactant, intermediates and transition states are also similar to that on the Cu-doped surface, and the relative energies are shown in Fig. 3 using the red line. The activation energies for the two elementary steps are 43.4 and 127.3 kJ mol⁻¹, respectively.

On the Co-doped α-Fe₂O₃ surface, the Mulliken charge of doped Co is 0.940e before interacting with H₂S, which is smaller than that of Fe atom with 1.090e because the electron is shared between Co and O. It is in good accordance with the results of Liao et al.,²⁵ in which the Bader charge has been analyzed, and covalent character in Co–O bond has been suggested. H₂S undergoes two dissociation steps leading to S/H/H on the Co-doped α-Fe₂O₃ surface via SH/H intermediate, and the potential energy with the green line in Fig. 3 shows that activation energies are 34.3 and 114.5 kJ mol⁻¹. The corresponding structures are not shown since those are similar to that on the Cu-doped α-Fe₂O₃ surface.

3.6 General discussion

The decomposition of H₂S on the Fe-vacancy, sulfurized, and Cu-, Zn- and Co-doped surfaces have been examined. In Fig. 3, as for the sulfurized surface, the highest energy point for the dissociation of H₂S occurs at TS1 with a relative energy of 243.1 kJ mol⁻¹, which is far higher than 72.0 kJ mol⁻¹ on the perfect surface. Whereas, the highest relative energies on the Fe-vacancy, Cu-, Zn- and Co-doped surfaces are 25.8, 51.6, 45.5 and 34.3 kJ mol⁻¹, respectively, which are smaller than that on the perfect surface. The above analyses suggest that the Fe-vacancy surface can accelerate the dissociation process of H₂S, which is advantage to improving the efficiency of the desulfurization. However, the sulfurized surface is disadvantageous to the dissociation of H₂S, so its regeneration is necessary. The regeneration of lots of desulfurizer, including CeO₂,⁶⁰ La₂O₃,⁶¹ CaCO₃,⁶² ZnO- and CaO-containing sorbents,⁶³ and Fe₂O₃–Al₂O₃ sorbents,⁶⁴ have been investigated during the desulfurization. What's more, the performance of desulfurization sorbent can be improved by doping other metal promoters. Wei et al.⁶⁵ have also found that Cu doping in SnO₂(110) can increase surface electrical conductivity and directly improve the sensitivity of SnO₂ toward H₂S. And Co is as an effective dopant to improve the catalytic activity of pure hematite for water oxidation.⁶⁶ Aiming at the three dopants, on the one hand, comparing with the highest energy barrier relative to the reactant for the dissociation of H₂S on the Cu-, Zn- and Co-doped surfaces, Cu-doped surface is the highest, Zn-doped surface takes second place, while Co-doped surface is the lowest one. On the other hand, considering the economy, Zn is the cheapest, Cu is the second, and Co is the most expensive. It can draw a conclusion that Zn addition is the best doped candidate. Zn has been doped into Fe₂O₃ to improve the sensitivity and selectivity for gases in experiment.⁶⁷ In addition, ZnO–Fe₂O₃ mixed metal oxide sorbent has shown better sensitivity⁶⁸ and higher removal capacity for H₂S (ref. 8) than the pure Fe₂O₃ sorbent.

4. Conclusions

In this work, to probe into the effects of the defective, sulfurized and different metal doped α-Fe₂O₃ surfaces on the desulfurization, the mechanisms of H₂S adsorption and decomposition on these distinct surfaces are studied by periodic DFT slab calculations.

On the Fe-vacancy surface, the removal of one surface Fe atom results in the three surrounding O atoms exhibiting a strong electron accepter. The highest energy point is 25.8 kJ mol⁻¹, which is smaller than that on the perfect α-Fe₂O₃(0001) surface leading to the dissociation of H₂S easier. Therefore, the presence of Fe vacancy on the surface can accelerate the dissociation of H₂S, which is advantage to improving the efficiency of the desulfurization.

On the O-vacancy surface, O-vacancy leads to the collapse of Fe atom and the disappearance of surface activity sites. Therefore, the existence of O-vacancy on the α-Fe₂O₃(0001) surface has an adverse effect on the desulfurization. Pretreatment of the desulfurization sorbent by oxygen is necessary.

Sulfurized surface leads to the increment of energy barrier for dissociating H₂S, which has a negative effect on the desulfurization. The result is the same as the experimental results. So the regeneration of desulfurization sorbent is necessary to prolong its working life.

Doping effects on surface chemistry are evaluated by direct cation substitutions. The results show that the performance of desulfurization sorbent can be improved by doping other metals. Zn addition is candidate to improve the performance of hematite desulfurization sorbent by overall consideration among the doped metals such as Cu, Zn and Co.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (grant nos 20976115, 21276171, 21276003), the National Younger Natural Science Foundation of China (grant no. 21103120), the Doctoral Fund of Ministry of Education (grant no. 20091402110013), China Postdoctoral Science Foundation (grant no. 2012M520608) and the State Key Laboratory of Fine Chemicals (KF1205).

References

1. H. Atakül, J. P. Wakker, A. W. Gerritsen and P. J. Berg, Fuel, 1995, 74, 187–191.
2. X. Y. Wang, Y. H. Liu, Z. W. Sun and D. F. Che, Energy Fuels, 2011, 25, 4865.
3. R. L. Bain, D. C. Dayton, D. L. Carpenter, S. R. Czernik, C. J. Feik, R. J. French, K. A. Magrini-Bair and S. D. Phillips, Ind. Eng. Chem. Res., 2005, 44, 7945–7956.
4. J. Koningen and K. Sjostrom, Ind. Eng. Chem. Res., 1998, 37, 341–346.
5. J. Hepola, J. McCarty, G. Krishnan and V. Wong, Appl. Catal., B, 1999, 20, 191–203.
6. J. Hepola and P. Simell, Appl. Catal., B, 1997, 14, 287–303.
7. W. Xie, L. P. Chang, D. H. Wang, K. C. Xie, T. Wall and J. L. Yu, Fuel, 2010, 89, 868–873.
8. Y. S. Lee, H. T. Kim and Y. O. Yoo, Ind. Eng. Chem. Res., 1995, 34, 1181–1188.
9. X. R. Ren, L. P. Chang, F. Li and K. C. Xie, Fuel, 2010, 89, 883–887.
10. T. V. Reshetenko, S. R. Khairulin, Z. R. Ismagilov and V. V. Kuznetsov, Int. J. Hydrogen Energy, 2002, 27, 387–394.
11. C. Y. Kim, A. A. Escuadro and M. J. Bedzyk, Surf. Sci., 2007, 601, 4966–4970.
12. L. X. Ling, R. G. Zhang, P. D. Han and B. J. Wang, Fuel Process. Technol., 2013, 106, 222–230.
13. W. F. Wang, H. T. Chen and M. C. Lin, J. Phys. Chem. C, 2009, 113, 20411–20420.
14. H. T. Chen, Y. M. Choi, M. L. Liu and M. C. Lin, J. Phys. Chem. C, 2007, 111, 11117–11122.
15. R. G. Zhang, H. Y. Liu, J. R. Li, L. X. Ling and B. J. Wang, Appl. Surf. Sci., 2012, 258, 9932–9943.
16. J. J. Song, X. Q. Niu, L. X. Ling and B. J. Wang, Fuel Process. Technol., 2013, 115, 26–33.
17. T. Liu, X. Guo and C. G. Zheng, Proc. Combust. Inst., 2013, 34, 2803–2810.
18. Y. F. Zhukovskii, E. A. Kotomin and G. Borstel, Vacuum, 2004, 74, 235–240.
19. M. S. Palmer, M. Neurock and M. M. Olken, J. Am. Chem. Soc., 2002, 124, 8452–8461.
20. O. Warschkow, D. E. Ellis, J. Hwang, N. Mansourian-Hadavi and T. O. Mason, J. Am. Ceram. Soc., 2002, 85, 213–220.
21. C. R. A. Catlow, J. Corish, J. Hennessy and W. C. Mackrodt, J. Am. Ceram. Soc., 1988, 71, 42–49.
22. S. X. Yin and D. E. Ellis, Surf. Sci., 2008, 602, 2047–2054.
23. J. A. Rodriguez, J. Hrbek, Z. P. Chang, J. Dvorak and T. Jirsak, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 235414.
24. E. Ozdogan and J. Wilcox, J. Phys. Chem. B, 2010, 114, 12851–12858.
25. P. Liao, J. A. Keith and E. A. Carter, J. Am. Chem. Soc., 2012, 134, 13296–13309.
26. J. A. Rodriguez and A. Maiti, J. Phys. Chem. B, 2000, 104, 3630–3638.
27. B. J. Wang, R. X. Yan and H. Y. Liu, Appl. Surf. Sci., 2012, 258, 8831–8836.
28. M. Nolan, J. Phys. Chem. C, 2009, 113, 2425–2432.
29. M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097.
30. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
31. J. A. White and D. M. Bird, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 4954–4957.
32. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
33. K. Wong, Q. H. Zeng and A. B. Yu, J. Phys. Chem. C, 2011, 115, 4656–4663.
34. T. Yang, X. D. Wen, C. F. Huo, Y. W. Li, J. G. Wang and H. J. Jiao, J. Phys. Chem. C, 2008, 112, 6372–6379.
35. P. Guo, X. Guo and C. G. Zheng, Appl. Surf. Sci., 2010, 256, 6991–6996.
36. P. Guo, X. Guo and C. G. Zheng, Fuel, 2011, 90, 1840–1846.
37. Y. Hou, D. Wang, X. H. Yang, W. Q. Fang, B. Zhang, H. F. Wang, G. Z. Lu, P. Hu, H. J. Zhao and H. G. Yang, Nat. Commun., 2013, 2547, 1–8.
38. A. Rohrbach, J. Hafner and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 125426.
39. A. Bandyopadhyay, J. Velev, W. H. Butler, S. K. Sarker and O. Bengone, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 174429.
40. G. Rollmann, A. Rohrbach, P. Entel and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 165107.
41. M. N. Huda, A. W. Y. Yan, S. H. Wei and M. M. Al-Jassim, J. Appl. Phys., 2010, 107, 123712.
42. G. J. Martin, R. S. Cutting, D. J. VauGhan and M. C. Warren, Am. Mineral., 2009, 94, 1341–1350.
43. L. M. Sandratskii, M. Uhl and J. Kübler, J. Phys.: Condens. Matter, 1996, 8, 983–989.
44. J. A. Glasscock, P. R. F. Barnes, I. C. Plumb, A. Bendavid and P. J. Martin, Thin Solid Films, 2008, 516, 1716–1724.
45. P. Merchant, R. Collins, R. Kershaw, K. Dwight and A. Wold, J. Solid State Chem., 1979, 27, 307–315.
46. M. N. Hunda, A. Walsh, Y. F. Yan, S. H. Wei and M. M. Al-Jassim, J. Appl. Phys., 2010, 107, 123712.
47. T. P. Trainor, A. M. Chaka, P. J. Eng, M. Newville, G. A. Waychunas, J. G. Catalano and G. E. Brown Jr, Surf. Sci., 2004, 573, 204–224.
48. X. G. Wang, W. Weiss, S. K. Shaikhutdinov, M. Ritter, M. Petersen, F. Wagner, R. Schlögl and M. Scheffler, Phys. Rev. Lett., 1998, 81, 1038–1041.
49. S. Thevuthasan, Y. J. Kim, S. I. Yi, S. A. Chambers, J. Morais, R. Denecke, C. S. Fadley, P. Liu, T. Kendelewicz and G. E. Brown Jr, Surf. Sci., 1999, 425, 276–286.
50. F. Alvarez-Ramírez, J. M. Martínez-Magadán, J. R. B. Gomes and F. Illas, Surf. Sci., 2004, 558, 4–14.
51. P. Liu, T. Kendelewicz, G. E. Brown Jr, E. J. Nelson and S. A. Chambers, Surf. Sci., 1998, 417, 53–65.
52. W. Qin, Q. L. Chen, T. C. Wang, N. Wang, W. Y. Li, Q. Lu and C. Q. Dong, Adv. Mater. Res., 2012, 403–408, 2285–2288.
53. T. A. Halgren and W. N. Lipscomb, Chem. Phys. Lett., 1977, 49, 225–232.
54. A. F. Kohan, G. Ceder and D. Morgan, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 15019–15027.
55. J. A. Rodriguez and J. Hrbek, Acc. Chem. Res., 1999, 32, 719–728.
56. J. A. Rodriguez, T. Jirsak, A. Freitag, J. C. Hanson, J. Z. Larese and S. Chaturvedi, Catal. Lett., 1999, 62, 113–119.
57. J. A. Rodriguez, T. Jirsak and S. Chaturvedi, J. Chem. Phys., 1999, 111, 8077–8087.
58. L. X. Ling, J. B. Wu, J. J. Song, P. D. Han and B. J. Wang, Comput. Theor. Chem., 2012, 1000, 26–32.
59. Z. X. Yang, B. L. He, Z. S. Lu and K. Hermansson, J. Phys. Chem. C, 2010, 114, 4486–4494.
60. Y. Zeng, S. Zhang, F. R. Groves and D. P. Harrison, Chem. Eng. Sci., 1999, 54, 3007–3017.
61. M. Flytzani-Stephanopoulos, M. Sakbodin and Z. Wang, Science, 2006, 312, 1508–1510.
62. J. Adánea, F. García-Labiano, A. Abad, L. F. de Diego and P. Gayán, Energy Fuels, 2001, 15, 85–94.
63. S. C. Christoforou, E. A. Efthimiadis and A. A. Vasalos, Environ. Sci. Technol., 1995, 29, 372–383.
64. V. Patrick and G. R. Gavalas, Ind. Eng. Chem. Res., 1993, 32, 519–532.
65. W. Wei, Y. Dai and B. B. Huang, J. Phys. Chem. C, 2011, 115, 18597–18602.
66. P. L. Liao, J. A. Keith and E. A. Carter, J. Am. Chem. Soc., 2012, 134, 13296–13309.
67. Z. H. Jing, Mater. Sci. Eng., A, 2006, 441, 176–180.
68. N. K. Pawar, D. D. Kajale, G. E. Patil, S. D. Shinde, V. B. Gaikwad and G. H. Jain, New Dev. Appl. Sens. Technol., 2011, 83, 123–132.

---