The self-assembly of linear–dendritic and lipid-like copolymers investigated by computer simulations
Juan-mei Huab,
Wen-de Tian*ab and
Yu-qiang Ma*abc
aCenter for Soft Condensed Matter Physics and Interdisciplinary Research, Soochow University, Suzhou 215006, China
bCollege of Physics, Optoelectronics and Energy, Soochow University, Suzhou 215006, China
cNational Laboratory of Solid State Microstructures and Department of Physics, Nanjing University, Nanjing 210093, China. E-mail: tianwende@suda.edu.cn; myqiang@nju.edu.cn
First published on 5th November 2014
Abstract
Amphiphiles have long been attractive for their spontaneous formation of diverse structures and potential applications. Here, the self-assembly of binary mixtures with various hydrophilic/hydrophobic ratios is systematically investigated by dissipative particle dynamics simulations. On increasing the proportion of linear–dendritic copolymers, the self-assembled structure changes from a compound vesicle to a netlike micelle. Additionally, more structures including the high-genus vesicle, toroidal vesicle, oblate vesicle, and the perforated vesicle are obtained at different mixing ratios. The spontaneous curvature of self-assembling morphologies is the critical factor for shaping their final structures. Furthermore, stress is released as much as possible via the intelligent distribution of two amphiphiles, which makes the structures more stable than those obtained in pure amphiphile systems. Moreover, the slow release of the potential energy stored in the initially self-assembled components may induce the system into a metastable state and the self-assembly can be kinetically controlled by a pathway-directing process.
1. Introduction
Self-assembly is useful in designing and developing novel materials. In particular, the self-assembly of amphiphiles has received tremendous attention due to their application versatility,1–6 such as surface modification, drug delivery carriers, and biomimetic mineralization. Therefore, it is important to regulate the self-assembled nanostructures and predict their specific functions from the building molecules. Previous studies7–10 found that the self-assembled structures of amphiphiles are definitively determined by their architectures, such as the size of the hydrophilic and hydrophobic components. Generally, if the hydrophilic part is larger than the hydrophobic part, the micelles form. With the decrease of the hydrophilic volume fraction, the micelles change to lamellar structures. For intermediate architectures, cylindrical micelles such as wormlike structures or branched networks can be obtained.However, the picture becomes more sophisticated when two types of amphiphiles are mixed.11–13 Many structures that have not been observed in the monomodal dispersion are obtained.14–16 Cooperative self-assembly in the hybrid amphiphiles has been proven to be a promising strategy to fabricate aggregates with the controllable structures and novel properties. For example, morphologies, such as smaller vesicles, disk-like micelles, ring-like micelles, and elongated thread-like micelles have been observed by the addition of a micelle-forming surfactant to a vesicular system.17 By mixing single-tailed cationic and anionic surfactants (cetyltrimethylammoniumtosylate (CTAT) and sodium dodecyl-benzene sulfonate (SDBS)) in aqueous, Kaler et al.18 found the long term stable vesicles. Meanwhile, the properties of the vesicles, such as size, surface charge and permeability, can be simply adjusted by varying the mixing ratios or the chain length of the individuals. Chiruvolu et al.19 got the entangled tubular vesicles in the mixtures of DMPC, geraniol, and water at appropriate ratios. By coarse-grained simulations, Zheng et al.20 observed sphere, biconcave, starfish, capsule, budding and budding off vesicles in multicomponent membrane when the effects of spontaneous curvature and fluidity were included. Bressel et al.21 successfully fabricated vesicles with extremely low polydispersity and high stability by admixture of amphiphilic copolymers.
Although, the cooperative self-assembly of mixed amphiphiles has become a promising method to fabricate aggregates with novel properties, it is still difficult to precisely refine the complex factors that affect the self-assembly process and final structures due to the polydispersity, mixing uniformity, etc. Thus, the picture of self-assembly in mixed amphiphiles still remains unclear and there is a need to define some appropriate model systems for research. To systematically study the self-assembled structures in a binary mixture, the mesoscopic simulation (dissipative particle dynamics (DPD))22 becomes a good candidate as a complementarity of experiments. The complicated factors that affect the self-assembly can be investigated separately and the self-assembling process can be reproduced in simulations. Additionally, the simulation can provide molecular information about the self-assembled aggregates, which may not be discerned using currently available experimental techniques.
In this study, we employed the DPD simulations to investigate the self-assembling behaviors of the mixture systems composed of the lipid-like polymers and linear–dendritic copolymers (LDCs). To avoid the immiscible phases, the two amphiphiles were considered to have the similar polarity and chain length with different hydrophilic/hydrophobic ratios. The schematic diagrams of the two amphiphiles are given in Fig. 1. We found that the binary mixtures are able to self-assemble into various structures including high-genus vesicles, toroidal vesicles, oblate vesicles and perforated vesicles. These morphologies are determined by spontaneous curvature of the two amphiphiles under condition of different mixing ratios. The intelligent distribution of the amphiphiles based on the global and local curvature makes these structures more stable than those found in pure amphiphile systems. Furthermore, the self-assembled structures can be influenced by kinetics and the assembled morphologies could be regulated through different preparing methods of the initial structures.
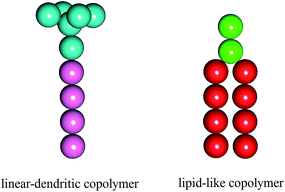 | ||
| Fig. 1 Schematic diagrams of the two amphiphiles: linear–dendritic copolymer (left) and lipid-like molecule (right) and. Cyan and green beads are hydrophilic, pink and red beads are hydrophobic. | ||
2. Simulation method and model
DPD simulation is a coarse-grained computer simulation technique for discovering the mesoscale hydrodynamic phenomena introduced by Hoogerbrugge and Koelman in 1992.22 In the DPD technique, each bead represents a group of atoms, whose time evolution is governed by Newton's equation of motion. The main interaction between the beads is the soft conservative force, which can be denoted as
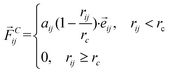 | (1) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij =
ij = ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i −
i − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) j,
j, ![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) ij =
ij = ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij/rij. rc is the cut-off radius.
ij/rij. rc is the cut-off radius.
In the simulation, the lipid-like molecule is modeled by two hydrophilic beads (Hl) and two tails, each have four hydrophobic beads (Tl), while the linear–dendritic copolymer is modeled by a branch cluster with six hydrophilic beads (Hd) and one tail with four hydrophobic beads (Td). Water is explicitly included as the solvent (W). A harmonic spring with a constant of ks = 128 kBT/rc2 is applied to connect the neighboring beads in a single molecule and the equilibrium bond length is set to r0 = 0.5rc. The rigidity of the hydrocarbon chains is ensured by a three-body bond angle potential E = ka[1 − cos(θijk − θ0)] with the force constant ka = 5 kBT/rc2 and the equilibrium angle θ0 = 180°. In the simulation, the physical quantities are scaled with cutoff radius (rc), bead mass (m) and temperature (kBT). The interaction parameters aij between different beads are chosen based on their hydrophobicity or hydrophilicity properties,23 as shown in Table 1.
| aij | W | Hl | Tl | Hd | Td |
|---|---|---|---|---|---|
| W | 25 | 25 | 100 | 25 | 100 |
| Hl | 25 | 25 | 100 | 25 | 100 |
| Tl | 100 | 100 | 25 | 100 | 25 |
| Hd | 25 | 25 | 100 | 25 | 100 |
| Td | 100 | 100 | 25 | 100 | 25 |
All simulations are performed in the canonical ensemble (NVT) using LAMMPS package.24 The simulation box is set to 50 × 50 × 50 with periodic boundary conditions. The bead density is 3 with the concentration fixed at 6.4% independent of mixing ratios. Here, both the LDCs and lipid-like molecules contain 10 beads, thus, 2400 total amphiphiles are used. In order to be fully mixed, all the amphiphiles are randomly distributed in the simulation box at the initial state unless otherwise indicated. The velocity-Verlet algorithm is used to integrate the equation of motion with the time step of Δt = 0.04τ (τ = [mr2c/kBT]1/2). The reduced temperature, kBTc, is fixed at kBTc = 1.0 for all static self-assemblies. Each mixing ratio is performed three times with different initial states to make sure our results are reliable. All the simulations are carried out at least 3.0 × 106 simulation steps.
3. Results and discussion
3.1 The self-assembled structures at different mixing ratios
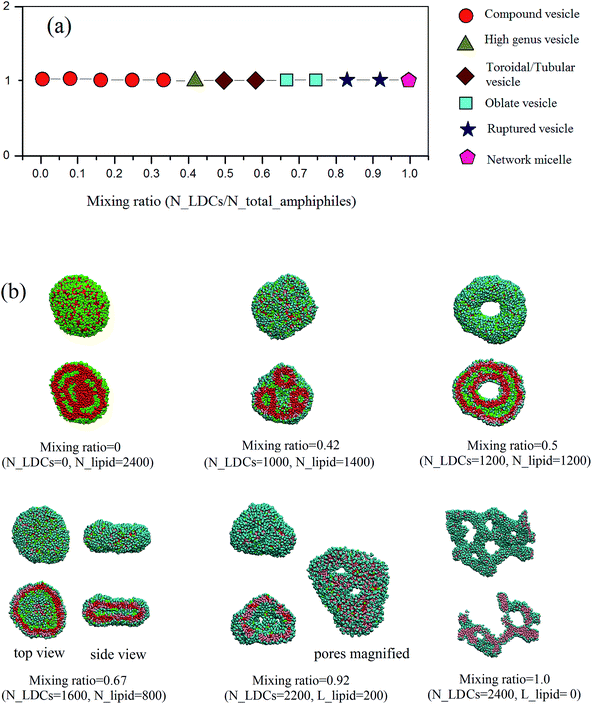
Fig. 2 gives the self-assembled structures from DPD simulations with different mixing ratios of LDCs and lipid-like molecules. The morphologies, including compound vesicles (in pure lipid-like molecule system), high genus vesicles, toroidal vesicles, oblate vesicles, perforated vesicles, and network micelles(in pure LDCs system), were obtained. By analyzing the architectures of the two amphiphiles, we can see that with increasing the ratio of LDCs, the hydrophilic/hydrophobic fraction increases monotonously. It well satisfies the widely accepted rule that with the increase of the hydrophilic volume fraction, the aggregations change from lamellar structures to micelles.9,10 The detailed morphologies and the mechanism of the morphological changing from the compound vesicles to network micelles will be discussed in the following.During the self-assembly, the randomly mixed amphiphiles first aggregate to small disk-like micelles driven by their hydrophobic interactions. Then these micelles grow up and wrap to spherical vesicles forced by the line tension. The minimal vesicle size is determined by the balance of line tension γ and bending modulus k as Rv = 2k/γ.25 In our simulation, the size of these minimal vesicles is evaluated by accounting the water packaged by the vesicles, as shown in Fig. 3. It shows that with the increase of LDCs ratio, the size of the first stage vesicles increases monotonously. It results from the competition between bending energy and line tension at different mixing ratios.
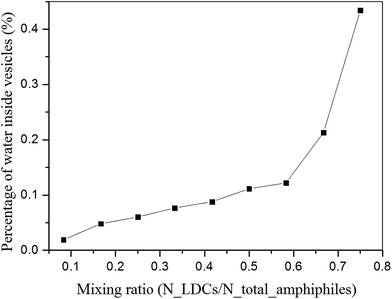 | ||
| Fig. 3 Percentage of water inside the first stage vesicles at different ratios of LDCs and lipid-like molecules. | ||
At low ratio of LDCs, the bending energy of the disk-like micelles is small while the line tension is quite large. Thus, the disk-like micelles are unstable and tend to envelop themselves easily. Due to the compensation of bending energy during the wrapping of small disk-like micelles, the vesicles are far from saturation. Meanwhile, the bending energy in the outer layer is much larger than that in the inner layer. When two small vesicles are interconnected, the inner layers nearly remain while the outer layers fuse together to cause the whole vesicles losing the interface energy. Therefore, compound vesicles appear when the first stage vesicles are encountered.
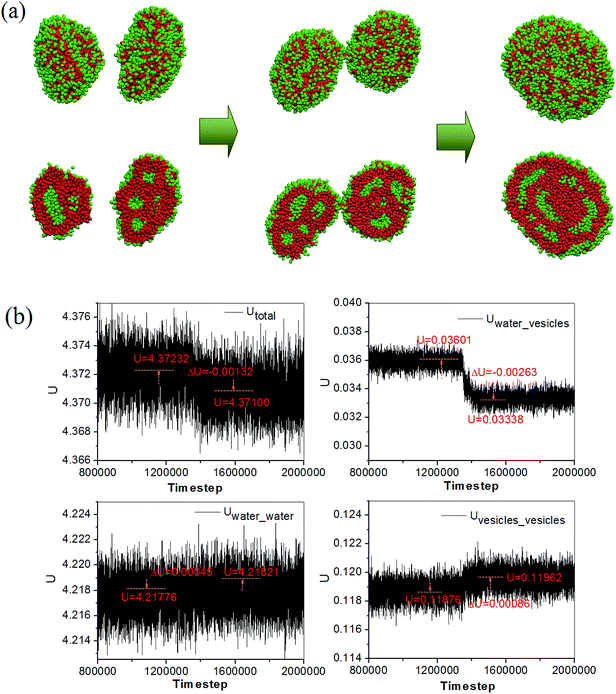
The morphology evolution accompanying with the energy change during the fusion of two compound vesicles in the pure lipid-like system is given in Fig. 4. Here, the Utotal is the summation of all pair interactions between water and vesicles, Utotal = Uwater_water + Uwater_vesicles + Uvesicles_vesicles. We can see that the interaction energy between water and vesicle drops down while the interaction energy between water and water (vesicle and vesicle) increases. This means that the interface energy between water and vesicle decreases and the vesicles become more stable after fusion. Meanwhile, the decrease of the Utotal implies that the fusion is a spontaneous process. The compound vesicles in our simulation are quite similar to those observed from block copolymers by Zhang et al.26 Both the compound vesicles are self-assembled from the building units with large size of the hydrophobic tails, and the formation involves a secondary aggregation of individual vesicles and a subsequent fusion process. The compound vesicles is a complex aggregate analogous to the aggregated soap bubble, which have been considered to have potential application in controllable drug release.27
With increasing the ratio of LDCs, the line tension decreases quickly and the disk-like aggregates can take up more aggregates before becoming a large vesicle. Meanwhile, the bending energy of the vesicles' inner layer increases while that of the outer decreases. Thus, when two initial vesicles encounter, the fusion happens to release both layers' bending energy. After fusion, a tubular vesicle with the fixed area-to-volume ratio is formed.28 The tubular vesicle extends via continually fusing with other vesicles, or bends to a toroidal vesicle. Fig.5 gives the pathway of a toroidal vesicle formation at the mixing ratio of 0.5. It clearly shows that when a tubular vesicle meets a toroidal vesicle, the tubular vesicle can fuse into the toroidal vesicle and expand the ring to become a large toroid.
Interestingly, a high-genus vesicle (n > 1) was observed at the mixing ratio of 0.42, as shown in Fig. 2. Under the competition between the line tension and the bending energy, the size of first stage vesicles at mixing ratio of 0.42 is smaller than that at mixing ratio of 0.5. Under this condition, small tubular or toroidal vesicles were formed by the fusion of two spherical vesicles. However, the residual bending energy of the outer layers is not low enough, and part of the outer layers will stick to each other when a toroidal vesicle encounter with other toroidal vesicles or tubular vesicles. Then the two types of amphiphiles will redistribute through lateral diffusion to get the comfortable structures with more than one pore. Similar high-genus vesicles have also been reported in experiments and theoretical predictions, especially in studying vesicle–micelle transitions in phospholipid and surfactant mixtures.29–31 It was considered as a state of minimum curvature energy for the fluid membrane under the constraints of constant area, volume and area difference between the inner and outer layers of the bilayer.
When the mixing ratio of LDCs reaches 0.67, the size of first stage vesicles increases sharply and the structure changes to be an oblate vesicle (see Fig. 2). Quasi-saturated spherical vesicles were observed when the ratio exceeds 0.75. The saturated vesicles start to appear pores when we continuously increasing LDCs ratios and the pore size is proportional to the amount of LDCs. The pores are the results of appropriate hydrophilic/hydrophobic ratio accompanied with the appropriate distribution of the two amphiphiles in the binary mixing system. The change from intact vesicles to vesicles with controllable pore size by adding LDCs is similar to intelligent vesicles with tunable water channels. It opens a new way for therapeutic drug release at a defined rate. Similar perforated vesicles have been observed by Cryo-TEM experiments in studying the vesicle–micelle transition of egg phosphatidylcholine and sodium cholate.16 The amphiphiles first aggregate into short worm-like micelles instead of disk-like micelles when the ratios of LDCs further increases. At last, the network micelles were obtained in the case of pure LDCs in aqueous solution.
We have to mention that the morphologies obtained in our simulations have already been observed in different mixed systems. Additionally, the surfaces of most morphologies in Fig. 2 are bumpy, which has also been observed in the system of mixed surfactants.32 It may result from the non-uniformly distributions of the two amphiphiles.
3.2 The stability of the self-assembled structures
The distribution of the two amphiphiles in the inner and outer layers of the self-assembled vesicles was investigated by calculating the percentages of LDCs at different mixing ratios. The results are shown in Fig. 6. Here, the uniform distribution profile is given as a reference. We can see that the LDCs, which have positive spontaneous curvature, are in favor of locating in the outer layer of the vesicles independent of the mixing ratios.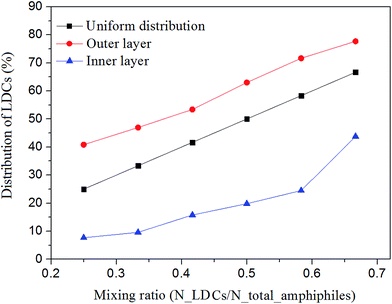 | ||
| Fig. 6 The percentage of LDCs in the inner and outer layers of the vesicles at different mixing ratios. | ||
The asymmetric distribution implies that compared with pure amphiphilic vesicles, more bending energy is released in the mixed system by rearranging the two amphiphiles in the inner and outer layers. This result manifests Safran's33 statement that the spontaneous vesicles formed in amphiphile mixtures are more stable than lamellar phases when the two amphiphiles provide opposite spontaneous curvatures at two sides of the bilayers. Similar distribution has also been observed in fluorescence-labeled diblock copolymers.34,35 It shows that polymeric vesicles prepared from a diblock mixture of PSb300-b-PAA11/ps310-b-p(4-vp)33 could be tailored by changing the length of PAA and P4VP, and the short block chains tend to reside inside the vesicles while the outside consists of long block copolymers.
Besides the asymmetric distribution between the inner and outer layers, the distribution of the two amphiphiles in the same layer is also curvature dependent. From the cross-section of the high-genius vesicle, we can see that in the outer layer lipid-like molecules prefer locating at negative curvature. Similar behavior is also observed in the inner layer's annulus of the oblate vesicles (see the cross-section in Fig. 2). The non-uniform distribution is caused by the inconsistent curvature of the aggregates in the same layer. It is a result of the minimization of bending energy under the constraints of area and volume. Thus, compared with the transitional oblate vesicles from pure amphiphiles, the mixing oblate vesicles are much stable. For the perforated vesicles, we can see that the pores are surrounded by LDCs (see the magnified pore). In this case, the relatively large hydrophilic heads of the LDCs can interact with water to reduce the hydrocarbon contact of the lipid tail with the aqueous phase. The situation is quite similar to the experimental observation in ref. 36 that the cholate concentration at the edges of an open bilayer sheet is greater than in the center.
The intelligent distribution of the two amphiphiles in the mixed system depending on the effective curvature makes as much as curvature energy released. That's why the structures can be more thermodynamically stable and more self-assembled structures have been observed in mixed experiments compared with the pure lipid or pure block-copolymer systems.18,37 The diversified structures with improved stability in the mixed systems make them promising candidates for potential applications.
3.3 The pathway-directing vesicle formation at the mixing ratio of 0.5
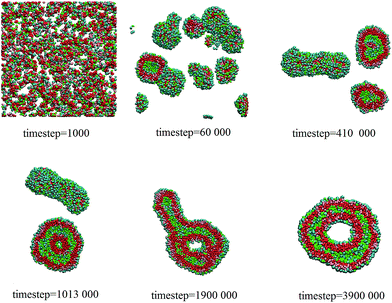
To study the kinetic effect on the self-assembled structures, pure LDCs and lipid-like solutions at the concentration of 3.2% are mixed after initially self-assembly (105 and 106 steps, respectively). The snapshots of the two self-assembling processes are shown in Fig. 7.In the first case (see Fig. 7(a)), short cylindrical micelles and small compound vesicles form before the LDCs and lipid-like solutions are mixed. After mixture, the two amphiphiles inter-diffuse quickly between the two structures, and tubular or small spherical vesicles similar to those obtained in the randomly mixed solution appear. Later, a quasi-toroidal vesicle with a tubular tail forms and the vesicle keeps relatively stable in our simulation time. In the second case (see Fig 7(b)), the self-assembled structures are worm-like micelles and large compound vesicles in the two pure solutions at the beginning. We mixed the two solutions and found that the degree of mixture keeps quite low due to the low probability of inter-contacting. Thus, compound vesicles and perforated vesicles are clearly observed during the simulation. After the two types of vesicles run into each other and fully undergo diffusion, a structure between toroid vesicle and bowl forms.
Our study shows that the morphology of the mixed amphiphiles can be influenced by the preparation pathways. Due to the local curvature-dependent distribution of the two amphiphiles, the system easily traps into a low dynamical process. The kinetic effect on the morphologies in the binary mixture has also been confirmed by experiments.38,39 That's why two or more structures were observed in experiments, simultaneously.40
In addition, the two self-assembled structures are heated to kBT = 1.3 and kBT = 1.2, respectively, and then cooled to kBT = 1.0. The toroidal vesicles similar to that of the random initial state are obtained in both cases (see Fig. 7). The recent experiments have suggested that the final structure may be dependent on the mechanistic pathway of the assembly, rather than the thermodynamic endpoint.41 Our results indicate that the self-assembly at the first stage can establish an energy barrier (without the anneal simulations) that hinders the reach of equilibrium thermodynamic structure. It implies that the slow release of the potential energy stored in the initially self-assembled components can drive the system into the non-equilibrium structures. One can incorporate pathway-directing information into the process of self-assembly.
4. Conclusions
In summary, the self-assembly processes of binary mixing amphiphiles, which respectively prefer the compound vesicles and network-like micelles, were investigated by computer simulations. By varying the mixing ratios of the two amphiphiles, a variety of self-assembled structures were obtained, including high genus vesicles, toroidal vesicles, oblate vesicles and perforated vesicles. Energetic and structural analysis suggests that the key factor that drives the appearance of diverse morphologies is the effective spontaneous curvature of the two amphiphiles in the mixed system. Furthermore, these structures are more stable than similar structures obtained from pure amphiphiles due to their intelligent distribution in the two layers. In other words, due to tunable spontaneous curvature at different mixing ratios and the flexible distribution of the two amphiphiles, more structures with improved stability can form in the mixing surfactant systems. In addition, we suggested that the pathway-directing assembly can provide a physical barrier to prevent the appearance of equilibrium thermodynamic structure. Our findings would be helpful for designing versatile nanostructures with unique properties.42Acknowledgements
The work was supported by the National Natural Science Foundation of China (nos 91027040, 21104056, 21474074), the National Basic Research Program of China (973 program of no. 2012 CB 821500), China Postdoctoral Science Foundation funded project (no. 2013M541713) and the Postdoctor Fundation of Jiangsu Province (no. 1301053C).References
- P. Alexandridis and B. Lindman, Amphiphilic Block Copolymers: Self-Assembly and Applications, Elsevier, Amsterdam, 2000 Search PubMed.
- X. B. Zhao, F. Pan, H. Xu, M. Yaseen, H. H. Shan, C. A. E. Hauser, S. G. Zhang and J. R. Lu, Chem. Soc. Rev., 2010, 39, 3480–3498 RSC.
- Y. W. Chung, J. K. Lee, W. C. Zin and B. K. Cho, J. Am. Chem. Soc., 2008, 130, 7139–7147 CrossRef CAS PubMed.
- A. Blanazs, S. P. Armes and A. J. Ryan, Macromol. Rapid Commun., 2009, 30, 267–277 CrossRef CAS PubMed.
- J. del Barrio, L. Oriol, C. Sáchez, J. L. Serrano, A. D. Cicco, P. Keller and M. H. Li, J. Am. Chem. Soc., 2010, 132, 3762–3769 CrossRef CAS PubMed.
- Y. Mai and A. Eisenberg, Chem. Soc. Rev., 2012, 41, 5969–5985 RSC.
- M. Ramanathan, L. K. Shrestha, T. Mori, Q. Ji, J. P. Hillbc and K. Ariga, Phys. Chem. Chem. Phys., 2013, 15, 10580–10611 RSC.
- R. J. Hickey, A. S. Haynes, J. M. Kikkawa and S. J. Park, J. Am. Chem. Soc., 2011, 133, 1517–1525 CrossRef CAS PubMed.
- M. J. Greenall and G. Gompper, Macromolecules, 2012, 45, 525–535 CrossRef CAS.
- Z. B. Li, M. A. Hillmyer and T. P. Lodge, Nano Lett., 2006, 6, 1245–1249 CrossRef CAS PubMed.
- P. F. Long and J. C. Hao, Adv. Colloid Interface Sci., 2012, 171–172, 66–76 CrossRef CAS PubMed.
- S. Ghosh, C. Ghatak, C. Banerjee, S. Mandal, J. Kuchlyan and N. Sarkar, Langmuir, 2013, 29, 10066–10076 CrossRef CAS PubMed.
- H. Noguchi, J. Chem. Phys., 2013, 138, 024907 CrossRef PubMed.
- E. Betthausen, C. Hanske, M. Müller, A. Fery, F. H. Schacher, A. H. E. Müller and D. J. Pochan, Macromolecules, 2014, 47, 1672–1683 CrossRef CAS.
- K. Eduards, J. Gustavsson, M. Almgren and G. Karlsson, J. Colloid Interface Sci., 1993, 161, 299–309 CrossRef.
- A. Walter, P. K. Vinson, A. Kaplun and Y. Talmon, Biophys. J., 1991, 60, 1315–1325 CrossRef CAS.
- A. Bernheim-Groswasser, R. Zana and Y. Talmon, J. Phys. Chem. B, 2000, 104, 12192–12201 CrossRef CAS.
- E. W. Kaler, A. K. Murthy, B. Z. Rodroguez and J. A. Zasadzinski, Science, 1989, 245, 1371–1374 CAS.
- S. Chiruvolu, H. E. Warriner, E. Naranjo, S. H. Idziak, J. O. Rädler, R. J. Piano, J. A. Zasadzinski and C. R. Safinya, Science, 1994, 266, 1222–1225 CAS.
- C. Zheng, P. Liu, J. Li and Y. W. Zhang, Langmuir, 2010, 26, 12659–12666 CrossRef CAS PubMed.
- K. Bressel, M. Muthig, S. Prevost, J. Gummel, T. Narayanan and M. Gradzielski, ACS Nano, 2012, 6, 5858–5865 CrossRef CAS PubMed.
- P. J. Hoogerbrugge and J. M. V. Koelman, Europhys. Lett., 1992, 19, 155–160 CrossRef.
- H. M. Ding, W. D. Tian and Y. Q. Ma, ACS Nano, 2012, 6, 1230–1238 CrossRef CAS PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- M. Antonietti and S. Förster, Adv. Mater., 2003, 15, 1323–1333 CrossRef CAS.
- L. F. Zhang, K. Yu and A. Eisenberg, Science, 1996, 272, 1777–1779 CAS.
- Y. Y. Mai, Y. F. Zhou and D. Y. Yan, small, 2007, 3, 1170–1173 CrossRef CAS PubMed.
- J. H. Fuhrhop, D. Spiroskit and C. Boettchert, J. Am. Chem. Soc., 1993, 115, 1600–1601 CrossRef CAS.
- B. Fourcade, M. Mutz and D. Bensimon, Phys. Rev. Lett., 1992, 68, 2551–2554 CrossRef CAS.
- X. Michalet and D. Bensimon, Science, 1995, 269, 666–668 CAS.
- H. S. Zhu, Q. R. Geng, W. Q. Chen, Y. Q. Zhu, J. Chen and J. Z. Du, J. Mater. Chem. B, 2013, 1, 5496–5504 RSC.
- R. H. Zheng, G. J. Liu and X. H. Yan, J. Am. Chem. Soc., 2005, 127, 1358–15359 CrossRef PubMed.
- S. A. Safran, P. Pincus and D. Andelman, Science, 1990, 248, 354–356 CAS.
- L. Luo and A. Eisenberg, Angew. Chem., Int. Ed., 2002, 41, 1001–1004 CrossRef CAS.
- J. Cui and W. Jiang, Langmuir, 2010, 26, 13672–13676 CrossRef CAS PubMed.
- S. A. Meeuwissen, S. M. C. Bruekers, Y. Chen, D. J. Pochanb and J. C. M. van Hest, Polym. Chem., 2014, 5, 489–501 RSC.
- H. Noguchi, Soft Matter, 2012, 8, 8926–8935 RSC.
- P. Schuetz, M. J. Greenall, J. Bent, S. Furzeland, D. Atkins, M. F. Butler, T. C. B. McLeish and D. M. A. Buzza, Soft Matter, 2011, 7, 749–759 RSC.
- S. Jain and F. S. Bates, Macromolecules, 2004, 37, 1511–1523 CrossRef CAS.
- F. Li, S. Prévost, R. Schweins, A. T. M. Marcelis, F. A. M. Leermakers, M. A. C. Stuart and E. J. R. Sudhölter, Soft Matter, 2009, 5, 4169–4172 RSC.
- J. S. Moore and M. L. Kraft, Science, 2008, 320, 620–621 CrossRef CAS PubMed.
- W. D. Tian and Y. Q. Ma, Chem. Soc. Rev., 2013, 42, 705–727 RSC.
| This journal is © The Royal Society of Chemistry 2014 |