Inaccessibility of the μ-hydride species in [FeFe] hydrogenases†
Arndt R.
Finkelmann
,
Martin T.
Stiebritz
and
Markus
Reiher
*
ETH Zürich, Laboratorium für Physikalische Chemie, Wolfgang-Pauli-Strasse 10, Zürich, Switzerland. E-mail: markus.reiher@phys.chem.ethz.ch; Fax: +41 44 633 15 94; Tel: +41 44 633 43 08
First published on 20th September 2013
Abstract
[FeFe] hydrogenases catalyse the reversible formation and oxidation of H2. They presumably feature a hydride species as a key intermediate. The H− ligand can either be bound between the iron atoms of the [2Fe]H subsite (μ-H) or terminally to the distal iron atom of the active site (terminal-H). Although the μ-H species is thermodynamically most stable, experimental evidence points to the terminal-H species as the relevant intermediate. In order to understand these contradictory results, we investigate the catalytic cycle of [FeFe] hydrogenases (including transition states) with a special focus on the role of the two possible hydride intermediates. For this, density functional theory calculations were carried out for a large quantum mechanical active-site model. It is shown that formation of the μ-H intermediate is prohibited by high activation barriers which are caused by interactions of the H cluster with surrounding amino acids. We provide direct evidence for the anchoring of the H cluster in the protein to be decisive for the kinetic hindrance of μ-H formation.
1 Introduction
The [2Fe]H subcluster of [FeFe] hydrogenases is the active site with the highest turnover frequency for the reduction of protons to form molecular hydrogen observed in biology.1 This diiron subcluster carries strong ligands and is bound to a [4Fe–4S] cubane via a cysteine bridge. Both form the so-called H cluster, which is found in all [FeFe] hydrogenases2–5 (see Fig. 1). Oxygen irreversibly inhibits [FeFe] hydrogenases, presumably by formation of reactive oxygen species and subsequent destruction of the cluster.6–9 The catalytic mechanism is believed to involve the formation of an intermediate hydride species10,11 which could be either bound terminally to the distal iron atom (Fed) or in a μ-bridging fashion between the proximal iron atom (Fep) and Fed. Although it has not been definitely clarified which form of these is the key hydride species as an experimental detection is challenging,12 the terminal-H intermediate appears to be widely accepted as the key intermediate. However, the μ-H species was found to be thermodynamically more stable (see below). Clearly, a detailed mechanistic investigation including transition states of all relevant elementary reactions is mandatory to resolve this puzzle.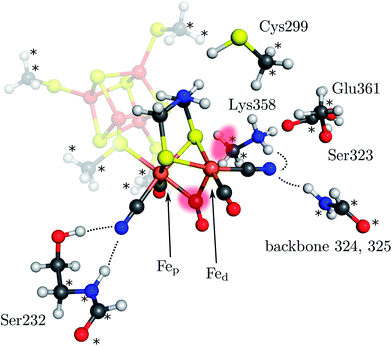 | ||
| Fig. 1 Model of the H cluster including the proximal Fe4S4 cubane, the side chains of Ser232, Cys299, Ser323, Lys358, Glu361 and the backbone atoms of residues 324 and 325 (labeling according to PDB entry 3C8Y). The atoms marked with an asterisk were fixed at their crystal structure positions (3C8Y). The transparent red spots indicate the terminal and μ-bridging ligand positions. Hydrogen bonds from H cluster surrounding residues are shown by dotted lines. | ||
Initial theoretical investigations into the mechanism of [FeFe] hydrogenases were performed by Hall and co-workers13,14 and by Liu and Hu.15,16 They employed a model for the [2Fe]H subcluster. The mechanistic key features found are the protonation of the bridging dithiomethylamine (dtma) ligand (which is a suitable base14,17) and successive formation of a hydride species which is terminally bound to Fed. Subsequently, this hydride is protonated to form H2.
However, for biomimetic model complexes which resemble the [2Fe]H subcluster it was found that a μ-hydride species (bridging the two Fe atoms) is formed.18–26 A mechanism comprising the μ-hydride was theoretically investigated by De Gioia and co-workers27,28 and Zhou et al.29,30 who considered a rotation of H2 from the bridging to the terminal position. Later Zampella et al.31 compared both mechanistic possibilities. For small models, which take only the [2Fe]H subcluster into account, the μ-hydride intermediate was always found to be more stable than the terminal hydride intermediate.
Later, the effect of the residues surrounding the H cluster on the mechanism was investigated by means of hybrid quantum mechanical/molecular mechanical calculations.32,33 Especially the relative stability of μ- vs. terminal-hydride species was addressed.34 The protein environment was found to reduce the difference in energy between both species but the μ-hydride was always more stable. It was concluded that, if the terminal hydride is the key intermediate, this must be due to kinetic effects, but barrier heights had not been calculated. Mutagenesis studies revealed that several key residues in the vicinity of the H cluster are crucial for catalytic activity providing experimental evidence for the importance of the protein matrix.35
Here, we present a quantum mechanical study into the H2-formation mechanism of [FeFe] hydrogenases based on a large active-site model that explicitly accounts for embedding effects of the protein matrix. This model includes the most important amino-acid residues surrounding the H cluster (see Fig. 1). These residues are anchored in the position they adopt in the protein structure as indicated in Fig. 1. The whole structure is then embedded in an electrostatic continuum. The full catalytic cycle is investigated, including all relevant transition states. For the formation of the μ-hydride species isomerization of the terminal hydride species and direct protonation of the Fe–Fe bond by Lys358 (Fig. 1), which has been discussed as a possible proton source,31 are considered. We show that the protein environment of the H cluster has a strong influence on the energetics of the H2 formation mechanism and kinetically hinders the formation of the μ-hydride species. All calculations were performed in the framework of density functional theory with the BP86 exchange-correlation functional36,37 (supported by B3LYP38–40 single-point calculations), the def2-TZVP basis set on all atoms,41 corrections for dispersion interactions (DFT-D3)42 and the COSMO model43 for a continuum electrostatics embedding (ε = 4) on optimised isolated structures as implemented in the TURBOMOLE program package.44 Note that the energy differences reported are differences in electronic energies since free-energy differences can hardly be obtained for molecular structures optimised under geometric constraints (in this case, anchoring of atoms in the amino-acid residues). However, the standard quantum-chemical (gas-phase) model for the calculation of Gibbs free energies would either provide similar results (i.e., temperature effects are negligible in the light of the overall accuracy of present-day density functional approximations) or artificially deviate from the electronic energy differences if the number of reactants differs on both sides of the reaction arrow.45 Differences in free energy from the literature are explicitly marked as ΔG. This methodology is in accordance with our previous work on hydrogenases6,8,46–48 and additional information on the model structures and computational methodology can be found in the ESI.†
2 Results and discussion
2.1 Mechanism at the terminal site of Fed
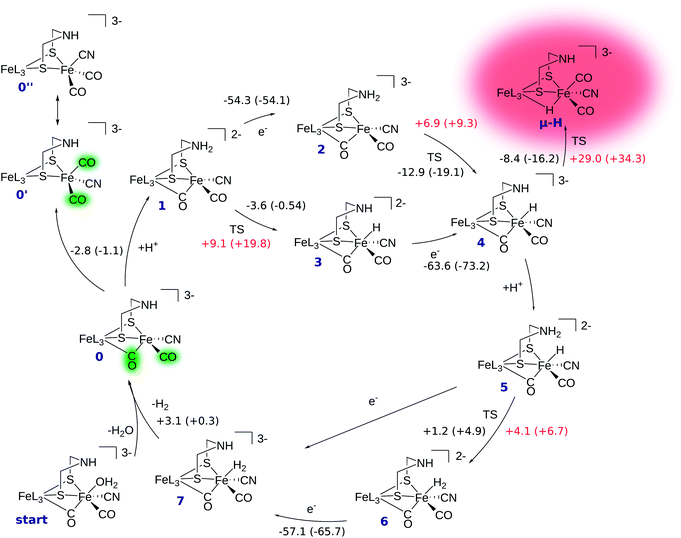
The reaction mechanism of [FeFe] hydrogenase consists of a cascade of successive protonations and proton reductions at the active site. Proton reduction leads to an intermediate hydride species which, with an additional proton, forms H2, the reaction product. The reaction site of the H cluster is believed to be the free terminal coordination site at Fed (see Fig. 1). The catalytic cycle with corresponding energetics is depicted in Fig. 2. It starts at intermediate 0 where the [2Fe]H subcluster is in the active oxidised oxidation state Fep(II)Fed(I) (Hcatox). Ligand rearrangement leads to an alternative conformation with one CO in the terminal position, one (formerly bridging) CO in the basal plane of Fed's coordination sphere and an open coordination site between the two iron atoms (compare intermediate 0′ in Fig. 2). This conformation will be called open conformation here.We first discuss the reaction mechanism with all reactions occurring at the terminal position of Fed. Then, we discuss whether and how the μ-hydride species is accessible.
In intermediate 0 the secondary amine group of the bridging dithiolate ligand is an ideal base and proton relay for H2 formation at Fed.14,49 Amine protonation leads to intermediate 1, which can be reduced by one electron to yield intermediate 2. Here, the formal oxidation state is the so-called active reduced state (Hcatred) with Fep(I)Fed(I). The terminal hydride species (intermediate 4) can be formed by proton transfer from the ammonium group to Fed. The hydride formation is exothermic by −12.9 kcal mol−1 and has a barrier of +6.9 kcal mol−1. Hydride formation may also be possible before reduction (reaction 1 → 3). In this oxidation state hydride formation is only slightly exothermic by −3.6 kcal mol−1 and has a barrier of +9.1 kcal mol−1. Successive reduction leads to intermediate 4.
After hydride formation, the bridgehead's amine group can be protonated again, leading to intermediate 5 (Fep(II)Fed(II)). H2 formation via proton transfer from the bridgehead atom to the hydride is slightly endothermic by +1.2 kcal mol−1 and has a small barrier of +4.1 kcal mol−1, resulting in intermediate 6. The low barrier indicates a fast equilibrium between the two species. Reduction of 6 yields intermediate 7, which is in the formal oxidation state Fep(II)Fed(I). The structure resulting from reduction of intermediate 5 before proton transfer is not a stable minimum on the potential energy hypersurface and structure optimization directly converges to intermediate 7. Thus, reduction of 5 leads to spontaneous hydrogen formation or, in other words, hydrogen formation can be driven by proton-coupled electron transfer. After detachment of H2 from intermediate 7 the cycle starts again.
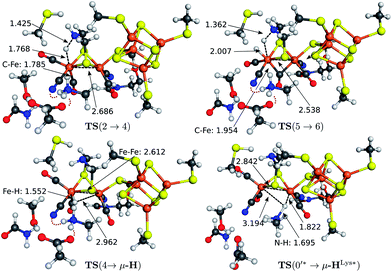
The transition state structures for hydride and H2 formation are depicted in Fig. 3. The hydride formation transition state TS(2 → 4) (Fig. 3, top left) has an elongated N–H bond and the Fed–H bond is partially formed. The μ-bridging CO ligand is still close to Fed. In the transition state TS(5 → 6) (Fig. 3, top right), which emerges from a straightforward transfer of the proton from the ammonium group, the N–H bond is slightly elongated and the Fe–H bond partially formed.
2.2 Incorporation of the μ-H species
In the mechanism described, all reactions occur at the terminal coordination site of Fed. However, the bridging hydride species is thermodynamically more stable than the terminal hydride species. In our model the difference in energy between terminal and bridging hydride (called intermediate μ-H) is −8.4 kcal mol−1, which compares well to the results of Bruschi et al.34 who obtained differences of −8.9 kcal mol−1 to −11.4 kcal mol−1 for different model sizes (−9.4 kcal mol−1 for a QM/MM model). There are two possible pathways to obtain the μ-bridging hydride species. First, ligand rearrangement from the terminal hydride, and second, direct protonation of the Fe–Fe bond in the open conformation. For the first possibility, we found a transition state directly connecting intermediates 4 and μ-H (compare Fig. 2) by ligand rearrangement. This reaction consists of a rotation of both CO ligands and the bound H− species, while the CN− remains fixed by the salt bridge to Lys358. The transition state TS(4 → μ-H) is depicted in Fig. 3 (bottom left). The formerly μ-bridging CO ligand has almost completely moved into the basal position at Fed and the formerly basal CO into the apical position at Fed. The Fe–Fe bond is elongated, compared to the educt, and the hydride ligand is still close to Fed but moving into the μ-bridging position. However, the barrier is +29.0 kcal mol−1 for this process. Thus, this reaction would be slow and μ-H formation via this pathway is therefore kinetically hindered. To elucidate the effect of the salt bridge from Lys358 to the cyanide, the reaction and barrier were re-calculated with a small structural model consisting only of the H cluster (cubane plus [2Fe]H subcluster). With this small model a similar rearrangement is found, which is exothermic by −7.5 kcal mol−1 (compared to −8.4 kcal mol−1 for the large model) and also possesses a significant barrier of +23.5 kcal mol−1 (compared to the +29.0 kcal mol−1 for the large model). Hence, the effect of the salt bridge on the reaction energy is small, but leads to a 5.5 kcal mol−1 higher barrier.It is interesting to note that the direct isomerization reaction for model complexes is known (e.g., ref. 50) and is believed to proceed according to a Bailar51 or a Ray–Dutt52 isomerization pathway.53 Both pathways feature two 120° rotations of three (Bailar) or four (Ray–Dutt) ligands and the Ray–Dutt pathway is stated to be energetically favoured.53 The reaction we found cannot be described by a Bailar or Ray–Dutt twist, since both require an intermediate with a basal hydride species. However, given the ligand arrangement in the product and educt structures, the reaction roughly resembles a distorted (because of the fixed cyanide) Bailar isomerization. A Ray–Dutt isomerization leads to a different isomer. For the Bailar isomerization Zampella et al. calculated a reaction barrier of +17.7 to +24.4 kcal mol−1 for different model compounds.53 This is in agreement with the barrier obtained for our small H-cluster model (+23.5 kcal mol−1). Recall, however, that the reaction pathway for our small model resembles the pathway of our large model. Other reactions might be possible for the small model (Bailar or Ray–Dutt) but are not considered here as they are not relevant for the enzyme. They could only come into play if the salt bridge was easily broken. Lys358 forms a salt bridge to CN− at Fed and at the same time to Glu361. We calculate a total binding energy of 98.9 kcal mol−1 for the bifurcated salt bridge (the binding energy is defined as the energy difference between the model with salt bridge 0 and the two optimized fragments Lys358 and the large model fragment without Lys358). Hence, the Glu361–Lys358–CN− arrangement is very stable and unlikely to break. This blockade of reaction pathways known for model complexes is another illustration of the important role of the Lys358–CN− salt bridge in the enzyme.
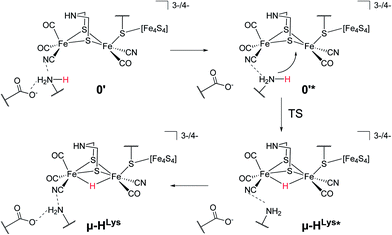
For the second hydride formation pathway (Fig. 4), the Fe–Fe bond must be protonated in the open conformation. In oxidation state Fep(II)Fed(I) intermediate 0′ (open conformation) is −2.8 kcal mol−1 more stable than intermediate 0. We could not locate any transition state for a hypothetical conversion 0 → 0′. A scan of the angle between the Fe–CO bond and the Fe–S bond (trans to the basal CO), which resembles the rearrangement process, has a flat energy profile and gives an estimate of +1.8 kcal mol−1 for the barrier which can be considered to be an upper bound. Note that the strong salt bridge between Lys358 and the CN− ligand at Fed prevents the cyanide ligand from being moved into the apical position, where it could form a hydrogen bridge to the bridgehead amine group (intermediate 0′′ in Fig. 2). Intermediate 0′ is 5.0 kcal mol−1 more stable than intermediate 0′′. It was suggested that the ammonium group of Lys358 could act as a proton donor for hydride formation in the open conformation.31 For calculating the energy of this reaction, Zampella et al. placed an unconstrained butylammonium molecule at the lysine's position and obtained an exergonic reaction with low barrier for the oxidation state Fep(I)Fed(I) (Zampella et al. give reaction energy and barrier height as ΔG = −18 kcal mol−1 and ΔG‡ = +3.5 kcal mol−1, respectively, at T = 298.15 K and p = 100 kPa) and a slightly endergonic reaction with high barrier in oxidation state Fep(II)Fed(I) (ΔG = +6.2 kcal mol−1 and ΔG‡ = +21.4 kcal mol−1). In our setup the carbon and hydrogen atoms representing the link to the protein backbone of the methylammonium are fixed at the crystallographic position of Lys358 (see Fig. 1). The reaction is depicted in Fig. 4. In the educt, which is derived from the crystal structure, Lys358 is in a salt bridge with Glu361 and CN−. Recall from above that the salt bridge, which keeps Lys358 in place, is stabilized by a binding energy of 98.9 kcal mol−1.
To transfer a proton in the μ-bridging position between Fep and Fed, the first step is a twist of the lysine accompanied by cleavage of the salt bridge to arrive at 0′*. This species is marked by an asterisk because it is a ‘transient species’. It is 5.0 and 13.3 kcal mol−1 higher in energy than the educt in the Hcatred respectively Hcatox oxidation states. We could not locate the transition state for the back reaction 0′* → 0′. However, a scan of the reaction pathway shows a very low barrier of about 1.3 kcal mol−1 for the back reaction in oxidation state Hcatox. Hence, this species does not significantly influence the overall reaction and is thus called ’transient’. From 0′* the hydride can be formed 0′* → μ-HLys* leading to another transient species (μ-HLys*) which upon back rotation of the amine leads to the product μ-HLys. This back rotation is exothermic in both oxidation states (−4.1 and −5.5 kcal mol−1 for Hcatred and Hcatox, respectively) and has a low barrier (estimated in a minimum energy path calculation to be +2.1 kcal mol−1 for Hcatox). Here the superscript “Lys” denotes the μ-hydride formed by the direct protonation of the Fe–Fe bond via Lys358. The reaction energies for both oxidation states are shown in Table 1. The overall reaction (without considering the transient species) is endothermic by +11.8 kcal mol−1 and has an overall barrier, from intermediate 0′ to hydride transfer TS, of +39.2 kcal mol−1 (Hcatred, compare Table 1). Also for the oxidised state Hcatox it is endothermic by +27.2 kcal mol−1 and possesses a barrier of +52.1 kcal mol−1. Thus, the reaction is highly unlikely to occur in the protein.
| Reaction | ΔE | ΔE‡ |
|---|---|---|
| [H]catox | ||
| 0′ → μ-HLys | +27.2 | +52.1 |
| 0′ → 0′* | +13.3 | |
| μ-HLys* → μ-HLys | −5.5 | |
| [H]catred | ||
| 0′ → μ-HLys | +11.8 | +39.2 |
| 0′ → 0′* | +5.0 | |
| μ-HLys* → μ-HLys | −4.1 | |
The transition state for the direct protonation of the Fe–Fe bond, TS(0′* → μ-HLys*), in the reduced oxidation state (Hcatred) is shown in Fig. 3 (bottom right). The ammonium group of the lysine residue is rotated away from the salt bridge to the glutamate's carboxylate group and the [2Fe]H subcluster is distorted in the course of this motion. The N–H bond of the transferred proton is significantly elongated and pointing towards the μ-bridging position, closer to Fep. This is reflected in the product, where the Fep–H bond is shorter than the Fed–H bond. A major difference to the model by Zampella et al. is the presence of the salt bridge between Lys358 and Glu361 in our large model which is broken in the course of the μ-HLys formation via direct protonation of the Fe–Fe bond. To further elaborate on the role of this salt bridge, the overall reaction (0′ → μ-HLys) was calculated without residues Glu361 and Ser323. Note that without these residues the proton of the lysine's ammonium group pointing towards the CN− ligand at Fed in the educt structure significantly shifts towards CN− in both oxidation states. In the oxidation state Hcatred the reaction is exothermic by −11.6 kcal mol−1 and has a hydride transfer barrier of +14.9 kcal mol−1. With the iron atoms being in oxidation state Hcatox the reaction is exothermic by −4.7 kcal mol−1 and shows a hydride transfer barrier of +17.6 kcal mol−1. The removal of the salt bridge results in a much more favourable μ-H formation reaction. This clearly illustrates the importance of the conserved hydrogen-bond network between Glu361, Ser323 and Lys358.
The reaction-energy differences reported for the model by Zampella et al.31 and calculated for our large model can be rationalised with these considerations as well. It appears that taking the transient species as educt and product yields reaction energies in better agreement with those reported by Zampella et al. For Hcatox we obtained ΔE = +38.7 kcal mol−1 and ΔE‡ = +8.4 kcal mol−1, whereas Zampella et al. obtained ΔG = +6.2 kcal mol−1 and ΔG‡ = +21.4 kcal mol−1 (note that the calculation of free energies for a given temperature can be expected to only modulate the electronic energy differences in this case). For Hcatred we have ΔE = +2.7 kcal mol−1 and ΔE‡ = +34.2 kcal mol−1, whereas Zampella et al. obtained ΔG = −18 kcal mol−1 and ΔG‡ = +3.5 kcal mol−1. Considering the reaction without Glu361 and Ser323 yields reaction energies even more similar to those reported by Zampella et al. as well.
A comparison of results from the literature with the reaction energies and barriers of this work is provided in Table 2. The BP86-D3 results compare well to recent studies of a large QM model and of a QM/MM model, which is an indication that our model is of sufficient size for studying the reaction mechanism. Note, however, that hydride and H2 formation are already well described by small active-site models. For reaction 5 → 7 an intermediate and a transition state had been found in the QM/MM approach and for QM models optimised within a COSMO dielectric environment. In this work, we were able to also locate a transition state for the reaction 4 → μ-H.
| Reaction | This work | Ref. 15 and 16 a | Ref. 14 b, ΔG | Ref. 31 c, ΔG | Ref. 56 d | Ref. 32 e | Ref. 34 f | Ref. 57 d |
|---|---|---|---|---|---|---|---|---|
| a GGA-PW91 plane wave/model for the [2Fe]H subcluster. b B3LYP/improved split valence basis set/model for the [2Fe]H subcluster. c BP86/TZVP/COSMO(ε = 4)/model of [2Fe]H subcluster. d BP86/TZVP/COSMO(ε = 4)/model of the H cluster. e BP86/TZVP/QM/MM model. f BP68/TZVP/model of the H-cluster and important surrounding amino acids; full QM/MM model (second row of each reaction). | ||||||||
| 2 → 4 | −12.9 (+6.9) | −17.8 (+0.7) | −9.5 (+1.1) | −10.5 | −11.9 | −13.9 | ||
| −19.1 (+9.3) | −14.3f | |||||||
| 1 → 3 | −3.6 (+9.1) | −4.7 (+11.6) | ||||||
| −0.5 (+19.8) | ||||||||
| 5 → 6 | +1.2 (+4.1) | +1.2 (+4.2) | −3.5 (+1.4) | +2.6 (+2.8) | ||||
| +4.9 (+6.7) | ||||||||
| 5 → 7 | +2.4 (+8.4) | −8.1 (+1.0) | ||||||
| 7 → 0 | +3.1 | +2.1 | −12.8 | −5.5 | −7.2 | −3.3 | ||
| +0.3 | ||||||||
| 4 → μ-H | −8.4 (+29.0) | −8.3 | −11.0 | −9.3 | ||||
| −16.2 (+34.3) | −9.4f | |||||||
| Hcatox | ||||||||
| 0′ → μ-HLys | +27.2 (+52.1) | +6.2 (+21.4) | ||||||
| +35.3 (+69.1) | ||||||||
| Hcatred | ||||||||
| 0′ → μ-HLys | +11.8 (+39.2) | −18.0 (+3.5) | ||||||
2.3 Effect of structural constraints
To investigate the influence of the constraints imposed on the model due to the fixation of certain amino-acid backbone and side-chain atoms, calculations with relaxed constraints and an enlarged model were conducted. The relative stability of terminal-H and μ-H species was calculated for another (even larger) model that takes into account the full side chains of Lys358, Ser323 and Glu361. The backbone atoms connected to Cα were replaced by hydrogen and fixed in space (Cα was fixed, too). The difference in energy between the two hydride species with this enlarged and thus structurally more flexible model is −8.4 kcal mol−1, which is exactly the same as for the original model and hence confirms the internal consistency of our approach. Furthermore, the isomerization reaction was calculated with relaxed constraints on Lys358 (no atom fixations for this residue). The reaction for the model without constrained Lys shows similar energetics as the one for the constrained Lys. It is exothermic by −8.1 kcal mol−1 and has a barrier of +28.9 kcal mol−1 compared to a reaction energy of −8.4 kcal mol−1 and barrier of +29.0 kcal mol−1 for the constrained lysine.2.4 Hydride–metal vibrational frequencies
Vibrational signatures of the different hydride species are important for the spectroscopic detection. Metal–hydride vibrations have been investigated for active-site model complexes for different hydrogenases. We first shortly review the findings obtained for [NiFe] and [FeFe] hydrogenase model complexes and then compare to our active site model.[NiFe] hydrogenases have an active site structure similar to [FeFe] hydrogenases2 and a bimetallic Ni–Fe core. A detailed computational and experimental study on a model complex of the μ-hydride intermediate of [NiFe] hydrogenases ([(dppe)Ni(μ-pdt)(μ-H)Fe(CO)3][BF4]) was conducted by Shafaat et al.54 Hydride–metal stretching frequencies were identified. In particular, it was concluded that the hydride–metal stretching modes of the μ-hydride species have an anharmonic potential. The line width can be expected to be broad and the anharmonicity can lead to a significant deviation of the calculated harmonic frequency from the experimental frequency, especially for the Fe–H bond in the investigated μ-hydride model complex.54 This effect may occur in μ-hydride species with a diiron center as well.
The symmetric [FeFe] hydrogenase model complex (μ-edt)[Fe2(PMe3)4(CO)2(H)]+, has a μ-bridging- and terminal-hydride conformation.50 Calculations predicted the stretching modes for the μ-hydride to be at 1151 (antisymmetric) and 1352 cm−1 (symmetric). For the terminal-hydride conformation a Fe–H stretching frequency of 1908 cm−1 has been calculated.55
In our active-site model the μ-H species features two Fe–H− stretching vibrations. The Fed–H− stretching band is found at 1071 cm−1 and the Fep–H− at 1462 cm−1 (unscaled frequencies). The different wavenumbers reflect the asymmetric binding. The Fep–H− distance is 1.643 Å, whereas the Fed–H− distance is 1.743 Å. Hence, the shorter Fep–H bond has a higher wavenumber (larger force constant). Both vibrations are isolated. The Fed–H− stretching wavenumber of intermediate 4 (terminal-H species) is 1816 cm−1. This mode has a small contribution of μ-CO stretching as the μ-CO stretching vibration is close in frequency (1872 cm−1). Accordingly, the latter has a small admixture of Fed–H− stretching.
Hence, there is a shift of the wavenumbers for the H cluster compared to the symmetric model complex investigated by Galinato et al.55 The asymmetric hydride binding in the μ-hydride species is reflected in a larger difference of the two Fe–H− stretching wavenumbers. For the terminal-H species the Fe–H− stretching mode is found at a lower wavenumber as was the case in the model complex. The signatures obtained may be useful for a spectroscopic detection of the hydride species in [FeFe] hydrogenases.
3 Conclusion
We have presented the full proton reduction mechanism of [FeFe] hydrogenases calculated with a large quantum mechanical active-site model (embedded in a dielectric continuum) that considers the interaction of the H cluster with its direct protein environment. Assuming a mechanism that only contains reactions at the terminal position of Fed, hydride formation is exothermic and has a small barrier of +6.9 kcal mol−1. Successive H2 formation features also a low barrier of +4.1 kcal mol−1 and is driven by reduction. The formation of the thermodynamically more stable μ-bridging hydride species has been shown to be kinetically hindered: the unavoidable ligand rearrangement features a large overall barrier (+29 kcal mol−1). Moreover, direct protonation of the Fe–Fe bond via Lys358 is endothermic and associated with even larger barriers of +52.1 and +39.2 kcal mol−1 for the Hcatox and Hcatred oxidation states, respectively. This is due to the cleavage of the very stable Glu361–Lys358 salt bridge, which would have to occur first. Thus, the surrounding of amino-acid residues of the active site of [FeFe] hydrogenases is crucial to prevent μ-hydride formation, and thus enables fast proton reduction with low barriers. In accordance to results obtained for [NiFe] and [FeFe] model complexes, we reported and discussed characteristic vibrations of the hydride species which might allow for their identification in experiment.Acknowledgements
This work has been financially supported by the Schweizerischer Nationalfonds (Project no. 200021L_138536).References
- M. Frey, ChemBioChem, 2002, 3, 153–160 CrossRef CAS.
- J. C. Fontecilla-Camps, A. Volbeda, C. Cavazza and Y. Nicolet, Chem. Rev., 2007, 107, 4273–4303 CrossRef CAS PubMed.
- J. W. Peters, W. N. Lanzilotta, B. J. Lemon and L. C. Seefeldt, Science, 1998, 282, 1853–1858 CrossRef CAS.
- Y. Nicolet, C. Piras, P. Legrand, C. E. Hatchikian and J. C. Fontecilla-Camps, Structure, 1999, 7, 13–23 CrossRef CAS.
- A. S. Pandey, T. V. Harris, L. J. Giles, J. W. Peters and R. K. Szilagyi, J. Am. Chem. Soc., 2008, 130, 4533–4540 CrossRef CAS PubMed.
- M. T. Stiebritz and M. Reiher, Inorg. Chem., 2009, 48, 7127–7140 CrossRef CAS PubMed ; erratum: M. T. Stiebritz and M. Reiher, Inorg. Chem., 2010, 49, 8645 CrossRef.
- S. T. Stripp, G. Goldet, C. Brandmayr, O. Sanganas, K. A. Vincent, M. Haumann, F. A. Armstrong and T. Happe, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 17331–17336 CrossRef CAS PubMed.
- M. K. Bruska, M. T. Stiebritz and M. Reiher, J. Am. Chem. Soc., 2011, 133, 20588–20603 CrossRef CAS PubMed.
- M. T. Stiebritz and M. Reiher, Chem. Sci., 2012, 3, 1739–1751 RSC.
- A. I. Krasna, Enzyme Microb. Technol., 1979, 1, 165–172 CrossRef CAS.
- M. W. Adams, L. E. Mortenson and J. S. Chen, Biochim. Biophys. Acta, 1981, 594, 105–176 Search PubMed.
- W. Lubitz, E. Reijerse and M. van Gastel, Chem. Rev., 2007, 107, 4331–4365 CrossRef CAS PubMed.
- Z. Cao and M. B. Hall, J. Am. Chem. Soc., 2001, 123, 3734–3742 CrossRef CAS PubMed.
- H.-J. Fan and M. B. Hall, J. Am. Chem. Soc., 2001, 123, 3828–3829 CrossRef CAS.
- Z.-P. Liu and P. Hu, J. Am. Chem. Soc., 2002, 124, 5175–5182 CrossRef CAS PubMed.
- Z.-P. Liu and P. Hu, J. Chem. Phys., 2002, 117, 8177–8180 CrossRef CAS.
- Y. Nicolet, A. L. de Lacey, X. Vernède, V. M. Fernandez, E. C. Hatchikian and J. C. Fontecilla-Camps, J. Am. Chem. Soc., 2001, 123, 1596–1601 CrossRef CAS PubMed.
- X. Zhao, I. P. Georgakaki, M. L. Miller, J. C. Yarbrough and M. Y. Darensbourg, J. Am. Chem. Soc., 2001, 123, 9710–9711 CrossRef CAS.
- F. Gloaguen, J. D. Lawrence, M. Schmidt, S. R. Wilson and T. B. Rauchfuss, J. Am. Chem. Soc., 2001, 123, 12518–12527 CrossRef CAS PubMed.
- X. Zhao, I. P. Georgakaki, M. L. Miller, R. Mejia-Rodriguez, C.-Y. Chiang and M. Y. Darensbourg, Inorg. Chem., 2002, 41, 3917–3928 CrossRef CAS PubMed.
- S. J. Borg, T. Behrsing, S. P. Best, M. Razavet, X. Liu and C. J. Pickett, J. Am. Chem. Soc., 2004, 126, 16988–16999 CrossRef CAS PubMed.
- X. Liu, S. K. Ibrahim, C. Tard and C. J. Pickett, Coord. Chem. Rev., 2005, 249, 1641–1652 CrossRef CAS PubMed.
- L. Schwartz, G. Eilers, L. Eriksson, A. Gogoll, R. Lomoth and S. Ott, Chem. Commun., 2006, 520–522 RSC.
- S. D. Brown, M. P. Mehn and J. C. Peters, J. Am. Chem. Soc., 2005, 127, 13146–13147 CrossRef CAS PubMed.
- A. Jablonskytė, J. A. Wright and C. J. Pickett, Dalton Trans., 2010, 39, 3026–3034 RSC.
- S. Tschierlei, S. Ott and R. Lomoth, Energy Environ. Sci., 2011, 4, 2340–2352 CAS.
- M. Bruschi, P. Fantucci and L. De Gioia, Inorg. Chem., 2002, 41, 1421–1429 CrossRef CAS PubMed.
- M. Bruschi, P. Fantucci and L. De Gioia, Inorg. Chem., 2003, 42, 4773–4781 CrossRef CAS PubMed.
- T. Zhou, Y. Mo, A. Liu, Z. Zhou and K. Tsai, Inorg. Chem., 2004, 43, 923–930 CrossRef CAS PubMed.
- T. Zhou, Y. Mo, Z. Zhou and K. Tsai, Inorg. Chem., 2005, 44, 4941–4946 CrossRef CAS PubMed.
- G. Zampella, C. Greco, P. Fantucci and L. De Gioia, Inorg. Chem., 2006, 45, 4109–4118 CrossRef CAS PubMed.
- C. Greco, M. Bruschi, L. De Gioia and U. Ryde, Inorg. Chem., 2007, 46, 5911–5921 CrossRef CAS PubMed.
- C. Greco, M. Bruschi, P. Fantucci, U. Ryde and L. De Gioia, J. Am. Chem. Soc., 2011, 133, 18742–18749 CrossRef CAS PubMed.
- M. Bruschi, C. Greco, M. Kaukonen, P. Fantucci, U. Ryde and L. De Gioia, Angew. Chem., Int. Ed., 2009, 48, 3503–3506 CrossRef CAS PubMed.
- P. Knörzer, A. Silakov, C. E. Foster, F. A. Armstrong, W. Lubitz and T. Happe, J. Biol. Chem., 2012, 287, 1489–1499 CrossRef PubMed.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3010 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- M. Reiher and B. A. Hess, Chem.–Eur. J., 2002, 8, 5332–5339 CrossRef CAS.
- M. T. Stiebritz and M. Reiher, Inorg. Chem., 2010, 49, 5818–5823 CrossRef CAS PubMed.
- M. T. Stiebritz, A. R. Finkelmann and M. Reiher, Eur. J. Inorg. Chem., 2011, 1163–1171 CrossRef CAS.
- M. Bruska, M. T. Stiebritz and M. Reiher, Dalton Trans., 2013, 42, 8729–8735 RSC.
- A. Silakov, B. Wenk, E. Reijerse and W. Lubitz, Phys. Chem. Chem. Phys., 2009, 11, 6592–6599 RSC.
- J. I. van der Vlugt, T. B. Rauchfuss, C. M. Whaley and S. R. Wilson, J. Am. Chem. Soc., 2005, 127, 16012–16013 CrossRef CAS PubMed.
- J. C. Bailar, Jr, J. Inorg. Nucl. Chem., 1958, 8, 165–175 CrossRef.
- P. Ray and N. K. Dutt, J. Indian Chem. Soc., 1943, 20, 81–92 CAS.
- G. Zampella, P. Fantucci and L. De Gioia, Chem. Commun., 2010, 46, 8824–8826 RSC.
- H. S. Shafaat, K. Weber, T. Petrenko, F. Neese and W. Lubitz, Inorg. Chem., 2012, 51, 11787–11797 CrossRef CAS PubMed.
- M. G. I. Galinato, C. M. Whaley, D. Roberts, P. Wang and N. Lehnert, Eur. J. Inorg. Chem., 2011, 1147–1154 CrossRef CAS PubMed.
- M. Bruschi, C. Greco, P. Fantucci and L. D. Gioia, Inorg. Chem., 2008, 47, 6056–6071 CrossRef CAS PubMed.
- C. Greco, M. Bruschi, P. Fantucci, U. Ryde and L. De Gioia, Chem.–Eur. J., 2011, 17, 1954–1965 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Computational details; cartesian coordinates. See DOI: 10.1039/c3sc51700d |
| This journal is © The Royal Society of Chemistry 2014 |