Structural re-arrangement in two hexanuclear Cu^II complexes: from a spin frustrated trigonal prism to a strongly coupled antiferromagnetic soluble ring complex with a porous tubular structure

Abstract

The addition of water to a chloroform solution of the Cu₆ trigonal prism complex [Cu₆(μ₆F)(μ₂OH)(μ₃OCH₃)₂(μ₂OCH₃)₂(3,5-Me₂pz)₆] (1) (3,5-Me₂pz⁻ = 3,5-dimethylpyrazolate) results in the formation of the Cu₆ planar hexagonal ring complex [Cu₆(μ₂OH)₆(3,5-Me₂pz)₆]·CH₃CN·CHCl₃ (2). A simple mechanism for this structural re-arrangement is proposed, in which 2 can be viewed as a hydrolysis product of 1. This process is clearly noticeable in the magnetic properties, which change from spin frustrated with a weak antiferromagnetic coupling in 1, to strongly antiferromagnetic in 2. Interestingly, the hexagonal ring complex 2 self-assembles in the solid state to form a porous hexagonal tubular structure containing guest solvent molecules that can be removed and CO₂-exchanged without loss of crystallinity.

---

Introduction

A recurrent topic in coordination chemistry is that of searching for new polynuclear complexes based on copper(II). In fact, thanks to its coordination plasticity and large affinity towards N-donor ligands, this ion has provided a huge variety of polynuclear structures showing different nuclearities and dimensionalities,^1,2 which have been shown to be of interest in diverse areas such as catalysis,³ bio-inorganic chemistry,^4–7 materials chemistry^8,9 and molecular magnetism, just to name a few. In molecular magnetism, for example, polynuclear Cu^II complexes have been extensively studied as model systems to gain insight into the exchange interaction phenomenon in both discrete units and extended structures.¹⁰

An aspect that has been much less investigated is how the structures of these polynuclear Cu^II complexes change under the influence of a chemical stimulus. Here the coordination plasticity around Cu^II can also play a key role. For example, in the solid state there are many examples of flexible coordination polymers in which the structural changes caused by the uptake/release of physisorbed or chemisorbed molecules are facilitated by changes induced in the Cu^II coordination environment.^11,12 In solution these chemically-induced structural rearrangements are also present, although it is often difficult to isolate the different chemical species involved in the process.

Here we report the synthesis of two new hexanuclear Cu^II complexes that form crystals of formula [Cu₆(μ₆F)(μ₂OH)(μ₃OCH₃)₂(μ₂OCH₃)₂(3,5-Me₂pz)₆] (1) and [Cu₆(μ₂OH)₆(3,5-Me₂pz)₆]·CH₃CN·CHCl₃ (2), where 3,5-Me₂pz⁻ (3,5-dimethylpyrazolate) is a pyrazole derivative which acts as a bridging ligand. In solution, complex 1 is transformed into 2 upon addition of water. Thus, complex 1 exhibits a trigonal prismatic geometry, which transforms into a hexagonal ring geometry (complex 2) when water is added to a CHCl₃ solution of 1. Here we propose a possible hydrolysis mechanism for the transformation of 1 into 2. We show that these structural changes have a strong influence on their magnetic properties and finally, we examine the porosity properties of crystals of 2, which exhibit a hexagonal tubular structure that allows partial removal of the internal solvent molecules and absorption of CO₂.

Experimental

Synthesis of the complexes

All chemicals were of reagent grade and used without further purification.

[Cu₆(μ₆F)(μ₂OH)(μ₃OCH₃)₂(μ₂OCH₃)₂(3,5-Me₂pz)₆] (1). 3,5-Dimethylpyrazole (288 mg, 3 mmol) and diethylamine (220 mg, 3 mmol) were dissolved in 15 mL of CHCl₃ and stirred for 20 minutes. This solution was added drop-wise into a solution of Cu(BF₄)₂·H₂O (712 mg, 3 mmol) in 15 mL of CH₃OH. The greenish solution was stirred for 3 hours. Diethyl ether was diffused into the solution, and green crystals suitable for X-ray diffraction were obtained within one day (yield = 360 mg, 65%). This compound can also be prepared using CH₃OH instead of CHCl₃ to prepare the first solution. Phase purity was established by XRPD (Fig. S1†). Elemental analysis for 1: found: C, 35.5; N, 14.6; H, 4.9%. Calc. for C₃₄H₅₅N₁₂O₅FCu₆: C, 36.7; N, 15.1; H, 5.0%. Elemental ratio estimated by electron probe microanalysis (EPMA): found: Cu : F = 6.0. Calc. for C₃₄H₅₅N₁₂O₅FCu₆: Cu : F = 6.0.

[Cu₆(μ₂OH)₆(3,5-Me₂pz)₆]·CH₃CN·CHCl₃ (2). 5 mL of water was added with stirring to a green solution containing 637 mg (0.57 mmol) of compound 1 in 20 mL of CHCl₃, resulting in the separation of two phases and a colour change from green to purple in the organic phase. The two phases were separated, and the diffusion of acetonitrile into the organic phase yielded purple crystals of compound 2 suitable for X-ray diffraction within one day (yield = 284 mg, 45%). Phase purity was established by XRPD (Fig. S2†). Elemental analysis for 2: found: C, 32.6; N, 14.6; H, 4.0%. Calc. for C₃₃H₅₂N₁₃Cl₃O₆Cu₆: C, 32.6; N, 15.0; H, 4.3%. The EPMA analysis ruled out the presence of any F⁻ in complex 2 and showed a Cu : Cl ratio of 2.0, in agreement with the proposed formula.

Single crystal X-ray diffraction

Single crystals of compounds 1 and 2 were mounted on a glass fibre using a viscous hydrocarbon oil to coat the crystal. X-ray data were collected at room temperature for 1. A single crystal of 2 was structurally characterized at 120 K, then heated to 373 K for 6 h, after which most of the solvent molecules were removed, as shown after the structural determination (2′-373). The crystal was then cooled to 120 K and crystal structure determination was re-undertaken (2′-120). X-ray data were collected on a Supernova diffractometer equipped with a graphite-monochromated Enhance (Mo) X-ray source (λ = 0.71073 Å). The program CrysAlisPro, Oxford Diffraction Ltd., was used for unit cell determinations and data reduction. Empirical absorption correction was performed using spherical harmonics, implemented in the SCALE3 ABSPACK scaling algorithm. Crystal structures were solved and refined against all F² values using the SHELXTL suite of programs.¹³ Non-hydrogen atoms were refined anisotropically and hydrogen atoms were placed in calculated positions that were refined using idealized geometries (riding model) and assigned fixed isotropic displacement parameters except for that of the hydroxido ligand, which was located and refined with distance restraints. In 2, the non-coordinated solvent molecules (CHCl₃ and CH₃CN) are disordered over two sites (related by an inversion centre) and have been modelled with 50 : 50 ratios. The void volumes in 2′-373 and 2′-120 were estimated using PLATON to be 16.7% and 14.7% of the unit cell, respectively. SQUEEZE¹⁴ analysis shows that no solvent molecules are present in 2′-373, whereas a small amount of residual electron density (8 electrons) is found in 2′-120. This is attributed to the presence of some interstitial solvent molecules that remain in the channel, which are highly disordered at high temperature and freeze upon lowering the temperature. All efforts to model this residual electron density were unsuccessful. A summary of the data collection and structure refinements is provided in Table S1.†

Physical characterisation

Variable temperature susceptibility measurements were carried out in the temperature range 2–300 K with an applied magnetic field of 0.1 T on ground polycrystalline samples of compounds 1 and 2 (with masses of 20.44 and 5.68 mg, respectively), using a Quantum Design MPMS XL-5 SQUID magnetometer. The susceptibility data were corrected for the sample holders previously measured under the same conditions and for the diamagnetic contributions of the sample using tables of Pascal's constants.¹⁵

ESI-mass spectra were obtained with a Waters Micromass ZQ spectrometer in the positive ion mode. The cone voltage was set to 10 V and the extractor voltage to 5 V, in order to avoid fragmentation. In all cases, well-resolved isotopic patterns consisting of mono-isotopic peaks separated by 1/z Da were obtained.

Elemental analysis (C, N, H) of bulk samples was performed by microanalytical procedures using an EA 1110 CHNS-O elemental analyzer from CE instruments. The Cu : F and Cu : Cl ratios of the bulk samples were estimated by electron probe microanalysis (EPMA) performed with a Philips SEM XL30 equipped with an EDAX DX-4 microprobe.

The phase purity of polycrystalline samples 1 and 2 was established by XRPD. Polycrystalline samples were lightly ground in an agate pestle and mortar and placed into 0.7 mm borosilicate capillaries. Data were collected at room temperature in the 2θ range of 2–30° on a Empyrean PANalytical powder diffractometer, using Cu Kα radiation (λ = 1.54177 Å). In both cases, the powder diffraction pattern of the bulk sample was consistent with the pattern calculated from single-crystal data (see Fig. S1 and S2†).

Thermogravimetric analysis of 2 was carried out with a Mettler Toledo TGA/SDTA 851 apparatus in the 25–1000 °C temperature range under a 5 °C min⁻¹ scan rate and an air flow of 30 mL min⁻¹.

UV-visible spectra were recorded for 1 and 2 on a Perkin-Elmer Lambda 1050 Wideband UV-Vis-NIR spectrophotometer in CHCl₃ solutions in the range 300 to 850 nm. To follow the inter-conversion, compound 1 (or 2) was dissolved in 160 μL of CH₃OH (CHCl₃ for 2) and successive 10 μL aliquots of CHCl₃ (CH₃OH for 2) were added to the solution.

Results and discussion

Synthesis

As a ligand we used the pyrazole derivative 3,5-dimethylpyrazolate (3,5-Me₂pz⁻). In its anionic form this ligand has shown a marked tendency to form polynuclear Cu^II complexes containing Cu–N–N–Cu bridges (see Scheme 1), leading to nuclearities ranging from two^16–23 to twelve,^24,25 including three,^26,27 five,¹⁸ eight²⁸ and eleven,¹⁸ although to date, none with six.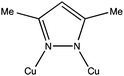

Scheme 1 The 3,5-dimethylpyrazolate (3,5-Me₂pz⁻) ligand connecting two copper atoms, as found in complexes 1 and 2.

The reaction of this ligand in chloroform/methanol or methanol with Cu(BF₄)₂·H₂O in a basic medium gives a green solution that after slow diffusion of diethyl ether yields bluish-green single crystals of 1. Addition of water to a green chloroform solution of 1 yields a purple organic phase that, upon slow diffusion of acetonitrile, affords single crystals of 2.

X-ray crystal structures

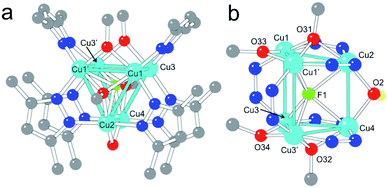
Complex 1 contains six Cu^II centres distributed in two eclipsed, almost parallel isosceles triangles (Cu1Cu1′Cu2 and Cu3Cu3′Cu4, see Fig. 1), forming an uncommon trigonal prismatic geometry. This trigonal prism has a central F⁻ ligand shared by the six Cu^II centres, resulting in a sandglass-shaped complex with a μ₆-F⁻ bridge (Fig. 1). The Cu–Cu distances inside the triangles (2.833(1)–3.112(1) Å) are slightly shorter than those between the triangles (3.056(2)–3.382(2) Å). Each copper atom presents a distorted square pyramidal geometry with Addison parameters of 0.14, 0.04, 0.13 and 0.12 for Cu1–Cu4, respectively.²⁹ In each case, the basal plane is formed by two nitrogen atoms from two 3,5-Me₂pz⁻ ligands and by two oxygen atoms from a μ₃-OCH₃⁻ and a μ₂-OCH₃⁻ ligand. The axial ligand is in all cases the fluorine atom (F1) of the central μ₆-F⁻ bridge, located between the two copper triangles (Fig. 1).

Fig. 1 (a) Top view of complex 1 showing the 3,5-Me₂pz⁻ ligands and the π–π overlap of the pyrazolate rings. (b) Central portion of the structure of the same complex showing the atom labelling of Cu, F and O atoms and the coordination environments of the six Cu^II centres. (H atoms have been omitted for clarity except that of the OH group). Colour code: Cu = cyan, O = red, N = dark blue, C = grey, H = yellow, F = green.

Both isosceles triangles are similar and present a symmetry plane that passes through Cu2 and Cu4 and intersects the Cu1–Cu1′ and Cu3–Cu3′ edges. Besides the common μ₆-F⁻ bridge, both triangles are also connected by: (i) a μ₂-OH⁻ bridge (O2) connecting Cu2 with Cu4, with a Cu2–O2–Cu4 bond angle of 103.0(3)°; and (ii) two 3,5-Me₂pz⁻ ligands connecting Cu1 with Cu3 and Cu1′ with Cu3′ through a Cu–N–N–Cu bridge. Each triangle has a μ₃-OCH₃⁻ bridge connecting the three Cu atoms. The corresponding μ₃-O atoms (O31 and O32) are located 0.97 Å and 0.99 Å out of the Cu2Cu1Cu1′ and Cu4Cu3Cu3′ planes, respectively. Besides these μ₃-OCH₃⁻ bridges, connectivity inside each triangle is also provided by (i) a μ₂-CH₃O⁻ bridge connecting the two equivalent copper atoms (Cu1 with Cu1′ and Cu3 with Cu3′); and (ii) two μ₂-3,5-Me₂pz⁻ bridges connecting the non-equivalent copper atoms (Cu2 with Cu1 and Cu1′ in one triangle and Cu4 with Cu3 and Cu3′ in the other). As observed in the μ₃-OCH₃⁻ bridges, the oxygen atoms of the μ₂-OCH₃⁻ bridges (O33 and O34) are not co-planar with the corresponding triangles: O33 is located 0.158 Å above the Cu2Cu1Cu1′ plane and O34 is located 0.276 Å below the Cu4Cu3Cu3′ plane, leading to dihedral angles of 7.0° (Cu2Cu1Cu1′O33) and 11.6° (Cu4Cu3Cu3′O34). In summary, complex 1 has six Cu^II ions in an uncommon trigonal prismatic geometry connected by a central μ₆-F⁻ bridge. The connectivity of the cluster is completed by a μ₂-OH⁻ bridge (O2), two μ₂-OCH₃⁻ bridges (O33 and O34), two μ₃-OCH₃⁻ bridges (O31 and O32) and six μ₂-3,5-Me₂pz⁻ bridges, leading to a total anionic charge of −12 that compensates the charge of the six Cu^II ions.

Although the presence of a central μ₆-F⁻ bridge is not straightforward to observe from the X-ray crystal analysis (it could also be a OH⁻ or even a O²⁻ bridge), we have confirmed the presence of fluorine in compound 1 through electron probe microanalysis (EPMA), which indicates the presence of one F atom per Cu₆ cluster. Note that, although in the synthetic procedure there is no addition of F⁻, the partial dissociation of the BF₄⁻ counter-anion of the precursor Cu(BF₄)₂ salt can release F⁻ anions, as has been previously reported.^30–37 Once the nature of the central atom is established, the O2 bridge has to be assigned to a OH⁻ group in order to maintain the balance of charge (if this was also a F⁻ atom, it would imply a Cu : F ratio of 3 instead of 6).

The presence of a μ₆-F⁻ bridge is not unprecedented and has been reported in a family of three compounds, in which the F⁻ ion is surrounded by six Ag⁺ ions in a octahedral environment.^38,39 Compound 1 is, however, the first example of a μ₆-F⁻ bridge with a trigonal prismatic geometry. Notice also that the presence of any μ₆-X bridge surrounded by six Cu^II ions is very unusual in coordination chemistry. Thus, only four μ₆-Cl⁻,^40–42 three μ₆-V,^43–45 two μ₆-S,^46,47 one μ₆-Br,⁴⁸ one μ₆-I,⁴⁹ one μ₆-O²⁻,⁵⁰ and one μ₆-H⁵¹ have been reported to date. Among these 13 examples, there is only one (the μ₆-Cl⁻ complex [Cu₆(μ₆Cl)(μ₃OCH₃)₂(μ₂pyrazolate)₉],⁴²) in which the six copper atoms present a trigonal prismatic geometry as in 1. In summary, 1 is the first copper complex with a μ₆-F⁻ bridge, and the first example for any metal with trigonal prismatic geometry around a μ₆-F atom.

Besides the central μ₆-F⁻ bridge, the trigonal prismatic arrangement of the six Cu^II ions is stabilized by two μ₂-3,5-Me₂pz⁻ bridges connecting Cu1–Cu3 and Cu1′-Cu3′, a μ₂-OH⁻ bridge connecting Cu2 and Cu4 and by two quite strong π–π interactions between the rings of the μ₂-Me₂pz⁻ bridges, forming two of the three edges of the triangles (the distance between the average planes of the 3,5-Me₂pz⁻ ligands is 3.73 Å, Fig. 1a).⁵² Note that an octahedral arrangement of the six Cu^II ions would weaken all these interactions except the central μ₆-F⁻ one.

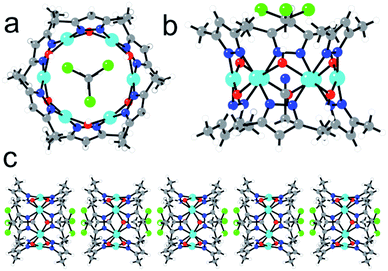
Complex 2 also contains a Cu₆ cluster, although with a regular planar hexagonal arrangement of the six equivalent Cu^II ions (Fig. 2a). This hexagonal wheel-like structure is packed in the solid state forming hexagonal channels along the c axis (Fig. 3) with an internal diameter of 6.355 Å (measured as the Cu–Cu distance along the diagonal), and a free pore diameter of ca. 3.5 Å. The Cu^II ions present a square planar geometry with two trans N atoms (N1 and N2) from two μ₂-3,5-Me₂pz⁻ ligands, and two trans oxygen atoms (O1) from two μ₂-OH⁻ bridges (Fig. 2b). Note that the channel structure of compound 2 suggests the possible inclusion of guest molecules, as will be discussed below.

Fig. 2 (a) Top view of the Cu₆ wheel showing the CHCl₃ molecule and the three H atoms of the CH₃CN molecule located in the central channel. (b) Side view of the same molecule showing one of the two possible locations of the CHCl₃ and CH₃CN molecules. (c) Side view of the hexagonal channels showing the two possible locations of the CHCl₃ and CH₃CN molecules. Colour code: Cu = cyan, O = red, N = dark blue, Cl = green, C = grey, H = white.

Fig. 3 Perspective view along the c direction of the hexagonal channels in the structure of 2. H and solvent atoms are omitted for clarity. Colour code: Cu = cyan, O = red, N = dark blue, C = grey.

Each pair of two consecutive Cu^II ions are connected by two different bridges, alternating on one or the other side of the ring: (i) a –N–N– bridge from a μ₂-3,5-Me₂pz⁻ bridge and (ii) a μ₂-OH⁻ bridge with a Cu1–O1–Cu1 bond angle of 110.18° (Fig. 2b). The Cu–O and the Cu–N bond lengths are all similar (in the range 1.936–1.960 Å). The Cu–Cu distance along the side of the hexagon is 3.178(2) Å.

The hexagonal ring in 2 resembles the numerous examples of metalla-crown complexes, whose very interesting host–guest interactions and potentialities have been reviewed by Pecoraro et al.,⁵³ although in 2 the connecting unit between two oxygen atoms is a Cu^II centre instead of a –M–N– bridging group. In addition, an interesting feature of this structure is the presence of a CHCl₃ and a CH₃CN molecule inside the Cu₆ ring (confirmed by thermo-gravimetric analysis, Fig. S3†). Both molecules present a positional disorder over two related positions with occupancy factors of 1/2. The CHCl₃ molecules are always located above (or below) the Cu₆ plane with the three Cl atoms pointing out of the ring and the H atom pointing towards the centre of the ring (Fig. 2c). The CH₃CN molecules are in the centre of the molecule with the N atom located in the Cu₆ plane and the two C atoms pointing to one or the other side, depending on the position of the CHCl₃ molecule (Fig. 2). Since single crystals of compound 2 are only obtained from a CHCl₃ solution after slow diffusion of CH₃CN, it seems that both solvent molecules play an important templating role in the crystallization of the Cu₆ metalla-cycle.

This kind of Cu₆ ring structure with double bridges (O and –N–N–) has already been described in a few cases,^54–59 although they are all charged or contain an ion (mainly Cl⁻, Br⁻, I⁻ or NO₂⁻). Interestingly, in 2 the Cu₆ ring structure is charge-balanced and, therefore, 2 is the first example of a neutral Cu₆ ring of this type without any counter-ion inside. This fact explains the eclipsed packing of the rings leading to an unprecedented tubular structure with hexagonal channels that can be evacuated (Fig. 3).

One-dimensional pores are highly interesting, since their tubular topology can afford a high adsorption capacity with size selectivity and one dimensional diffusion properties. The presence of the solvent molecules in the Cu₆ channels prevents the crystal from exhibiting a well-defined nano-porous structure, as occurs in other metalla-cycles. Still, as these solvent molecules are neutral, they can be partially removed upon heating in a single-crystal-to-single-crystal process, without loss of crystallinity. This affords a porous material (15–17% of the unit cell volume) with a pore diameter of ca. 3.55 Å, slightly larger than the kinetic CO₂ diameter (3.30 Å). Indeed, preliminary gas sorption studies show that CO₂ molecules can partially enter into the one-dimensional pores with an uptake of up to ca. 30% v/v of CO₂ in the hexagonal channels of a de-solvated sample of compound 2 with a CO₂ pressure of ca. 1 atm (Fig. S4†).

Stability in solution of the Cu₆ compounds

A green CHCl₃ solution of compound 1 presents an ESI-mass spectrum with four main signals centred at m/z = 1069.23, 1049.13, 1021.25 and 1003.18 Da in the positive region (Fig. 4). These four signals can be attributed to hexanuclear Cu^II complexes with 3,5-Me₂pz⁻ (L) bridges presenting different degrees of hydrolysis and different amounts of O²⁻, OH⁻ and CH₃O⁻ bridges: {Cu₆(L)₆(F)(OH)₃(O)(CH₃O) − 2e⁻}⁺ (m/z = 1069.06), [Cu₆(L)₆(F)(O)(CH₃O)₂]⁺ (m/z = 1049.08), [Cu₆(L)₆(F)(O)(OH)₂]⁺ (m/z = 1021.07) and [Cu₆(L)₆(F)(O)₂]⁺ (m/z = 1003.01), with isotopic patterns matching those observed experimentally (Fig. 4), confirming the presence of the μ₆-F⁻ hexanuclear Cu^II complex 1 in solution and its stability.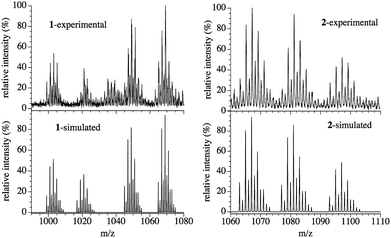

Fig. 4 Experimental (top) and simulated (bottom) ESI-mass spectra of compounds 1 (left) and 2 (right).

The ESI-mass spectrum of compound 2 dissolved in a 1 : 1 CHCl₃–CH₃OH mixture shows three main signals centred at m/z = 1067.17, 1081.18 and 1097.21 Da in the positive region (Fig. 4). These three signals correspond to those expected for an ionized Cu₆ wheel with a partial substitution of one, two or three μ-OH⁻ bridges by the corresponding μ-OCH₃⁻ bridges, together with the loss (or gain) of H atoms and electrons (Fig. 4). We can conclude that the {[Cu₆(3,5-Me₂pz)₆(OH_n)(OH)_5−x(CH₃O)_x] − ze⁻}⁺ monocations with x = 1 and 2 (n/z = 0/2), and x = 3 (n/z = 2/0) with average masses of 1067.07, 1081.10 and 1097.14 Da and with isotopic patterns matching those observed experimentally are present in the solution, showing the stability of the Cu₆ wheel and the progressive OH⁻/CH₃O⁻ ligand exchange.

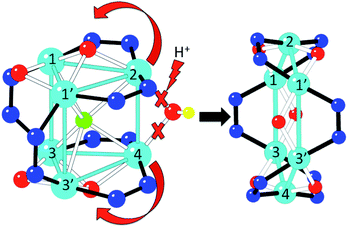
Conversion from 1 to 2

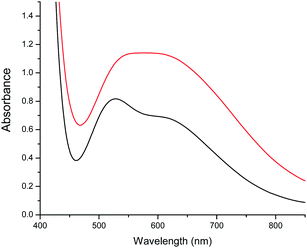
When a CHCl₃ solution of 1 is left to stand in open air, a colour change from green to purple is observed on the surface after a few hours. This colour change is caused by the diffusion of water molecules from the air, and can indeed be promoted by addition of water, yielding a purple solution that, upon slow diffusion of acetonitrile, affords single crystals of 2. Thus, conversion of 1 into 2 can be achieved in this way. A possible pathway for this conversion is depicted in Fig. 5. The addition of water molecules may cause the hydrolysis of the easily accessible μ₂-OH⁻ (O2) and the two μ₃-OCH₃⁻ bridges (O32 and O33 in Fig. 1). This kind of process has already been observed in other similar trinuclear pyrazolato-Cu^II complexes with alkoxido bridges.⁶⁰ Once hydrolysed, these three bridges are released, allowing the unfolding of the Cu₆ trigonal prism into a planar Cu₆ hexagon by a simple rotation of 90° of both triangles around the Cu3–Cu3′ and Cu1–Cu1′ edges (Fig. 5). Note that this mechanism does not imply cleavage nor formation of any Cu–N bond during the process, since the number and connectivity of the μ₂-3,5-Me₂pz⁻ ligands remains the same in both compounds. The transformation of the Cu₆ arrangement is clearly followed by the change of colour of the solution (from green to purple). Addition of CH₃CN to the purple solution containing the wheels permits the crystallization of 2.

Fig. 5 Proposed mechanism for the transformation of 1 into 2.

In order to check if the conversion of 1 into 2 is reversible, we have followed the changes in colour of a solution containing these species upon changing the solvent mixture. We have found that by adding methanol to the purple solution of 2, the colour changes to a green colour very close to that of the original solution of 1, but not identical, indicating that complex 2 is transformed into a complex very similar to 1 under these conditions. These colour changes have been monitored in a more precise way by recording UV-vis absorption spectra. In the visible region 1 shows a broad double maximum in the range of 550 to 600 nm, while 2 shows a maximum at 528 nm (ε = 512) and a shoulder at ca. 610 nm (Fig. 6).

Fig. 6 Absorption spectra of 1 (red) and 2 (black) in CHCl₃.

The spectra of a solution of 2 in 160 μL of CHCl₃ with different added aliquots of CH₃OH (10 μL to 160 μL) are shown in Fig. 7. These show that the maximum at 528 nm decreases in intensity upon addition of CH₃OH, and eventually disappears. At the same time a new maximum starts to appear when 60 μL of CH₃OH is added. This new maximum increases in intensity and moves to lower energies to reach a constant value of 630 nm when 160 μL has been added. This maximum is similar, although not identical, to that observed in the spectrum of 1 in a solution of CHCl₃ and 160 μL of CH₃OH (Fig. S5†), and indicates that compound 2 converts into a compound closely related to 1. Two isosbestic points at approximately 473 and 525 nm are also observed, indicating that an equilibrium between both species is established when small quantities of CH₃OH are added to an initial CHCl₃ solution (Fig. 7).

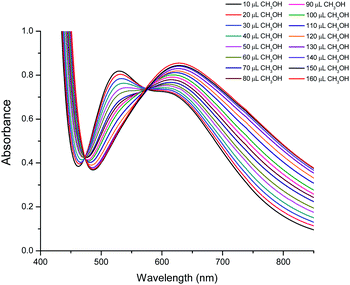Fig. 7 Visible spectra of compound 2 in CHCl₃ with different quantities of CH₃OH, showing the transformation of 2 into a complex similar to 1.

Finally, it should be mentioned that when 10 μL of H₂O was added to a solution of 1 in CHCl₃ plus 160 μL of CH₃OH, the colour of the solution changed from green to blueish-purple, indicating that 2 is formed. When larger amounts of water were added, the visible spectra of these solutions remained practically identical to that of a solution of 2 in these solvents (Fig. S6†), until the addition of 30 μL of H₂O; at that point the organic solution formed a suspension.

All these transformations have also been followed with ESI-mass spectroscopy. The addition of water to a green solution containing 1 leads to the formation of a purple solution whose ESI-mass spectrum is the same as a solution of 2 in CHCl₃ (Fig. 4), which clearly demonstrates the transformation of 1 into 2. Finally, the addition of an excess of CH₃OH to the purple solution of 2 results in a green solution that contains trimeric Cu^II units connected by 3,5-Me₂pz⁻ (L) ligands with a presumed structure very similar to that present in 1. The ESI-mass spectrum of this resulting green solution presents three main signals centred at m/z = 666.24, 602.42 and 571.23 Da (Fig. S8†), corresponding to Cu^II trimers with different hydrolysis degrees and different amounts of CH₃OH and CH₃O⁻ bridges: {[Cu₃(L)₃(CH₃OH)₄(CH₃O)₂]}⁺ (m/z = 666.24), {[Cu₃(L)₃(CH₃OH)₂(CH₃O)₂]}⁺ (m/z = 602.16) and {[Cu₃(L)₃(CH₃OH)₂(CH₃O)]+1e⁻}⁺ (m/z = 571.12). These spectra indicate that 1 transforms into 2, whereas 2 transforms into a trimeric Cu^II cluster very similar to each of the two trimeric species that form compound 1, although containing only CH₃O⁻ and CH₃OH bridges but no hydroxido or fluoride ones.

A possible explanation of the non-reversibility of the reaction is the lack of F⁻ anions in the medium that could act as μ₆-bridges. However, even in the presence of an excess of F⁻ (or BF₄⁻), the Cu₆ wheel does not convert back into 1.

Magnetic properties

These two Cu₆ complexes exhibit strong differences in their magnetic behaviour, which can be correlated with their molecular structures. Thus, for 1 a smooth decrease of the product of the molar magnetic susceptibility and temperature (χ_mT) is observed upon cooling, exhibiting a χ_mT value of ca. 1.9 emu K mol⁻¹ at 300 K, which decreases to reach an intermediate χ_mT value of 0.7 emu K mol⁻¹ at 10 K, and finally shows a sharp decrease at lower temperatures. In contrast, for 2 this decrease is much sharper, exhibiting a much lower χ_mT value even at room temperature (0.5 emu K mol⁻¹), which tends to be zero below 50 K (Fig. 8). Qualitatively this difference indicates that in these magnetic clusters the Cu^II spins are much more strongly antiferromagnetically coupled in 2 than in 1. It also indicates that for 2, the antiferromagnetic spin state S = 0 is the ground state, being well separated in energy from the first excited spin states, while for 1 the spin states S = 0 and S = 1 must be quasi-degenerate to explain the tendency of χ_mT to reach an intermediate value (ca. 0.7 emu K mol⁻¹) at low temperatures. In other words, in this last cluster the behaviour is dominated by two antiferromagnetic triangles, each having a ground spin state of S = 1/2. In the frame of this model, the sharp decrease in χ_mT observed in the low temperature limit should indicate the presence of weaker antiferromagnetic coupling between these two triangular units.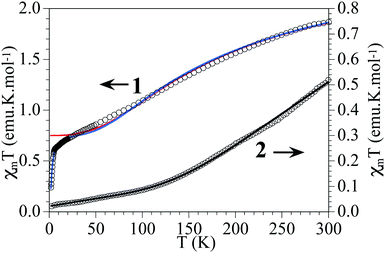

Fig. 8 Thermal variation of χ_mT per Cu₆ unit in 1 and 2. Solid lines are the best fit to the models (see text).

In order to give a quantitative explanation, these magnetic data have been fitted to spin models that take into account the structural features of these Cu₆ magnetic clusters using the package MAGPACK.^61,62 In these models, the Hamiltonian describing the exchange interaction between sites i and j is written as −JS_iS_j. Structurally, 1 possesses two isosceles triangles connected through three different bridges (two μ₂-3,5-Me₂pz⁻, one μ₂-OH⁻ and the central μ₆-F⁻, Fig. 1). This low symmetry leads to a complex exchange network formed by two exchange interactions inside the triangles and two different exchange interactions connecting the two triangles (Scheme 2). Taking into account the above remarks, we first extracted the exchange interactions within the triangles (J₁ and J₂) by fitting the magnetic data in the temperature range 30 K < T < 300 K to an isolated triangle (i.e., J₃ and J₄ have been fixed to 0). The resulting curve is plotted as a red line in Fig. 8 (extrapolated down to 2 K). In a second step, to fit the low temperature behaviour, we fixed J₁ and J₂ to these values, while allowing J₃ and J₄ to vary. As these two parameters have been found to be strongly correlated, we have performed DFT calculations to estimate J₃ (ESI†). The obtained value for J₃ (−22 cm⁻¹) agrees well with the calculated values for two similar pyrazolato bridges in two closely related Cu₆ trigonal prisms.^42,63 Note that this J₃ exchange pathway involves a pyrazolato Cu–N–N–Cu bridge, and that this bridge gives rise to antiferromagnetic coupling when the pyrazolate bridge connects two basal positions, but the magnitude strongly depends on the angle formed by the two basal planes. Thus, when the two basal planes are coplanar, the antiferromagnetic coupling is strong, but when this angle decreases, the magnetic coupling significantly decreases.^64–66 In 1 the two basal planes are far from being coplanar, forming an angle of 58.6° and, therefore it is expected to lead to a weak antiferromagnetic coupling, in agreement with the calculated J₃ value (−22 cm⁻¹). Fixing this value in the fitting procedure, the final set of exchange parameters is J₁ = −94 cm⁻¹; J₂ = −131 cm⁻¹, J₃ = −22 cm⁻¹ and J₄ = −4 cm⁻¹ (the fit with these values corresponds to the blue line in Fig. 8). As can be seen in Scheme 2, J₁ (−94 cm⁻¹) corresponds to a double bridge formed by a pyrazolate (–N–N–) and a methoxido bridge. This kind of bridge is well known to produce moderate to strong antiferromagnetic (AF) couplings (in the range ca. −160 to −550 cm⁻¹),¹⁶ with stronger AF coupling as the Cu–O–Cu angle increases. In 1 this angle is very small (102.1(2)°) compared with most of the reported examples (with angles in the range ca. 120–130° and, accordingly, this AF coupling is weaker than those observed in the other examples). The second coupling constant, J₂, (−131 cm⁻¹) corresponds to a double methoxido bridge (Scheme 2 and Fig. 1). The coupling through this kind of bridge is mainly determined by the Cu–O–Cu bond angle (α) and the angle formed by the C–O bond with the Cu₂O₂ central unit (τ) when this central unit is planar.^67,68 These correlations establish that when τ = 0, the coupling is AF for α angles above ca. 88.5°, but for τ = 40° the crossing point shifts to ca. 94.5°. In 1 the Cu–O–Cu angles are 90.8(2)° (Cu1–O31–Cu1′) and 96.5(3)° (Cu1–O33–Cu1′) and the corresponding τ angles are ca. 40° and ca. 10°, respectively (the lack of planarity of the central Cu₂O₂ unit precludes a precise calculation of τ). These values suggest that the Cu1–O31–Cu1′ exchange pathway should be weak and ferromagnetic, whereas the Cu1–O33–Cu1′ pathway should be stronger and AF, resulting in the observed moderate AF coupling for this double methoxido bridge. Note also that the lack of planarity in the basal planes of Cu1 and Cu1′ or Cu3 and Cu3′ (the dihedral angles between their average planes are 135.5° and 133.6°, respectively) is expected to further decrease the resulting magnetic exchange. Finally, J₄ (−4 cm⁻¹) corresponds to a hydroxido bridge with a Cu–O–Cu bond angle of 103.0(3)°. Note that previous magneto-structural correlations in this kind of bridge^67,68 indicate that, in general, this coupling should be strongly antiferromagnetic. The much weaker coupling observed for this bridge in 1 has to be attributed to the fact that the basal planes of the two Cu^II ions are almost orthogonal (the dihedral angle is 94.9°), resulting in an almost null orbital overlap.

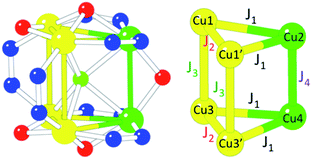Scheme 2 Magnetic exchange scheme and coupling constants used to fit the magnetic properties of the Cu₆ cluster in 1.

Compound 2 at room temperature shows a χ_mT value of ca. 0.5 emu K mol⁻¹ per Cu₆ ring, well below that expected for six independent Cu^II ions. When the temperature is decreased, χ_mT shows a continuous decrease to reach a value of ca. 0.02 emu K mol⁻¹ at 2 K (Fig. 8). This behaviour indicates that compound 2 shows a strong antiferromagnetic coupling inside the Cu₆ cluster with a small contribution from paramagnetic impurities. The isothermal magnetization at 2 K (Fig. S9†) confirms this behaviour. In compound 2 the model used to fit the magnetic properties is much more simple, since the six coupling constants inside the Cu₆ ring are identical, and therefore we only need to consider one exchange constant. The fitting was done by the same methodology used for 1.^61,62 With this simple model the magnetic properties of compound 2 can be very well reproduced over the whole temperature range, including a paramagnetic monomeric Cu^II impurity (ρ) with the following parameters: J₁ = −454 cm⁻¹ and ρ = 0.23%, with a fixed value of g = 2.1 (solid line in Fig. 8).

The value found for the coupling constant in compound 2 is close to those found in other similar Cu complexes with the same kind of double bridge and similar structural parameters.¹⁶

Furthermore, from previous magneto-structural correlations in Cu^II complexes with hydroxido bridges,^67,68 in compound 2 we can estimate a J value of ca. −450 cm⁻¹, in very good agreement with the experimental value.

Conclusions

In this work we present the structural and magnetic characterization of two new hexanuclear Cu^II complexes: [Cu₆(μ₆F)(μ₂OH)(μ₃OCH₃)₂(μ₂OCH₃)₂(3,5-Me₂pz)₆] (1) and [Cu₆(μ₂OH)₆(3,5-Me₂pz)₆]·CH₃CN·CHCl₃ (2), and a possible mechanism of the transformation of 1 into 2. Complex 1 exhibits a sandglass-like structure, and represents the first copper complex with a μ₆-F⁻ bridge and the first metallic complex with trigonal prismatic geometry around a μ₆-F atom. Compound 2 is formed from a neutral and soluble wheel-like Cu₆ complex, which packs in the solid state to give a tubular structure that contains CH₃CN and CHCl₃ molecules in the hexagonal channels formed by the eclipsed packing of the Cu₆ rings. These solvent molecules can be removed and partially exchanged with CO₂ since the removal of the solvent molecules does not alter the crystal structure of 2. Visible and mass spectra confirm the conversion of 1 into 2 by simply changing the solvent conditions. The stability of the Cu₆ wheel in solution opens up the possibility of preparing thin films of this entity with a mono-disperse porous tubular structure by using different solution-based techniques. These two compounds exhibit very different magnetic behaviours, in agreement with their structural features. Thus, the spin structure of 1 shows a ground state formed of quasi-degenerate S = 0 and S = 1 spin levels, as it is dominated by a spin frustration effect within the two antiferromagnetic triangles. In turn, 2 shows an antiferromagnetic ground spin state S = 0, which is well separated in energy from the first excited S = 1 spin state (by more than 62 cm⁻¹), as a consequence of the very strong antiferromagnetic Cu–Cu interactions and of the hexagonal topology of the exchange network.

Acknowledgements

We acknowledge the European Union (Advanced ERC grant SPINMOL), the Spanish MINECO (projects Consolider-Ingenio in Molecular Nanoscience, CTQ2011-26507 and MAT2011-22785) and the Generalidad Valenciana (Prometeo and ISIC-Nano Programs) for financial support. The work in Chile has been supported by the Financiamiento Basal Program FB0807. WCM thanks CONICYT for Doctoral Scholarships (21080445 and AT24100006), and Becas Chile. The authors also thank Powered@NLHPC. This research was partially supported by the Supercomputing Infrastructure of the National Laboratory for High Performance Computing, NLHPC (ECM-02), Centre for Mathematical Modeling (CMM), Universidad de Chile. Thanks are given to the Spanish CSIC for the award of a license for the use of the Cambridge Crystallographic Data Base (CSD). We thank Dr J. M. Clemente for helpful discussions in the fitting of the magnetic data.

References

1. M. Fu, I. Issac, D. Fenske and O. Fuhr, Angew. Chem., Int. Ed., 2010, 49, 6899–6903.
2. B. Murphy and B. Hathaway, Coord. Chem. Rev., 2003, 243, 237–262.
3. A. M. Kirillov, M. V. Kirillova and A. J. L. Pombeiro, Coord. Chem. Rev., 2012, 256, 2741–2759,  DOI:10.1016/j.ccr.2012.07.022.
4. E. I. Solomon, U. M. Sundaram and T. E. Machonkin, Chem. Rev., 1996, 96, 2563–2606.
5. D. Desbouis, I. P. Troitsky, M. J. Belousoff, L. Spiccia and B. Graham, Coord. Chem. Rev., 2012, 256, 897–937.
6. I. Blain, P. Slama, M. Giorgi, T. Tron and M. Réglier, Rev. Mol. Biotechnol., 2002, 90, 95–112.
7. M. C. Feiters, Comments Inorg. Chem., 1990, 11, 131–174.
8. V. Wing-Wah Yam, K. Kam-Wing Lo, W. Kit-Mai Fung and C. Wang, Coord. Chem. Rev., 1998, 171, 17–41.
9. G. Givaja, P. Amo-Ochoa, C. J. Gómez-García and F. Zamora, Chem. Soc. Rev., 2012, 41, 115–147.
10. O. Kahn, Molecular Magnetism, VCH Publishers, USA, 1993.
11. E. Coronado, M. Giménez-Marqués, G. Mínguez Espallargas and L. Brammer, Nat. Commun., 2012, 3, 828.
12. E. Coronado and G. Minguez Espallargas, Chem. Soc. Rev., 2013, 42, 1525–1539.
13. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122.
14. A. Spek, J. Appl. Crystallogr., 2003, 36, 7–13.
15. G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532–536.
16. Y. Elerman, H. Kara and A. Elmali, Z. Naturforsch., A: Phys. Sci., 2003, 58, 363–372.
17. G. A. Ardizzoia, M. A. Angaroni, G. La Monica, N. Masciocchi and M. Moret, J. Chem. Soc., Dalton Trans., 1990, 2277–2281.
18. T. O. Denisova, E. V. Amel'chenkova, I. V. Pruss, Z. V. Dobrokhotova, O. P. Fialkovskii and S. E. Nefedov, Russ. J. Inorg. Chem., 2006, 51, 1020–1064.
19. G. Mezei and R. G. Raptis, Inorg. Chim. Acta, 2004, 357, 3279–3288.
20. Y. Elerman and A. Elmali, Z. Naturforsch., B: J. Chem. Sci., 2001, 56, 970–974.
21. Y. Elerman, H. Kara and A. Elmali, Z. Naturforsch., B: J. Chem. Sci., 2001, 56, 1129–1137.
22. H. Kara, Y. Elerman and K. Prout, Z. Naturforsch., B: J. Chem. Sci., 2001, 56, 719–727.
23. H. Kara, Y. Elerman and K. Prout, Z. Naturforsch., B: J. Chem. Sci., 2000, 55, 796–802.
24. V. Chandrasekhar, L. Nagarajan, R. Clerac, S. Ghosh, T. Senapati and S. Verma, Inorg. Chem., 2008, 47, 5347–5354.
25. V. Chandrasekhar and S. Kingsley, Angew. Chem., Int. Ed., 2000, 39, 2320–2322.
26. J. He, Y. Yin, T. Wu, D. Li and X. Huang, Chem. Commun., 2006, 2845–2847.
27. M. K. Ehlert, S. J. Rettig, A. Storr, R. C. Thompson and J. Trotter, Can. J. Chem., 1990, 68, 1444–1449.
28. G. A. Ardizzoia, M. A. Angaroni, G. La Monica, F. Cariati, S. Cenini, M. Moret and N. Masciocchi, Inorg. Chem., 1991, 30, 4347–4353.
29. A. W. Addison, T. N. Rao, J. Reedijk, J. van Rijn and G. C. Verschoor, J. Chem. Soc., Dalton Trans., 1984, 1349–1356.
30. J. A. Carroll, R. E. Cobbledick, F. W. B. Einstein, N. Farrell, D. Sutton and P. L. Vogel, Inorg. Chem., 1977, 16, 2462–2469.
31. M. Hidai, T. Kodama, M. Sato, M. Harakawa and Y. Uchida, Inorg. Chem., 1976, 15, 2694–2697.
32. P. B. Hitchcock, M. F. Lappert and R. G. Taylor, J. Chem. Soc., Chem. Commun., 1984, 1082–1084.
33. F. J. Rietmeijer, R. A. G. De Graaff and J. Reedijk, Inorg. Chem., 1984, 23, 151–156.
34. R. H. Crabtree, G. G. Hlatky and E. M. Holt, J. Am. Chem. Soc., 1983, 105, 7302–7306.
35. S. Herold and S. J. Lippard, Inorg. Chem., 1997, 36, 50–58.
36. Y. Zang, H. G. Jang, Y. Chiou, M. P. Hendrich and L. Que, Jr, Inorg. Chim. Acta, 1993, 213, 41–48.
37. V. Terruzzi, U. Comin, F. De Grazia, G. L. Toti, A. Zambelli, S. Beretta and G. Minoli, Gastrointest. Endosc., 2000, 51, 23–27.
38. Q. Wang, G. Guo and T. C. W. Mak, Polyhedron, 2003, 22, 217–223.
39. Q. Wang and T. C. W. Mak, Chem. Commun., 2000, 1435–1436.
40. E. V. Lider, E. V. Peresypkina, A. I. Smolentsev, V. N. Elokhina, T. I. Yaroshenko, A. V. Virovets, V. N. Ikorskii and L. G. Lavrenova, Polyhedron, 2007, 26, 1612–1618.
41. E. V. Govor, A. B. Lysenko, D. Quinonero, E. B. Rusanov, A. N. Chernega, J. Moellmer, R. Staudt, H. Krautscheid, A. Frontera and K. V. Domasevitch, Chem. Commun., 2011, 47, 1764–1766.
42. A. Kamiyama, T. Kajiwara and T. Ito, Chem. Lett., 2002, 980–981.
43. D. G. Chen, H. H. Zhang and X. F. Yu, Chin. J. Struct. Chem., 2003, 22, 591–594.
44. C. D. Scattergood, P. G. Bonney, J. M. Slater, C. D. Garner and W. Clegg, J. Chem. Soc., Chem. Commun., 1987, 1749–1750.
45. F. Zheng, H. H. Zhang, R. P. Zhou, Y. S. Wu, X. F. Yu and J. S. Huang, Chin. J. Struct. Chem., 1997, 16, 392.
46. R. E. Marsh, Acta Crystallogr., Sect. B: Struct. Sci., 1997, 53, 317–322.
47. P. Lin, X. Wu, L. Chen, L. Wu and W. Du, Polyhedron, 2000, 19, 2189–2193.
48. Z. Wei, H. Li, M. Cheng, X. Tang, Y. Chen, Y. Zhang and J. Lang, Inorg. Chem., 2009, 48, 2808–2817.
49. E. Jalilian and S. Lidin, CrystEngComm, 2011, 13, 5730–5736.
50. B. Li, J. Zhao, S. Zheng and G. Yang, Inorg. Chem., 2009, 48, 8294–8303.
51. R. D. Kohn, Z. Pan, M. F. Mahon and G. Kociok-Kohn, Chem. Commun., 2003, 1272–1273.
52. C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5525–5534.
53. G. Mezei, C. M. Zaleski and V. L. Pecoraro, Chem. Rev., 2007, 107, 4933–5003.
54. J. J. Henkelis, L. F. Jones, M. P. de Miranda, C. A. Kilner and M. A. Halcrow, Inorg. Chem., 2010, 49, 11127–11132.
55. A. A. Mohamed, A. Burini, R. Galassi, D. Paglialunga, J. Galán-Mascarós, K. R. Dunbar and J. P. Fackler, Inorg. Chem., 2007, 46, 2348–2349.
56. E. V. Govor, A. B. Lysenko, D. Quinonero, E. B. Rusanov, A. N. Chernega, J. Moellmer, R. Staudt, H. Krautscheid, A. Frontera and K. V. Domasevitch, Chem. Commun., 2011, 47, 1764–1766.
57. A. A. Mohamed, S. Ricci, A. Burini, R. Galassi, C. Santini, G. M. Chiarella, D. Y. Melgarejo and J. P. Fackler, Inorg. Chem., 2011, 50, 1014–1020.
58. G. Mezei, P. Baran and R. G. Raptis, Angew. Chem., Int. Ed., 2004, 43, 574–577.
59. J. Liu, J. Zhuang, X. You and X. Huang, Chem. Lett., 1999, 28, 651–652.
60. G. Mezei, R. G. Raptis and J. Telser, Inorg. Chem., 2006, 45, 8841–8843.
61. J. J. Borrás-Almenar, J. M. Clemente-Juan, E. Coronado and B. S. Tsukerblat, Inorg. Chem., 1999, 38, 6081–6088.
62. J. J. Borrás-Almenar, J. M. Clemente-Juan, E. Coronado and B. S. Tsukerblat, J. Comput. Chem., 2001, 22, 985–991.
63. E. M. Zueva, M. M. Petrova, R. Herchel, Z. Travnicek, R. G. Raptis, L. Mathivathanan and J. E. McGrady, Dalton Trans., 2009, 5924–5932.
64. S. O. Malinkin, Y. S. Moroz, L. V. Penkova, V. V. Bon, E. Gumienna-Kontecka, V. A. Pavlenko, V. I. Pekhnyo, F. Meyer and I. O. Fritsky, Polyhedron, 2012, 37, 77–84.
65. M. F. Iskander, T. E. Khalil, W. Haase, R. Werner, I. Svoboda and H. Fuess, Polyhedron, 2001, 20, 2787–2798.
66. V. Mishra, F. Lloret and R. Mukherjee, Eur. J. Inorg. Chem., 2007, 2161–2170.
67. E. Ruiz, P. Alemany, S. Alvarez and J. Cano, Inorg. Chem., 1997, 36, 3683–3688.
68. E. Ruiz, P. Alemany, S. Alvarez and J. Cano, J. Am. Chem. Soc., 1997, 119, 1297–1303.

---

Footnote

† Electronic supplementary information (ESI) available: CCDC 927862–927865. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c3sc52628c

---