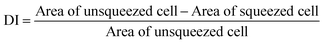Squeezing red blood cells on an optical waveguide to monitor cell deformability during blood storage†
Balpreet Singh
Ahluwalia
*a,
Peter
McCourt
b,
Ana
Oteiza
b,
James S.
Wilkinson
c,
Thomas R.
Huser
d and
Olav Gaute
Hellesø
a
aDepartment of Physics and Technology, University of Tromsø, N-9037 Tromsø, Norway. E-mail: balpreet.singh.ahluwalia@uit.no
bDepartment of Medical Biology, University of Tromsø, N-9037 Tromsø, Norway
cOptoelectronics Research Center, University of Southampton, SO17 1BJ, UK
dDepartment of Physics, University of Bielefeld, Bielefeld, Germany
First published on 23rd October 2014
Abstract
Red blood cells squeeze through micro-capillaries as part of blood circulation in the body. The deformability of red blood cells is thus critical for blood circulation. In this work, we report a method to optically squeeze red blood cells using the evanescent field present on top of a planar waveguide chip. The optical forces from a narrow waveguide are used to squeeze red blood cells to a size comparable to the waveguide width. Optical forces and pressure distributions on the cells are numerically computed to explain the squeezing process. The proposed technique is used to quantify the loss of blood deformability that occurs during blood storage lesion. Squeezing red blood cells using waveguides is a sensitive technique and works simultaneously on several cells, making the method suitable for monitoring stored blood.
Introduction
The flexible membranes and a large ratio of surface area to volume make it easy for red blood cells (RBCs) to change shape. RBCs typically have a biconcave profile, like a disk-shaped donut, with a diameter of 7–8 μm, a thickness of 0.8–1 μm at the center and 2–2.5 μm at the periphery. During their life span of 120 days, RBCs have to squeeze through tiny micro-capillaries in the blood circulatory system (<3 μm diameter) and through sieves in the spleen (1 μm openings).1,2 Recent clinical studies link a loss in blood deformability with several diseases such as diabetes, obesity, sickle cell anaemia, cardiovascular diseases, malaria, hypertension and the side-effects of heavy smoking.3,4The loss of blood cell deformability is also associated with blood storage lesion.5,6 Blood storage lesion refers to the collective bio-chemical, functional and structural changes occurring in the blood during storage. The functional and biochemical changes include decreased 2,3-diphosphoglycerate levels, ATP depletion, reduction in the concentrations of nitric oxide and adenosine triphosphate. The structural changes include a progressive loss of deformability, increased adhesiveness and aggregability.7 The health of stored blood has been debated because clinical studies show adverse effects associated with the transfusion of older stored blood (storage time > 2 weeks),8–10 while blood is typically stored for up to six weeks in blood banks. Clinical studies have recently reported increased post-surgical complications such as multiple organ failure in patients transfused with old stored blood as compared to fresh blood (storage time < 2 weeks).8 Some chemical changes in stored blood can occur within the first few hours of storage, e.g., a decrease in pH and an increase in potassium and lactate. Morphological changes are significantly slower to observe and take weeks to develop. The storage of blood is essential for blood transfusion during modern medical surgery. It is thus important to develop sensitive diagnostic tools to identify minute changes in the biochemical and structural properties of stored blood, affecting its ability to hold and transport oxygen, and to deform during circulation in micro-capillaries.
In vitro, the elasticity and deformability of RBCs are studied using physical pressure (non-optical techniques) from micropipette aspiration, micro-pores and micro-fabricated channels.11–14 Non-contact methods, such as optical tweezers are also used to trap red blood cells.15–22 Optical tweezers typically characterize a single cell at a time and use a strongly focused laser beam. The intensity gradient generated by the focused beam traps a cell in the vicinity of the focus. By using multiple beams or by trapping beads attached to a cell, the red blood cell can be stretched to monitor its elasticity.17,18 The force imparted on the blood cells for deformation studies using optical tweezers is typically 50–400 pN.17,18
The evanescent field of an optical waveguide can trap and propel red blood cells along the waveguide.23–25 The cells are trapped on the surface of the waveguide and several cells can be trapped simultaneously at various positions along the waveguide. The optical force imparted by the evanescent field in waveguide trapping is typically an order of magnitude lower than the optical forces used in optical tweezers (<10 pN). In this work, we demonstrate that the intensity gradient at the edge of narrow waveguides can be used to deform and squeeze cells. This technique is demonstrated to be a sensitive tool for detecting the loss of blood deformability during blood storage lesion. The novel phenomenon of waveguide cell squeezing is explained using comprehensive numerical simulations on a computer cluster.
Experimental methods
Waveguides
Optical waveguides were made of tantalum pentoxide (Ta2O5) on oxidised silicon substrates. The refractive index of Ta2O5 is 2.15 (at 1070 nm wavelength), which gives a high refractive index contrast (Δn) of 0.7 relative to the silica-cladding underneath (n = 1.45). The thickness of the optical waveguides was around 180 nm. The relatively high refractive index combined with thin and narrow waveguide dimensions provide high surface intensity in the evanescent field. Straight and tapered waveguides were fabricated. Further information about waveguide fabrications is provided in the ESI.†Experimental apparatus
A 5 W Ytterbium fiber laser at 1070 nm wavelength was used for the experiment, with power incident on the waveguide end adjusted down to a maximum of 700 mW. Laser light was coupled into the waveguides using a long working distance infrared-coated objective lens (Nachet 100×, N.A. 0.8). The coupling objective lens was held on a piezoelectric translation stage to optimize the coupling efficiency. The cells were kept in thin chambers made of polydimethylsiloxane (PDMS) and covered with a coverslip. The cells were observed with an upright microscope equipped with a long working distance objective lens (Olympus 50× N.A. 0.5 and 20× N.A. 0.4) and a CCD camera (Lumenera Infinity2). The experimental set-up is shown in the ESI.†Cell preparation
Fresh blood samples were collected in standard blood bags as used in blood banks. The blood bag contains a saline solution including adenine, glucose, and mannitol and is commonly referred to as SAGMAN. To isolate red blood cells, the blood sample was mixed with phosphate buffered saline (PBS) and centrifuged at 600 g for 10 minutes. This accumulates RBC pellets at the bottom of the test tube. A supernatant solution containing white blood cells and plasma was carefully removed from the top. This process was repeated three times in PBS to remove most of the platelets and white blood cells. The red blood cells were then stored in an SAGMAN medium at 4 °C. The sample was divided into several tubes, which were opened only on specified days for monitoring deformability. For waveguide trapping, the blood sample was diluted and submerged into an isotonic sucrose medium (0.25 M)24 and the experiment was completed within 3 hours. The replacement of phosphate buffer solution (PBS) with an isotonic sucrose medium avoided cell sticking to the waveguide surface.Squeezing red blood cells with optical waveguides
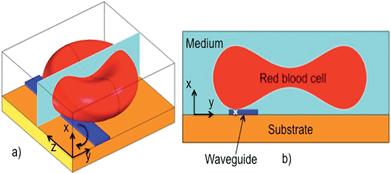
When a cell is positioned in the vicinity of an optical waveguide as depicted in Fig. 1, the cell interacts with the evanescent field of the waveguide. The optical forces experienced by the cell can be classified as a scattering force along the waveguide (Fz, along z in Fig. 1a), vertical gradient force (Fx in Fig. 1a and b), and lateral gradient force (Fy in Fig. 1b). For the axes defined in Fig. 1, Fx is negative, Fz is positive and the sign of Fy depends on the position of the cell along the y-axis. As the refractive index of the cell is close to that of the surrounding aqueous medium, the scattering force Fz is weak and the forward push is thus small. The vertical gradient force Fx attracts the cell down towards the waveguide, while the lateral gradient force Fy holds the cell laterally in position on top of the waveguide. The extent of the evanescent field is typically 150 nm, which is also the extent of the vertical gradient force. The extent of the lateral gradient force is dictated by the width of the waveguide. The additional experimental details are described in the ESI Fig. 1 and 2.†The lateral gradient force of a narrow waveguide (1.3 μm wide) is used to deform a red blood cell as shown in Fig. 2 (Movie 1) and ESI Fig. 3.† When the laser is switched on, the rim (i.e. the thickest part) of the cell is attracted to the waveguide and is held in place there (Fig. 2a). Subsequently, the part of the cell not on the waveguide is pulled in across the waveguide (Fig. 2b–e). The result (Fig. 2e) is a cell squeezed down to a significantly smaller width (from 7 μm to 4.8 μm). The rim (bulge) of the cell on the waveguide becomes darker, which could be due to the increased thickness and accumulation of hemoglobin in the part that interacts with the evanescent field of the waveguide. As the volume of the cell remains constant, a reduction in the observed area must be accompanied by an expansion upwards, either by rotation or by the cell becoming thicker. The central part of the cell (donut) remains comparatively transparent (thin) during the initial phase of cell squeezing, as noticed in Fig. 2a–e and ESI Fig. 3b–e.† As the central part of the cell is visible and the entire cell remains in focus until the laser is switched off, the cell must remain in the yz-plane. Note that the part of the rim that is on the waveguide is straight (see ESI Fig. 3 and 4 and Movie 1†). This straightening effect is also predicted by the simulation results discussed below. Fig. 2e also shows that cells can squeeze differently even if they are next to each other. When the laser is switched off, the cell regains its original donut shape (Fig. 2f).
 | ||
| Fig. 2 Time lapsed images of RBCs trapped and squeezed on a 1.3 μm wide and 180 nm thick waveguide. The laser beam was on in images a–f, and switched off from g–h. See also associated media file (associated Movie 1†). | ||
Fig. 3 shows four cases of cell squeezing. A cell trapped on an 8 μm wide waveguide (Fig. 3a) shows no structural deformation (see also ESI Movie 2†). The cell has a donut-shape with a transparent center. The strong dependence of the optical force (ESI Fig. 5†) and the pressure (ESI Fig. 6†) on the waveguide width explains why squeezing is not observed on wide waveguides. For a narrower waveguide, most of the cells are squeezed with the center faintly visible and the entire cell in focus, suggesting that the cell is placed horizontally. The last image, Fig. 3d, shows a highly compressed cell where the center of the cell is not visible. Thus, the entire rim of the cell must either be squeezed tightly together onto the waveguide, or a part of the rim or the complete cell must be rotated upwards. In our experiments (>100 cells) only 6 cells were squeezed such that we could not see the central donut (similar to Fig. 3d). For the large majority of cells, an upward rotation around the edge can be ruled out. In a conventional laser beam trap the RBC is flipped (rotated) on its edge, and the flipping time is typically 300–500 ms.15 While, in waveguide deformation cell squeezing takes 2–40 seconds. Fig. 3 suggests that cells in close proximity could squeeze differently depending on the cell shape, size, age and deformability index (see section below).
 | ||
| Fig. 3 Squeezing of red blood cells on waveguides with different widths of (a) 8 μm, (b) 2 μm, and (c and d) 1.3 μm. | ||
Waveguide cell squeezing is a slow phenomenon, which can take 2–40 seconds depending on the waveguide width, guided power and cell age. The reverse process of a cell regaining its shape after the laser is switched off, is usually faster than the squeezing phenomenon. The intermediate steps of cell deformation vary from cell to cell and are also dependent on the waveguide width. As it is propelled along a waveguide, a cell can readjust and change its deformed shape (see ESI Movie 3†).
To mimic the sudden change in the stress level acting on RBCs encountering micro-capillaries during blood circulation, a tapered waveguide was employed as schematically shown in Fig. 4. At the wider end of the taper (8 μm wide), cells are propelled along the waveguide without any deformation as shown in Fig. 4a and b. At the narrow end (1.3 μm wide), cells experience large lateral optical forces and deform to a narrower shape (Fig. 4d). The tapered structure was used to measure cell deformation as a function of storage dates, as discussed below.
 | ||
| Fig. 4 Time lapsed images of RBC propelling on a waveguide that tapers down from an original width of 8 μm to 1.3 μm. Associated media file (Movie 2†). | ||
Numerical simulation
Optical forces have been used to stretch red blood cells,17,18 while the observations of squeezing on waveguides is a new phenomenon. Thus, numerical simulations of optical forces and pressure are important to explain the squeezing process. The force density f on a non-magnetic, isotropic dielectric body in an electromagnetic field is:26,27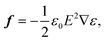 | (1) |
The finite element method was used to compute the optical forces and the optical pressure that a cell experiences during waveguide trapping. A biconcave shape with a diameter of 7 μm was used for the red blood cell. The waveguide width and thickness were 1.3 μm and 180 nm, respectively. The guided power was 15 mW, corresponding to the experimental values. Further details can be found in the ESI.†
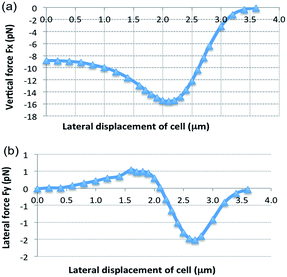
Fig. 5 shows the simulated optical forces. The vertical force Fx is negative, pulling the cell down to the waveguide surface as long as the cell is in contact with the evanescent field. The lateral force Fy is zero for zero displacement as expected for a symmetric model (Fig. 5b). As the cell is moved away from the center of the waveguide, the lateral force increases (Fy > 0 for y > 0). A cell centered on the waveguide is thus not stable as a small displacement will push the cell away from the center (no restoring force). On the other hand, stable (lateral) trapping with Fy = 0 is found for a displacement of 2.1 μm (the center of the cell at y = 2.1 μm). Around this position, Fy > 0 for y < 2.1 μm, pushing the cell towards the stable position, and Fy < 0 for y > 2.1 μm, pulling it back to the stable position. According to the simulation, stable trapping thus initially occurs when the cell is displaced from the center of the waveguide. This is consistent with the experimental result shown in Fig. 2 and ESI Fig. 3 and the associated movie files.†
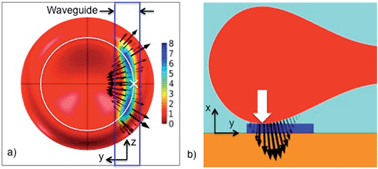
The optical pressure on the cell in the stable position is shown in Fig. 6. The black arrows give the direction of the force density (i.e. pressure multiplied with surface normal). The central point of contact with the waveguide is shown with a white cross in Fig. 6a and a white arrow in Fig. 6b. The sum of the force densities taken along the y-axis is zero, as Fy = 0 for the stable position (see Fig. 6a). However, the force densities point towards the center of the cell in the vicinity of the white cross, while further away from the white cross, the force densities point away from the center of the cell. As the cell is an elastic body, the net effect of the force densities is thus to straighten the part of the cell that is overlapping with the evanescent field and make it parallel to the waveguide. This straightening effect was also observed experimentally in Fig. 2 and ESI Fig. 3 and Movie 1.† When this part of the cell becomes straight, mechanical forces will pull the rest of the cell towards the waveguide in the yz-plane. The cell is thus squeezed onto the waveguide. It is interesting that the evanescent field, which stretches about 150 nm from the surface, induces a localized optical pressure sufficient to squeeze the entire red blood cell (7 μm wide and 2 μm thick), see ESI Fig. 7.† The elastic membrane of the cell plays a crucial role in spreading the localized optical pressure over the entire cell.17
Fig. 7 shows the pressure distribution on the cell as it is moved relative to the waveguide (along the y-axis). Fig. 6a corresponds to Fig. 7c. For a zero offset and thus a symmetric model, the force is entirely along the waveguide, pushing the cell forward (see Fz in the ESI Fig. 5†). As the offset increases, Fig. 7b and c, the forces act to straighten the part of the cell that is on the waveguide. For large offsets, Fig. 7d, the forces mainly act to pull the cell back onto the waveguide. More simulation results are given and discussed in the ESI Fig. 5–9.†
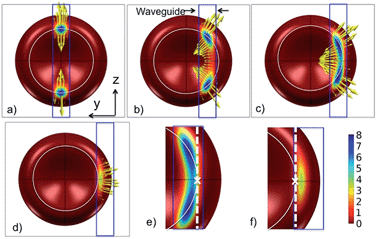 | ||
| Fig. 7 Pressure distribution and the direction of force density as the cell is moved sideways relative to the waveguide (along the y axis). The waveguide is 1.3 μm wide. The cell is seen from below through the waveguide and the substrate. The offsets are: (a) Zero, (b) 1.6 μm, (c) 2.1 μm (stable position) and (d) 3.0 μm. (e) and (f) are zoomed in on the contact areas of (c) and (d), respectively. A white circle shows the bottom of the cell, the white cross shows the central point of contact (similar to the arrow shown in Fig. 6b) and the dotted white line is the axis of rotation for which the torque is calculated in Fig. 8. | ||
The largest force component is along the x-axis (pointing downwards), as shown in Fig. 5 and 6b. The cell is thus pressed down and the bottom of the cell will become flat. The forces acting on the cell also give rise to a torque. The simulation shows that a cell experiences a positive torque (see the direction in Fig. 1a) at a stable trapping location (see ESI Fig. 9†). Thus, the simulation predicts that the cell will be pressed down towards the substrate due to the positive torque and therefore ruling out flipping or rotation of the cell.
Waveguide cell squeezing as a storage lesion marker
To demonstrate the capabilities of the proposed technique, we monitored the deformability of fresh and stored RBCs. A healthy RBC under no stress has, as noted previously, a biconcave shape. When an RBC is trapped on a narrow waveguide, the cell is squeezed and its surface area is reduced. By measuring the surface area of cells before and during squeezing, the deformability of blood cells can be obtained (see ESI†). We define a deformability index (DI) as:The DI of RBCs was measured on fresh and stored cells (up to thirty days). The measurement was done on cells (>100) from blood samples from different donors. The experiments were performed on similar waveguides and the DI was measured on the narrow section of a tapered waveguide (1.3 μm wide). The input power to the waveguide was kept constant at 500 mW, giving a guided power of approximately 15 mW. The deformability index shifts when the input power is changed, as highlighted in ESI Fig. 10.† The experimental procedures are further described in the methods section.
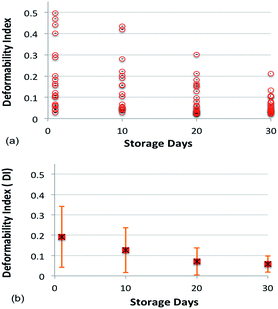
Fig. 8a and b show the value and average, respectively, of DI for blood cells with respect to the number of days stored.
The average DI of the cell population on Day 1 was 0.19 and it progressively decreased with the number of days stored. After ten and thirty days of blood storage, the average DI of the cell population decreased to 0.12 and 0.05, respectively. This corresponds to a reduction of RBC deformability by 37% and 74% as compared to Day 1. The large standard deviation of the DI reflects a large spread in cell deformability for each day, with some cells showing low deformability throughout the study. The result shown in Fig. 8 uses over 100 cells from different healthy donors and the cells were stored in the SAGMAN medium.
Discussion and conclusions
Squeezing of red blood cells on an optical waveguide is a novel and sensitive method to measure the loss of blood deformability. The technique to some extent bio-mimics the squeezing of blood cells inside micro-capillaries during blood circulation. The proposed method provides a new alternative for exploring the deformation and stress handling capabilities of RBCs. Using this technique, we found a fast and significant loss of blood deformability due to storage lesion. The average deformability index decreased from 0.19 on the first day to 0.12 after 10 days, and further to 0.05 after 30 days of storage. We found a large variation in deformability on all days, which may partly explain the variation in the published results.28–32 Using a rotational cell analyser, a larger loss of deformability was found for low pressure (15% at 3 Pa) than for high pressure (5% at 30 Pa).29 The maximum pressure applied with our method was intermediate, on the order of 8 Pa, which may explain the large spread in the deformability measured. Most of this pressure is directed downwards, while only some 10% is used for squeezing (see Fxvs. Fy in Fig. 5). By increasing the optical power, the optical pressure increases and gives a larger deformation of the cells (see ESI Fig. 10†). However, to detect even minute losses of deformability, an optimum pressure that gives a measureable deformation throughout the storage period should be applied.In waveguide trapping a blood cell is deformed with an optical force that is an order of magnitude smaller than what is conventionally used by laser tweezers.17 This can be explained by the localized optical pressure generated by the evanescent field.33 The evanescent field is dominant up to 150 nm from the surface, thus the optical forces generated are confined to a small surface area of the cell that is interacting with the evanescent field (see ESI Fig. 7b†). As the area is small the pressure thus becomes relatively large. With a guided power of 15 mW inside the waveguide, optical forces and pressures of around 10 pN and 10 Pa are generated, respectively. An optical pressure of 10 Pa has been found sufficient to deform RBCs with other methods.29,34
We used extensive numerical simulations to compute the distribution of optical pressure in three dimensions in order to explain the squeezing process. The simulations predict the off-center trapping of biconcave blood cells, followed by a straightening process, in correspondence with the experimental observations. The simulations show that a positive torque is experienced by the cell (i.e. the cell is pressed onto the substrate) at the stable trapping location. Our simulations are on a perfect, undeformed single RBC. As squeezing proceeds, the distribution of forces and the torque will change. Moreover, if cells are touching each other it might affect the force distribution. Experimentally, the center of the cell was in most cases visible with the entire rim in focus. The majority of cells (low DI < 0.3) are thus believed to be in the plane of observation, i.e. horizontal. For a few cells (6%) on days 1 and 10 (4 and 2 cells, respectively, Fig. 8a), the center was not visible (see Fig. 3d) and such cells had a large DI (>0.4). It is possible that these cells have rotated around the z-axis, although the cell deformation process starts in the same way as for the other cases. Rotation would change the observed area and thus the value of DI. However, as rotation is not confirmed and the number of cells concerned is small, we have included all the experimental results in Fig. 8.
The experiments in this work were performed at room temperature. A decrease in temperature increases the rigidity of the RBC membrane,35 the viscosity of the cell membrane and the viscosity of the internal cytosol of blood cells. The accumulative effect of a decrease in the temperature is cells with lower deformability. We thus anticipate that higher values of the deformability index will be obtained if cell squeezing experiments are performed at 37 °C (in vivo temperature).
The loss of blood deformability during storage is due to the cumulative alterations of structural and biochemical changes that stored blood undergoes. The oxidation in the stored blood causes an alteration in the lipid molecules and proteins present in the cell membrane.31 This consequently alters the linkage between the membrane and the cytoskeleton influencing the deformability of blood cells.36 The depletion of adenosine triphosphate and 2,3-diphosphoglycerate during blood storage is also associated with the loss of blood deformability.29 The storage also modifies the viscoelasticity properties of the cell membrane and the internal cytosol. Stored blood undergoes structural changes and a loss in the surface area to volume ratio that will affect the shape and the curvature of the blood cell. A change in the curvature, size and shape of a blood cell will influence the lateral stable trapping location of a cell (see Fig. 5) and consequently will influence the squeezing behaviour. Moreover, any change in the refractive index of an RBC will also influence the result in waveguide deformation. The scope of the manuscript was to study the cumulative effect of blood storage on the loss of deformability.
The loss of blood deformability during storage may have important consequences on blood transfusion. A few hours after a blood transfusion, the patient's body removes a relatively large percentage of transfused blood (up to 30%).32 A possible cause of removal is the loss of blood cell deformability and the subsequent removal of non-elastic blood cells by the spleen.1,2 It was also reported that the major change in RBC deformability might occur during the processing of the blood by a blood bank.31 The on-going debate on the health of stored blood and the adverse effects of blood transfusion5–10,28–32 might lead to a further scrutiny of the mechanical and structural properties of stored blood before transfusion. This can be accomplished by the proposed technique of waveguide cell squeezing. As the distribution in deformability is large, a large number of cells (>100) must be characterized to yield statistically viable data. To determine the loss of blood deformability, the area of a cell before and after waveguide trapping should be determined. Each experiment (deformation and relaxation) takes around 20–40 seconds and the throughput depends on the number of cells examined during each experiment. As cells can be deformed along the entire length of several straight and narrow waveguides in parallel, the ultimate limiting factor is the field-of-view and the optical resolution of the objective lens. In this work, a tapered waveguide was used, limiting the length where cells could be deformed, and a maximum of 10 cells were observed simultaneously, giving a throughput of 0.25 cells per s. The measurements were done with a 50× objective with a 300 μm field-of-view, which gave good resolution for the measurements. As the diameter of the cells is around 7 μm, it can be foreseen to have 10 waveguides in parallel and observe 20 cells along each waveguide, thus observing 200 cells simultaneously. With an observation period of 20 seconds, the throughput of a future commercial system can be estimated to 10 cells per s. By using an objective with a lower magnification and larger field-of-view, e.g. 20× as in the ESI Movie 5,† a larger number of cells can be analyzed simultaneously and the throughput can thus be significantly increased.
The challenges associated with waveguide trapping are cell adhesion, insertion loss, and non-specificity. In the present work, cell adhesion is avoided by immersing cells in an isotonic sucrose medium.24 Functionalization of a waveguide surface such as with PEG–PLL (poly(ethylene glycol)–poly(L-lysine)) can be explored to avoid cell adhesion. In waveguide trapping, only a fraction of the input power is present in the evanescent field that is used for trapping application. The advantages of this technique are that it can be automated and integrated with microfluidics and with other measurement techniques to characterize red blood cells, such as the measurement of refractive index37 and absorption spectroscopy.38
Acknowledgements
The authors would like to thank Ananth Z. Subramanian for his contribution on waveguide fabrication, Wenche Bakkelund for cell preparation, Pål Løvhaugen, Per Jakobsen and Iver Brevik for their advice on simulations. BSA and OGH acknowledge funding from The Research Council of Norway.References
- L. T. Chen and L. Weiss, Blood, 1973, 41, 529–537 CAS.
- G. Deplaine, et al. , Blood, 2011, 117, E88–E95 CrossRef CAS PubMed.
- K. Tsukada, E. Sekizuka, C. Oshio and H. Minamitani, Microvasc. Res., 2011, 61, 231–239 CrossRef PubMed.
- M. Wiewiora, K. Sosada, M. Wylezol, L. Slowinska and W. Zurawinski, Obes. Surg., 2007, 17, 365–371 CrossRef PubMed.
- R. R. Huruta, et al., Mechanical properties of stored red blood cells using optical tweezers, Blood, 1998, 92, 2975–2977 CAS.
- T. L. Berezina, S. B. Zaets, C. Morgan, C. R. Spillert, M. Kamiyama, Z. Spolarics, E. A. Deitch and G. W. Machiedo, J. Surg. Res., 2002, 102, 6–12 CrossRef CAS PubMed.
- C. Lelubre, M. Piagnerelli and J. L. Vincent, Acta Clin. Belg., 2010, 65, 456 Search PubMed.
- C. G. Koch, L. Li, D. I. Sessler, P. Figueroa, G. A. Hoeltge, T. Mihaljevic and E. H. Blackstone, N. Engl. J. Med., 2008, 358, 1229–1239 CrossRef CAS PubMed.
- C. Lelubre, M. Piagnerelli and J. L. Vincent, Transfusion, 2009, 49, 1384–1394 CrossRef PubMed.
- G. Edgren, M. Kamper-Jørgensen, S. Eloranta, K. Rostgaard, B. Custer, H. Ullum, E. L. Murphy, M. P. Busch, M. Reilly, M. Melbye, H. Hjalgrim and O. Nyrén, Transfusion, 2010, 50, 1185–1195 CrossRef PubMed.
- E. Evans, Biophys. J., 1983, 43, 27–30 CrossRef CAS.
- E. Ogura, P. J. Abatti and T. Moriizumi, IEEE Trans. Biomed. Eng., 1991, 38, 721–726 CrossRef CAS PubMed.
- J. L. McWhirter, H. Noguchi and G. Gompper, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 6039–6043 CrossRef CAS PubMed.
- D. J. Quinn, I. Pivkin, S. Y. Wong, K. H. Chiam, M. Dao, G. E. Karniadakis and S. Suresh, Ann. Biomed. Eng., 2011, 39, 1041–1050 CrossRef PubMed.
- S. K. Mohantya, K. S. Mohanty and P. K. Guptaa, Opt. Express, 2005, 13, 4745 CrossRef.
- S. C. Grover, R. C. Gauthier and A. G. Skirtach, Opt. Express, 2000, 7, 533–539 CrossRef CAS.
- M. Dao, C. T. Lim and S. Suresh, J. Mech. Phys. Solids, 2003, 51, 2259–2280 CrossRef PubMed.
- H. Zhang and K. K. Liu, J. R. Soc., Interface, 2008, 5, 671–690 CrossRef CAS PubMed.
- J. Guck, R. Ananthakrishnan, H. Mahmood, T. J. Moon, C. C. Cunningham and J. Käs, Biophys. J., 2001, 81, 767–784 CrossRef CAS.
- J. M. A. Mauritz, A. Esposito, T. Tiffert, J. N. Skepper, A. Warley, Y.-Z. Yoon, P. Cicuta, V. L. Lew, J. R. Guck and C. F. Kaminski, Med. Biol. Eng. Comput., 2010, 48, 1055–1063 Search PubMed.
- N. Bellini, K. C. Vishnubhatla, F. Bragheri, L. Ferrara, P. Minzioni, R. Ramponi, I. Cristiani and R. Osellame, Opt. Express, 2010, 18, 4679–4688 CrossRef CAS PubMed.
- S. Unterkofler, M. K. Garbos, T. G. Euser and P. St. J. Russell, J. Biophotonics, 2013, 6, 743–752 CrossRef PubMed.
- S. Gaugiran, S. Gétin, J. Fedeli, G. Colas, A. Fuchs, F. Chatelain and J. Dérouard, Opt. Express, 2005, 13, 6956–6963 CrossRef CAS.
- B. S. Ahluwalia, P. McCourt, T. Huser and O. G. Helleso, Opt. Express, 2010, 18, 21053–21061 CrossRef CAS PubMed.
- O. G. Helleso, P. Lovhaugen, A. Z. Subramanian, J. S. Wilkinson and B. S. Ahluwalia, Lab Chip, 2012, 12, 3436–3440 RSC.
- I. Brevik, Phys. Rep., 1979, 52, 133–201 CrossRef.
- I. Brevik and R. Kluge, J. Opt. Soc. Am. B, 1999, 16, 976–985 CrossRef CAS.
- E. Farges, R. Grebe and M. Baumann, Clin. Hemorheol. Microcirc., 2002, 27, 1–11 CAS.
- E. Bennett-Guerrero, T. H. Veldman, A. Doctor, M. J. Telen, T. L. Ortel, T. S. Reid, M. A. Mulherin, H. Zhu, R. D. Buck, R. M. Califf and T. J. McMahon, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 17063–17068 CrossRef CAS PubMed.
- A. Fontes, M. L. B. Castro, M. M. Brandão, H. P. Fernandes, A. A. Thomaz, R. R. Huruta, L. Y. Pozzo, L. C. Barbosa, F. F. Costa, S. T. O. Saad and C. L. Cesar, J. Opt., 2011, 13, 044012 CrossRef.
- J. C. A. Cluitmans, M. R. Hardeman, S. Dinkla, R. Brock and G. J. C. G. M. Bosman, Blood Transfusion, 2012, 10, S12–S18 Search PubMed.
- M. Luten, B. Roerdinkholder-Stoelwinder, N. P. Schaap, W. J. de Grip, H. J. Bos and G. J. Bosman, Transfusion, 2008, 48, 1478–1485 CrossRef CAS PubMed.
- M. Gu, S. Kuriakose and X. Gan, Opt. Express, 2007, 15, 1369–1375 CrossRef.
- M. R. Hardeman, G. A. Besselink, I. Ebbing, D. de Korte, C. Ince and A. J. Verhoeven, Transfusion, 2003, 43, 1533–1537 CrossRef.
- T. Lecklin, S. Egginton and G. B. Nash, Pfluegers Arch., 1996, 432, 753–759 CrossRef CAS.
- G. M. D'Amici, S. Rinalducci and L. Zolla, J. Proteome Res., 2007, 6, 3242–3255 CrossRef PubMed.
- Y. K. Park, D. S. Monica, G. Popescu, G. Lykotrafitis, W. Choi, M. S. Feld and S. Suresh, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 13730–13735 CrossRef CAS PubMed.
- M. Wojdyla, S. Raj and D. Petrov, J. Biomed. Opt., 2012, 17, 97006 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details of numerical simulations, materials and methods, and seven supplementary video files with description. See DOI: 10.1039/c4an01181c |
| This journal is © The Royal Society of Chemistry 2015 |