Revisiting large volume injection in non-miscible diluents: an on-line reversed phase supported liquid extraction/liquid chromatography scenario†
Paul
Lazăr
a,
Ştefan
Udrescu
a,
Florentin
Tache
a,
Florin
Albu
ab,
Nelu
Grinberg
c and
Andrei
Medvedovici
*a
aUniversity of Bucharest, Faculty of Chemistry, Department of Analytical Chemistry, #90 Panduri Av., Bucharest – 050663, Romania. E-mail: avmedved@yahoo.com; Fax: +40 214 102 279; Tel: +40 723 330 423
bAnalytical Application Laboratory, Agilrom, # 40S Th. Pallady Ave., Bucharest – 032266, Romania
cChemical Development Department, Boehringer Ingelheim Pharmaceuticals Inc., 900 Ridgebury Rd, Ridgefield, CT 06877-0368, USA
First published on 20th November 2014
Abstract
According to some recently published studies, large volume injection (LVI) of diluents immiscible with the eluents used in reversed phase liquid chromatography (RPLC) appears to be feasible, despite the widely accepted rules governing injection related phenomena. The process was previously described and was successfully applied in practice. The present study describes a simple theoretical model explaining LVI of diluents immiscible with the mobile phase in RPLC; the model relies on the on-line coupling of reversed phase supported liquid extraction (RP-SLE) to the chromatographic separation. The compliance of the theoretical model with experimental observations was tested by using data collected for LVI of a homologous series of para-hydroxy alkyl benzoates (methyl, ethyl, propyl, butyl, pentyl, hexyl and octyl congeners) in liquid alkanes (hexane, heptane, iso-octane, decane and dodecane). The SP consisted of an octadecyl chemically modified silica gel eluted with a mixture of acetonitrile![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 4
water 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 (v/v). Although the model mainly focuses on explaining the linear reduction of the retention time with the injected volume, some aspects relating to zone spreading and thermodynamic aspects are also discussed.
6 (v/v). Although the model mainly focuses on explaining the linear reduction of the retention time with the injected volume, some aspects relating to zone spreading and thermodynamic aspects are also discussed.
1. Introduction
Large Volume Injection (LVI) in chromatography relates to the continuous challenge of increasing method sensitivity.1,2 Injection phenomena arising in liquid chromatography (LC) were extensively studied with respect to the strength3–7 and viscosity8–10 of the sample diluent (D) and their recurrent impact on the chromatographic parameters illustrating retention, band spread, and peak shape. The injection produces a thermodynamic disturbance in the chromatographic system. Column loadability in a LVI complex phenomenon depends directly on its intrinsic characteristics (length, internal diameter, particle size, and phase ratio), mobile phase (MP) composition and elution conditions, D characteristics, and the specific properties of the analytes (A). LC injection phenomena should be also considered in a close relationship with the widely applied sample preparation methods, primarily delivering the target compounds in a wide variety of organic solvents.11 Moreover, removal of solvents producing unwanted phenomena in LC and their replacement by adequate ones strongly impacts on the characteristics of the sample preparation approaches and directly influences the overall accuracy and precision.The possibility of using D immiscible with the MP in RPLC was already demonstrated.12–14 The process was successfully applied in the pharmaceutical field15–19 and in bioanalysis.20–24 Injection in immiscible D was also used for estimation of the hydrophobic characteristics of a series of pharmaceutical compounds.25 However, determination of the retention corresponding to a hypothetical condition assuming the absence of the D is more related to the intrinsic behavior of the analyte in the chromatographic column, rather than an illustration of injection related phenomena.
The possibility of introduction in the chromatographic column of large volumes of samples in immiscible D to the MP was explained through the competitional equilibria between the analyte and the D molecules for the adsorption sites in the stationary phase (SP).12 Consequently, the process becomes experimentally possible, without affecting peak shapes, if the affinity of the D for the SP is higher than that of the analyte. As a direct consequence, a part of the SP in the column's head becomes unavailable for the compounds contained in the sample, their retention linearly decreasing with the increase of the injection volume. It results that an essential condition for achieving LVI of immiscible D in RPLC is an increased hydrophobic character of the D compared to analytes. The process generally occurs with a loss in the peak efficiency, although band focusing was also reported in some specific conditions.13 In some specific cases, acceptable peak fronting or tailing may be observed.
However, these explanations seem to only superficially describe the real chromatographic phenomena. A new theoretical model of LVI in immiscible D in the RPLC MP is presented herein. This new approach assumes that immediately after the filling of the column's head with the sample dissolved in an immiscible D, the latter acts as a liquid phase immobilized on the SP. The MP penetrates the D plug from behind through running channels, with the analyte(s) being extracted between the D and the MP. Once extracted from the D, the analytes are separated in the part of the chromatographic column remaining available for interaction. The scenario involves the creation, after injection, in the column's head, of a reversed phase supported liquid–liquid extraction (SLE) “cartridge”, followed by the on-line removal of analytes by the MP and their separation in the remaining part of the chromatographic column. The theoretical model focuses on explaining the linear reduction of the retention in the system when the injected volume increases. To validate the theoretical model, a homologous series of para-hydroxy alkyl benzoates (methyl, ethyl, propyl, butyl, pentyl, hexyl and octyl congeners) dissolved in liquid alkanes (hexane, heptane, iso-octane, decane and dodecane) were used. The SP consisted of an octadecyl chemically modified silica gel eluted with a MP consisting of a mixture of acetonitrile![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 4
water 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 (v/v). The thermodynamics of the phenomena as well as band spreading are also discussed.
6 (v/v). The thermodynamics of the phenomena as well as band spreading are also discussed.
2. Experimental
2.1. Reagents
Acetonitrile (HPLC gradient grade), hexane, heptane, i-octane (all Lichrosolv® grade), decane (for synthesis) and dodecane (Msynth®plus) from Merck (Darmstadt, Germany) were used during experiments. Water for chromatography (resistivity of minimum 18.2 MΩ and total residual organic carbon content – TOC – of maximum 30 ng mL−1) was produced within the laboratory by using a TKA Lab HP 6UV/UF instrument (TKA Instruments as part of Thermo Fischer Scientific, Niederelbert, Germany). Methyl, ethyl, propyl and butyl para-hydroxybenzoates (further denoted MeP, EtP, PrP, and BuP, respectively) of secondary standard pharmaceutical purity grade were purchased from Sigma-Aldrich (Taufkirchen, Germany). Pentyl para-hydroxybenzoate (PeP) was obtained from Santa Cruz Biotechnology Inc. (Delaware, USA). The hexyl congener (HeP) was purchased from TCI Europe N.V. (Zwijndrecht, Belgium) while the octyl one (OcP) was obtained from Alfa Aesar (Massachusetts, USA).2.2. Equipment
Experiments were performed with an Agilent 1260 Infinity series LC/MWD (Agilent Technologies, Waldbronn, Germany) system consisting of the following modules: a quaternary pump (G1311B), an automated injector (ALS-G1329B), a column thermostat (TCC-G1316C), and a multi-channel UV-Vis detector (DVL-G1365D). Occasionally, the refractive index detector (RID-G1362A) was used to monitor the retention behavior of the D. System control and data acquisition were made with the Agilent Chemstation for LC 3D, version 04.03(16).2.3. Chromatographic experiments
A Zorbax SB-C18 column (50 mm L × 4.6 mm i.d. × 1.8 μm d.p.) from Agilent Technologies (cat. no. 827975-902) was used and thermostatted at 25 °C. The SP consists of spherical silica particles (1.8 μm) with a pore size of 80 Å densely covered (10% carbon load) with octadecyl moieties. The MP consisted of a mixture of acetonitrile and water, in the volumetric ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6. The flow rate was 1.5 mL min−1. Elution was made under isocratic conditions. To prepare the column for consecutive injections, the composition of the MP was brought to 100% acetonitrile in a 0.1 min stepwise ramp, followed by a period of time used to eliminate the D plug from the column. The time required for the elimination of D from the column depends upon the injected volume. To accommodate experiments that require working in unassisted sequences, the period for D exclusion was set to 20 min. To shorten this period, stepwise increase of the flow rate simultaneous to the jump at 100% acetonitrile may be used. Next, the composition of the MP was set at the initial mixing ratio (4
6. The flow rate was 1.5 mL min−1. Elution was made under isocratic conditions. To prepare the column for consecutive injections, the composition of the MP was brought to 100% acetonitrile in a 0.1 min stepwise ramp, followed by a period of time used to eliminate the D plug from the column. The time required for the elimination of D from the column depends upon the injected volume. To accommodate experiments that require working in unassisted sequences, the period for D exclusion was set to 20 min. To shorten this period, stepwise increase of the flow rate simultaneous to the jump at 100% acetonitrile may be used. Next, the composition of the MP was set at the initial mixing ratio (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6) followed by 3 min of equilibration. Spectrometric UV detection was applied, using 270 nm as the analytical wavelength. For samples dedicated to 1 μL injection volume, stock solutions of the analyte mixture of 2 mg mL−1 each in methanol (for hexane, heptane and iso-octane) and in ethyl acetate (for decane and dodecane) were 1/20 diluted with the respective D. From these intermediate stock solutions, 1/5, 1/10, 1/20, 1/50 and 1/100 dilutions in the appropriate D were made, in order to keep the absolute amounts of analytes constant when 5, 10, 20, 50 and 100 μL injection volumes were applied. Separately, serial injection of 1, 5, 10, 20, 50, and 100 μL mixtures of the analytes in the MP was also achieved (individual injected amounts were kept constant during experiments).
6) followed by 3 min of equilibration. Spectrometric UV detection was applied, using 270 nm as the analytical wavelength. For samples dedicated to 1 μL injection volume, stock solutions of the analyte mixture of 2 mg mL−1 each in methanol (for hexane, heptane and iso-octane) and in ethyl acetate (for decane and dodecane) were 1/20 diluted with the respective D. From these intermediate stock solutions, 1/5, 1/10, 1/20, 1/50 and 1/100 dilutions in the appropriate D were made, in order to keep the absolute amounts of analytes constant when 5, 10, 20, 50 and 100 μL injection volumes were applied. Separately, serial injection of 1, 5, 10, 20, 50, and 100 μL mixtures of the analytes in the MP was also achieved (individual injected amounts were kept constant during experiments).
2.4. Complementary approaches
The distribution constants (K) of the considered compounds between heptane and the acetonitrile![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water mixture 4
water mixture 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 (v/v) were determined according to the shake flask method after vortexing for 24 h (vortexing speed 500 rpm) of equal volumes of phases (the initial concentration of each compound in the organic layer was 10 μg mL−1). Quantitative determinations of the compounds were made in both layers separately, by means of the chromatographic method. The mass balance for the sum of the determined compounds in the two phases with respect to the initial amounts varied from 98.1 to 100.6% in recovery.
6 (v/v) were determined according to the shake flask method after vortexing for 24 h (vortexing speed 500 rpm) of equal volumes of phases (the initial concentration of each compound in the organic layer was 10 μg mL−1). Quantitative determinations of the compounds were made in both layers separately, by means of the chromatographic method. The mass balance for the sum of the determined compounds in the two phases with respect to the initial amounts varied from 98.1 to 100.6% in recovery.
The retention of model compounds was studied separately when the MP was deliberately saturated with heptane. Saturation was achieved through vortexing the pre-mixed MP (acetonitrile/water = 4/6, v/v) with heptane for 24 h, in a volumetric ratio of 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The injected volume was 1 μL from a solution in methanol at 1000 μg mL−1 from each compound of the homologous series. Subsequent injections were made in order to obtain constant retention times.
1. The injected volume was 1 μL from a solution in methanol at 1000 μg mL−1 from each compound of the homologous series. Subsequent injections were made in order to obtain constant retention times.
For the thermodynamic studies, BuP dissolved in heptane was used, and injected in incremental volumes of 20, 40, 60, 80 and 100 μL. The temperature interval used in the study was between 20 and 45 °C, in 5 °C increments. Van't Hoff plots were used for the calculation of apparent standard enthalpies and entropies.
3. Results and discussion
3.1. Rationale for the choice of the experimental conditions
Homologous series of para-hydroxyalkyl benzoates were used as model compounds, covering a large scale of hydrophobicity. The values of the logarithms of their partition coefficients between n-octanol and water (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow), calculated according to the fragment theory (KOWWIN v1.67, Environmental Protection Agency, USA), are in the order: MeP – 2.00; EtP – 2.48; PrP – 2.98; BuP – 3.47; PeP – 3.96; HeP – 4.45; OcP – 5.43.
Kow), calculated according to the fragment theory (KOWWIN v1.67, Environmental Protection Agency, USA), are in the order: MeP – 2.00; EtP – 2.48; PrP – 2.98; BuP – 3.47; PeP – 3.96; HeP – 4.45; OcP – 5.43.
The chosen D are characterized by the following computed log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow values: hexane – 3.29; heptane – 3.78; iso-octane – 4.09; decane – 5.25; dodecane – 6.23. According to the previous theory, no suitable results should be obtained in cases where the log
Kow values: hexane – 3.29; heptane – 3.78; iso-octane – 4.09; decane – 5.25; dodecane – 6.23. According to the previous theory, no suitable results should be obtained in cases where the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow of the analyte is higher than the log
Kow of the analyte is higher than the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow of the D.
Kow of the D.
The column was chosen with a minimal length (50 mm) for two main reasons. Firstly, it was chosen to produce lower retention and to achieve separation of the model compounds under isocratic conditions while keeping the MP composition with the highest percentage of water. This has the effect of producing the lowest solubility of the D in the MP. Secondly, the column geometry makes injections of 10 to 100 μL possible, representing a significant part of the kinetic void volume. The column void volume (V0) was 447 μL, which was determined by injection of a solution of potassium nitrate. As such, the injected volumes of D represented 2.24 to 22.4% from the void volume.
3.2. The theoretical model
The theoretical model being advanced herein is based on the scenario of an RP-SLE process on-line coupled to RPLC (see Fig. 1).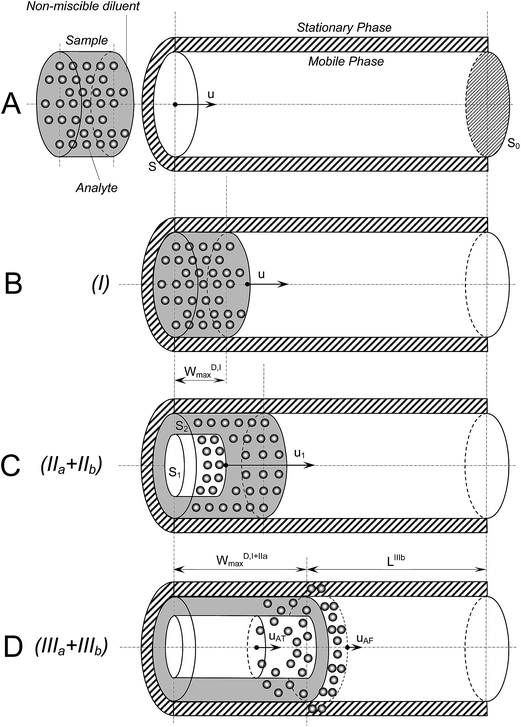 | ||
| Fig. 1 Steps of the on-line reversed phase supported liquid extraction/liquid chromatography (RP-SLE/LC) on injection of large volumes of immiscible diluents. | ||
The steps of the process are: (I) the transport of the D plug in the head of the chromatographic column (filling – Fig. 1A and B); (IIa) inflation of the D plug produced by the penetration of the MP (formation of channels) and its diffusion in the SP; (IIb) liquid–liquid extraction (LLE) of the analyte from the D in the MP until the D/MP front interface is reached (stages IIa and IIb are simultaneous) – see Fig. 1C; (IIIa) beginning of reinjection of the MP containing the extracted analyte into the rest of the chromatographic column and continuation of the LLE process; (IIIb) LLE process ends and the normal chromatographic process occurs in the remaining portion of the column.
Some general simplifying assumptions are necessary: (i) the D completely replaces the MP during loading (no intra- and extra-particle entrapping of the MP arises); (ii) the D plug remains immobile after its transport in the column's head and its inflation (due to its larger affinity to SP as compared with that of MP); (iii) the reciprocal solubility of the D and the MP should be considered as negligible; (iv) the hydrophobic character of the D is significantly similar to the SP character; (v) the model ignores the effect of the longitudinal/axial and radial/transversal mass transfer widening the analyte zone; thus, the short range (at the order of magnitude of particle size dimensions) mass transfer via radial/transversal diffusion is considered instantaneous but axial/longitudinal diffusion is considered 0; (vi) the number of the MP penetrating channels through the D soaking the SP is significantly similar to the number of chromatographic elution channels through the packing material; (vii) the SP contribution to the analyte partition in the D plug is negligible (the surface retention activity of the SP is quenched by the presence of the D existing in a much larger amount); the contribution of the SP to the dilution effect of the analyte in the D zone is negligible; (viii) no fingering effects at the interfaces between the immiscible liquid zones were considered.
The elimination of the fingering effects from the theoretical model was not made for simplification reasons, only. Fingering effects which may appear at the front interface between the D and the MP are hindered by the consecutive inflation of the D plug (step IIa). Fingering effects arising at the rear interface between the MP and the D are hindered by the penetration of the MP in the D plug and the channel formation process. Experimental results confirm the absence of the fingering effects.
The following mathematical relationships were used to describe the RP-SLE process on-line coupled to RPLC.
During the first stage (I) of the process, the following relationships are established:
The D maximum longitudinal spread on loading (WD,Imax) is
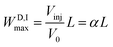 | (1) |
The D maximum filling time in the column's head (tD,Imax) is
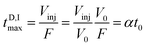 | (2) |
Obviously, the filling speed of the D plug is the MP speed 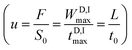 , where S0 is the effective MP cross-section through the column packing.
, where S0 is the effective MP cross-section through the column packing.
The MP evolution during stage (IIa) (channel formation) of the process may be described by the following relationships:
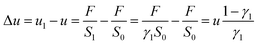 | (3) |
The period needed for MP channel formation should thus be considered as:
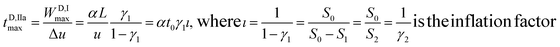 | (4) |
The cumulative period needed for D filling and MP channel formation through the D plug is:
| tD,I+IIamax = αt0 + αγ1ιt0 = αt0(1 + γ1ι) = αt0ι | (5) |
The longitudinal spatial spread of D during steps (I) and (IIa) may be calculated as
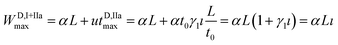 | (6) |
During the liquid–liquid extraction step (IIb), the evolution of the analyte's (A) rear front may be described starting from the mass conservation relationship:
| S1[A]MP(u1 − uAT) = S2[A]DuAT | (7) |
Consequently
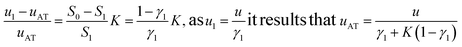 | (8) |
Thus, the compression speed of the analyte front is
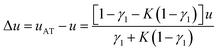 | (9) |
The maximum rear analyte depleted zone width WIIbA,void may be calculated as:
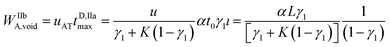 | (10) |
The compressed analyte zone is characterized by the width WIIbA, resulting from the following relationship:
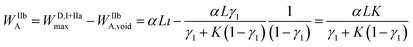 | (11) |
For the reinjection stage (IIIa), the mass conservation relationship gives:
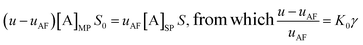 | (12) |
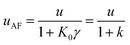 | (13) |
The virtual duration of the reinjection process of the analyte (tIIIaA) is:
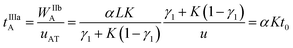 | (14) |
The maximum spatial width of the analyte's zone after reinjection WIIIbA is:
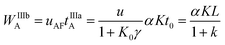 | (15) |
The remaining length of the column available for the chromatographic separation of the analyte LIIIb is:
| LIIIb = L − WD,I+IIamax = L − αLι = L(1 − αι) | (16) |
The retention time corresponding to the remaining length of the column available for the chromatographic separation is
| tIIIbR = tR(1 − αι) = (1 − αι)(1 + k)t0 | (17) |
It follows that the apparent retention time of the analyte tappR may be computed according to the following relationship:
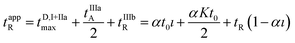 | (18) |
The term 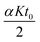 is actually the half width (in time units) of the peak, if diffusion does not contribute to zone spreading as the model considers. If tappR = t0(1 + kapp) is considered, it follows that:
is actually the half width (in time units) of the peak, if diffusion does not contribute to zone spreading as the model considers. If tappR = t0(1 + kapp) is considered, it follows that:
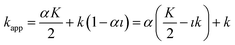 | (19) |
If the linear relationship19 must fit the experimental findings, the slope 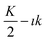 should be negative (the apparent retention factor decreases linearly with the increase of the injected volume). This is equivalent to the situation where
should be negative (the apparent retention factor decreases linearly with the increase of the injected volume). This is equivalent to the situation where
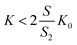 | (20) |
Experimental results show that the apparent retention factor, kapp, is less influenced by the distribution constant K, its functional dependence on α being mainly due to the ιk term (the inflation factor and the chromatographic retention factor). As a direct consequence, one can conclude that the variation of the apparent retention with α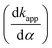 is mainly determined by the inflation factor (ι). The inflation factor is a geometrical parameter which does not depend directly on any chromatographically related parameter, but only on the shear forces developed at the D/MP interface (influenced by viscosity) and the interfacial forces of the D/MP interface. A reasonable explanation for the stabilization to a given thickness of the D film covering the SP can be the so-called “disjoining pressure”.
is mainly determined by the inflation factor (ι). The inflation factor is a geometrical parameter which does not depend directly on any chromatographically related parameter, but only on the shear forces developed at the D/MP interface (influenced by viscosity) and the interfacial forces of the D/MP interface. A reasonable explanation for the stabilization to a given thickness of the D film covering the SP can be the so-called “disjoining pressure”.
3.3. Correlation with experimental results
As illustrated in Table 1, linear relationships between kapp and α are established for all D and studied compounds. This is not surprising at all, as the linear decrease of the retention factor with the injected volume was observed during the previous works relating to the use of immiscible D in RPLC.12,13,19,25 One can observe that the coefficients describing the correlations between experimental data are higher than 0.99.| Diluent | Characteristics of the linear regression kapp = f(α) | Model compounds | ||||||
|---|---|---|---|---|---|---|---|---|
| MeP | EtP | PrP | BuP | PeP | HeP | OcP | ||
| Hexane | Slope | −2.387 | −5.144 | −10.912 | −22.374 | −45.845 | −95.813 | −392.974 |
| Intercept | 1.26 | 2.33 | 4.57 | 9.06 | 18.00 | 35.88 | 131.34 | |
| Correlation coefficient | 0.9976 | 0.9990 | 0.9995 | 0.9997 | 0.9997 | 0.9996 | 0.9991 | |
| Heptane | Slope | −2.295 | −5.045 | −10.715 | −21.925 | −44.822 | −93.271 | −411.107 |
| Intercept | 1.27 | 2.35 | 4.60 | 9.09 | 18.09 | 35.96 | 140.45 | |
| Correlation coefficient | 0.9964 | 0.9984 | 0.9994 | 0.9996 | 0.9995 | 0.9996 | 0.9997 | |
| Iso-octane | Slope | −2.114 | −4.796 | −10.366 | −21.387 | −43.902 | −92.047 | −409.310 |
| Intercept | 1.26 | 2.34 | 4.59 | 9.10 | 18.08 | 36.08 | 142.22 | |
| Correlation coefficient | 0.9960 | 0.9987 | 0.9996 | 0.9999 | 0.9998 | 0.9998 | 0.9997 | |
| Decane | Slope | −2.025 | −4.970 | −11.103 | −23.005 | −47.240 | −99.732 | −444.952 |
| Intercept | 1.51 | 2.72 | 5.23 | 10.26 | 20.32 | 40.54 | 160.11 | |
| Correlation coefficient | 0.9938 | 0.9984 | 0.9996 | 0.9999 | 0.9998 | 0.9997 | 0.9996 | |
| Dodecane | Slope | −2.137 | −5.102 | −10.971 | −22.113 | −46.101 | −97.501 | −445.343 |
| Intercept | 1.528 | 2.735 | 5.250 | 10.297 | 20.402 | 40.694 | 161.327 | |
| Correlation coefficient | 0.9979 | 0.9997 | 0.9996 | 0.9998 | 0.9999 | 0.9999 | 0.9997 | |
The partition constants (K) of the analytes between heptane and the MP were available from the shake flask experiments. The chromatographic equilibrium constants (calculated with K0 = kγ−1i.e. using the formalism of the partition based retention) were also available from the injection of the analytes dissolved in the MP. The retention factor, k, and the phase ratio (γ) are calculated using a void volume of 0.447 mL, and a SP volume of 0.1 mL (an approximation of the bulk octadecyl moieties volume covering the surface of the silica material). It is thus possible to compute some of the key parameters of the model, more precisely ι, γ2, and WD,I+IImax. Results are illustrated in Table 2.
| V inj (μL) | α × 103 | k | k app | K | K 0 | K 0/K | ι | γ 2 | Mean ι | Mean γ2 | W D,I+IImax(αLι) | L IIIb (mm) | L IIIb/L | N app | N | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MeP | 1 | 2.237 | 1.27 | 1.27 | 0.011 | 28.5 | 2537.6 | — | — | M = 2.0; s = 0.13; RSD% = 6.7 | M = 0.508; s = 0.04; RSD% = 7.0 | 0.27 | 49.73 | 0.995 | 7128 | 6988 |
| 5 | 11.186 | 1.25 | — | — | 1.35 | 48.65 | 0.973 | 5757 | 5602 | |||||||
| 10 | 22.371 | 1.21 | 2.1 | 0.470 | 2.70 | 47.30 | 0.946 | 5550 | 5087 | |||||||
| 20 | 44.743 | 1.16 | 2.0 | 0.513 | 5.39 | 44.61 | 0.892 | 5096 | 3860 | |||||||
| 50 | 111.857 | 0.98 | 2.1 | 0.486 | 13.48 | 36.52 | 0.730 | 4830 | 1541 | |||||||
| 100 | 223.714 | 0.77 | 1.8 | 0.564 | 26.96 | 23.04 | 0.461 | 4577 | 485 | |||||||
| EtP | 1 | 2.237 | 2.34 | 2.35 | 0.028 | 52.4 | 1890.9 | — | — | M = 2.2; s = 0.09; RSD% = 4.2 | M = 0.465; s = 0.02; RSD% = 4.0 | 0.27 | 49.73 | 0.995 | 8845 | 7951 |
| 5 | 11.186 | 2.31 | — | — | 1.35 | 48.65 | 0.973 | 7569 | 7030 | |||||||
| 10 | 22.371 | 2.23 | 2.1 | 0.472 | 2.70 | 47.30 | 0.946 | 6944 | 6800 | |||||||
| 20 | 44.743 | 2.12 | 2.1 | 0.479 | 5.39 | 44.61 | 0.892 | 6972 | 5465 | |||||||
| 50 | 111.857 | 1.74 | 2.3 | 0.433 | 13.48 | 36.52 | 0.730 | 6113 | 2671 | |||||||
| 100 | 223.714 | 1.24 | 2.1 | 0.475 | 26.96 | 23.04 | 0.461 | 4817 | 906 | |||||||
| PrP | 1 | 2.237 | 4.57 | 4.59 | 0.062 | 102.2 | 1661.3 | — | — | M = 2.3; s = 0.11; RSD% = 4.8 | M = 0.443; s = 0.02; RSD% = 4.8 | 0.27 | 49.73 | 0.995 | 9601 | 8711 |
| 5 | 11.186 | 4.50 | — | — | 1.35 | 48.65 | 0.973 | 8923 | 8037 | |||||||
| 10 | 22.371 | 4.35 | 2.1 | 0.472 | 2.70 | 47.30 | 0.946 | 8576 | 7785 | |||||||
| 20 | 44.743 | 4.12 | 2.2 | 0.452 | 5.39 | 44.61 | 0.892 | 7031 | 7003 | |||||||
| 50 | 111.857 | 3.34 | 2.4 | 0.415 | 13.48 | 36.52 | 0.730 | 6889 | 4514 | |||||||
| 100 | 223.714 | 2.23 | 2.3 | 0.435 | 26.96 | 23.04 | 0.461 | 4615 | 2071 | |||||||
| BuP | 1 | 2.237 | 9.04 | 9.06 | 0.144 | 202.3 | 1407.6 | — | — | M = 2.0; s = 0.04; RSD% = 1.9 | M = 0.419; s = 0.01; RSD% = 1.9 | 0.27 | 49.73 | 0.995 | 9705 | 8596 |
| 5 | 11.186 | 8.92 | — | — | 1.35 | 48.65 | 0.973 | 9435 | 8181 | |||||||
| 10 | 22.371 | 8.57 | 2.3 | 0.432 | 2.70 | 47.30 | 0.946 | 8581 | 8050 | |||||||
| 20 | 44.743 | 8.06 | 2.4 | 0.413 | 5.39 | 44.61 | 0.892 | 7351 | 7744 | |||||||
| 50 | 111.857 | 6.59 | 2.4 | 0.412 | 13.48 | 36.52 | 0.730 | 6717 | 6627 | |||||||
| 100 | 223.714 | 4.22 | 2.4 | 0.418 | 26.96 | 23.04 | 0.461 | 3832 | 4289 | |||||||
| PeP | 1 | 2.237 | 17.95 | 17.94 | 0.318 | 401.6 | 1262.5 | — | — | M = 2.4; s = 0.11; RSD% = 4.4 | M = 0.417; s = 0.02; RSD% = 4.7 | 0.27 | 49.73 | 0.995 | 8790 | 8028 |
| 5 | 11.186 | 17.81 | — | — | 1.35 | 48.65 | 0.973 | 8468 | 7807 | |||||||
| 10 | 22.371 | 17.06 | 2.2 | 0.451 | 2.70 | 47.30 | 0.946 | 8001 | 7824 | |||||||
| 20 | 44.743 | 15.98 | 2.5 | 0.405 | 5.39 | 44.61 | 0.892 | 6593 | 7669 | |||||||
| 50 | 111.857 | 13.01 | 2.5 | 0.405 | 13.48 | 36.52 | 0.730 | 5945 | 7379 | |||||||
| 100 | 223.714 | 8.11 | 2.5 | 0.407 | 26.96 | 23.04 | 0.461 | 3327 | 6292 | |||||||
| HeP | 1 | 2.237 | 35.81 | 35.69 | 0.690 | 801.1 | 1161.2 | — | — | M = 2.6; s = 0.04; RSD% = 1.5 | M = 0.386; s = 0.01; RSD% = 1.6 | 0.27 | 49.73 | 0.995 | 7525 | 7042 |
| 5 | 11.186 | 35.31 | — | — | 1.35 | 48.65 | 0.973 | 7625 | 7206 | |||||||
| 10 | 22.371 | 33.79 | 2.5 | 0.395 | 2.70 | 47.30 | 0.946 | 6542 | 7066 | |||||||
| 20 | 44.743 | 31.61 | 2.6 | 0.380 | 5.39 | 44.61 | 0.892 | 5385 | 7077 | |||||||
| 50 | 111.857 | 25.32 | 2.6 | 0.380 | 13.48 | 36.52 | 0.730 | 5039 | 6939 | |||||||
| 100 | 223.714 | 15.22 | 2.6 | 0.388 | 26.96 | 23.04 | 0.461 | 2674 | 6609 | |||||||
| OcP | 1 | 2.237 | 141.34 | 139.80 | 2.938 | 3161.9 | 1076.3 | — | — | M = 3.1; s = 0.12; RSD% = 3.8 | M = 0.324; s = 0.01; RSD% = 3.8 | 0.27 | 49.73 | 0.995 | 4353 | 5001 |
| 5 | 11.186 | 136.89 | — | — | 1.35 | 48.65 | 0.973 | 4542 | 5115 | |||||||
| 10 | 22.371 | 131.38 | 3.2 | 0.316 | 2.70 | 47.30 | 0.946 | 4326 | 5015 | |||||||
| 20 | 44.743 | 120.98 | 3.2 | 0.310 | 5.39 | 44.61 | 0.892 | 3647 | 4972 | |||||||
| 50 | 111.857 | 93.47 | 3.0 | 0.329 | 13.48 | 36.52 | 0.730 | 3458 | 5044 | |||||||
| 100 | 223.714 | 49.12 | 2.9 | 0.342 | 26.96 | 23.04 | 0.461 | 1413 | 5212 | |||||||
| Mean | 2.4 | 0.423 | ||||||||||||||
| s | 0.33 | 0.05 | ||||||||||||||
| RSD% | 13.8 | 12.8 |
It can be observed that the conditions described in eqn (20) are fulfilled in all cases. The chromatographic equilibrium constants (K0) are significantly higher than the LLE ones (K). As one can observe from the γ2 calculations, the cross-section of the column occupied by the supported D (S2) is roughly one-half of the column cross-section occupied by the MP (S0).
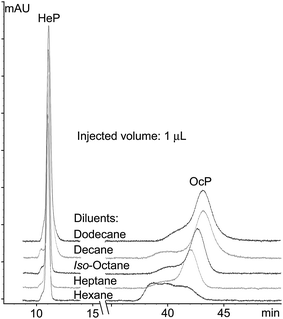
ι (and its inverse γ2) values should depend mainly on the nature of the D and the nature of the SP. Experimental results in Table 2 support this assumption, with ι and γ2 values being significantly similar for all analytes at injected volumes equal to or higher than 10 μL. The relative standard deviations (RSD%) computed for the ι and γ2 data sets are placed below 15% (n = 28). Data obtained for 1 and 5 μL injection volumes for all analytes were deliberately discarded. Such volumes are most probably not homogeneously occupying the cross-section of the chromatographic column during the transfer of the D plug in the head of the column, immediately after injection. Such a process should be the basis, at least for the last eluting compounds (for which the LLE from the D plug to the MP remains unfavorable), of severe peak shape distortion, and fits to the experimental observations (Fig. 2 illustrates peak shapes corresponding to the last two eluting compounds when injecting 1 μL from all used D).
Injection volumes higher than 10 μL in all tested D lead to a fair peak symmetry and efficiency for the considered compounds (see Fig. 3 and the ESI,† Part 1). It appears that the condition for successful chromatographic results stated in previous studies (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KDiluentow > log
KDiluentow > log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAnalyteow) does not necessarily apply.
KAnalyteow) does not necessarily apply.
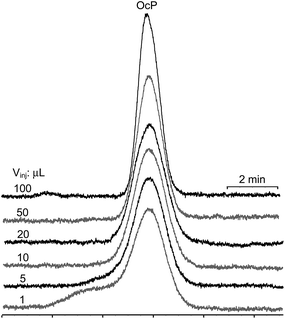 | ||
| Fig. 3 Peak shapes of para-octyl (OcP) hydroxybenzoate on injection of progressive volumes (1, 5, 10, 20, 50, 100 μL) in heptane. | ||
From Table 2 one can see that the inflated zone of the D (WD,I+IImax) for the 100 μL injected volume is occupying almost one-half of the chromatographic column. Reduction of the column length produces a proportional decrease of the peak efficiency. When injecting large volumes of solutions in the MP, the first four eluting compounds suffer a reduction of peak efficiency. This is due to the inability of the SP to re-focus analytes on injection (Table 2 and the ESI,† Part 2). For the earlier eluting compounds (poorly retained in D and SP), on injection of the immiscible D, the MP channels formed in the D plug are focusing analytes (eqn (9)), due to their favorable partition from the D to the MP. Consequently, the apparent peak efficiency (Napp) will increase with the increase of the injected volume, compared to the situation when the MP is used as D. For the later eluting compounds (strongly retained in the D and SP), partition from the D to the MP during the channels' formation is not favored, but the SP in the head of the remaining chromatographic column focuses the analytes and compensates (at least partially) for the band spread. Consequently, the initial spread of the analyte zone due to the filling of a large amount of D may not be entirely compensated by either compression or refocusing, and the virtual re-injected volume can be larger than Vinj if K ≫ 1.
The simplifying conditions assumed by the mathematical model (specifically, the assumptions relying on the reciprocal lack of solubility between the D and the MP, on one hand, and the immobility of the D plug after column percolation and the inflation process, on the other hand) are not obeyed in experimental practice. As illustrated in the ESI,† Part 3, around 25 min after the injection of 100 μL of heptane, the D plug starts to be evacuated from the column. This can be observed under RID conditions, but also in the UV trace (as a noisy baseline due to the formation of a micro-emulsion of the D in the MP). In real conditions, the D plug should act as a MP saturator. A MP saturated with the D would also decrease the chromatographic retention. As a result it was decided to study the effect of the saturation of the MP with the D, under the conditions of small volume injection in methanol (1 μL). Experimental conditions are described in Complementary approaches under the Experimental section. Results are presented in the ESI,† Part 4. As expected, on repetitive injections, retention continuously decreases until equilibrium of the partition of the saturating D between phases is obtained. Surprisingly, the equilibration period is extremely long, largely exceeding 800 void volumes. Under such conditions, for the assumed on-line RP-SLE/RPLC scenario, MP saturation with the D should not produce any measurable effects and fully explains why the experimental results fit to the proposed mathematical model. From the number of void volumes needed to equilibrate the column when the MP is saturated with D one can also conclude that the displacement mechanism of the D plug is mainly based on mechanically driven forces and not through a chromatographic process.
3.4. Thermodynamic considerations
To have a better insight, a thermodynamic study was also conducted. The global thermodynamic behavior of the system should take into account the individual contributions of both consecutive processes, the LLE extraction and the chromatographic separation on the remaining available chromatographic column. A study of the relationships between the logarithms of the apparent retention factor (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kapp) versus the inverse of the temperature was carried out (van't Hoff plots). The considered temperature interval ranged from 20 to 45 °C (in steps of 5 °C). The chosen model compound was BuP dissolved in heptane and injected in volumes of 20, 40, 60, 80 and 100 μL, respectively. A comparison with the situation involving only the chromatographic separation, meaning the injection of 1 μL of a solution of the model compound in methanol, is also presented. Resulting data are given in Table 3. The graphical plots are also provided in the ESI,† Part 5.
kapp) versus the inverse of the temperature was carried out (van't Hoff plots). The considered temperature interval ranged from 20 to 45 °C (in steps of 5 °C). The chosen model compound was BuP dissolved in heptane and injected in volumes of 20, 40, 60, 80 and 100 μL, respectively. A comparison with the situation involving only the chromatographic separation, meaning the injection of 1 μL of a solution of the model compound in methanol, is also presented. Resulting data are given in Table 3. The graphical plots are also provided in the ESI,† Part 5.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kapp = f(1/T)) for para-hydroxybutyl benzoate (BuP) on injection of different volumes in heptane or methanol
kapp = f(1/T)) for para-hydroxybutyl benzoate (BuP) on injection of different volumes in heptane or methanol
| V inj (μL) | Diluent | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k k |
T (°C) | 1/T (K−1) | B | A | r xy | ΔH0 (kJ) | ΔS0 (J K−1) | ΔG0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Slope of the linear relationship. b Intercept of the linear relationship. c Correlation coefficient of the linear relationship. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | MeOH | 2.28 | 20 | 0.003411 | 1391.98 | −2.4680 | 0.9972 | −11.57 | −8.07 | −9.21 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2.20 | 25 | 0.003354 | −9.17 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2.13 | 30 | 0.003299 | −9.13 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2.05 | 35 | 0.003245 | −9.09 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.96 | 40 | 0.003193 | −9.05 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.92 | 45 | 0.003143 | −9.01 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | Heptane | 2.15 | 20 | 0.003411 | 1385.08 | −2.5681 | 0.9990 | −11.52 | −8.90 | −8.91 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2.08 | 25 | 0.003354 | −8.86 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2.01 | 30 | 0.003299 | −8.82 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.93 | 35 | 0.003245 | −8.77 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.85 | 40 | 0.003193 | −8.73 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.78 | 45 | 0.003143 | −8.68 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40 | Heptane | 2.02 | 20 | 0.003411 | 1407.81 | −2.7765 | 0.9994 | −11.71 | −10.64 | −8.59 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.95 | 25 | 0.003354 | −8.53 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.87 | 30 | 0.003299 | −8.48 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.79 | 35 | 0.003245 | −8.43 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.72 | 40 | 0.003193 | −8.37 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.64 | 45 | 0.003143 | −8.32 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 60 | Heptane | 1.89 | 20 | 0.003411 | 1443.71 | −3.0312 | 0.9998 | −12.00 | −12.75 | −8.27 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.81 | 25 | 0.003354 | −8.20 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.73 | 30 | 0.003299 | −8.14 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.66 | 35 | 0.003245 | −8.07 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.58 | 40 | 0.003193 | −8.01 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.50 | 45 | 0.003143 | −7.95 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 80 | Heptane | 1.73 | 20 | 0.003411 | 1522.24 | −3.4613 | 0.9999 | −12.66 | −16.33 | −7.87 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.64 | 25 | 0.003354 | −9.17 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.56 | 30 | 0.003299 | −9.13 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.48 | 35 | 0.003245 | −9.09 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.40 | 40 | 0.003193 | −9.05 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.32 | 45 | 0.003143 | −9.01 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 100 | Heptane | 1.54 | 20 | 0.003411 | 1601.70 | −3.9236 | 0.9936 | −13.32 | −20.17 | −7.40 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.44 | 25 | 0.003354 | −7.30 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.34 | 30 | 0.003299 | −7.20 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.31 | 35 | 0.003245 | −7.10 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.18 | 40 | 0.003193 | −7.00 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.11 | 45 | 0.003143 | −6.90 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
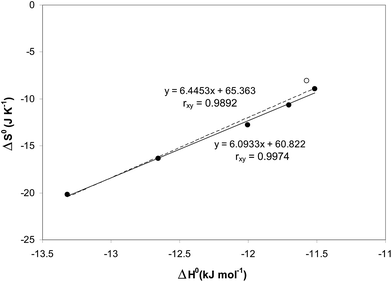
Surprisingly, all the van't Hoff plots were linear, despite the two different processes acting additively (LLE and the chromatographic separation). The resulting standard enthalpies (ΔH0) vary from −11.52 to −13.32 kJ, on increasing the injected volumes from 20 to 100 μL. The entropic terms were determined through the relationship 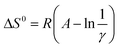 considering the volumes of the MP and SP as 0.447 and 0.1 mL, respectively, and the phase ratio being invariant with respect to the temperature. One can observe from Table 3 that the standard entropy ΔS0 varies from −8.90 to −20.17 J K−1 on increasing the injected volumes from 20 to 100 μL. As illustrated in Fig. 4, the relationship between ΔH0 and ΔS0 was found to be linear (correlation coefficient of 0.9974) when considering injection volumes in heptane ranging from 20 to 100 μL. Such a behavior may be explained through the enthalpy–entropy compensation effects.26 Consideration of data resulting after injections of 1 μL of solutions in methanol (the empty circle in Fig. 4) negatively affects the linearity of the functional relationship (correlation coefficient is reduced to 0.9892).
considering the volumes of the MP and SP as 0.447 and 0.1 mL, respectively, and the phase ratio being invariant with respect to the temperature. One can observe from Table 3 that the standard entropy ΔS0 varies from −8.90 to −20.17 J K−1 on increasing the injected volumes from 20 to 100 μL. As illustrated in Fig. 4, the relationship between ΔH0 and ΔS0 was found to be linear (correlation coefficient of 0.9974) when considering injection volumes in heptane ranging from 20 to 100 μL. Such a behavior may be explained through the enthalpy–entropy compensation effects.26 Consideration of data resulting after injections of 1 μL of solutions in methanol (the empty circle in Fig. 4) negatively affects the linearity of the functional relationship (correlation coefficient is reduced to 0.9892).
The plot of the natural logarithm of capacity factors of the solute (BuP) measured at a given temperature under different injection volume conditions against the corresponding enthalpy change should appear linear when compensation occurs. It has been stated26 that, for purposes of enhancing the accuracy of the experimental data, the working temperature should be placed near the harmonic means of the temperature values used in the van't Hoff study. As illustrated in the ESI,† part 6, the plot of the logarithm of the apparent retention factor (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kapp) at 30 °C (the computed harmonic mean was 32.26 °C) versus ΔH0 is described by a linear relationship characterized by a correlation coefficient of 0.9884, in the case of increasing injection volumes of heptane. If the point corresponding to the injection of 1 μL solution in methanol (accounted only for the chromatographic separation process) is added to the plot, the correlation coefficient is reduced to 0.9609.
kapp) at 30 °C (the computed harmonic mean was 32.26 °C) versus ΔH0 is described by a linear relationship characterized by a correlation coefficient of 0.9884, in the case of increasing injection volumes of heptane. If the point corresponding to the injection of 1 μL solution in methanol (accounted only for the chromatographic separation process) is added to the plot, the correlation coefficient is reduced to 0.9609.
One can conclude that the thermodynamic study revealed the existence of the distinctive LLE and the RP chromatographic stages. As both stages are based on similar interactions of the analyte distributed between a hydrophobic phase (D and SP) and the MP, van't Hoff plots remain linear. The slight increase of the enthalpy on increasing the D volume is well compensated by the entropy change. Through analyzing the compensation plots, the small difference between the chromatographic separation taken alone and the on-line coupling between RP-SLE and RPLC resulted in a reduction of the correlation coefficients. A large entropy change indicates that the solute molecules are retained with less random movement in the SP than they were in the D layer.
3.5. Hydrophobicity indicating scale
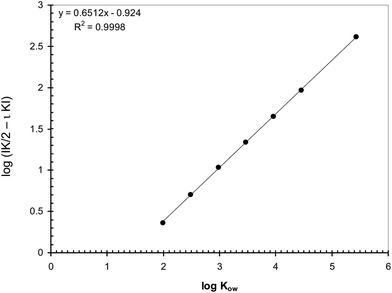
From eqn (19) it results that the slope of the linear regression kapp = f(α) depends on the retention factor of the model compound in the chromatographic column and its partition constant from the MP to the D (K). Consequently, the slope of the linear regression should globally express the affinity of the analyte towards hydrophobic media (the D and the SP), or towards the hydrophilic MP. Thus, a correlation between the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow of the analytes and the slope of the linear regression kapp = f(α) should be observable. Fig. 5 illustrates the correlation between the calculated log
Kow of the analytes and the slope of the linear regression kapp = f(α) should be observable. Fig. 5 illustrates the correlation between the calculated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow values of the target compounds and the logarithms of the slopes of the linear regressions kapp = f(α), taken as absolute values, when using heptane as D on injection. One can observe the excellent correlation between the two sets of data.
Kow values of the target compounds and the logarithms of the slopes of the linear regressions kapp = f(α), taken as absolute values, when using heptane as D on injection. One can observe the excellent correlation between the two sets of data.
Similar correlations were established between log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow and the logarithms of the absolute slopes resulting from the injection of all analytes in the other D (see the ESI,† Part 7). In fact, the data generated in all D are similar, as long as their hydrophobic characteristics are similar with respect to the hydrophobic characteristics of the SP. It appears that the slope of the linear relationship between kapp and α may successfully act as a hydrophobicity descriptor.
Kow and the logarithms of the absolute slopes resulting from the injection of all analytes in the other D (see the ESI,† Part 7). In fact, the data generated in all D are similar, as long as their hydrophobic characteristics are similar with respect to the hydrophobic characteristics of the SP. It appears that the slope of the linear relationship between kapp and α may successfully act as a hydrophobicity descriptor.
4. Conclusions
Large volume injection (LVI) of immiscible D in reversed phase liquid chromatography (RPLC) may be successfully described by means of a reversed phase supported liquid extraction process (RP-SLE) on-line coupled to the chromatographic separation. The simple mathematic model being developed fully explains the linear relationship experimentally established between the apparent retention factor (kapp) and the reduced injected volume (α = VinjV0−1). The model is based on the immobilization of the D plug immediately after its transfer in the column's head, followed by the formation of MP channels. The formation of MP channels leads to inflation of the D plug and allows liquid–liquid extraction of the analytes. The chromatographic separation follows the SLE process in the part of the column remaining after inflation of the D plug up to its maximal extent. The model allows the calculation of the column cross-section occupied by the D. The model was verified on a homologous series of para-alkyl hydroxybenzoates, using hexane, heptane, iso-octane, decane, and dodecane as D. A rapid liquid–liquid extraction from the D in the MP leads to analyte focusing and improves band spreading in the case of rapidly eluting compounds, as compared to the situation of injection of large volumes of samples dissolved in the MP. For analytes poorly extracted from the D by the MP, band spreading is limited by re-focusing in the SP. It was experimentally proven that D saturation of the MP is not responsible for the retention factor reduction under the given conditions. The SLE and RPLC processes consecutively acted according to the proposed mechanism, and are observable in the enthalpy–entropy compensation plots, if compared to the chromatographic separation conditions taken alone. It also results that the logarithm of the slope of the linear relationship between kapp and α, taken as the absolute value, may successfully act as a hydrophobicity descriptor. LVI of immiscible D in RPLC is also one of the most direct proofs that the chromatographic retention mechanism is based on adsorption. Under the experimental conditions, the adsorption based chromatographic retention is “quenched” by the D.Acknowledgements
Some of the authors (Ş. Udrescu, F. Tache, F. Albu and A. Medvedovici) acknowledge the financial support given by the Romanian project PNII_ID_PCE_2011_3_0152.References
- C. F. Poole and S. K. Poole, in Chromatography Today, Elsevier, Amsterdam, 5th edn, 1991, ch. 5, pp. 563–567 Search PubMed.
- M. A. Rezai, G. Famiglini and A. Cappiello, J. Chromatogr. A, 1996, 742, 69–78 CrossRef CAS.
- E. Loeser and P. Drumm, J. Sep. Sci., 2006, 29, 2847–2852 CrossRef CAS.
- S. Keunchkarian, M. Reta, L. Romero and C. Castells, J. Chromatogr. A, 2006, 1119, 20–28 CrossRef CAS PubMed.
- M. Mishra, C. Rana, A. De Wit and M. Martin, J. Chromatogr. A, 2013, 1297, 46–55 CrossRef CAS PubMed.
- B. J. VanMiddlesworth and G. Dorsey, J. Chromatogr. A, 2012, 1236, 77–89 CrossRef CAS PubMed.
- J. Samuelsson, L. Edström, P. Forssén and T. Fornstedt, J. Chromatogr. A, 2010, 1217, 4306–4312 CrossRef CAS PubMed.
- D. Cherrak, E. Guernet, R. Cardot, C. Herrenknecht and M. Czok, Chromatographia, 1997, 46, 647–654 CAS.
- G. Rousseaux, A. De Wit and M. Martin, J. Chromatogr. A, 2007, 1149, 254–273 CrossRef CAS PubMed.
- M. Mishra, M. Martin and A. DeWit, Chem. Eng. Sci., 2010, 65, 2392–2398 CrossRef CAS PubMed.
- D. David, M. Cheregi and A. Medvedovici, Bioanalysis, 2013, 5, 3051–3061 CrossRef PubMed.
- A. Medvedovici, V. David, V. David and C. Georgita, J. Liq. Chromatogr. Relat. Technol., 2007, 30, 199–213 CrossRef CAS.
- V. David, T. Galaon and H. Y. Aboul-Enein, J. Chromatogr. A, 2014, 1323, 115–122 CrossRef CAS PubMed.
- E. Loeser, S. Babiak and P. Drumm, J. Chromatogr. A, 2009, 1216, 3409–3412 CrossRef CAS PubMed.
- V. David, C. Bărcuţean, C. Georgita and A. Medvedovici, Rev. Roum. Chim., 2006, 51, 447–453 CAS.
- T. Galaon, M. Radulescu, V. David and A. Medvedovici, Cent. Eur. J. Chem., 2012, 10, 1360–1368 CrossRef CAS PubMed.
- N. Grinberg, F. Albu, K. Fandrick, E. Iorgulescu and A. Medvedovici, J. Pharm. Biomed. Anal., 2013, 75, 1–6 CrossRef CAS PubMed.
- S. Udrescu, I. D. Sora, V. David and A. Medvedovici, J. Liq. Chromatogr. Relat. Technol., 2010, 33, 133–149 CrossRef CAS.
- S. Udrescu, A. Medvedovici and V. David, J. Sep. Sci., 2008, 31, 2939–2945 CrossRef CAS PubMed.
- A. Medvedovici, S. Udrescu, F. Albu, F. Tache and V. David, Bioanalysis, 2011, 3, 1935–1947 CrossRef CAS PubMed.
- S. Udrescu, I. D. Sora, F. Albu, V. David and A. Medvedovici, J. Pharm. Biomed. Anal., 2011, 54, 1163–1172 CrossRef CAS PubMed.
- M. Cheregi, F. Albu, Ş. Udrescu, N. Rǎducanu and A. Medvedovici, J. Chromatogr. B: Anal. Technol. Biomed. Life Sci., 2013, 927, 124–132 CrossRef CAS PubMed.
- S. Udrescu, I. D. Sora, F. Albu, V. David and A. Medvedovici, J. Pharm. Biomed. Anal., 2011, 54, 1163–1172 CrossRef CAS PubMed.
- A. Medvedovici, S. Udrescu and V. David, Biomed. Chromatogr., 2013, 27, 48–57 CrossRef CAS PubMed.
- C. Sârbu, R. D. Naşcu-Briciu, D. Casoni, A. Kot-Wasik, A. Wasik and J. Namiesnik, J. Chromatogr. A, 2012, 1266, 53–60 CrossRef PubMed.
- W. Melander, D. E. Campbell and C. Horvath, J. Chromatogr., 1978, 158, 215–225 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ay02332c |
| This journal is © The Royal Society of Chemistry 2015 |