Open Access Article
Open Access ArticleStructural directing roles of isomeric phenylenediacetate ligands in the formation of coordination networks based on flexible N,N′-di(3-pyridyl)suberoamide†
Yang-Chih
Lo
a,
Wayne
Hsu
a,
Hsiu-Yi
He
a,
Stephen T.
Hyde
*b,
Davide M.
Proserpio
 *cd and
Jhy-Der
Chen
*a
*cd and
Jhy-Der
Chen
*a
aDepartment of Chemistry, Chung-Yuan Christian University, Chung-Li, Taiwan, ROC. E-mail: jdchen@cycu.edu.tw
bApplied Maths Department, Research School of Physics, Australian National University, Canberra, ACT 0200, Australia. E-mail: stephen.hyde@anu.edu.au
cUniversità degli Studi di Milano, Dipartimento di Chimica, Via Golgi 19, 20133 Milano, Italy. E-mail: davide.proserpio@unimi.it
dSamara Center for Theoretical Materials Science (SCTMS), Samara State University, Ac. Pavlov St. 1, Samara 443011, Russia
First published on 2nd October 2014
Abstract
Reactions of the flexible N,N′-di(3-pyridyl)suberoamide (L) with Cu(II) salts in the presence of the isomeric phenylenediacetic acids under hydrothermal conditions afforded three new coordination networks, {[Cu(L)(1,2-pda)]·H2O}n (1,2-H2pda = 1,2-phenylenediacetic acid), 1, {[Cu(L)(1,3-pda)]·2H2O}n (1,3- H2pda = 1,3-phenylenediacetic acid), 2, and {[Cu(L)(1,4-pda)]·2H2O}n (1,4-H2pda = 1,4-phenylenediacetic acid), 3, which have been structurally characterized by X-ray crystallography. Complex 1 forms a single 3,5-coordinated 3D net with the (42·65·83)(42·6)-3,5T1 topology, which can be further simplified as a 6-coordinated (412·63)-pcu topology. Complex 2 is a 5-fold interpenetrated 3D structure with the (65·8)-cds topology, which exhibits the maximum number of interpenetration presently known for cds and complex 3 is the first 1D self-catenated coordination network. The ligand isomerism of the phenylenediacetate ligands is important in determining the structural types of the Cu(II) coordination networks based on the flexible L ligands.
Introduction
The design and synthesis of coordination networks with interesting topologies and potential applications have attracted great attention during recent years.1 These new complexes thus synthesized are widely applied in catalysis, magnetism materials, gas storage, separation, ion exchange and optics. Entanglement is a very interesting phenomenon in coordination networks, and it is also a major factor contributing to the diversities of coordination networks.2The coordination networks of metal complexes containing flexible bidentate ligands are less predictable due to the possible occurrence of supramolecular isomerism involving the adoption of different ligand conformations.3 However, the flexible ligands with long spacer lengths are prone to form entangled structures due to their inclination to show large voids. Moreover, the dicarboxylate ligands that show diverse coordination ability can be used as auxiliary building blocks in the construction of coordination networks.4 Recently, we have reported two highly interpenetrated diamondoid nets of Zn(II) and Cd(II) coordination networks, {[Zn(L1)(1,4-BDC)]·H2O}n (L1 = N,N′-di(4-pyridyl)adipoamide; 1,4-H2BDC = 1,4-benzenedicarboxylic acid) and {[Cd(L1)(1,4-BDC)]·2H2O}n, which show distorted cages with 8- and 9-fold interpenetrating modes.3f The combination of a long flexible L1 ligand with short rigid 1,4-BDC2− ligands reduced the number of interpenetration compared with the complex [CuSO4(L1)(H2O)2]n featuring a 12-fold interpenetration.3c We have also shown that increasing the number of the backbone carbon atom of the neutral spacer ligand not only decreases the degree of interpenetration but also changes the structural type.3f
With this background information, we sought to investigate the influence of geometry and flexibility of the auxiliary dicarboxylate ligand on the structural diversity of coordination networks containing the flexible N,N′-di(3-pyridyl)suberoamide (L) ligands. The syntheses, structures and properties of {[Cu(L)(1,2-pda)]·H2O}n [H2(1,2-pda) = 1,2-phenylenediacetic acid], 1, {[Cu(L)(1,3-pda)]·2H2O}n [H2(1,3-pda) = 1,3-phenylenediacetic acid], 2, and {[Cu(L)(1,4-pda)]·2H2O}n [H2(1,4-pda) = 1,4-phenylenediacetic acid], 3, form the subject of this report.
Experimental
General procedures
IR spectra (KBr disk) were obtained using a JASCO FT/IR-460 plus spectrometer. Elemental analyses were performed using a PE 2400 series II CHNS/O analyzer or a HERAEUS VaruoEL analyzer. Thermal gravimetric analyses (TGA) measurements were carried out with a TG/DTA 6200 analyzer from SII Nano Technology Inc. from 30 to 900 °C at a heating rate of 10 °C min−1 under nitrogen. Powder X-ray diffraction was carried out using a PANalytical PW3040/60 X'Pert Pro diffractometer with CuKα (λα = 1.54 Å) radiation.Materials
The reagent Cu(OAc)2·H2O was purchased from SHOWA, 1,3-phenylenediacetic acid from Alfa Aesar, and 1,2-phenylenediacetic acid and 1,4-phenylenediacetic acid from ACROS. The ligand N,N′-di(3-pyridyl)suberoamide (L) was prepared according to a published procedure.3dPreparation
X-ray crystallography
The diffraction data for complexes 1–3 were collected with a Bruker AXS SMART APEX II CCD diffractometer at 22 °C, which was equipped with graphite-monochromated Mo Kα (λα = 0.71073 Å) radiation.5 Data reduction was carried out by standard methods with the use of a well-established computational procedure.6 The structure factors were obtained after Lorentz and polarization corrections. An empirical absorption correction based on “multi-scan” was applied to the data for all complexes. The positions of some of the heavier atoms were located by direct methods and the remaining atoms were found in a series of alternating difference Fourier maps and least-square refinements, except that the hydrogen atoms were added by using the HADD command in SHELXTL 5.10. In complexes 1 and 2, some of the carbon [C(6)–C(9) and C(17)–C(18) for 1 and C(14) for 2] and oxygen [O(1) and O(17) for 1] atoms are disordered such that two orientations can be found for each disordered atom. Basic information pertaining to crystal parameters and structure refinement is summarized in Table 1. Selected bond distances and angles are listed in Table 2.| Compound | 1 | 2 | 3 |
|---|---|---|---|
| a R 1 = Σ||Fo| − |Fc||/Σ|Fo|. b wR2 = [Σw(Fo2 − Fc2)2/Σw(Fo2)2]1/2. w = 1/[σ2(Fo2) + (ap)2 + (bp)], p = [max(Fo2 or 0) + 2(Fc2)]/3. a = 0.1048, b = 0.4275, 1; a = 0.1051, b = 0.7142, 2; a = 0.1126, b = 5.7921, 3. c Quality of fit = [Σw(|Fo2| − |Fc2|)2/(Nobserved − Nparameters)]1/2. | |||
| Formula | C28H32N4O7Cu | C28H34N4O8Cu | C28H34N4O8Cu |
| F w | 600.12 | 618.13 | 618.13 |
| Crystal system | Triclinic | Monoclinic | Orthorhombic |
| Space group |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
C2/C | Pmna |
| a, Å | 8.3326(4) | 29.5458(9) | 15.8723(8) |
| b, Å | 10.3780(5) | 6.3519(2) | 12.1103(6) |
| c, Å | 16.5929(9) | 18.5588(6) | 14.8539(7) |
| α, ° | 87.460(3) | 90 | 90 |
| β, ° | 77.784(3) | 125.320(2) | 90 |
| γ, ° | 74.322(3) | 90 | 90 |
| V, Å3 | 1350.09(12) | 2841.88(15) | 2855.2(2) |
| Z | 2 | 4 | 4 |
| D calc, g cm−3 | 1.476 | 1.445 | 1.438 |
| F(000) | 626 | 1292 | 1292 |
| μ(Mo Kα), mm−1 | 0.863 | 0.825 | 0.821 |
| Range(2θ) for data collection, deg | 4.76 ≤ 2θ ≤ 52.00 | 3.38 ≤ 2θ ≤ 52.00 | 3.76 ≤ 2θ ≤ 52.00 |
| Independent reflections | 5302 | 2799 | 2924 |
| [R(int) = 0.1066] | [R(int) = 0.0759] | [R(int) = 0.1033] | |
| Data/restraints/parameters | 5302/0/383 | 2799/0/201 | 2924/0/206 |
| Quality-of-fit indicatorc | 1.028 | 1.009 | 1.053 |
| Final R indices [I > 2σ(I)] a,b | R 1 = 0.0652, wR2 = 0.1670 | R 1 = 0.0624, wR2 = 0.1577 | R 1 = 0.0750, wR2 = 0.1865 |
| R indices (all data) | R 1 = 0.1205, wR2 = 0.2012 | R 1 = 0.1121, wR2 = 0.1864 | R 1 = 0.1229, wR2 = 0.2242 |
| 1 | |||
|---|---|---|---|
| Cu–O(6A) | 1.959(4) | Cu–O(3) | 1.997(3) |
| Cu–N(1) | 2.001(5) | Cu–N(3) | 2.006(5) |
| Cu–O(5B) | 2.173(4) | ||
| O(6A)–Cu–O(3) | 150.3(2) | O(6A)–Cu–N(1) | 85.3(2) |
| O(3)–Cu–N(1) | 90.9(2) | O(6A)–Cu–N(3) | 88.0(2) |
| O(3)–Cu–N(3) | 90.9(2) | N(1)–Cu–N(3) | 169.5(2) |
| O(6A)–Cu–O(5B) | 122.9(2) | O(3)–Cu–O(5B) | 86.8(1) |
| N(1)–Cu–O(5B) | 97.0(2) | N(3)–Cu–O(5B) | 93.4(2) |
| 2 | |||
|---|---|---|---|
| Cu–O(2A) | 1.952(3) | Cu–O(2) | 1.952(3) |
| Cu–N(1) | 2.011(4) | Cu–N(1A) | 2.011(4) |
| O(2A)–Cu–O(2) | 180.0 | O(2A)–Cu–N(1) | 90.0(2) |
| O(2)–Cu–N(1) | 90.0(2) | O(2A)–Cu–N(1A) | 90.0(2) |
| O(2)–Cu–N(1A) | 90.0(2) | N(1)–Cu–N(1A) | 180.0 |
| 3 | |||
|---|---|---|---|
| Symmetry transformations used to generate equivalent atoms: (A) x − 1, y, z. (B) −x + 1, −y + 1, −z + 1 for 1; (A) −x + 1/2, −y + 1/2, −z + 1 for 2; (A) x, y − 1, z. (B) −x + 1, y, z. (C) −x + 1, −y + 1, −z + 1 for 3. | |||
| Cu–O(4A) | 1.949(5) | Cu–O(2) | 1.970(4) |
| Cu–N(1B) | 2.046(4) | Cu–N(1) | 2.046(4) |
| Cu–O(2C) | 2.393(5) | ||
| O(4A)–Cu–O(2) | 177.4(2) | O(4A)–Cu–N(1B) | 87.4(1) |
| O(2)–Cu–N(1B) | 92.7(1) | O(4A)–Cu–N(1) | 87.4(1) |
| O(2)–Cu–N(1) | 92.7(1) | N(1B)–Cu–N(1) | 173.7(2) |
| O(4A)–Cu–O(2C) | 95.6(2) | O(2)–Cu–O(2C) | 81.8(2) |
| N(1B)–Cu–O(2C) | 92.0(1) | N(1)–Cu–O(2C) | 92.0(1) |
Results and discussion
Structure of 1
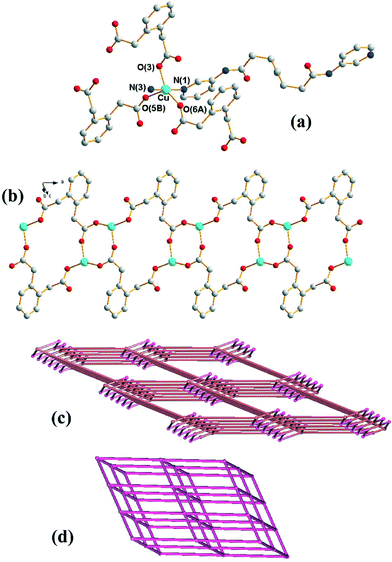
Crystals of 1 conform to the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with one Cu(II) cation, two halves of two different L ligands and one 1,2-PDA2− anion in the asymmetric unit. Fig. 1(a) shows the coordination environment of the Cu(II) metal center, which is five-coordinated by two pyridyl nitrogen atoms from two L ligands and three oxygen atoms from three 1,2-PDA2− ligands, resulting in a distorted square pyramidal geometry with a τ value of 0.32.7 The Cu(II) ions are linked together by the 1,2-PDA2− ligands that adopt the μ3-κ1,κ,1κ1 coordination mode to afford 1D looped chains with dinuclear metal units (Fig. 1(b)) which are further connected by the L ligands through the pyridyl nitrogen atoms to form a 3D structure. In the structure, 1,2-PDA2− interact with the L ligand through N–H⋯O (H⋯O = 2.02 Å, N⋯O = 2.86 Å, ∠N–H–O = 162°) hydrogen bonds.
with one Cu(II) cation, two halves of two different L ligands and one 1,2-PDA2− anion in the asymmetric unit. Fig. 1(a) shows the coordination environment of the Cu(II) metal center, which is five-coordinated by two pyridyl nitrogen atoms from two L ligands and three oxygen atoms from three 1,2-PDA2− ligands, resulting in a distorted square pyramidal geometry with a τ value of 0.32.7 The Cu(II) ions are linked together by the 1,2-PDA2− ligands that adopt the μ3-κ1,κ,1κ1 coordination mode to afford 1D looped chains with dinuclear metal units (Fig. 1(b)) which are further connected by the L ligands through the pyridyl nitrogen atoms to form a 3D structure. In the structure, 1,2-PDA2− interact with the L ligand through N–H⋯O (H⋯O = 2.02 Å, N⋯O = 2.86 Å, ∠N–H–O = 162°) hydrogen bonds.
If the Cu(II) cations are defined as 5-coordinated nodes and the 1,2-PDA2− ligands as 3-coordinated nodes, topological analysis reveals that the structure of 1 can be regarded as a 3,5-coordinated net with the (42·65·83)(42·6)-3,5T1 topology (Fig. 1(c)), as determined using TOPOS.8 If the Cu2(μ-COO)2 dimer is considered as a node, the structure of 1 can be further simplified as a 6-coordinated net with a single (412·63)-pcu topology (Fig. 1(d)). The underlying 3,5T1 net is observed in 81 crystals (interpenetrated in 13) as can be found in TTD TOPOS database.9 Interestingly five compounds present M2(μ-COO)2 dimers that allow the same alternative cluster description of the net as pcu,10 with [Cd(adp)(bpfp)]n [adp = adipate; bpfp = bis(4-pyridylformyl)piperazine] the only one with two different ligands of very different lengths.10a
Structure of 2
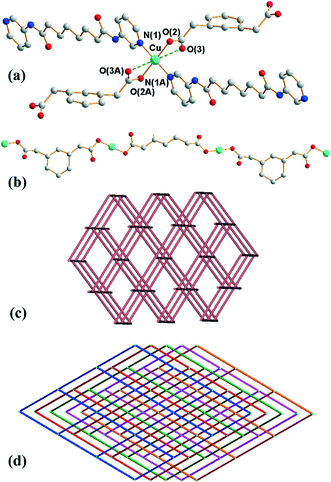
Crystals of 2 conform to the monoclinic space group C2/c with the Cu(II) cation on the inversion center, with half of L and 1,3-PDA2− ligands in the asymmetric unit. The coordination environment of the Cu(II) metal center is shown in Fig. 2(a), which is four-coordinated by two pyridyl nitrogen atoms from two L ligands and two oxygen atoms from two 1,3-PDA2− ligands, resulting in a distorted square planar geometry. Two weak Cu⋯O interactions with a distance of 2.620(4) Å are also observed in the axial positions. The Cu(II) ions are linked together by the 1,3-PDA2− ligands that adopt the μ2-κ1,κ,1 coordination mode to afford 1D linear chains (Fig. 2(b)), which are further linked by the L ligands through the pyridyl nitrogen atoms to form a 3D structure.Each Cu(II) ion is connected to four neighboring Cu(II) ions through two 1,3-PDA2− and two L ligands with distances of 12.08 Å (through 1,3-PDA2−) and 21.69 (through L), and thus each Cu(II) ion can be considered as a four-coordinated node. Topological analysis reveals that complex 2 forms a 5-fold interpenetrated 3D coordination network with the (65·8)-cds topology (Fig. 2(c) and (d)). The 5 nets are related by a single translation [0,1,0]; thus they belong to Class Ia.11 According to the TTO database of TOPOS,8,9 the maximum number of interpenetrations that has been reported for cds in coordination networks is four and there are three examples. Complex 2 thus exhibits the maximum number of interpenetrations presently known for cds. The five interpenetrated nets are joined in a single net by N–H⋯O [H⋯O = 2.06 Å, N⋯O = 2.90 Å ∠N–H⋯O = 164°] hydrogen bonds from the amine hydrogen atoms of the L ligands to the carboxylate oxygen atoms of the 1,3-PDA2− ligands (Fig. S4†). The water molecules are also involved in hydrogen bonds with the 1,3-PDA2− ligands through O–H⋯O (H⋯O = 1.91 and 2.25 Å, O⋯O = 2.76 and 3.02 Å, ∠O–H⋯O = 179 and 151°).
Structure of 3
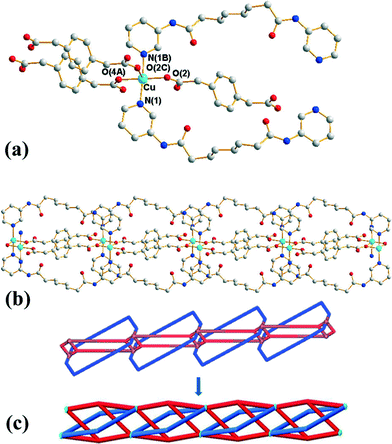
Crystals of 3 conform to the orthorhombic space group Pmna with the Cu(II) cation lying on a mirror plane, with half of L and 1,4-PDA2− ligand and two cocrystallized water molecules in the asymmetric unit. Fig. 3(a) shows the coordination environment of the Cu(II) metal center, which is five-coordinated by two pyridyl nitrogen atoms from two L ligands and three oxygen atoms from three 1,4-PDA2− ligands, resulting in a distorted square pyramidal geometry with a τ value of 0.06. The Cu(II) ions are bridged by the 1,4-PDA2− anions that adopt the μ3-κ1,κ1,κ1 coordination mode to form dinuclear units with a Cu⋯Cu distance of 3.309(1) Å, which are further linked by the L ligands and the 1,4-PDA2− ligands to form a 1D self-catenated coordination network (Fig. 3(b) and (c)). It can be seen that each 34-membered ring that involves two Cu(II) ions and two L ligands is penetrated by two 1,4-PDA2− ligands. Adjacent 1D chains are connected by water molecules through N–H⋯O (H⋯O = 2.14 Å, N⋯O = 3.00 Å, ∠N–H⋯O = 177°) hydrogen bonds originating from the amine hydrogen atoms of the L ligands to the water molecules and O–H⋯O (H⋯O = 1.82–1.93 Å, O⋯O = 2.65–2.76 Å ∠O–H⋯O = 164–168°) hydrogen atoms to the carboxylate oxygen atoms of 1,3-PDA2− ligands (Fig. S5†).Self-catenated nets are single nets that exhibit the peculiar feature of containing shortest rings through which pass other components of the same network.12 Catenation can be identified by the presence of edges that thread a ring; in other words, they share at least one point with a disc-like film bounded by the ring. Since infinite nets with three lattice vectors inevitably contain large cycles that are threaded, we restrict “rings” to smallest cycles in the net that cannot be decomposed into sums of still smaller cycle, such as “strong rings”.13 If both the threaded edge and the ring belong to a single connected component of the structure, it is self-catenated. Most coordination networks showing the feature of self-catenation are 3D nets,14 and there are only several 2D cases that are presently known.15 Complex 3 thus appears to be the first 1D coordination network showing self-catenation.
This network has an additional feature that is worth noting, namely, it is entangled. To see this, it is convenient to redraw complex 3 as a “ladder” (with single back- “/” and paired forward-slash “\” stringers), as shown in Fig. 4(a). Here the structure has been redrawn to preserve its topology. Further, although its geometric details (such as vertex locations and bonding geometries) are distorted, its tangled features, namely, the mutual catenation of edges and cycles, are also preserved. This means that the structure in Fig. 4(a) is an equivalent “tangled-isotope” that preserves both the topology and the edge crossings. Here we adopt the term “tangled-isotope” from the mathematical operation of “ambient isotopy”, corresponding to distortions of a structure that do not alter its inherent entanglement.16 The ring formed by a pair of forward-slashes – one above and one below – sharing two vertices is threaded by (two parallel) back-slashes, describing the self-catenation. A simpler, untangled-isotope is that whose pair of forward-slash stringers is either both above or both below the back-slash stringers, as illustrated in Fig. 4(b). The edges of this untangled-isotope reticulate a cylinder without any edge crossings (with forward- and back-slashes running on opposite faces of the cylinder). In contrast, the edges of complex 3 cannot reticulate a cylinder without edge crossings: a multi-handled surface made of a pair of parallel cylinders with connecting tubes is necessary to support a crossing-free reticulation. Since this latter surface is topologically more complex than the simple cylinder, complex 3 is (according to the definition advanced in ref. 15) entangled.
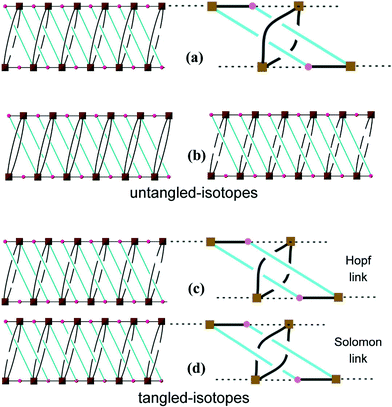 | ||
| Fig. 4 (a) A schematic drawing of 3. (b) Two equivalent representations of the same arrangement but NOT entangled. (c) A drawing showing the Hopf links. (d) A drawing showing the Solomon links. | ||
Closely related tangled-isotopes to complex 3 are knotted, with more common signatures of entangled networks in terms of constituent knots or links. For example, permutations of the crossings between forward- and back-slash stringers result in patterns containing threaded links, or pairs of catenated rings. Two of the simpler tangled-isotopes are those with Hopf links (Fig. 4(c)) and Solomon links (Fig. 4(d)). In stark contrast to complex 3, both of these are tangled-isotopes since they contain pairs of interwoven cycles that cannot be separated without breaking edges, as illustrated in the figures. They are distinguished by the crossings of one cycle (blue in the figures) with the interlocked (black) cycle. If we denote crossings of blue edges over/under black edges by the symbols “+”/“−”, an anticlockwise walk around a blue cycle made of four edges in Fig. 4(c) crosses black edges in the order “− + + +” (or cyclic permutations); the analogous walk in Fig. 4(d) is “+ − + −”. These sequences of over and under crossings characterise Hopf and Solomon links, respectively (see, for example, ref. 17). However, the entanglement in complex 3 is a peculiar and hitherto unrecognised one. It has neither knots nor links. Further, it is also free of “ravels” – a subtle entanglement mode distinct from knots or links – that can be formed in tangled nets.18 To date, knots, links and ravels have all been identified in metal–organic complexes.2,19 Complex 3 is, to our knowledge, the first example of a tangled net that does not contain knots, links or ravels, thus exemplifying a new mode of entanglement.
Ligand conformations and structural comparisons
Twenty ligand conformations can be found for L if the A and G conformations are given when the C–C–C–C torsion angle (θ) is 0 ≤ θ ≤ 90° and 90 ≤ θ < 180°, respectively. In addition, based on the relative orientation of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups, each conformation can adopt a cis or a trans arrangement. Moreover, due to the difference in the orientations of the pyridyl nitrogen atom positions, three more orientations, anti–anti, syn–anti and syn–syn, based on the relative positions of the pyridyl nitrogen and amide oxygen atom can also be derived (Fig. 5).
O groups, each conformation can adopt a cis or a trans arrangement. Moreover, due to the difference in the orientations of the pyridyl nitrogen atom positions, three more orientations, anti–anti, syn–anti and syn–syn, based on the relative positions of the pyridyl nitrogen and amide oxygen atom can also be derived (Fig. 5).
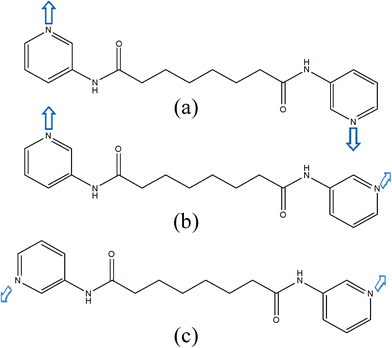 | ||
| Fig. 5 Three possible orientations for the pyridyl nitrogen atoms of the L ligand: (a) syn–syn (b) syn–anti (c) anti–anti. | ||
Table 3 lists all of the ligand conformations of the L ligand in complexes 1–3. The structural parameters of the reported complexes [Cu(L)(1,2-bdc)]n (1,2-H2bdc = 1,2-benzenedicarboxylic acid) and [Cu(L)(1,3-bdc)(H2O)·3H2O]n (1,3-H2bdc = 1,3-benzenedicarboxylic acid) that contain L are also shown for comparison.20 A comparison of these structures shows that the flexibility of the dicarboxylate ligands, in which the pda2− ligands in 1–3 hold two more CH2 groups than the bdc2–ligands, significantly affects the structural diversity. In 1 and [Cu(1,2-bdc)(L)]n, the 1,2-pda2− and 1,2-bdc2− ligands adopt the μ3-κ1,κ1,κ1 mode and μ2-κ2,κ2 mode, respectively, resulting in AAAAA trans anti–anti and GGAGG trans anti–anti conformations for the L ligands in 1 and AAAAA trans syn–syn conformation for the L ligands in [Cu(1,2-bdc)(L)]n, forming a 3D structure with 3,5T1 topology and a 2D wavelike structure, respectively. In contrast, the 1,3-pda2− and 1,3-bdc2− ligands of 2 and [Cu(1,3-bdc)(L)(H2O)]·3H2O adopt the same μ2-κ1,κ1 coordination mode, but lead to the formation of AAAAA trans anti–anti conformation for the L ligands in 2 and GAAAG trans syn–syn and AAAAA trans syn–syn conformations for the L ligands in [Cu(1,3-bdc)(L)(H2O)]·3H2O, resulting in 5- and 3-fold interpenetration, respectively. In each single cds structure, the distances between the Cu(II) nodes are 12.08 Å (through 1,3-pda2−) and 21.69 Å (through L) for 2 significantly longer than those of 9.66 Å (through 1,3-bdc2−) and 19.46 Å (through L) for [Cu(1,3-bdc)(L)(H2O)]·3H2O, indicating the importance of the length of the spacer ligand in determining the number of interpenetrations. The cis- and trans-conformations of the phenylenediacetate ligands have been investigated recently.21 For example, in the 1D ladder-like silver(I) complex [Ag3(cis-pda)(bipy)3]n·0.5n(trans-pda)·5nH2O (bipy = 4,4′-bipyridine), both of the two different formations (cis- and trans) of the 1,2-pda2− ligands were observed.21a Inspection of the structures of the three isomeric pda2− ligands in 1–3 reveals that they all adopt the trans conformation.
| Complex | Coordination mode of the dicarboxylate ligand | Conformation of L | Structure |
|---|---|---|---|
| a Derived from the crystallographic data for [Cu(L)(1,2-BDC)]n and {[Cu(L)(1,3-BDC)(H2O)]·3H2O}n. | |||
| {[Cu(L)(1,2-pda)]·H2O}n, 1 | μ3-κ1,κ1,κ1 | AAAAA trans anti–anti | 3,5T1 |
| GGAGG trans anti–anti | |||
| {[Cu(L)(1,3-pda)]·2H2O}n,2 | μ2-κ1,κ1 | AAAAA trans anti–anti | cds, 5-fold interpenetration |
| {[Cu(L)(1,4-pda)]·2H2O}n, 3 | μ3-κ1,κ1,κ1 | GAAAG cis syn–syn | 1D self-catenation |
| [Cu(L)(1,2-bdc)]n | μ2-κ2,κ2 | AAAAA trans syn–syna | sql |
| {[Cu(L)(1,3-bdc)(H2O)]·3H2O}n | μ2-κ1,κ1 | GAAAG trans syn–syna | cds, 3-fold interpenetration |
| AAAAA trans syn–syna | |||
Thermal properties
In order to estimate the stability of the frameworks, thermogravimetric analysis (TGA) of complexes 1–3 was carried out in nitrogen from 30 to 900 °C (Fig. S6 and Table S1†). The TGA curve of 1 shows the gradual weight loss of water molecules (calculated 5.02%; observed 3.53%) in 50–190 °C. The weight loss between 200 and 460 °C corresponds to the decomposition of the L ligand and 1,4-pda2− ligand (calculated 84.96%; observed 86.41%). The TGA curve of 2 shows the gradual weight loss of water molecules (calculated 3.00%; observed 2.16%) in 45–200 °C, and the weight loss of 86.19% between 200 and 510 °C corresponds to the decomposition of the L ligand and 1,4-pda2− ligand (calculated 86.41%). For complex 3, the TGA curve shows the gradual weight loss of water molecules (calculated 5.83%, observed 6.56%) in 50–200 °C. The weight loss of 83.26% between 200 and 460 °C can be ascribed to the decomposition of the L ligand and 1,4-pda2− ligand (calculated 83.89%). The TGA results show that the weight losses that are due to the removal of cocrystallized and the bonded water molecules occurred in 45–200 °C, and the organic ligands decomposed at temperatures above 200 °C. The different structural types of 1–3 do not affect the decomposition of the organic ligands significantly. The PXRD patterns of complexes 1–3 heated at 150 °C for 3 hours shown in Fig. S1–S3† reveal that their structures are stable upon solvent removal. It is noted that the solvent-accessible volumes of complexes 1–3 calculated with PLATON22 after the removal of water molecules are as small as 67.5, 161.0 and 196.2 Å3, which are 5.0%, 5.7% and 6.9% of each of the unit cell volumes, respectively.Conclusion
Three new coordination networks containing L and isomeric phenylenediacetate ligands have been successfully synthesized under hydrothermal conditions. The different structures in 1–3 can be attributed to the ligand isomerism of the PDA2− ligands that result in different L conformations. Obviously, the L ligands are sufficiently flexible to adjust to the stereochemical requirements for the formation of complexes 1–3, which adopt the conformations that maximize their intra- and intermolecular forces. To our best knowledge, complex 1 is a rare example with two different ligands of very different lengths, with underlying 3,5T1 nets further simplified to pcu; complex 2 shows the maximum number of interpenetrations presently known for cds coordination networks; and complex 3 is the first 1D self-catenated, entangled, unknotted and unravelled coordination network.Acknowledgements
We are grateful for the Ministry of Science and Technology of the Republic of China for support. DMP acknowledges the Ministry of Education and Science of Russia (grant 14.B25.31.0005).References
- (a) E. R. T. Tiekink and J. J. Vittal, Frontiers in Crystal Engineering, John Wiley & Sons, Ltd., England, 2006 Search PubMed; (b) C. B. Aakeröy, N. R. Champness and C. Janiak, CrystEngComm, 2010, 12, 22 RSC; (c) M. O'Keeffe, M. A. Peskov, S. J. Ramsden and O. M. Yaghi, Acc. Chem. Res., 2008, 41, 1782 CrossRef PubMed; (d) J. R. Li, R. J. Kuppler and H. C. Zhou, Chem. Soc. Rev., 2009, 38, 1477 RSC; (e) M. D. Allendorf, C. A. Bauer, R. K. Bhakta and R. J. T. Houk, Chem. Soc. Rev., 2009, 38, 1330 RSC; (f) B. Moulton and M. J. Zaworotko, Chem. Rev., 2001, 101, 1629 CrossRef CAS PubMed; (g) W. L. Leong and J. J. Vittal, Chem. Rev., 2011, 111, 688 CrossRef CAS PubMed; (h) Z. Niu and H. W. Gibson, Chem. Rev., 2009, 109, 6014 CrossRef PubMed.
- (a) L. Carlucci, G. Ciani and D. M. Proserpio, Coord. Chem. Rev., 2003, 246, 247 CrossRef CAS; (b) D. M. Proserpio, Nat. Chem., 2010, 2, 435 CrossRef CAS PubMed; (c) L. Carlucci, G. Ciani, D. M. Proserpio, T. G. Mitina and V. A. Blatov, Chem. Rev., 2014, 114, 7557 CrossRef CAS PubMed; (d) G.-P. Yang, L. Hou, X.-J. Luan, B. Wu and Y.-Y. Wang, Chem. Soc. Rev., 2012, 41, 6992 RSC; (e) J.-Q. Liu, Y.-Y. Wang, P. Liu, Z. Dong, Q.-Z. Shia and S. R. Batten, CrystEngComm, 2009, 11, 1207 RSC.
- See, for examples: (a) L. Carlucci, G. Ciani, D. M. Proserpio and S. Rizzato, CrystEngComm, 2002, 4, 121 RSC; (b) H.-C. Chen, H.-L. Hu, Z.-K. Chan, C.-W. Yeh, H.-W. Jia, C.-P. Wu, J.-D. Chen and J.-C. Wang, Cryst. Growth Des., 2007, 7, 698 CrossRef CAS; (c) Y.-F. Hsu, C.-H. Lin, J.-D. Chen and J.-C. Wang, Cryst. Growth Des., 2008, 8, 1094 CrossRef CAS; (d) Y.-F. Hsu, H.-L. Hu, C.-J. Wu, C.-W. Yeh, D. M. Proserpio and J.-D. Chen, CrystEngComm, 2009, 11, 168 RSC; (e) Y.-F. Hsu, W. Hsu, C.-J. Wu, P.-C. Cheng, C.-W. Yeh, W.-J. Chang, J.-D. Chen and J.-C. Wang, CrystEngComm, 2010, 12, 702 RSC; (f) J.-J. Cheng, Y.-T. Chang, C.-J. Wu, Y.-F. Hsu, C.-H. Lin, D. M. Proserpio and J.-D. Chen, CrystEngComm, 2012, 14, 537 RSC.
- (a) M. Du, X.-J. Jiang and X.-J. Zhao, Chem. Commun., 2005, 5521 RSC; (b) M. Du, Z.-H. Zhang, X.-G. Wang, L.-F. Tang and X.-J. Zhao, CrystEngComm, 2008, 10, 1855 RSC; (c) M. Du, X.-J. Jiang and X.-J. Zhao, Inorg. Chem., 2007, 46, 3984 CrossRef CAS PubMed; (d) J. Yang, J.-F. Ma, Y.-Y. Liu, J.-C. Ma and S. R. Batten, Cryst. Growth Des., 2009, 9, 1894 CrossRef CAS.
- Bruker AXS, APEX2, V2008.6, SADABS V2008/1, SAINT V7.60A, SHELXTL V6.14, Bruker AXS Inc., Madison, Wisconsin, USA, 2008.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112 CrossRef CAS PubMed.
- A. W. Addison, T. N. Rao, J. Reedijik, J. V. Rijn and G. C. Verschoor, J. Chem. Soc., Dalton Trans., 1984, 1349 RSC.
- V. A. Blatov, A. P. Shevchenko and D. M. Proserpio, Cryst. Growth Des., 2014, 14, 3576 CAS . See also: http://www.topos.samsu.ru/.
- E. V. Alexandrov, V. A. Blatov, A. V. Kochetkov and D. M. Proserpio, CrystEngComm, 2011, 13, 3947 RSC.
- PECJIS: (a) A. L. Pochodylo and R. L. LaDuca, Inorg. Chim. Acta, 2012, 389, 191 CrossRef CAS PubMedSUNHEP, SUNHIT, SUNHOZ: (b) J. Zhang, T. Wu, S. Chen, P. Feng and X. Bu, Angew. Chem., Int. Ed., 2009, 48, 3486 CrossRef PubMedQUJHIN: (c) F. Guo, J. Coord. Chem., 2009, 62, 3621 CrossRef CAS.
- V. A. Blatov, L. Carlucci, G. Ciani and D. M. Proserpio, CrystEngComm, 2004, 6, 377 RSC.
- L. Carlucci, G. Ciani and D. M. Proserpio, in Making crystals by design: methods, techniques and applications, ed. D. Braga and F. Grepioni, Wiley-VCH, Weinheim, 2007, ch. 1.3, p. 58 Search PubMed.
- O. Delgado-Friedrichs and M. O'Keeffe, J. Solid State Chem., 2005, 178, 2480 CrossRef CAS PubMed.
- X.-J. Ke, D.-S. Li and Du Miao, Inorg. Chem. Commun., 2001, 14, 788 CrossRef PubMed.
- See for examples: (a) M. J. Plater, M. R. S. J. Foreman, T. Gelbrich and M. B. Hursthouse, J. Chem. Soc., Dalton Trans., 2000, 1995 RSC; (b) L.-P. Zhang, J. Yang, J.-F. Ma, Z.-F. Jia, Y.-P. Xie and G.-H. Wei, CrystEngComm, 2008, 10, 1410 RSC; (c) Y.-Y. Liu, Z.-H. Wang, J. Yang, B. Liu, Y.-Y. Liu and J.-F. Ma, CrystEngComm, 2011, 13, 3811 RSC; (d) Y.-Y. Liu, H.-Y. Liu, J.-F. Ma, Y. Yang and J. Yang, CrystEngComm, 2013, 15, 1897 RSC; (e) Y. Gong, P. G. Jiang, J. Li, T. Wu and J. H. Lin, Cryst. Growth Des., 2013, 13, 1059 CrossRef; (f) D.-R. Xiao, Y.-G. Li, E.-B. Wang, L.-L. Fan, H.-Y. An, Z.-M. Su and L. Xu, Inorg. Chem., 2007, 46, 4158 CrossRef CAS PubMed; (g) R. Custelcean and M. G. Gorbunova, CrystEngComm, 2005, 7, 297 RSC; (h) K. Zhou, F.-L. Jiang, L. Chen, M.-Y. Wu, S.-Q. Zhang, J. Ma and M.-C. Hong, Chem. Commun., 2012, 5521 Search PubMed; (i) G. O. Lloyd, J. L. Atwood and L. J. Barbour, Chem. Commun., 2005, 1845 RSC; (j) J.-K. Sun, Q.-X. Yao, Z.-F. Ju and J. Zhang, CrystEngComm, 2010, 12, 1709 RSC; (k) C.-C. Wang, S.-M. Tseng, S.-Y. Lin, F.-C. Liu, S.-C. Dai, G.-H. Lee, W.-J. Shih and H.-S. Sheu, Cryst. Growth Des., 2007, 7, 1783 CrossRef CAS.
- (a) P. Cromwell, Knots and Links, Cambridge University Press, England, 2004 Search PubMed; (b) T. Castle, M. E. Evans and S. T. Hyde, Prog. Theor. Phys. Supp., 2011, 191, 235 CrossRef.
- R. S. Forgan, J.-P. Sauvage and J. F. Stoddart, Chem. Rev., 2011, 111, 5434 CrossRef CAS PubMed.
- (a) T. Castle, M. E. Evans and S. T. Hyde, New J. Chem., 2008, 32, 1484 RSC; (b) T. Castle, Entangled graphs on surfaces in space, Ph.D. Thesis, Australian National University, Canberra, 2013, http://hdl.handle.net/1885/11978 Search PubMed.
- F. Li, J. K. Clegg, L. F. Lindoy, R. B. Macquart and G. V. Meehan, Nat. Commun., 2011, 2, 205 CrossRef PubMed.
- X.-L. Wang, F.-F. Sui, H.-Y. Lin, C. Xu, G.-C. Liu, J.-W. Zhang and A.-X. Tian, CrystEngComm, 2013, 15, 7274 RSC.
- (a) G.-P. Yang, J.-H. Zhou, Y.-Y. Wang, P. Liu, C.-C. Shi, A.-Y. Fu and Q.-Z. Shi, CrystEngComm, 2011, 13, 33 RSC; (b) G.-P. Yang, Y.-Y. Wang, P. Liu, A.-Y. Fu, Y.-N. Zhang, J.-C. Jin and Q.-Z. Shi, Cryst. Growth Des., 2010, 10, 1443 CrossRef CAS; (c) T. Liu, J. Lu, L. Shi, Z. Guo and R. Cao, CrystEngComm, 2009, 11, 583 RSC.
- A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: PXRD patterns of 1–3 (Fig. S1–S3). Drawings showing the hydrogen bonds in 2 and 3 (Fig. S4–S5). TGA curves of 1–3 (Fig. S6). Thermal properties of 1–3 (Table S1). CCDC 1014134–1014136. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4ce01752h |
| This journal is © The Royal Society of Chemistry 2015 |