Towards chiral distributions of dopants in microporous frameworks: helicoidal supramolecular arrangement of (1R,2S)-ephedrine and transfer of chirality

Abstract

A molecular-mechanics computational study is performed in order to analyze the arrangement of (1R,2S)-(–)-ephedrine molecules within the 12-MR channels of the AFI aluminophosphate microporous framework and the influence on the spatial distribution of dopants embedded in the tetrahedral network. Results showed that ephedrine molecules arrange exclusively as dimers by π–π stacking of the aromatic rings within the AFI channels. Interestingly, the asymmetric nature of ephedrine and the presence of H-bond-forming groups (NH₂ and OH) involve a preferential orientation where consecutive dimers within the channels are rotated by an angle of +30°; this is driven by the establishment of inter-dimer H-bonds. This preferential orientation leads to the development of a supramolecular enantiomerically-pure helicoidal (chiral) arrangement of ephedrine dimers. In addition, the computational results demonstrate that the particular molecular structure of ephedrine imparts a strong trend to attract negative charges to the vicinity of the NH₂⁺ positively-charged groups. Hence divalent dopants such as Mg, whose replacement by trivalent Al in the aluminophosphate network involves the generation of a negative charge, will tend to locate close to the NH₂⁺ molecular groups, suggesting that an imprinting of the organic arrangement to the spatial distribution of dopants would be feasible. Combined with the trend of ephedrine to arrange in a helicoidal fashion, an enantiomerically-pure helicoidal distribution of dopants would be expected, thus inducing a new type of chirality in microporous materials.

---

Introduction

Chirality is ubiquitous in nature. Indeed, homochirality (chirality in enantiopure form) is fundamental for life as we understand it, since life in nature decided to work in an asymmetric fashion,¹ although the origin of this is still unresolved and a matter of intense research. Most of the biochemical building-blocks of living organisms, specifically amino acids and nucleotides that build proteins and nucleic acids, are homochiral.² As a consequence, chiral molecules usually lead to a different biological response in living organisms depending on their absolute configuration, with very often only one of the enantiomers having the desired effect. Therefore, the quest for materials that can perform enantioselective operations, i.e. asymmetric catalytic synthesis and separation, represents nowadays a great challenge for chemists. The most attractive feature of this challenge is the effect of chiral multiplication, where minor amounts of a chiral material can produce large amounts of chiral compounds.³

Although more rarely, chirality also occurs in inorganic systems. However, homochirality is hardly found in inorganic compounds: even though quartz was soon recognized as being chiral, it occurs in nature in both right- and left-handed configurations.⁴ Nevertheless, such inorganic chiral systems can potentially transfer their chirality to organic processes and lead to enantioselective operations, as was found by using enantiopure crystals of quartz.⁵ In this context, zeolite-type materials are considered as optimum candidates for achieving chiral inorganic materials because they can potentially combine two crucial features in chemical processes, porosity and their characteristic shape-selectivity, with enantioselectivity.^6,7 Early attempts to induce chirality in zeolitic materials considered the immobilization of homogeneous chiral catalysts⁸ or the anchoring of chiral additives,⁹ which led to some enantiomeric excesses. However, a much preferred alternative consists of the production of chiral zeolite-type materials in which chirality is intrinsic to the framework and is not contained in an extra-framework, and thus weakly-retained, component. Indeed, several chiral zeolitic materials do exist, as was soon recognized by Treacy and Newsam with polymorph A of zeolite BEA;¹⁰ interesting examples have been recently discovered,¹¹ as the mesoporous chiral ITQ-37 zeolite¹² and HPM-1,¹³ the silica-form of the chiral SU-32 silicogermanate.¹⁴ However, these materials almost invariably crystallize as racemic mixtures, limiting their use for enantioselective operations. Homochirality in microporous materials is hardly found, although some examples do spontaneously (and normally unpredictably) occur through chiral symmetry breaking effects.^15,16 Moreover, an interesting strategy by using nucleotides as chiral inductors has also led to a certain enantioenrichment of a chiral zeotype crystal.¹⁷

Several strategies have been followed in an attempt to induce the crystallization of zeolite-type chiral structures.^18,19 Zeolitic materials are built from achiral units (TO₄), and therefore their chirality comes from a chiral long-range ordering of such units, usually in the form of helicoidal channels.¹¹ Hence, the induction of chirality must come from elements external to the frameworks, like chiral solvents or additives.¹⁸ A particular feature of the synthesis of zeolitic materials is that it usually involves the addition of organic molecules (referred to as structure-directing agents or templates) to the synthesis gels to direct the crystallization pathway towards a particular framework type.^20–22 This provided what seemed a direct obvious strategy in an attempt to induce chirality through the use of chiral structure-directing agents (SDAs). However, although chiral SDAs effectively led to zeolitic materials, the failure of this strategy to transfer the chirality from the molecular component to the inorganic framework was soon recognized.¹⁹ Such failure of the transfer of chirality might be associated, on the one hand, to the typical lack of strong non-bonding interactions between the frameworks and the SDA molecules during zeolite crystallization, and the consequent free rotational movement of the molecules within the porous frameworks. Such movement would cancel the asymmetric micro-environment generated around the chiral SDA molecule. Indeed, Yu and coworkers established the important role of H-bonds during the transfer of chirality to an inorganic chiral framework.²³ A second reason for the lack of success in the transfer of chirality during templating might come from the different dimensions of the chiral nature associated with organic molecules, which comes from the presence of stereogenic centres that creates a very local (short-ranged) asymmetric micro-environment, and that of microporous frameworks, where chirality comes from the asymmetric long-range ordering of achiral TO₄ units.

In an attempt to overcome such problems, we recently proposed a new concept of chirality in microporous materials.^24,25 Since the tetrahedral dopant substituents embedded in microporous frameworks are in general the ones involved in catalytic processes, we proposed a helicoidal, and hence chiral, ordering of only these active atoms in order to produce chiral materials. Indeed, a Co-containing aluminophosphate material with such a feature has been already found.¹⁵ The problem resides on how to drive the incorporation of dopants in microporous frameworks in such a way, taking into account that the chiral nature of such materials would come from the long-range ordering of the dopants. In this sense, we consider as a crucial issue the change, during templating, from single-unit chiral SDA molecules, which will create local chiral microenvironments, to self-assembling chiral organic molecules that can develop supramolecular long-ranged helicoidal (and hence chiral) arrangements, which will induce long-ranged chiral environments, thus adapting the dimensions of the chirality to that of the microporous frameworks.

An attractive way of achieving such supramolecular long-range helicoidal organic arrangements is by using self-assembling chiral aromatic amines. Our group has been for some time working on the use of aromatic amines that self-assemble through π–π type interactions leading to supramolecular aggregates as SDAs for the synthesis of microporous aluminophosphates.^26–30 Computational simulations showed that (S)-(N)-benzyl-2-pyrrolidinemethanol (BPM), a chiral SDA that directed the crystallization of the AFI framework, the structure of which is composed of non-interconnected 12-membered-ring one-dimensional channels, tended to form dimers when occluded within this framework. Interestingly, the most stable packing of these dimers within the pores involved consecutive dimers always rotated by an angle of −90°, thus leading to a long-range helicoidal supramolecular arrangement of BPM dimers.²⁴ The asymmetric nature of BPM provided by the presence of a methanol-substituent in the pyrrolidine ring involves the presence of a particular preferred inter-dimer rotation (−90°) driven by a better fit between pyrrolidine rings of consecutive dimers. However, we should note that the formation of dimers is strongly dependent on the nature of the dopant incorporated in the AFI network,²⁸ and is limited by the electrostatic repulsion between adjacent protonated BPM molecules.³⁰ In any case, this represents a feasible strategy to induce a long-range supramolecular chiral organic arrangement that could be potentially imprinted into a microporous framework, in particular into the spatial distribution of dopants. For such a transfer of chirality (chiral imprinting) to occur, a strong and localized interaction between a particular area of the SDA molecule and the dopant to be incorporated must occur. In this regard, the substitution of trivalent Al by Si⁴⁺ in zeolites or divalent metals (such as Mg, Co or Zn) by Al³⁺ in aluminophosphate networks involves the generation of a negative charge on the framework which is compensated for by the positive charge of the SDA molecules. We recently observed that secondary amines with protonated NH₂⁺ groups show a great trend to locate dopants in their vicinity through the formation of H-bonds, and thus these SDA molecules can drive the spatial distribution of dopants in zeolitic frameworks.³¹ It is worth noting that secondary amines are more efficient in the synthesis of zeolite-type materials with aluminophosphate composition. Besides, heteroatom-containing microporous aluminophosphates represent ideal candidates to imprint chirality since these atoms can stabilize particular angles required for chiral frameworks that pure-silica compositions do not.¹⁵

As previously mentioned, the most common driving-force for the self-assembly of organic molecules is the presence of aromatic rings. On the other hand, the most common driving-force for molecular-recognition phenomena is the development of intermolecular H-bonds between particular donor–acceptor groups of different molecules. The possibility of forming H-bonds would in principle facilitate a supramolecular ordering through molecular recognition phenomena among the SDA molecules occluded within nanoporous frameworks. Based upon these grounds, we have rationally selected (1R,2S)-(–)-ephedrine as a potential SDA for the synthesis of AFI aluminophosphate frameworks in an attempt to induce chirality in this structure.³² This molecule has been rationally selected based on (i) the presence of aromatic rings which tend to self-assemble through π–π type interactions, (ii) the presence of two stereogenic centres that impart a strong asymmetric nature to the molecule, and (iii) the presence of –NH_x and –OH groups susceptible of developing intermolecular H-bonds. The synergy of these three molecular features might potentially lead to the development of supramolecular helicoidal organic arrangements. Moreover, the presence of NH_x⁺ groups may lead to a strong and localized H-bond interaction with dopants, thus potentially driving the spatial distribution of dopants during the crystallization of the framework. The combination of both issues could lead to a helicoidal arrangement of dopants within the AFI network.

In a recent work, we demonstrated that (1R,2S)-(–)-ephedrine directs the crystallization of the AFI framework in the presence of different dopants.³² Interestingly, we observed that ephedrine incorporates exclusively as dimers within this structure, regardless of the dopant introduced; this is most important since it is a crucial condition for the helicoidal organic arrangement to occur. In this work, we perform a computational study in order to determine the arrangement of ephedrine dimers within the AFI channel and the potential transfer of chirality to the spatial distribution of Mg dopants.

Computational details

Molecular-mechanics-based simulations were performed to analyze the supramolecular arrangement of (1R,2S)-ephedrine (EPH) molecules occluded within the 12-MR channels of the AFI framework, as well as their interaction with Mg dopants. Molecular structures of ephedrine molecules and their packing and non-bonding interactions with the AFI framework were described using the CVFF forcefield;³³ this forcefield contains a large series of energy terms which suitably describes the molecular structure of organic molecules as well as their interaction with AlPO-based zeolite-like frameworks. The AFI structure was kept fixed during the calculations. All calculations were performed under periodic boundary conditions (PBC).

Due to the basicity of EPH (pK_a = 9.6),³⁴ the acidic pH of the synthesis medium (between 3 and 5), as well as the necessity of compensating the negative charge introduced by the isomorphic substitution of Al³⁺ by Mg²⁺, protonated EPH (EPH⁺) molecules were studied (unless in specified cases). The atomic charge-distribution of EPH⁺ was obtained from DFT calculations, using the B3LYP hybrid functional and the ESP charge calculation method, setting the total net charge to +1 (unless in specified cases). The framework charges were generally fixed to −1.2 for O, 3.4 for P, 1.4 for Al and 0.4 for Mg. In the cases where there is an excess of positive charge (provided by the EPH⁺ molecules), this excess was compensated for by uniformly reducing the Mg and Al atomic charge until neutrality.

All the calculations were performed using the Forcite and Discover modules, as implemented in Material Studio 6.1.^35,36 Molecular Dynamics (MD) were performed in the NVT ensemble; simulated annealing calculations consisted of heating the system from 300 K to 700 K with temperature increments of 10 K, and then cooling to 300 K in the same way, with five hundred MD NVT steps of 1.0 fs run in every heating–cooling step; this cycle was repeated 10 times, and at the end of each cycle the system was geometry optimised. The reported MD energies were averaged and made relative to the most stable case, and are given in kcal per mol per u.c. Details of the particular models employed are given in the corresponding results section.

Results

A previous fluorescence study showed that EPH molecules tend to arrange as dimers when occluded within the one-dimensional pores of the AFI framework, an essential condition for a helicoidal organic arrangement to occur.³² In this work molecular simulations are applied in order to study the assembly (packing) of these EPH dimers within the one-dimensional 12-MR channels of the AFI framework. In practice this involves the study of the interface between the non-aromatic (polar) sides of the EPH molecules in consecutive dimers. First we looked for a potential preferential orientation between consecutive dimers, in terms of rotation (around the channel axis) between consecutive dimers. This meant searching for the most stable inter-dimer angle (defined as the rotation angle around the channel axis between consecutive dimers, see Fig. S1 in the ESI†) to establish if a supramolecular helicoidal arrangement of EPH dimers would be expected (Section A), as occurred for BPM.²⁴ The second step involved the study of the interaction between the protonated EPH dimers and Mg dopants, in an attempt to determine the most probable spatial distribution of Mg ions embedded in the AFI framework as a function of the EPH supramolecular arrangement (Section B).

A Arrangement of protonated EPH dimers within an undoped AFI framework

We first examined the stability of different types of EPH dimers that can be occluded within the AFI framework (model 3AFI-4EPH). 4 EPH molecules (2 dimers) were loaded in 1 × 1 × 3 AFI supercells; simulated annealing procedures were applied to find the most stable location and the interaction energies. EPH molecules can adopt two different orientations within the AFI channels to form dimers, which are referred to as 1 and 2 (Fig. 1); the two EPH orientations have the same conformation, but are rotated ∼60° around an axis perpendicular to the channel direction. This gives place to three possible dimer configurations, with both EPH molecules in orientation 1 (1–1, top), in orientation 2 (2–2, middle), or one on each (1–2, bottom). Simulated annealing calculations showed clearly that dimers with (1–1) orientation fit better within the AFI channels (Fig. 1, top). In fact, the other configurations reverted the molecules to orientation 1 during the simulated annealing procedure, clearly demonstrating their lower stability. This preferential (1–1) configuration might be associated to the formation of inter-dimer H-bonds between the H(N) and O atoms of consecutive dimers, which is only possible in orientation (1–1) (Fig. 1, dashed blue lines). Moreover, these results suggest a preferential packing value of 1.33 EPH per u.c. (2 dimers every 3 u.c.).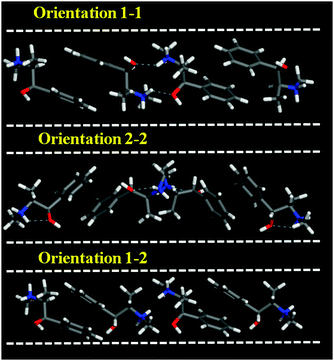

Fig. 1 Three different orientations of 2 EPH molecules to form dimers within the AFI channels (model 3AFI-4EPH); dashed blue lines indicate H-bonds.

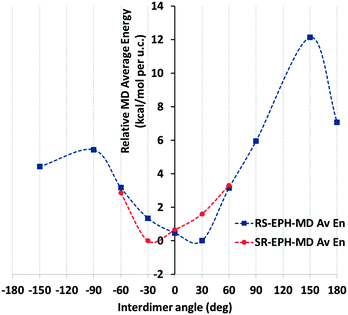
We then investigated the packing interaction between consecutive dimers through the polar (non-aromatic) molecular sides, looking for a preferential orientation between consecutive dimers as a function of the inter-dimer rotation angle (as defined in Fig. S1 in the ESI†). 1 × 1 × 18 AFI supercells were built and 24 EPH molecules (12 dimers) were loaded in order to have fully periodic systems with all the dimers at a certain inter-dimer angle, thus developing helicoidal supramolecular arrangements (model 18AFI-24EPH). Inter-dimer angles of 0°, ±30°, ±60°, ±90°, ±120°, ±150° and 180° have been studied (following the hexagonal symmetry of the AFI framework). After an initial geometry optimization (to avoid accidental overlapping), the systems were relaxed by running 100 ps of MD at 300 K in order to avoid trapping in local minima. The stability of the systems as a function of the inter-dimer angle was determined by looking at the relative averaged energy (with respect to the most stable case) during the MD simulations of the systems (Fig. 2) and the variation of the inter-dimer angle during the MD simulations (Fig. S2 in the ESI†).

Fig. 2 Relative average energy (with respect to the most stable case) of the systems (in kcal per mol per u.c.) during the MD simulations as a function of the interdimer angle (model 18AFI-24EPH) for (1R,2S)-ephedrine (blue squares) and (1S,2R)-ephedrine (red circles).

Results for (1R,2S)-ephedrine (Fig. 2, blue line) showed that the inter-dimer angles of −30, 0 and especially +30° represent the most stable packing orientations. Indeed, these inter-dimer angles were maintained during all the MD simulations (see the angle distributions in Fig. S2, ESI†). Inter-dimer orientations of +60 and −60° were less stable, and in these cases the angles varied along the MD simulations and the angle distributions were broader, a consequence of their lower stability (Fig. S2, ESI†). Systems with inter-dimer angles of −150, +90, −90 and 180° were notably unstable, and indeed they strongly varied during the simulations (Fig. S2, ESI†). Finally, the least stable system had inter-dimer angles of +150°, although in this case the rotation barrier to modify such an angle must be high and the angles were maintained during the simulation (Fig. S2, ESI†). The asymmetry of the inter-dimer-angle energy diagram for (1R,2S)-ephedrine (Fig. 2, blue line; the ordinate axis represents the 0° rotation) is worth noting. Such asymmetry is especially true in the +30/−30° rotation, which is a direct consequence of the asymmetric nature of EPH. These results indicate that the most stable packing of (1R,2S)-EPH dimers within the AFI channels involves a rotation of +30° around the channel axis between consecutive dimers, thus developing a helicoidal supramolecular arrangement of EPH dimers (Fig. 3).

Fig. 3 Helicoidal arrangement of (1R,2S)-EPH dimers with a verse of rotation of +30°; inter-dimer H-bonds are represented as dashed blue lines. One of the H atoms bonded to N (the one closer to the framework walls) is displayed as balls (bottom) to highlight the helicoidal nature of the arrangement.

In order to test the robustness of our computational model, we repeated the calculations but for the mirror-image system, with the (1S,2R)-ephedrine enantiomer (Fig. 2, red line). Indeed, a mirror-image behaviour for the rotation energy diagram was observed, where in this case the −30° rotation was the most stable one, as expected. Hereafter, all calculations will consider only the previous (1R,2S)-enantiomer.

We then considered the origin for such distinct stability of the systems as a function of the inter-dimer angle. Fig. 3 shows that inter-dimer H-bonds are developed between the H(N) and O atoms of (1R,2S)-EPH molecules in consecutive dimers (a detail is shown in Fig. 4, bottom). Hence we examined the development of such inter-dimer H-bonds as a function of the inter-dimer angle by looking at the intermolecular Radial Distribution Functions (RDFs) between O and H(N) atoms of EPH molecules (Fig. 4, top). RDF results showed that the H-bonds are exclusively developed with one of the two H(N) atoms, the one referred to as H1 (see Fig. 4, bottom), but not with H2 (see Fig. S3 in the ESI;† only the 180° and −150° systems develop a minor H-bond formation with this H atom). Except for the 180° angle (black line in Fig. 4, top), these intermolecular H-bonds are developed at all the inter-dimer angles, suggesting that the interface between consecutive dimers is determined by the establishment and strength of such H-bonds (see Fig. S4 in the ESI† for a picture of all the dimer interfaces). If we now compare these RDFs for the different angles, a much more intense peak is observed for the most stable inter-dimer orientations, i.e. angles of ±60, ±30 and 0°, with the highest intensity corresponding to the most stable systems (+30, 0 and −30°). This evidences that their higher stability is due to the formation of stronger – probably because of less steric repulsions – H-bonds between consecutive dimers at such particular orientations (rotations); the higher stability for +30° rotations might then be associated with a lower steric repulsion between the methyl substituents. If we now decompose the non-bond energy in the Van der Waals and electrostatic terms, we observe that the main difference as a function of the inter-dimer angles comes from the Van der Waals term (Fig. S5, left in the ESI,† red line), suggesting again that the different packing stabilities come from steric repulsions. The main differences in the electrostatic term are in the +60 → +150° rotations, which should come from electrostatic repulsions, but these differences are not relevant since those correspond to unstable situations. Finally, in order to ensure that the energy differences observed are not an artefact of the atomic charge distribution selected for EPH molecules (calculated by B3LYP methodology), we repeated the calculations using in this case force-field-assigned charges (Fig. S5, right, ESI†), and we found essentially the same energy profile (with some differences only in unstable angles), providing confidence to our computational model.

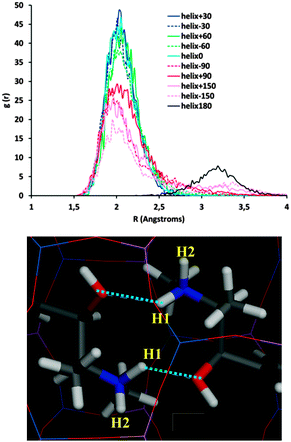Fig. 4 Intermolecular H-bond formation as a function of the inter-dimer angle. Top: RDF (during the MD simulations) between O and H(1)-N atoms. Bottom: detail of the development of two H-bonds (dashed blue lines) in the most stable helicoidal system of +30° (detail of dashed white square in Fig. 3-top).

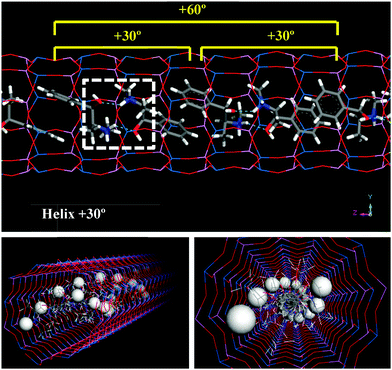
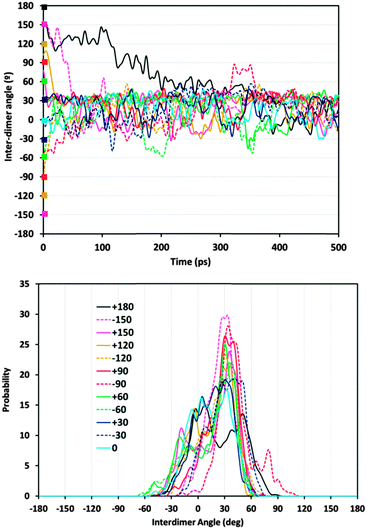
Given the preferential orientation of dimers rotated consecutively by +30°, we then considered if a self-assembly of (1R,2S)-EPH dimers into such (+30°)-helicoidal supramolecular arrangement would spontaneously occur during crystallization of the AFI framework. In an attempt to simulate this, 500 ps of MD simulations at the synthesis temperature (453 K) were performed (model 4AFI-4EPH-2Ar); in this case, 2 dimers were inserted in a 1 × 1 × 4 AFI supercell and manually rotated to the required initial inter-dimer angle. 2 Ar atoms were kept fixed at both extremes of the channel in order to ensure an inter-dimer separation similar to that in the periodic helicoidal system. Initial inter-dimer angles of 0°, ±30°, ±60°, ±90°, ±120°, ±150° and 180° were tried. Evolution of the inter-dimer angles along the MD simulations showed all of them to converge to a value close to +30° (Fig. 5, top), regardless of the initial orientation (displayed as color squares at 0 ps time).³⁷ The angle distribution (between 250 and 500 ps, once the orientation of the dimers has relaxed) showed a clear preference in most cases for an inter-dimer rotation of +30° (Fig. 5, bottom). These results suggest that (1R,2S)-EPH molecules tend to self-assemble as dimers, and these spontaneously rotate an angle of +30° when approaching the consecutive dimer, thus developing a supramolecular helicoidal arrangement during the growth of the AFI 12-MR channels. It should be noted that the enantiomeric purity of the molecule used (1R,2S-ephedrine) requires the helicoidal arrangement to also be enantiomerically pure, i.e. with +30° verse of rotation (and not with −30°).

Fig. 5 Evolution of the inter-dimer angle during the 453 K MD simulations starting from different initial angles (top) and angle distribution in the second half of the MD simulation (250–500 ps) (bottom). The color code is common for both graphs.

In order to analyse the influence of the protonation state of (1R,2S)-EPH on the helicoidal arrangement, (indeed we also observed the formation of the AFI framework with half of the Mg (0.67 Mg per u.c.) required to compensate a fully-loaded system with protonated EPH dimers, suggesting either the presence of neutral molecules or a lower total amount of protonated EPH), we also studied a helicoidal arrangement in which only half of the molecules are protonated (EPH) and half are neutral (EP0). Energy results showed that the ephedrine species, protonated and neutral, tend to alternate consecutively in the dimers ([EPH·EP0]–[EPH·EP0] dimers), as expected due to the lower electrostatic repulsions between charged molecules. A very similar energy profile as a function of the inter-dimer angle (for such alternate EPH·EP0 configuration) as when all the molecules were protonated was observed (Fig. S6 in the ESI†), with the +30° inter-dimer angle being the most stable one. This result strengthens the hypothesis for the high trend of ephedrine dimers to pack with an inter-dimer angle of +30°, regardless of the protonation state.

B Transfer of chirality to the spatial distribution of dopants

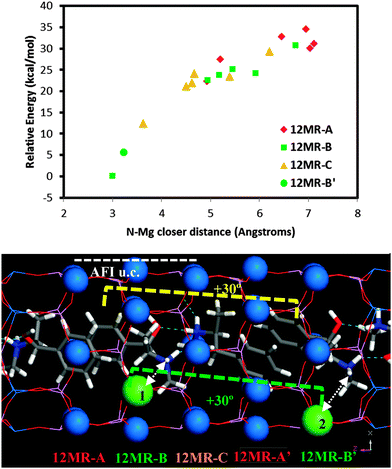
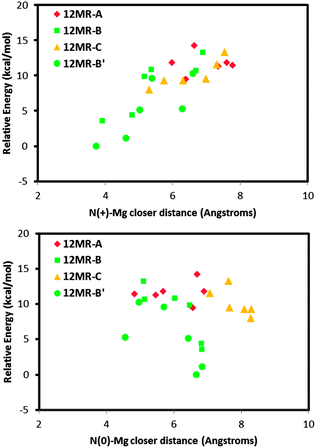
Following the demonstration of the helicoidal, and hence chiral, supramolecular arrangement of the (1R,2S)-EPH molecules, in this section we examine if such supramolecular chiral arrangement could be imprinted onto the AFI framework through the spatial distribution of Mg dopants. In principle, a strong electrostatic interaction between the negative charge associated with the incorporation of Mg²⁺ (replacing Al³⁺) and the positive charge of protonated (1R,2S)-EPH molecules is presumed. Moreover, the positive charge of protonated EPH molecules is well-localized around the amino group (NH₂⁺), and is not shielded by bulky groups as occurs in tetraalkylammonium salts.³¹ Such charge localization would anticipate a strong and localized electrostatic interaction, and hence a potential transfer of the supramolecular organic arrangement to the spatial distribution of dopants.

To analyse such potential transfer of chirality, one Al was replaced by one Mg (in all the non-equivalent Al positions) in the previous 18AFI-24EPH model with EPH dimers (all protonated molecules) in the +30° helicoidal arrangement, and the systems were geometry optimized (model 18AFI-24EPH-1Mg). Three 12-rings along the main AFI channels are distinguished in relation to the position of the EPH dimers (Fig. 6, bottom): 12-ring-A, where the main interaction of the framework is developed with the aromatic rings, and 12-ring-B and -C, where the main interaction is established with the polar side of the EPH molecules (note that AFI consecutive 12-rings separated by 1/2c are rotated ±30° around the channel axis). Due to the packing value of 1.33 EPH per u.c. (which means a packing of 2 dimers every 3 u.c., i.e. 1 dimer per 1.5 u.c.) (there are two 12-rings per AFI unit cell), the next (fourth) 12-ring again interacts with the aromatic side of the subsequent dimer, and hence is equivalent to 12-ring-A (12MR-A′ in Fig. 6, bottom). Energy results (Fig. 6, top) show a lower stability when Mg is in 12-ring-A (red diamonds, with relative energies above 25 kcal mol⁻¹), where it interacts mostly with the aromatic molecular side; this is due to the apolar nature of these rings. A much more stable situation is found when Mg locates in 12-ring-B and -C (green squares and orange triangles, respectively) close to the N atoms of EPH, especially in 12-ring-B (position 1 in Fig. 6, bottom), where the smallest N⋯Mg distance is found (∼3 Å). A clear relationship between the relative energy and the N⋯Mg distance is observed (Fig. 6, top). This is a consequence of the electrostatic interaction established between the negative-charge associated with Mg dopants embedded in the AFI framework and the positive charge of the NH₂⁺ moieties. Indeed, the second most stable location for Mg (after position 1 in 12-ring B) is in the subsequent 12-ring-B (12MR-B′, position 2 in Fig. 6, bottom), again due to a closer N⋯Mg distance. Interestingly, this position is rotated by +30° (around the channel axis) with respect to position 1, i.e. following the helicoidal arrangement of the EPH dimers. In order to support this Mg⋯NH₂⁺ spatial association, we ran 500 ps of NVT MD simulations at room temperature of a system which contained 1 Mg in a 1 × 1 × 3 AFI supercell loaded with a single protonated EPH molecule, locating the molecule initially far from Mg. We observed that the molecule rapidly moves close to Mg (Fig. S7, left in the ESI†), and then stays there for all the simulation time, developing a strong interaction between NH₂⁺ and Mg (at a distance of 3.25 Å) (Fig. S7, right, ESI†). These results suggest that the location of Mg is driven by the establishment of a strong electrostatic interaction between the negative charge induced by the replacement of Mg²⁺ by Al³⁺ and the positively-charged NH₂⁺ groups through the formation of H-bonds between these protons and the O atoms nearest neighbor to Mg, presuming a transfer of chirality from the supramolecular organic arrangement into a long-ranged helicoidal distribution of Mg in the AFI framework.

Fig. 6 Stability as a function of the Mg location (for systems with all protonated molecules). Top: relative energy for the different Mg positions as a function of the N–Mg closer distance. Bottom: schematic picture of the two most stable locations for Mg along the different 12MR channels; dashed white arrows indicate the closest distances between Mg and H(N) atoms; atoms displayed as balls represent all the positions studied.

We then repeated the same type of calculations, but this time with the helicoidal system where half of the molecules were protonated and half were neutral. Fig. 7 shows the relative energy (with respect to the most stable case) as a function of the N⋯Mg distance for the protonated (top) or neutral (bottom) ephedrine species, for the different Mg locations. Again we observed that the most stable Mg locations correspond to those where they locate close to the polar side of the molecules (12MR-B rings, as previously defined, green circles and squares); the least favourable Mg locations correspond to those cases where the dopant locates close to the aromatic rings (red diamonds). On the other hand, there is a clear relationship between the relative stability and the interatomic distance between the dopant and the N atom of the protonated EPH (top); in contrast, such relationship is not observed for the N⋯Mg distance with the neutral molecule (bottom). This clearly evidences the directing-role of the protonated NH₂⁺ group of ephedrine to drive the location of divalent dopants, which only occurs when the molecules are protonated.

Fig. 7 Stability as a function of the Mg location (for systems with half protonated and half neutral molecules): relative energy for the different Mg positions as a function of the N⋯Mg closer distance of protonated (top) or neutral (bottom) molecules.

Following the demonstration of the trend of (1R,2S)-EPH to drive the Mg incorporation, we finally studied a more realistic case for the transfer of the helicoidal feature from the EPH supramolecular arrangement to a potential helicoidal arrangement of Mg. In these models, we built helicoidal arrangements of Mg with +30 or −30° pitches (1 Mg per helical pitch, i.e. per dimer, i.e. per 1.5 u.c.), and with EPH dimers in +30 or −30° helicoidal arrangements; EPH molecules were located to have the NH₂⁺ group as close as possible to Mg. The systems were then relaxed with MD simulations, and the averaged relative energies (in kcal per mol per u.c.) are reported in Table 1. Energy results clearly indicate that Mg will tend to follow the helicoidal arrangement of the EPH molecules in order to minimize the distance between the net charges, Mg and NH₂⁺ of EPH, thus maximizing the electrostatic interaction (cases 1 and 4). Cases 2 and 3, where Mg does not follow the helicoidal arrangement of EPH, are rather less stable. On the other hand, of the two cases where Mg follows the EPH helicoidal arrangement, 1 and 4, that with a pitch of +30° is more stable due to the better packing of the EPH molecules with a rotation angle of +30° compared to that of −30°, as observed in Section A. These results provide further evidence for the trend of Mg to follow the +30° helicoidal arrangement that (1R,2S)-EPH molecules tend to adopt within the AFI framework.

Table 1 Averaged MD relative energies (in kcal per mol per u.c.) (relative to the most stable case, case 1) of the systems as a function of the helicoidal Mg and (1R,2S)-EPH arrangements

Case	Mg helix	EPH helix	Relative E
1	+30	+30	0.0
2	+30	−30	5.4
3	−30	+30	6.5
4	−30	−30	1.0

---

Discussion

The computational study performed in this work has allowed us to gain insights into a potential new strategy to induce chirality in microporous materials. As mentioned in the introduction, we recently proposed a new concept of chirality in zeolitic materials consisting of a chiral spatial distribution of dopants embedded in a zeolitic framework. This is in contrast with the common concept of chirality in zeolites which is given by a chiral ordering of all the T atoms conforming the framework, giving place to chiral frameworks. However, this strategy has so far been severely hindered by the usually unavoidable crystallization of racemic conglomerates. Our strategy proposes an alternative way of inducing chirality in zeolitic materials, which should be in principle more easily achievable, where only the dopants are arranged in a chiral fashion. We remark that these dopants will be the ones involved in a potential enantioselective process.

For such a helicoidal distribution of dopants to occur, for instance in the AFI framework, two conditions must be satisfied: first, a helicoidal supramolecular long-range order of the organic SDA molecules must occur during the crystallization process; second, a strong interaction between a localized area of the SDA molecules and the dopant must exist, so that the chirality of the molecular arrangement is imprinted onto the solid through the spatial distribution of dopants.

Our work shows that the first condition is satisfied by the molecule employed in this work, (1R,2S)-ephedrine: it is incorporated as dimers within the AFI channels, and these dimers show a strong trend to rotate consecutively by +30° due to the establishment of stronger inter-dimer H-bonds and a better packing (less repulsive interactions).

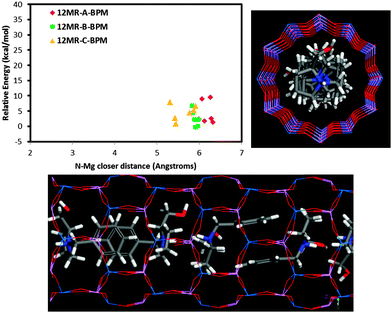
On the other hand, our results also show that there is a very strong trend of Mg to locate close to the charged NH₂⁺ group of the protonated EPH molecules due to the establishment of strong H-bonds between the H(N) atoms and the O-nearest-neighbor to Mg atoms. Indeed, molecular simulations of an aqueous solution of ephedrinium chloride (EPH⁺·Cl⁻)³² showed a close location of chloride anions and NH₂⁺ groups of EPH in solution (see Fig. S8 in the ESI†), confirming the trend of the protonated ammonium groups to attract negative charges. This strong trend to drive the spatial distribution of dopants is a consequence of the particular molecular structure of ephedrine, with a highly mobile NH₂⁺ group that can locate close to the framework wall in order to interact with it. Indeed, we have observed a lower trend of our previously studied (S)-N-benzyl-pyrrolidinemethanol molecule (BPM) to drive the incorporation of dopants. When we analysed the relative energy for the different Mg locations as a function of the N⋯Mg distance (Fig. 8), we did not observe a relationship between the energy and the N⋯Mg distance as was found for ephedrine (Fig. 8, top-left). This is so because in the BPM supramolecular helicoidal arrangement, the N–H groups locate close to the centre of the channels, and hence do not interact with the framework walls (Fig. 8). Therefore, the trend of BPM to drive the location of dopants should be weaker.

Fig. 8 Stability as a function of the Mg location (for systems with all protonated (S)-benzyl-pyrrolidine-methanol molecules): relative energy for the different Mg positions as a function of the N–Mg closer distance (top-left), and two views of the −90° helicoidal arrangement of these molecules (N atoms are displayed in blue).

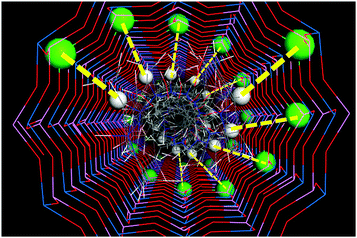
In summary, the trend of EPH to drive the location of dopants, together with the trend of EPH dimers to arrange helicoidally, would suggest a potential imprinting of the helicoidal supramolecular arrangement of the EPH dimers onto the framework through a helicoidal spatial distribution of Mg dopants (Fig. 9). Such potential transfer of chirality is closely associated with the AlPO composition, where Al and P atoms strictly alternate, thus reducing the positions available for the divalent dopants. We want to note that the presence of two molecules (i.e. two NH₂⁺ groups) per dimer (which represents the verse of rotation of the helicoidal arrangement) would involve the occurrence of a double helix of dopants (Fig. 9), where each dopant would be closely associated with one NH₂⁺ group of each EPH cation. In the case of having half of the molecules without protonation (with a Mg content of 0.67 atoms per u.c.), we would have a single helix of dopants (with 1 Mg per dimer).

Fig. 9 Illustration of the transfer of chirality from the supramolecular helicoidal arrangement of EPH dimers (external H(N) atoms displayed as white balls) to a double helicoidal spatial distribution of Mg dopants (displayed as green balls).

In any case, we are aware of the simplifications assumed by our computational model. The crystallization of microporous materials assisted by the presence of organic molecules is a very complex phenomenon, which nowadays is only poorly understood. Therefore, it is a difficult task to predict the exact distribution of dopants that will actually occur during the crystallization of the AFI framework. However, there are two clear issues demonstrated in this work: first the trend of EPH molecules to aggregate as dimers, and their consecutive rotation by a particular angle because of the asymmetric nature of EPH combined with the possibility of developing H-bonds; and second, the strong trend of negative charges to locate closely to the positive charge of EPH. Both these issues would predict a helicoidal spatial distribution of dopants, even if these are different from the ones predicted here.

Experimental demonstration of the occurrence of these chiral distributions of dopants is extremely difficult to perform (by diffraction techniques) due to the subtle nature of the chirality involved. However, work is currently under way in an attempt to see if these materials can perform enantioselective operations. We finally remark here that, in the absence of racemization processes during crystallization, the SDA employed is enantiomerically pure ((1R,2S)-ephedrine), and therefore an enantiomerically pure helicoidal spatial distribution of dopants would be produced, overcoming the common problem of chiral zeolitic structures. After calcination of the SDA molecules, the framework should maintain its chiral nature given by the dopant distribution, as long as the dopant atoms remain in the framework.

Conclusions

In this work we have analyzed computationally the potential of (1R,2S)-ephedrine molecules to induce chirality in the AFI framework through a helicoidal spatial distribution of dopants. The particular molecular structure of ephedrine imparts a strong trend to form dimers within the AFI channels. Interestingly, the two stereogenic atomic centres of ephedrine provide a strongly asymmetric nature to the molecule, which combined with the possibility of forming intermolecular H-bonds due to the presence of NH₂ and OH groups, involves a preferential inter-dimer rotation of +30° when these dimers are packed along the one-dimensional 12-ring AFI channels. Such preferred particular rotation involves the development of a supramolecular helicoidal (and hence chiral) arrangement of the EPH dimers.

Interestingly, the molecular structure of (1R,2S)-ephedrine, specifically the presence of positively-charged H-bonded-to-N atoms susceptible of forming strong H-bonds with negatively-charged framework atoms, also imparts a strong trend to this SDA to drive the incorporation of dopants within the framework because of the establishment of strong electrostatic interactions with the negative charge associated with the replacement of trivalent Al by divalent Mg dopants. Combined with the preferential helicoidal arrangement of ephedrine dimers, and assisted by the chemical nature of AlPO networks and the AFI particular framework structure, a transfer of chirality from the organic supramolecular arrangement to an enantiomerically-pure double helix of dopants in the AFI channels is predicted, inducing a new type of chirality in microporous materials.

Acknowledgements

The research leading to these results has received funding from the Spanish Ministry of Science and Innovation MICINN (projects MAT2009-13569 and MAT2012-31127) and the European Research Council, under the Marie Curie Career Integration Grant program (FP7-PEOPLE-2011-CIG), Grant Agreement PCIG09-GA-2011-291877. LGH and BBM acknowledge the Spanish Ministry of Economy and Competitivity for Ramón y Cajal and predoctoral contracts, respectively.

Notes and references

1. M. Gardner, The Ambidextrous Universe. Symmetry and Asymmetry from Mirror Reflections to Superstrings, 3rd revised edn, 1964.
2. S. F. Mason, Nature, 1984, 311, 19.
3. K. D. M. Haris and S. J. M. Thomas, ChemCatChem, 2009, 1, 223.
4. R. M. Hazen and D. S. Sholl, Nat. Mater., 2003, 2, 367.
5. P. R. Kavasmaneck and W. A. Bonner, J. Am. Chem. Soc., 1977, 99, 44.
6. T. S. Van Erp, T. P. Caremans, D. Dubbeldam, A. Martín-Calvo, S. Calero and J. A. Martens, Angew. Chem., Int. Ed., 2010, 49, 3010.
7. J. M. Castillo, T. J. H. Vlugt, D. Dubbeldam, S. Hamad and S. Calero, J. Phys. Chem. C, 2010, 114, 22207.
8. P. Mc Morn and G. J. Hutchings, Chem. Soc. Rev., 2004, 33, 108.
9. M. E. Davis, Microporous Mesoporous Mater., 1998, 21, 173.
10. M. M. J. Treacy and J. M. Newsam, Nature, 1988, 332, 249–251.
11. J. Yu and R. Xu, J. Mater. Chem., 2008, 18, 4021.
12. J. Sun, C. Bonneau, A. Cantín, A. Corma, M. J. Díaz-Cabañas, M. Moliner, D. Zhang, M. Li and X. Zou, Nature, 2009, 458, 1154.
13. A. Rojas and M. A. Camblor, Angew. Chem., Int. Ed., 2012, 51, 3854.
14. L. Q. Tang, L. Shi, C. Bonneau, J. L. Sun, H. J. Yue, A. Ojuva, B. L. Lee, M. Kritikos, R. G. Bell, Z. Bacsik, J. Mink and X. D. Zou, Nat. Mater., 2008, 7, 381.
15. X. W. Song, Y. Li, L. Gan, Z. P. Wang, J. H. Yu and R. R. Xu, Angew. Chem., Int. Ed., 2009, 48, 314.
16. X. Liu, Y. Xing, X. Wang, H. Xu, X. Liu, K. Shao and Z. Su, Chem. Commun., 2010, 46, 2614.
17. J. Zhang, S. M. Chen and X. H. Bu, Angew. Chem., Int. Ed., 2009, 49, 6049.
18. R. E. Morris and X. H. Bu, Nat. Chem., 2010, 2, 353.
19. M. E. Davis, Top. Catal., 2003, 25, 3.
20. J. Pérez-Pariente and L. Gómez-Hortigüela, The role of templates in the synthesis of zeolites, in Zeolites: from model materials to industrial catalysts, ed. J. Čejka, J. Peréz-Pariente and W. J. Roth, 2008, ISBN: 978-81-7895-330-4.
21. C. S. Cundy and P. A. Cox, Chem. Rev., 2003, 103, 663.
22. M. E. Davis and R. F. Lobo, Chem. Mater., 1992, 4, 756.
23. Y. Wang, J. H. Yu, Y. Li, Z. Shi and R. R. Xu, Chem. – Eur. J., 2003, 9, 5048.
24. L. Gómez-Hortigüela, F. Corà, C. R. A. Catlow and J. Pérez-Pariente, Phys. Chem. Chem. Phys., 2006, 8, 486.
25. L. Gómez-Hortigüela, F. Corà and J. Pérez-Pariente, Microporous Mesoporous Mater., 2012, 155, 14.
26. L. Gómez-Hortigüela, F. Corà, C. R. A. Catlow and J. Pérez-Pariente, J. Am. Chem. Soc., 2004, 126, 12097.
27. L. Gómez-Hortigüela, F. López-Arbeloa, F. Corà and J. Pérez-Pariente, J. Am. Chem. Soc., 2008, 130, 13274.
28. L. Gómez-Hortigüela, F. López-Arbeloa and J. Pérez-Pariente, Microporous Mesoporous Mater., 2009, 119, 299.
29. L. Gómez-Hortigüela, S. Hamad, A. B. Pinar, F. López-Arbeloa, J. Pérez-Pariente and F. Corà, J. Am. Chem. Soc., 2009, 131, 16509.
30. L. Gómez-Hortigüela, F. López Arbeloa, C. Márquez-Álvarez and J. Pérez-Pariente, J. Phys. Chem. C, 2013, 117, 8832.
31. L. Gómez-Hortigüela, A. B. Pinar, F. Corà and J. Pérez-Pariente, Chem. Commun., 2010, 46, 2073.
32. T. Álvaro-Muñoz, F. López-Arbeloa, J. Pérez-Pariente and L. Gómez-Hortigüela, J. Phys. Chem. C, 2014, 118, 4835.
33. P. Dauber-Osguthorpe, V. A. Roberts, D. J. Osguthorpe, J. Wolff, M. Genest and A. T. Hagler, Proteins: Struct., Funct., Genet., 1988, 4, 31.
34. L. S. Schanker, P. A. Shore, B. B. Brodie and C. A. M. Hogben, J. Pharmacol. Exp. Ther., 1957, 120, 528.
35. Discover module, Material Studio, version 6.1, Accelrys Inc., San Diego, CA, 2013.
36. Forcite module, Material Studio, version 6.1, Accelrys Inc., San Diego, CA, 2013.
37. Note: indeed, in many cases the angles already changed to more stable values upon the initial geometry optimization.

---

Footnote

† Electronic supplementary information (ESI) available: Additional RDFs, energy diagrams, angle distributions and pictures. See DOI: 10.1039/c4cp03957b

---