Genetics of superionic conductivity in lithium lanthanum titanates

Abstract

The self-diffusion of ions is a fundamental mass transport process in solids and has a profound impact on the performance of electrochemical devices such as the solid oxide fuel cell, batteries and electrolysers. The perovskite system lithium lanthanum titanate, La_2/3−xLi_3xTiO₃ (LLTO) has been the subject of much academic interest as it displays very high lattice conductivity for a solid state Li conductor; making it a material of great technological interest for deployment in safe durable mobile power applications. However, so far, a clear picture of the structural features that lead to efficient ion diffusion pathways in LLTO, has not been fully developed. In this work we show that a genetic algorithm in conjunction with molecular dynamics can be employed to elucidate diffusion mechanisms in systems such as LLTO. Based on our simulations we provide evidence that there is a three-dimensional percolated network of Li diffusion pathways. The present approach not only reproduces experimental ionic conductivity results but the method also promises straightforward investigation and optimisation of the properties relating to superionic conductivity in materials such as LLTO. Furthermore, this method could be used to provide insights into related materials with structural disorder.

---

Introduction

There is an increasing need for reliable electrical energy storage for both mobile and static applications.^1–4 Solid-state lithium ion conducting batteries are of particular relevance in this regard due to their inherent high energy densities. A key component in such a device is the solid electrolyte, which must have a high ionic conductivity at the temperature of operation and be easily processed into a thin dense membrane. In addition it must be compatible with the electrode materials. Polymeric and glass materials have, until now, been favoured because of their ease of processing, however oxide ceramics are also strong candidates for this role. In particular, LLTO is an interesting material for the electrolyte in such batteries, due to its conductivity, however it does suffer from limitations in such devices due to the easy reducibility of the Ti⁴⁺ cation, e.g. in contact with metallic Li. The study of Inaguma et al.⁵ was the first to demonstrate the excellent bulk lithium conductivity of LLTO, which is circa 1 × 10⁻³ S cm⁻¹ at room temperature. The bulk conduction of Li ions in LLTO is described as non-Arrhenius as the activation energy changes with temperature.⁷ Despite significant research effort^6–19 the actual mechanism of Li ion migration in LLTO has yet to be clearly and fully described. Without this basic understanding, designing improved materials within the LLTO family may be problematic hindering their commercialisation.

LLTO is classed as a perovskite (ABO₃) although the stoichiometry is somewhat unusual. The parent structure is a 2,4 perovskite, similar to SrTiO₃, in which 2/3 of the divalent A-cations are replaced by La³⁺, with the remaining 1/3 of the sites being unoccupied, leaving vacancies. This La_2/3TiO₃ structure is further modified by the replacement of a small fraction, x, of the trivalent cations by Li⁺ to give La_2/3−xLi_3xTiO₃. LLTO systems with low lithium contents (x ≤ 0.08) have predominantly been found to adopt an orthorhombic structure and at lithium contents above this, a tetragonal structure forms,²⁰ with space group P4/mmm, as shown in Fig. 1a. The unit cell of LLTO is made from corner shared TiO₆ octahedra with the central A-cation cages formed by 12 oxygen ions belonging to the octahedral faces (see Fig. 1a).^21,22

Fig. 1 (a) Crystal structure of tetragonal La_2/3−xLi_3xTiO₃ (x = 0.115). The alternating rich and poor layers within the A-site sub-lattice are indicated, their correspondence with the Li densities within the simulated systems can be seen in sub-figures (b) and (c). A bottleneck exists between these layers through which Li ions must pass when migrating along the c-axis. This is delineated by the four, corner shared oxygen ions sitting between layers on the edges of the unit-cell. Sub-figure (b) calculated Li density plot showing the Li distribution in cell shown in (a), for a value of S = 0.2. The distribution shows significant Li density along the c-axis as well as in the ab plane indicating the isotropic nature of Li diffusion. (c) Calculated Li density plot showing the Li distribution in the cell depicted in (a), for a value of S = 0.8. The distribution shows that Li density is more localised within ab planes corresponding to La poor (i.e. Li rich) layer for S values that emphasise layering.

It is difficult to describe a defect nomenclature based on the La_2/3TiO₃ lattice and thereby to ensure a consistent notation and set of effective charges. As a consequence in order to describe the extensive point defect population using Kröger–Vink notation²³ the A²⁺B⁴⁺O₃ stoichiometry of the parent structure will be used. The distribution of La³⁺ ions on to the A-sites is nominally random, however, there is a small degree of ordering whereby rich and poor 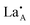layers are formed perpendicular to the c-axis. Lithium ions and A site vacancies also occupy the A-sites, leaving a network of 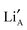and available for lithium ion migration.⁷ In the notation chosen for this representation the crystal neutrality condition becomes;

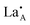The effect of the layering is of particular importance to the migration and movement of 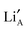ions between the layers.²⁴ The degree of ordering of cations and vacancies on the A-sites in the layers strongly influences the crystal structure and Li ion conductivity¹⁷ and it is important to define the stoichiometry, degree of ordering and crystal structure when comparing conductivity results. The crystal is described as having rich and poor La layers¹⁷ and an order parameter describing the degree of order is defined as;
where R_(La-rich) and R_(dis) are the occupancies of the A-sites by La³⁺ ions in a structure with ordered La-rich layers and a disordered structure respectively. For structures where S = 0, the ions are completely disordered and the diffusion is isotropic. When S = 1, however, the La rich planes are fully occupied and the diffusion is restricted to the La poor planes perpendicular to the c-axis.²⁵ The layering effect is an important structural feature since the migration energy barrier for Li⁺ ions will depend upon the individual local environment of each of the A-sites along the percolating and network. As such, there will be no single activation energy for diffusion to describe the transport of Li⁺ ions. Therefore, the distribution of the 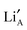and in and between the layers is investigated in this work.

Previous computational investigations of LLTO failed to reproduce the ionic conductivities determined experimentally. The aim of the present study is to explore the importance of atomic configuration and the structural features that result in high ionic conductivity in LLTO. To achieve this we employed a genetic algorithm (GA) in conjunction with molecular dynamics (MD) to search configurational space for structures with high conductivities. Finally, we examine whether there is a percolated network of Li diffusion pathways in LLTO.

Methodology

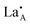In order to establish the structural features giving rise to LLTO's high ionic conductivity and its correspondence to the rich-poor layering of the material it was necessary to generate model systems exhibiting high Li ion mobility. These could then be investigated using molecular dynamics calculations to discover the local ordering of and species associated with areas of significant Li diffusion and as a consequence provide greater insight into the properties of the LLTO system.

Genetic algorithms have been used previously within the field of atomic scale simulation to perform configurational searches and structural refinement.^26–28 In light of this, a GA was adopted for this work and it was found it could be used to optimise initially random and configurations to yield much higher Li diffusion values and in so doing emphasise the local 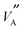and arrangements relevant to the present study. A GA was coupled to MD simulations to give an approach, that did not rely on significant prior assumptions on structure and migration mechanisms for its operation, which could have introduced unwanted bias into the final results. The details of the GA are described in considerable detail within the ESI† accompanying this paper, however, the major features of the algorithm and MD simulation methods employed are now described.

GA's represent a class of heuristic optimization/search techniques^27–29 that adopt principles from evolutionary biology, whereby the Darwinian idea of survival of the fittest is applied to a problem in order to simulate evolution, with the intention of obtaining solutions that are improved over the course of several generations. The GA used to search for the and configurations, described in the results section, is summarised in Fig. 2. An initial population of 100 random configurations was generated; the mean squared displacement (MSD) of the Li ions within these structures was calculated using molecular dynamics calculations (this defines the merit function within the selection step of the genetic algorithm). Then, pairs of structures from this population were combined using single point crossover to produce child structures in which characteristics from each of parent structures were present (the details of this simulated inheritance are given in full detail within the ESI†). By preferentially selecting those structures exhibiting high MSD values, it was possible to emphasise and arrangements consistent with high Li diffusivity over a number of iterations of the GA loop (Fig. 2). In order to maintain variation between the configurations two mutations were employed, the position of entire layers were swapped and secondly atom positions were swapped within layers of the La sub-lattice of LLTO. Please refer to the ESI† for a more complete description of the algorithm and MD simulations.

Fig. 2 Schematic describing how the GA encourages inheritance from structures with high ionic conductivity to yield iterative refinement of structures. (1) Initialisation: each structure's La sub-lattice contained 14 layers (each with 196 sites), initially Li and were distributed at random amongst the La sites such that the desired composition and rich-poor order parameter were obtained. (2) Selection: each structure's Li MSD was calculated via MD simulation. Parents for the next generation were selected using roulette wheel selection²⁷ which biased selection towards those configurations with high MSD values. (3) Cross-over: child configurations were generated using single point cross-over with the intention of allowing characteristics of each parent to be inherited within the next generation. (4) Mutation: to preserve variety between structures, a small number of mutations were introduced (a) layer order effects were explored by swapping entire layers and (b) heterogeneous , La and pairs were swapped within layers.

Following twenty generations of the genetic algorithm, the ten structures with highest Li MSD were further examined. This involved further MD equilibration and data-collection stages: 20 ps of constant pressure molecular dynamics at each temperature of interest within the range 400–1200 K followed by 100 ps of dynamics within the NVE ensemble during which atomic positions were sampled every 100 fs. It is the results of these data-collection runs that are used within the results section unless otherwise stated.

For its operation, MD requires a good description of the forces acting between the atoms in the system. Here, empirical pair potentials were used in which the forces between pairs of ions were described using the Buckingham form. Initially the existing potential set of Cleave.³⁰ was used to describe interactions between the ionic species La, Ti and O. However, as seen in Fig. 3 the Li⁺ conductivity produced from this model did not reproduce experimental properties well. Therefore, a new set of potentials was developed using static³¹ and dynamic multi-component fitting. By using experimental data for Li₂O and La₃Li₇Zr₂O₁₂ the fitting process led to a potential model that was better able to reproduce the thermal expansion of these related materials. It is important to ensure that the potentials can describe such temperature induced structural effects well, as the resultant rotation or tilt of TiO₆ octahedra changes the shape and size of the regions through which the Li ions migrate (Fig. 1a, also known as the bottleneck^18,19). Changes to the shape of the bottleneck could alter the migration pathway of Li⁺ ions. The benefit of developing this improved potential model (refer to Table S1 of the ESI†) can be seen in Fig. 3, where it is shown to reproduce experimental conductivity values well.⁷ In addition, the figure also demonstrates the importance of the structural optimisation achieved using the GA: purely random atomic configurations showed significantly lower conductivities than optimised structures. The major effect of the GA was to produce structures containing long chains of nearest of and sites, which facilitated longer and more interconnected migration networks, discussed later. The high conductivity structures are not necessarily the lowest lattice energy structures but energy differences to random configurations are of the order of 0.1 eV per unit cell. This energy difference is small given that the materials used in the experimental studies were held at high temperatures (circa 1300 °C) for extended periods of time to sinter dense ceramics. At these temperatures the thermal energy is of the same order as these energy differences and thus such structures can be frozen into the low temperature structure of the material where the conductivity is usually measured.

Fig. 3 A comparison of Li conductivity produced in this work against other simulated and experimental literature values. The simulation values are for LLTO with S = 0.2, values are given for the original potential model with random layering (), original potentials with GA optimised structures and random layering (■), original potentials with GA optimised structure and rich-poor layering (◆) and finally GA optimization, rich-poor layering and the potentials derived for this work (▲). Experimental values taken from literature are as follows: Šalkus et al.⁷ (), Katsumata et al.³² for x = 0.066 (), Hirakuri et al.³³ (), for x = 0.066.

Results and discussion

Values of the order parameter, S, from 0 to 0.8 were investigated at 1000 K using the GA approach: the highest ionic conductivity was obtained for S = 0.2. This is consistent with previous experimental work,¹⁷ which also shows a broad maximum for S = 0.0–0.2 which then tails off as S → 0.8, see Fig. 4 (although this data was collected at 300 K, rather than the higher temperatures considered here). Given the agreement with experimental data^32,33 demonstrated in Fig. 3 and 4, the layered structure at S = 0.2 was investigated further.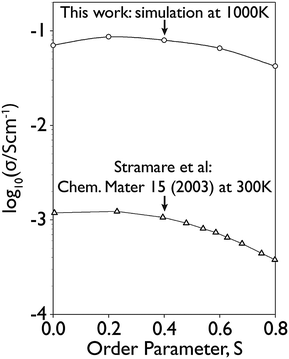

Fig. 4 This plot gives a comparison of Li conductivity for x = 0.115, for the S values considered in this work (at 1000 K) against experimental data from Stramare et al.¹⁷ (at 298 K and x = 0.11).

Insight into the nature of Li ion migration through the LLTO structure can be obtained from the “self” part of the van Hove correlation function³⁴G_S(r⃑,t), this gives information about particle motion by considering the time evolution of their positions (r⃑) with time and is defined as:

where, N is the total number of Li ions. G_S(r⃑,t) then defines the probability of an atom being found at a distance r from its position at t = 0 after a given period of time (t).³⁵ Applying this technique to data acquired from MD simulations at 1000 K performed on the S = 0.2 configurations obtained from the GA reveals the manner in which Li ions move in LLTO. After 0.05 ps, this indicates that the Li ions still occupied their initial sites as shown by peak close to r = 0 (this initial peak is offset slightly from r = 0 due to the thermal vibration of the atoms about their sites). After longer time periods, the correlation functions within Fig. 5 show a series of distinct peaks, as before, there is a large initial peak however after 5 ps and 50 ps a series of peaks at larger r values are apparent. These subsequent peaks correspond with the separation to nearest, second nearest and further neighbour A sites (indicated by crosses on the x-axis). This confirms that the long-range diffusion of Li proceeds through a sequence of hops between adjacent A-sites. If the G_S(r⃑,t) functions were continuous, rather than peak like, then this would suggest an entirely different mechanism.

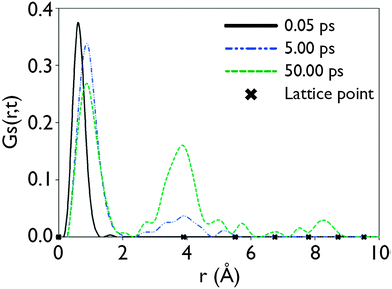Fig. 5 The self-part of the van Hove correlation function G_S(r⃑,t), for Li ions at 1000 K. The time/space dependence for t = 0.05 ps, 5 ps and 50 ps is plotted. x = 0.115 and S = 0.2.

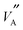Considering the atomistic details of diffusion in LLTO, a number of important features emerge. As S → 0.0, the rich-poor layering effect becomes less pronounced with isotropic diffusion observed along all three of the a, b and c axes. The lack of layering is such that there is no discernible difference in the composition of the rich-poor layers and so hops between the ions and are possible in all three dimensions; this can be seen in Fig. 1b. This profile of Li density, closely matches the occupation probability for Li ions obtained by X-ray and neutron scattering intensities calculated by Ohara et al.²⁴ Conversely, as S → 0.8 (Fig. 1c), less diffusion occurs along the c-axis and more in the ab directions. This is because, the La rich layers contain fewer of the vacancies required for Li hopping; the possibility of many aligning in consecutive layers is reduced.

As mentioned previously,^36,37 the local ordering of the and ions will have a profound effect on the Li ion migration pathways possible in the structure. Indeed, as discussed by Gao et al.³⁷ the structure of LLTO is far from ideal and significant variations in local chemistry are present; this is supported by the present study. It has been noted that if Li is completely coordinated by La, then it effectively becomes trapped and cannot contribute to overall migration. This is consistent with the suggestion by Šalkus et al.⁷ that migration is vacancy mediated; since La atoms are effectively immobile in the structure, they restrict Li and migration. For example, in S = 0.2 structures about 2–4% of Li are surrounded by six La ions and are therefore, immobile.

The main image within Fig. 6 shows and sites within a GA optimised structure. Given that diffusion proceeds by a series of hops between neighbouring and sites, it is instructive to draw white rods between such neighbours. In this way an effective three dimensional map of possible hopping routes through the structure in Fig. 6 has been revealed. This graphically illustrates that a percolating network of 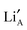and A site vacancies exists within the A site sub-lattice of these structures. To further clarify these spatial relationships, inset to the side of Fig. 6, are three schematic representations of alternating La rich and La poor layers, in which the connecting ‘hop’ rods are further colour coded with blue showing connections to the layer above and red to that below. The percolating network of interlayer associations is significant as it is shown to be continuous for S = 0.2 meaning that the Li atoms can use multiple routes to travel between layers. This maze of different possibilities will be temperature and also disorder dependent.

Fig. 6 Schematic of LLTO showing La poor (blue) and rich (yellow) layers. Green points and connections highlight the possible pathways created by and . The layer plans (right) highlight the pathways in ab planes and within these, a blue sticks indicate connections to the layer above and red to the layer below. The structure shown is for LLTO where S = 0.2 and has been optimised using the GA.

The activation energy for Li transport of LLTO has been found to be thermally activated^17,21,38 and is non-Arrhenius over the whole temperature range.^17,37 However, local Arrhenius fits can be made to Fig. 3, giving an activation energy of 0.14 eV (600–1000 K). This closely matches the activation energy proposed by Inaguma et al.⁵ that is 0.15 eV (>400 K).

Conclusions

This study provides an in-depth description of the complex structure of LLTO and the importance of local ordering and how it affects the migration pathways for Li ions and consequently, properties that make LLTO technologically significant. The experimental conductivity and activation energy (in the range 600–1000 K) for Li ions in La_2/3−xLi_3xTiO₃ (x = 0.115) has been replicated using classical MD simulations and the new Buckingham³⁹ potentials developed here. The van Hove analysis,³⁴ shows that Li ions move freely between nearest neighbour A-sites, utilising vacancies. 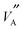Observing the mechanism reveals that Li ions can move individually into vacant sites or as concerted long chains of Li ions moving together into a vacancy, also discussed by Catti.⁴⁰ The GA used in this work improves Li conductivity by creating areas of local order which align and species in the ab and c directions, ensuring that very few Li ions are blocked in by immobile La ions, shown in Fig. 6. Recent TEM studies by Gao et al.⁴¹ also discuss the importance of local ordering in this material.

This work concludes that while the layer ordering in tetragonal LLTO has an effect on the conductivity, the local ordering between the layers is also crucial. It is interesting to note that as the ordering factor S → 0.8, the ability to align these species in the c axis decreases, simply because of the reduced number of Li ions in the La rich layers. This leads to the majority of the Li ion migration occurring within the ab planes and reduced 3D migration accessing the c planes; demonstrated experimentally and by the density plots shown in Fig. 1b and c and by, Yashima et al.¹⁹

Acknowledgements

This study was funded in part by the UK EPSRC research grant EP/F009720/1 “New Research Directions for Solid Oxide Fuel Cell Science and Engineering”. Computing resources were provided by the Imperial College High Performance Computing Service.

Notes and references

1. E. Kendrick, J. Kendrick, K. S. Knight, M. S. Islam and P. R. Slater, Nat. Mater., 2007, 6, 871.
2. S. I. Nishimura, G. Kobayashi, K. Ohoyama, R. Kanno, M. Yashima and A. Yamada, Nat. Mater., 2008, 7, 707.
3. M. Armand and J. M. Tarascon, Nature, 2008, 451, 652.
4. A. R. Armstrong, C. Lyness, P. M. Panchmatia, M. S. Islam and P. G. Bruce, Nat. Mater., 2011, 10, 223.
5. Y. Inaguma, L. Chen, M. Itoh, T. Nakamura, T. Uchida, H. Ikuta and M. Wakihara, Solid State Commun., 1993, 86, 689.
6. T. Onishi, Solid State Ionics, 2009, 180, 592.
7. T. Šalkus, E. Kazakevičius, A. Kežionis, A. F. Orliukas, J. C. Badot and O. Bohnke, Solid State Ionics, 2011, 188, 69.
8. M. Nakayama, A. Shirasawa and T. Saito, J. Ceram. Soc. Jpn., 2009, 117, 911.
9. Y. Maruyama, H. Ogawa, M. Kamimura, S. Ono and M. Kobayashi, Ionics, 2008, 14, 357.
10. M. Catti, J. Phys.: Conf. Ser., 2008, 117, 12008.
11. M. Catti, J. Phys. Chem. C, 2008, 112, 11068.
12. M. Catti, Chem. Mater., 2007, 19, 3963.
13. S. Ono, Y. Seki, S. Kashida and M. Kobayashi, Solid State Ionics, 2006, 177, 1145.
14. T. Okumura, A. Dodomi, M. Saito and J. Kuwano, Computational simulations of Li ion conduction in (Li,La)TiO₃, in Electroceramics in Japan IX, ed. K. Katayama, 2006, vol. 320, p. 275.
15. Y. Maruyama, H. Ogawa, M. Kamimura and M. Kobayashi, J. Phys. Soc. Jpn., 2006, 75, 064602.
16. D. Mazza, S. Ronchetti, O. Bohnke, H. Duroy and J. L. Fourquet, Solid State Ionics, 2002, 149, 81.
17. S. Stramare, V. Thangadurai and W. Weppner, Chem. Mater., 2003, 15, 3974.
18. K. Ohara, Y. Kawakita, L. Temleitner, L. Pusztai, S. Kohara, A. Jono, H. Shimakura, N. Inoue and S. Takeda, J. Phys.: Condens. Matter, 2010, 22, 404203.
19. M. Yashima, M. Itoh, Y. Inaguma and Y. Morii, J. Am. Chem. Soc., 2005, 127, 3491.
20. J. Ibarra, A. Várez, C. León, J. Santamara, L. M. Torres-Martinez and J. Sanz, Solid State Ionics, 2000, 134, 219.
21. O. Bohnke, C. Bohnke and J. L. Fourquet, Solid State Ionics, 1996, 91, 21.
22. J. L. Fourquet, H. Duroy and M. P. Crosnier-Lopez, J. Solid State Chem., 1996, 127, 283.
23. F. Vink and H. Kröger, Solid State Phys., 1956, 3, 307.
24. K. Ohara, Y. Kawakita, L. Pusztai, L. Temleitner, S. Kohara, N. Inoue and S. Takeda, J. Phys.: Condens. Matter, 2010, 22, 404203.
25. Y. Inaguma, J. Ceram. Soc. Jpn., 2006, 114, 1103.
26. S. M. Woodley, P. D. Battle, J. D. Gale and C. R. A. Catlow, Phys. Chem. Chem. Phys., 1999, 1, 2535–2542.
27. R. L. Johnston, Dalton Trans., 2003, 4193.
28. W. Paszkowicz, Mater. Manuf. Processes, 2009, 24, 174–197.
29. D. E. Goldberg, Genetic algorithms in search optimization and machine learning, Addison-Wesley, Reading-Mass, 1988.
30. A. Cleave, PhD thesis, Imperial College London, 2006.
31. L. Minervini, R. W. Grimes and K. E. Sickafus, J. Am. Ceram. Soc., 2000, 83, 1873.
32. T. Katsumata, Y. Inaguma, M. Itoh and K. Kawamura, Chem. Mater., 2002, 14, 3930.
33. M. Hirakuri, T. Okumura, M. Saito and J. Kuwano, Key Eng. Mater., 2009, 388, 61.
34. L. Van Hove, Phys. Rev., 1954, 95, 249.
35. A. Tilocca, J. Chem. Phys., 2010, 133, 014701.
36. T. Tsurui, T. Katsumata and Y. Inaguma, Solid State Ionics, 2009, 180, 607.
37. X. Gao, C. A. J. Fisher, T. Kimura, Y. H. Ikuhara, H. Moriwake, A. Kuwabara, H. Oki, T. Tojigamori, R. Huang and Y. Ikuhara, Chem. Mater., 2013, 25, 1607.
38. B. Youmbi, S. Zékeng, S. Domngang, F. Calvayrac and A. Bulou, Ionics, 2012, 18, 371.
39. R. A. Buckingham, Proc. R. Soc. London, Ser. A, 1938, 168, 264.
40. M. Catti, Solid State Ionics, 2011, 183, 1.
41. X. Gao, C. A. J. Fisher, T. Kimura, Y. H. Ikuhara, H. Moriwake, A. Kuwabara, H. Oki, T. Tojigamori, R. Huang and Y. Ikuhara, J. Am. Chem. Soc., 2012, 25, 1607.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp04834b

---