Length dependence of electron transport through molecular wires – a first principles perspective
Khoong Hong
Khoo
abc,
Yifeng
Chen
ab,
Suchun
Li
acd and
Su Ying
Quek
*ab
aDepartment of Physics, Faculty of Science, National University of Singapore, 2 Science Drive 3, Singapore 117551, Singapore. E-mail: phyqsy@nus.edu.sg
bCentre for Advanced 2D Materials and Graphene Research Centre, National University of Singapore, 6 Science Drive 2, Singapore 117546, Singapore
cInstitute of High Performance Computing, Agency for Science Technology and Research, 1 Fusionopolis Way, #16-16 Connexis, Singapore 138632, Singapore
dNUS Graduate School for Integrative Sciences and Engineering, National University of Singapore, 28 Medical Drive, Singapore 117456
First published on 12th November 2014
Abstract
One-dimensional wires constitute a fundamental building block in nanoscale electronics. However, truly one-dimensional metallic wires do not exist due to Peierls distortion. Molecular wires come close to being stable one-dimensional wires, but are typically semiconductors, with charge transport occurring via tunneling or thermally-activated hopping. In this review, we discuss electron transport through molecular wires, from a theoretical, quantum mechanical perspective based on first principles. We focus specifically on the off-resonant tunneling regime, applicable to shorter molecular wires (<∼4–5 nm) where quantum mechanics dictates electron transport. Here, conductance decays exponentially with the wire length, with an exponential decay constant, beta, that is independent of temperature. Different levels of first principles theory are discussed, starting with the computational workhorse – density functional theory (DFT), and moving on to many-electron GW methods as well as GW-inspired DFT + Sigma calculations. These different levels of theory are applied in two major computational frameworks – complex band structure (CBS) calculations to estimate the tunneling decay constant, beta, and Landauer–Buttiker transport calculations that consider explicitly the effects of contact geometry, and compute the transmission spectra directly. In general, for the same level of theory, the Landauer–Buttiker calculations give more quantitative values of beta than the CBS calculations. However, the CBS calculations have a long history and are particularly useful for quick estimates of beta. Comparing different levels of theory, it is clear that GW and DFT + Sigma calculations give significantly improved agreement with experiment compared to DFT, especially for the conductance values. Quantitative agreement can also be obtained for the Seebeck coefficient – another independent probe of electron transport. This excellent agreement provides confirmative evidence of off-resonant tunneling in the systems under investigation. Calculations show that the tunneling decay constant beta is a robust quantity that does not depend on details of the contact geometry, provided that the same contact geometry is used for all molecular lengths considered. However, because conductance is sensitive to contact geometry, values of beta obtained by considering conductance values where the contact geometry is changing with the molecular junction length can be quite different. Experimentally measured values of beta in general compare well with beta obtained using DFT + Sigma and GW transport calculations, while discrepancies can be attributed to changes in the experimental contact geometries with molecular length. This review also summarizes experimental and theoretical efforts towards finding perfect molecular wires with high conductance and small beta values.
 Su Ying Quek † | Su Ying Quek graduated with BA Honors (1st class) in Mathematics from the University of Cambridge in 2000 and obtained her PhD in Applied Physics from Harvard University in 2006, working with Efthimios Kaxiras and Cynthia Friend. After a year of exchange studies at University of California, Berkeley, in 2005 with Steven G. Louie, she joined Jeff Neaton in Lawrence Berkeley National Laboratory as his first postdoctoral associate, from 2006 to 2010. From 2011 to 2013, she was an Independent Investigator in the Institute of High Performance Computing, Singapore. In August 2013, she joined the National University of Singapore as an Assistant Professor, supported by the Singapore National Research Foundation Fellowship. Her research interests include the electronic structure and transport properties of emerging materials. |
The field of molecular electronics has seen remarkable progress during the past few decades. The vision of using molecular components for electronics applications was proposed back in the 1970s,1,2 and experimental advancements such as scanning probe techniques and break junctions have provided the necessary tools for the fabrication and characterization of these molecular electronic devices.
Molecular wires, which are usually understood as one-dimensional rod-like molecular structures made from single molecules or their assemblies, constitute one of the most important building blocks of molecular electronics. Typical molecular wires studied extensively in the literature include oligo(phenylene ethynylene)s (OPEs), oligo(phenylene vinylene)s (OPVs), oligo-thiophenes, oligo-phenyls, oligoynes, oligoacenes, oligo-porphyrins, DNA, and alkane chains.3–11 Electron transport studies through these molecular wires are particularly important for both understanding their fundamental properties from a scientific perspective and guiding their utilization in practical devices, such as in molecular circuits, organic solar cells, organic light-emitting diodes (OLED), and organic field-effect transistors (OFET).12,13 π-Conjugated molecular wires are usually more conductive, hence they are often proposed as potential linking structures in molecular circuits. On the other hand, saturated molecular wires like alkane chains have higher resistance, but are less susceptible to extrinsic effects in experimental measurements, which makes them suitable for fundamental studies.
In this review, we focus on the study of electron transport through molecular wires, from a first principles perspective. That is, we shall discuss methodologies that treat the electron transport problem by solving Schrodinger's equation, without any empirical parameters but with some well-defined approximations.
The paper is organized as follows. Section 1 provides a general introduction to transport through molecular wires, including phenomena that are not typically studied using first principles methodologies. In Section 2, we begin our focus on first principles studies, providing a background for the first principles methods involved in the study of electron transport across molecular wire junctions. In Section 3, we present detailed examples of these first principles methods applied to different molecular wire systems and compare results with experimental measurements. In Section 4, we summarize different transport characteristics within the tunneling regime for a number of different wire systems, in efforts towards understanding and predicting perfect molecular wires. Section 5 presents concluding remarks, including some future perspectives on problems which still remain open in the field.
1. Introduction and background
Earlier studies of molecular electronics systems started with molecular assemblies such as Langmuir–Blodgett (LB) films or self-assembled monolayers (SAMs).14–16 These ingeniously synthesized molecular assemblies routinely reach single-molecule thicknesses. Sandwiched between a back electrode and top metal contacts or probes, electron transport through these systems can be systematically studied in experiments, providing the first results at the single-molecular level. Although short-range intermolecular interactions are usually not negligible in these monolayer systems, results from SAMs or LB films are routinely used to provide insight into truly single-molecular junctions wherever appropriate. Device contacting and measuring strategies usually include nanopores, nanoparticle top contacts, conducting-probe atomic force microscopy (CP-AFM), crossed wire junctions, mercury drop junctions, and conducting polymer top contacts.17For single molecular systems, an experimental breakthrough came during the late 1990s, when M. A. Reed et al.18 first used mechanically controlled break junctions (MCBJs) to successfully obtain electron conductance data through a molecular benzenedithiol (BDT) system sandwiched between two gold electrodes. This method subsequently became one of the most important fabrication techniques for single-molecule electronic devices. Besides MCBJs, electrochemical break junctions (BJs) and scanning tunneling microscopy (STM) based BJs were also developed by several groups to investigate molecular systems in solution.19,20 STM-BJs have the advantage that they can be repeatedly formed and broken over numerous cycles very easily.
However, interpretation of results from single-molecule experiments is usually non-trivial. Initially, discrepancies between theory and experiments and between experiments from different groups were prevalent. Eventually, it was realized that various effects such as device contact geometry, metal/molecule interfaces, molecular anchoring and side groups, inelastic effects, molecular conformation, and stochastic fluctuations can all influence experimental results considerably.21–29 A statistical analysis method was employed by Xu and Tao30 to unambiguously determine transport characteristics through single molecular junctions. By constructing a conductance histogram using data from thousands of molecular junctions formed between a gold STM tip and gold substrate, well-defined histogram peaks were identified at integer multiples of a fundamental conductance value (usually a small fraction of G0 for alkanedithiol systems). The lowest conductance histogram peak is interpreted to correspond to single molecular junctions while higher conductance peaks are attributed to junctions having multiple molecules linking the gold electrodes. This kind of statistical analysis has subsequently become a standard procedure in data analysis for single molecule experiments.
In spite of the seminal work by Xu and Tao, subsequent experiments by numerous groups on alkanedithiol–Au junctions still produce qualitatively different conductance histograms from previous results. These differences have since been attributed to variations in the atomic configurations of the thiol–gold bonds and changes in the conformation of alkane molecules.31,32 The strong dependence of conductance on molecular conformation has also been observed in phenyl molecules. Experimental studies by L. Venkataraman et al.26 have demonstrated a cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ conformational dependence of the electron conductance through a series of diamine–biphenyl junctions at various twist angles θ, consistent with theoretical predictions.
θ conformational dependence of the electron conductance through a series of diamine–biphenyl junctions at various twist angles θ, consistent with theoretical predictions.
Although the thiol anchoring group is popular in the literature for single molecular systems because it readily forms strong bonds with metallic electrodes, it also suffers from serious shortcomings, such as high variability of conductance with details of the junction geometry, hindering junction reliability and measurement reproducibility. Other anchoring groups used for molecular wire studies include amine, nitro, cyano, pyridine, carboxyl, and heterocycle groups as well as molecules directly bound to the contacts.20,33–35 In particular, the amine anchoring group is found to bind preferentially with under-coordinated gold atoms, enabling well-defined conductance characteristics for single molecular devices, even though the coupling of amines with metallic contacts is usually weak.20
Electron transport mechanisms in molecular wire junctions can largely be classified into two categories, coherent tunneling and incoherent hopping, with a length-dependent mechanism crossover between the two regimes.36
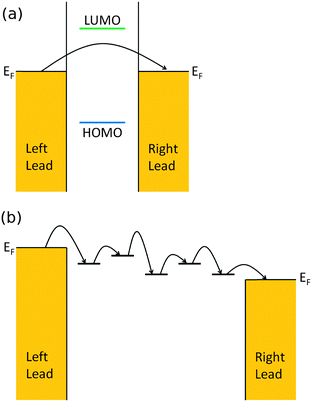
For short or saturated wires with large EF-LUMO (or HOMO, whichever is closer) separation, the dominant transport mechanism is a one-step coherent off-resonant tunneling of the carriers through the molecular bridge, as shown in Fig. 1(a). In the coherent off-resonant tunneling regime, inelastic effects such as electron–phonon couplings do not significantly affect the room temperature conductance of single molecules. Since the molecular wire bridge effectively acts as a guiding barrier for the charge carriers to tunnel through, the differences between electron tunneling through molecular assemblies versus single molecular wires are less significant. In particular, through-molecule tunneling has been found to be dominant over through-space tunneling (tunneling between molecules in the SAM).37
For longer conjugated molecular wires at moderate temperatures, there will be localized sites on the bridge where charge carriers can temporarily reside; the longer bridge length means that carriers need to spend more time on the molecules, which subsequently increases the chances of coupling with molecular vibrational modes. Furthermore, it is easier to distort backbones and excite or absorb vibrational modes in longer wires. Thus the dominant transport mechanism here changes into a multi-step incoherent hopping of carriers from site to site on the bridge, as shown in Fig. 1(b). The inter-site hopping transition is usually believed to be thermally-activated, following the Marcus picture of electron transfer.
There are substantial characteristic differences between tunneling and hopping transport mechanisms. For coherent off-resonant tunneling transport, the electron conductance (resistance) usually displays an exponentially decreasing (increasing) behavior with respect to the bridge length L:
| G = Gce−βL or R = RceβL | (1) |
Here Gc (Rc) is the contact conductance (resistance) of the molecular wire junction, while β is the tunneling decay constant that depends on the molecular backbone. Also, tunneling transport is largely temperature independent.
For incoherent hopping transport, junction resistance increases linearly with the bridge length:
| R ∝ αL | (2) |
For electron transport through molecular wire systems, the transition from tunneling to hopping mechanism has been observed for both molecule assemblies and single molecular systems. Choi et al.41 used the CP-AFM method to measure the length-dependent transport of a set of oligo-phenyleneimine (OPI) SAMs with lengths ranging from 1.5 to 7.3 nm. The resistance data taken from averages of I–V traces were plotted as shown in Fig. 2(a). The transition point can be clearly identified at OPI 5 where the wire length is about 4 nm. The linearly increasing behavior of molecular resistance from OPI 6 to OPI 10 shown in the inset indicates the onset of hopping dominated transport for longer wires. These conclusions are also corroborated by temperature-dependence measurements in the same report. In another study, Hines et al.42 used the STM-BJ technique and investigated the length and temperature dependence of electron conductance through one group of conjugated single molecular wires ranging from 3.1 to 9.4 nm in length (1- to 4-mer). The collected data from conductance histograms are shown in Fig. 2(b). The mechanism transition point is clearly determined as between 2-mer and 3-mer, which means a length between 5.2 and 7.3 nm. Temperature dependence studies also revealed strong conductance variations for longer 3, 4-mer wires, while showing no significant variation for shorter 1, 2-mer wires, consistent with the mechanism crossover picture.
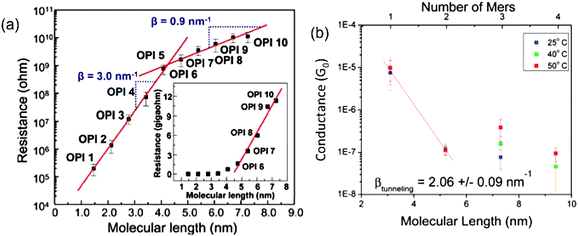 | ||
| Fig. 2 (a) CP-AFM measured electron resistance data of OPI molecular wires with respect to their lengths in a semi-log plot. Insert: linear scale plot. (b) STM-BJ measured electron conductance of one group of conjugated single molecular wire junctions from 1-mer to 4-mer in a semi-log plot. (Panel (a) is reproduced by permission of the American Association for the Advancement of Science (ref. 41)). (Panel (b) is reproduced by permission of the American Chemical Society (ref. 42)). | ||
Aside from electron conductance G or resistance R properties through nanoscale molecular wires, thermal transport and thermoelectric properties are emerging as new important research directions.43,44 In particular, the thermoelectric response across various types of molecular wires have been successfully measured from experiments and investigated from theory.45,46
As the focus of our present review is on a first principles perspective of electron transport, we now comment on which of the transport phenomena discussed above are amenable to first principles studies. Since first principles methods are inherently quantum mechanical, they are ideal tools for investigating electron transport in the coherent off-resonant tunneling regime. First principles methods can provide predictions of the tunneling decay factor β, and the conductance G at low finite biases. As long as transport is within the tunneling regime and not too far from equilibrium, first principles methods can also be used to predict the thermopower, or Seebeck coefficient S, in molecular wire junctions. Inelastic effects within the tunneling regime can also be treated using first principles within perturbation theory; we refer the reader to excellent reviews on this topic, in particular in relation to low temperature inelastic tunneling spectroscopy experiments.47–53 On the other hand, incoherent hopping transport is rarely treated fully from first principles. As the reorganization energies in Marcus theory result from the rearrangement of solvent molecules in addition to geometric changes in the conducting molecule, first principles studies of such processes are computationally demanding. Instead, semi-empirical techniques are more commonly applied.13
2. First principles methods
The workhorse of first principles calculations is density functional theory (DFT). However, an issue of DFT is the notorious underestimation of the HOMO–LUMO gap, owing to the fact that the Kohn–Sham eigenenergies are Lagrange multipliers with no physical significance. Since tunneling transport depends critically on the energy barrier, the inaccurate HOMO–LUMO gap can lead to serious quantitative errors, especially for the conductance G.54,55 The decay factor β and thermopower S are also affected by this error, although to a smaller extent. Despite these issues, DFT transport calculations can often still yield qualitatively meaningful results, as demonstrated in the studies on the geometry dependence of conductance.56–58 One way to improve the DFT quasiparticle spectrum is to introduce a non-local energy dependent self-energy correction using the GW approximation.59,60 Transport properties computed using the GW approximation have significantly improved agreement with experiment.61,62 However, a drawback of this method is that it is computationally intensive and scales badly with system size, so that it can only be applied to systems having a small number of atoms. Recently, a “multiscale” method called DFT + Σ has been introduced to quantitatively predict conductance values at the same computational expense as DFT calculations.11 The DFT + Σ method uses a DFT Hamiltonian, but corrects for inaccuracies in the molecular levels using a self-energy correction term based on GW calculations. This method is able to yield quantitatively accurate conductances, however, it is only applicable to systems where the molecular resonances are sufficiently far from the Fermi level so that the broadened resonance is either fully occupied or fully unoccupied, and where the polarizability of the molecule is sufficiently small.63,64While DFT or GW tells us how to treat the electron–electron interactions in the many-body system, a theoretical framework is required in order to compute transport properties. The Landauer–Buttiker formalism allows one to directly compute the transmission spectra of a two-electrode system, and is often the method of choice to compute the conductance G and thermopower S in molecular junctions. On the other hand, the decay constant β can also be estimated using simpler complex band structure (CBS) calculations.
Another promising framework for studying non-equilibrium transport, which we shall introduce only briefly here, is time dependent current-density functional theory (TDCDFT) that directly probes the time development of the system. Conductances of prototypical systems have been studied and a dynamical exchange–correlation correction to the conductance has been identified.65–67 A complication of this method is that the Runge–Gross theorem, which underpins TDCDFT, is not proven for non-equilibrium open-systems. Possible workarounds include the use of large but finite leads68,69 or the inclusion of complex absorbing potentials that make the leads essentially finite.70 In addition, currently available exchange–correlation potentials are unable to account for non-local effects, essential for accurately describing molecular conductance.
In the following, we introduce the CBS and Landauer–Buttiker formalisms, and finally provide a detailed description of the DFT + Σ method, which is used in the Landauer–Buttiker formalism.
2.1 Complex bandstructure calculations
For molecular wires, which consist of a set of repeating units, the tunneling decay constant β can be evaluated from the complex band structure (CBS) of the corresponding periodic polymer,71 computed by considering the energy E as input and solving for the set of wavevectors k that produce this energy for a given Hamiltonian. The output k-values are generally complex, and in particular, for E in the band gap of the polymer, the k-values are purely imaginary. At the interface between a metal and the polymer, incoming states from the metal decay as e−Im[k(E)]L while their tunneling probability decays as e−2Im[k(E)]L. Thus β can be obtained as 2Im[k(EF)], where EF is the Fermi energy of the metal. Such evanescent states within the band gap of the polymer, which originate from the adjacent metal, are known as metal-induced gap states.A simple way of estimating the Fermi level lineup within the CBS was suggested by Tersoff.72 In general, if the density of the metal-induced gap states is sufficiently large, the Fermi level should be pinned at the charge neutrality level (CNL), and this can be estimated to be at the branch point 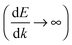 within the band gap having the smallest Im(k), as shown in Fig. 3(a). This method provides a reasonable first estimate of the Fermi level alignment.
within the band gap having the smallest Im(k), as shown in Fig. 3(a). This method provides a reasonable first estimate of the Fermi level alignment.
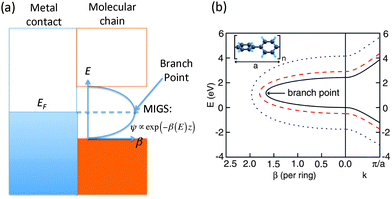 | ||
| Fig. 3 (a) Schematic of the molecule–contact interface including the imaginary part of the complex band structure. The Fermi level is typically pinned at the branch point within the band gap having the smallest Im(k). (b) Right (left) panels are real (imaginary) band structures of periodic chain with different band gaps Eg. Right: highest valence and lowest conduction bands. Left: complex band corresponding to the smallest imaginary k within the gap. The energy E is plotted against β(E) = 2aIm(kmin(E)). All other bands are explicitly omitted. Inset: atomic geometry of a repeat unit of the periodic polyphenyl chain. (Panel (b) is reproduced by permission of the American Chemical Society (ref. 11)). | ||
Compared to evaluating β from transport calculations involving the full molecular junction, such as in the Landauer–Buttiker formalism, the CBS method has the advantage that it is more direct and computationally efficient. Also, the CBS carries detailed information about the tunneling layer and its evanescent states, which makes it an interesting analysis and characterization tool. However, the CBS method does have several limitations. The metal contacts, anchoring groups, and contact geometry can only influence β through the placement of the Fermi level within the CBS. This implicitly assumes that the interfacial interactions are not dominant. In addition, the band gap of the periodic polymer is usually smaller than the HOMO–LUMO gaps obtained for short oligomers. A possible solution to this is to add a ‘scissor-shift’ operator to the Hamiltonian when computing the CBS, as illustrated in the CBS for oligophenyls in Fig. 3(b).11 However, this HOMO–LUMO gap is also generally length-dependent, especially for short molecules. Overall, the CBS method provides a reasonable estimate for the value of β, but it does lack quantitative accuracy that may be accessible through direct transport calculations.11
The above discussion has focused on extracting transport properties from the CBS. Alternatively, if the transmission spectra is known, one can also derive an “effective complex band structure” βN,N′(E) defined as 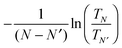 .11 This function avoids the ambiguities of EF alignments and represents a decay constant encompassing the physical features of the molecular junction. The effective CBS allows one to obtain information such as the sensitivity of β to differences in junction level alignment and also analyze contact-dependent features not available in regular CBS calculations.
.11 This function avoids the ambiguities of EF alignments and represents a decay constant encompassing the physical features of the molecular junction. The effective CBS allows one to obtain information such as the sensitivity of β to differences in junction level alignment and also analyze contact-dependent features not available in regular CBS calculations.
2.2 Landauer–Buttiker formalism
In mesoscopic systems where the length scale becomes comparable to electron wavelengths, quantum effects dominate electron transport. Landauer showed that for coherent transport in this regime, the conductance is closely related to the probability of electron transmission, and this is summarized in the following equation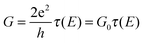 | (3) |
In the linear response regime, when the thermally induced electrical voltage ΔV is proportional to the applied temperature difference ΔT, we can define the thermopower S as S = −(ΔV/ΔT)|I=0 at the steady state zero current. Under conditions that the average junction temperature T is relatively small so that the electron transmission varies smoothly within kBT of the Fermi level, and for ΔT much smaller than T, we can write the thermopower S in the following form
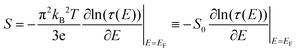 | (4) |
Starting from first-principles electronic structure methods such as DFT, the electron transmission spectrum can be computed either by the non-equilibrium Green's function (NEGF) method, as implemented in transport packages such as TranSIESTA76 and SMEAGOL,77 or the scattering-state method as implemented in SCARLET.78,79
In these transport calculations, one first constructs an open-boundary system consisting of a left lead, right lead, and central resistive region. For the NEGF method, the retarded Green's function Gr of the resistive region is evaluated along with the self-energies of the leads. These quantities are then used to evaluate the transmission spectrum using the following expression
| τ(E) = Tr[ΓL(E)Ga(E)ΓR(E)Gr(E)] | (5) |
When a finite bias V is applied across the resistive region, a self-consistent procedure is employed to obtain the steady-state non-equilibrium transmission spectrum τ(E,V), and the current–voltage (I–V) characteristics for electron transport is evaluated from the following integration
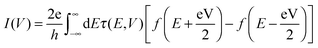 | (6) |
Compared to the complex band structure method described previously, Landauer transport calculations are much more computationally intensive. However, the advantage is that one obtains not just the decay constant β, but also the contact conductance G. Also, these calculations account for the contact, anchoring groups, and variations in the junction geometry explicitly, all of which have been shown to have non-negligible effects in determining transport properties in single molecule junctions. The Landauer calculations are also much more general, and can be used to describe electron transport in other regimes, such as coherent resonant tunneling.
2.3 DFT, GW and DFT + Σ
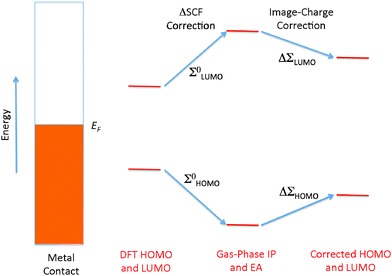
The simplest physical picture of coherent off-resonant tunneling consists of electrons tunneling across a one-dimensional potential barrier V(V > E), with the tunneling decay constant given by β ∼ (2m(V − E))1/2/ℏ. A predictive theory for transport in single-molecule junctions thus relies on an accurate prediction of the tunneling barrier Ebarrier = V − E, which is approximately given by the quasiparticle energy of the frontier molecular orbital relative to the Fermi level. The quasiparticle energy can be predicted accurately using the GW method,59,60 which can be understood as being analogous to Hartree–Fock except that the screened Coulomb potential is used instead of the bare Coulomb potential. As such, GW considers the effect of electronic screening in response to the removal of an electron or hole from the system, in addition to exchange interactions that are already present in Hartree–Fock. On the other hand, DFT Kohn–Sham eigenvalues are introduced as Lagrange multipliers in the formalism, but are often used as a qualitative approximation to the quasiparticle energies. The actual value of the Kohn–Sham HOMO–LUMO gap depends on the flavor of the exchange–correlation potential used in the DFT calculation. Typically, the local density approximation (LDA) and generalized gradient-corrected approximations (GGA) give HOMO–LUMO gaps that are too small. Hybrid functionals81,82 that explicitly include a percentage of Hartree–Fock exchange interactions widen this gap, as do self-interaction corrections.83Several transport calculations have been performed explicitly in the GW framework, and these have resulted in significantly more accurate level alignments and conductance values compared to DFT.61,84–86 In addition, first-principles GW calculations have been used to provide physical insight into many-body and dynamical effects involved in image charge formation.87,88 Despite the success of the GW transport formalism, its high computational cost has prompted the development of a GW motivated parameter-free self-energy operator on DFT that corrects for level alignments and predicts quantitatively accurate conductances within the single-particle picture.11,35,89 This DFT + Σ method is inspired by studies performed by Neaton et al. to investigate the difference between GW and DFT LDA eigenvalues for the energy level alignment of physisorbed molecules on a metallic surface.90 In addition to the underestimation of the HOMO–LUMO gap by DFT LDA, it was found that long-range correlation effects due to surface electrostatic screening of the metal electrodes leads to a substantial decrease of the HOMO–LUMO quasiparticle gap, shown schematically as ΔΣLUMO and ΔΣHOMO in Fig. 4. This correction is completely missing from the corresponding Kohn–Sham gap, as can be seen in Table 1, where the GW HOMO–LUMO gap for benzene on graphite reflects variations in screening effects due to differences in the molecular environment, while DFT LDA yields a gap that is nearly constant. This lack of transferability to different environments is characteristic also of hybrid functionals in DFT, where the non-local nature of the exchange–correlation effect is not fully taken into account.90–93 The results of Table 1 imply that for a physisorbed molecule on a metal substrate, the self-energy correction to the DFT HOMO and LUMO levels can be obtained as a sum of two parts: (1) the self-energy correction in the gas phase, which typically increases the HOMO–LUMO gap, and (2) the self-energy correction due to image charge effects in the substrate, which reduces the HOMO–LUMO gap (Fig. 4). This method has also been applied to benzenediamine on Au(111), and obtained excellent agreement with photoemission results.94 The two-part self-energy correction in Fig. 4 is also applicable to molecules chemisorbed on metal substrates, provided that the molecular resonances are sufficiently far from the Fermi level so that the broadened resonance is either fully occupied or fully unoccupied, and that the polarizability of the molecule is sufficiently small.63,64
| Gas phase | Flat on graphite | Crystal phase | |
|---|---|---|---|
| ΔEgap (LDA) | 5.16 | 5.05 | 5.07 |
| ΔEgap (GW) | 10.51 | 7.35 | 7.91 |
The gas-phase correction Σ0HOMO and Σ0LUMO can be easily obtained by comparing the DFT, HOMO and LUMO levels of the gas-phase molecule with the ionization potential (IP) and electron affinity (EA) computed from total energy differences within the ΔSCF method. The image-charge correction ΔΣ can be obtained using electrostatics and details are provided in the next subsection. Self-energy corrections for the metallic leads are usually small compared with the molecule, and can be safely neglected. Therefore, in order to correct for the self-energy errors in DFT, we can add to the DFT Hamiltonian a self-energy operator
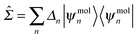 | (7) |
DFT + Σ has been implemented for both NEGF85 and scattering-state formalisms.11,35,89,95 In both cases, the charge density is first converged from transport calculations using standard-DFT XC functionals. The self-energy operator ![[capital Sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e139.gif) is then added to the Hamiltonian and the calculation carried out in a “one-shot” non-self-consistent fashion based on the converged DFT charge density to obtain the transmission spectrum. This procedure has been shown to yield accurate molecule-contact level alignments and conductances for molecular systems satisfying the necessary conditions. DFT + Σ transport calculations have been shown to be equivalent to static GW transport calculations.88
is then added to the Hamiltonian and the calculation carried out in a “one-shot” non-self-consistent fashion based on the converged DFT charge density to obtain the transmission spectrum. This procedure has been shown to yield accurate molecule-contact level alignments and conductances for molecular systems satisfying the necessary conditions. DFT + Σ transport calculations have been shown to be equivalent to static GW transport calculations.88
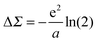 using the method of images, where a is the electrode separation. Applying this formula to the benchmark case of Au–BDA junctions, and using an image plane position ∼1 Å from the Au surface, we obtain a ΔΣHOMO of ∼ +1 eV. Combining this with the bare HOMO self-energy correction of −3 eV yields a ΣHOMO correction of −2 eV. This shift modifies the calculated conductance from 0.046 G0 to 0.007 G0, giving much better agreement with the experimental value of 0.0064 G0.58
using the method of images, where a is the electrode separation. Applying this formula to the benchmark case of Au–BDA junctions, and using an image plane position ∼1 Å from the Au surface, we obtain a ΔΣHOMO of ∼ +1 eV. Combining this with the bare HOMO self-energy correction of −3 eV yields a ΣHOMO correction of −2 eV. This shift modifies the calculated conductance from 0.046 G0 to 0.007 G0, giving much better agreement with the experimental value of 0.0064 G0.58
In actual DFT + Σ calculations, a more refined model is employed where the orbital charge density is represented by Mulliken charges centered on each atom. Here, the image charge correction is
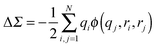 | (8) |
3 Comparison between calculations and experiment
3.1 Complex band structure calculations
In general, the CBS method has been used to investigate tunneling in a wide variety of molecular systems including alkanes,71,98,99 alkenes,71,100 silanes,98 polyphenyls,11,100 DNA strands,101 PPE,56,71,102 and carbon nanotubes.103 In addition, there has also been a GW CBS study on alkanes, alkenes, PPE, and PPI molecules, with comparisons made to DFT local, semilocal, and hybrid-exchange density functionals.104 It was found that local and semilocal density functionals systematically underestimate the β parameter, while hybrid-exchange schemes partially correct for this discrepancy, resulting in much better agreement with GW calculations and experiments.CBS calculations of β have proven to be particularly predictive in the case of alkane chains. Experiments on alkane chains sandwiched between Au contacts have yielded a β of 0.94–1.0731,105,106 and 0.9120 per methyl group for thiol and amine terminated molecules respectively. Junctions where alkane molecules are directly linked to Au contacts have also been fabricated to give a β value of 0.97.39 Earlier DFT–CBS calculations that align EF using Tersoff's method have yielded β between 0.9–1.0,71,99 while a more recent DFT study utilizing the B3LYP hybrid-functional and EF from junction calculations gives β ∼ 0.81 and 0.93 per methyl group for Au–alkanedithiol and Au–alkanediamine junctions respectively.98 It can be seen from these calculations that the anchoring group does not have a strong effect on the tunneling decay constant for alkane chains, and CBS calculation gives β values in fairly good agreement with experiment. The insensitivity of β to environmental factors and DFT errors, as well as to the exact placement of EF, has been attributed to the large band gap of alkane chains producing a relatively flat CBS with nearly constant β over a broad energy range.107
As for oligophenyls, another common class of molecular wires, the decay constant β for self-assembled monolayers (SAMs) of oligophenylene thiolates on Au substrates has been measured to be 1.8 per phenyl group.108 Similarly, β for single oligophenyldiamine molecules sandwiched between Au and Ag contacts have been measured to be between 1.7–1.8 per phenyl ring,26,109 while oligophenyls directly connected to Au leads give a higher value of 2.0.40 For oligophenyl chains, DFT–CBS calculations employing the Tersoff approach give a β of 1.6 per phenyl group, slightly below the experimental range.100 In another CBS study, a scissor shift was applied to match the CBS gap to the HOMO–LUMO band gap in oligophenyldiamine–Au junctions (a DFT + Σ type calculation).11 The Fermi level EF is then placed above the VBM using EF-HOMO alignments from molecular-junction calculations, giving a β of 2.0 per phenyl ring.
3.2 Landauer–Buttiker transport calculations
Numerous transport studies invoking the GW approximation have been shown to predict accurate conductances.61,62,84–86,117 However, the poor scaling of many-body calculations with system size means that correlations can only be introduced in a small calculation region, and it is necessary to use highly simplified representations of junction structures. This may present issues as the junction conductance has been shown to be sensitive to atomic structure.118–120
Let us now consider studies on several prototypical single molecule junctions. Unless otherwise stated, DFT values reported from the literature are obtained within LDA or GGA.
Just as DFT CBS calculations have been particularly effective for predicting β in alkane chains, we see from Table 2 that DFT transport calculations are similarly effective. In contrast, the value obtained from higher-level CI calculations is clearly too small.
It is interesting in particular to note that both the medium and high conductance families (corresponding to different contact geometries) in the alkanedithiol–Au junctions have very similar β values, although the conductances in the two families differ by a magnitude of ∼5.31 This indicates that β is much less sensitive to contact geometry than actual conductance values, especially for the alkanedithiol molecules. Experimentally, three families of junctions with distinct conductance values have been found for these molecules, with each family corresponding to a different atomic configuration at the molecule–electrode bond.31,32,125–127 DFT calculations on Au–alkanedithiol–Au junctions have also found a strong dependence of conductance on the binding geometry, consistent with the family behavior observed in experiments.120,123 In contrast to alkanedithiol–Au junctions, alkanediamine–Au junctions exhibit a unique contact conductance Gc instead of the family behavior observed for alkanedithiol junctions. This unique contact conductance comes from the fact the amine groups bind selectively to undercoordinated Au sites, while the thiol group can bind to different Au binding sites with very similar binding energies. Experiments have reported a Gc of 0.030 G0 (ref. 20) while DFT calculations predict a much larger value of 0.11 G0.84 Introducing GW corrections brings Gc down to 0.04 G0,84 in very good agreement with experiment. Recently, metal–alkane junctions with direct Au–C bonding without anchoring groups were synthesized.128 These junctions show almost a 100-fold increase in conductance relative to their thiol or amine linked counterparts due to the strong Au–C bonding. As mentioned previously, the decay constant β is found to be 0.97 ± 0.2 per carbon, which is similar to those obtained from experiments on alkane chains with anchoring groups. DFT based transport calculations indicate that the transmission at the Fermi level is dominated by the Au–C σ-bonding orbitals. With its unambiguous bonding geometry and high conductance, it would be interesting to investigate transport through these junctions from first-principles with proper self-energy corrections.
Moving on to discuss the conjugated molecular wires, we begin with the prototypical single molecule junctions, benzenedithiol (BDT)–Au and benzenediamine (BDA)–Au junctions (Table 3).
For BDT–Au, conductance values spanning several orders of magnitude from 5 × 10−5G0 to 0.1 G0 were reported from earlier experiments,18,19,130,131 while recent measurements have settled to more consistent values ranging between 0.005 and 0.01 G0.23,132 On the theoretical front, many authors have performed DFT calculations on BDT–Au junctions, giving conductances in the range of 0.067–0.9 G0. It was also found from DFT calculations that the conductance is strongly dependent on the binding geometry, similar to the alkanethiol–Au case, and typical for Au–thiol contacted systems.56,57 This finding is consistent with the large range of experimental conductance values. A GW transport calculation for BDT–Au junctions with the sulfur attached to flat Au surfaces gave a conductance value of 0.83 G0, much larger than experimentally measured values. However, a similar calculation with benzene-dithiolate (BDT + H) on pyramidal Au contacts gives a reasonable conductance value of 0.01 G0. More recently, a DFT + Σ calculation for BDT attached to Au pyramidal contacts also gave a conductance of 0.01 G0.129
For better comparison between theory and experiments, junctions containing benzenediamine have been considered, as amine end-groups are found experimentally to have less variability in conductance.20,23,26,134 Experiments on BDA–Au junctions report conductance values between 0.005 and 0.01 G0,23,26 while DFT calculations predict a significantly larger value of 0.046 G0.58 Inclusion of GW corrections lowers the conductance to 0.0042 G0 and brings it much closer to the experimental range.61 Similarly, DFT + Σ calculations have yielded a value of 0.005 G0, in agreement with experimental measurements and GW calculated values.11 The conductance of BDA molecules was further investigated by chemical functionalization. Experimentally, the conductance of BDA was varied between 5.5 × 10−3G0 and 8.2 × 10−3G0 by substituting H atoms on the phenyl ring with a series of electron-donating/withdrawing functional groups.24 By performing GW and DFT + Σ calculations on these molecules, it was found that both methods yield conductances in good agreement with experiments. However, DFT + Σ predicts conductances that are closer to the measured values while GW calculations give better conductance trends across various functional groups.85
In addition to amines, other anchoring groups such as pyridine have also been found to have less variability in conductance and therefore more suitable for benchmark studies.20,35,58 Through a combined experimental and theoretical analysis,35 it was found that the conductance histogram in pyridine–Au junctions has two conductance peaks (the high-G and low-G peaks), corresponding to two different molecular geometries. The low-G geometry has the molecular backbone aligned perpendicular to the metal surface, while the high-G geometry has molecules tilted in the junction between the metal electrodes.
In Fig. 5, the zero-bias conductance data from calculations and experiments are plotted for a number of junctions with amine and pyridine terminated molecules sandwiched between Au-leads. From this plot, it is obvious that DFT substantially over-estimates the electron conductance relative to experimental values while both DFT + Σ and GW give much better agreement with experiment. In addition to overestimating the conductance, DFT can also yield incorrect conductance trends. For example, the conductance of BP–Au junctions (molecule 7) is smaller than that of 1,2-bis(4-pyridyl)ethylene–Au junctions (molecule 8) within DFT, while DFT + Σ correctly predicts a larger conductance for BP relative to molecule 8 in agreement with experiment.
 | ||
| Fig. 5 Conductance obtained from DFT (black circles), DFT + Σ (red squares), and GW (blue diamonds) plotted against experimental conductances on a log–log scale for Au junctions containing (1) 1,4-benzenediamine (BDA), (2) 4,4′-dibenzenediamine (DBDA), (3) 4,4′′-tribenzenediamine (TBDA), (4) 4,4′-diamino-stilbene (DAS), (5) bis-(4-aminophenyl)acetylene (APA), (6) 1,6-hexanediamine (HDA), (7) 4,4-bipyridine (BP), (8) 1,2-bis(4-pyridyl)ethylene, (9) 4,4′′-bis(4-terpyridine), and (10) 1,2-bis(4-pyridyl)ethane. DFT, DFT + Σ and experimental results for molecules 1–3 are obtained from ref. 11 and 26, molecules 4–6 from ref. 135 and 136, and molecules 7–10 from ref. 89 (low G values). GW results are obtained from ref. 85 and 137. | ||
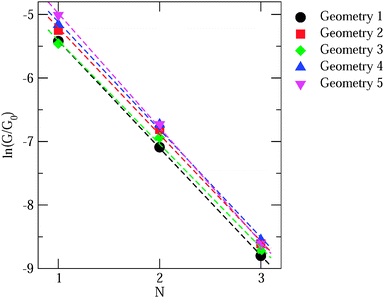
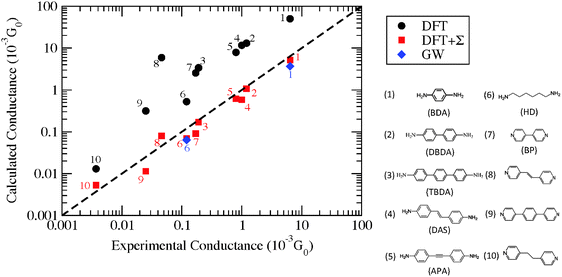
Now we consider the exponential decay constant β in molecular wires of oligophenyldiamine–Au junctions as well as wires based on pyridine–Au junctions. Although errors for β are not as dramatic as for G, at a quantitative level, DFT Landauer calculations still under-estimate its magnitude relative to experiments in the case of oligophenyldiamine–Au junctions. Fig. 6(a) shows a plot of ln(G/G0) against the number of phenyl rings N for oligophenyldiamine molecular junctions. Here DFT + Σ predicts a decay constant β equal to 1.7 per phenyl ring and experiments yield a value of 1.7 ± 0.1 per ring, while DFT under-estimates β to be 1.3 per ring.11,26 These results show that the DFT + Σ method predicts both G and β that are in agreement with experiments, and a proper inclusion of self-interaction corrections is necessary for the successful prediction of these quantities.
 | ||
| Fig. 6 (a) Plot of logarithmic conductance against the number of rings for oligophenyldiamine junctions. N equals 1, 2 and 3 correspond to one, two and three phenyl rings respectively. Inset: calculated conductance of N up to 7. (b) Similar plot for a number of pyridine junctions. Color legends: green (molecule 7), blue (molecule 8), orange (molecule 9), red (molecule 10), following the numbering scheme in Fig. 5. (Panel (a) is reproduced by permission of the American Chemical Society (ref. 11)). (Panel (b) is reproduced by permission of the American Chemical Society (ref. 89)). | ||
The same exponentially decaying behavior of conductance with length is found for a number of pyridine-terminated aromatic molecular junctions, as shown in Fig. 6(b). Molecule 10 is orders of magnitude less conductive than the other molecules being considered because of conjugation breaking at the C–C single bond. The experimentally determined decay constants are ∼0.5 Å−1 for both low and high G junctions of molecules 7–9. Experimental histograms show that the high conductance plateaus are more complicated than the low G ones, indicative of variability in the junction geometries. On the other hand, DFT + Σ correctly predicts the conductance of the low G series and its length dependence, as shown in Fig. 6(b). An eigenchannel analysis shows that electron transmission through these conjugated molecules are dominated by the LUMO level with π* character on the pyridine rings. This explains the relatively small decay constant observed in experiments.
While we have shown some representative results from the literature, comparing the predicted value of conductance with experiment still requires sampling a significant number of geometries. Generally, the DFT + Σ predicted value of conductance falls within the experimentally measured range (given by the full-width-at-half-maximum of the conductance histogram). Since conductance of individual junctions depends on the specific contact geometry, one has to be careful about quantitative comparisons of predicted β values with the experimentally determined β. This is because the experimentally determined β is obtained from the conductance histogram peaks for molecules of different lengths, but molecules of different lengths could conceivably have very different contact geometries. At present, a proper prediction of contact geometry as a function of molecular length is still beyond computational means. Instead, typically, an unbiased prediction of β will use very similar models of the contact geometry for molecules of different lengths. In Fig. 7, we plot in detail the conductance values for different contact geometries used to obtain the β value in Fig. 6(a). From Fig. 7, we see that the β value obtained from considering all data points is almost the same as that obtained by considering data points for different lengths using the same contact geometry. However, if one were to pick Geometry 5 for N = 1 and Geometry 1 for N = 3, the predicted β value would be quite different. The variability of contact geometry with molecule length in experiment is likely to be the reason for the discrepancy between experiment and DFT + Σ values for β in oligophenyl–diamine–Ag junctions.11,109 Indeed, the variation in conductance upon junction elongation is found to be larger for Ag junctions than for Au junctions, leading to sloped conductance plateaus and broader peaks in the conductance histograms.109 This has been shown to result from a larger sensitivity of electronic coupling to details of the Ag–N binding geometry.109
From eqn (4) in Section 2.2, it is clear that thermopower S is an intensive quantity, proportional to the logarithmic derivative of the electron transmission at the Fermi level EF. If the transmission near the Fermi level is dominated by off-resonant tunneling, thus showing an exponential decay with the number of molecular units τ(E) = A(E)exp(−β(E)N), eqn (4) implies that the thermopower S depends linearly on N with the linear slope given by
| βS = S0(∂(βN(E))/(∂E))|E=EF. | (9) |
Because thermopower S arises from an imbalance of charge carriers close to EF, a positive S implies that hole transport is dominant near EF, while a negative S implies that electron transport is dominant. Often, this concept is extended to conclude that a positive S implies HOMO-dominated transport, while a negative S implies LUMO-dominated transport, by using a Lorentzian function to approximate the transmission function. Likewise, within the Lorentzian model, a positive (negative) βS implies HOMO (LUMO)-dominated transport. However, in the case of molecular junctions, interface states can result in non-Lorentzian transmission functions,46 changing the gradient of transmission significantly, thus underscoring the importance of both first principles calculations and experiments in understanding the thermopower in these systems.
To illustrate the relevance and importance of interface states in thermopower measurements, we consider the case of oligophenyldiamine–Au junctions. DFT and DFT + Σ calculations were performed for these junctions, with different number of phenyl rings in the molecule.95 Two contact geometries were considered, with amine binding to single Au adatoms on Au(111), or a trimer of three Au atoms on Au(111). Au d-orbital derived interface states result in highly non-Lorentzian transmission functions close to EF for the adatom case; on the other hand, the transmission function is quite smooth close to EF for the trimer case. Since S is sensitive to the gradient of transmission close to EF, the derived values of S are quite different for the adatom and trimer cases, although the computed values of βS were almost the same for the two contact geometries.95 Interestingly, the experiment by Segalman et al.142 gave S values that are in excellent agreement with the DFT + Σ values for the trimer case, while the experiment by Venkataraman et al.46 gave S values in good agreement with the DFT + Σ values for the adatom case. This is consistent with the fact that the experiments by Segalman et al. probe the thermopower of molecular junctions without crashing the scanning tunneling microscope (STM) tip into the Au surface (thus leaving a relatively smooth Au surface), whereas the experiments by Venkataraman et al. probe the thermopower of single molecule junctions obtained by first crashing the STM tip into the Au surface to form a rough surface. Regardless of the experimental details, the DFT + Σ values of S are within the full-width half-maximum in experiments, while the DFT values are too large.95 This discussion underscores the need to consider interface states in interpreting thermopower measurements, while also emphasizing the importance of proper energy level alignments in first principles transport calculations for S.
We now summarize the key results for the length dependence of thermopower in molecular junctions,40,45,95,142 where interface states can at times lead to an unexpected sign for βS.142 Specifically, it was found that thermopower S increases linearly with length for oligophenyldiamines and oligophenyldithiols, but decreases linearly with length for alkanedithiols. The former behavior is understood as HOMO dominated tunneling in which the HOMO resonance moves closer to EF with increasing length for conjugated systems, while the latter is attributed to the presence of metal-induced gap states between the HOMO and LUMO levels.142 On the other hand, for highly conducting Au–C linked junctions, the thermopower S is found to increase non-linearly with length and saturate for oligophenyls, but to remain constant with length for alkanes.40 Comparison of computed βS values for oligophenyldiamine–Au junctions with experiments showed that DFT overestimates this quantity, while DFT + Σ gives values in agreement with experiment.95
Numerical convergence of the thermopower S with respect to the sampling density of k∥ is significantly more challenging than that for the conductance, especially when interface states affect the transmission spectra.95 Nevertheless, several GW calculations have been performed to compute the thermopower of single molecule junctions. In Table 4, we present the predicted values of S for different molecules, using DFT, DFT + Σ and GW methods, and compare the results with experiment. In general, DFT overestimates the magnitude of the thermopower, while both DFT + Σ and GW give better agreement with experiment. In addition, S.-H. Ke et al.143 used a DFT single particle Green's function method with the hybrid B3LYP and PBE0 exchange–correction functional to study the thermopower of a range of molecular junctions. They were able to get very good quantitative agreement of thermopower compared with experiments, but the predicted electronic conductance under the same framework is still over-estimated.
| Molecule | DFT | DFT + Σ | GW | Experiment |
|---|---|---|---|---|
| Data are froma Ref. 95.b Ref. 86.c Ref. 142.d Ref. 144.e Ref. 145.f Ref. 45.g Ref. 129.h Ref. 46.i Ref. 146. | ||||
| Benzenediamine | 12.3a | 3.9a | 7.8b | 2.3 ± 0.3c |
| Benzenedithiol | 7.49d; 6.4g | 2.4g | 7.2 ± 0.2e; 8.7 ± 2.1f | |
| Benzenedicyanide | −69.9g | −11.5g | −9.2b | −1.3 ± 0.5e |
| Biphenyldiamine | 17.9a | 5.4a | 4.9 ± 1.9c | |
| Triphenyldiamine | 24.3a | 8.1a | 6.4 ± 0.4c | |
| 4,4′-Bipyridine | −38.17h | −7.88h | −9.5h | |
| B4APA | 2.8i | 4.71h; 0.9–1.1i | 11.6i | 9.7 ± 0.3h |
In general, getting good agreement between theory and experiment for both thermopower and conductance is still a challenge for many molecules. Yet, the agreement that has been achieved thus far, with DFT + Σ95,141 and GW146 approaches, gives clear evidence of the validity of off-resonant tunneling transport in these single-molecule junctions. On the other hand, it is interesting to highlight one particularly simple case: that of pyridine–Au junctions, where the LUMO-derived transmission can be well described by a simple Lorentzian function. Accordingly, Lorentzian models can be used to derive the level alignments and lead-molecule coupling from simultaneously measured values of S and G in pyridine–Au junctions, and this has been shown to agree well with DFT + Σ results.141
4. Towards perfect molecular wires
A one-dimensional (1D) metal tends to slightly rearrange the atomic positions to gain electronic energy at the price of elastic energy associated with lattice distortion. This Peierls distortion effect opens a gap in most 1D wires such as polyacetylene, and armchair graphene nanoribbons (AGNRs),147 therefore transport through these semiconducting 1D or quasi-1D wires has to occur via the tunneling or hopping mechanisms. Even so-called metallic carbon nanotubes typically have a very small band gap due to curvature and strain effects.148,149 Within the tunneling regime, the low-bias conductance G of a molecular wire decays exponentially with length, and high performance molecular wires are characterized by a large contact conductance Gc and small decay constant β. In general, as the Fermi level approaches the frontier orbitals, Gc increases and approaches its peak value at resonance while β decreases.So far, there have been many experimental and theoretical efforts devoted to understanding the factors determining β in the search for high performance molecular wires. Table 5 lists the experimentally measured and theoretically calculated β and Gc values for many different types of molecular wires.
| Molecule | Link group | β (Å−1) | G c (G0) |
|---|---|---|---|
| Extended viologen molecules150 | S | 0.006 ± 0.0004 | 8.4 × 10−5 |
| Oligoporphyrins containing coordinated zinc cations151 | Thioacetates | 0.04 ± 0.006 | 8.6 × 10−5 |
| OPEs | Carbodithioate152 | 0.05 | 7 × 10−3 |
| Thiol152–155 | 0.2–0.34 | 10−3 | |
| [3 × n] gold-ion clusters enclosed within self-assembled cages156 | Panel ligands | 0.05 (DFT: 0.02) | 1.1 × 10−2 |
| Oligoynes | Py = 4-pyridyl | 0.06 ± 0.03157 | 2 × 10−4 (LC), 6 × 10−4 (MC)157 |
| 0.31 ± 0.04158 | 6.3 × 10−2 (ref. 158) | ||
| CN158 | 0.17 ± 0.01 | 8.1 × 10−4 | |
| NH2 (ref. 158) | ∼0.25 | 4.8 × 10−2 | |
| BT158 | 0.29 ± 0.02 | 1.2 | |
| –SH158 | ∼0.318 | 0.96 | |
| Oligothiophenes5 | Thiocyanate group | 0.1 | 1.7 × 10−2 |
| Benzene-furan oligoaryls159 | Thiolated (–SH) | 0.11–0.13 (conformation by stretching the molecule develops a smaller β) | 3.3 × 10−4 |
| Carotenoid polyenes | Pyridine160 | 0.17 ± 0.03 | (1.8 ± 1.5) × 10−4 |
| Thiol161 | 0.22 ± 0.04 | (4.8 ± 2.3) × 10−4 | |
| Oligophenyleimine (OPI)41 | S | 0.3 (tunnelling regime) | |
| 0.09 (hopping regime) | |||
| 7-AGNR162 | No link group | 0.45 ± 0.06 (low bias) | ∼10−2 |
| 0.1–0.2 (high bias) | ∼10−2 | ||
| AGNR sheet163 | Zigzag edge atom (gold chain as leads) | Hybrid-DFT: ∼0.117 | Hybrid-DFT: ∼10−3 |
| AGNR164 | Zigzag edge (wider AGNR as leads) | DFT: ∼0 | DFT: 0–1 tunable with bias |
| (8,0) CNT103 | DFT–CBS: ∼0.12 |
We see from the table that there are many organic molecules with very small measured β (<0.1 Å−1), including oligoynes,157 conjugated porphyrin oligomers,151 and extended viologen molecules.150 However, many of these systems also have a relatively small conductance, with G ranging between 10−5 and 10−4G0. As can be seen, extended viologen molecules150 show one of the smallest β measured, and its conductance is likely to be dominated by the LUMO. There have also been several studies showing that the junction conductances can be strongly affected by the link groups.152,158,160,161 In particular, the carbodithioate link group is found to lower the effective barrier for charge transport and enhance the conductance by an order of magnitude.152 In addition, there have also been theoretical predictions that oligopolyynes165 and oligoperylenes166 attached to Au electrodes can have very small β and large Gc values.
Recently, bottom-up synthesis of AGNRs of specific widths has been achieved,162,167–170 and molecular wires made of AGNRs have been proposed and studied. AGNRs can be classified into three families, according to the number of carbon atoms, n, across the width of the AGNR. The three families are n = 3p, 3p + 1 and 3p + 2 where p is an integer. Following standard convention, we call an AGNR with n carbon atoms across its width an n-AGNR. A recent report finds that a finite 7-AGNR molecule attached to gold electrodes shows a very low Gc but fast decay rate at low bias. Higher Gc and lower β can be reached as the bias window approaches the delocalized HOMO and LUMO levels.162 However, if we attach an AGNR segment to gold chains via its zigzag edge at both ends, an unusual exponential increase of transmission with wire length (β = −0.117 Å−1) has been predicted based on the extended Caroli, Combescot, Nozieres, and Saint-James (CCNS) formulation for tunneling currents with the Hamiltonian derived from hybrid DFT-B3LYP calculations.163,171 This phenomenon has been attributed to the localization of orbital amplitude at the two zigzag terminations and the remarkable decrease in the HOMO–LUMO gap with molecule length.163
When a 3p + 2-AGNR is seamlessly attached to a wider AGNR leads incorporating zigzag edges at the interface, as shown in Fig. 8(a), it is found to show frontier transmission peaks that are almost independent of the wire length (Fig. 8(b)).164 This length-independence is attributed to special link groups, i.e. the zigzag edges at the interface between the narrower AGNR molecule and wider AGNR leads. Such link groups provide two effects to the frontier peaks. First, they eliminate the confinement effect within the AGNR molecule in the sense that they keep the eigenenergies and eigenchannel wavefunctions of the two frontier resonances similar to that of the infinite AGNR ribbon, independent of the length of the AGNR fragment (see Fig. 8(c)–(f)). This property is related to the fact that the states in the infinite 3p + 2-AGNR can match very well to the zigzag edge states without any frustration or distortion. Secondly, these link groups serve as electrons “sources” and “drains” (zigzag edge) that absorb any change in the coupling to the leads as the wire lengthens. Further details can be found in ref. 164. In addition to 3p + 2-AGNRs, it is also very likely that metallic carbon nanotubes are excellent candidates for perfect molecular wires.173–175
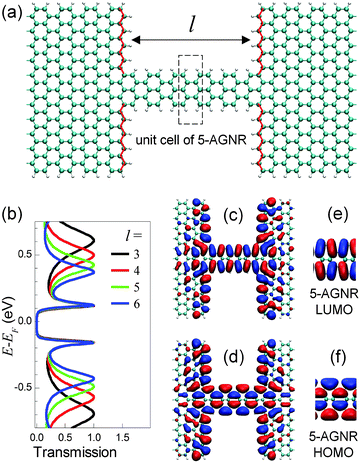 | ||
| Fig. 8 (a) Atomic structure of a 5-AGNR seamlessly attached to wider AGNR leads incorporating zigzag edges at the interface (denoted by red lines). The length of the 5-AGNR segment l = 5 unit cells. (b) Transmission curves of junction shown in (a) with varying l, calculated using the first-principles scattering-state approach as implemented in SCARLET.78 (c, d) Real parts of eigenchannel-wavefunction isosurfaces with isovalue = ±0.025 calculated using SCARLET at the two frontier peaks of the junction with l = 3. (e, f) The Γ-point HOMO and LUMO isosurfaces with isovalue = ±0.03 of the perfect 5-AGNR calculated using SIESTA.172 | ||
5. Concluding remarks
In this review, we have focused on a first principles theory perspective of electron transport through molecular wires, applicable in the off-resonant tunneling regime. We show that complex band structure calculations are helpful to provide a quick estimate of the decay constant beta, but they neglect effects of the metal–molecule geometry, which are significant and need to be considered for quantitative predictions of conductance and beta. The Landauer–Buttiker formalism, which explicitly takes into account contact geometries, is a useful tool to predict conductance, thermopower and beta values in molecular wires. Within this formalism, GW and DFT + Σ calculations can accurately predict conductance values, compared to DFT calculations which tend to overestimate the conductance by orders of magnitude, especially in the off-resonant tunneling regime. The reason for this significant improvement is that off-resonant tunneling conductance is very sensitive to the energy barrier for transport, and only GW and DFT + Σ calculations incorporate accurate values of this energy barrier. DFT + Σ calculations are particularly useful as they are of similar computational expense to DFT calculations, thus allowing a number of different contact geometries to be considered. However, at present, a truly effective search for typical contact geometries in experiment is still elusive due to the large number of atoms involved and the need to consider atomic-scale dynamics. Therefore, while DFT + Σ can give values of conductance close to the peaks in experimental conductance histograms, disagreement between calculated and measured values of beta can arise when the experimental contact geometry changes significantly with molecule length. However, the fact that DFT + Σ can accurately predict not only conductance, but also the thermopower of oligophenyldiamine–Au junctions, provides evidence that transport in these systems occurs via off-resonant tunneling, and sets the framework for a consistent understanding of independent experimental probes of charge transport through these wires.GW calculations go beyond DFT + Σ by taking into account dynamical effects and are in principle applicable to all classes of systems; therefore, GW is by far the gold standard in terms of making accurate predictions for charge transport in single molecule junctions. However, in practice, the high computational cost of GW restricts this method to relatively small system sizes. Furthermore, very high energy cutoffs and a large number of conduction bands are involved in accurately predicting the ionization potential or electron affinity of molecules within GW.176 This implies that similarly large cutoffs are required to obtain correct level alignments for molecule–metal systems within GW, an issue that is critical for transport calculations.
The present review is not exhaustive, and special mention must be given here to several other topics that we have omitted. In recent years, the study of quantum interference pathways in single molecule junctions has been performed by both experiment and theory, providing yet another confirmation of quantum coherence in these systems.177,178 Increasingly sophisticated experiments are being set up to perform vibrational spectroscopy on single molecule junctions, simultaneously to the measurement of conductance and/or thermopower.43 These experiments would provide valuable information on the contact geometry of the junctions, and can be combined with first principles calculations to directly relate electron transport properties with the atomic structure. Finally, the transport of electron spin in molecular wires has also been studied using DFT179–181 and DFT + Σ182 calculations, but so far, there have been no benchmark experiments to compare these results against. In general, spin transport is much more sensitive to details of the interface geometry than non-spin-polarized transport.
Moving forwards, it would be extremely helpful to develop effective classical potentials to treat the interactions between typical metal electrodes and organic molecules. This would be an important step towards using more representative model geometries for transport calculations. Investigating the effects of solvent molecules on transport properties is another important consideration. Furthermore, electron transport through very long molecular wires typically occurs via thermally-activated hopping. To this end, it would be interesting to develop multi-scale methods incorporating first principles theory to compute the conductance. The full power of Marcus theory has yet to be exploited to study hopping transport in open quantum systems of molecular junctions including contact with electron reservoirs.
Acknowledgements
The authors gratefully acknowledge the Singapore National Research Foundation for funding via the NRF Fellowship Grant (NRF-NRFF2013-07).References
- A. Aviram and M. A. Ratner, Molecular Rectifiers, Chem. Phys. Lett., 1974, 29(2), 277–283 CrossRef CAS.
- E. E. Polymeropoulos and J. Sagiv, Electrical-Conduction through Adsorbed Monolayers, J. Chem. Phys., 1978, 69(5), 1836–1847 CrossRef CAS.
- R. Huber, et al., Electrical conductance of conjugated oligorners at the single molecule level, J. Am. Chem. Soc., 2008, 130(3), 1080–1084 CrossRef CAS PubMed.
- J. C. Cuevas, et al., Theoretical description of the electrical conduction in atomic and molecular junctions, Nanotechnology, 2003, 14(8), R29–R38 CrossRef CAS.
- R. Yamada, et al., Electrical conductance of oligothiophene molecular wires, Nano Lett., 2008, 8(4), 1237–1240 CrossRef CAS PubMed.
- C. Wang, et al., Oligoyne Single Molecule Wires, J. Am. Chem. Soc., 2009, 131(43), 15647–15654 CrossRef CAS PubMed.
- B. Kim, et al., Molecular Tunnel Junctions Based on pi-Conjugated Oligoacene Thiols and Dithiols between Ag, Au, and Pt Contacts: Effect of Surface Linking Group and Metal Work Function, J. Am. Chem. Soc., 2011, 133(49), 19864–19877 CrossRef CAS PubMed.
- D. Porath, et al., Direct measurement of electrical transport through DNA molecules, Nature, 2000, 403(6770), 635–638 CrossRef CAS PubMed.
- V. B. Engelkes, J. M. Beebe and C. D. Frisbie, Length-dependent transport in molecular junctions based on SAMs of alkanethiols and alkanedithiols: Effect of metal work function and applied bias on tunneling efficiency and contact resistance, J. Am. Chem. Soc., 2004, 126(43), 14287–14296 CrossRef CAS PubMed.
- G. Sedghi, et al., Long-range electron tunnelling in oligo-porphyrin molecular wires, Nat. Nanotechnol., 2011, 6(8), 517–523 CrossRef CAS PubMed.
- S. Y. Quek, et al., Length Dependence of Conductance in Aromatic Single-Molecule Junctions, Nano Lett., 2009, 9(11), 3949–3953 CrossRef CAS PubMed.
- P. Bujak, et al., Polymers for electronics and spintronics, Chem. Soc. Rev., 2013, 42(23), 8895–8999 RSC.
- J. L. Bredas, et al., Charge-transfer and energy-transfer processes in pi-conjugated oligomers and polymers: A molecular picture, Chem. Rev., 2004, 104(11), 4971–5003 CrossRef CAS PubMed.
- B. Mann and H. Kuhn, Tunneling through Fatty Acid Salt Monolayers, J. Appl. Phys., 1971, 42(11), 4398–4405 CrossRef CAS.
- E. E. Polymeropoulos, D. Mobius and H. Kuhn, Monolayer Assemblies with Functional Units of Sensitizing and Conducting Molecular-Components – Photo-Voltage, Dark Conduction and Photoconduction In Systems with aluminum and barium electrodes, Thin Solid Films, 1980, 68(1), 173–190 CrossRef CAS.
- M. Fujihira, K. Nishiyama and H. Yamada, Photoelectrochemical responses of optically transparent electrodes modified with Langmuir-Blodgett-films consisting of surfactant derivatives of electron-donor, acceptor and sensitizer molecules, Thin Solid Films, 1985, 132(1–4), 77–82 CrossRef CAS.
- L. Luo, S. H. Choi and C. D. Frisbie, Probing Hopping Conduction in Conjugated Molecular Wires Connected to Metal Electrodes, Chem. Mater., 2011, 23(3), 631–645 CrossRef CAS.
- M. A. Reed, et al., Conductance of a molecular junction, Science, 1997, 278(5336), 252–254 CrossRef CAS.
- X. Y. Xiao, B. Q. Xu and N. J. Tao, Measurement of single molecule conductance: Benzenedithiol and benzenedimethanethiol, Nano Lett., 2004, 4(2), 267–271 CrossRef CAS.
- L. Venkataraman, et al., Single-molecule circuits with well-defined molecular conductance, Nano Lett., 2006, 6(3), 458–462 CrossRef CAS PubMed.
- K. H. Khoo, et al., Contact dependence of the conductance of H-2 molecular junctions from first principles, Phys. Rev. B, 2008, 77(11), 115326 CrossRef.
- C. Jia and X. Guo, Molecule-electrode interfaces in molecular electronic devices, Chem. Soc. Rev., 2013, 42(13), 5642–5660 RSC.
- M. Kiguchi, et al., Effect of Anchoring Group Position on Formation and Conductance of a Single Disubstituted Benzene Molecule Bridging Au Electrodes: Change of Conductive Molecular Orbital and Electron Pathway, J. Phys. Chem. C, 2010, 114(50), 22254–22261 CAS.
- L. Venkataraman, et al., Electronics and chemistry: Varying single-molecule junction conductance using chemical substituents, Nano Lett., 2007, 7(2), 502–506 CrossRef CAS PubMed.
- M. Galperin, M. A. Ratner and A. Nitzan, Inelastic electron tunneling spectroscopy in molecular junctions: Peaks and dips, J. Chem. Phys., 2004, 121(23), 11965–11979 CrossRef CAS PubMed.
- L. Venkataraman, et al., Dependence of single-molecule junction conductance on molecular conformation, Nature, 2006, 442(7105), 904–907 CrossRef CAS PubMed.
- R. A. Wassel, et al., Stochastic variation in conductance on the nanometer scale: A general phenomenon, Nano Lett., 2003, 3(11), 1617–1620 CrossRef CAS.
- V. Fatemi, et al., Environmental Control of Single-Molecule Junction Transport, Nano Lett., 2011, 11(5), 1988–1992 CrossRef CAS PubMed.
- B. Capozzi, et al., Tunable Charge Transport in Single-Molecule Junctions via Electrolytic Gating, Nano Lett., 2014, 14(3), 1400–1404 CrossRef CAS PubMed.
- B. Q. Xu and N. J. J. Tao, Measurement of single-molecule resistance by repeated formation of molecular junctions, Science, 2003, 301(5637), 1221–1223 CrossRef CAS PubMed.
- C. Li, et al., Charge transport in single Au vertical bar alkanedithiol vertical bar Au junctions: Coordination geometries and conformational degrees of freedom, J. Am. Chem. Soc., 2008, 130(1), 318–326 CrossRef CAS PubMed.
- M. Teresa González, et al., Conductance values of alkanedithiol molecular junctions, New J. Phys., 2008, 10(6), 065018 CrossRef.
- F. Chen, et al., Effect of anchoring groups on single-molecule conductance: Comparative study of thiol-, amine-, and carboxylic-acid-terminated molecules, J. Am. Chem. Soc., 2006, 128(49), 15874–15881 CrossRef CAS PubMed.
- W. Chen, et al., Highly conducting pi-conjugated molecular junctions covalently bonded to gold electrodes, J. Am. Chem. Soc., 2011, 133(43), 17160–17163 CrossRef CAS PubMed.
- S. Y. Quek, et al., Mechanically controlled binary conductance switching of a single-molecule junction, Nat. Nanotechnol., 2009, 4(4), 230–234 CrossRef CAS PubMed.
- D. Nozaki, et al., Disorder and dephasing effects on electron transport through conjugated molecular wires in molecular junctions, Phys. Rev. B, 2012, 85(15), 155327 CrossRef.
- Y. Qi, et al., Mechanical and charge transport properties of alkanethiol self-assembled monolayers on a Au(111) surface: The role of molecular tilt, Langmuir, 2008, 24(5), 2219–2223 CrossRef CAS PubMed.
- J. Vura-Weis, et al., Crossover from Single-Step Tunneling to Multistep Hopping for Molecular Triplet Energy Transfer, Science, 2010, 328(5985), 1547–1550 CrossRef CAS PubMed.
- Z. L. Cheng, et al., In situ formation of highly conducting covalent Au–C contacts for single-molecule junctions, Nat. Nanotechnol., 2011, 6(6), 353–357 CrossRef CAS PubMed.
- J. R. Widawsky, et al., Length-Dependent Thermopower of Highly Conducting Au–C Bonded Single Molecule Junctions, Nano Lett., 2013, 13(6), 2889–2894 CrossRef CAS PubMed.
- S. H. Choi, B. Kim and C. D. Frisbie, Electrical resistance of long conjugated molecular wires, Science, 2008, 320(5882), 1482–1486 CrossRef CAS PubMed.
- T. Hines, et al., Transition from Tunneling to Hopping in Single Molecular Junctions by Measuring Length and Temperature Dependence, J. Am. Chem. Soc., 2010, 132(33), 11658–11664 CrossRef CAS PubMed.
- S. V. Aradhya and L. Venkataraman, Single-molecule junctions beyond electronic transport, Nat. Nanotechnol., 2013, 8(6), 399–410 CrossRef CAS PubMed.
- W. Lee, et al., Heat dissipation in atomic-scale junctions, Nature, 2013, 498(7453), 209–212 CrossRef CAS PubMed.
- P. Reddy, et al., Thermoelectricity in molecular junctions, Science, 2007, 315(5818), 1568–1571 CrossRef CAS PubMed.
- J. R. Widawsky, P. Darancet, J. B. Neaton and L. Venkataraman, Simultaneous Determination of Conductance and Thermopower of Single Molecule Junctions, Nano Lett., 2012, 12(1), 354–358 CrossRef CAS PubMed.
- W. Y. Kim, et al., Application of quantum chemistry to nanotechnology: electron and spin transport in molecular devices, Chem. Soc. Rev., 2009, 38(8), 2319–2333 RSC.
- M. Galperin, A. Nitzan and M. A. Ratner, Inelastic effects in molecular junctions in the Coulomb and Kondo regimes: Nonequilibrium equation-of-motion approach, Phys. Rev. B, 2007, 76(3), 035301 CrossRef.
- Y. C. Chen, M. Zwolak and M. Di Ventra, Inelastic effects on the transport properties of alkanethiols, Nano Lett., 2005, 5(4), 621–624 CrossRef CAS PubMed.
- N. Sergueev, D. Roubtsov and H. Guo, Ab initio analysis of electron-phonon coupling in molecular devices, Phys. Rev. Lett., 2005, 95(14), 146803 CrossRef CAS PubMed.
- A. Troisi, M. A. Ratner and A. Nitzan, Vibronic effects in off-resonant molecular wire conduction, J. Chem. Phys., 2003, 118(13), 6072–6082 CrossRef CAS.
- Y. C. Chen, M. Zwolak and M. Di Ventra, Inelastic current-voltage characteristics of atomic and molecular junctionsm, Nano Lett., 2004, 4(9), 1709–1712 CrossRef CAS.
- Y. Asai, Theory of inelastic electric current through single molecules, Phys. Rev. Lett., 2004, 93(24), 246102 CrossRef PubMed.
- K. Stokbro, et al., Theoretical study of the nonlinear conductance of Di-thiol benzene coupled to Au(111) surfaces via thiol and thiolate bonds, Comput. Mater. Sci., 2003, 27(1–2), 151–160 CrossRef CAS.
- F. Evers, F. Weigend and M. Koentopp, Conductance of molecular wires and transport calculations based on density-functional theory, Phys. Rev. B, 2004, 69(23), 235411 CrossRef.
- J. Tomfohr and O. F. Sankey, Theoretical analysis of electron transport through organic molecules, J. Chem. Phys., 2004, 120(3), 1542–1554 CrossRef CAS PubMed.
- H. Kondo, et al., Contact-structure dependence of transport properties of a single organic molecule between Au electrodes, Phys. Rev. B, 2006, 73(23), 235323 CrossRef.
- S. Y. Quek, et al., Amine-gold linked single-molecule circuits: Experiment and theory, Nano Lett., 2007, 7(11), 3477–3482 CrossRef CAS PubMed.
- L. Hedin, New method for calculating 1-particle greens function with application to electron-gas problem, Phys. Rev., 1965, 139(3A), A796 CrossRef.
- M. S. Hybertsen and S. G. Louie, Electron correlation in semiconductors and insulators – band-gaps and quasi-particle energies, Phys. Rev. B, 1986, 34(8), 5390–5413 CrossRef CAS.
- M. Strange, et al., Self-consistent GW calculations of electronic transport in thiol- and amine-linked molecular junctions, Phys. Rev. B, 2011, 83(11), 115108 CrossRef.
- P. Darancet, et al., Ab initio GW electron-electron interaction effects in quantum transport, Phys. Rev. B, 2007, 75(7), 075102 CrossRef.
- S. Y. Quek and K. H. Khoo, Predictive DFT-based approaches to charge and spin transport in single-molecule junctions and two-dimensional materials: Successes and challenges, Acc. Chem. Res., 2014 DOI:10.1021/ar4002526.
- S. Y. Quek, D. A. Strubbe, H. J. Choi, S. G. Louie and J. B. Neaton, First-Principles Approach to Charge Transport in Single-Molecule Junctions with Self-Energy Corrections: a “DFT + Sigma Method”, in preparation.
- G. Vignale and W. Kohn, Current-dependent exchange-correlation potential for dynamical linear response theory, Phys. Rev. Lett., 1996, 77(10), 2037–2040 CrossRef CAS PubMed.
- N. Sai, et al., Dynamical corrections to the DFT-LDA electron conductance in nanoscale systems, Phys. Rev. Lett., 2005, 94(18), 186801 CrossRef.
- S. Kurth and G. Stefanucci, Dynamical Correction to Linear Kohn-Sham Conductances from Static Density Functional Theory, Phys. Rev. Lett., 2013, 111(3), 030601 CrossRef CAS PubMed.
- M. Di Ventra and T. N. Todorov, Transport in nanoscale systems: the microcanonical versus grand-canonical picture, J. Phys.: Condens. Matter, 2004, 16(45), 8025–8034 CrossRef CAS.
- G. Stefanucci and C. O. Almbladh, Time-dependent quantum transport: An exact formulation based on TDDFT, Europhys. Lett., 2004, 67(1), 14–20 CrossRef CAS.
- K. Varga, Time-dependent density functional study of transport in molecular junctions, Phys. Rev. B, 2011, 83(19), 195130 CrossRef.
- J. K. Tomfohr and O. F. Sankey, Complex band structure, decay lengths, and Fermi level alignment in simple molecular electronic systems, Phys. Rev. B, 2002, 65(24), 235105 CrossRef.
- J. Tersoff, Schottky-Barrier Heights and the Continuum of Gap States, Phys. Rev. Lett., 1984, 52(6), 465–468 CrossRef CAS.
- P. N. Butcher, Thermal and Electrical Transport Formalism for Electronic Microstructures with Many Terminals, J. Phys.: Condens. Matter, 1990, 2(22), 4869–4878 CrossRef.
- M. Paulsson and S. Datta, Thermoelectric effect in molecular electronics, Phys. Rev. B, 2003, 67(24), 241403 CrossRef.
- J. A. Malen, et al., Fundamentals of energy transport, energy conversion, and thermal properties in organic-inorganic heterojunctions, Chem. Phys. Lett., 2010, 491(4–6), 109–122 CrossRef CAS.
- M. Brand byge, et al., Density-functional method for nonequilibrium electron transport, Phys. Rev. B, 2002, 65(16), 165401 CrossRef.
- A. R. Rocha, et al., Spin and molecular electronics in atomically generated orbital landscapes, Phys. Rev. B, 2006, 73(8), 085414 CrossRef.
- H. J. Choi, M. L. Cohen and S. G. Louie, First-principles scattering-state approach for nonlinear electrical transport in nanostructures, Phys. Rev. B, 2007, 76(15), 155420 CrossRef.
- H. J. Choi and J. Ihm, Ab initio pseudopotential method for the calculation of conductance in quantum wires, Phys. Rev. B, 1999, 59(3), 2267–2275 CrossRef.
- S. Liu, Y. P. Feng and C. Zhang, Communication: Electronic and transport properties of molecular junctions under a finite bias: A dual mean field approach, J. Chem. Phys., 2013, 139(19), 191103 CrossRef PubMed.
- J. P. Perdew, M. Emzerhof and K. Burke, Rationale for mixing exact exchange with density functional approximations, J. Chem. Phys., 1996, 105(22), 9982–9985 CrossRef CAS.
- A. D. Becke, Density-Functional Thermochemistry.3. the Role of Exact Exchange, J. Chem. Phys., 1993, 98(7), 5648–5652 CrossRef CAS.
- J. P. Perdew and A. Zunger, Self-Interaction Correction to Density-Functional Approximations For Many-Electron Systems, Phys. Rev. B, 1981, 23(10), 5048–5079 CrossRef CAS.
- M. Strange and K. S. Thygesen, Towards quantitative accuracy in first-principles transport calculations: The GW method applied to alkane/gold junctions, Beilstein J. Nanotechnol., 2011, 2, 746–754 CrossRef CAS PubMed.
- C. J. Jin, et al., Energy level alignment and quantum conductance of functionalized metal-molecule junctions: Density functional theory versus GW calculations, J. Chem. Phys., 2013, 139(18), 184307 CrossRef PubMed.
- T. Markussen, C. Jin and K. S. Thygesen, Quantitatively accurate calculations of conductance and thermopower of molecular junctions, Phys. Status Solidi B, 2013, 250(11), 2394–2402 CrossRef CAS.
- M. Strange and K. S. Thygesen, Image-charge-induced localization of molecular orbitals at metal-molecule interfaces: Self-consistent GW calculations, Phys. Rev. B, 2012, 86(19), 195121 CrossRef.
- C. Jin and K. S. Thygesen, Dynamical image-charge effect in molecular tunnel junctions: Beyond energy level alignment, Phys. Rev. B, 2014, 89(4), 041102 CrossRef.
- M. Kamenetska, et al., Conductance and Geometry of Pyridine-Linked Single-Molecule Junctions, J. Am. Chem. Soc., 2010, 132(19), 6817–6821 CrossRef CAS PubMed.
- J. B. Neaton, M. S. Hybertsen and S. G. Louie, Renormalization of molecular electronic levels at metal-molecule interfaces, Phys. Rev. Lett., 2006, 97(21), 216405 CrossRef CAS PubMed.
- A. Biller, et al., Electronic level alignment at a metal-molecule interface from a short-range hybrid functional, J. Chem. Phys., 2011, 135(16), 164706 CrossRef PubMed.
- J. M. Garcia-Lastra, et al., Polarization-induced renormalization of molecular levels at metallic and semiconducting surfaces, Phys. Rev. B, 2009, 80(24), 245427 CrossRef.
- M. Jain, J. R. Chelikowsky and S. G. Louie, Reliability of Hybrid Functionals in Predicting Band Gaps, Phys. Rev. Lett., 2011, 107(21), 216806 CrossRef PubMed.
- M. Dell'Angela, et al., Relating Energy Level Alignment and Amine-Linked Single Molecule Junction Conductance, Nano Lett., 2010, 10(7), 2470–2474 CrossRef PubMed.
- S. Y. Quek, et al., Thermopower of Amine – Gold-Linked, Aromatic Molecular Junctions from First Principles, ACS Nano, 2011, 5(1), 551–557 CrossRef CAS PubMed.
- M. L. Perrin, et al., Large tunable image-charge effects in single-molecule junctions, Nat. Nanotechnol., 2013, 8(4), 282–287 CrossRef CAS PubMed.
- S. C. Lam and R. J. Needs, 1ST-Principles Calculations of the Screening of Electric-Fields at the Aluminum(111) And (110) Surfaces, J. Phys.: Condens. Matter, 1993, 5(14), 2101–2108 CrossRef CAS.
- S. McDermott, et al., Tunnel Currents across Silane Diamines/Dithiols and Alkane Diamines/Dithiols: A Comparative Computational Study, J. Phys. Chem. C, 2009, 113(2), 744–750 CAS.
- F. Picaud, et al., Complex band structures and decay length in polyethylene chains, J. Phys.: Condens. Matter, 2003, 15(22), 3731–3740 CrossRef CAS.
- J. Li, J. K. Tomfohr and O. F. Sankey, Theoretical study of carotene as a molecular wire, Phys. E, 2003, 19(1–2), 133–138 CrossRef CAS.
- H. Wang, J. P. Lewis and O. F. Sankey, Band-gap tunneling states in DNA, Phys. Rev. Lett., 2004, 93(1), 016401 CrossRef PubMed.
- G. Fagas, A. Kambili and M. Elstner, Complex-band structure: a method to determine the off-resonant electron transport in oligomers, Chem. Phys. Lett., 2004, 389(4–6), 268–273 CrossRef CAS.
- P. Pomorski, C. Roland and H. Guo, Quantum transport through short semiconducting nanotubes: A complex band structure analysis, Phys. Rev. B, 2004, 70(11), 115408 CrossRef.
- A. Ferretti, et al., Ab initio complex band structure of conjugated polymers: Effects of hydrid density functional theory and GW schemes, Phys. Rev. B, 2012, 85(23), 235105 CrossRef.
- B. Xu and N. J. Tao, Measurement of single-molecule resistance by repeated formation of molecular junctions, Science, 2003, 301(5637), 1221–1223 CrossRef CAS PubMed.
- X. L. Li, et al., Conductance of single alkanedithiols: Conduction mechanism and effect of molecule-electrode contacts, J. Am. Chem. Soc., 2006, 128(6), 2135–2141 CrossRef CAS PubMed.
- E. Prodan and R. Car, Tunneling conductance of amine-linked alkyl chains, Nano Lett., 2008, 8(6), 1771–1777 CrossRef PubMed.
- D. J. Wold, et al., Distance dependence of electron tunneling through self-assembled monolayers measured by conducting probe atomic force microscopy: Unsaturated versus saturated molecular junctions, J. Phys. Chem. B, 2002, 106(11), 2813–2816 CrossRef CAS.
- T. Kim, et al., Conductance of molecular junctions formed with silver electrodes, Nano Lett., 2013, 13(7), 3358–3364 CrossRef CAS PubMed.
- K. S. Thygesen and K. W. Jacobsen, Conduction mechanism in a molecular hydrogen contact, Phys. Rev. Lett., 2005, 94(3), 4 CrossRef.
- A. Marchenkov, et al., Atomic dimer shuttling and two-level conductance fluctuations in Nb nanowires, Phys. Rev. Lett., 2007, 98(4), 4 CrossRef.
- C. Toher and S. Sanvito, Efficient atomic self-interaction correction scheme for nonequilibrium quantum transport, Phys. Rev. Lett., 2007, 99(5), 056801 CrossRef CAS PubMed.
- S.-H. Ke, H. U. Baranger and W. Yang, Role of the exchange-correlation potential in ab initio electron transport calculations, J. Chem. Phys., 2007, 126(20), 201102 CrossRef PubMed.
- A. Cehovin, et al., Role of the virtual orbitals and HOMO-LUMO gap in mean-field approximations to the conductance of molecular junctions, Phys. Rev. B, 2008, 77(19), 195432 CrossRef.
- P. Delaney and J. C. Greer, Correlated electron transport in molecular electronics, Phys. Rev. Lett., 2004, 93(3), 036805 CrossRef CAS PubMed.
- I. Baldea and H. Koeppel, Electron transport through correlated molecules computed using the time-independent Wigner function: Two critical tests, Phys. Rev. B, 2008, 78(11), 115315 CrossRef.
- T. Rangel, et al., Transport properties of molecular junctions from many-body perturbation theory, Phys. Rev. B, 2011, 84(4), 045426 CrossRef.
- Y. B. Hu, et al., Conductance of an ensemble of molecular wires: A statistical analysis, Phys. Rev. Lett., 2005, 95(15), 4 Search PubMed.
- H. Basch, R. Cohen and M. A. Ratner, Interface geometry and molecular junction conductance: Geometric fluctuation and stochastic switching, Nano Lett., 2005, 5(9), 1668–1675 CrossRef CAS PubMed.
- K. H. Muller, Effect of the atomic configuration of gold electrodes on the electrical conduction of alkanedithiol molecules, Phys. Rev. B, 2006, 73(4), 045403 CrossRef.
- C. C. Kaun and H. Guo, Resistance of alkanethiol molecular wires, Nano Lett., 2003, 3(11), 1521–1525 CrossRef CAS.
- G. Fagas, P. Delaney and J. C. Greer, Independent particle descriptions of tunneling using the many-body quantum transport approach, Phys. Rev. B, 2006, 73(24), 241314 CrossRef.
- M. H. Lee, G. Speyer and O. F. Sankey, Electron transport through single alkane molecules with different contact geometries on gold, Phys. Status Solidi B, 2006, 243(9), 2021–2029 CrossRef CAS.
- M. Paulsson, et al., Conductance of Alkanedithiol Single-Molecule Junctions: A Molecular Dynamics Study, Nano Lett., 2009, 9(1), 117–121 CrossRef CAS PubMed.
- W. Haiss, et al., Anomalous length and voltage dependence of single molecule conductance, Phys. Chem. Chem. Phys., 2009, 11(46), 10831–10838 RSC.
- M. Fujihira, et al., Currents through single molecular junction of Au/hexanedithiolate/Au measured by repeated formation of break junction in STM under UHV: Effects of conformational change in an alkylene chain from gauche to trans and binding sites of thiolates on gold, Phys. Chem. Chem. Phys., 2006, 8(33), 3876 RSC.
- A. Nishikawa, et al., Accurate determination of multiple sets of single molecular conductance of Au/1,6-hexanedithiol/Au break junctions by ultra-high vacuum-scanning tunneling microscope and analyses of individual current-separation curves, Nanotechnology, 2007, 18(42), 424005 CrossRef PubMed.
- Z. L. Cheng, et al., In situ formation of highly conducting covalent Au-C contacts for single-molecule junctions, Nat. Nanotechnol., 2011, 6(6), 353–357 CrossRef CAS PubMed.
- L. A. Zotti, et al., Heat dissipation and its relation to thermopower in single-molecule junctions, New J. Phys., 2014, 16, 25 CrossRef.
- M. Tsutsui, et al., High-conductance states of single benzenedithiol molecules, Appl. Phys. Lett., 2006, 89(16), 163111 CrossRef.
- E. Loertscher, H. B. Weber and H. Riel, Statistical approach to investigating transport through single molecules, Phys. Rev. Lett., 2007, 98(17), 176807 CrossRef.
- M. Tsutsui, M. Taniguchi and T. Kawai, Atomistic Mechanics and Formation Mechanism of Metal-Molecule-Metal Junctions, Nano Lett., 2009, 9(6), 2433–2439 CrossRef CAS PubMed.
- M. Strange, et al., Benchmark density functional theory calculations for nanoscale conductance, J. Chem. Phys., 2008, 128(11), 114714 CrossRef CAS PubMed.
- M. S. Hybertsen, et al., Amine-linked single-molecule circuits: systematic trends across molecular families, J. Phys.: Condens. Matter, 2008, 20(37), 14 CrossRef PubMed.
- J. R. Widawsky, et al., Measurement of voltage-dependent electronic transport across amine-linked single-molecular-wire junctions, Nanotechnology, 2009, 20(43), 434009 CrossRef CAS PubMed.
- P. Darancet, et al., Quantitative Current-Voltage Characteristics in Molecular Junctions from First Principles, Nano Lett., 2012, 12(12), 6250–6254 CrossRef CAS PubMed.
- M. Strange and K. S. Thygesen, Towards quantitative accuracy in first-principles transport calculations: The GW method applied to alkane/gold junctions, Beilstein J. Nanotechnol., 2011, 2, 746–754 CrossRef CAS PubMed.
- R. Y. Wang, R. A. Segalman and A. Majumdar, Room temperature thermal conductance of alkanedithiol self-assembled monolayers, Appl. Phys. Lett., 2006, 89(17), 3 Search PubMed.
- G. D. Mahan and J. O. Sofo, The best thermoelectric, Proc. Natl. Acad. Sci. U. S. A., 1996, 93(15), 7436–7439 CrossRef CAS.
- T. E. Humphrey and H. Linke, Reversible thermoelectric nanomaterials, Phys. Rev. Lett., 2005, 94(9), 096601 CrossRef CAS PubMed.
- T. Kim, et al., Determination of Energy Level Alignment and Coupling Strength in 4,4′-Bipyridine Single-Molecule Junctions, Nano Lett., 2014, 14(2), 794–798 CrossRef CAS PubMed.
- J. A. Malen, et al., Identifying the Length Dependence of Orbital Alignment and Contact Coupling in Molecular Heterojunctions, Nano Lett., 2009, 9(3), 1164–1169 CrossRef CAS PubMed.
- S.-H. Ke, et al., Thermopower of Molecular Junctions: An ab Initio Study, Nano Lett., 2009, 9(3), 1011–1014 CrossRef CAS PubMed.
- F. Pauly, J. K. Viljas and J. C. Cuevas, Length-dependent conductance and thermopower in single-molecule junctions of dithiolated oligophenylene derivatives, A density functional study, Phys. Rev. B, 2008, 78(3), 035315 CrossRef.
- K. Baheti, et al., Probing the chemistry of molecular heterojunctions using thermoelectricity, Nano Lett., 2008, 8(2), 715–719 CrossRef CAS PubMed.
- C. J. Jin, T. Markussen and K. S. Thygesen, Simultaneous description of conductance and thermopower in single-molecule junctions from many-body ab initio calculations, Phys. Rev. B, 2014, 90(7), 8 CrossRef.
- Y.-W. Son, M. L. Cohen and S. G. Louie, Energy gaps in graphene nanoribbons, Phys. Rev. Lett., 2006, 97(21), 216803 CrossRef PubMed.
- M. J. Biercuk, S. Ilani, C. M. Marcus and P. L. McEuen, in Electrical Transport in Single-Wall Carbon Nanotubes, ed. A. D. G. Jorio and M. S. Dresselhaus, Springer, Berlin Heidelberg, 2008, pp. 455–493 Search PubMed.
- M. Ouyang, et al., Energy gaps in “metallic” single-walled carbon nanotubes, Science, 2001, 292(5517), 702–705 CrossRef CAS PubMed.
- V. Kolivoska, et al., Single-Molecule Conductance in a Series of Extended Viologen Molecules, J. Phys. Chem. Lett., 2013, 4(4), 589–595 CrossRef CAS PubMed.
- G. Sedghi, et al., Single molecule conductance of porphyrin wires with ultralow attenuation, J. Am. Chem. Soc., 2008, 130(27), 8582–8583 CrossRef CAS PubMed.
- Y. J. Xing, et al., Optimizing Single-Molecule Conductivity of Conjugated Organic Oligomers with Carbodithioate Linkers, J. Am. Chem. Soc., 2010, 132(23), 7946–7956 CrossRef CAS PubMed.
- V. Kaliginedi, et al., Correlations between Molecular Structure and Single-Junction Conductance: A Case Study with Oligo(phenylene-ethynylene)-Type Wires, J. Am. Chem. Soc., 2012, 134(11), 5262–5275 CrossRef CAS PubMed.
- Q. Lu, et al., From Tunneling to Hopping: A Comprehensive Investigation of Charge Transport Mechanism in Molecular Junctions Based on Oligo(p-phenylene ethynylene)s, ACS Nano, 2009, 3(12), 3861–3868 CrossRef CAS PubMed.
- K. Liu, et al., Length dependence of electron conduction for oligo(1,4-phenylene ethynylene)s: A conductive probe-atomic force microscopy investigation, J. Phys. Chem. C, 2008, 112(11), 4342–4349 CAS.
- M. Kiguchi, et al., Highly Conductive 3 × n Gold-Ion Clusters Enclosed within Self-Assembled Cages, Angew. Chem., Int. Ed., 2013, 52(24), 6202–6205 CrossRef CAS PubMed.
- C. S. Wang, et al., Oligoyne Single Molecule Wires, J. Am. Chem. Soc., 2009, 131(43), 15647–15654 CrossRef CAS PubMed.
- P. Moreno-Garcia, et al., Single-Molecule Conductance of Functionalized Oligoynes: Length Dependence and Junction Evolution, J. Am. Chem. Soc., 2013, 135(33), 12228–12240 CrossRef CAS PubMed.
- I. W. P. Chen, et al., The effect of molecular conformation on single molecule conductance: measurements of pi-conjugated oligoaryls by STM break junction, Chem. Commun., 2007, 3074–3076 RSC.
- I. Visoly-Fisher, et al., Conductance of a biomolecular wire, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(23), 8686–8690 CrossRef CAS PubMed.
- J. He, et al., Electronic decay constant of carotenoid polyenes from single-molecule measurements, J. Am. Chem. Soc., 2005, 127(5), 1384–1385 CrossRef CAS PubMed.
- M. Koch, et al., Voltage-dependent conductance of a single graphene nanoribbon, Nat. Nanotechnol., 2012, 7(11), 713–717 CrossRef CAS PubMed.
- T. Tada and K. Yoshizawa, Reverse exponential decay of electrical transmission in nanosized graphite sheets, J. Phys. Chem. B, 2004, 108(23), 7565–7572 CrossRef CAS.
- S. Li, et al., Anomalous length-independent frontier resonant transmission peaks in armchair graphene nanoribbon molecular wires, Carbon, 2014, 76, 285–291 CrossRef CAS.
- Z. Crljen and G. Baranovic, Unusual conductance of polyyne-based molecular wires, Phys. Rev. Lett., 2007, 98(11), 116801 CrossRef CAS PubMed.
- A. Bilic and S. Sanvito, Anomalous length dependence of conductance of aromatic nanoribbons with amine anchoring groups, Phys. Rev. B, 2012, 86(12), 125409 CrossRef.
- J. M. Cai, et al., Atomically precise bottom-up fabrication of graphene nanoribbons, Nature, 2010, 466(7305), 470–473 CrossRef CAS PubMed.
- H. Huang, et al., Spatially Resolved Electronic Structures of Atomically Precise Armchair Graphene Nanoribbons, Sci. Rep., 2012, 2, 983 Search PubMed.
- S. Linden, et al., Electronic Structure of Spatially Aligned Graphene Nanoribbons on Au(788), Phys. Rev. Lett., 2012, 108(21), 216801 CrossRef CAS PubMed.
- Y.-C. Chen, D. G. de Oteyza, Z. Pedramrazi, C. Chen, F. R. Fischer and M. F. Crommie, Tuning the Band Gap of Graphene Nanoribbons Synthesized from Molecular Precursors, ACS Nano, 2013, 7(7), 6123–6128 CrossRef CAS PubMed.
- C. Caroli, R. Combescot, P. Nozieres and D. Saint-James, Direct calculation of the tunneling current, J. Phys. C: Solid State Phys., 1971, 4(8), 916–929 CrossRef.
- J. M. Soler, et al., The SIESTA method for ab initio order-N materials simulation, J. Phys.: Condens. Matter, 2002, 14(11), 2745–2779 CrossRef CAS.
- A. Bachtold, et al., Scanned probe microscopy of electronic transport in carbon nanotubes, Phys. Rev. Lett., 2000, 84(26), 6082–6085 CrossRef CAS PubMed.
- S. J. Tans, et al., Individual single-wall carbon nanotubes as quantum wires, Nature, 1997, 386(6624), 474–477 CrossRef CAS.
- D. Mann, et al., Ballistic transport in metallic nanotubes with reliable Pd ohmic contacts, Nano Lett., 2003, 3(11), 1541–1544 CrossRef CAS.
- S. Sharifzadeh, et al., Quantitative molecular orbital energies within a G(0)W(0) approximation, Eur. Phys. J. B, 2012, 85(9), 323 CrossRef.
- S. V. Aradhya, et al., Dissecting Contact Mechanics from Quantum Interference in Single-Molecule Junctions of Stilbene Derivatives, Nano Lett., 2012, 12(3), 1643–1647 CrossRef CAS PubMed.
- C. M. Guedon, et al., Observation of quantum interference in molecular charge transport, Nat. Nanotechnol., 2012, 7(5), 304–308 CrossRef PubMed.
- R. Pilevarshahri, et al., Spin transport in higher n-acene molecules, Phys. Rev. B, 2011, 84(17), 174437 CrossRef.
- S. Bhattacharya, A. Akande and S. Sanvito, Spin transport properties of triarylamine-based nanowires, Chem. Commun., 2014, 50(50), 6626–6629 RSC.
- S. H. Liang, et al., Organic magnetic tunnel junctions: The role of metal-molecule interface, Phys. Rev. B, 2012, 86(22), 224419 CrossRef.
- N. Gorjizadeh and S. Y. Quek, Interface effects on tunneling magnetoresistance in organic spintronics with flexible amine-Au links, Nanotechnology, 2013, 24(41), 415201 CrossRef PubMed.
Footnote |
| † Photo is copyrighted by A*STAR/SCEI. |
| This journal is © the Owner Societies 2015 |