Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Orbital entanglement and CASSCF analysis of the Ru–NO bond in a Ruthenium nitrosyl complex
Leon
Freitag
a,
Stefan
Knecht
b,
Sebastian F.
Keller
b,
Mickaël G.
Delcey
c,
Francesco
Aquilante
cd,
Thomas
Bondo Pedersen
e,
Roland
Lindh
f,
Markus
Reiher
*b and
Leticia
González
*a
aInstitut für theoretische Chemie, Universität Wien, Währinger Str. 17, 1090 Vienna, Austria. E-mail: leticia.gonzalez@univie.ac.at
bETH Zürich, Laboratory of Physical Chemistry, Vladimir-Prelog-Weg 2, 8093 Zürich, Switzerland. E-mail: markus.reiher@phys.chem.ethz.ch
cDepartment of Chemistry – Ångström, The Theoretical Chemistry Programme, Uppsala University, Box 518, 751 20 Uppsala, Sweden
dDipartimento di Chimica “G. Ciamician”, Università di Bologna, V. F. Selmi 2, 40126 Bologna, Italy
eCentre for Theoretical and Computational Chemistry, Department of Chemistry, University of Oslo, P.O. Box 1033 Blindern, 0315 Oslo, Norway
fUppsala Center for Computational Chemistry - UC3, Uppsala University, Box 518, 751 20 Uppsala, Sweden
First published on 10th March 2015
Abstract
Complete active space self-consistent field (CASSCF) wavefunctions and an orbital entanglement analysis obtained from a density-matrix renormalisation group (DMRG) calculation are used to understand the electronic structure, and, in particular, the Ru–NO bond of a Ru nitrosyl complex. Based on the configurations and orbital occupation numbers obtained for the CASSCF wavefunction and on the orbital entropy measurements evaluated for the DMRG wavefunction, we unravel electron correlation effects in the Ru coordination sphere of the complex. It is shown that Ru–NO π bonds show static and dynamic correlation, while other Ru–ligand bonds feature predominantly dynamic correlation. The presence of static correlation requires the use of multiconfigurational methods to describe the Ru–NO bond. Subsequently, the CASSCF wavefunction is analysed in terms of configuration state functions based on localised orbitals. The analysis of the wavefunctions in the electronic singlet ground state and the first triplet state provides a picture of the Ru–NO moiety beyond the standard representation based on formal oxidation states. A distinct description of the Ru and NO fragments is advocated. The electron configuration of Ru is an equally weighted superposition of RuII and RuIII configurations, with the RuIII configuration originating from charge donation mostly from Cl ligands. However, and contrary to what is typically assumed, the electronic configuration of the NO ligand is best described as electroneutral.
1 Introduction
The electronic structure and properties of transition metal nitrosyl complexes have been a subject of interest in inorganic and bioinorganic chemistry for a long time. Nitric oxide (NO) plays a role in neurotransmission, blood pressure control and even control of tumour growth.1 A number of transition metal nitrosyl complexes have been employed in photodynamical therapy to deliver targeted NO to biological tissues.2 Particularly interesting are ruthenium nitrosyls, since they are postulated to be intermediates3,4 in the mechanism of action of novel ruthenium anti-cancer drugs such as NAMI-A5 and KP1019.6 Understanding the electronic structure of the metal–NO moiety is therefore essential to rationalise the mechanisms for NO delivery from nitrosyl complexes and thus obtain a fundamental understanding of the mode of action of ruthenium anti-cancer drugs.Furthermore, NO is a well-known non-innocent ligand in coordination chemistry,7 which leads to an intricate and ambiguous electronic structure of the transition metal nitrosyls. NO can attach to the metal both in a linear or a bent configuration, depending on the electronic structure of the metal, charge of the free NO and the remaining coordination sphere. The metal-nitrosyl moiety M–NO usually shows strongly delocalised electron density and a strong covalency. Enemark and Feltham8,9 have suggested to describe the electronic structure of this moiety as {M(NO)}n, with n being the total number of electrons in the metal d and nitrosyl π* orbitals. Within this framework, however, the electronic character of neither the Ru nor the NO fragment is known, and it is not possible to assign a particular oxidation state to either fragment. For example, it is unclear whether {RuNO}6 structures should be treated as RuII–NO+ or RuIII–NO0. A correct description of the oxidation states of the metal and ligands is important, e.g., for the study of the redox processes involved in the metabolism of redox-active anti-cancer drugs.
Attempts to resolve the ambiguity in the metal–NO bond and to assign oxidation states to the metal and the ligands have been carried out in many theoretical, spectroscopic and electrochemical studies.4,10–14 It has been largely accepted that most linear {RuNO}6 complexes15 and many {FeNO}6 complexes16 are best described as MII–NO+. Interestingly, and in contrast to this picture, a recent extensive joint experimental and computational study4 on one particular {RuNO}6 complex concluded that the physical electronic structure of the Ru–NO moiety is better described by RuIII–NO0, rather than RuII–NO+.
The majority of computational studies on transition metal complexes employ density functional theory (DFT).17 However, many structures belong to the class of the so-called strongly correlated systems which cannot be described by Kohn–Sham DFT18 due to its single Slater determinant approximation. In this respect, Kohn–Sham DFT is conceptually similar to Hartree–Fock theory, which does not incorporate electron correlation (i.e. movement of electrons depending on the instantaneous positions of other electrons). Electron correlation can be classified as19–21dynamic and static (split further into static and nondynamic correlation by some authors19,21). Dynamic correlation is responsible for keeping the electrons apart and is found in any quantum mechanical system with more than one electron. Static correlation corresponds to significant mixtures of several electronic configurations and is largely present, e.g., in dissociating molecules and many transition metal compounds. While dynamic correlation can be effectively described by DFT and post-Hartree–Fock methods, such as Møller–Plesset perturbation theory or coupled cluster (CC) methods, the proper description of static correlation requires several Slater determinants or configurations in the ansatz. Multiconfigurational methods – such as the complete active space self consistent field (CASSCF),22 the restricted active space SCF (RASSCF),23 or the density matrix renormalization group (DMRG)24 method in its quantum chemical formulation25 as well as their corresponding refinements by second-order perturbation theory23,26,27 – are then mandatory to describe such systems.
Sizova et al.11 were the first to apply a multiconfigurational/valence-bond treatment to a variety of {RuNO}6 complexes. Radoń et al.13 applied CASSCF localised orbitals and spin densities to analyse the Fe–NO bond in several {FeNO}7 complexes, as well as calculated the doublet-quartet energy gap with CASPT2/CASSCF. Recently, we have also used CASPT2/CASSCF to study the electronic structure of another {RuNO}6 complex.14 Boguslawski et al.28 compared the CASSCF spin densities of several Fe–NO complexes with DFT results, deeming both unsatisfactory. This unpleasant situation could only be resolved by calculating the spin density from a large-CAS DMRG wavefunction, in which the complete double-d shell correlation effects could be taken into account.29 Double-d shell correlation effects are related to the presence of a large number of electrons in compact d shells, resulting in large radial correlation effects in these shells. The second more diffuse d shell gives additional flexibility to describe such correlation effects, and for many 3d transition metal compounds the second d shell must be present to obtain quantitative accuracy with the CASPT2 method.30
The last example illustrates the major limitation of CASSCF – the factorial growth of computational time with the number of correlating electrons and orbitals. Presently, CASSCF calculations are typically limited to active spaces comprising approximately 16 electrons in 16 orbitals. Over the past few decades, several attempts have been made to overcome the CASSCF factorial scaling problem and allow the usage of larger active spaces: the RASSCF method introduces additional subspaces with a restricted number of excitations; the generalised active space (GAS)31 concept takes the RAS concept one step further by introducing an arbitrary number of subspaces. RAS and GAS methods allow us to extend the active spaces at the price of having to choose a restriction of the excitation levels; however this degree of freedom makes these methods less straightforward to use than CASSCF. Recently, the GAS method has been combined with Löwdin's partitioning technique32 resulting in the SplitGAS method,33 which, despite its demonstrated capability to effectively employ up to 1022 Slater determinants, still requires algorithmic advances and further development before it can be widely used.
The conceptually different DMRG algorithm employs the reduced density matrix of the system studied to construct and optimise a CAS-like wavefunction, allowing for a polynomial instead of factorial scaling with the number of active orbitals. As a consequence, DMRG allows much larger active spaces than conventional CASSCF, explaining its value for calculations on transition metal complexes dominated by strong static electron correlation34 and its remarkable success in transition metal chemistry in recent years.29,35
Using the DMRG algorithm, n-orbital reduced density matrices are easily obtained from the full density matrix by tracing out contributions from all orbitals in the complementary set of orbitals in the active space. As a consequence, entanglement measures such as the single-orbital entropy36 and mutual information37,38 calculated from the one-orbital and two-orbital reduced density matrix, respectively, are easily accessible. These orbital-based entanglement measures can be applied to examine the multi-reference character of the electronic wave function. In particular, they can be correlated with the amount of static and dynamic electron correlation in an electronic wavefunction21 or exploited to study chemical bonding in molecule formation and dissociation processes.39 Thus, they complement the traditional orbital-based correlation measures such as the natural orbital and geminal analysis.40
In addition to the factorial scaling with the active space size, the cost of multiconfigurational calculations also scales as O(n4) with the number of basis functions. Efficient calculations on large molecules, including large transition metal complexes, cannot be performed unless this scaling is reduced. Using approximate representations of the electron repulsion integrals based on density-fitting (DF) and Cholesky decomposition (CD)41 reduces the scaling to cubic, thus enabling multiconfigurational calculations on larger molecules.42 Analytical gradients employing combined DF and CD techniques extend the applicability to geometry optimisations.43,44
In this work we investigate the electronic structure of the {RuNO}6 moiety in the trans-[RuCl4(NO)(1H-indazole)]-complex (RuHIndNO),45 which is closely related to the anti-cancer drug KP1019. We perform CASSCF calculations of the S0 and T1 state of RuHIndNO, describe the electronic structure of the coordination sphere around Ru and analyse the wavefunction in terms of contributions of different configurations and natural orbital occupation numbers. Note that CASPT2/CASSCF singlet-triplet energy splittings have been addressed in ref. 44. Here we also perform orbital entanglement analyses21,38,39 based on DMRG calculations of the S0 state. We examine different types of electron correlation present in the Ru–ligand bonds and assess the ability of multiconfigurational methods to describe the Ru–NO coordination sphere in RuHIndNO.
To shed more light on the electronic structure of the {RuNO}6 complex, we transform the CASSCF wavefunctions of the S0 and T1 states into a localised orbital basis and analyse the Ru–NO bond and the Ru coordination sphere in terms of configuration state functions (CSFs) based on localised orbitals; we compare the results obtained from the localised orbital analysis to the Mulliken population of Ru d orbitals based on both single-configurational DFT and the CASSCF wavefunction. At the end of our analysis we adress the non-innocence of the NO ligand: in particular, whether NO is to be considered ionic or neutral and the true 4d occupation of the Ru center.
Noting the importance of the double-d shell effects in transition metal compounds,29,30,46 we also investigate the double-d-shell effect using entanglement analysis. We perform another DMRG calculation with an active space incorporating another pair of correlating orbitals and a second d shell on Ru.
2 Computational details
Geometry optimisation of the lowest singlet (S0) and the triplet state (T1) has been performed with DFT, using the BP86 functional47,48 and the def2-TZVPP basis set.49,50 For Ru, the MWB28 effective core potential51 (ECP) has been used, and RI-J and MARI-J52 approximations were employed for computational efficiency. The triplet geometry has been optimised with the unrestricted Kohn–Sham procedure. The DFT calculations have been performed using the TURBOMOLE 6.553 suite of programs.Using the optimised S0 and T1 geometries, single-point CASSCF calculations employing the ANO-RCC-VTZP basis set54 and atomic compact Cholesky decomposition (acCD)-based algorithms41 with the Cholesky decomposition threshold of 10−4 have been performed with the MOLCAS 7.8 program package.55 Mulliken population analyses have been done at the CASSCF and PBE56 levels of theory with the ANO-RCC-VTZP basis set, as implemented in MOLCAS.57
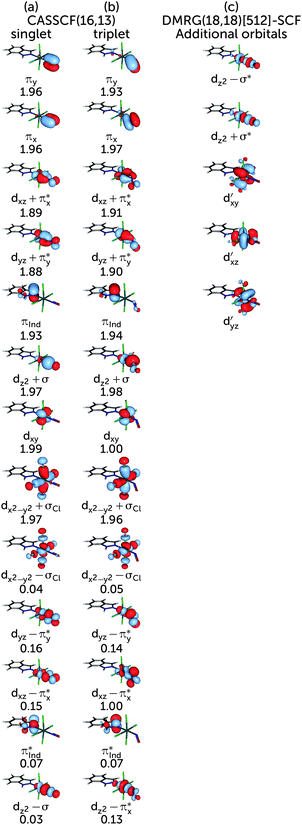
The choice of the CASSCF active space is motivated by its feasibility for a configuration analysis of the Ru coordination sphere. Accordingly, all Ru 4d orbitals and the ligand orbitals interacting with them must be included, resulting in a total active space of 13 orbitals with 16 electrons (denoted (16,13)), including the five Ru 4d orbitals, two pairs of NO π and π* orbitals, one pair of indazole π and π* orbitals, one combination of p orbitals on the Cl atoms (denoted σCl) as well as the NO σ orbital. The last two orbitals are particularly important because they participate in the covalent bond formed between the metal and the NO and Cl ligands, respectively; accordingly, each of them mixes with the dz2 and the dx2−y2 orbitals of the Ru atom, respectively. A fair comparison of the CASSCF wavefunction analyses on the S0 and T1 geometry should be done using the same active spaces in both calculations. For RuHIndNO, this can be only achieved in the S0 calculation by a state-average (SA)-CASSCF calculation over the lowest three singlet states. Thus, the T1 calculation was similarly averaged over three states, to ensure that the deterioration of the wavefuction quality due to state averaging is similar in both spin states. The resulting orbitals and corresponding natural orbital occupation numbers of the optimised S0 and T1 geometries are collected in Fig. 1a and b, respectively.
For the entanglement measures, a DMRG-CASCI calculation based on the optimised CASSCF orbitals (cf.Fig. 1a) has been performed for the S0 state employing the same geometry, active space and basis set as in the CASSCF calculation using the MAQUIS58,59 DMRG program, interfaced to the development version of the MOLCAS program package. The number of renormalised active-subsystem states (m-value)58 is set to 1000. With this value, the DMRG calculation reproduces the absolute energy of the CASSCF calculation up to 10−6 a.u., so that the properties of the DMRG wavefunction can be considered identical to those of the CASSCF wavefunction. This calculation will be denoted DMRG(16,13)[1000], using the shorthand notation DMRG(nelectrons,norbitals)[m]. From the CI-type expansion coefficients of the DMRG wavefunction, a density matrix is constructed, in which environment states can be traced out. These states are states defined on orbitals of the active space that are not considered part of a selected subsystem of orbitals. In the single-orbital case, the selected subsystem consists of only one spatial orbital with four possible states (empty, spin-up, spin-down and doubly-occupied) quantum-mechanically embedded into all other orbitals of the active space. States defined on these complementary orbitals are the environment states traced out in the (then) reduced density matrix. The four eigenvalues of this reduced density matrix, wα,i, enter a von Neumann entropy expression, which yields the single-orbital entropy, s(1)i, for a given orbital i, which can be understood as a measure of the interaction of one orbital with all other orbitals:
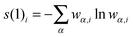 | (1) |
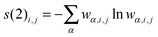 | (2) |
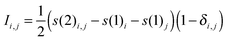 | (3) |
To evaluate the correlation contribution of additional orbitals, including the second d shell effect, another DMRG calculation and entanglement analysis was performed with a larger active space. The previous (16,13) active space (Fig. 1a) was augmented with another pair of orbitals consisting of Ru dz2 and NO σ* orbitals and the second Ru dxy, dxz and dyz shells (cf.Fig. 1c). From all orbitals not present in the (16,13) active space, these orbitals were expected to give the largest contribution to the correlation in the Ru coordination sphere. The new active space consists of 18 electrons in 18 orbitals. Since this active space is out of reach for the traditional CASSCF implementation, the orbitals were optimised with the DMRG-SCF approach as implemented in the development version of MOLCAS. We carried out the DMRG(18,18)[512]-SCF orbital optimisation with the smaller ANO-RCC-MB basis set, augmented with an additional d shell on Ru because the ANO-RCC-VTZP basis set yielded additional p shells on N or O atoms of NO instead of the Ru double shell orbitals. The subsequent DMRG-CASCI step, which is based on the DMRG-SCF orbitals, was done increasing the m-value back to 1000, to be consistent with the DMRG(16,13)[1000] calculation. The orbital entanglement analysis was carried out for the DMRG-CASCI wavefunction, analogous to what has been explained before.
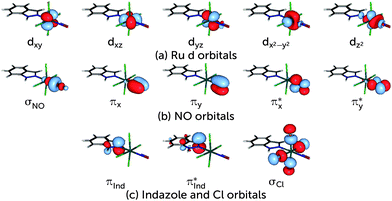
To perform the characterisation of the electronic structure in terms of CSFs based on localised orbitals, all active space orbitals have been localised using the Cholesky algorithm.60 As for any rotation among the active orbitals only, this procedure does not change the total energy of the CASSCF wavefunction. The Cholesky localisation yielded orbitals predominantly localised on single atoms, including single p orbitals at the N and O atoms of NO. These were converted into a set of proper π and π* orbitals by forming normalised linear combinations of the form 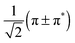 . This procedure yields π and π* orbitals almost exclusively localised on the NO molecule, and together with the other Cholesky orbitals they form the localised active space. The remaining Cholesky orbitals (cf.Fig. 2) are d orbitals localised on the metal, the σ orbital localised at the NO molecule and an orbital consisting of the p orbitals of the four Cl ligands. This localised active space is used in the discussion of the electronic structure of the complex.
. This procedure yields π and π* orbitals almost exclusively localised on the NO molecule, and together with the other Cholesky orbitals they form the localised active space. The remaining Cholesky orbitals (cf.Fig. 2) are d orbitals localised on the metal, the σ orbital localised at the NO molecule and an orbital consisting of the p orbitals of the four Cl ligands. This localised active space is used in the discussion of the electronic structure of the complex.
3 Results and discussion
Based on the CASSCF wavefunction expressed in natural orbitals (cf.Fig. 1a), the singlet, S0, and triplet, T1, states are predominantly described by the electronic configurations (cf.Fig. 1a)| |S0〉 = |(dxz + πx*)2(dyz + πy*)2(dxy)2(dxz − πx*)0〉 |
| |T1〉 = |(dxz + πx*)2(dyz + πy*)2(dxy)1(dxz − πx*)1〉 |
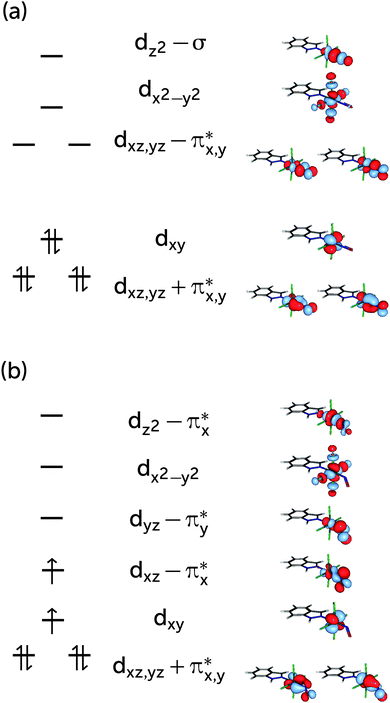 | ||
| Fig. 3 Principal configurations expressed in terms of CASSCF natural orbitals for the S0 (a) and the T1 (b) state. | ||
The major configurations discussed above correspond to 77% of the singlet and 78% of the triplet wavefunctions of RuHIndNO. These weights are lower than the typical value of over 90% for a molecule where the ground state is well described with a single configuration. The remaining ≈20% are distributed among many other configurations, each with weights below 3%. One might then be tempted to conclude that a single-configurational description is sufficient in this case, arguing that the remaining wavefunction contributions are negligible or that they arise due to the dynamic correlation of the system, present in every molecule. If that was the case, however, double excitations would dominate the remaining configurations and single excitations would have much less weight due to the Brilloin theorem. Indeed, one can find that the configuration with the second largest weight of (3% and 2%) in the S0 and T1 wavefunctions, respectively, is a local π → π* double excitation on the indazole ligand; this configuration can be attributed to dynamic correlation between these orbitals. However, a number of single excitations with comparable weight are also present in the wavefunction, for instance, the (dxz + πx*) → (dxz − πx*) and (dyz + πy*) → (dyz − πy*) excitations in the S0 wavefunction, and excitations to the (dxz,yz − πx,y*) and dz2 − πx* orbitals, in the T1 state, which points to the presence of static correlation. For comparison, the former contributions amount to 18% of the S0 wavefunction in the related [Ru(PaPy3)(NO)]2+ complex.14
The presence of both static and dynamic correlation in the Ru–NO bond of RuHIndNO is also reflected by the occupation numbers of the orbitals involved in the Ru–NO bonds, which differ significantly from the formal values of 2 (doubly occupied) and 0 (unoccupied). In the S0 state these are the (dxz,yz + πx,y*) and (dxz,yz − πx,y*) orbitals with occupation numbers of 1.89, 1.88, 0.15 and 0.16 respectively (cf.Fig. 1). Similar occupation numbers for these orbitals are also found in the T1 state, although here the role of the (dyz − πy*) orbital is taken over by the (dz2 − πy*) orbital: the occupation number of the former orbital is exactly 1, which indicates that it does not contribute to the electron correlation. The discrepancies from the formal uncorrelated values of 2 and 0 are also larger than those of the orbitals providing dynamic correlation only, e.g. the π, π* pair of indazole (πInd and πInd*) (1.93/1.94 and 0.07). Not surprisingly, similar behaviour has been found in {FeNO}7 complexes before,13 although the effects are even more pronounced there – with occupation numbers of antibonding orbitals as large as 0.3.
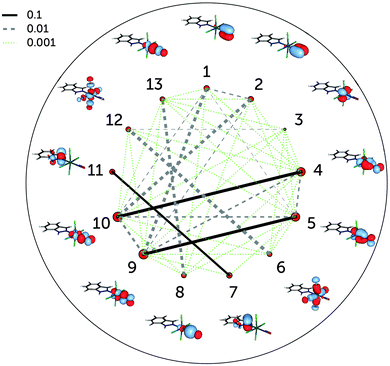
Fig. 4 shows the single-orbital entropies and mutual information for the S0 structure, as defined in eqn (1)–(3), as obtained from the DMRG(16,13)[1000] calculation. One can immediately recognise that orbitals 4, 5, 9 and 10 (corresponding to the dxz,yz ± πx,y* orbitals) have the largest single-orbital entropy (as indicated by the size of the corresponding red circles in Fig. 4), while e.g. orbital 3 (dxy) shows very low entropy. Orbitals 4, 5, 9 and 10 also show high entanglement with each other, and additionally 9 and 10 are also entangled with the πx,y orbitals, labelled 1 and 2. Large single-orbital entropies and strong entanglement with more than one orbital are a signature of static correlation. In contrast, small single-orbital entropies combined with weak entanglement among many orbitals or strong entanglement between two orbitals only is an indication of dynamic correlation. Accordingly, the πx,y − dxz,yz − πx,y* orbitals (1, 2, 4, 5, 9, 10), corresponding to two Ru–NO π bonds, are strongly entangled (i.e. interact strongly) and are responsible for static correlation. The entanglement of the orbitals 1 with 9 and 2 with 10 is due to dynamic correlation, as expected from ππ* pairs. One can distinguish other orbital pairs which show largely dynamic correlation, i.e. have smaller single-orbital entropy and are strongly entangled only with each other, but not with other orbitals of the active space, such as orbitals 7 and 11 (πInd and πInd*, which are again a textbook example of dynamic correlation), 6 and 12 (dx2–y2 ± σCl) and 8 and 13 (dz2 ± σ). The latter two orbital pairs correspond to Ru bonds with chlorido ligands and the Ru–NO σ bond. The single-orbital entropy values correlate well with the deviation of the occupation numbers from 2 or 0 (recall Fig. 1a). The orbitals with the largest deviation (4, 5, 9, 10) show both static and dynamic correlation, whereas orbitals with smaller deviations (7 and 11, 6 and 12, 8 and 13) show mostly dynamic correlation.
The incorporation of the additional dz2–NO σ* pair and the double-shell d orbitals in the active space (DMRG(18,18)[1000] calculation) does not change the entanglement picture (Fig. 5). Compared to DMRG(16,13)[1000], only a few weak interactions with the newly added orbitals can be seen. The dz2–NO σ pair (orbitals 8 and 13) has similar single-orbital entropies to the newly added dz2–NO σ* orbitals (14 and 15) and is weakly-entangled with them; similarly weak is the interaction of the dxy orbital (3) with its double shell (16). The entanglement of the two other double shells is even smaller – they are not affecting the entanglement in the Ru–NO bond in any way. Single-orbital entropies of other orbitals, present in the smaller active space, remain also unaffected. The few additional weak interactions added with the extension of the active space thus should be attributed to the dynamic correlation and do not affect the overall entanglement picture of the Ru coordination sphere found with the smaller (16,13) active space. The lack of strong entanglement and small single-orbital entropies of the double-shell d orbitals shows that their overall effect on the correlation is negligible, similar to what has been found by Pierloot and coworkers for the description of electronic excitations in other 4d transition metals.30,46 The negligible effect of the double-shell d orbitals also explains why the orbital optimisation of the DMRG(18,18)[512]-SCF calculation could only be done with the small ANO-RCC-MB basis set, which excludes the additional p shells of the N, C and O atoms. If the larger ANO-RCC-VTZP basis set is used, the double-shell d orbitals will then be replaced by these p shells. Notably, a similar problem was faced in an earlier study of a ruthenocene complex reported by Phung et al.61 We thus emphasise that despite the difference in the basis set, the entanglement picture is similar in both cases.
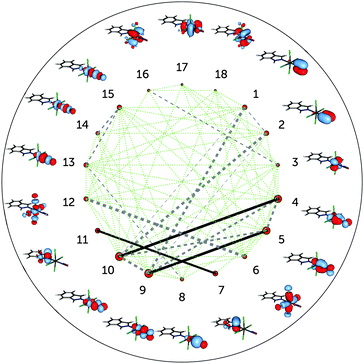 | ||
| Fig. 5 Single-orbital entropy, s(1), and mutual information, I, for the DMRG(18,18)[1000] wavefunction. Labels as in Fig. 4; additional orbitals have been labelled 14–18. | ||
Summarising, the configurational analysis in terms of CASSCF natural orbitals and the entanglement analyses reveal that the Ru–NO σ bond and other Ru–ligand bonds exhibit mostly dynamic correlation and therefore they are well described with single-configurational methods, whereas the Ru–NO π bonds show static correlation and therefore require a multiconfigurational treatment. It is precisely the electronic structure of these π bonds that contributes to the non-innocence of the NO ligand and, hence, a multiconfigurational analysis is best suited to determine the electronic structure of the {RuNO}6 moiety.
An attempt to determine the electronic configuration of Ru can be performed with the help of Mulliken population analysis. For illustrative purposes and for the sake of comparison with the DFT work of Bučinský et al.,4 we contrast Mulliken population differences of Ru 4d orbitals from wavefunctions obtained from CASSCF and DFT calculations. The total Ru 4d atomic orbital population of the single-determinantal wavefunction is 6.47, in very good agreement with the total Ru d population of 6.54 obtained in a similar Ru nitrosyl complex by Bučinský et al.4 The value obtained from the CASSCF wavefunction is 6.02. Given that a single-determinant wavefunction corresponds to a RuII(d6)–NO+ configuration, i.e. to a theoretical Ru 4d occupation of 6, the Mulliken population analysis “overestimates” the d population by approximately half an electron (0.47). Assuming that the intrinsic overestimation of the Mulliken analysis is the same for both wavefunctions, a corrected Mulliken 4d population for the CASSCF wavefunction can be estimated to be 6.02 – 0.47 = 5.55 electrons. A d population value below 6 within a multiconfigurational calculation is due to the mixture of RuII(d6)–NO+ and RuIII(d5)–NO0 configurations in the wavefunction. Although these values should be considered purely qualitative, the difference in Mulliken populations between single-determinant and the CASSCF wavefunction hints to the need of a multiconfiguration treatment.
Further insight into the Ru coordination sphere can be gained from transforming the CSFs into the basis of localised orbitals (Fig. 2) and analysing the CASSCF wavefunctions in terms of the transformed CSFs. The S0 wavefunction expressed in terms of localised orbitals results in a very diffuse expansion, with a large amount of configurations having small but comparable weights, none above 6%. The configurations with the highest weights of 6% and 4% are (σCl)2(dxy)2(dyz)2(dxz)1(dz2)0(dx2–y2)0(πInd)1(πInd*)1(σNO)2(πx)2(πy)2(πx*)1(πy*)0 and
| (σCl)2(dxy)2(dyz)1(dxz)2(dz2)0(dx2–y2)0(πInd)1(πInd*)1(σNO)2(πx)2(πy)2(πx*)0(πy*)1 |
| (σCl)2(dxy)2(dyz)2(dxz)2(dz2)0(dx2–y2)0(πInd)1(πInd*)1(σNO)2(πx)2(πy)2(πx*)0(πy*)0 |
| Character | Contr. S0 (%) | Contr. T1 (%) | |
|---|---|---|---|
| (a) | RuIV(d4) | 7.7 | 8.9 |
| RuIII(d5) | 42.0 | 44.9 | |
| RuII(d6) | 39.9 | 38.4 | |
| (b) | NO− | 18.3 | 23.1 |
| NO0 | 58.0 | 62.3 | |
| NO+ | 21.5 | 12.2 | |
| (c) | RuIV(d4) and NO− | 7.3 | 8.2 |
| RuIII(d5) and NO0 | 31.9 | 31.2 | |
| RuII(d6) and NO+ | 14.3 | 8.8 | |
| RuII(d6) and NO0 | 24.7 | 28.7 | |
| (d) | RuII(d6) and (σCl)1 | 24.6 | 28.7 |
| NO− and (σCl)1 | 10.0 | 13.2 | |
From the analysis of Table 1a we see that the contribution of RuII(d6) and RuIII(d5) configurations to the S0 state is almost the same, yielding a formal oxidation state of Ru of 2.5. This value is in accordance with the corrected Mulliken d population in the CASSCF wavefunction of 5.55 determined previously, despite the fact that Mulliken populations should be treated only qualitatively. A similar process is carried out with NO (Table 1b). The RuII to RuIII ratios do not correspond to the ratios of ionic to neutral NO: the NO0 contribution is the predominant one in this complex (58%). Moreover, NO+ contributions are largely cancelled out by NO− contributions.
Since the net charge (−1) of the complex cannot be explained with a Ru formal oxidation state of 2.5 and a NO0 ligand, we also consider the class of configurations combining the Ru and NO occupancies. Table 1c shows that the RuIII–NO0 configurations have the largest collective weight, above 30%, which is 2.2 times as large as that of the RuII–NO+ configurations. This weight ratio is slightly smaller than the weight ratio of NO0 to NO+ configurations, which is approximately 2.7. This shows that the Ru–NO bond situation is dominated by a strong d → πNO* back donation leading to NO0 and the d6 character of Ru comes from elsewhere. Indeed, we find a large amount of configurations with RuII(d6) and NO0 character, with an even larger weight than that of the RuII(d6) and NO+ configurations. Table 1d reveals that these configurations entirely correspond to the σCl → dx2–y2 excitations, i.e. to a charge transfer from Cl ligands.
Summarising the configuration analysis for the S0 state, we may conclude that the electronic structure of {RuNO}6 is a mixture of several important contributions from which the RuIII–NO0 configurations are most important, indicating a strong d → πNO* back donation. The RuII–NO+ configurations are about half as important if compared by total contributions to the wavefunction, and give Ru some of its RuII character. Despite the lesser significance of RuII–NO+ configurations, Ru shows a large amount of RuII character, almost equal to its RuIII character by having a formal oxidation state of 2.5. A larger amount of the d6 character of Ru, however, does not arise from these configurations, but rather from an electron transfer from the Cl ligands, which can be seen from the contribution of RuII(d6)–(σCl)1 configurations: this contribution is almost identical to that of RuII(d6)–NO0.
Very similar results are obtained for the T1 state, despite its different molecular structure and electronic wavefunction. Most notably, the weights of Ru d5 and d6 configurations are alike and hence the formal oxidation state of Ru is also approximately 2.5. The CSFs with the largest weight have the same electronic configurations as in the case of S0, albeit with a different spin and weights under 3%. At first glance, this is quite unexpected since the T1 state involves an excitation to a metal–NO π* antibonding orbital and Ru–NO back donation gets stronger. As such one would expect a withdrawal of electron density from the metal to NO. Indeed, we observe it to some extent, as the weight of NO+ and RuII(d6)–NO+ configurations decreases compared to the S0 state (8.8% in T1vs. 14.3% in S0): the bent-coordinated NO has even less NO+ contributions than the linear-coordinated one. However, this electron withdrawal from the metal is compensated by the stronger Ru → Cl dative bond: the cumulative weight of RuII(d6)–(σCl)1 configurations increases to 28.7%. This stronger dative bond compensates for the electron density loss on Ru due to a stronger back donation, yielding a similar Ru electronic configuration to that in S0.
4 Conclusion
In this work, we have employed multiconfigurational methods to analyse the electronic structure of the lowest singlet and triplet states of RuHIndNO, a ruthenium nitrosyl complex. We performed a CASSCF calculation on the optimised geometries for the S0 and T1 states of RuHIndNO and analysed the resulting wavefunction both in terms of CASSCF natural orbitals and localised orbitals. The Ru–NO bond shows strong electronic correlation, both static and dynamic, which is supported by the weight of the dominant configuration being significantly below 100%, comparably large weights of single excitations and large fractional populations of the orbitals involved in this bond and the analysis of orbital entanglement. An orbital entanglement analysis based on the one- and two-orbital reduced density matrices calculated from the DMRG wavefunction of the S0 state provides further evidence of strong static correlation in the Ru–NO π bonds, while the Ru–NO σ bond and other Ru–ligand bonds are largely dominated by dynamic correlation. An additional entanglement analysis based on a larger active-space calculation shows a negligible effect of the double-shell d orbitals on the static correlation effects. Furthermore, Mulliken Ru d orbital population based on the single-reference DFT and CASSCF wavefunction shows a discrepancy of approximately 0.5 electrons. In view of these results, we advocate the usage of multiconfigurational methods such as CASSCF to describe the correct bonding situation in the Ru–NO moiety.CASSCF-type methods also allow for an extensive electronic structure analysis of the metal centre, ligands and metal-ligand bonds in the Ru coordination sphere. By a comparatively straightforward unitary transformation of the active-space orbitals, an operation which does not change the physical content of the wavefunction, we obtain a possibility to quantify the contributions from different electronic configurations and therefore to describe the electronic structure of {RuNO}6 more precisely than any assigned formal oxidation state would do. As we have shown, a single structure e.g. RuIII–NO0 or RuII–NO+ does not account for the complexity of the {RuNO}6 electronic structure. Although the electronic structure of the RuHIndNO complex is a superposition of configurations like RuIII–NO0, RuII–NO+ and many others, we gain more details about the structure when we describe the Ru and NO fragments of the Ru–NO bond separately. In this view, our results show that the electronic configuration of Ru consists of approximately equal amounts of d5(RuIII) and d6(RuII) contributions, resulting in a formal Ru oxidation state of 2.5. The NO electronic configuration, on the other hand, shows a predominantly neutral character, which is in contrast to the commonly accepted picture of the RuII–NO+ description. The NO neutral character arises mainly due to the d → πNO* back donation, but a dative contribution by the Cl ligands compensates the outflux of the electron density due to this back donation. This description of Ru and NO is almost the same for both the S0 and T1 state, despite the different electronic structures, with the only difference that metal → NO back donation is even stronger in the T1 structure. This increase of the metal → NO back donation is additionally supported by the increase of the bond length in the triplet state.
Acknowledgements
Financial support from the University of Vienna, the COST Action CM1305 “Explicit Control Over Spin-states in Technology and Biochemistry”, the Research Council of Norway through a Centre of Excellence Grant (Grant No. 179568/V30), the Italian Ministry of Education and Research (MIUR)-Grant No. RBFR1248UI, the Uppsala University, eSSENCE, and the Swedish Research Council (VR) is gratefully acknowledged. Furthermore, we thank Yingjin Ma for the help with the MAQUIS-MOLCAS interface, as well as Vladimir Arion and Gabriel Büchel for fruitful discussions.References
- (a) E. Culotta and D. E. Koshland, Science, 1992, 258, 1862–1865 CAS; (b) F. C. Fang, Nitric Oxide and Infection, Springer, 1999 Search PubMed; (c) L. J. Ignarro, Nitric Oxide: Biology and Pathobiology, Academic Press, 2000 Search PubMed.
- (a) P. Ford, J. Bourassa, K. Miranda, B. Lee, I. Lorkovic, S. Boggs, S. Kudo and L. Laverman, Coord. Chem. Rev., 1998, 171, 185–202 CrossRef CAS; (b) P. C. Ford and I. M. Lorkovic, Chem. Rev., 2002, 102, 993–1018 CrossRef CAS PubMed; (c) A. R. Butler and I. L. Megson, Chem. Rev., 2002, 102, 1155–1166 CrossRef CAS PubMed; (d) J. L. Bourassa and P. C. Ford, Coord. Chem. Rev., 2000, 200–202, 887–900 CrossRef CAS; (e) M. Hoshino, L. Laverman and P. C. Ford, Coord. Chem. Rev., 1999, 187, 75–102 CrossRef CAS; (f) C. F. Works, C. J. Jocher, G. D. Bart, X. Bu and P. C. Ford, Inorg. Chem., 2002, 41, 3728–3739 CrossRef CAS PubMed; (g) C. F. Works and P. C. Ford, J. Am. Chem. Soc., 2000, 122, 7592–7593 CrossRef CAS; (h) A. K. Patra and P. K. Mascharak, Inorg. Chem., 2003, 42, 7363–7365 CrossRef CAS PubMed; (i) E. Tfouni, D. R. Truzzi, A. Tavares, A. J. Gomes, L. E. Figueiredo and D. W. Franco, Nitric Oxide, 2012, 26, 38–53 CrossRef CAS PubMed.
- B. Serli, E. Zangrando, E. Iengo, G. Mestroni, L. Yellowlees and E. Alessio, Inorg. Chem., 2002, 41, 4033–4043 CrossRef CAS PubMed.
- L. Bučinský, G. E. Büchel, R. Ponec, P. Rapta, M. Breza, J. Kožíšek, M. Gall, S. Biskupič, M. Fronc, K. Schiessl, O. Cuzan, D. Prodius, C. Turta, S. Shova, D. A. Zając and V. B. Arion, Eur. J. Inorg. Chem., 2013, 2505–2519 CrossRef PubMed.
- (a) J. M. Rademaker-Lakhai, D. v. d. Bongard, D. Pluim, J. H. Beijnen and J. H. M. Schellens, Clin. Cancer Res., 2004, 10, 3717–3727 CrossRef CAS PubMed; (b) E. Alessio, G. Mestroni, A. Bergamo and G. Sava, Curr. Top. Med. Chem., 2004, 4, 1525–1535 CrossRef CAS.
- C. G. Hartinger, S. Zorbas-Seifried, M. A. Jakupec, B. Kynast, H. Zorbas and B. K. Keppler, J. Inorg. Biochem., 2006, 100, 891–904 CrossRef CAS PubMed.
- (a) C. Jørgensen, Coord. Chem. Rev., 1966, 1, 164–178 CrossRef; (b) W. Kaim, Eur. J. Inorg. Chem., 2012, 343–348 CrossRef CAS PubMed.
- J. Enemark and R. Feltham, Coord. Chem. Rev., 1974, 13, 339–406 CrossRef CAS.
- J. H. Enemark and R. D. Feltham, J. Am. Chem. Soc., 1974, 96, 5002–5004 CrossRef CAS.
- (a) M. Li, D. Bonnet, E. Bill, F. Neese, T. Weyhermüller, N. Blum, D. Sellmann and K. Wieghardt, Inorg. Chem., 2002, 41, 3444–3456 CrossRef CAS PubMed; (b) R. G. Serres, C. A. Grapperhaus, E. Bothe, E. Bill, T. Weyhermüller, F. Neese and K. Wieghardt, J. Am. Chem. Soc., 2004, 126, 5138–5153 CrossRef CAS PubMed; (c) P. Singh, B. Sarkar, M. Sieger, M. Niemeyer, J. Fiedler, S. Záliš and W. Kaim, Inorg. Chem., 2006, 45, 4602–4609 CrossRef CAS PubMed; (d) G. F. Caramori and G. Frenking, Organometallics, 2007, 26, 5815–5825 CrossRef CAS; (e) G. F. Caramori and G. Frenking, Croat. Chem. Acta, 2009, 82, 219–232 CAS; (f) G. F. Caramori, A. G. Kunitz, K. F. Andriani, F. G. Doro, G. Frenking and E. Tfouni, Dalton Trans., 2012, 41, 7327–7339 RSC; (g) A. G. De Candia, J. P. Marcolongo, R. Etchenique and L. D. Slep, Inorg. Chem., 2010, 49, 6925–6930 CrossRef CAS PubMed; (h) J. Conradie and A. Ghosh, J. Phys. Chem. B, 2007, 111, 12621–12624 CrossRef CAS PubMed; (i) H.-Y. Cheng, S. Chang and P.-Y. Tsai, J. Phys. Chem. A, 2004, 108, 358–361 CrossRef CAS; (j) J. Oláh and J. N. Harvey, J. Phys. Chem. A, 2009, 113, 7338–7345 CrossRef PubMed; (k) K. F. Andriani, G. F. Caramori, F. G. Doro and R. L. T. Parreira, Dalton Trans., 2014, 43, 8792–8804 RSC.
- O. V. Sizova, V. I. Baranovski, N. V. Ivanova and V. V. Sizov, Mol. Phys., 2003, 101, 715–720 CrossRef CAS.
- M. Radoń and K. Pierloot, J. Phys. Chem. A, 2008, 112, 11824–11832 CrossRef PubMed.
- M. Radoń, E. Broclawik and K. Pierloot, J. Phys. Chem. B, 2010, 114, 1518–1528 CrossRef PubMed.
- L. Freitag and L. González, Inorg. Chem., 2014, 53, 6415–6426 CrossRef CAS PubMed.
- M. J. Rose and P. K. Mascharak, Coord. Chem. Rev., 2008, 252, 2093–2114 CrossRef CAS PubMed.
- F. Roncaroli, M. Videla, L. D. Slep and J. A. Olabe, Coord. Chem. Rev., 2007, 251, 1903–1930 CrossRef CAS PubMed.
- C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2009, 11, 10757–10816 RSC.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Science, 2008, 321, 792–794 CrossRef CAS PubMed.
- R. J. Bartlett and J. F. Stanton, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, John Wiley & Sons, Inc., 1994, pp. 65–169 Search PubMed.
- O. Sinanoğlu and D. F. Tuan, J. Chem. Phys., 1963, 38, 1740–1748 CrossRef PubMed.
- K. Boguslawski, P. Tecmer, Ö. Legeza and M. Reiher, J. Phys. Chem. Lett., 2012, 3, 3129–3135 CrossRef CAS.
- B. O. Roos, P. R. Taylor and P. E. Siegbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- P. A. Malmqvist, K. Pierloot, A. R. M. Shahi, C. J. Cramer and L. Gagliardi, J. Chem. Phys., 2008, 128, 204109 CrossRef PubMed.
- (a) S. R. White, Phys. Rev. Lett., 1992, 69, 2863–2866 CrossRef; (b) S. R. White, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 10345–10356 CrossRef CAS.
- (a) K. H. Marti and M. Reiher, Z. Phys. Chem., 2010, 224, 583–599 CrossRef CAS; (b) G. K.-L. Chan and S. Sharma, Annu. Rev. Phys. Chem., 2011, 62, 465–481 CrossRef CAS PubMed; (c) Y. Kurashige, Mol. Phys., 2013, 112, 1485–1494 CrossRef; (d) S. Wouters and D. van Neck, Eur. Phys. J. D, 2014, 68, 272 CrossRef; (e) T. Yanai, Y. Kurashige, W. Mizukami, J. Chalupský, T. N. Lan and M. Saitow, Int. J. Quantum Chem., 2015, 115, 283–299 CrossRef CAS PubMed; (f) S. Sharma and G. K.-L. Chan, J. Chem. Phys., 2012, 136, 124121 CrossRef PubMed; (g) Ö. Legeza, R. M. Noack, J. Sólyom and L. Tincani, in Computational Many-Particle Physics, ed. H. Fehske, R. Schneider and A. Weiße, Springer Berlin Heidelberg, 2008, pp. 653–664 Search PubMed.
- K. Andersson, P. A. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488 CrossRef CAS.
- (a) Y. Kurashige and T. Yanai, J. Chem. Phys., 2011, 135, 094104 CrossRef PubMed; (b) S. Sharma and G. K.-L. Chan, J. Chem. Phys., 2014, 141, 111101 CrossRef PubMed.
- K. Boguslawski, C. R. Jacob and M. Reiher, J. Chem. Theory Comput., 2011, 7, 2740–2752 CrossRef CAS.
- K. Boguslawski, K. H. Marti, Ö. Legeza and M. Reiher, J. Chem. Theory Comput., 2012, 8, 1970–1982 CrossRef CAS PubMed.
- K. Pierloot, in Computational Organometallic Chemistry, ed. T. R. Cundari, Marcel Dekker Inc., New York, 2001, pp. 123–158 Search PubMed.
- D. Ma, G. Li Manni and L. Gagliardi, J. Chem. Phys., 2011, 135, 044128 CrossRef PubMed.
- P.-O. Löwdin, J. Chem. Phys., 1951, 19, 1396–1401 CrossRef PubMed.
- G. Li Manni, D. Ma, F. Aquilante, J. Olsen and L. Gagliardi, J. Chem. Theory Comput., 2013, 9, 3375–3384 CrossRef CAS.
- K. H. Marti, I. Malkin Ondík, G. Moritz and M. Reiher, J. Chem. Phys., 2008, 128, 014104 CrossRef PubMed.
- (a) Y. Kurashige, G. K.-L. Chan and T. Yanai, Nat. Chem., 2013, 5, 660–666 CrossRef CAS PubMed; (b) S. Wouters, T. Bogaerts, P. V. D. Voort, V. V. Speybroeck and D. V. Neck, J. Chem. Phys., 2014, 140, 241103 CrossRef PubMed; (c) S. Sharma, K. Sivalingam, F. Neese and G. K.-L. Chan, Nat. Chem., 2014, 6, 927–933 CrossRef CAS PubMed; (d) J. Chalupský, T. A. Rokob, Y. Kurashige, T. Yanai, E. I. Solomon, L. Rulíšek and M. Srnec, J. Am. Chem. Soc., 2014, 136, 15977–15991 CrossRef PubMed.
- Ö. Legeza and J. Sólyom, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 195116 CrossRef.
- Ö. Legeza and J. Sólyom, Phys. Rev. Lett., 2006, 96, 116401 CrossRef.
- J. Rissler, R. M. Noack and S. R. White, Chem. Phys., 2006, 323, 519–531 CrossRef CAS PubMed.
- (a) K. Boguslawski, P. Tecmer, G. Barcza, Ö. Legeza and M. Reiher, J. Chem. Theory Comput., 2013, 9, 2959–2973 CrossRef CAS; (b) M. Mottet, P. Tecmer, K. Boguslawski, Ö. Legeza and M. Reiher, Phys. Chem. Chem. Phys., 2014, 16, 8872–8880 RSC.
- (a) P. Pulay and T. P. Hamilton, J. Chem. Phys., 1988, 88, 4926–4933 CrossRef CAS PubMed; (b) M. S. Gordon, M. W. Schmidt, G. M. Chaban, K. R. Glaesemann, W. J. Stevens and C. Gonzalez, J. Chem. Phys., 1999, 110, 4199–4207 CrossRef CAS PubMed.
- (a) N. H. F. Beebe and J. Linderberg, Int. J. Quantum Chem., 1977, 12, 683–705 CrossRef CAS PubMed; (b) H. Koch, A. Sánchez de Merás and T. B. Pedersen, J. Chem. Phys., 2003, 118, 9481–9484 CrossRef CAS PubMed; (c) T. B. Pedersen, F. Aquilante and R. Lindh, Theor. Chem. Acc., 2009, 124, 1–10 CrossRef CAS; (d) F. Aquilante, L. Boman, J. Boström, H. Koch, R. Lindh, A. Sánchez de Merás and T. B. Pedersen, in Challenges and Advances in Computational Chemistry and Physics, ed. M. G. Papadopoulos, R. Zalesny, P. G. Mezey and J. Leszczynski, Springer, 2011, vol. 13, pp. 301–344 Search PubMed.
- (a) F. Aquilante, T. B. Pedersen, R. Lindh, B. O. Roos, A. Sánchez de Merás and H. Koch, J. Chem. Phys., 2008, 129, 024113 CrossRef PubMed; (b) F. Aquilante, P.-Å. Malmqvist, T. B. Pedersen, A. Ghosh and B. O. Roos, J. Chem. Theory Comput., 2008, 4, 694–702 CrossRef CAS; (c) F. Aquilante, T. K. Todorova, T. B. Pedersen, L. Gagliardi and B. O. Roos, J. Chem. Phys., 2009, 131, 34113 CrossRef PubMed; (d) D. Roca-Sanjuán, F. Aquilante and R. Lindh, WIREs Comput. Mol. Sci., 2012, 2, 585–603 CrossRef PubMed.
- (a) F. Aquilante, R. Lindh and T. B. Pedersen, J. Chem. Phys., 2008, 129, 034106 CrossRef PubMed; (b) J. Boström, F. Aquilante, T. B. Pedersen and R. Lindh, J. Chem. Theory Comput., 2013, 9, 204–212 CrossRef.
- M. G. Delcey, L. Freitag, T. B. Pedersen, F. Aquilante, R. Lindh and L. González, J. Chem. Phys., 2014, 140, 174103 CrossRef PubMed.
- A. Gavriluta, G. E. Büchel, L. Freitag, G. Novitchi, J. B. Tommasino, E. Jeanneau, P.-S. Kuhn, L. González, V. B. Arion and D. Luneau, Inorg. Chem., 2013, 52, 6260–6272 CrossRef CAS PubMed.
- K. Pierloot, Int. J. Quantum Chem., 2011, 111, 3291–3301 CrossRef CAS PubMed.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124 CrossRef CAS.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- (a) K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290 CrossRef CAS; (b) M. Sierka, A. Hogekamp and R. Ahlrichs, J. Chem. Phys., 2003, 118, 9136–9148 CrossRef CAS PubMed.
- TURBOMOLE V6.5 2013, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com.
- B. O. Roos, R. Lindh, P.-A. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2005, 109, 6575–6579 CrossRef CAS PubMed.
- F. Aquilante, L. de Vico, N. Ferré, G. Ghigo, P.-Å. Malmqvist, P. Neogrády, T. B. Pedersen, M. Pitoňák, M. Reiher, B. O. Roos, L. Serrano-Andrés, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224–247 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef CAS PubMed.
- S. F. Keller and M. Reiher, Chimia, 2014, 68, 200–203 CrossRef CAS PubMed.
- M. Dolfi, B. Bauer, S. Keller, A. Kosenkov, T. Ewart, A. Kantian, T. Giamarchi and M. Troyer, Comput. Phys. Commun., 2014, 185, 3430–3440 CrossRef CAS PubMed.
- F. Aquilante, T. B. Pedersen, A. Sánchez de Merás and H. Koch, J. Chem. Phys., 2006, 125, 174101 CrossRef PubMed.
- Q. M. Phung, S. Vancoillie, A. Delabie, G. Pourtois and K. Pierloot, Theor. Chem. Acc., 2012, 131, 1–9 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2015 |