Open Access Article
Open Access ArticleSynthesis, structure and properties of [Co(NCS)2(4-(4-chlorobenzyl)pyridine)2]n, that shows slow magnetic relaxations and a metamagnetic transition†
Julia
Werner
a,
Zbigniew
Tomkowicz
b,
Michał
Rams
b,
Stefan G.
Ebbinghaus
c,
Tristan
Neumann
a and
Christian
Näther
*a
aInstitut für Anorganische Chemie, Christian-Albrechts-Universität zu Kiel, Max-Eyth-Straße 2, 24118 Kiel, Germany. E-mail: cnaether@ac.uni-kiel.de; Fax: +49 431-880 1520; Tel: +49 431-880 1520
bInstitute of Physics, Jagiellonian University, 30-348 Kraków, Łojasiewicza 11, Poland
cMartin-Luther-Universität Halle-Wittenberg, Institut für Chemie, Kurt-Mothes-Straße 2, 06120 Halle/Saale, Germany
First published on 1st July 2015
Abstract
The reaction of Co(NCS)2 with 4-(4-chlorobenzyl)pyridine (ClBP) leads to the formation of Co(NCS)2(4-(4-chlorobenzyl)pyridine)4 (1) and [Co(NCS)2(4-(4-chlorobenzyl)pyridine)2]n (2). In the crystal structure of 1 the Co(II) cations are octahedrally coordinated by two terminal bonded thiocyanato anions and four ClBP ligands, whereas in 2 the Co(II) cations are linked into chains by pairs of μ-1,3-bridging thiocyanato anions. Magnetic measurements of 2 show an antiferromagnetic phase transition with TN = 3.9 K. A metamagnetic transition is observed at the critical magnetic field of 260 Oe. Magnetic relaxations in the zero field are consistent with single chain magnetic behavior. These results are compared with those obtained for similar compounds reported recently.
Introduction
Low-dimensional magnetic materials, because of their unusual properties, attracted wide interest of researchers over several decades. The last wave of interest is related with the discovery of the so-called Single Chain Magnets (SCM) and an increasing number of such compounds have been continuously reported.1–9 In this regard compounds which show a slow relaxation of the magnetization that can be traced back to the relaxation of single chains are of special interest because of their potential for future applications as high-density storage material.10–27 To get more insight into the influence of a chemical and a structural modification on the magnetic properties of such compounds systematic investigations using strongly related compounds are needed.For the creation of such materials, it is necessary that cations of large magnetic anisotropy are linked into chains by small ligands like, e.g. azido anions that can mediate strong magnetic exchange along the chains.28–31 In this context thiocyanato ligands are also useful because they offer a broad number of different bonding modes, which allows the selective preparation of coordination compounds with a different dimensionality of the coordination network.32–53
In our ongoing project on the synthesis, structure and properties of thio- or selenocyanato coordination polymers we are especially interested in compounds, in which Co(II) or Fe(II) cations are connected by pairs of these anionic ligands into chains, because several of them show a slow relaxation of magnetization, indicative of SCM behavior. For the first time we observed such relaxations in [Co(NCS)2(pyridine)2]n.54 A similar behavior is observed for the corresponding selenocyanato coordination polymer [Co(NCSe)2(pyridine)2]n, with significantly stronger intrachain interactions.55 In contrast, the analogous Fe(II) compound [Fe(NCS)2(pyridine)2]n reported by Foner et al. is a metamagnet that shows no relaxations but this behavior can be induced by an exchange of the anionic ligand.56,57 [Fe(NCSe)2(pyridine)2]n is also a metamagnet but it shows slow relaxation of magnetization and it is assumed that the lower magnetic anisotropy of Fe(II) cations is compensated by stronger intrachain interactions.58
To study the influence of the co-ligand onto the relaxation properties, compounds with different co-ligands were prepared which also consist of 1D Co(NCS)2 chains and show these relaxations. This includes, e.g., [Co(NCS)2(4-acetylpyridine)2]n that exhibits a ferromagnetic ground state.59 In contrast, [Co(NCS)2(4-ethylpyridine)2]n has an antiferromagnetic ground state and shows a metamagnetic transition.60 A similar behavior is also observed for [Co(NCS)2(bis-(4-pyridyl)ethylene)2]n and for [Co(NCS)2(bis-(4-pyridyl)ethane)2]n.39,61 We also tried to investigate the influence of the interchain interactions by using the relatively large 4-(3-phenylpropyl)pyridine as a co-ligand. [Co(NCS)2(4-(3-phenylpropyl)pyridine)2]n exhibits a ferromagnetic ground state and also shows magnetic relaxations that, however, cannot be clearly attributed to single chain relaxations.62
To investigate the influence of the co-ligand on the magnetic properties in more detail we tried to prepare a compound based on the relatively large co-ligand 4-(4-chlorobenzyl)pyridine, in which the Co cations are linked by pairs of μ-1,3-bridging thiocyanato anions into chains. Here we report on our investigations.
Results and discussion
Synthesis and crystal structures
The reaction of different ratios of Co(NCS)2 and 4-(4-chlorobenzyl)pyridine leads to the formation of two different compounds as indicated by X-ray powder diffraction. The results of the elemental analysis reveal a composition of Co(NCS)2(ClBP)4 (1) and Co(NCS)2(ClBP)2 (2). In compound 1 the asymmetric stretching vibration νas(CN) is observed at 2064 cm−1, which proves that only N-terminally bonded thiocyanato anions are present. In contrast, in compound 2 the asymmetric stretching vibration νas(CN) is shifted to 2105 cm−1, which indicates that μ-1,3 bridging thiocyanato anions are present (Fig. S1 and S2 in the ESI†). Based on these results it can be concluded that compound 1 consists of octahedrally coordinated discrete complexes, whereas in compound 2 the cations are linked by the anionic ligands into a coordination polymer. To verify whether compound 1 could be used as a precursor to prepare a ligand deficient phase by thermal decomposition, measurements using simultaneous differential thermoanalysis and thermogravimetry were performed. This shows that compound 1 decomposes in only one step at about 120 °C, without the formation of any further intermediate (Fig. S3 in the ESI†). Single crystals were obtained from acetonitrile (1) or methanol (2) and were characterized by single crystal X-ray diffraction.Co(NCS)2(ClBP)4 (1) crystallizes in the monoclinic space group C2/c with four formula units in the unit cell. The asymmetric unit consists of one cobalt cation which is located on a center of inversion as well as of one thiocyanato anion and two 4-(4-chlorobenzyl)pyridine ligands in general positions. The metal center is octahedrally surrounded by two thiocyanato anions and four 4-(4-chlorobenzyl)pyridine ligands (Fig. 1).
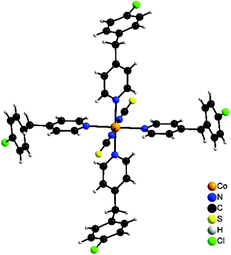 | ||
| Fig. 1 Coordination sphere of 1. An ORTEP plot of this structure can be found in Fig. S4 in the ESI.† | ||
The cobalt nitrogen distances range between 2.0943(15) and 2.241(2) Å and the bond angles have values between 88.66(6) and 91.34(6)° and of 180.00(8)° (Table S1 in the ESI†).
[Co(NCS)2(ClBP)2]n (2) crystallizes in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with two formula units in the unit cell. The asymmetric unit consists of two crystallographically independent cobalt cations which are located on centers of inversion as well as of two thiocyanato anions and two 4-(4-chlorobenzyl)pyridine ligands in general positions. The cobalt cations are in an octahedral environment and are coordinated by two ClBP ligands and by two N and two S atoms of four thiocyanato anions in the trans position (Fig. 2). The cobalt nitrogen distances range from 2.060(2) to 2.165(2) Å and the Co–S distances are between 2569(1) and 2.607(1) Å (Table S2 in the ESI†). The overall coordination of both crystallographically independent Co cations is almost identical.
with two formula units in the unit cell. The asymmetric unit consists of two crystallographically independent cobalt cations which are located on centers of inversion as well as of two thiocyanato anions and two 4-(4-chlorobenzyl)pyridine ligands in general positions. The cobalt cations are in an octahedral environment and are coordinated by two ClBP ligands and by two N and two S atoms of four thiocyanato anions in the trans position (Fig. 2). The cobalt nitrogen distances range from 2.060(2) to 2.165(2) Å and the Co–S distances are between 2569(1) and 2.607(1) Å (Table S2 in the ESI†). The overall coordination of both crystallographically independent Co cations is almost identical.
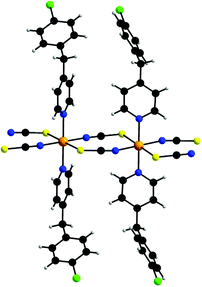 | ||
| Fig. 2 View of the coordination sphere of 2. An ORTEP plot of 2 can be found in Fig. S5 in the ESI.† | ||
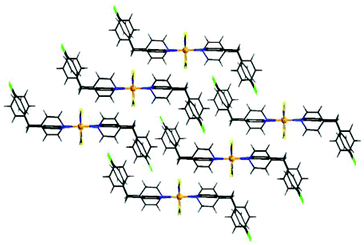
The Co cations are linked by pairs of μ-1,3-bridging thiocyanato anions into chains with an interchain distance of 5.6348 Å between neighboring Co cations (Fig. 2). The shortest interchain Co⋯Co distance is close to 8.2413 Å. In the crystal structure the cobalt thiocyanato chains are orientated parallel to each other and this arrangement is similar to that in [Co(NCS)2(pyridine)2]n and [Co(NCS)2(4-Acpy)2]n reported recently (Fig. 3).54,59
Based on the crystallographic data powder patterns were calculated for compounds 1 and 2 and were compared with those measured, which proves that both compounds were obtained as pure phases (Fig. S6 and S7 in the ESI†). Scanning electron microscopy shows that for 2 crystalline particles of several μm were obtained (Fig. S8 in the ESI†).
Magnetic investigations
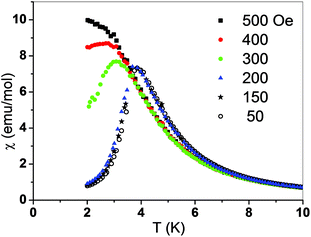
For the chain compound 2 the magnetic susceptibility was measured in the temperature range 2–300 K. The χ(T) dependence is presented in Fig. 4. It has a sharp maximum at 3.9 K characteristic for an antiferromagnetic transition. In the inset the temperature dependence of the χT product is shown. The room temperature value of χT equals 3.3 emu K mol−1 and is much greater than the spin only value 1.87, expected for s = 3/2, pointing to the orbital contribution in Co(II) which is also responsible for a small decrease of χT with decreasing temperature (not seen in the scale of the figure). However, below about 20 K a strong increase of χT is observed due to ferromagnetic intrachain interactions. Thus, the above mentioned antiferromagnetic transition can only be caused by weak antiferromagnetic interchain interactions.
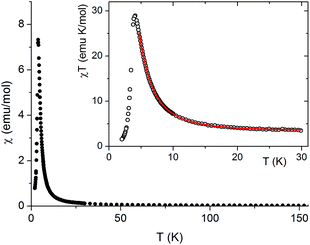 | ||
| Fig. 4 Temperature dependence of magnetic susceptibility χ and the χT product (inset) measured for 2 at 50 Oe. Solid line is a fit; see the text. | ||
For quasi one-dimensional anisotropic magnetic systems the temperature dependence of χT is often presented in the form of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χT vs. reciprocal temperature plot (Fig. S10 in the ESI†). The slope of the linear part of this plot Δξ/kB = 11.9 K equals the energy for the creation of a domain wall and is a measure of the intrachain exchange interaction J. The value of J may be estimated from the relation Δξ = 2s2J,27 thus, assuming s = 1/2 one obtains J/kB ∼ 23.8 K. The rounding down near the maximum may indicate antiferromagnetic interchain interactions. This behavior may be well described by the Ising Hamiltonian adequate for linear chain of Co(II) ions in an axially distorted octahedral coordination
χT vs. reciprocal temperature plot (Fig. S10 in the ESI†). The slope of the linear part of this plot Δξ/kB = 11.9 K equals the energy for the creation of a domain wall and is a measure of the intrachain exchange interaction J. The value of J may be estimated from the relation Δξ = 2s2J,27 thus, assuming s = 1/2 one obtains J/kB ∼ 23.8 K. The rounding down near the maximum may indicate antiferromagnetic interchain interactions. This behavior may be well described by the Ising Hamiltonian adequate for linear chain of Co(II) ions in an axially distorted octahedral coordination
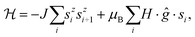 | (1) |
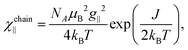 | (2) |
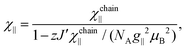 | (3) |
| χ = χ‖/3 + χtip. | (4) |
The term χtip takes into account the increasing population of excited Kramers doublets of single Co(II) centers at elevated temperatures. Fitting such a model into experimental data in the 5–30 K temperature range leads to the following values: J = 29.8(2) K, zJ′ = −0.43(2) K, g|| = 7.2(1) and χtip = 0.034(1) emu mol−1 (Fig. 4).
Such small interchain interaction zJ′ may be easily overcome by a magnetic field. To show this effect, the temperature dependent magnetic susceptibility was measured in various magnetic fields. The data obtained prove that a metamagnetic transition occurs between 200 and 400 Oe (Fig. 5). It is noted that the fields given in the figure refer to the external fields and therefore, at 300 Oe an antiferromagnetic-like maximum is still visible especially, considering the fact that the sample is powdered and not all crystallites undergo metamagnetic transition at the same field.64
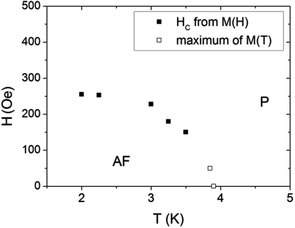
This transition is also clearly visible in field dependent magnetization measured at 2.0 K (Fig. 6). The rapid increase of M below 2 kOe is followed by a slower increase up to 2.4μB at 90 kOe. There is no saturation, seemingly because of the high anisotropy of Co(II) ions. No hysteresis loop is observed. The inset in Fig. 6 shows M(H) in the vicinity of the metamagnetic transition. The critical field Hc = 258 ± 5 Oe at 2.0 K was determined from crossing of tangents to M(H) curve below and above the transition. The values for Hc at higher temperatures were determined in the same way and used for the construction of the magnetic phase diagram (Fig. 7). The additional points at higher temperatures were taken from the DC measurements at different fields (Fig. 5).
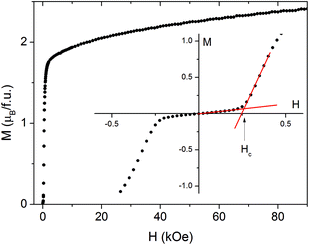 | ||
| Fig. 6 Magnetization vs. field measured at T = 2.0 K for 2. The inset magnifies the low-field region and shows the way of critical field determination. | ||
Additional temperature dependent DC measurements were performed under the field cooling (FC) and zero-field cooling (ZFC) regimes. Only a small bifurcation between FC and ZFC curves in the limits of experimental uncertainties was observed, which does not clearly prove the presence of long time magnetic relaxations (Fig. S11 in the ESI†).
φ = ΔTm/[TmΔ(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f)]. f)]. | (5) |
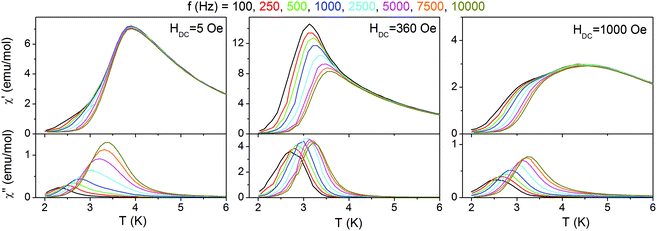 | ||
| Fig. 8 Temperature dependent AC magnetic susceptibilities for 2 measured for various frequencies in different DC magnetic fields. | ||
In Fig. 9 frequency dependent AC susceptibility measured at various temperatures in DC field of 5 Oe is presented. All frequency dependencies can be well described by the generalized Debye model with one mean relaxation time according to the equation
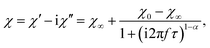 | (6) |
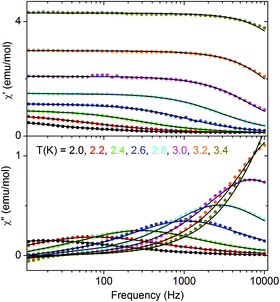 | ||
| Fig. 9 Frequency dependent AC susceptibility for 2 measured at various temperatures. Solid lines are fits with the generalized Debye model. | ||
The table with the best fit parameters is given in the ESI (Table S3†). As seen in the table, τ strongly increases with decreasing temperature. The simultaneous increase of α means that the width of relaxation time distribution increases with decreasing temperature, which should be caused by interchain interactions. The Cole–Cole plots, which present χ′′ vs. χ′ dependence are shown in Fig. 10. They are an arc of circles which are shifted down with respect to the χ′ axis according to the non-zero α parameter.
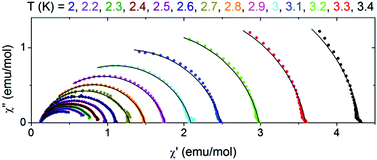 | ||
| Fig. 10 Cole–Cole plots for 2 at various temperatures. Solid lines are fits with the generalized Debye model. | ||
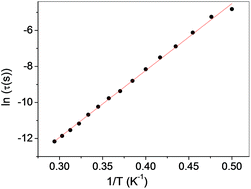
The temperature dependence of τ is shown in Fig. 11 as a plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ vs. 1/T, from which the energy barrier ΔE and prefactor τ0 in the Arrhenius equation
τ vs. 1/T, from which the energy barrier ΔE and prefactor τ0 in the Arrhenius equation
τ = τ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(ΔE/kBT) exp(ΔE/kBT) | (7) |
Discussion of the magnetic properties
Compound 2, built from ferromagnetic Co–(NCS)2–Co chains, shows an antiferromagnetic transition at a Néel temperature of 3.8 K. It undergoes a metamagnetic transition in the field of ∼260 Oe. The magnetic relaxations existing in the antiferromagnetic state are well described with one mean relaxation time and a single energy barrier for thermal activation ΔE/kB = 37.1 K, which may originate from single chain relaxations.67According to Coulon et al.27 the activation energy of the relaxation time may be discussed using the following equation
| ΔE = kΔξ + ΔA, | (8) |
A crossover from k = 1 to k = 2 is expected with increasing temperature around T*, that can be related to the chain length n (ref. 27)
2n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−2Js2/kBT*) = 1. exp(−2Js2/kBT*) = 1. | (9) |
As mentioned in the Introduction compound 2 is a member of a family of compounds we have investigated in the past. All of these compounds of the general composition [Co(NCS)2(L2)]n (L = co-ligand) consist of octahedrally coordinated Co(II) cations that are linked into chains by pairs of thiocyanato anions. When the magnetic properties of these compounds are compared always similar values for the intrachain interaction are noted, which can be traced back to the fact that always the same thiocyanato chains are involved (Table 2). It is not clear if the small differences between the J values originate from the influence of the co-ligand.
However, all of these compounds can be divided into two different groups. The first group consists of compounds that exhibit an antiferromagnetic ground state and show a metamagnetic transition as it is the case for compound 2. For all of these compounds the Mydosh parameter points to superparamagnetic behaviour, the magnetic relaxations can be well fitted using the Debye model leading to similar values for the anisotropy energy ΔA and the Glauber criterion is also fulfilled. In this context it is noted that ΔA can also be calculated in a more general way, without assuming the Fisher model restrictions, by using the Δξ values obtained from the ln(χT)(1/T) dependence. The values of ΔA obtained in such a way do not differ very much from those given in Table 2. Therefore, their relaxations seem to originate from the relaxation of single chains. However, for α, which is a measure for the distribution of the relaxation times, relatively large values are observed (Table 1). Even if such high values are frequently discussed in the literature in context of single chain magnetic behaviour the question arises if this might always be adequate. With decreasing temperatures α increases dramatically which suggests that at higher temperatures single chain relaxations are observed, whereas at lower temperatures interchain interactions must come into play.
| 2 | Etpy | bpe | bpa | Acpy | PPP | |
|---|---|---|---|---|---|---|
| The parameters zJ′ and J given in the table differ slightly from the values given in ref. 59–62. This is due to different models used to fit χT(T) in some of these reports, particularly different definitions of zJ′ and the temperature range used in the fitting procedures. To be able to compare directly between zJ′ parameters for all compounds of this family, we estimated the parameters zJ′ and J again, fitting χT(T) data, but using the identical model as for 2. For better comparison the value if ΔA for the compound with Etpy was recalculated assuming k = 1. Thus, it deviates from that given in ref. 60 where arbitrarily k = 2 was selected. J = intrachain interaction; zJ′ = interchain interaction; Tc = critical temperature; AF = antiferromagnetic ground state; FO = ferromagnetic ground state; Hc = critical field; ΔE = Arrhenius law energy; τ0 = prefactor; ΔA = see eqn (8); α = distribution of the relaxation times determined at different temperatures; φ = Mydosh parameter. | ||||||
| Ground state | AF | AF | AF | AF | FM | FM |
| H c (Oe) | ∼260 (2 K) | ∼175 (1.5 K) | ∼400 (2 K) | ∼40 (2 K) | — | — |
| T c (K) | 3.9 | 3.4 | 4.0 | 3.1 | 3.8 | 3.3 |
| J/kB (K) | 29.8 | 27.0 | 26.8 | 27.8 | 30.2 | 28.4 |
| zJ′/kB (K) | −0.43 | −0.42 | −0.66 | −0.22 | +0.17 | +0.15 |
| ΔE/kB (K) | 37.1 | 45.3 | 33.3 | 39.2 | 74 | 116 |
| τ 0 (s) | 9.5 × 10−11 | 2 × 10−12 | 1.2 × 10−11 | 1.2 × 10−11 | 6 × 10−13 | 10−19 |
| Δ A/kB (K) | 22.2 (k = 1) | 31.8 (k = 1) | 19.9 (k = 1) | 25.3 (k = 1) | — | — |
| α | 0.09–0.37 | 0.1–0.4 | 0.10–0.46 | 0.06–0.41 | 0.4–0.52 | — |
| φ | 0.14 | 0.14 | 0.16 | 0.11 | 0.074 | 0.059 |
| Compound | 1 | 2 |
|---|---|---|
| Formula | C50H40Cl4CoN6S2 | C26H20Cl2CoN4S2 |
| M W/g mol−1 | 989.73 | 582.41 |
| Crystal system | Monoclinic | Triclinic |
| Space group | C2/c |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
| Z | 4 | 2 |
| D calc/mg cm−3 | 1.382 | 1.482 |
| μ/mm−1 | 0.715 | 1.045 |
| a/Å | 18.8098(13) | 9.0456(15) |
| b/Å | 9.5685(5) | 10.8405(16) |
| c/Å | 27.6126(17) | 14.941(3) |
| α/° | 90 | 73.393(19) |
| β/° | 106.867(7) | 83.37(2) |
| γ/° | 90 | 68.356(17) |
| V/Å3 | 4756.0(5) | 1304.9(4) |
| T/K | 293(2) | 200(2) |
| Scan range 2θ/° | 2.26 to 25.97 | 2.10 to 26.99 |
| Measured refl. | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 774 774 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 952 952 |
| R int | 0.0389 | 0.0413 |
| Min./max. transm. | 0.7998, 0.8759 | 0.7951, 0.9070 |
| Unique reflns | 4584 | 5692 |
| Refl. [F0 > 4σ(F0)] | 3894 | 4342 |
| Parameters | 296 | 320 |
| R 1 [F0 > 4σ(F0)] | 0.0357 | 0.0441 |
| wR2 [all data] | 0.0946 | 0.1021 |
| GOF | 1.057 | 1.034 |
| Δρmax/min/e Å−3 | 0.428 and −0.394 | 0.380 and −0.437 |
The second group consists of compounds with a ferromagnetic ground state. For these two compounds with 4-(3-phenylpropyl)pyridine (PPP) and 4-acetylpyridine (Acpy) as co-ligands, a relatively small Mydosh parameter is observed indicating spin glass-like behaviour (Table 2). Interestingly, for the Acpy compound the frequency dependent AC data can be fitted using the Debye model but in this case relatively high values of α and ΔE/kB are obtained together with much smaller τ0 value, which clearly shows that this compound behaves differently from that with the AF ground state. Moreover, temperature dependent AC data obtained for the compound with PPP lead to an unrealistic small τ0, so obtained ΔE cannot be linked with the relaxation process of single chains. All these findings indicate that for the ferromagnetic compounds the relaxation might not be traced back to the relaxation of single chains and that it is more reasonable to assume that these are relaxations of walls of 3-dimensional ferromagnetic domains.
The reason why some of these compounds exhibit an antiferromagnetic ground state whereas some others exhibit a ferromagnetic ground state is still unclear. There is, e.g., no simple correlation between the interchain distances and their magnetic properties. It is noted that two different arrangements of the Co(NCS)2 chains are observed in their crystal structures. In some of these compounds the N–N vector of the two coordinating pyridine ligands of neighboring chains are parallel, whereas in some others they are canted. Unfortunately this does not correlate with the magnetic ground state of these compounds. Most probably, the type of the magnetic ground state is due to different arrangements of the anisotropic Co chains in the crystal structures, which lead to different dipolar interactions changing the sign of effective zJ′. The basis for the simulations of dipolar interactions and expected ground state is however single ion Co anisotropy and its direction, which is not obvious. To gain such information magnetic investigations with a single crystal would be desirable.
Conclusions
In the present contribution a new thiocyanato compound with the relatively large co-ligand 4-(4-chlorobenzyl)pyridine was prepared, in which the Co(II) cations are linked by pairs of thiocyanato anions into chains. This new compound is a member of a family of compounds that we have recently investigated to examine the influence of a chemical and a structural modification on the magnetic properties in detail. For some of these compounds the magnetic properties can be discussed as a single chain magnetic behavior, while for some other compounds this seems to be inadequate. Within this family, compound 2 presented in this report, in spite of undergoing an antiferromagnetic transition, most clearly demonstrates the relaxation behavior characteristic for single chain magnets.In this context it is noted that the stem compound Co(NCS)2(pyridine)2 mentioned in the Introduction obviously also exhibits a ferromagnetic ground state but shows relaxations which were interpreted as SCM relaxations on the basis of the Mydosh parameter, α and the analysis of the relaxation times.54 In that work these parameters were determined by a different procedure and the temperature dependence of α was not investigated and therefore, these results cannot be compared here. However, in the light of the results of this work the question arises how this compound can be classified and what the real nature of its relaxations is. Consequently, these questions must be answered in future investigations.
Experimental section
Co(NCS)2 and 4-(4-chlorobenzyl)pyridine (ClBP) were obtained from Alfa Aesar. The solvents were used without further purification. The crystalline powders of all compounds were prepared by stirring the reactants in the respective solvents at room temperature. The purity of the compounds was checked by X-ray powder diffraction and elemental analysis.Synthesis of Co(NCS)2(4-(4-chlorobenzyl)pyridine)4 (1)
Single crystals suitable for single crystal X-ray diffraction were prepared using Co(NCS)2 (26.3 mg, 0.15 mmol) and 4-(4-chlorobenzyl)pyridine (105.4 μL, 0.60 mmol) in 1.5 mL acetonitrile. A crystalline powder was synthesized by stirring Co(NCS)2 (175.1 mg, 1.00 mmol) and 4-(4-chlorobenzyl)pyridine (702.3 μL, 4.00 mmol) in 5 mL acetonitrile for 6 d. Yield: 85% elemental analysis calcd (%) for C50H40Cl4CoN6S2: C 60.67, H 4.07, N 8.49; S 6.48; found C 59.33, H 4.24, N 8.31, S 6.89. IR (ATR): νmax = 3075 (w), 3039 (w), 2915 (w), 2064 (s), 2084 (s), 1615 (s), 1558 (m), 1488 (s), 1422 (s), 1348 (w), 1311 (w), 1222 (m), 1091 (m), 1048 (m), 1014 (s), 923 (w), 855 (s), 805 (s), 799 (s), 733 (m), 714 (m), 675 (w), 592 (s), 490 (s), 423 (m).Synthesis of [Co(NCS)2(4-(4-chlorobenzyl)pyridine)2]n (2)
Single crystals suitable for single crystal X-ray diffraction were prepared using Co(NCS)2 (52.5 mg, 0.30 mmol) and 4-(4-chlorobenzyl)pyridine (26.4 μL, 0.15 mmol) in 1.5 mL methanol. A crystalline powder was synthesized by stirring Co(NCS)2 (175.1 mg, 1.00 mmol) and 4-(4-chlorobenzyl)pyridine (93.8 μL, 0.50 mmol) in 5 mL water for 3 d. Yield: 77% elemental analysis calcd (%) for C26H20Cl2CoN4S2: C 53.62, H 3.46, N 9.62; S 11.01; found C 53.36, H 3.35, N 9.40, S 10.86. IR (ATR): νmax = 3086 (w), 3027 (w), 2905 (w), 2105 (s), 2084 (s), 1692 (w), 1612 (s), 1558 (m), 1488 (s), 1423 (s), 1274 (w), 1223 (m), 1094 (m), 1068 (m), 1014 (s), 919 (w), 852 (m), 805 (s), 787 (s), 733 (m), 656 (w), 597 (s), 503 (s), 489 (s), 423 (m).Elemental analysis
CHNS analysis was performed using an EURO EA elemental analyzer fabricated by EURO VECTOR Instruments.IR-spectroscopy
All IR data were obtained using an ATI Mattson Genesis Series FTIR Spectrometer, control software: WINFIRST, from ATI Mattson.Differential thermal analysis and thermogravimetry (DTA-TG)
The DTA-TG measurements were performed under a nitrogen atmosphere (purity: 5.0) in Al2O3 crucibles using a STA-409CD instrument from Netzsch. All measurements were performed with a flow rate of 75 mL min−1 and were corrected for buoyancy and current effects. The instrument was calibrated using standard reference materials.Scanning electron microscopy (SEM)
The SEM measurements were performed with a Philips Environmental Scanning Electron Microscope ESEM XL30, which is equipped with an EDAX detector.Magnetic measurements
Magnetic measurements were performed using a PPMS (Physical Property Measurement System) from Quantum Design. All AC data were obtained with the amplitude of the AC field equal to 5 Oe. The data were corrected for core diamagnetism.X-Ray powder diffraction (XRPD)
The measurements were performed using (1) a PANalytical X'Pert Pro MPD Reflection Powder Diffraction System with CuKα radiation (λ = 154.0598 pm) equipped with a PIXcel semiconductor detector from PANalytical and (2) a Stoe Transmission Powder Diffraction System (STADI P) with CuKα radiation (λ = 154.0598 pm) that was equipped with a linear position-sensitive detector from STOE & CIE.Single crystal structure analysis
The data collection was performed with imaging plate diffraction systems (STOE IPDS-1 (1) and STOE IPDS-2 (2)) using MoKα radiation. The structure solution was done with direct methods using SHELXS-97 and structure refinement was performed against F2 using SHELXL-97.68 For both compounds a numerical absorption correction was applied using X-red and X-shape of the Program Package X-area.69–71 All non-hydrogen atoms were refined with anisotropic displacement parameters. All hydrogen atoms were positioned with idealized geometry and were refined isotropically with Uiso(H) = −1.2Ueq(C) (1.5 for methyl H). Selected crystal data and details of the structure determinations are given in Table 2.CCDC 1401785 (1) and 1401784 (2) contain the supplementary crystallographic data for this paper.
Acknowledgements
This project was supported by the Deutsche Forschungs-gemeinschaft (Project No. Na 720/5-1) and the State of Schleswig-Holstein. We thank Prof. Dr Wolfgang Bensch for access to his experimental facilities. Z. T. thanks National Science Centre Poland for financial support granted under decision DEC-2013/11/B/ST3/03799.References
- W. L. Leong and J. J. Vittal, Chem. Rev., 2011, 111, 688–764 CrossRef CAS PubMed.
- H. Arora, F. Lloret and R. Mukherjee, Inorg. Chem., 2009, 48, 1158–1167 CrossRef CAS PubMed.
- L. Bogani, C. Sangregorio, R. Sessoli and D. Gatteschi, Angew. Chem., Int. Ed., 2005, 117, 5967–5971 CrossRef PubMed.
- S. W. Choi, H. Y. Kwak, J. H. Yoon, H. C. Kim, E. K. Koh and C. S. Hong, Inorg. Chem., 2008, 47, 10214–10216 CrossRef CAS PubMed.
- E. Shurdha, C. E. Moore, A. L. Rheingold, S. H. Lapidus, P. W. Stephens, A. M. Arif and J. S. Miller, Inorg. Chem., 2013, 52, 10583–10594 CrossRef CAS PubMed.
- X. Shen, Q. Zhang, H. Zhou, H. Zhou and A. Yuan, New J. Chem., 2012, 36, 1180–1186 RSC.
- P. P. Chakrabarty, S. Saha, D. Schollmeyer, A. K. Boudalis, A. D. Jana and D. Luneau, J. Coord. Chem., 2012, 66, 9–17 CrossRef PubMed.
- C. Näther, S. Wöhlert, J. Boeckmann, M. Wriedt and I. Jeß, Z. Anorg. Allg. Chem., 2013, 639, 2696–2714 CrossRef PubMed.
- M. Bałanda, Z. Tomkowicz, W. Haase and M. Rams, J. Phys.: Conf. Ser., 2010, 303, 012036 CrossRef.
- A. Caneschi, D. Gatteschi, N. Lalioti, C. Sangregorio, R. Sessoli, G. Venturi, A. Vindigni, A. Rettori, M. G. Pini and M. A. Novak, Angew. Chem., Int. Ed., 2001, 113, 1810–1813 CrossRef.
- E. Pardo, R. Ruiz-García, F. Lloret, J. Faus, M. Julve, Y. Journaux, M. Novak, F. Delgado and C. Ruiz-Pérez, Chem. – Eur. J., 2007, 13, 2054–2066 CrossRef CAS PubMed.
- H.-L. Sun, Z.-M. Wang and S. Gao, Coord. Chem. Rev., 2010, 254, 1081–1100 CrossRef CAS PubMed.
- L. Bogani, A. Vindigni, R. Sessoli and D. Gatteschi, J. Mater. Chem., 2008, 18, 4733–4880 RSC.
- W.-X. Zhang, R. Ishikawa, B. Breedlovea and M. Yamashita, RSC Adv., 2013, 3, 3772–3798 RSC.
- J. Ru, F. Gao, T. Wu, M.-X. Yao, Y.-Z. Li and J.-L. Zuo, Dalton Trans., 2014, 43, 933–936 RSC.
- E. V. Peresypkina, A. M. Majcher, M. Rams and K. E. Vostrikova, Chem. Commun., 2014, 50, 7150–7153 RSC.
- H. Miyasaka and R. Clérac, Bull. Chem. Soc. Jpn., 2005, 78, 1725–1748 CrossRef CAS.
- A. V. Palii, O. S. Reu, S. M. Ostrovsky, S. I. Klokishner, B. S. Tsukerblat, Z.-M. Sun, J.-G. Mao, A. V. Prosvirin, H.-H. Zhao and K. R. Dunbar, J. Am. Chem. Soc., 2008, 130, 14729–14738 CrossRef CAS PubMed.
- M. Bałanda, M. Rams, S. K. Nayak, Z. Tomkowicz, W. Haase, K. Tomala and J. V. Yakhmi, Phys. Rev. B: Condens. Matter, 2006, 74, 224421 CrossRef.
- Z. Tomkowicz, M. Rams, M. Bałanda, S. Foro, H. Nojiri, Y. Krupskaya, V. Kataev, B. Büchner, S. K. Nayak, J. V. Yakhmi and W. Haase, Inorg. Chem., 2012, 51, 9983–9994 CrossRef CAS PubMed.
- S.-Y. Zhang, W. Shi, Y. Lan, N. Xu, X.-Q. Zhao, A. K. Powell, B. Zhao, P. Cheng, D.-Z. Liao and S.-P. Yan, Chem. Commun., 2011, 47, 2859–2861 RSC.
- X. Feng, T. David Harris and J. R. Long, Chem. Sci., 2011, 2, 1688–1694 RSC.
- R. Liu, L. Li, X. Wang, P. Yang, C. Wang, D. Liao and J.-P. Sutter, Chem. Commun., 2010, 46, 2566–2568 RSC.
- V. Mougel, L. Chatelain, J. Hermle, R. Caciuffo, E. Colineau, F. Tuna, N. Magnani, A. de Geyer, J. Pécaut and M. Mazzanti, Angew. Chem., Int. Ed., 2014, 126, 838–842 CrossRef PubMed.
- Y.-L. Hou, R.-R. Cheng, G. Xiong, J.-Z. Cui and B. Zhao, Dalton Trans., 2014, 43, 1814–1820 RSC.
- H. Miyasaka, T. Madanbashi, A. Saitoh, N. Motokawa, R. Ishikawa, M. Yamashita, S. Bahr, W. Wernsdorfer and R. Clérac, Chem. – Eur. J., 2012, 18, 3942–3954 CrossRef CAS PubMed.
- C. Coulon, H. Miyasaka and R. Clérac, Struct. Bonding, 2006, 122, 163–206 CrossRef CAS.
- J. H. Yoon, J. W. Lee, D. W. Ryu, S. W. Yoon, B. J. Suh, H. C. Kim and C. S. Hong, Chem. – Eur. J., 2011, 17, 3028–3034 CrossRef CAS PubMed.
- J. H. Yoon, W. R. Lee, D. W. Ryu, J. W. Lee, S. W. Yoon, B. J. Suh, H. C. Kim and C. S. Hong, Inorg. Chem., 2011, 50, 10777–10785 CrossRef CAS PubMed.
- X.-B. Li, G.-M. Zhuang, X. Wang, K. Wang and E.-Q. Gao, Chem. Commun., 2013, 49, 1814–1816 RSC.
- A. Escuer, G. Vlahopoulou and F. A. Mautner, Inorg. Chem., 2011, 50, 2717–2719 CrossRef CAS PubMed.
- F. A. Mautner, M. Scherzer, C. Berger, R. C. Fischer, R. Vicente and S. S. Massoud, Polyhedron, 2015, 85, 20–26 CrossRef CAS PubMed.
- B. Machura, A. Świtlicka, P. Zwoliński, J. Mroziński, B. Kalińska and R. Kruszynski, J. Solid State Chem., 2013, 197, 218–227 CrossRef CAS PubMed.
- B. Machura, A. Świtlicka, J. Mroziński, B. Kalińska and R. Kruszynski, Polyhedron, 2013, 52, 1276–1286 CrossRef CAS PubMed.
- J. G. Małecki, T. Groń and H. Duda, Polyhedron, 2012, 36, 56–68 CrossRef PubMed.
- Q. Ma, M. Zhu, L. Lu, S. Feng and J. Yan, Inorg. Chim. Acta, 2011, 370, 102–107 CrossRef CAS PubMed.
- M. Wriedt and C. Näther, Chem. Commun., 2010, 46, 4707–4709 RSC.
- J. Boeckmann and C. Näther, Polyhedron, 2012, 31, 587–595 CrossRef CAS PubMed.
- S. Wöhlert, J. Boeckmann, M. Wriedt and C. Näther, Angew. Chem., Int. Ed., 2011, 50, 6920–6923 CrossRef PubMed.
- P. Bhowmik, S. Chattopadhyay, M. G. B. Drew, C. Diaz and A. Ghosh, Polyhedron, 2010, 29, 2637–2642 CrossRef CAS PubMed.
- S. Wöhlert, U. Ruschewitz and C. Näther, Cryst. Growth Des., 2012, 12, 2715–2718 Search PubMed.
- S. Wöhlert, J. Boeckmann, I. Jess and C. Näther, CrystEngComm, 2012, 14, 5412–5420 RSC.
- S. Wöhlert, L. Peters and C. Näther, Dalton Trans., 2013, 42, 10746–10758 RSC.
- C. J. Adams, M. F. Haddow, D. J. Harding, T. J. Podesta and R. E. Waddington, CrystEngComm, 2011, 13, 4909–4914 RSC.
- A. Barasiński, P. Sobczak, A. Drzewiński, G. Kamieniarz, A. Bieńko, J. Mroziński and D. Gatteschi, Polyhedron, 2010, 29, 1485–1491 CrossRef PubMed.
- S. Wöhlert, T. Runčevski, R. E. Dinnebier, S. G. Ebbinghaus and C. Näther, Cryst. Growth Des., 2014, 14, 1902–1913 Search PubMed.
- S. Wöhlert, M. Wriedt, T. Fic, Z. Tomkowicz, W. Haase and C. Näther, Inorg. Chem., 2013, 52, 1061–1068 CrossRef PubMed.
- J. G. Małecki and P. Zwoliński, Polyhedron, 2012, 39, 85–90 CrossRef PubMed.
- J.-F. Létard, S. Asthana, H. J. Shepherd, P. Guionneau, A. E. Goeta, N. Suemura, R. Ishikawa and S. Kaizaki, Chem. – Eur. J., 2012, 18, 5924–5934 CrossRef PubMed.
- S. Das, K. Bhar, S. Chattopadhyay, P. Mitra, V. J. Smith, L. J. Barbour and B. K. Ghosh, Polyhedron, 2012, 38, 26–35 CrossRef CAS PubMed.
- J. G. Małecki, B. Machura, A. Świtlicka, T. Groń and M. Bałanda, Polyhedron, 2011, 30, 746–753 CrossRef PubMed.
- J. Palion-Gazda, B. Machura, F. Lloret and M. Julve, Cryst. Growth Des., 2015, 15, 2380–2388 CAS.
- R. González, A. Acosta, R. Chiozzone, C. Kremer, D. Armentano, G. De Munno, M. Julve, F. Lloret and J. Faus, Inorg. Chem., 2012, 51, 5737–5747 CrossRef PubMed.
- J. Boeckmann and C. Näther, Dalton Trans., 2010, 39, 11019–11026 RSC.
- J. Boeckmann and C. Näther, Chem. Commun., 2011, 47, 7104–7106 RSC.
- S. Foner, R. B. Frankel, W. M. Reiff, B. F. Little and G. J. Long, Solid State Commun., 1975, 16, 159–161 CrossRef CAS.
- S. Foner, R. B. Frankel, W. M. Reiff, H. Wong and G. J. Long, J. Chem. Phys., 1978, 68, 4781–4783 CrossRef CAS PubMed.
- J. Boeckmann, M. Wriedt and C. Näther, Chem. – Eur. J., 2012, 18, 5284–5289 CrossRef CAS PubMed.
- M. R. Julia Werner, Z. Tomkowicz, T. Runčevski, R. E. Dinnebier, S. Suckert and C. Näther, Inorg. Chem., 2015, 54, 2893 CrossRef PubMed.
- S. Wöhlert, T. Fic, Z. Tomkowicz, S. G. Ebbinghaus, M. Rams, W. Haase and C. Näther, Inorg. Chem., 2013, 52, 12947–12957 CrossRef PubMed.
- S. Wöhlert, Z. Tomkowicz, M. Rams, S. G. Ebbinghaus, L. Fink, M. U. Schmidt and C. Näther, Inorg. Chem., 2014, 53, 8298–8310 CrossRef PubMed.
- J. Werner, M. Rams, Z. Tomkowicz and C. Nather, Dalton Trans., 2014, 43, 17333–17342 RSC.
- M. E. Fisher, J. Math. Phys., 1963, 4, 124–135 CrossRef PubMed.
- R. L. Carlin and A. J. van Duyneveldt, Acc. Chem. Res., 1980, 13, 231–236 CrossRef CAS.
- R. Hoogerbeets, S. A. J. Wiegers, A. J. van Duyneveldt, R. D. Willett and U. Geiser, Physica B, 1984, 125, 135–149 CrossRef CAS.
- C. Coulon, R. Clérac, W. Wernsdorfer, T. Colin and H. Miyasaka, Phys. Rev. Lett., 2009, 102, 164204–164207 CrossRef.
- H. Miyasaka, K. Takayama, A. Saitoh, S. Furukawa, M. Yamashita and R. Clérac, Chem. – Eur. J., 2010, 16, 3656–3662 CrossRef CAS PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- X-Area, Version 1.44, Program Package for Single Crystal Measurements, STOE & CIE GmbH, Darmstadt, Germany, 2008 Search PubMed.
- X-Red, Version 1.11, Program for Data Reduction and Absorption Correction, STOE & CIE GmbH, Darmstadt, Germany, 1998 Search PubMed.
- X-Shape, Version 1.03, Program for the Crystal Optimization for Numerical Absorption Correction, STOE & CIE GmbH, Darmstadt, Germany, 1998 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: X-Ray powder pattern and IR-spectra of compounds 1 and 2. DTA, DTG and TG curves for compounds 1 and 2. Additional magnetic measurements for compound 2. CCDC 1401784 and 1401785. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5dt01898f |
| This journal is © The Royal Society of Chemistry 2015 |