Photochemical upconversion: present status and prospects for its application to solar energy conversion
Tim F.
Schulze
a and
Timothy W.
Schmidt
*b
aHelmholtz-Zentrum Berlin für Materialien und Energie GmbH, Institute Silicon Photovoltaics, Kekuléstr. 5, D-12489 Berlin, Germany
bSchool of Chemistry, UNSW, Sydney, NSW 2052, Australia. E-mail: timothy.schmidt@unsw.edu.au
First published on 18th November 2014
Abstract
All photovoltaic solar cells transmit photons with energies below the absorption threshold (bandgap) of the absorber material, which are therefore usually lost for the purpose of solar energy conversion. Upconversion (UC) devices can harvest this unused sub-threshold light behind the solar cell, and create one higher energy photon out of (at least) two transmitted photons. This higher energy photon is radiated back towards the solar cell, thus expanding the utilization of the solar spectrum. Key requirements for UC units are a broad absorption and high UC quantum yield under low-intensity incoherent illumination, as relevant to solar energy conversion devices, as well as long term photostability. Upconversion by triplet–triplet annihilation (TTA) in organic chromophores has proven to fulfil the first two basic requirements, and first proof-of-concept applications in photovoltaic conversion as well as photo(electro)chemical energy storage have been demonstrated. Here we review the basic concept of TTA-UC and its application in the field of solar energy harvesting, and assess the challenges and prospects for its large-scale application, including the long term photostability of TTA upconversion materials.
Broader contextWhile solar energy is abundant and free, efficiently harvesting solar energy in cheaply manufactured devices remains a challenge. All photovoltaic energy conversion devices forgo a portion of the solar spectrum with photon energies below the bandgap. This is especially so for high bandgap materials such as amorphous silicon, polythiophenes and lead halide perovskites. Photochemical upconversion achieved by triplet–triplet annihilation (TTA-UC) in organic molecules is a spectrally versatile approach to harvesting this unused light and converting it into wavelengths useful to the device in question. TTA-UC has been applied to several thin film devices to date, including a-Si:H, OPV and DSC devices. The improvements to short circuit current are still in the few microamps range under one sun pumping. This needs to be increased by orders of magnitude. Here we present a review of the state-of-the-art of applications of TTA-UC to solar energy harvesting. We further outline several strategies by which improvements to TTA-UC might be brought about. An organic upconvertor placed under (filtered) sunlight must also withstand years of sunlight without suffering degradation. We present data to suggest that existing devices should last hundreds of days if effectively encapsulated. |
1 Introduction
Photovoltaic solar energy conversion devices waste a major part of the incident energy, due to the requirement of a gap in the continuum of electronic states in the light-harvesting material, acting as an absorption threshold. For photon energies higher than this bandgap, the excess energy is converted into heat by thermalization of excited charge carriers, while light with sub-bandgap energies cannot be harvested at all. These effects dominate the fundamental losses of single-threshold photovoltaic (PV) devices, and restrain their conversion efficiency to 34% under the AM1.5G spectrum, or about 30% under a model 6000 K spectrum1–3 (Fig. 1).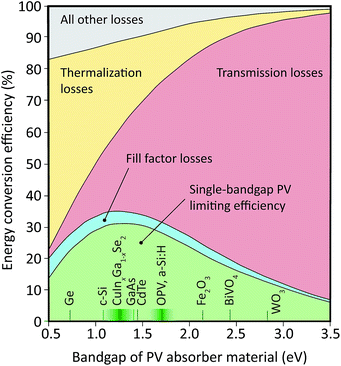 | ||
| Fig. 1 Relative importance of fundamental loss mechanisms in solar energy conversion as a function of the PV absorber bandgap, and examples of absorber materials. Figure inspired by Hirst et al.,7 plotted for a 6000 K spectrum. | ||
While power conversion losses in low-bandgap materials such as germanium or crystalline silicon (c-Si) are dominated by thermalization, transmission of sub-bandgap light is dominant for bandgaps of greater than 1.3 eV, that is, for most thin-film photovoltaic absorber materials and for all known oxide-based electrode materials of interest to photoelectrochemical energy storage.4,5 Even solar cells made from c-Si sacrifice a considerable part of the solar spectrum by transmission.
Sub-bandgap losses can be remedied by the application of photonic upconversion, whereby transmitted light is converted to light of higher energy, which can then be harvested by the cell and contribute to current generation. Based on detailed balance considerations it has been shown that upconversion can boost the maximum energy conversion efficiency to about 43% under one sun for a solar cell with a bandgap of 1.76 eV, and >50% under solar concentration.6 Crystalline silicon cells could still reach about 38%, although the potential gain is smaller than for the high-bandgap devices.
In recent years, upconversion has been an active area in the field of so-called ‘third-generation photovoltaics’ which comprises all thin-film device concepts that are, in principle, capable of circumventing the detailed balance efficiency limit (Shockley–Queisser limit1) for a single-threshold PV device.8,9 Research has focused mainly on two different and essentially complementary approaches:6,10 firstly, the application of lanthanoid cations (mostly erbium and ytterbium) in a solid-state matrix,11 making use of their discrete and long-lived atomic states that can facilitate absorption of multiple photons, followed by upconverted luminescence. The rare-earth materials absorb in the infrared region of the solar spectrum and lanthanoid upconversion (L-UC) is thus most interesting for application to c-Si solar cells.12–14
The second active field of research is the exploitation of triplet–triplet-annihilation in organic chromophores to achieve upconversion (TTA-UC).15–17 TTA-UC exploits the longevity of molecular triplet states. However, as the longevity diminishes with energy, TTA-UC is most readily applied to solar cells with bandgaps above about 1.5 eV. This review is devoted to summarizing the state-of-the-art in TTA-UC and its application to solar energy conversion.
2 Triplet–triplet annihilation upconversion: potential and limits
2.1 Description of TTA-UC systems
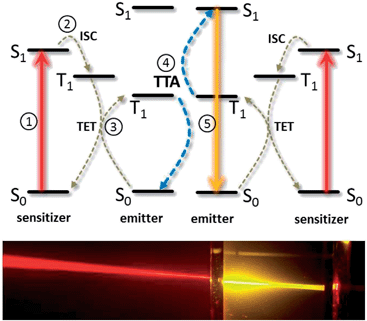
TTA-UC exploits the strong oscillator strength of singlet–singlet transitions to absorb and emit the light, while intermediate energy storage (necessary in incoherent UC processes as the energy of two photons, incident at different times, is merged) is facilitated by long-lived T1 triplet states. This represents an inherent advantage as compared to upconverting lanthanoid-based phosphors, which use the same electronic manifold to absorb, store and re-emit the photon energy, leading to low absorptivity and inherent competition of non-radiative losses with the UC process. Consequently, high upconversion yields, where >30% of absorbed photons give rise to emitted photons, have been measured for TTA-UC.17,20
TTA-upconversion is an incoherent process, and the intrinsic intermediate energy storage in the triplet states allows for its efficient operation under low-light conditions. There are examples of lanthanoid upconversion proceeding efficiently under broadband, pulsed supercontinuum radiation,21,22 but several studies have shown TTA-upconversion under broad-band white-light illumination,23,24 with some demonstrations even employing sunlight itself as the excitation source.25,26
(i) A sensitizer species with
• A strong absorption in the desired region (peaking at several Å2 absorption cross-section),
• A high intersystem crossing yield, usually obtained by incorporating a heavy metal atom (ΦISC ∼ 1 is desirable),
• A long triplet lifetime (>10 μs), and
• Ideally a small singlet–triplet gap (few kBT) so as to minimize energy sacrifice in the process of intersystem crossing.
(ii) An emitter species with
• A long triplet lifetime (>100 μs),
• A singlet state at just below double the energy of the first triplet, to make TTA energetically favourable, and
• A high fluorescence quantum yield (ΦF ∼ 1 is desirable).
Additionally, it is beneficial if the second excited triplet state of the emitter cannot be accessed by combining the energy of two sensitizer triplet states, as this would open a loss channel (see Section 2.2).27
Commonly employed molecular species for TTA-UC systems are metallated porphyrins as sensitizers while polycyclic aromatic hydrocarbons (PAHs, for example rubrene, anthracene, perylene etc.) are the most commonly used emitters. However, efficient TTA-UC is not restricted to these classes of molecules, as others can also satisfy the above-mentioned conditions: transition metal complexes such as Ir(ppy)3 (ref. 28) or Ru(dmb)3 (ref. 29) also facilitate efficient ISC by incorporating a heavy atom and can act as triplet sensitizers. Boron-dipyrromethene derivatives (so-called BODIPY dyes)30 were found to function as rare-metal-free triplet sensitizers at reasonable efficiency, and can also be combined with Ir complexes31 to increase their absorption strength. Regarding emitter species, most studies have focussed on PAHs, with BODIPY- and conjugated polymer-based emitters being notable exceptions.16,32 Comprehensive review articles regarding the plethora of molecular species employed in TTA systems include the works of Singh-Rachford et al.16 and Zhao et al.17
The large variety of molecules that satisfy the conditions outlined above allows for tailored spectral tuning of the absorption and emission wavelengths exhibited by the TTA system. So far, obtainable excitation wavelengths range from the blue (440 nm)33 across the visible16 and down into the near infrared (NIR) out to >800 nm,34,35 while emission wavelengths of the upconverted light range from the deep red (720 nm) as far up as the near ultraviolet (NUV) at about 360 nm.33,34 The obtained upconversion margins (that is, the energetic difference between peak absorbed and emitted light) range from 0.3 eV (ref. 36) to 1 eV,37 with typical values being around 0.5 eV.
2.2 Dynamics and efficiency of homogeneous solution-based TTA systems
The simplest realization of a TTA-UC system is obtained by the dissolution of the active molecules in a suitable solvent. Most of the fundamental studies on TTA dynamics, as well as the first device applications of TTA-UC, were based on this architecture. Commonly employed solvents are toluene, benzene, chloroform, acetonitrile, dimethylformamide or 1,1,2-trichloroethane, among others.In order to assess the efficiency of the TTA-UC process, two aspects have been considered in detail: firstly, the sensitivity of the desired energetic pathways, sketched in Fig. 2, to unwanted relaxation/back-reaction processes such as the non-radiative loss of triplet excitons, phosphorescence and reverse intersystem crossing, and secondly, the details of the spin physics underlying the actual triplet–triplet annihilation process between two excited emitter molecules. Both aspects will be discussed in the following.
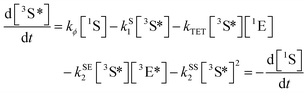 | (1) |
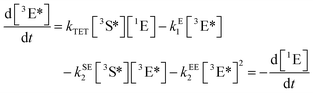 | (2) |
Some of the processes depicted in Fig. 2 are not explicitly accounted for in the rate equations, such as the photo-excitation to the sensitizer singlet S1 and the intersystem crossing to T1, which are assumed to have unit efficiency and be relatively instantaneous. Indeed, intersystem crossing (ISC) in the PQ4Pd sensitizer used in much of our work proceeds with a time constant of approximately 10 ps. The prepared singlet state would otherwise radiate with a lifetime of some nanoseconds, and as such it can be seen that the ISC yield is near unity.
Typical values for the rate constants are listed in Table 1, assuming a slowly diffusing sensitizer and a rapidly diffusing emitter such as those studied by Castellano and co-workers.38,43
| Quantity | Value | Unit | Reference |
|---|---|---|---|
| a In the case of a slowly diffusing sensitizer, the hetero-TTA rate will be approximately half that of the emitter homo-TTA rate, and similar to the triplet energy transfer rate. | |||
| k ϕ | 4 | s−1 | [39] |
| k S1 | 2.5 × 104 | s−1 | [39] |
| k E1 | 1 × 104 | s−1 | [39] |
| k TET | 1 × 109 | M−1 s−1 | |
| k SE2 | 1 × 109 | M−1 s−1 | |
| k SS2 | 1 × 108 | M−1 s−1 | [39] |
| k EE2 | 2 × 109 | M−1 s−1 | [38 and 43] |
| 3E* + 3E* ⇄ 1|E⋯E|* → 1E + 1E* | (3) |
| 3E* + 3E* ⇄ 3|E⋯E|* → 1E + 3E** | (4) |
| 3E* + 3E* ⇄ 5|E⋯E|* → 1E + 5E* | (5) |
Due to the degeneracies of the spin states, the complex formation probabilities are statistically weighted with regard to their multiplicity. That is, in the ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, respectively. Only the singlet complex (1 in 9) can dissociate to the emitter S1 state (1E*) and thus yield the desired upconverted fluorescence (pathway from eqn (3)).
5, respectively. Only the singlet complex (1 in 9) can dissociate to the emitter S1 state (1E*) and thus yield the desired upconverted fluorescence (pathway from eqn (3)).
For a time it was unclear whether these spin statistics fundamentally limited the efficiency of the TTA-UC process and thereby constrained its applicability to solar cells. Some studies claimed a fundamental limit of 11% emitter S1 yield based on this statistical argument, which would correspond to a maximum 5.5% quantum yield of the upconversion process, disregarding any other losses.36 However, it had already been observed in organic light emitting diodes that triplet–triplet annihilation could bring about excited singlet states with an efficiency exceeding the statistical limit,44 and this simple argument has been dismissed based on energetic considerations:27,32,44,45 the emitter quintet state Q1 always lies above the lowest excited singlet state (S1) and above the lowest excited triplet state (T1), and, for the vast majority of candidate emitter molecules, Q1 is energetically inaccessible by combining their T1 states.46 This means that the quintet channel (eqn (5)) is never open, and a quintet encounter complex must dissociate back to the two initial emitter triplets without loss of stored energy.
The question, then, becomes whether or not the triplet channel is open (eqn (4)). If it is, then the respective TTA process will create an emitter in its second excited triplet (3E**), which will rapidly internally convert to the first excited triplet state (3E*) following Kasha's rule. Therefore, this process would recover one of the initial triplets, meaning that five emitter triplets would be quenched for every emitted photon (taking into account the spin statistical ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 between the singlet and triplet channels), corresponding to a quantum yield of 20%. The fact that several studies have observed quantum yields exceeding this number shows that there must be systems in which 3E** is inaccessible. Currently, the highest reported TTA quantum yields are above 30% in solution,27 effectively ruling out full participation of the triplet channel.
3 between the singlet and triplet channels), corresponding to a quantum yield of 20%. The fact that several studies have observed quantum yields exceeding this number shows that there must be systems in which 3E** is inaccessible. Currently, the highest reported TTA quantum yields are above 30% in solution,27 effectively ruling out full participation of the triplet channel.
The rate at which photons are generated in the TTA-UC process, per unit volume irradiated, is at most 0.5 × kEE2[3E*]2, where it is assumed that each two triplets lost will yield a photon, that is, that both the triplet and quintet channels are closed. We introduced the factor ηconv to express the probability that the loss of a pair of triplets yields a photon by the bimolecular process. In rubrene, this was found to be about ηconv = 0.6.27 For an operational triplet channel, we expect that one excited singlet is produced for each five triplets lost giving ηconv of 0.4 (five triplets is 2.5 pairs). Finally, we need to consider that the excited singlet state may not decay radiatively, and so the fluorescence quantum yield, ΦF, should be considered. As such, we arrive at the expression for the rate of photon output by TTA-UC per unit volume irradiated, WTTA = 0.5 × ηconvΦFkEE2[3E*]2.
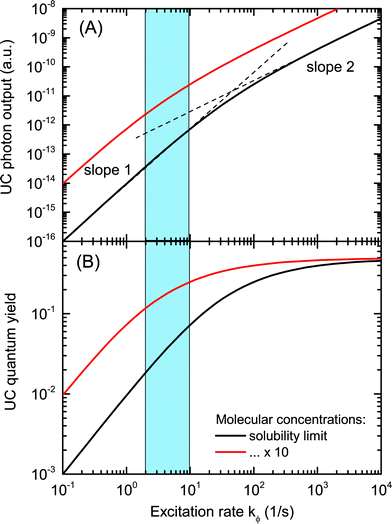
The model reproduces the prototypical intensity behaviour of TTA systems under variation of the illumination, seen in many experiments:40,41 a quadratic increase of the photon output for low illumination density, saturating into a linear regime for high illumination conditions. The quantum yield linearly increases for small kϕ, and begins to saturate in the transition region between the quadratic and linear photon output regimes. The transition from quadratic to linear behaviour has been characterized by Monguzzi and co-workers as the threshold intensity, Ith.40 This behaviour correlates with that observed for rare-earth upconversion, where the efficiency increases linearly in the low-pump regime and rolls over to sub-linear and saturates under high pumping conditions.48
In the present case, no spin-physical limitations and no further hindrances to the operation of the system have been assumed (ηconv = ΦTTA = 1), therefore the quantum yield saturates at the physical maximum of 50%. It is easy to see that for operation under sunlight illumination, the given TTA system is inefficient. The quantum yield for kϕ = 4 s−1, which was measured for PQ4Pd, is around 3–4%, even in the solubility limit of PQ4Pd and rubrene in toluene (black curve).
In order to increase the quantum yield to application-relevant levels, the model suggests two strategies: increasing the concentration of active species, and/or increasing the illumination density. If it were possible to increase [E] and [S] by a factor of 10 at constant rates (red curve), the quantum yield increases significantly to around 20%. To this end, overcoming the solubility limit is the prime goal, which is currently being pursued mainly by solid-state approaches to TTA materials. These are to be discussed in the next section. Other approaches aiming at increasing molecular concentrations as well as ideas to (locally) increase the excitation rate will be covered in Section 4.
2.3 Towards solid-state TTA
So far, the most widely followed approach to creating solid-state TTA-UC materials is the blending of the active species into a photophysically inert polymeric host matrix, which serves as a mechanical support for the chromophores. It has been determined that a crucial requirement for the matrix material is a low glass-transition temperature as the bimolecular interactions leading to the TET and TTA events require some residual diffusivity.49 Consequently, most of the reported systems are based on soft ‘rubbery’ polymers. Up to now, TTA-UC has been demonstrated in several host matrices including, but not limited to, cellulose acetate,50 polystyrene,51 a copolymer of ethyleneoxide and epichlorohydrin,49,52 polyurethane,53,54 or poly-butylacrylate.55 It was further shown that upconverting nanoparticles can be formed using the blending approach with different polymeric host media, including polystyrene56 or poly-butylacrylate.57 Concerning the attainable efficiency of such blended solid-state systems, aggregation or even phase-segregation of the dye species, at concentrations above a few percent, has been found to be a serious issue which has so-far prevented the realization of higher UC quantum yields as compared to the liquid systems.58A strategy that might help to overcome part of this problem is the use of a polymer host which, at the same time, acts as the TTA emitter species, and is doped with only one triplet sensitizing species. Several groups have investigated these materials, including porphyrin-doped polyfluorene,59 porphyrin-doped poly-pentaphenylene60 and porphyrin-doped super-yellow.32 Again, in most cases the aggregation of the porphyrin triplet sensitizers appeared to be a major problem.
To summarize the state-of-the-art in solid-state TTA-UC it can be said that although fairly efficient TTA-UC has been demonstrated in the solid phase by the blending approach (up to 17% quantum yield55), this strategy will most likely not allow much higher quantum yields than the liquid approach without a precise and tailored control over the microscopic arrangement of the active species in order to prevent aggregation and phase separation. The reader is referred to the review article of Simon and Weder, who discuss the pending issues in great detail.58 Strategies that might allow such control will be discussed below in Section 4.2.3.
3 Application of TTA in solar energy conversion
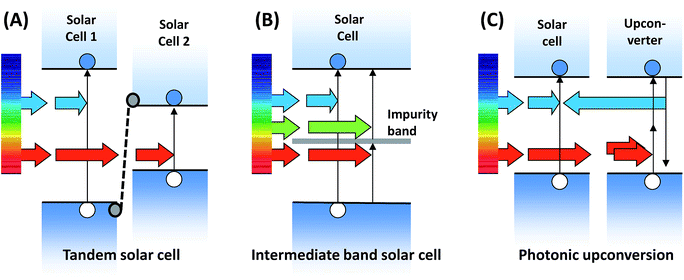
3.1 Approaches for harvesting sub-bandgap light
Since the early beginnings of photovoltaic energy conversion research it has been clear that sub-bandgap transmission is among the two most severe fundamental efficiency losses.1 Thus, the challenge of harvesting sub-bandgap light has stood for decades. Several approaches, aimed at circumventing these losses, have been proposed and, in part, realized in devices. These are depicted in Fig. 4.Irrespective of the undoubtedly higher conversion efficiencies with respect to single-junction PV – culminating in the impressive 44.7% record – the vast majority of the multijunction cells struggle on the global PV market. One of the major drawbacks is the rather complex manufacturing, which requires series-connection of complete solar cells, each of which is a multilayer structure itself. Also, the series connection requires matching of the photocurrents delivered by the sub-cells, which puts additional constraints on device design and leads to less robust operation, as the solar altitude as well as atmospheric and environmental parameters impact the relative performance of the sub-cells. That said, these cells can operate under hundreds of suns and as such can tolerate manufacturing costs hundreds of times higher providing the concentrator system can be built for negligible cost.
Very recent research activities have focused on quantum dot arrays71 and highly mismatched alloys72 as potential realizations of multi-band IBSCs, with promising initial results. However, in order to design an economically competitive IBSC, the main drawback remains the necessity to electronically re-engineer the absorber material while at the same time preserving the excellent bulk electronic quality which has become state-of-the-art in PV technology.
The most studied incoherent upconversion processes besides triplet–triplet annihilation (TTA) are energy transfer upconversion (ETU, also known as ‘addition of photons by transfer of energy’, APTE) and excited state absorption (ESA), which are observed for several classes of ions in solid-state matrices and were first reported by Auzel in 1966.73 Concerning ETU and ESA, the required long lifetimes of the respective excited states and a ladder-like arrangement of the energy levels with similar spacings are realized for certain ions of the d and f elements. Transition-metal ions with open 3d, 4d or 5d shells have been reported to show upconversion in different host materials. The highest upconversion efficiencies realized to date for inorganic materials have been observed for solid matrices doped with lanthanoid ions, such as Gd3+, Dy3+, Er3+, Yb3+ or Tm3+. One of the most efficient UC phosphors to date is NaYF4, doped with Er3+ or co-doped with Yb3+ and Er3+, which was introduced in 1972 by Menyuk et al.74 Comprehensive reviews of ETU by f-shell ions in solid bulk matrices and nanoparticles include the works by Auzel11 and Haase et al.75
The first realization of an upconversion-assisted solar cell was based on Yb3+ and Er3+ ions in a vitroceramic host, placed behind a GaAs solar cell.76 The first application of the same system to c-Si solar cells was demonstrated in 2005 by Shalav et al.,13,77 and current lanthanoid-based upconversion efforts are mainly focused around crystalline silicon,14,78–80 due to the energetically favorable absorption of Er3+ around 1523 nm, below the c-Si band edge in energy and within a local maximum of the solar spectral irradiance.12 Currently, the most efficient lanthanoid upconversion phosphor for c-Si PV applications appears to be β-NaYF4:20–25%Er3+ powder.14,81,82 However, a very recent record result was obtained with mono-crystalline BaY2F8:30%Er3+, which indicates that there is still potential for further efficiency increase of lanthanoid-UC aiming at c-Si solar cells.83
Furthermore, also other types of solar cells have been assisted by lanthanoid-based upconversion: De Wild et al. have applied the Yb/Er system to amorphous silicon solar cells, in the form of a NaYF4:(18%Yb3+,2%Er3+) phosphor,84,85 as well as in a more recent study employing a Gd2O2S:(10%Yb3+,5%Er3+) phosphor.86 Liu et al. have employed an yttrium–aluminium garnet (YAG) transparent ceramic co-doped with 3.0%Yb3+ and 0.5%Er3+ behind a dye-sensitized solar cell (DSSC),87 while Shan et al. integrated Er3+ and Yb3+ co-doped into LaF3 in a nanocomposite with TiO2 to serve as upconversion layer in DSSCs.88 Other examples of lanthanoid-based upconversion applied to DSSCs include the employment of fluorescence resonance energy transfer from upconversion centres,89 the use of colloidal upconversion nanocrystals as an energy relay,90 and direct electron injection from up-conversion nanoparticles to the TiO2 photoanode.91 For a useful review on upconversion nanophosphors for solar cell applications, see the recent review of Ramasamy et al.92
In 2012, our group demonstrated the first solar cell assisted by triplet–triplet annihilation upconversion, using the example of an amorphous silicon thin-film solar cell.47,93,94 The approach was successively applied to organic solar cells95 as well as dye-sensitized solar cells.96 Details about these results and a comparison to the lanthanoid upconversion system are given below.
3.2 Limiting efficiency for UC-enhanced solar cells
There is general agreement that, regarding the maximum possible efficiency from an idealized thermodynamic perspective, upconversion-assisted solar cells are on par with tandem and intermediate band solar cells. Trupke et al. have calculated 47.6% maximum conversion efficiency for an upconversion-assisted solar cell under non-concentrated sunlight,9 using a detailed balance calculation based on equivalent circuits and assuming 6000 K blackbody radiation. Importantly, they considered an unconstrained model allowing for two different low-energy absorption thresholds, that is, the upconvertor was modeled equivalently to two low-bandgap bottom cells connected in series which drive an LED illuminating the high-bandgap top cell. Tayebjee and Schmidt calculated a maximum efficiency of 48.2% for the same system using the actual AM1.5G solar spectrum as illumination source.6,97Both ETU by lanthanoid ions and TTA-UC are based on the interaction of identical excited states – either within the 4f manifold of the lanthanoid ions or of the first excited triplet state of the TTA emitter species – which restricts the detailed balance model to a symmetrical case. Tayebjee and Schmidt have calculated a limiting efficiency of 43.3% for this case, with an optimum solar cell absorption threshold of 1.76 eV and an upconvertor absorption threshold of 1.11 eV.6,97
For comparison, within the same modeling approach, tandem solar cells, symmetric IBSCs and asymmetric IBSCs were found to have limiting efficiencies of 45.7%, 45.9% and 51.9% respectively. It has been determined that the luminescent coupling to the ‘top cell’ PV device brought about by the UC approach is slightly inferior to the direct electrical coupling manifested in tandems or IBSCs, due to an additional free energy sacrifice by the re-emission process. Indeed, Schmidt and Ekins-Daukes proposed that direct injection by emitters acting as dyes in DSSCs would in effect be a symmetric IBSC – a molecular intermediate band solar cell.98 On the other hand, and unlike for tandems and IBSCs, a radiatively coupled upconvertor does not interfere with the electronic structure of the absorber and the electrical layout of the solar cell, which makes it much easier to implement into current PV technology.
Recently, modeling work has been undertaken in order to assess the limiting efficiency of solar cell/UC couples under more realistic boundary conditions. Johnson and Conibeer have analyzed non-ideal c-Si solar cells coupled to ideal UC units, and their results are quite specific to crystalline silicon PV.99 Atre and Dionne have attempted to formulate a model for upconversion-assisted solar cells incorporating non-idealities such as recombination in solar cell and upconvertor, non-radiative relaxation within the upconvertor, narrow absorption bands of the UC materials as well as non-ideal absorption of solar cell and upconvertor.100,101 They also explicitly include the characteristics of real UC systems from the domains of both TTA and lanthanoids. Due to the plethora of parameters in the respective model a rather complex picture emerges, but the general conclusions are that high-bandgap thin-film PV technologies are most interesting for combining with UC, and that ‘bimolecular upconverting materials are already well-suited to enhance the efficiency of high-bandgap devices by almost one absolute percent’.101
3.3 Design considerations of TTA upconversion systems
Before discussing the results achieved to date in applying TTA-upconversion to solar cells and photochemical solar energy storage devices, we outline the general design principles of TTA-UC systems for solar energy applications below.As seen in Fig. 2, there are energy losses associated with ISC and there may be energy losses in the TET and TTA processes.37 The largest contribution to the overall energy loss usually stems from intersystem crossing, as the singlet–triplet gaps of common sensitizer species are in the order of 0.4 eV. The triplet energy transfer between the sensitizer and emitter manifold is driven by a free energy gradient, and so does not necessarily rely solely on an enthalpic difference between sensitizer and emitter triplets. Indeed, a difference in concentration between the two species can be exploited to drive TET via the entropic gain associated with the exciton transfer from the smaller reservoir of states in the sensitizer manifold to a larger reservoir among the emitter species.37 It has to be noted, though, that the overall efficiency of the TTA process is affected if TET is endergonic. TTA itself is not necessarily associated with an energy loss either, as a careful choice of the emitter species allows the energy of the S1 singlet to be at twice the triplet energy T1. But, a small energy sacrifice can help mitigate the effects of singlet fission reversing the TTA process. Providing the emitter demonstrates delayed fluorescence by TTA, the non-radiative decay rate of the emitter triplet states has a more direct impact on the overall efficiency.
Typical widths of the main molecular absorption band of common sensitizer species (for example, the Q-band of a porphyrin) are around 50 nm, which constrains the region within the solar spectrum that can be upconverted with a single TTA system. However, it has already been demonstrated that a family of sensitizers can be combined with a single emitter species in such way that the sensitizer absorption bands are staggered in order to provide a quasi-continuous absorption band over more than 125 nm width.102,103
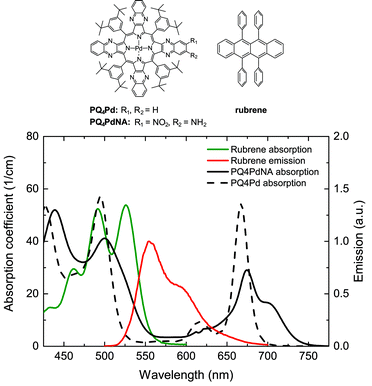
In order to minimize parasitic absorption, the overlap between the emission band of the TTA emitter and the absorption bands of both emitter and sensitizer must be minimized. Fig. 5 shows the situation for two TTA solutions employed in our studies,47,93,95 plotted for typical concentrations. It can be seen that there are slight overlaps between the rubrene emission and its own absorption band (self-absorption) as well as with the porphyrin sensitizer Q- and Soret bands. In the given situation, the characteristic decay length of the absorbed light due to sensitizer absorption is on the order of some 100 μm, while the baseline absorption of the porphyrin around the emitter peak emission wavelength is close to negligible. However, we note that upon shifting the absorption band of the PQ4Pd porphyrin further into the NIR by adding nitro- and amino-groups, resulting in PQ4PdNA (cf.Fig. 5), the baseline absorption slightly increases to 7000 M−1 cm−1, about 10% of the peak absorbance in the red region of the spectrum. Similar effects were observed by Yakutkin et al. upon extending the π-system of a tetra-naphthaloporphyrin to bring about a tetra-anthraporphyrin: while the distance between the Q- and Soret band was still favourably large, the baseline absorption increased to a level which might affect the suitability for application.35
Optical modeling of the system shown in Fig. 5, as well as experiments with varying thickness of the UC unit, revealed that a TTA-UC layer in the presence of a rear reflector yields the highest overall photon output at a thickness which is roughly the characteristic decay length of the incident light at the peak absorption wavelength.47,104 This shows that the optics are dominated by absorption of the incident light and that parasitic absorption of the emitted light cannot play an important role as the ideal thickness would otherwise shift to lower values. Optical modeling predicts that a Lambertian back-scattering layer behind an UC layer of ideal thickness would enhance the UC photon yield by a factor of 3.6. A simple specular mirror would improve the device by a factor of 2.6.47
In solution at mM concentrations, the porphyrin sensitizers employed in our studies require an optimum thickness of the active upconverting layer of between 50 and 150 μm. In a-Si:H and OPV systems, the absorber layer is on the order of 1000 times thinner. Eventually, it is desired to bring about upconverting layers of comparable thickness. Such a device will require nano-structured sensitizer supports and is the subject of present research.94 The requirement of realizing a TTA system with a thickness of around 100 μm poses a challenge in combination with the necessity to rigorously deaerate the UC device in order to suppress triplet quenching by oxygen. The latter is usually achieved by sequentially freezing the TTA solution with liquid nitrogen, evacuating the volume over the frozen solution to the 10−5 mbar range, and successive thawing (freeze–pump–thaw cycle). This procedure requires a mechanically stable cuvette, which is not easily available with a 100 μm gap. In our first UC-enhanced solar cell device, we placed a 1 cm diameter cuvette behind the solar cell which was optically connected to the cell by means of immersion oil.47 This arrangement has several drawbacks. Firstly, about half of the upconverted light is lost as it is emitted away from the solar cell and secondly, the cell itself suffers from very poor light-trapping without any back reflector.
In the next realization of the UC unit we implemented a crude back-scatterer comprising 100 μm-diameter silver-coated glass spheres, which were introduced into the 1 cm diameter cuvette.93 The effect of the resulting textured surface was to multi-pass the incoming light to improve absorption, while also improving the out-coupling of upconverted light. Indeed, with a close-packed structure of 100 μm spheres, most of the surface area presents an optical depth less than this value. Nevertheless, most of the light rays impinging on the spheres are reflected at oblique angles. The solution to the ray-tracing equations required to model this device are complicated, yielding fractal patterns of reflections.105 The region between three spheres represents a so-called fractal vortex, with multiple reflections ensuring complete light absorption. The remainder of the illuminated volume can out-couple the upconverted light in at most one refection. With this topology inside a standard 1 cm diameter cuvette we realized a twofold increase of the UC-related current increase as compared to the quasi-infinite case.93 The comparison to the optical modeling results47,104 shows that the configuration is not optimal, but reasonably close to the optimum situation. At the same time it allows for facile freeze–pump–thaw deaeration which led us to adapt this configuration to be the standard experimental setup.
Nonetheless, we fabricated a custom ‘half cuvette’ which directly connects to the backside glass sheet of the solar cell and allows for a continuous variation of the upconvertor thickness, for further studies of the UC optics.104 Additionally, different reflectors can be employed and compared in an in situ experiment. With this device we validated the optical modeling regarding the optimal thickness of the UC layer and could show, for the first time, that local concentration of the incident light leads to an additional enhancement of the UC yield. These results will be discussed in Section 4. Based on the results obtained, regarding optimum UC layer thickness and reflectors, we finally employed a device-integrated cavity at the correct thickness, incorporating a dielectric reflecting backside layer, which was integrated into a dye-sensitized solar cell.96 Details are given below in Section 3.5.2.
Given the finite absorption range of lanthanoid-based UC materials, strategies have been developed in order to increase the harvest of sub-bandgap light. One possibility would be to combine the UC material with a downshifting luminescent solar concentrator (LSC), as proposed within the so-called NanoSpec concept.107 The LSC would serve to both funnel more spectral weight of the solar spectrum into the UC absorption range and at the same time to geometrically concentrate the incident light, thus exploiting the non-linearity of the UC process for an increase of the quantum yield. As a side effect, the use of UC material would be reduced. While conceptually convincing, the main drawback currently lies in the low quantum efficiency of downshifting phosphors in the infrared range.
While the mentioned concept would in principle be applicable to TTA-UC materials as well, it appears more promising to employ combinations of multiple sensitizers whose combined absorption regions are staggered such that they straddle a larger region of the solar spectrum – a strategy first introduced by Baluschev et al.,102,103 which was shown to work with a single emitting species if the energy levels are correctly aligned. Broadening the upconvertor's spectral response through sensitization with semiconductor nanocrystals has been attempted, but this introduces reabsorption of upconverted light at the expense of a back-reflector.108 Strategies towards realizing concentration of the incident light in combination with TTA-UC units will be discussed below in Section 4.2.2.
3.4 How to measure UC-assisted solar cells
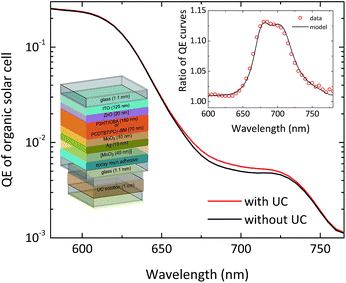
In order to verify the extended utilization of the solar spectrum by a solar cell, brought about by an attached upconvertor unit, the straightforward approach is to measure precisely the spectral response of the solar cell in the presence of the upconvertor and compare it to the situation without the UC effect. It turns out that this is a nontrivial task, for the following two reasons:(1). Usual spectral response or (external) quantum efficiency (QE) measurement schemes use monochromated white light as the (modulated) probe, which results in sensitizer excitation rates much below 1-sun operation conditions. As the response of the upconvertor, upon changing the illumination density, is nonlinear at low flux (cf.Fig. 3), the net contribution of the upconvertor to the QE will be close to zero. Therefore, one has to use a detection and analysis scheme which takes into account the nonlinear nature of the upconversion process.
(2). To deconvolute the contribution of the upconvertor from the solar cell characteristics, it is required to measure the solar cell with and without a contribution from the upconvertor. However, the upconversion unit comprises a reflector which is an integral part of the overall optical system and acts also for wavelengths outside the active region of the UC unit. Therefore, physically removing the upconversion unit will alter the optical behaviour of the solar cell and obstruct the interpretation of the measurement.
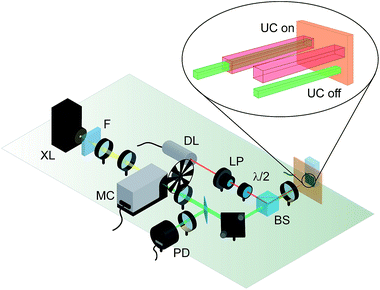 | ||
| Fig. 6 Measurement scheme for solar cells enhanced by TTA-UC. A diode laser selectively pumping the sensitizer absorption but not disturbing the solar cell is used to bias the triplet concentration in the upconvertor unit, to allow for its measurement with a chopped monochromated white light probe as commonly employed in quantum efficiency measurements. The upconvertor is characterized by comparing the situation with the two beams aligned with those where the beams are misaligned, rendering the UC yield negligible. XL – xenon arc lamp, F – long-pass filter, MC – monochromator, BS – beamsplitter, DL – diode laser, LP – linear polariser, λ/2 – half-wave plate, PD – photodiode. Figure adapted from ref. 109. | ||
The setup described above allows circumvention of the nonlinear response of the UC unit, but leaves us with the second challenge of how to compare the UC-augmented with the standard response of the cell. Regarding this issue we exploited the before-mentioned drawback: as the unbiased upconvertor shows negligible response upon illumination by the probe beam alone, we may take this situation to be the baseline for the QE measurement. However, just switching off the bias beam might again change the solar cell behaviour in cases where the cell absorbs slightly in the bias energy region and shows nonlinear effects – which cannot be excluded a priori. We therefore keep the bias beam switched on at all times, and misalign the two beams for the baseline measurement (Fig. 6). By doing this, the solar cell still sees the same overall DC bias illumination, but the upconvertor response in the geometrical region probed by the probe beam is negligible.
This measurement scheme is based on two assumptions: firstly, any nonlinearity of the solar cell does not depend on the position of the illuminated spot, and secondly, the probe beam is sufficiently faint as to ensure a negligible UC response. The first assumption is usually fulfilled for well-behaved solar cells, and can be easily tested, for example by misaligning the bias to a different spot on the cell area and repeating the measurement. The second assumption might become untrue for highly efficient upconvertor materials, but in any case would lead to an underestimation of the UC performance. An alternative method for switching off the contribution of a liquid UC unit is to aerate the TTA-UC solution.24 This, on the other hand, leads to destruction of the dye molecules by singlet oxygen created upon illumination, changing the optical characteristics of the upconvertor.
We have generalized the above scheme, using standard photodetectors in place of solar cells, to measure raw upconversion efficiencies.110 While many of the researchers reporting upconversion efficiencies do so using relative actinometry, this method is inappropriate for use with the optically dense samples required for efficient operation under one-sun excitation. We have coupled broadband, white-light biasing with a modulated monochromatic probe to measure excitation spectra of upconvertors under solar-relevant conditions. The analysis is similar to that laid out below, and is detailed in ref. 110.
| kΦ⊙ = ∫ρ⊙(λ)TSC(λ)σ(λ)dλ. | (6) |
As mentioned in Section 2.2, typical values for kϕ⊙ are in the 2–10 s−1 range. The irradiation Ib of the bias beam in photons per area per time is used to calculate the pump rate under the given experimental conditions, that is kϕb = σ(λb)TSC(λb)Ib with the bias laser wavelength λb. The ratio C = kϕb/kϕ⊙ then gives the effective solar concentration sensed by the upconvertor.
In the nonlinear regime (cf.Fig. 3), that is, under inefficient operating conditions of the upconvertor, and assuming efficient triplet energy transfer, the rate equations from Section 2.2 can be simplified to yield the steady-state emitter triplet concentration
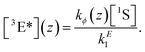 | (7) |
Here we introduced a spatial coordinate z which denotes the depth inside the upconverting material, to account for the decay of the incident photon flux as the light penetrates the UC unit. Since the upconverted light production is proportional to the triplet concentration squared, one can write that the UC photon production rate is
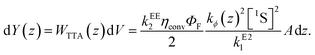 | (8) |
Under experimental conditions, kϕ has contributions from the bias beam and the monochromated probe beam. Denoting these additive contributions kϕb and kϕp,
dY(z) ∝ [1S]2(kΦb(0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−αbz + kΦp(0) e−αbz + kΦp(0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−αpz)2dz, e−αpz)2dz, | (9) |
| αb = σb[1S] | (10) |
| αp = σp[1S]. | (11) |
Integration over z gives
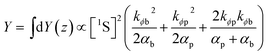 | (12) |
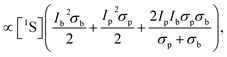 | (13) |
Now, the linear response of the upconvertor with probe light is the quantity of interest which is determined in a QE measurement employing lock-in detection. The intensity of the probe impinging on the solar cell is larger than Ip by a factor 1/TSC(λp), where TSC(λp) is the solar cell transmission at the probed wavelength. Thus
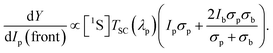 | (14) |
Since the probe light is indeed small compared to the bias, the first term inside the parentheses can be ignored, and the augmentation of the QE curve is proportional to the second term. Denoting the QE in the absence of upconversion QE0, we obtain
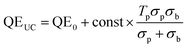 | (15) |
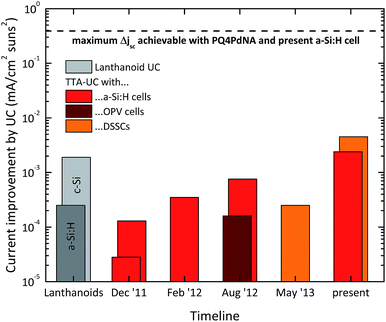
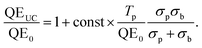 | (16) |
This means that the experimentally observed QE ratio can be modelled using the absorption spectrum of the sensitizer molecules, and the transmission and baseline QE curves of the solar cell. Indeed we have found that this model describes the measured QE data of TTA-UC-enhanced solar cells of various types very well, as can be seen for the example of a P3HT:ICBA organic bulk heterojunction solar cell95 in Fig. 7.
We calculate the current enhancement that results from the augmentation of the solar cell with the upconvertor at the effective number of suns imposed by the bias light, by the equation
| ΔjSC = Ce∫ΦAM1.5G(λ)(QEUC(λ) − QE0(λ))dλ, | (17) |
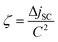 | (18) |
Table 2 shows our best experimental results for different types of thin-film solar cells augmented with TTA-upconversion, as well as the best results for thin-film and crystalline wafer-based solar cells enhanced by lanthanoid-UC reported in the literature. In the following section we will briefly discuss the performance reached with each solar cell, and the pending issues in the optimization of the respective UC unit.
| Solar cell type | Upconvertor | C (⊙) | Δjsc (mA cm−2) | FOM ζ (mA cm−2 ⊙−2) | Ref. | ||
|---|---|---|---|---|---|---|---|
| Type | Constituent A | Constituent B | |||||
| a Mixture of rubrene and 9,10-bis-phenylethynylanthracene. | |||||||
| PCDTBT:PC71PM | TTA-UC | 1.3 mM PQ4PdNA | 11 mM rubrene | 28.9 | 0.129 | 0.15 × 10−3 | 95 |
| P3HT:ICBA | TTA-UC | 1.4 mM PQ4PdNA | 35 mM rubrene | 17.3 | 0.048 | 0.16 × 10−3 | 95 |
| DSSC | TTA-UC | 0.6 mM PQ4PdNA | 33 mM rubrene | 3.0 | 2.25 × 10−3 | 0.25 × 10−3 | 96 |
| a-Si:H | TTA-UC | 0.9 mM PQ4PdNA | 13 mM rubrene | 19 | 0.275 | 0.76 × 10−3 | 95 |
| DSSC | TTA-UC | 0.8 mM PQ4PdNA | Hybrid emittera | 0.3 | 4.05 × 10−4 | 4.50 × 10−3 | 111 |
| a-Si:H | TTA-UC | 0.8 mM PQ4PdNA | Hybrid emittera | 1.4 | 4.70 × 10−3 | 2.40 × 10−3 | 111 |
| DSSC | YAG:(Er,Yb) | 3% Yb3+ | 0.5% Er3+ | ? | 0.2 | ? | 87 |
| a-Si:H | Gd2O2S:(Er,Yb) | 10% Yb3+ | 5% Er3+ | 20 | 0.1 | 0.25 × 10−3 | 86 |
| c-Si | Mono-BaY2F8:Er | 30% Er3+ | — | 94 | 17.0 | 1.92 × 10−3 | 83 |
3.5 Organic and dye-sensitized solar cells
Both organic and dye-sensitized solar cells are ideal candidates for the combination with TTA-upconversion due to their comparably large absorption thresholds. The latest generation of organic bulk heterojunction solar cells can provide significant spectral response as far into the infrared as 800–900 nm based on low-bandgap polymers such as PCPDTBT and its derivatives,112 but for most standard blends such as P3HT:PCBM the QE does not extend beyond 650–700 nm.113 There are already DSSCs with considerable spectral response down to roughly 900 nm, mostly based on the black dye,114 but even some of the newest highly efficient DSSC architectures such as porphyrin-based co-sensitized DSSCs115,116 do not reach above the wavelength range of 750 nm in terms of spectral response. This means that for both classes of solar cells, the porphyrin-based TTA-sensitizers reported so-far35 suffice to extend the utilization of the solar spectrum for most present devices. In our recent publication we have combined two different organic bulk heterojunction cells with a semitransparent design with an external UC unit.95 We further adapted a DSSC to host the upconvertor inside the device.96Our cells had the layer sequence glass/ITO cathode/ZnO buffer/photoactive blend/MoO3 interlayer/semi-transparent silver anode. The active blends employed in the two cell types were PCDTBT:PC71BM, as well as P3HT:ICBA, with the latter cell type also incorporating a topmost MoO3 light coupling layer (cf.Fig. 7). The PCDTBT:PC71BM cells achieved notable power conversion efficiencies of up to 3.8% under illumination through the ITO cathode and 2.4% for illumination through the silver anode. The P3HT:ICBA solar cells exhibited efficiencies of up to 3.1% and 1.7%, respectively. Further details on the fabrication can be found in ref. 95. We employed the UC unit hosted in a standard cuvette, filled with 100 μm diameter Ag-coated glass beads as discussed above in Section 3.3.2.
The upconversion FOMs reached with the polymer solar cells were between 0.24–1.60 × 10−4 mA cm−2 and thus the lowest among the range of thin-film solar cells studied so-far, and showed pronounced differences with respect to the orientation of the cell. Upon illumination of the cell through the ITO layer we measured FOMs that were 50% lower than upon illumination through the Ag electrode. The apparent reason for this is the dependence of the solar cell QEs on orientation which stems from limited exciton diffusion lengths and the resulting sensitivity on the spatial positions of the electric field amplitude maxima,120 as well as from optical losses in the Ag electrode. In the usual operation scheme with illumination through the substrate glass and ITO cathode, the upconvertor is penalized by the absorptive Ag layer on the rear which is then positioned in between the active blend and the upconverting material. This leads to a lower FOM for this orientation. For illumination through the Ag anode on the other hand, the upconverted photons can be harvested by the cell with fewer optical losses, but with a significantly lower quantum efficiency, leading to an improved FOM as compared to the other orientation, but still somewhat lower than for the other thin-film solar cells. A next development step would be to combine the TTA-UC unit with an inverted OPV cell comprising a PEDOT:PSS top contact layer to avoid the mentioned parasitic optical losses. In case semitransparent OPV devices reach efficiencies in the range of a-Si:H devices in the future, they are to be expected to exhibit comparable UC-related photocurrent gains. For low-bandgap polymer absorbers112 it might be required to employ sensitizers absorbing further in the infrared, which are however available already now.35
In our study on UC-enhanced DSSCs we therefore pursued an integrated UC device, in which a solution-based UC system is contained within an encapsulated chamber on the back of the DSSC, similar to that which holds the active DSSC system (Fig. 8B). DSSCs were made at the University of Wollongong (UoW). This chamber included an Al2O3 back-reflector coated onto the glass back-sheet and was engineered to have a thickness of 120 μm that allows optimal optical output from the TTA-UC solution in combination with the used concentrations, based on the considerations presented in Section 3.3.2. This architecture bears resemblance to tandem DSSC architectures. However, no extra TCO layer is required because the second cavity uses plain soda lime glass resulting in minimal additional cost. We chose D149 to be the active dye in our cell concept as its peak absorption (when adsorbed onto TiO2) matches the peak emission wavelength of rubrene (cf.Fig. 8A and 5).
 | ||
| Fig. 8 (A) Absorption characteristics of the dye D149 employed in the upconversion-enhanced dye-sensitized solar cell96 (picture adapted from Mitsubishi Paper Mills Ltd.). Comparison with Fig. 5 shows the good overlap with the rubrene emission. (B) Device structure of the UC-enhanced DSSC with an integrated cavity to host the TTA-upconvertor. | ||
Indeed, we found that the good match of the dye absorption and the direct incorporation of the UC unit minimizing optical losses leads to FOMs around 0.25 × 10−3 mA cm−2 – higher than for the organic solar cells but still inferior to a-Si:H cells (to be discussed in the next Section). The integration strategy might be a practical method for incorporating TTA-UC into PV devices in general. However, the organic solvent hosting the TTA system poses a challenge to the encapsulation. We used Surlyn (Solaronix SA) hot melt adhesive to join the glass sheets when forming the cavities for the electrolyte and TTA system, which is not compatible with highly volatile solvents such as toluene. This points to the importance of finding alternative, less volatile host media for TTA-UC systems, such as ionic liquids.123 Using a hybrid-emitter TTA system we have recently obtained a FOM of 4.50 × 10−3 mA cm−2 with a DSSC using our classical backreflector design based on silver-coated glass beads. To our knowledge, this represents the highest enhancement figure-of-merit for upconversion-enhanced solar cells (cf.Table 2). Details about the experiments and the novel hybrid TTA systems will be published elsewhere soon.111
3.6 Thin-film silicon solar cells
Hydrogenated amorphous silicon (a-Si:H) solar cells are probably the most straightforward candidate for combination with a TTA-upconvertor as they provide reasonably high efficiencies of up to 10.1% but show an absorption threshold of roughly 700 nm.124 At the same time it is fairly easy to implement a semitransparent design as a-Si:H absorbers withstand the deposition of a backside TCO layer. We therefore used a-Si:H solar cells as the workhorse during our optimization of the TTA materials and optics of the combined system.47,93,95,104The cells we employed were a-Si:H p–i–n solar cells with i-layer thicknesses of between 90–150 nm. In the course of our studies we found that the UC performance is increased when the light trapping of the solar cell is reduced, as the near-threshold transmission is thereby increased. For this reason we omitted texturing of the front-side TCO which, at the same time, allowed us to increase the i-layer thickness while maintaining high sub-threshold transmittance. Our best bifacial a-Si:H p–i–n cells employed a smooth ZnO:Al front TCO layer, a p-doped μc-Si/μc-SiOx/a-Si:H triple layer stack,125 a 150 nm thick (i) a-Si:H absorber, a μc-Si backside n-doped layer and a ZnO:Al back contact TCO layer. We employed industrial thin-film processing by plasma-enhanced chemical vapor deposition (PECVD) and reactive sputtering on 30 × 30 cm2 glass sheets at Helmholtz-Zentrum Berlin für Materialien und Energie (HZB). The substrates were cut into 10 × 10 cm2 pieces afterwards, each containing 20 1 × 1 cm2 individual solar cells. The overall conversion efficiency of the semitransparent a-Si:H cells was a notable 7.0% without any backside reflector.
During the measurements of UC-enhanced a-Si:H solar cells we connected the UC unit by different means: in a standard cuvette without back-scattering medium47 and filled with 100 μm diameter Ag-coated glass beads,93,95 or using the half cuvette and different back-reflecting or -scattering media. The best results, including our record 2.40 × 10−3 mA cm−2 current increase (cf.Table 2) following the implementation of a hybrid-emitter TTA system,20,111 were obtained with the cuvette filled with Ag-coated beads.
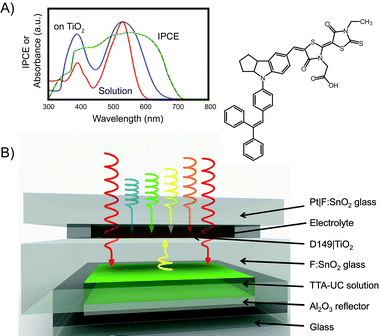
Fig. 9 shows the history of the FOM obtained with the different classes of devices, as compared to the best result of a thin-film solar cell enhanced with lanthanoid upconversion.14 The dashed line represents the maximum current enhancement of our best a-Si:H solar cell that would be possible with our present flagship TTA system if it was operating at the maximum quantum yield that has been experimentally demonstrated for high illumination density. This number of roughly 0.4 mA cm−2 is based on detailed optical modeling in combination with the rate equation description. In our opinion it also marks the region where commercial application might become feasible in case the UC unit can be made inexpensive and durable. Although we have realized a significant increase of the FOM by two orders of magnitude since our first results, there are another two orders of magnitude to be gained in order to fully exploit the potential of the TTA system. Section 4 will be devoted to sketching ways that might lead to bridging this gap. Before we open this discussion we briefly review concepts for TTA-enhanced solar energy storage in the next section.
 | ||
| Fig. 9 History of the figure of merit for thin-film solar cells enhanced by TTA-upconversion as obtained by our group.47,93,95,96,111 For comparison, the best results for lanthanoid upconversion-enhanced silicon solar cells are shown in grey.83,86 | ||
3.7 TTA-enhanced solar energy storage
TTA upconversion hosts great potential for sensitizing photo(electro)chemical (PC/PEC) energy storage, as the respective materials and mechanisms usually have threshold energies well into the visible or even UV range of the spectrum. PEC-driven water splitting, for instance, requires a voltage of 1.23 V plus the over-potentials of the electrodes (thus, in practice, 2 V), and respective devices are therefore restrained to high-bandgap absorber materials. One way of achieving the required high voltage is to invoke multijunction PV devices, which either efficiently utilise the spectrum but are highly expensive to manufacture such as III–V-based systems,126 or consist of thin-film multijunction cells incorporating high-bandgap absorber materials such as a-Si:H (ref. 127) and again suffer from dominant sub-bandgap losses.The domain of metal oxide PEC electrode materials faces similar issues: respective materials have large bandgaps of >2 eV, giving rise to very significant sub-bandgap losses, and even for the combination with a driver solar cell, the choices are again limited to high-voltage high-bandgap PV devices that leave a large part of the long-wavelength region of the spectrum unused.128
This means that harvesting and converting sub-bandgap photons by upconversion is highly relevant for PEC and PC devices, as inexpensive tandem PV devices which efficiently use the solar spectrum and deliver a high voltage are presently unavailable. TTA-UC is particularly interesting for this purpose as relevant energy ranges for harvesting and re-emission can lie well in the visible or even (in the case of high-gap metal oxide electrodes) in the UV region of the spectrum.
Until now, only few reports are documented in the literature where TTA-UC has been used to augment PEC/PC processes and devices. The majority of those concerns the sensitization of the oxygen evolution half-reaction of water splitting using a WO3 photoanode by green-to-blue TTA-upconversion based on a platinum(II)- or palladium(II)-octaethylporphyrin/9,10-diphenylanthracene ([Pt/Pd]OEP/DPA) TTA couple. Khnayzer et al. employed the TTA materials in a liquid solution in toluene and encapsulated them in a glass cuvette, thus separating them from the aqueous phase,24 while Kim et al. used a hexadecane/polyisobutylene host which was enclosed in microcapsules made from ethoxylated trimethylolpropane triacylate ester (ETPTA) which allowed the introduction of the TTA system into the aqueous phase.129 While the first example employed truncated white light as the excitation source, the second and also the following used a 532 nm laser. Monguzzi et al. dispersed the TTA couple into an elastomeric poly-butylacrylate host, and immersed the resulting solid medium into water.55 These proof-of-concept studies convincingly illustrate the potential of TTA in the field of PEC devices and highlight strategies that can render TTA-UC compatible with an aqueous environment. However, they rely on a photoanode which is not state-of-the-art and employ a very crude optical design of the system, which leaves ample space for optimization of respective device concepts.
TTA-UC has also been employed to augment photochemical reactions that might be used for solar energy storage. Börjesson et al. used the aforementioned PdOEP/DPA system to sensitize a photoisomerization reaction of a fulvalene diruthenium derivative. Upon thermal or catalytic activation, the isomerism can be reversed and the compound releases the stored energy as heat, thus acting as a recyclable solar fuel. The liquid molecular solar thermal (MOST) storage medium and the liquid TTA system, both dissolved in toluene, were cycled through a microfluidic chip as the light-harvesting surface.23
TTA-UC was further employed to sensitize photochemical reactions for other applications: Islangulov et al. sensitized TTA between anthracene with the metal-to-ligand charge-transfer (MLCT) sensitizer [Ru(dmb)3] in order to produce reactive excited singlet species prone to cycloaddition chemistry, resulting in the formation of anthracene dimers.130 Jiang et al. used a red-absorbing porphyrin/anthracene-derivative TTA couple to sensitize trans-cis-photoisomerization of azotolane in a cross-linked liquid-crystal polymer, resulting in a photomechanical effect with potential application in soft actuation.131
4 Prospects for device applications
We have seen, so far, that there is a clear application case for TTA-upconversion aiming to remedy sub-bandgap losses in thin-film solar cells and photo(electro)chemical devices. In recent years, a number of proof-of-concept application examples and – in some areas – a successive technological optimization have shown that TTA-UC can indeed be feasibly integrated into devices. The major bottleneck at present is the limited quantum yield under relevant operation conditions. In order to result in low-cost, large-scale deployable systems, the UC-augmented devices must not rely on geometric-optical concentration in order to function at appreciable yield. We therefore have to strive for• Incorporating concepts that enable the remarkably high quantum yields of present TTA-UC systems also under 1-sun conditions,
• Tackling the longevity of TTA systems under operation conditions, and
• Developing facile and scalable concepts for oxygen defense and encapsulation.
4.1 Reported efficiencies under one-sun conditions
While there are many reports of TTA-UC upconversion efficiencies,132 these are mostly obtained under strong pumping conditions using CW laser excitation. Under one-sun equivalent broadband excitation, MacQueen and Schmidt reported a red to yellow rubrene emitter system with a TTA quantum yield of 0.55% (ΦTTA = 1.1%).110 Indeed, in that experiment upconversion excitation spectra were obtained with as low as 0.09 suns excitation. Monguzzi and co-workers recently reported a semiconductor nanocrystal-boosted system which exhibited a half-maximum output at 0.5 suns.108 The DPA emitter has a maximum upconversion yield of 25%. Thus, the quantum yield at 0.5 suns is taken to be 12.5%. For the same emitter, we obtain about 3% quantum yield (ΦTTA = 6%) under one sun excitation, increasing to 7% by three suns. Clearly, several percent quantum yields are possible under one-sun pumping. This must be increased several-fold. Below we outline several approaches one might take to bring about more efficient one-sun TTA-UC.4.2 How to further increase UC yield
A possible guideline for this task is given in the form of eqn (7), which is the steady-state solution of the rate equations. Here we see that in order to increase the steady-state concentration of emitter molecules in their triplet excited state [3S*] – and thus the UC yield – we have to increase the triplet lifetime 1/kE1, the sensitizer excitation rate kϕ as well as the concentration of sensitizers [1S].In case TTA materials with significantly higher dye concentrations become available (cf. the next section) and the characteristic absorption length approaches the wavelength of the light, near-field optical effects will become a very attractive route for increasing the sensitizer excitation rate. These might result from photonic structures such as distributed Bragg reflectors (DBR) or from plasmonic resonances hosted by metallic nanostructures.
DBRs have been employed to enhance lanthanoid-based upconversion134 by enhanced absorption of incident light via so-called slow light modes, and recent modeling work suggests beneficial effects also for TTA-upconversion.135 Plasmonic effects have been shown to enhance lanthanoid upconversion136 and were also employed in combination with TTA-UC systems: Baluschev et al. used a conjugated polyfluorene polymer acting as TTA emitter, sensitized with PtOEP blended into the blue-emitting host, which was coated onto a silver surface employing a 15 nm LiF spacer to prevent quenching of the triplets by the presence of the metal. Upon changing the orientation of the substrate with respect to an incident laser beam, the authors could clearly identify the TE and TM modes of the plasmonic resonance hosted by the Ag layer in the TTA yield.137 Recently, Poorkazem et al. dispersed plasmonically active silver nanoplates in a poly(methyl methacrylate) (PMMA) host which contained a PdOEP/DPA TTA-UC system, and observed a pronounced increase of the upconverted fluorescence signal as compared to a PdOEP/DPA/PMMA system lacking the silver nanoplates.138 Theoretical studies have further emphasized the possibility of enhancing TTA-UC in plasmonically active nanoparticles with crescent-shaped silver coatings.139
In summary, it is without doubt that plasmonics can provide great potential for increasing the TTA-UC yield by near-field enhancement of sensitizer transition rates, and possibly also by enhancing the outcoupling efficiency of the upconverted light. However, unlike for the geometrical concentration approach which has already proven to be useful, an in situ demonstration of the benefit of near-field optical effects in a solar energy conversion device is still lacking. Additionally, metal-induced exciton quenching might become an issue regarding plasmonic enhancement.
An elegant and straightforward approach would be covalently linking sensitizer and emitter species.140 Recent studies imply that this indeed increases the UC yield in liquid solutions,141 while earlier studies have found an increase of the TTA photon yield of a porphyrin sensitizer end-capped poly-pentaphenylene solid TTA emitter142 as compared to a porphyrin-doped host. Although others have argued that the gain in UC efficiency in this system was minute and relate this finding to a possible exciton back-diffusion,58 these strategies point in the right direction but require much more effort in order to realize efficient and robust TTA systems tailored for solar energy applications.
Another interesting strategy is omitting the host matrix completely by functionalizing the active species with branched alkyl chains, thus creating a nonvolatile organic liquid solely consisting of the active species. Duan et al. pursued this approach functionalizing the PtOEP/DPA system and realized a concentration of up to 10 mM of porphyrin sensitizer in the resulting DPA solution.143 The quantum yield was measured to be up to 28%.
Further, an increase of dye load should also be possible by tethering the active species onto nanoscopic support structures. Lissau et al. reported upconverted fluorescence from the PtOEP/DPA system adsorbed onto ZrO2 nanoparticles, but found their system to be limited by aggregation; sub-optimal dye loading and orientation; and oxygen quenching. An improved system featured functionalized DPA with carboxylate anchor groups on ZrO2 nanoparticles floating in a butyronitrile solution containing the PtOEP sensitizer, and showed improved performance.144
Our own activities in this field have been focussed around tethering the sensitizer species onto nanoscale scaffolds which are then immersed into a liquid emitter solution or interspersed with a polymeric emitter. First results of our red-absorbing porphyrins bound to silica nanoparticles in rubrene solution, in combination with amorphous silicon solar cells, showed a working system but no benefit with respect to the liquid system.94 Clearly, more work is required to shed light on the changes in dynamics, transfer and quenching rates associated with immobilized dyes in order to assess if this concept bears potential for improving TTA-UC efficiency.
Finally, an interesting strategy is to move away from the TTA couple paradigm and to introduce a third (or even more) active species. Successful attempts to combine two or more porphyrin sensitizers providing triplets to the same emitter were presented above and mainly aim at extending the spectral harvest of the TTA system.102,103 However, in contrast, employing more than one emitter species appears to yield a benefit in UC efficiency. First of all, the solubility problem can be mitigated if the sensitizer triplets are accepted by two separate species instead of one. In addition, there seems to be a synergetic effect in the combination of two emitting species which results in a clear gain in UC yield as compared to a classical TTA couple.20,145 Consequently, our newest and best solar cell results (cf.Table 2) were obtained with dual-emitter TTA systems. The exact reason for this effect is currently under investigation, and a respective analysis of our results will be published elsewhere soon.
4.3 Longevity
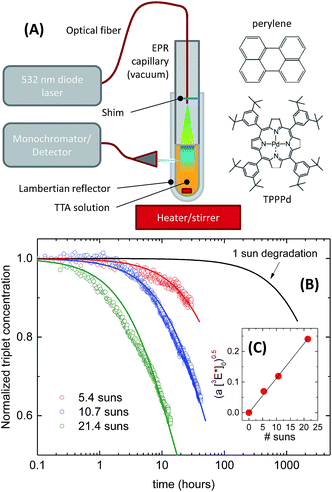
For applications in solar energy harvesting, an encapsulated TTA-UC system would be required to last for several years. Even if one might consider a liquid TTA system in a flow reactor where an exchange of the active solution is more easily achieved,23 the economic feasibility of applying a TTA-UC booster to a solar energy device crucially depends on the longevity. However, to our knowledge, no experimental results have been reported so-far regarding photodegradation of TTA systems under application-relevant conditions. To this end, we have collected preliminary data which we present here for the first time.The experimental setup consisted of a TPPPd/perylene TTA couple,37 dissolved in a highly nonvolatile synthetic silicone oil. We inserted a well-defined amount of this mixture into an EPR tube with 5 mm inner diameter, including a miniature magnetic stirrer. The outside of the tube was covered with a white Lambertian reflector, leaving only a roughly 1 mm sized hole for detection of the upconverted fluorescence through an optical fiber using a monochromator/CCD camera assembly (Princeton Instruments). A 532 nm diode laser coupled into an optical fiber was inserted into the EPR tube such that the light spot covered the entire surface of the TTA solution (Fig. 10A). The EPR tube was evacuated to the 10−5 mbar range using a diffusion pump and the pump line was connected during the entire duration of the experiment. After pumping on the solution for 2 h during stirring to deaerate and evaporate residual volatile components, the experiment was started by exposing the solution to the 532 nm light. Over the course of several hours, fluorescence spectra were taken every minute and the peak height of the perylene fluorescence around 455 nm was monitored. After the experiment, the effective solar concentration was again calculated to be C = kϕb/kϕ⊙, with kϕb in this case assumed to be the total incident photon flux divided by the number of molecules in the cuvette, that is, assuming an optically hermetic system and a quasi-homogeneous flooding of the solution with incident light.
The obtained decay traces of the fluorescence intensity were afterwards analyzed with the help of a model. We normalized the square root of the fluorescence intensity which results in data sets of the relative decay of the steady-state emitter triplet density [3E*]t/[3E*]0.27 We found that these curves could be reasonably fit assuming that the emitter species are destroyed by a second-order process,
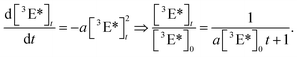 | (19) |
The fit results are shown in Fig. 10B.
We noted from UV-Vis absorption spectra taken after the degradation run that [E] and [S] had been diminished equally such that the ratio [S]/[E] was approximately constant. Thus, the photo-destruction mechanism must affect both molecular species.
We fit the decay curves for different effective light concentrations and found the square root of the time constant 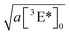 to vary linearly with the incident laser power (Fig. 10C). Extrapolating the respective linear fit to 1 sun conditions we arrive at the black model curve in panel (B), predicting that after 1000 h at 1 sun conditions – corresponding to one year of outdoor operation in central Europe – the triplet concentration would have dropped by 10%. After three years 30% loss would have occurred, corresponding to a loss in the UC photon yield of about 50%.
to vary linearly with the incident laser power (Fig. 10C). Extrapolating the respective linear fit to 1 sun conditions we arrive at the black model curve in panel (B), predicting that after 1000 h at 1 sun conditions – corresponding to one year of outdoor operation in central Europe – the triplet concentration would have dropped by 10%. After three years 30% loss would have occurred, corresponding to a loss in the UC photon yield of about 50%.
While this analysis is only a first and crude step towards assessing the longevity of TTA systems under relevant conditions, we consider the results to be promising, even though the lifetime is most likely not yet sufficient for an economically feasible operation. Given the fact that the employed excitation energies (hν) are 25% higher than for the red-absorbing TTA systems relevant to PV devices, and the energy accessible by second order processes might be up to 1 eV lower in those TTA couples, the destruction rate will likely be reduced. The fact that the PV device protects the upconvertor from high-energy photons will further help to extend the lifetime of the TTA system. However, further and more detailed studies are needed to conclude about the longevity in device-relevant configurations, and dedicated materials design will be required in order to increase the lifetime under 1 sun conditions towards the order of 10 years or more.
4.4 Encapsulation and oxygen defense
Oxygen is detrimental to the operation of TTA-UC as it scavenges triplet excitons from the active TTA species. The electronic ground-state of molecular oxygen has a triplet configuration of electron spins with a T0–S1 energy gap of 0.97 eV. This makes it an effective quencher of triplet-excited chromophores in TTA-UC systems by the reaction [3O2] + [3M*] → [1O*2] + [1M]. Sustainably excluding oxygen is therefore a prime directive in the design of device-appended TTA-UC systems. Additionally, replacing highly volatile solvents such as toluene, which are commonly used for lab-based TTA systems, becomes mandatory for long-term encapsulation of TTA systems. While the containment of the TTA system in a closed glass cuvette after freeze–pump–thaw cycles is a practical method in the lab, device application requires new routes for both oxygen defense and encapsulation. In the literature we already find documents of very different approaches that might be viable to this end, and partly include rendering the TTA-system to be bio- or aqueous-compatible.Polymeric micro- or nano-capsules filled with a liquid TTA system have been presented in a number of studies and allow stable operation in water,129,146–149 as do polymeric nanofibers containing nano-capsules filled with a liquid TTA system.150 Self-organized micellar carriers based on non-ionic surfactants have been presented and likewise allow transference of the system into water.151 There are also several alternatives to the highly volatile solvents: ionic liquids have been presented as a completely nonvolatile host matrix,123 while hexadecane/polyisobutylene was found to be a less volatile host, also providing some degree of oxygen protection.129 Finally, matrices which have oxygen-scavenging properties can further reduce the detrimental impact of atmospheric conditions.152,153
In summary it appears that several complementary strategies for oxygen exclusion and encapsulation are already available. As for the longevity issue discussed above, focussed efforts are needed to explore the feasibility of those approaches in a device context.
4.5 Materials cost
In the end, the uptake of photovoltaics is a trade-off between cost and efficiency, there being a market for cheap but reasonably efficient cells (η ≈ 10%), and a market for highly efficient yet expensive cells (η > 20%). The addition of an upconvertor to a thin-film solar cell must not add a considerable cost to its manufacture. The cost will comprise two components, the materials cost and the manufacturing cost. We begin with estimating the materials cost.In order to absorb the sub-bandgap light, the sensitizer materials must be in a high enough concentration such that their absorption cross sections, σ, could be used to tessellate the rear of the solar cell. At a surface coverage of 1/σ, 1/e of the incoming radiation would be absorbed at peak, which, in conjunction with a back-reflector, has been determined to be optimal.93
The PQ4Pd porphyrin has a peak absorption cross section of 4 Å2, which would yield an optimal surface concentration of 2.5 × 1019 m−2, or 4 × 10−5 mol m−2. With a molecular mass of ∼1500 amu, this translates to about 65 mg m−2. Now, while specialty research chemicals cost on the order of $1000 per g, vat dyes which are manufactured in bulk can be purchased for prices ranging from $1 to $50 per kg. At $50 per kg, the dye cost would be just a third of a cent per square metre. The emitters in widespread use are already manufactured in bulk: rubrene can be obtained for as little as $10 per kg, as can various perylene dyes, some of which are used in paints for vehicles. Phthalocyanines, which have been demonstrated as sensitizers,154 are available for as little as $1 per kg. Thus, given a choice of sensitizer and emitter species which are already in widespread use and having scalable synthesis, the cost for dye production could be well in the c/m2 range.
In terms of elemental raw materials use, the palladium or platinum metal currently incorporated in the porphyrin sensitizers is expected to dominate the price. The cost of palladium is $780 per oz at the time of writing. Assuming an absorption cross section of 4 Å2, this amounts to 4 mg m−2, which would cost about 12c m−2. Thus, the use of precious metals in the sensitizer species would be the main price driver given bulk synthesis prices as discussed above.
To pay for itself, the upconvertor must generate an additional Wp per $. Assuming a cell voltage of 0.5 V at its maximum power point, an additional 2A per $ is required. At an upconvertor cost of 1 $ per m2 – much higher than the more optimistic estimates outlined above – this amounts to 0.2 mA cm−2, which is at the upper end of what we believe is eventually achievable with a single sensitizer species.95 Note however that by broadening the absorption range through the use of multiple sensitizer species feeding the same emitter,35 the current harvest could be increased by adding a single molecular species, thus leveraging the cost of the entire UC system.
Clearly, there is a need to identify upconversion materials which are either already in widespread use, have scalable syntheses, and forgo the use of precious metals. With respect to upconversion without heavy metals, BODIPY dyes were shown to function as rare-metal-free triplet sensitizers.30 It has further been demonstrated that zinc porphyrins can sensitize TTA-UC systems.155,156 Zinc costs on the order $2 per kg, which is a tiny fraction of the cost of palladium. While zinc compounds do not usually have the ∼100% triplet yields of palladium and platinum compounds, they are still high (∼80–90%), and since intersystem crossing is not presently a bottleneck in TTA-UC efficiency the prospects for achieving photochemical upconversion with cheap materials are good.
Regarding the manufacturing cost for integration of an UC unit into a solar energy harvesting device, a sincere estimate is hard to make based on the currently available UC systems. Clearly, the realization of an efficient solid-state TTA-UC material would greatly improve the application perspective. However, incorporation of liquid materials does not generally preclude a large-scale application as can be seen from the example of liquid crystal flat panel displays. As a result, respective sealing and encapsulation methods are available, but a commercially viable application of liquid-based TTA-UC might ultimately be hindered by the requirement of a second glass sheet to form the cavity hosting the UC unit. Thus, the application perspective of TTA-UC will crucially depend on further materials development, mainly tackling the challenges of solid state matrices as well as photo-degradation.
5 Conclusion
In conclusion, we have shown the status and prospects of device application for triplet–triplet annihilation upconversion in the context of solar energy conversion and storage. The application perspective of TTA-UC for thin-film PV and photo(electro)chemical storage is clearly given, due to the inherently large bandgaps of respective absorbers and ensuing transmission losses. It is apparent that the quantum yield of TTA-upconversion systems under device operation conditions is the crucial quantity to be optimized in the near future. Although it approaches the physical limit under high excitation flux for some TTA systems, it is mostly in the low percent range under 1-sun conditions. The combination of micro- or nano-optical enhancement schemes with tailored engineering of TTA materials to facilitate higher concentrations of the active species might pave the way to higher QEs in device configuration. Alongside this challenge in material and optical design, the longevity of the UC unit needs to be addressed within a technological effort. There seems to be a plethora of possible complementary approaches to oxygen defense and encapsulation, making it realistic that this aspect will not hinder application. Photo-degradation of the organic species is more likely to be a crucial issue, but very preliminary results let us hope that it can be resolved. Finally, we believe that TTA-UC has a bright future for solar energy harvesting if we are able to rise to the challenges set out above.Acknowledgements
Much of the work summarized in this review was the result of sustained efforts by Y. Y. Cheng, R. W. MacQueen, A. N. Danos, M. J. Y. Tayebjee, B. Fückel, and R. G. C. R. Clady on TTA-UC characterization; and T. Khoury and M. J. Crossley on the synthesis of porphyrin sensitizers. We acknowledge K. Lips for initiating the German–Australian collaboration leading to many of the results presented herein. B. Stannowski, T. Hänel and S. Kirner from HZB are acknowledged for a-Si:H solar cell processing and characterization. We thank A. Colsmann, J. Czolk and U. Lemmer at KIT for OPV cell design and manufacturing. A. Nattestad, F. W. Thompson, A. J. Mozer and G. G. Wallace from UoW are acknowledged for the development and processing of the DSSCs. N. J. Ekins-Daukes is thanked for initiating our work on TTA-UC. TFS acknowledges the Alexander von Humboldt-Foundation for a Feodor Lynen fellowship. TWS acknowledges the Australian Research Council for a Future Fellowship. The research projects generating the results summarized herein from our laboratory were funded by the Australian Renewable Energy Agency (Project A-023), with contributions from The New South Wales Government and The University of Sydney. Aspects of the research were supported under Australian Research Council's Discovery Projects funding scheme (DP110103300).References
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS PubMed.
- M. C. Hanna and A. J. Nozik, J. Appl. Phys., 2006, 100, 074510 CrossRef PubMed.
- M. J. Y. Tayebjee, A. A. Gray-Weale and T. W. Schmidt, J. Phys. Chem. Lett., 2012, 3, 2749–2754 CrossRef CAS.
- T. Hisatomi, J. Kubota and K. Domen, Chem. Soc. Rev., 2014 Search PubMed.
- M. Grätzel, Nature, 2001, 414, 338–344 CrossRef PubMed.
- T. Schmidt and M. Tayebjee, in Comprehensive Renewable Energy, ed. A. Sayigh, Elsevier, Oxford, 2012, pp. 533–548 Search PubMed.
- L. C. Hirst and N. J. Ekins-Daukes, Prog. Photovoltaics, 2011, 19, 286–293 Search PubMed.
- M. A. Green, Third Generation Photovoltaics: Advances Solar Energy Conversion, Springer-Verlag, Heidelberg, 2003 Search PubMed.
- T. Trupke, M. A. Green and P. Würfel, J. Appl. Phys., 2002, 92, 4117–4122 CrossRef CAS PubMed.
- J. de Wild, A. Meijerink, J. K. Rath, W. G. J. H. M. van Sark and R. E. I. Schropp, Energy Environ. Sci., 2011, 4, 4835–4848 CAS.
- F. Auzel, Chem. Rev., 2004, 104, 139–173 CrossRef CAS PubMed.
- B. M. van der Ende, L. Aarts and A. Meijerink, Phys. Chem. Chem. Phys., 2009, 11, 11081–11095 RSC.
- A. Shalav, B. S. Richards, T. Trupke, K. W. Krämer and H. U. Güdel, Appl. Phys. Lett., 2005, 86, 013505 CrossRef PubMed.
- S. Fischer, B. Fröhlich, H. Steinkemper, K. Krämer and J. Goldschmidt, Sol. Energy Mater. Sol. Cells, 2014, 122, 197–207 CrossRef CAS PubMed.
- S. Baluschev, T. Miteva, V. Yakutkin, G. Nelles, A. Yasuda and G. Wegner, Phys. Rev. Lett., 2006, 97, 143903 CrossRef CAS.
- T. N. Singh-Rachford and F. N. Castellano, Coord. Chem. Rev., 2010, 254, 2560–2573 CrossRef CAS PubMed.
- J. Z. Zhao, S. M. Ji and H. M. Guo, RSC Adv., 2011, 1, 937–950 RSC.
- C. A. Parker and C. G. Hatchard, Proc. Chem. Soc., 1962, 386–387 CAS.
- C. A. Parker, Proc. R. Soc. A, 1963, 276, 125–135 CrossRef CAS.
- X. Cao, B. Hu and P. Zhang, J. Phys. Chem. Lett., 2013, 4, 2334–2338 CrossRef CAS.
- S. K. W. MacDougall, A. Ivaturi, J. Marques-Hueso, K. W. Krämer and B. S. Richards, Opt. Express, 2012, 20, A879–A887 CrossRef PubMed.
- R. Martn-Rodríguez, S. Fischer, A. Ivaturi, B. Froehlich, K. W. Krämer, J. C. Goldschmidt, B. S. Richards and A. Meijerink, Chem. Mater., 2013, 25, 1912–1921 CrossRef.
- K. Börjesson, D. Dzebo, B. Albinsson and K. Moth-Poulsen, J. Mater. Chem. A, 2013, 1, 8521–8524 Search PubMed.
- R. S. Khnayzer, J. Blumhoff, J. A. Harrington, A. Haefele, F. Deng and F. N. Castellano, Chem. Commun., 2012, 48, 209–211 RSC.
- S. Baluschev, V. Yakutkin, T. Miteva, Y. Avlasevich, S. Chernov, S. Aleshchenkov, G. Nelles, A. Cheprakov, A. Yasuda and K. Müllen, et al. , Angew. Chem., Int. Ed., 2007, 46, 7693–7696 CrossRef CAS PubMed.
- S. Baluschev, V. Yakutkin, T. Miteva, G. Wegner, T. Roberts, G. Nelles, A. Yasuda, S. Chernov, S. Aleshchenkov and A. Cheprakov, New J. Phys., 2008, 10, 013007 CrossRef.
- Y. Cheng, B. Fückel, T. Khoury, R. G. C. R. Clady, M. J. Y. Tayebjee, N. J. Ekins-Daukes, M. J. Crossley and T. W. Schmidt, J. Phys. Chem. Lett., 2010, 1, 1795–1799 CrossRef CAS.
- W. Zhao and F. N. Castellano, J. Phys. Chem. A, 2006, 110, 11440–11445 CrossRef CAS PubMed.
- R. R. Islangulov, D. V. Kozlov and F. N. Castellano, Chem. Commun., 2005, 3776–3778 RSC.
- C. Zhang, J. Zhao, S. Wu, Z. Wang, W. Wu, J. Ma, S. Guo and L. Huang, J. Am. Chem. Soc., 2013, 135, 10566–10578 CrossRef CAS PubMed.
- J. Sun, F. Zhong, X. Yi and J. Zhao, Inorg. Chem., 2013, 52, 6299–6310 CrossRef CAS PubMed.
- V. Jankus, E. W. Snedden, D. W. Bright, V. L. Whittle, J. A. G. Williams and A. Monkman, Adv. Funct. Mater., 2013, 23, 384–393 CrossRef CAS.
- T. N. Singh-Rachford and F. N. Castellano, J. Phys. Chem. A, 2009, 113, 5912 CrossRef CAS PubMed.
- B. Fückel, D. A. Roberts, Y. Cheng, R. G. C. R. Clady, R. B. Piper, N. J. Ekins-Daukes, M. J. Crossley and T. W. Schmidt, J. Phys. Chem. Lett., 2011, 2, 966–971 CrossRef.
- V. Yakutkin, S. Aleshchenkov, S. Chernov, T. Miteva, G. Nelles, A. Cheprakov and S. Baluschev, Chem.–Eur. J., 2008, 14, 9846–9850 CrossRef CAS PubMed.
- T. N. Singh-Rachford, A. Haefele, R. Ziessel and F. N. Castellano, J. Am. Chem. Soc., 2008, 130, 16164 CrossRef CAS PubMed.
- Y. Y. Cheng, B. Fückel, T. Khoury, R. G. C. R. Clady, N. J. Ekins-Daukes, M. J. Crossley and T. W. Schmidt, J. Phys. Chem. A, 2011, 115, 1047–1053 CrossRef CAS PubMed.
- T. N. Singh-Rachford and F. N. Castellano, Inorg. Chem., 2009, 48, 2541–2548 CrossRef CAS PubMed.
- J. E. Auckett, Y. Cheng, T. Khoury, R. G. C. R. Clady, N. J. Ekins-Daukes, M. J. Crossley and T. W. Schmidt, J. Phys.: Conf. Ser., 2009, 185, 012002 CrossRef.
- A. Monguzzi, J. Mezyk, F. Scotognella, R. Tubino and F. Meinardi, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 5 CrossRef.
- A. Haefele, J. Blumhoff, R. S. Khnayzer and F. N. Castellano, J. Phys. Chem. Lett., 2012, 3, 299–303 CrossRef CAS.
- R. B. Piper, M. Yoshida, D. J. Farrell, T. Khoury, M. J. Crossley, T. W. Schmidt, S. A. Haque and N. Ekins-Daukes, RSC Adv., 2014, 4, 8059–8063 RSC.
- T. N. Singh-Rachford, A. Nayak, M. L. Muro-Small, S. Goeb, M. J. Therien and F. N. Castellano, J. Am. Chem. Soc., 2010, 132, 14203–14211 CrossRef CAS PubMed.
- D. Y. Kondakov, T. D. Pawlik, T. K. Hatwar and J. P. Spindler, J. Appl. Phys., 2009, 106, 124510 CrossRef PubMed.
- Y. Cheng, T. Khoury, R. G. C. R. Clady, M. J. Y. Tayebjee, N. J. Ekins-Daukes, M. J. Crossley and T. W. Schmidt, Phys. Chem. Chem. Phys., 2010, 12, 66–71 RSC.
- B. Dick and B. Nickel, Chem. Phys., 1983, 78, 1–16 CrossRef CAS.
- Y. Y. Cheng, B. Fückel, R. W. MacQueen, T. Khoury, R. G. C. R. Clady, T. F. Schulze, N. J. Ekins-Daukes, M. J. Crossley, B. Stannowski, K. Lips and T. W. Schmidt, Energy Environ. Sci., 2012, 5, 6953–6959 CAS.
- G. E. Arnaoutakis, J. Marques-Hueso, A. Ivaturi, K. W. Krämer, S. Fischer, J. C. Goldschmidt and B. S. Richards, Opt. Express, 2014, 22, A452–A464 CrossRef CAS PubMed.
- R. R. Islangulov, J. Lott, C. Weder and F. N. Castellano, J. Am. Chem. Soc., 2007, 129, 12652–12653 CrossRef CAS PubMed.
- A. Monguzzi, R. Tubino and F. Meinardi, J. Phys. Chem. A, 2009, 113, 1171–1174 CrossRef CAS PubMed.
- T. Miteva, V. Yakutkin, G. Nelles and S. Baluschev, New J. Phys., 2008, 10, 103002 CrossRef.
- T. N. Singh-Rachford, J. Lott, C. Weder and F. N. Castellano, J. Am. Chem. Soc., 2009, 131, 12007–12014 CrossRef CAS PubMed.
- J.-H. Kim, F. Deng, F. N. Castellano and J.-H. Kim, Chem. Mater., 2012, 24, 2250–2252 CrossRef CAS.
- T. N. Singh-Rachford and F. N. Castellano, J. Phys. Chem. Lett., 2009, 1, 195–200 CrossRef.
- A. Monguzzi, F. Bianchi, A. Bianchi, M. Mauri, R. Simonutti, R. Ruffo, R. Tubino and F. Meinardi, Adv. Energy Mater., 2013, 3, 680–686 CrossRef CAS.
- A. Monguzzi, M. Frigoli, C. Larpent, R. Tubino and F. Meinardi, Adv. Funct. Mater., 2012, 22, 139 CrossRef CAS.
- Y. C. Simon, S. Bai, M. K. Sing, H. Dietsch, M. Achermann and C. Weder, Macromol. Rapid Commun., 2012, 33, 498–502 CrossRef CAS PubMed.
- Y. C. Simon and C. Weder, J. Mater. Chem., 2012, 22, 20817 RSC.
- P. E. Keivanidis, S. Baluschev, T. Miteva, G. Nelles, U. Scherf, A. Yasuda and G. Wegner, Adv. Mater., 2003, 15, 2095–2098 CrossRef CAS.
- S. Baluschev, P. Keivanidis, G. Wegner, J. Jacob, A. Grimsdale, K. Müllen, T. Miteva, A. Yasuda and G. Nelles, Appl. Phys. Lett., 2005, 86, 061904 CrossRef PubMed.
- S. Bedair, M. Lamorte and J. Hauser, Appl. Phys. Lett., 1979, 34, 38–39 CrossRef CAS PubMed.
- N. H. Karam, R. R. King, M. Haddad, J. H. Ermer, H. Yoon, H. L. Cotal, R. Sudharsanan, J. W. Eldredge, K. Edmondson and D. E. Joslin, et al. , Sol. Energy Mater. Sol. Cells, 2001, 66, 453–466 CrossRef CAS.
- http://www.ise.fraunhofer.de/de/presse-und-medien/presseinformationen/presseinformationen-2013/weltrekord-solarzelle-mit-44-7-prozent-wirkungsgrad, 2013.
- A. Shah, P. Torres, R. Tscharner, N. Wyrsch and H. Keppner, Science, 1999, 285, 692–698 CrossRef CAS.
- Thin-film Silicon Solar Cells, ed. A. Shah, EPFL Press, Lausanne, Switzerland, 2010 Search PubMed.
- M. Wolf, Proc. IRE, 1960, 48, 1246 CrossRef.
- G. Güttler and H. Queisser, Energy Convers., 1970, 10, 51–55 CrossRef.
- P. Würfel, Sol. Energy Mater. Sol. Cells, 1993, 29, 403–413 CrossRef.
- A. Luque and A. Martí, Phys. Rev. Lett., 1997, 78, 5014 CrossRef CAS.
- M. Keevers and M. Green, J. Appl. Phys., 1994, 75, 4022–4031 CrossRef CAS PubMed.
- L. Sang, M. Liao, Q. Liang, M. Takeguchi, B. Dierre, B. Shen, T. Sekiguchi, Y. Koide and M. Sumiya, Adv. Mater., 2014, 26, 1414–1420 CrossRef CAS PubMed.
- N. López, L. Reichertz, K. Yu, K. Campman and W. Walukiewicz, Phys. Rev. Lett., 2011, 106, 028701 CrossRef.
- F. Auzel, C. R. Acad. Sci., 1966, 263, 819 Search PubMed.
- N. Menyuk, K. Dwight and J. Pierce, Appl. Phys. Lett., 1972, 21, 159–161 CrossRef CAS PubMed.
- M. Haase and H. Schäfer, Angew. Chem., Int. Ed., 2011, 50, 5808 CrossRef CAS PubMed.
- P. Gibart, J.-C. Guillaume and K. Zahraman, et al. , Jpn. J. Appl. Phys., 1996, 35, 4401 CrossRef CAS.
- A. Shalav, B. S. Richards and M. A. Green, Sol. Energy Mater. Sol. Cells, 2007, 91, 829–842 CrossRef CAS PubMed.
- J. C. Goldschmidt, S. Fischer, P. Löper, K. W. Krämer, D. Biner, M. Hermle and S. W. Glunz, Sol. Energy Mater. Sol. Cells, 2011, 95, 1960–1963 CrossRef CAS PubMed.
- S. Fischer, J. C. Goldschmidt, P. Löper, G. H. Bauer, R. Brüggemann, K. Krämer, D. Biner, M. Hermle and S. W. Glunz, J. Appl. Phys., 2010, 108, 044912 CrossRef PubMed.
- S. Fischer, A. Ivaturi, B. Fröhlich, M. Rüdiger, A. Richter, K. W. Krämer, B. S. Richards and J. C. Goldschmidt, IEEE J. Photovoltaics, 2014, 4, 183–189 CrossRef.
- S. K. MacDougall, A. Ivaturi, J. Marques-Hueso, K. W. Krämer and B. S. Richards, Sol. Energy Mater. Sol. Cells, 2014, 128, 18–26 CrossRef CAS PubMed.
- A. Ivaturi, S. K. MacDougall, R. Martín-Rodríguez, M. Quintanilla, J. Marques-Hueso, K. W. Krämer, A. Meijerink and B. S. Richards, J. Appl. Phys., 2013, 114, 013505 CrossRef PubMed.
- J. Goldschmidt, S. Fischer, B. Herter, B. Fröhlich, K. Krämer, B. Richards, A. Ivaturi, S. MacDougall, J. M. Hueso, E. Favilla and M. Tonelli, Proceedings of the European Photovoltaic Solar Energy Conference and Exhibition (EU PVSEC), 2014, p. 1AP.1.2 Search PubMed.
- J. de Wild, J. K. Rath, A. Meijerink, W. G. J. H. M. van Sark and R. E. I. Schropp, Sol. Energy Mater. Sol. Cells, 2010, 94, 2395–2398 CrossRef CAS PubMed.
- J. de Wild, A. Meijerink, J. K. Rath, W. G. J. H. M. van Sark and R. E. I. Schropp, Sol. Energy Mater. Sol. Cells, 2010, 94, 1919–1922 CrossRef CAS PubMed.
- J. de Wild, T. Duindam, J. Rath, A. Meijerink, W. Van Sark and R. Schropp, IEEE J. Photovoltaics, 2013, 3, 17–21 CrossRef.
- M. Liu, Y. Lu, Z. Xie and G. Chow, Sol. Energy Mater. Sol. Cells, 2011, 95, 800–803 CrossRef CAS PubMed.
- G.-B. Shan and G. P. Demopoulos, Adv. Mater., 2010, 22, 4373–4377 CrossRef CAS PubMed.
- L. Li, Y. Yang, R. Fan, Y. Jiang, L. Wei, Y. Shi, J. Yu, S. Chen, P. Wang, B. Yang and W. Cao, J. Power Sources, 2014, 264, 254–261 CrossRef CAS PubMed.
- C. Yuan, G. Chen, P. N. Prasad, T. Y. Ohulchanskyy, Z. Ning, H. Tian, L. Sun and H. Agren, J. Mater. Chem., 2012, 22, 16709–16713 RSC.
- J. Chang, Y. Ning, S. Wu, W. Niu and S. Zhang, Adv. Funct. Mater., 2013, 23, 5910–5915 CrossRef CAS.
- P. Ramasamy, P. Manivasakan and J. Kim, RSC Adv., 2014, 4, 34873–34895 RSC.
- T. F. Schulze, Y. Y. Cheng, B. Fückel, R. W. MacQueen, A. Danos, N. J. L. K. Davis, M. J. Y. Tayebjee, T. Khoury, R. G. C. R. Clady, N. J. Ekins-Daukes, M. J. Crossley, B. Stannowski, K. Lips and T. W. Schmidt, Aust. J. Chem., 2012, 65, 480–485 CrossRef CAS.
- R. W. MacQueen, T. F. Schulze, T. Khoury, Y. Y. Cheng, B. Stannowski, K. Lips, M. J. Crossley and T. Schmidt, SPIE Solar Energy + Technology, 2013, pp. 882408–882408 Search PubMed.
- T. F. Schulze, J. Czolk, Y.-Y. Cheng, B. Fuckel, R. W. MacQueen, T. Khoury, M. J. Crossley, B. Stannowski, K. Lips and U. Lemmer, et al. , J. Phys. Chem. C, 2012, 116, 22794–22801 CAS.
- A. Nattestad, Y. Y. Cheng, R. W. MacQueen, T. F. Schulze, F. W. Thompson, A. J. Mozer, B. Fckel, T. Khoury, M. J. Crossley, K. Lips, G. G. Wallace and T. W. Schmidt, J. Phys. Chem. Lett., 2013, 4, 2073–2078 CrossRef CAS.
- M. J. Y. Tayebjee, Ph.D. thesis, The University of Sydney, School of Chemistry, 2012.
- N. J. Ekins-Daukes and T. W. Schmidt, Appl. Phys. Lett., 2008, 93, 063507 CrossRef PubMed.
- C. M. Johnson and G. J. Conibeer, J. Appl. Phys., 2012, 112, 103108 CrossRef PubMed.
- A. C. Atre and J. A. Dionne, J. Appl. Phys., 2011, 110, 034505 CrossRef PubMed.
- J. A. Briggs, A. C. Atre and J. A. Dionne, J. Appl. Phys., 2013, 113, 124509 CrossRef PubMed.
- S. Baluschev, V. Yakutkin, G. Wegner, T. Miteva, G. Nelles, A. Yasuda, S. Chernov, S. Aleshchenkov and A. Cheprakov, Appl. Phys. Lett., 2007, 90, 181103 CrossRef PubMed.
- S. Baluschev and T. Miteva, in Next Generation of Photovoltaics, New Concepts, Springer, 2012, pp. 157–190 Search PubMed.
- T. F. Schulze, Y. Y. Cheng, T. Khoury, M. J. Crossley, B. Stannowski, K. Lips and T. W. Schmidt, J. Photonics Energy, 2013, 3, 034598 CrossRef PubMed.
- D. Sweet, E. Ott and J. A. Yorke, Nature, 1999, 399, 315–316 CrossRef CAS PubMed.
- M. Rüdiger, S. Fischer, J. Frank, A. Ivaturi, B. S. Richards, K. W. Krämer, M. Hermle and J. C. Goldschmidt, Sol. Energy Mater. Sol. Cells, 2014, 128, 57–68 CrossRef PubMed.
- J. C. Goldschmidt, P. Loper, S. Fischer, S. Janz, M. Peters, S. Glunz, G. Willeke, E. Lifshitz, K. Kramer and D. Biner, Conference on Optoelectronic and Microelectronic Materials and Devices (COMMAD), 2008, pp. 307–311 Search PubMed.
- A. Monguzzi, D. Braga, M. Gandini, V. C. Holmberg, D. K. Kim, A. Sahu, D. J. Norris and F. Meinardi, Nano Lett., 2014, 14, 6644–6650 CrossRef CAS PubMed.
- R. W. MacQueen, Ph.D. thesis, The University of Sydney, School of Chemistry, 2014.
- R. W. MacQueen, Y. Y. Cheng, A. N. Danos, K. Lips and T. W. Schmidt, RSC Adv., 2014, 4, 52749–52756 RSC.
- Y. Y. Cheng, A. Nattestad, T. F. Schulze, R. W. MacQueen, B. Fückel, K. Lips, G. G. Wallace and T. W. Schmidt, Prog. Photovoltaics, 2014, submitted Search PubMed.
- J. You, L. Dou, K. Yoshimura, T. Kato, K. Ohya, T. Moriarty, K. Emery, C.-C. Chen, J. Gao and G. Li, et al. , Nat. Commun., 2013, 4, 1446 CrossRef PubMed.
- S. Günes, H. Neugebauer and N. S. Sariciftci, Chem. Rev., 2007, 107, 1324–1338 CrossRef PubMed.
- M. Grätzel, Acc. Chem. Res., 2009, 42, 1788–1798 CrossRef PubMed.
- A. Yella, C.-L. Mai, S. M. Zakeeruddin, S.-N. Chang, C.-H. Hsieh, C.-Y. Yeh and M. Grätzel, Angew. Chem., 2014, 126, 3017–3021 CrossRef.
- A. Yella, H.-W. Lee, H. N. Tsao, C. Yi, A. K. Chandiran, M. K. Nazeeruddin, E. W.-G. Diau, C.-Y. Yeh, S. M. Zakeeruddin and M. Grätzel, Science, 2011, 334, 629–634 CrossRef CAS PubMed.
- T. Ameri, G. Dennler, C. Waldauf, H. Azimi, A. Seemann, K. Forberich, J. Hauch, M. Scharber, K. Hingerl and C. J. Brabec, Adv. Funct. Mater., 2010, 20, 1592–1598 CrossRef CAS.
- A. Colsmann, M. Reinhard, T.-H. Kwon, C. Kayser, F. Nickel, J. Czolk, U. Lemmer, N. Clark, J. Jasieniak, A. Holmes and D. Jones, Sol. Energy Mater. Sol. Cells, 2012, 98, 118–123 CrossRef CAS PubMed.
- Z. He, C. Zhong, S. Su, M. Xu, H. Wu and Y. Cao, Nat. Photonics, 2012, 6, 591–595 Search PubMed.
- H. Hoppe, N. Arnold, N. Sariciftci and D. Meissner, Sol. Energy Mater. Sol. Cells, 2003, 80, 105–113 CrossRef CAS.
- M. Grätzel, J. Photochem. Photobiol., C, 2003, 4, 145–153 CrossRef.
- A. Hagfeldt, G. Boschloo, L. Sun, L. Kloo and H. Pettersson, Chem. Rev., 2010, 110, 6595–6663 CrossRef CAS PubMed.
- Y. Murakami, Chem. Phys. Lett., 2011, 516, 56–61 CrossRef CAS PubMed.
- M. A. Green, K. Emery, Y. Hishikawa, W. Warta and E. D. Dunlop, Prog. Photovoltaics, 2014, 22, 701–710 Search PubMed.
- M. Rohde, M. Zelt, O. Gabriel, S. Neubert, S. Kirner, D. Severin, T. Stolley, B. Rau, B. Stannowski and R. Schlatmann, Thin Solid Films, 2014, 558, 337–343 CrossRef CAS PubMed.
- O. Khaselev and J. A. Turner, Science, 1998, 280, 425–427 CrossRef CAS.
- S. Y. Reece, J. A. Hamel, K. Sung, T. D. Jarvi, A. J. Esswein, J. J. Pijpers and D. G. Nocera, Science, 2011, 334, 645–648 CrossRef CAS PubMed.
- F. F. Abdi, L. Han, A. H. Smets, M. Zeman, B. Dam and R. van de Krol, Nat. Commun., 2013, 4, 2195 Search PubMed.
- J.-H. Kim and J.-H. Kim, J. Am. Chem. Soc., 2012, 134, 17478–17481 CrossRef CAS PubMed.
- R. R. Islangulov and F. N. Castellano, Angew. Chem., Int. Ed., 2006, 45, 5957–5959 CrossRef CAS PubMed.
- Z. Jiang, M. Xu, F. Li and Y. Yu, J. Am. Chem. Soc., 2013, 135, 16446–16453 CrossRef CAS PubMed.
- V. Gray, D. Dzebo, M. Abrahamsson, B. Albinsson and K. Moth-Poulsen, Phys. Chem. Chem. Phys., 2014, 16, 10345–10352 RSC.
- A. N. Danos, R. W. MacQueen, Y. Y. Cheng, M. J. Y. Tayebjee, M. Dvorak, T. Darwish and T. W. Schmidt, 2014, in preparation.
- C. M. Johnson, P. J. Reece and G. J. Conibeer, Opt. Lett., 2011, 36, 3990–3992 CrossRef CAS PubMed.
- C. Hofmann, B. Herter, J. Gutmann, J. Löffler, S. Fischer, S. Wolf, R. Piper, N. Ekins-Daukes, N. Treat and J. C. Goldschmidt, Proc. SPIE, 2014, 91400H Search PubMed.
- S. Schietinger, T. Aichele, H.-Q. Wang, T. Nann and O. Benson, Nano Lett., 2009, 10, 134–138 CrossRef PubMed.
- S. Baluschev, F. Yu, T. Miteva, S. Ahl, A. Yasuda, G. Nelles, W. Knoll and G. Wegner, Nano Lett., 2005, 5, 2482–2484 CrossRef CAS PubMed.
- K. Poorkazem, A. V. Hesketh and T. L. Kelly, J. Phys. Chem. C, 2014, 118, 6398–6404 CAS.
- A. C. Atre, A. García-Etxarri, H. Alaeian and J. A. Dionne, J. Opt., 2012, 14, 024008 CrossRef.
- P. C. Boutin, K. P. Ghiggino, T. L. Kelly and R. P. Steer, J. Phys. Chem. Lett., 2013, 4, 4113–4118 CrossRef CAS.
- J. Peng, X. Jiang, X. Guo, D. Zhao and Y. Ma, Chem. Commun., 2014, 50, 7828–7830 RSC.
- S. Baluschev, J. Jacob, Y. S. Avlasevich, P. E. Keivanidis, T. Miteva, A. Yasuda, G. Nelles, A. C. Grimsdale, K. Müllen and G. Wegner, ChemPhysChem, 2005, 6, 1250–1253 CrossRef CAS PubMed.
- P. Duan, N. Yanai and N. Kimizuka, J. Am. Chem. Soc., 2013, 135, 19056–19059 CrossRef CAS PubMed.
- J. S. Lissau, D. Nauroozi, M.-P. Santoni, S. Ott, J. M. Gardner and A. Morandeira, J. Phys. Chem. C, 2013, 117, 14493–14501 CAS.
- A. Turshatov, D. Busko, Y. Avlasevich, T. Miteva, K. Landfester and S. Baluschev, ChemPhysChem, 2012, 13, 3112–3115 CrossRef CAS PubMed.
- J.-H. Kim, F. Deng, F. N. Castellano and J.-H. Kim, ACS Photonics, 2014, 1, 382–388 CrossRef CAS.
- Q. Liu, B. Yin, T. Yang, Y. Yang, Z. Shen, P. Yao and F. Li, J. Am. Chem. Soc., 2013, 135, 5029–5037 CrossRef CAS PubMed.
- C. Wohnhaas, A. Turshatov, V. Mailander, S. Lorenz, S. Baluschev, T. Miteva and K. Landfester, Macromol. Biosci., 2011, 11, 772–778 CrossRef CAS PubMed.
- J.-H. Kang and E. Reichmanis, Angew. Chem., 2012, 124, 12011–12014 CrossRef.
- C. Wohnhaas, K. Friedemann, D. Busko, K. Landfester, S. Baluschev, D. Crespy and A. Turshatov, ACS Macro Lett., 2013, 2, 446–450 CrossRef CAS.
- A. Turshatov, D. Busko, S. Baluschev, T. Miteva and K. Landfester, New J. Phys., 2011, 13, 083035 CrossRef.
- M. Filatov, I. Ilieva, K. Landfester and S. Baluschev, Title: Exploring the IR-limit of the Triplet–Triplet Annihilation Upconversion: Tetraaryltetraanthra[2,3]porphyrin – family, Solar Power Technologies & Materials, in Nanotechnology 2013: Bio Sensors, Instruments, Medical, Environment and Energy, Nano Science and Technology Institute (NSTI), 2013, vol. 3, ch. 6, pp. 531–534 Search PubMed.
- F. Marsico, A. Turshatov, R. Peköz, Y. Avlasevich, M. Wagner, K. Weber, D. Donadio, K. Landfester, S. Baluschev and F. R. Wurm, J. Am. Chem. Soc., 2014, 136, 11057–11064 CrossRef CAS PubMed.
- T. N. Singh-Rachford and F. N. Castellano, J. Phys. Chem. A, 2008, 112, 3550–3556 CrossRef CAS PubMed.
- N. K. Giri, C. P. Ponce, R. P. Steer and M. F. Paige, Chem. Phys. Lett., 2014, 598, 17–22 CrossRef CAS PubMed.
- S. K. Sugunan, U. Tripathy, S. M. K. Brunet, M. F. Paige and R. P. Steer, J. Phys. Chem. A, 2009, 113, 8548–8556 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2015 |