Electronic tunability of the frustrated triangular-lattice cluster magnet LiZn_2−xMo₃O₈

Abstract

LiZn₂Mo₃O₈ is an electrically insulating geometrically frustrated antiferromagnet in which inorganic Mo₃O₁₃ clusters each behaves as a single S = 1/2 unit, with the clusters arranged on a two-dimensional triangular lattice. Prior results have shown that LiZn₂Mo₃O₈ does not exhibit static magnetic order down to at least T = 0.05 K, and instead possesses a valence bond ground state. Here, we show that LiZn₂Mo₃O₈ can be hole doped by oxidation with I₂ and subsequent removal of Zn²⁺ cations to access the entire range of electron count, from one to zero unpaired electrons per site on the triangular lattice. Contrary to expectations, no metallic state is induced; instead, the primary effect is to suppress the number of sites contributing to the condensed valence-bond state. Further, diffraction and pair-distribution function analysis show no evidence for local Jahn–Teller distortions or other deviations from the parent trigonal symmetry as a function of doping or temperature. Taken together, the data and density functional theory calculations indicate that removal of electrons from the magnetic layers favors Anderson localization of the resulting hole and an increase in the electrical band-gap over the formation of a metallic and superconducting state. These results put strong constraints on the chemical conditions necessary to realize metallic states from parent insulating geometrically frustrated antiferromagnets.

---

Conceptual insights

Emergence of complex behavior from simple components gives rise to the most spectacular and fascinating phenomena of the world around us, from the flocking of birds to life itself. Geometric magnetic frustration is a materials design tool used to engineer exotic emergent magnetic states of matter. One such state, the resonating valence bond, is thought to give way to high temperature superconductivity when doped away from perfect filling. In this manuscript, we report the ability to hole dope the triangular lattice antiferromagnet LiZn₂Mo₃O₈ without disturbing the magnetic layers. However, instead of metallic behavior, we find that all specimens remain insulating and that valence bonds become trapped near vacant sites. This localization effect can be understood as a consequence of the change in molecular energy levels upon oxidation. Often neglected in theoretical treatments, our experimental results unambiguously demonstrate that such energy level shifts must be considered in designing and understanding quantum spin liquids such as the resonating valence bond.

Emergent phenomena result from an ensemble of entities interacting to yield properties that appear greater than the sum of their parts. These phenomena can exist on a macroscopic scale, such as flocking birds or schooling fish, and on a microscopic scale, such as in superconducting,^1–4 quantum spin liquid,^5,6 spin ice,^7–9 charge-density wave,¹⁰ or heavy fermion^11,12 materials. Since the discovery of high-T_c superconductivity in the cuprates,^13,14 a major effort in condensed matter physics has been devoted to a rational theoretical explanation of the superconducting state. A proposed mechanism put forth by P. W. Anderson explained superconductivity in the La₂CuO₄ system¹⁵ as arising from itinerant, resonating spin singlets, or resonating valence-bonds¹⁶ (RVBs), as the underlying magnetic ground state to cooper pairing and superconductivity in the cuprates. A system of spins on a geometrically frustrated lattice, such as those on a two-dimensional triangular^17,18 or kagome^5,19–21 lattice with nearest neighbor antiferromagnetic interactions, can prevent long-range static magnetic order and harbor a RVB state. A Mott insulating RVB state that is charge doped and results in superconductivity would yield strong evidence for the RVB state as the yet unresolved theoretical explanation of high-T_c superconductivity.

LiZn₂Mo₃O₈ is a material composed of magnetic Mo₃O₈ layers, which consist of a triangular lattice of edge-sharing Mo₃O₁₃ clusters, separated by alkali and alkali earth cations (inset, Fig. 1(a)).† Each cluster has seven d-orbital valence electrons: six forming Mo–Mo bonds and one unpaired providing an S = 1/2 magnetic moment.²² Mo–O–Mo links between Mo₃O₁₃ clusters provide a superexchange pathway for antiferromagnetic spin interactions, resulting in a geometrically frustrated magnetic state. Inelastic neutron scattering²³ and a host of local magnetic measurements²⁴ indicate LiZn₂Mo₃O₈ is a spin liquid candidate, as it lacks any long range magnetic order above T > 0.05 K. Bulk magnetic susceptibility measurements indicate that upon cooling LiZn₂Mo₃O₈ below T = 100 K, two-thirds of the paramagnetic spins that previously contributed to the susceptibility effectively disappear without any experimental signature of long-range magnetic order. This is attributed to the formation of a condensed valence-bond state,²² in which two-thirds of the spins form valence bonds (probably resonating), while the remaining one-third spins continue to act paramagnetic down to the lowest temperatures. The origin of the stabilization of this magnetic ground state is unclear, but several theoretical proposals exist.^24–26

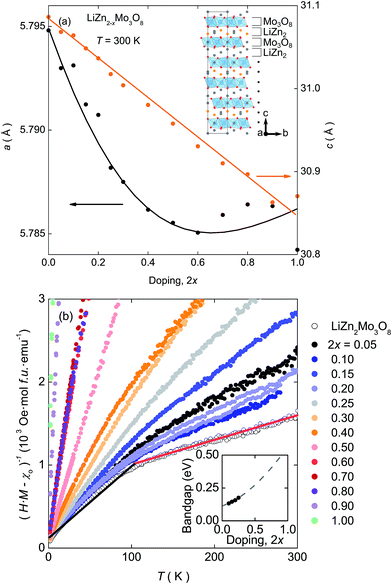Fig. 1 (a) Lattice parameters extracted from X-ray diffraction data over the entire doping range. The linear decrease in c is accompanied by an flattening and possible upturn in a at high doping levels. Inset: Structure of LiZn₂Mo₃O₈. The Zn-site where ∼90% of Zn²⁺ is removed upon doping† is shown in orange. (b) Curie–Weiss analysis of the magnetic susceptibility shows that the “kink” at T = 100 K (shown as the red and black lines on the 2x = 0 dataset), indicative of the formation of a condensed valence-bond state, is suppressed as holes are introduced into the lattice. Inset: Electronic bandgaps extracted from the electrical resistance measurements,† showing an increase upon hole doping.

Here we describe chemical hole doping of LiZn₂Mo₃O₈ over the range of one unpaired S = 1/2 electron per cluster to zero unpaired electrons per cluster via oxidation of LiZn₂Mo₃O₈ with elemental I₂. These doped samples are characterized by their magnetic, transport, and structural properties via magnetization, resistivity, X-ray powder diffraction (XRPD), neutron powder diffraction (NPD), and synchrotron X-ray powder diffraction (SXRD) experiments. Contrary to expectations, hole doping does not produce metallic behavior or superconductivity. Instead, the result is a smoothing of the transition into the condensed valence-bond state and an increase in the electrical bandgap, even though there are no average or local breaking of the trigonal symmetry. These results can be explained if the doped holes are trapped at individual sites, rather than being mobile on the lattice. Density functional theory (DFT) calculations provide a possible explanation for the lack of hole mobility in the form of a type of Anderson localization due to shifts in the individual energy levels of a Mo₃O₁₃ cluster when the electron count is changed from seven to six.

Hole doping LiZn₂Mo₃O₈ over the range LiZn₂Mo₃O₈ to LiZn_1.5Mo₃O₈ is accomplished by reacting LiZn₂Mo₃O₈ pellets or powder with elemental iodine²⁷ to form thermodynamically stable iodide salts with Li–Zn.† Surprisingly, reaction with I₂ vapor results in the formation of ZnI₂ as opposed to the more thermodynamically stable LiI. This was confirmed by the appearance of ZnI₂ crystals on the cold end of the quartz reaction vessels, identified as pure ZnI₂ by XRPD, with no detectable LiI phase in the product LiZn_2−xMo₃O₈. A possible explanation is that the higher vapor pressure of ZnI₂ compared to LiI allows it to be vapor transported to the cold end of the tube and irreversibly removed from the active reaction (Le Châtelier's principle). To test this, LiZn₂Mo₃O₈ was reacted with I₂ in tetramethylene sulfone at a temperature of T = 150 °C. The reaction was incomplete, as XRPD analysis indicated the formation of two phases by splitting the {00l} reflections. Nonetheless, a flame test revealed the presence of Li in the mothor liquor, and chemical analysis indicated that under these alternate, lower temperature, conditions both Li⁺ and Zn²⁺ were being deintercalated. This result suggests that the specificity for Zn²⁺ removal in the higher temperature conditions, even though Li is known to be highly mobile by NMR, is due to the irreversible removal of ZnI₂ by vapor transport. As it does not solely depend on relative ion mobilities in the host lattice, this method of chemical selectivity in a chimie douce reaction, i.e., irreversible removal of one product from the reaction, will likely have broader application in the preparation of metastable materials.

XRPD data of all samples are well described by the trigonal R3̄m structure of the parent compound.† The c lattice parameter, Fig. 1(a), follows Vegard's law and linearly decreases as a function of doping. However, the decrease is unexpected: in other systems where interlayer cations and anionic layers primarily interact via electrostatic attraction, removal of cations causes an increase in the c lattice parameter. The decrease indicates that in LiZn₂Mo₃O₈ there are more than simple electrostatic interactions between the Li–Zn layers and the Mo₃O₈ layers. Further, even though initially decreasing, there is an unusual flattening, and possible increase, in the in-plane a lattice parameter at high hole doping levels.

The electrical and magnetic properties also exhibit a continuous change as a function of electron count. The inverse susceptibility,†Fig. 1(b), shows a clear transition between two linear Curie–Weiss like regions in LiZn₂Mo₃O₈ that become less distinct as doping increases and disappear completely for 2x > 0.40. At the same time, resistivity measurements on polycrystalline pellets, inset Fig. 1(b), show a continuous increase in the electrical bandgap as holes are doped into LiZn_2−xMo₃O₈.†

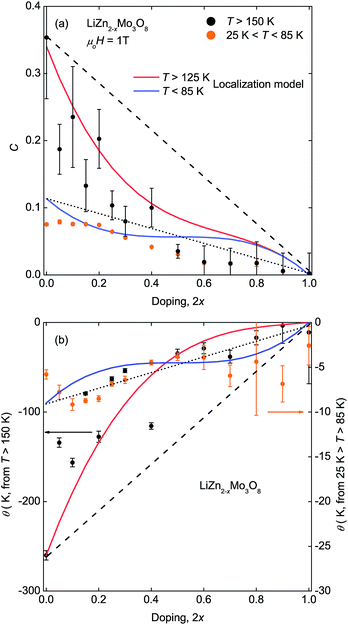
Extraction of the corresponding Curie constants, Fig. 2(a), and Weiss temperatures, Fig. 2(b), from the inverse susceptibility data reveals an interesting pattern. The Curie constant, proportional to the number of paramagnetic spins, starts close to the expected value of 0.375 for a full lattice of unpaired spins, but initially decreases three times faster than expected based on the change in electron count in the high temperature region (T ≥ 150 K). However, above 2x = 0.50, further increases in hole doping changes the Curie constants at high temperature more slowly and continuously toward zero. In contrast, the Curie constants extracted from the low temperature region (25 K ≤ T ≤ 85 K) vary more uniformly with hole doping. Similar trends are found for the Weiss temperatures, a measure of the net magnetic interactions present, for both the high temperature and low temperature regions.

Fig. 2 (a) Extracted Curie constants and (b) Weiss temperatures from two temperature ranges of the inverse susceptibility data, above T = 150 K and 25 K ≤ T ≤ 85 K. The experimental trends deviate strongly from simple linear behavior (dotted and dashed lines). Better agreement with experiment is obtained from a statistical calculation of the effect of removal of individual spins if each hole is fully localized and also localizes a neighboring valence bond (red and blue lines, see text).

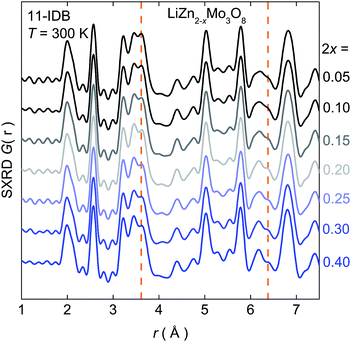
These deviations from simple expectations are not due to changes in crystallographic or local symmetry. Fig. 3 shows the pair distribution function (PDF), a scattering factor weighted atom–atom histogram, calculated from synchrotron X-ray data at room temperature on samples up to a doping level of 2x = 0.40. In addition to the series of nearest-neighbor metal–oxygen bonds around 2 Å, intra- and inter-cluster Mo–Mo distances are clearly resolved at 2.6 Å and 3.2 Å respectively.† These correlations remain sharp as holes are introduced, and rule out local structural changes of the Mo₃O₁₃ clusters that might explain the non-linearities in the physical properties. The only significant changes are those tied to the loss of Zn²⁺. Further, no changes are observed by neutron PDF at ambient or cryogenic conditions down to T = 2 K.† Rigorous analysis of synchrotron X-ray and neutron diffraction data similarly rules out large changes in the structure upon doping, beyond those expected from the change in the lattice parameters and removal of Zn²⁺.†

Fig. 3 X-ray pair-distribution functions as a function of r for doping up to 2x = 0.40. The orange lines at r ≈ 3.6 Å and r ≈ 6.3 Å correspond to Zn–Mo and Zn–O distances in the average structure, which decreases as Zn²⁺ is removed. There are no other significant changes in the local structure.

The most likely explanation of these data is that doped holes, rather than becoming mobile in the lattice, stay strongly localized. DFT band structure calculations and the resulting density of states (DOS), Fig. 4(a), provide insight into the origin of localization. The result of removing the magnetic valence electron from a cluster is a prominent increase in the energy of the now-empty orbital. Since the energy level is now significantly different than the filled states, it acts as a trap for the hole carrier and prevents free movement of electrons on the lattice. Put another way, the change in the electronic structure of each Mo₃O₁₃ cluster upon oxidation by one electron results in a form of Anderson localization²⁸ and is confirmed by the presence of three-dimensional variable range hopping in LiZn_2−xMo₃O₈ resistivity measurements.†

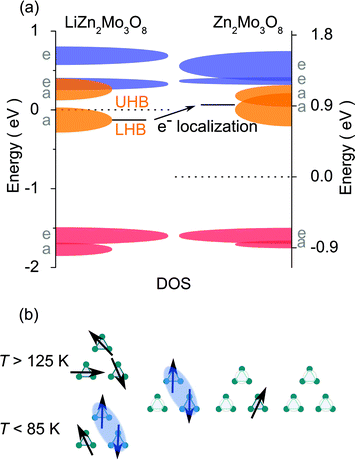Fig. 4 (a) Density of states diagram for LiZn₂Mo₃O₈ and Zn₂Mo₃O₈. Dashed lines are respective fermi energies. The “Zn₂Mo₃O₈” diagram has the same structure as LiZn₂Mo₃O₈, with the Li removed. Calculations suggest the effect of hole doping this material is an increase, relative to the fermi energy and the frontier orbitals, of the band corresponding to the highest filled orbital† once an electron is removed. (b) A local model of the effect of hole doping a triangular lattice antiferromagnet: when all sites are singlely occupied (left), there is a transition from a frustrated, paramagnetic state to a condensed valence bond one where two-thirds of the electrons collapse into singlets. Upon hole doping, a distribution of local configurations is formed: one hole localizes a valence bond singlet at all temperatures, two holes liberates a free paramagnetic spin, and three holes results in a non-magnetic state.

The non-linear trends in the a lattice parameter and Curie–Weiss parameters follow from this carrier localization. Because the hole carriers are localized, the effect on the underlying magnetic lattice can be modeled by assuming that, microscopically, the frustrated lattice is built of triangles of three Mo₃O₁₃ clusters containing three, two, one, or zero magnetic electrons, Fig. 4(b). The probability of occurance of each of these configurations is then set by statistics according to the fraction of holes put into the system. The easiest way to produce non-linear behavior is to assume, consistent with LiZn₂Mo₃O₈ being a frustrated antiferromagnet, that removal of one spin from a triangle will cause the other two to “disappear” into a singlet state. Thus, the only terms contributing to the measured susceptibility are when every site is full, and when two out of every three sites are empty. Fig. 2(a) shows the result of calculating the high- and low-temperature Curie constants from this model (red and blue lines). The qualitative features of the data are captured: initially there is a drop of the high-temperature Curie constant three times faster than expected due to formation of singlets even at T > 125 K, and then an extended plateau region where further addition of holes causes little change in the net Curie constant due to a competition between singlet localization and liberation of free spins due to two adjacent holes. Similar logic can be used to calculate the net magnetic interaction strength and Weiss temperature, shown in Fig. 2(b), with similar qualitative agreement with experiment that is substantially better than the naïve model. The agreement may be quantitative given the errors associated with the small signals being measured, but secondary effects, e.g., from hole (defect) clustering cannot be ruled out.

What do these results imply for the various theoretical models that have been proposed for the lack of a 120 degree magnetically ordered state in LiZn₂Mo₃O₈, the expectation for a nearest-neighbor triangular lattice antiferromagnet? The diffraction and local structure measurements put strict constraints on any deviations from the trigonal symmetry, on average or locally. This would seem to rule out the previously proposed cluster rotation model,²⁵ although small or highly dynamic (outside the energy range of the present measurements) distortions cannot be ruled out. This apparent adherence to trigonal symmetry also disfavors the explanation that the lack of magnetic order is simply due to a variation of local exchange interactions (due to Li–Zn mixing or other forms of disorder): if the frustration in LiZn₂Mo₃O₈ is only due to varying exchange interactions, then the magnetic ground state would be insensitive to the hole doping in LiZn_2−xMo₃O₈; instead, the formation of valence bonds (singlets) appears to be strongly favored in this material near doped holes. More recently, it was proposed that LiZn₂Mo₃O₈ may not fall into the fully localized molecular limit and instead possess a form of partial charge order.²⁶ In this model, all of the primary effects are in the electronic channel, and any structural changes would be secondary effects resulting from the electronic changes. Qualitatively, this is in better agreement with the present results, but more thorough calculations to understand the impact of the addition of holes on the partial charge order is needed in order to make a more definitive statement.

Here we described the reactions of LiZn₂Mo₃O₈ with increasing amounts of I₂ to remove Zn²⁺, thus hole doping the two dimensional triangular lattice antiferromagnet LiZn₂Mo₃O₈. The effect of Zn²⁺ doping is to systematically soften the transition between two linear Curie–Weiss regimes in the corrected inverse susceptibility. This doping is not accompanied by the appearance of metallic behavior or superconductivity as measured by magnetic susceptibility or resistivity. Instead, the doped holes undergo Anderson localization. This results in an increase in the electronic bandgap and the localization of neighboring singlets. Generally, these results suggest that cluster-based frustrated magnetic materials favor Anderson localization over a metal–insulator transition and/or superconductivity. It is yet to be seen if the same holds true for other (e.g. ionic based) GFM systems. Taken together, these findings imply that realizing a metallic or superconducting state in a doped frustrated antiferromagnet may require more careful control of the local energetics than previously thought.

Acknowledgements

This research was supported by the US Department of Energy (DOE), Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under Award DE-FG02-08ER46544 to The Institute for Quantum Matter at JHU. JPS would like to thank the William Hooper Grafflin Fellowship and Matt Suchomel (11-BM), Kevin Beyer (11-ID-B), and Mikhail Feygenson (NOMAD) for their assistance in collecting and reducing data. TMM acknowledges conversations with R. Flint, and G. Chen, and support from the donors of the American Chemical Society Petroleum Research Fund and the David and Lucile Packard Foundation. Use of the Advanced Photon Source, an Office of Science User Facility operated for the U.S. Department of Energy (DOE) Office of Science by Argonne National Laboratory, was supported by the U.S. DOE under Contract No. DE-AC02-06CH11357. A portion of this research at ORNL's Spallation Neutron Source was sponsored by the Scientific User Facilities Division, Office of Basic Energy Sciences, U.S. Department of Energy, under contract DE-AC05-00OR22725 with UT-Battelle, LLC.

References

1. Y. Kamihara, T. Watanabe, M. Hirano and H. Hosono, J. Am. Chem. Soc., 2008, 130, 3296–3297.
2. M. K. Wu, J. R. Ashburn, C. J. Torng, P. H. Hor, R. L. Meng, L. Gao, Z. J. Huang, Y. Q. Wang and C. W. Chu, Phys. Rev. Lett., 1987, 58, 908–910.
3. W. A. Phelan, D. C. Wallace, K. E. Arpino, J. R. Neilson, K. J. Livi, C. R. Seabourne, A. J. Scott and T. M. McQueen, J. Am. Chem. Soc., 2013, 135, 5372–5374.
4. K. Arpino, D. Wallace, Y. Nie, T. Birol, P. King, S. Chatterjee, M. Uchida, S. Koohpayeh, J.-J. Wen, K. Page, C. Fennie, K. Shen and T. McQueen, Phys. Rev. Lett., 2014, 112, 017002.
5. T.-H. Han, J. S. Helton, S. Chu, D. G. Nocera, J. A. Rodriguez-Rivera, C. Broholm and Y. S. Lee, Nature, 2012, 492, 406–410.
6. F. L. Pratt, P. J. Baker, S. J. Blundell, T. Lancaster, S. Ohira-Kawamura, C. Baines, Y. Shimizu, K. Kanoda, I. Watanabe and G. Saito, Nature, 2011, 471, 612–616.
7. D. J. P. Morris, D. A. Tennant, S. A. Grigera, B. Klemke, C. Castelnovo, R. Moessner, C. Czternasty, M. Meissner, K. C. Rule, J.-U. Hoffmann, K. Kiefer, S. Gerischer, D. Slobinsky and R. S. Perry, Science, 2009, 326, 411–414.
8. C. Castelnovo, R. Moessner and S. L. Sondhi, Nature, 2008, 451, 42–45.
9. S. Ladak, D. E. Read, G. K. Perkins, L. F. Cohen and W. R. Branford, Nat. Phys., 2010, 6, 359–363.
10. P. Cottingham, D. C. Miller, J. P. Sheckelton, J. R. Neilson, M. Feygenson, A. Huq and T. M. McQueen, J. Mater. Chem. C, 2014, 2, 3238–3246.
11. F. Steglich, J. Aarts, C. D. Bredl, W. Lieke, D. Meschede, W. Franz and H. Schfer, Phys. Rev. Lett., 1979, 43, 1892–1896.
12. J. R. Neilson, A. Llobet, A. V. Stier, L. Wu, J. Wen, J. Tao, Y. Zhu, Z. B. Tesanovic, N. P. Armitage and T. M. McQueen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 054512.
13. J. G. Bednorz and K. A. Mller, Zeitschrift fr Physik B Condensed Matter, 1986, 64, 189–193.
14. R. J. Cava, B. Batlogg, R. B. van Dover, D. W. Murphy, S. Sunshine, T. Siegrist, J. P. Remeika, E. A. Rietman, S. Zahurak and G. P. Espinosa, Phys. Rev. Lett., 1987, 58, 1676–1679.
15. P. W. Anderson, Science, 1987, 235, 11961198.
16. P. W. Anderson, Mater. Res. Bull., 1973, 8, 153160.
17. J. N. Reimers, J. R. Dahn, J. E. Greedan, C. V. Stager, G. Liu, I. Davidson and U. Von Sacken, J. Solid State Chem., 1993, 102, 542–552.
18. S. Nakatsuji, Y. Nambu, H. Tonomura, O. Sakai, S. Jonas, C. Broholm, H. Tsunetsugu, Y. Qiu and Y. Maeno, Science, 2005, 309, 1697–1700.
19. J. S. Helton, K. Matan, M. P. Shores, E. A. Nytko, B. M. Bartlett, Y. Yoshida, Y. Takano, A. Suslov, Y. Qiu, J.-H. Chung, D. G. Nocera and Y. S. Lee, Phys. Rev. Lett., 2007, 98, 107204.
20. I. S. Hagemann, Q. Huang, X. P. A. Gao, A. P. Ramirez and R. J. Cava, Phys. Rev. Lett., 2001, 86, 894–897.
21. M. S. Williams, J. P. West and S.-J. Hwu, Chem. Mater., 2014, 26, 1502–1504.
22. J. P. Sheckelton, J. R. Neilson, D. G. Soltan and T. M. McQueen, Nat. Mater., 2012, 11, 493496.
23. M. Mourigal, W. T. Fuhrman, J. P. Sheckelton, A. Wartelle, J. A. Rodriguez-Rivera, D. L. Abernathy, T. M. McQueen and C. L. Broholm, Phys. Rev. Lett., 2014, 112, 027202.
24. J. P. Sheckelton, F. R. Foronda, L. Pan, C. Moir, R. D. McDonald, T. Lancaster, P. J. Baker, N. P. Armitage, T. Imai, S. J. Blundell and T. M. McQueen, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 064407.
25. R. Flint and P. A. Lee, Phys. Rev. Lett., 2013, 111, 217201.
26. G. Chen, H.-Y. Kee and Y.-B. Kim, Unpublished, 2014, arXiv:1408.1963.
27. E. E. Rodriguez, P. Zavalij, P.-Y. Hsieh and M. A. Green, J. Am. Chem. Soc., 2010, 132, 10006–10008.
28. P. W. Anderson, Physical Review, 1958, 109, 1492–1505.

---

Footnotes

† Electronic supplementary information (ESI) available: Experimental methods, crystallographic tables, and additional data figures and in depth analysis. See DOI: 10.1039/c4mh00166d

‡ Present Address: Department of Chemistry, Colorado State University, Ft. Collins, Colorado 80523, USA.

---