Quaternary rare-earth selenides with closed cavities: Cs[RE9Mn4Se18] (RE = Ho–Lu)†
Hua
Lin
a,
Jin-Ni
Shen
ab,
Yong-Fang
Shi
a,
Long-Hua
Li
a and
Ling
Chen
*a
aKey Laboratory of Optoelectronic Materials Chemistry and Physics, Fujian Institute of Research on the Structure of Matter, Chinese Academy of Sciences, Fuzhou, Fujian 350002, People's Republic of China. E-mail: chenl@fjirsm.ac.cn; Tel: +(011)86-591-63173131
bUniversity of Chinese Academy of Sciences, Beijing 100039, People's Republic of China
First published on 21st January 2015
Abstract
New quaternary selenides, Cs[RE9Mn4Se18] (RE = Ho–Lu), have been synthesized by high temperature solid state reactions of elements with a reactive CsCl flux. These compounds adopt the BaV13O18-structure type in the trigonal space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) (no. 148) with a = 17.4867(8)–17.263(2) Å, c = 9.7996(8)–9.681(2) Å and Z = 3. The major structure motif is the 3D network that is constructed by octahedra of MSe6 (centered by disordered Mn and RE) and RESe6, in which closed cavities of cuboctahedra Cs@Se12 are embedded. This work extends the previously established empirical A/M-structure correlation in the ternary A/RE/Q system into quaternary A/RE/TM/Q, and A/M = 0.08 (A = the number of alkali metals, M = the sum of the numbers of RE and TM metals) represents the minimum ending value. The syntheses, properties, and theoretical analyses of the title compounds are also discussed.
(no. 148) with a = 17.4867(8)–17.263(2) Å, c = 9.7996(8)–9.681(2) Å and Z = 3. The major structure motif is the 3D network that is constructed by octahedra of MSe6 (centered by disordered Mn and RE) and RESe6, in which closed cavities of cuboctahedra Cs@Se12 are embedded. This work extends the previously established empirical A/M-structure correlation in the ternary A/RE/Q system into quaternary A/RE/TM/Q, and A/M = 0.08 (A = the number of alkali metals, M = the sum of the numbers of RE and TM metals) represents the minimum ending value. The syntheses, properties, and theoretical analyses of the title compounds are also discussed.
Introduction
Chalcogenides have attracted intense attention for not only their diverse structural chemistry,1 but also their interesting properties, such as superconducting, thermoelectric, nonlinear optical, or magnetic properties.2–5 The rich structural chemistry of ternary alkali metal/rare earth metal/chalcogenides (A/RE/Q) comes from the various linkages between the REQ6 octahedral building units. Previously, based on 70 ternary channel chalcogenides, we have proposed an interesting empirical structure correlation, that is the size of the channel within the anionic moiety decreases as the A/M ratio decreases (A = the number of alkali metals, M = the number of rare earth metals).6 For instance, as the A/M ratio decreases from 0.43, 0.33 to 0.20 on going from Rb3Yb7Se12,7 CsHo3Te5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 to RbSc5Te8,9 the number of A atoms accommodated per channel decreases monotonically from 4, 2, to 1 indicating the channel size reduction6 (Fig. 1, left). A/M = 1.0 is found in the infinite 2D layered structure, such as RbLaSe2.10 From the conceptual point of view, such adjacent 2D layers can be considered to be separated by channels with infinite radius. Thus, A/M = 1.0 represents the maximum ending value of the A/M-structure correlation.
8 to RbSc5Te8,9 the number of A atoms accommodated per channel decreases monotonically from 4, 2, to 1 indicating the channel size reduction6 (Fig. 1, left). A/M = 1.0 is found in the infinite 2D layered structure, such as RbLaSe2.10 From the conceptual point of view, such adjacent 2D layers can be considered to be separated by channels with infinite radius. Thus, A/M = 1.0 represents the maximum ending value of the A/M-structure correlation.
In this work, based on the systematic structure study of all available examples, we find that, in addition to ternary systems, the heterometallic anionic moiety in quaternary A/RE/TM/Q (TM = transition metals) systems also shows similar empirical A/M-correlation: as the A/M ratio decreases, the channel size decreases (note that M is now the sum of the numbers of RE and TM metals) (Fig. 1, right). Examples are ARETMQ3,11 ARE2TM3Q5,1 CsSc3Cu2Q6,12 K2CeAg3Te4,13 A3RE4Cu5Q10,1etc. On going from K2CeAg3Te4,13 K3Dy4Cu5Te10,1 to CsSc3Cu2Te6,12 as A/M decreases from 0.5, 0.33 to 0.2, the number of A atoms accommodated per channel drops from 4, 3 to 1 indicating the shrink of the channel. Note that TM and RE atoms usually have different local coordination behaviour, tetrahedron vs. octahedron, thus the corresponding monometallic and heterometallic anionic moieties differ in the structure considerably. Therefore, the A/M value may not be numerically equal for the corresponding ternary and quaternary structure-class (Fig. 1). For example, in the case of the 2D layered structure class, ternary compounds have an A/M of 1.0, but for quaternary it is 0.5. At A/M = 0.33, both ternary and quaternary compounds will be channel structures, but the former accommodates less A atoms per channel than the latter. Nevertheless, the principle A/M ratio–structure relationships coincide, and the channel size in both ternary and quaternary smoothly decreases until the A/M value drops to 0.2 (Fig. 1). Very interestingly, recent work shows that in the ternary system, when A/M = 0.14, the anionic moiety is no longer an open channel structure, instead it is a 3D network embedded with a closed cavity, such as in the CsLu7Q11 network, every two Cs atoms are captured into a dual-tricapped cube, Cs2@Se18.6 But if A/M in the quaternary system is further reduced, how the structure will change is yet unknown. Since low A/M ratio means low concentration of the reducing agent, it is also a great experimental challenge.
In this manuscript, we discover an even smaller A/M ratio of 0.08 in five new quaternary compounds, Cs[RE9Mn4Se18] (RE = Ho–Lu), with Cs atoms being captured into a smaller closed cavity of the Se12 cuboctahedron. The syntheses, crystal structure analyses, properties as well as theoretical analyses are reported.
Experimental section
Syntheses
Reactants were stored in an Ar-filled glovebox with controlled oxygen and moisture levels below 0.1 ppm. RE (99.95%) were purchased from Huhhot Jinrui Rare Earth Co., Ltd Se (99.999%) and Mn (99.99%) from Alfa Aesar, and CsCl (99.99%) from Sinopharm Chemical Reagent Co., Ltd.After numerous explorations on the experimental conditions including the starting reactant, loading ratio, and annealing temperature, the optimal synthesis conditions were established as loading a mixture (about 300 mg in total) of CsCl, RE, Mn and Se in a molar ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9
9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
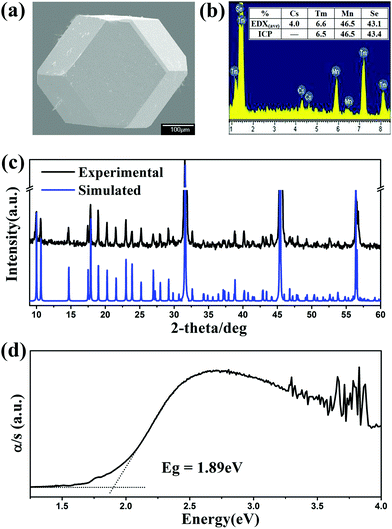
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 with a slight excess of CsCl as the reactive flux. The reactants were loaded in a fused-silica tube under vacuum, heated to 1223 K for 2 days, annealed at this temperature for 4 days, and then slowly cooled at 3 K h−1 to 473 K before switching off the furnace. Crystals of good quality were subsequently selected for single crystal X-ray diffraction studies, e.g. Cs[Tm9Mn4Se18] with a cuboctahedral crystal behaviour at room temperature (Fig. 2a). The EDX analyses carried out on several single crystals revealed the presence of Cs, RE, Mn, and Se in a ratio of 1
18 with a slight excess of CsCl as the reactive flux. The reactants were loaded in a fused-silica tube under vacuum, heated to 1223 K for 2 days, annealed at this temperature for 4 days, and then slowly cooled at 3 K h−1 to 473 K before switching off the furnace. Crystals of good quality were subsequently selected for single crystal X-ray diffraction studies, e.g. Cs[Tm9Mn4Se18] with a cuboctahedral crystal behaviour at room temperature (Fig. 2a). The EDX analyses carried out on several single crystals revealed the presence of Cs, RE, Mn, and Se in a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9
9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18. For example, CsTm9.1(3)Mn4.0(1)Se18.1(2) (Fig. 2b) was close to CsTm9.0(3)Mn4.0(3)Se18 as established by single-crystal diffraction data (Table 1 and Table S1 in ESI†). No other element was detected. The products were washed with distilled water to remove the excess CsCl and chloride by-products, and then dried with ethanol. After such a treatment, title compounds were obtained as pure phases according to the powder XRD patterns shown in Fig. 2c and Fig. S1 in ESI.† These compounds were stable in air for several months.
18. For example, CsTm9.1(3)Mn4.0(1)Se18.1(2) (Fig. 2b) was close to CsTm9.0(3)Mn4.0(3)Se18 as established by single-crystal diffraction data (Table 1 and Table S1 in ESI†). No other element was detected. The products were washed with distilled water to remove the excess CsCl and chloride by-products, and then dried with ethanol. After such a treatment, title compounds were obtained as pure phases according to the powder XRD patterns shown in Fig. 2c and Fig. S1 in ESI.† These compounds were stable in air for several months.
| Formula | Cs[Ho9Mn4Se18] | Cs[Er9Mn4Se18] | Cs[Tm9Mn4Se18] | Cs[Yb9Mn4Se18] | Cs[Lu9Mn4Se18] |
|---|---|---|---|---|---|
| a R 1 = ∑||Fo| − |Fc||/∑|Fo|, wR2 = [∑w(Fo2 − Fc2)2/∑w(Fo2)2]1/2. | |||||
| fw | 3258.31 | 3279.29 | 3294.32 | 3331.30 | 3348.64 |
| Crystal system | Trigonal | Trigonal | Trigonal | Trigonal | Trigonal |
| Space group |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) (no. 148) (no. 148) |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) (no. 148) (no. 148) |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) (no. 148) (no. 148) |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) (no. 148) (no. 148) |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) (no. 148) (no. 148) |
| a (Å) | 17.4867(8) | 17.441(4) | 17.360(2) | 17.3186(6) | 17.263(2) |
| c (Å) | 9.7996(8) | 9.785(3) | 9.724(2) | 9.6972(5) | 9.681(2) |
| V (Å3) | 2595.1(3) | 2577.9(2) | 2537.8(5) | 2518.9(2) | 2498.3(4) |
| Z | 3 | 3 | 3 | 3 | 3 |
| D c (g·cm−3) | 6.255 | 6.337 | 6.467 | 6.588 | 6.677 |
| μ (mm−1) | 41.679 | 43.215 | 45.174 | 46.800 | 48.590 |
| GOOF on F2 | 1.036 | 1.093 | 1.086 | 1.057 | 1.091 |
| R 1, wR2 (I > 2σ(I))a | 0.0285, 0.0653 | 0.0167, 0.0328 | 0.0411, 0.0868 | 0.0247, 0.0527 | 0.0305, 0.0768 |
| R 1, wR2 (all data) | 0.0305, 0.0663 | 0.0180, 0.0331 | 0.0459, 0.0888 | 0.0259, 0.0532 | 0.0308, 0.0770 |
| Largest diff. peak and hole (e Å−3) | 2.319, −1.379 | 2.250, −1.134 | 4.376, −3.865 | 1.448, −3.361 | 2.259, −2.127 |
Crystal structure determination
A Rigaku Mercury CCD diffractometer or a Rigaku Saturn724 CCD diffractometer equipped with graphite-monochromated Mo Kα radiation (λ = 0.71073 Å) was used for data collection at 293 K. The data were corrected for the Lorentz and polarization factor. Absorption corrections were based on the multiscan method.14 All structures were solved by direct methods and refined by the full-matrix least-squares fitting on F2 by SHELX-97.15 Taking Cs[Tm9Mn4Se18] as an example, the initial refinement generated one Cs, three Se, and three “Tm” atoms with R values of R1 = 9.86% and wR2 = 30.94%. Then, all three “Tm” sites were freely refined, after which the “Tm3” occupancy did not change, while those of the “Tm1” and “Tm2” sites decreased and the unbalanced formula “Cs3Tm25.37Se54” was converged. According to the EDX results, the compound should consist of Mn as well. Subsequently, Tm and Mn atoms were constrained to the same site (with identical coordinates and temperature factors) in SHELX. Meanwhile, the Tm to Mn ratio was fixed as 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to keep the charge balance, which is also in agreement with the EDX results. Finally, the structure refinement converged to R1 = 3.94%, wR2 = 8.54% with all atoms refined anisotropically and a formula of CsTm9.0(3)Mn4.0(3)Se18. Crystallographic data and structural refinement details are summarized in Table 1, the positional coordinates and isotropic equivalent thermal parameters are given in Table 2, and important bond distances are listed in Table 3.
1 to keep the charge balance, which is also in agreement with the EDX results. Finally, the structure refinement converged to R1 = 3.94%, wR2 = 8.54% with all atoms refined anisotropically and a formula of CsTm9.0(3)Mn4.0(3)Se18. Crystallographic data and structural refinement details are summarized in Table 1, the positional coordinates and isotropic equivalent thermal parameters are given in Table 2, and important bond distances are listed in Table 3.
| Atom | Symmetry | x | y | z |
U
(eq)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b (Å2) b (Å2) |
Occu. |
|---|---|---|---|---|---|---|
| a The RE and Mn were restricted to sum up 100% occupancy at each of M1 and M2 sites. b U (eq) is defined as one-third of the trace of the orthogonalized Uij tensor. | ||||||
CsHo9.0(3)Mn4.0(3)Se18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
||||||
| Cs1 | 3b | 0 | 0 | 0.5 | 0.0437(3) | 1 |
| M1 = Ho1/Mn1 | 18f | 0.24085(2) | 0.27636(2) | 0.33554(2) | 0.0086(2) | 0.84(2)/0.16(2) |
| M2 = Ho2/Mn2 | 18f | 0.40509(2) | 0.17719(2) | 0.33403(3) | 0.0107(2) | 0.49(2)/0.51(2) |
| Ho3 | 3a | 0 | 0 | 0 | 0.0090(2) | 1 |
| Se1 | 18f | 0.26808(3) | 0.15976(3) | 0.49798(4) | 0.0102(2) | 1 |
| Se2 | 18f | 0.12506(3) | 0.14042(3) | 0.16153(4) | 0.0100 (2) | 1 |
| Se3 | 18f | 0.38269(3) | 0.29806(3) | 0.16872(4) | 0.0080(2) | 1 |
CsEr9.0(3)Mn4.0(3)Se18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
||||||
| Cs1 | 3b | 0 | 0 | 0.5 | 0.0424(2) | 1 |
| M1 = Er1/Mn1 | 18f | 0.05694(2) | 0.42580(2) | 0.00200(2) | 0.0107(2) | 0.84(2)/0.16(2) |
| M2 = Er2/Mn2 | 18f | 0.15606(2) | 0.26151(2) | 0.00124(3) | 0.0110(2) | 0.49(2)/0.51(2) |
| Er3 | 3a | 0 | 0 | 0 | 0.0102(2) | 1 |
| Se1 | 18f | 0.01538(2) | 0.14024(3) | 0.16183(2) | 0.0104(2) | 1 |
| Se2 | 18f | 0.17362(2) | 0.39874(3) | 0.16483(2) | 0.0100(2) | 1 |
| Se3 | 18f | 0.28404(2) | 0.24875(3) | 0.16477(2) | 0.0101(2) | 1 |
CsTm9.0(3)Mn4.0(3)Se18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
||||||
| Cs1 | 3b | 0 | 0 | 0.5 | 0.0434(5) | 1 |
| M1 = Tm1/Mn1 | 18f | 0.05715(3) | 0.42611(3) | 0.00214(4) | 0.0136(2) | 0.82(2)/0.18(2) |
| M2 = Tm2/Mn2 | 18f | 0.15598(4) | 0.26149(4) | 0.00124(6) | 0.0159(2) | 0.51(2)/0.49(2) |
| Tm3 | 3a | 0 | 0 | 0 | 0.0155(3) | 1 |
| Se1 | 18f | 0.01525(5) | 0.13995(5) | 0.16192(8) | 0.0136(3) | 1 |
| Se2 | 18f | 0.17349(5) | 0.39881(5) | 0.16504(8) | 0.0140(3) | 1 |
| Se3 | 18f | 0.28447(5) | 0.24910(6) | 0.16443(8) | 0.0126(3) | 1 |
CsYb9.0(3)Mn4.0(3)Se18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
||||||
| Cs1 | 3b | 0 | 0 | 0.5 | 0.0352(2) | 1 |
| M1 = Yb1/Mn1 | 18f | 0.05696(2) | 0.42590(2) | 0.00194(2) | 0.0063(2) | 0.81(2)/0.19(2) |
| M2 = Yb2/Mn2 | 18f | 0.15606(2) | 0.26151(2) | 0.00124(3) | 0.0078(2) | 0.52(2)/0.48(2) |
| Yb3 | 3a | 0 | 0 | 0 | 0.0078(2) | 1 |
| Se1 | 18f | 0.01530(3) | 0.13988(3) | 0.16225(4) | 0.0069(2) | 1 |
| Se2 | 18f | 0.17347(3) | 0.39897(3) | 0.16543(4) | 0.0070(2) | 1 |
| Se3 | 18f | 0.28448(3) | 0.24905(3) | 0.16474(4) | 0.0056(2) | 1 |
CsLu9.0(3)Mn4.0(3)Se18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
||||||
| Cs1 | 3b | 0 | 0 | 0.5 | 0.0377(3) | 1 |
| M1 = Lu1/Mn1 | 18f | 0.05690(2) | 0.42596(2) | 0.00181(3) | 0.0107(2) | 0.82(2)/0.18(2) |
| M2 = Lu2/Mn2 | 18f | 0.15601(2) | 0.26155(2) | 0.00132(3) | 0.0120(2) | 0.52(2)/0.48(2) |
| Lu3 | 3a | 0 | 0 | 0 | 0.0118(2) | 1 |
| Se1 | 18f | 0.01530(3) | 0.13967(3) | 0.16247(5) | 0.0109 (2) | 1 |
| Se2 | 18f | 0.17355(3) | 0.39925(3) | 0.16547(5) | 0.0108(2) | 1 |
| Se3 | 18f | 0.28436(3) | 0.24904(4) | 0.16480(5) | 0.0093(2) | 1 |
| RE = Ho | RE = Er | RE = Tm | RE = Yb | RE = Lu | |
|---|---|---|---|---|---|
| M1–Se2 | 2.7782(5) | 2.7727(6) | 2.7556(9) | 2.7508(4) | 2.7437(6) |
| M1–Se1 | 2.8009(5) | 2.7946(7) | 2.7802(9) | 2.7740(4) | 2.7677(6) |
| M1–Se2 | 2.8087(5) | 2.8042(6) | 2.7874(9) | 2.7827(4) | 2.7761(6) |
| M1–Se3 | 2.8331(5) | 2.8257(7) | 2.8075(9) | 2.7994(5) | 2.7938(6) |
| M1–Se2 | 2.8358(5) | 2.8282(7) | 2.8126(9) | 2.8020(5) | 2.7944(6) |
| M1–Se3 | 2.8728(5) | 2.8661(7) | 2.8535(9) | 2.8438(4) | 2.8356(6) |
| M2–Se1 | 2.7650(6) | 2.7616(7) | 2.752(2) | 2.7480(5) | 2.7446(6) |
| M2–Se2 | 2.7720(6) | 2.7693(7) | 2.755(2) | 2.7524(5) | 2.7472(6) |
| M2–Se1 | 2.7961(6) | 2.7903(7) | 2.776(2) | 2.7717(5) | 2.7658(6) |
| M2–Se3 | 2.8413(5) | 2.8366(7) | 2.824(2) | 2.8186(5) | 2.8110(6) |
| M2–Se3 | 2.8516(5) | 2.8459(7) | 2.832(2) | 2.8250(5) | 2.8176(6) |
| M2–Se3 | 2.8538(5) | 2.8484(7) | 2.835(2) | 2.8260(5) | 2.8193(6) |
| RE3–Se1 × 6 | 2.8192(5) | 2.8120(6) | 2.7944(8) | 2.7879(4) | 2.7785(5) |
Powder X-ray diffraction
The powder XRD patterns were obtained at room temperature on a Rigaku DMAX 2500 powder X-ray diffractometer by using Cu Kα radiation (λ = 1.5418 Å) at room temperature. The purity and homogeneity of all phases were confirmed by comparison of the results from powder XRD with those calculated from single-crystal data.Elemental analysis
The semiquantitative microprobe elemental analysis was performed using a field emission scanning electron microscope (JSM6700F) equipped with an energy-dispersive X-ray (EDX) spectroscope (Oxford INCA) on clean single crystal surfaces. The Ultima-2 inductively coupled plasma (ICP) optimal emission spectrometer was used to quantitatively determine the composition of the hand-picked single crystals. The mass percentage of 46.3(2)% Tm, 6.5(3)% Mn and 43.4(2)% Se is also in good agreement with the single-crystal refinement stoichiometry (CsTm9Mn4Se18 mass percentage: 46.2% Tm, 6.7% Mn and 43.1% Se).UV-Vis-near IR spectroscopy
The optical diffuse reflectance spectra of powder samples were measured at room temperature using a Perkin-Elmer Lambda 900 UV-Vis spectrophotometer equipped with an integrating sphere attachment and BaSO4 as a reference in the range of 0.19–2.5 μm. The absorption spectrum was calculated from the reflection spectrum via the Kubelka–Munk function: α/S = (1 − R)2/2R, in which α is the absorption coefficient, S is the scattering coefficient, and R is the reflectance.16Magnetic susceptibility
The direct current magnetic susceptibility was measured using a Quantum Design PPMS-9 T magnetometer at a field of 1000 Oe in the temperature range of 2–300 K. The handpicked single crystals were ground to fine powder to minimize possible anisotropic effects and loaded into a gelatin capsule. The data were corrected for the susceptibility of the container and for the diamagnetic contribution from the ion core.Electronic structure calculations
The geometry optimization, band structure and density of states (DOS) were calculated by the Vienna ab initio simulation package (VASP).17a The generalized gradient approximation (GGA)17b was chosen as the exchange–correlation functional and a plane wave basis with the projector augmented wave (PAW)17c,d potentials was used. The plane-wave cut-off energy of 270 eV, and a threshold of 10−6 eV were set for the self-consistent-field convergence of the total electronic energy. The k integration over the Brillouin zone was performed by the tetrahedron method17e using total 172 k-points in the irreducible Brillouin zone (IBZ) and the Fermi level (EF = 0 eV) was selected as the reference of the energy. During the geometry optimization, an energy cutoff of 385 eV and a 3 × 3 × 3 Monkhorst–Pack k-point grid and the quasi-Newton minimization method were employed to make sure that the force on each atom is less than 0.02 eV Å−1. The results suggested that model-b5 is the most energetically favorable configuration (from Fig. 7 and Table S2†). To understand the distribution of Mn atoms in Cs[Tm9Mn4Se18], VASP calculations were carried out. As shown in Fig. 7 and Table S2,† 18 models of possible Mn-distribution were calculated. All models were constructed in a P1 primitive cell (ainit = binit = cinit = 10.538 Å, α = β = γ = 110.97°) instead of R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) . The optimal structural parameters were aopt ≈ bopt ≈ copt ≈ 10.565 Å, and α ≈ β ≈ γ ≈ 110.61°.
. The optimal structural parameters were aopt ≈ bopt ≈ copt ≈ 10.565 Å, and α ≈ β ≈ γ ≈ 110.61°.
Results and discussion
Structure description
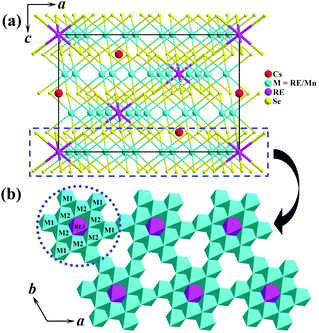
Compounds Cs[RE9Mn4Se18] crystallize in the BaV13O18 structure type18 in the trigonal space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) (no. 148) (Fig. 3). In the unit cell, M1 and M2 sites are disordered by RE1/Mn1 and RE2/Mn2 atoms with occupancies of 0.83/0.17 and 0.50/0.50, respectively. As usual, on going from Ho to Lu as indicated in Fig. 4, the lattice parameters of these compounds contract monotonically with the increase of the atomic number of the rare earth metal. In the structure, Cs and Se ions form a cubic close-packed arrangement along the c axis. Each M (or RE) is coordinated by 6 Se atoms forming an MSe6 (or RESe6) octahedron that is propagated by sharing edges and corners. Alternatively, the major structure motif can be described as the 3D framework condensed by MSe6 octahedra and RESe6 octahedra, in which the closed cavities, Cs centering Se12 cuboctahedra, are embedded (Fig. 5). As shown in Fig. 3b, the asymmetric unit, REM12Se42, is fused by 6 M1Se6, 6 M2Se6 and 1 RE3Se6 octahedra via edge-sharing with the normal M–Se or RE–Se bond distance (Table 3). Each REM12Se42 asymmetric unit is interconnected with other 6 neighbouring units into a 2D single layer parallel to the ab plane (Fig. 3b). Such layers connect to each other along the c direction via strong M–Se or RE–Se covalent bonding interactions into a trigonal 3D structure.
(no. 148) (Fig. 3). In the unit cell, M1 and M2 sites are disordered by RE1/Mn1 and RE2/Mn2 atoms with occupancies of 0.83/0.17 and 0.50/0.50, respectively. As usual, on going from Ho to Lu as indicated in Fig. 4, the lattice parameters of these compounds contract monotonically with the increase of the atomic number of the rare earth metal. In the structure, Cs and Se ions form a cubic close-packed arrangement along the c axis. Each M (or RE) is coordinated by 6 Se atoms forming an MSe6 (or RESe6) octahedron that is propagated by sharing edges and corners. Alternatively, the major structure motif can be described as the 3D framework condensed by MSe6 octahedra and RESe6 octahedra, in which the closed cavities, Cs centering Se12 cuboctahedra, are embedded (Fig. 5). As shown in Fig. 3b, the asymmetric unit, REM12Se42, is fused by 6 M1Se6, 6 M2Se6 and 1 RE3Se6 octahedra via edge-sharing with the normal M–Se or RE–Se bond distance (Table 3). Each REM12Se42 asymmetric unit is interconnected with other 6 neighbouring units into a 2D single layer parallel to the ab plane (Fig. 3b). Such layers connect to each other along the c direction via strong M–Se or RE–Se covalent bonding interactions into a trigonal 3D structure.
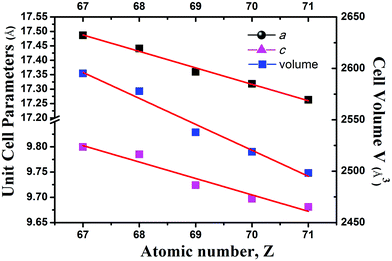 | ||
| Fig. 4 Plots of the unit cell parameters vs. the atomic number for Cs[RE9Mn4Se18] (RE = Ho–Lu) and the red lines represent the least-square fitting. | ||
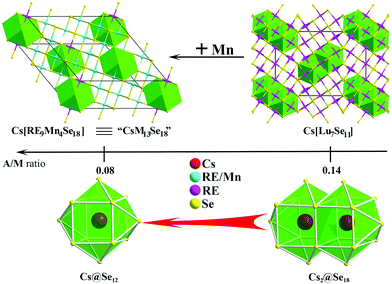 | ||
| Fig. 5 The structure comparison (up), A/M ratio (middle), and Cs-centering polyhedron (bottom) of Cs[RE9Mn4Se18] (left) and Cs[Lu7Se11] (right). | ||
Selected bond distances of Cs[RE9Mn4Se18] are shown in Table 3. All metal atoms (RE and M) are octahedrally coordinated by six Se atoms with distances of 2.7785(5)–2.8192(5) Å and 2.7437(6) Å–2.8661(5) Å for RE–Se and M–Se, respectively. These bond distances are consistent with those in CsREMnSe3 (RE–Se: 2.8360(5)–2.9325(5) Å and Mn–Se: 2.4996(8)–2.5898(7) Å),19 CsLu7Se11 (Lu–Se: 2.701(2)–2.911(1) Å),6 and Cs2Mn3Se4 (Mn–Se: 2.540(2)–2.576(3) Å).20 The Se–M–Se angles deviate from the ideal values (90° and 180°), ranging from 86.84(7)–94.71(9)°, and 175.9(2)–179.6(2)°, respectively. The Cs centering-cuboctahedron exhibits a 12-fold site symmetry with Cs–Se distances ranging from 3.9904(6) to 4.0846(5) Å, in comparison with those in CsLu7Se11 (3.634–4.133 Å),6 CsTaSe3 (3.996–4.004 Å),21 and CsRe6I3Se8 (3.955–4.076 Å).22 The same Se12 cuboctahedron is also observed in KCd4Ga5S12-type compounds.4b,23
Considering RE and Mn having the same coordination environment, the formula of title compounds can be written as [CsRE9Mn4Se18] ≡ “CsM13Se18”. As shown in Fig. 5, the title compounds and Cs[Lu7Se11]6 are 3D network structures made by metal–Se octahedra, within which cavities of either small cuboctahedra Cs@Se12 or large dual-tricapped cubes Cs2@Se18 are embedded. As the A/M ratio decreases from 0.14 to 0.08, the cavity size decreases from Se18 atoms to Se12. Previous studies suggest that when the A/M ratio drops from 1 to 0.2 (Fig. 1), the anionic moiety varies from infinite 2D layers to open channel structures, of which, the channel size gradually narrows and reaches the minimum at A/M = 0.2.6 The Cs[Lu7Q11] example illustrates that at A/M = 0.14, the open channel has been closed up into individual closed cavities.6 Here, we demonstrate nicely that the cavity size also reduces with the A/M decrease.
Optical and magnetic properties
According to the diffuse-reflectance spectra at room temperature, the band gaps were estimated to be 1.90 eV showing semiconducting behavior (Fig. 2d and S2†), which are in agreement with the color of the title compounds. These values are similar to those of CsYbMnSe3 (1.60 eV)19 and CsLu7Se11 (1.78 eV).6The magnetic susceptibility was measured at an applied field of 1000 Oe in the temperature range 2–300 K and shown as χ−1–T plots in Fig. 6. The susceptibility data in the temperature range 40–300 K were fit by a least-squares method to the Curie–Weiss equation χ = C/(T − θ), where χ is the magnetic susceptibility, C is the Curie constant and θ is the Weiss constant. The theoretical total effective magnetic moment can be calculated by the equation μeff(cal.) = [9μeff(RE)2 + 4μeff(Mn)2]1/2μB, and the experimental effective magnetic moment was calculated from the equation μeff(obsd.) = (7.997C)1/2μB.24 The resulting values for C, θ, and μeff are summarized in Table 4. The negative θ value suggests significant antiferromagnetic interactions existing between the magnetic ions. Furthermore, the experimental value of μeff for Cs[Ho9Mn4Se18] is smaller than the theoretical value calculated for Ho3+ and Mn2+. This presumably is attributed to that the 3d electrons of Mn lie in the outermost shell and are responsible for the magnetic behavior of Cs[Ho9Mn4Se18], whereas the electrons of the 4f shell of Ho lie deep inside the ion, within the 5s and 5p shells. Such a result is similar to that in CsTmMnSe3.19 The magnetic interactions should occur mainly between the centers M–M or RE–M (the nearest distance is around 3.90 Å).
 | ||
| Fig. 6 Temperature dependence of the inverse molar magnetic susceptibility (χ−1) of Cs[RE9Mn4Se18] (RE = Ho–Lu). | ||
| C (emu K mol−1) | θ (K) | μ eff (μB) obsd | μ eff (μB) cal. | |
|---|---|---|---|---|
| Cs[Ho9Mn4Se18] | 133.52 | −10.05 | 32.91 | 33.93 |
| Cs[Er9Mn4Se18] | 118.34 | −9.20 | 30.77 | 31.11 |
| Cs[Tm9Mn4Se18] | 79.43 | −18.29 | 25.20 | 25.61 |
| Cs[Yb9Mn4Se18] | 39.14 | −54.22 | 17.71 | 18.05 |
| Cs[Lu9Mn4Se18] | 16.06 | −6.28 | 11.53 | 11.84 |
Electronic structure
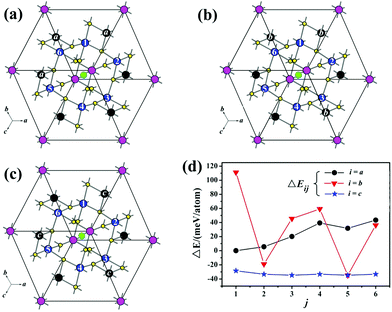
According to the single crystal structure refinement results, Mn and Tm atoms share each of the two sites (M1: blue and M2: black sites as shown in Fig. 7) with Mn occupancies of about 1/6 and 1/2, respectively. All the equivalent blue M1 sites are numbered by 1–6, of which only one can be occupied by Mn. Meanwhile, half of the six black M2 sites will be occupied by Mn according to one of the patterns of a, b, c. Consequently, total 18 possible configurations of the Mn-distribution had been designed and donated as model-ij (i = a, b and c; j = 1, 2, 3, 4, 5, 6) to probe the site preference of Mn atoms (Fig. 7a–c). The energy difference between each model and model-a1, ΔE (ΔE = Etol − Ea1), is calculated and listed in Table S2.† And the results reveal that the more the Mn ions are dispersed, the lower ΔE of the compound is (Fig. 7d), such as model-b5 and model-cj are the most energetically favorable configurations.To check the influence of the strong correlation effect at Mn sites, additionally GGA + U calculations were performed. The analyses indicated that the band gap of Cs[Tm9Mn4Se18] can be significantly widened by increasing U from 2 to 4 eV (see Fig. 8). Further increasing the effective Hubbard parameter does not alter significantly the calculated band gap value, which reaches a constant value of 1.68 eV. Consequently, the effective U (Ueff) of 5.0 eV was used for Mn in all the calculations carried out in this work. Similar Ueff was utilized in previous work.25
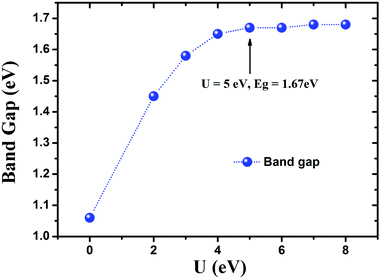 | ||
| Fig. 8 The Hubbard U effect on the band gap of Cs[Tm9Mn4Se18], calculated by the GGA + U method. The Hubbard correction is made to the Mn 3d states. | ||
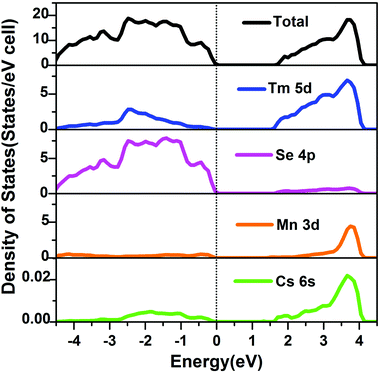
The on-site Coulomb correction was only applied to the Mn 3d electrons, which mostly increase the energy of empty 3d states, and widen the optical band gap. In order to simplify the calculation, the Tm 4f electrons were treated as core electrons. The total and partial DOSs of CsTm9Mn4Se18 were calculated, and the results revealed the semiconducting behavior and a band gap of about 1.67 eV (Fig. 9). The Ecal value is slightly smaller than Eexp (1.89 eV).
The valence band (VB) maximum near the Fermi level is mostly Se 4p states mixed with small contributions from Tm 5d and Mn 3d states, whereas the conduction band (CB) minimum is dominated by Tm 5d and Mn 3d states with minor contributions from Se 4p states. Cs atoms almost make no contribution around EF and act as electron donors to stabilize the structure. Accordingly, the optical absorptions are mainly assigned the charge transfer from Se 4p to Tm 5d and Mn 3d states.
Conclusion
In summary, new quaternary selenides, Cs[RE9Mn4Se18] (RE = Ho–Lu), have been synthesized by high temperature solid state reactions of elements with the reactive CsCl flux. They adopt the BaV13O18-structure type and the major structure motif is the 3D network that is constructed by octahedra of RESe6 and MSe6 (with disordered Mn and RE center), within which long-range ordered closed cavities of cuboctahedra Cs@Se12 are embedded. The Mn distribution on the anionic network (on M1 and M2 sites) is probed using single crystal diffraction data and is further discussed with the aid of VASP calculations. This work extends the empirical A/M-structure correlation established in the ternary A/RE/Q system into quaternary A/RE/TM/Q, and demonstrates that as the A/M ratio decreases from 0.14 to 0.08 (the minimum ending value to date), the cavity size decreases from Se18 atoms to Se12. To sum up, the A/M-structure correlation for chalcogenides can be better described as follows: when the A/M ratio drops from 1 to 0.2, the anionic moiety varies from infinite 2D layered to open channel structures with a gradually reduced channel size; at A/M = 0.14 for ternary, and 0.08 for quaternary, the anionic moiety is no longer an open channel structure, instead it is a 3D network embedded with individual closed cavities, of which the size also reduces with the A/M decrease. More examples to support such a regulation are in anticipation.Acknowledgements
This research was supported by the National Natural Science Foundation of China (21225104, 21233009, 91422303, 21301175 and 21171168).Notes and references
- K. Mitchell and J. A. Ibers, Chem. Rev., 2002, 102, 1929–1952 CrossRef CAS PubMed.
- (a) C. D. Malliakas, D. Y. Chung, H. Claus and M. G. Kanatzidis, J. Am. Chem. Soc., 2013, 135, 14540–14543 CrossRef CAS PubMed; (b) E. Gosøawska and M. Matlak, Phys. Status Solidi B, 1998, 207, 469–477 CrossRef.
- (a) D. Y. Chung, T. Hogan, P. Brazis, M. Rocci-Lane, C. Kannewurf, M. Bastea, C. Uher and M. G. Kanatzidis, Science, 2000, 287, 1024–1027 CrossRef CAS; (b) K. F. Hsu, S. Loo, F. Guo, W. Chen, J. S. Dyck, C. Uher, T. Hogan, E. K. Polychroniadis and M. G. Kanatzidis, Science, 2004, 303, 818–821 CrossRef CAS PubMed.
- (a) I. Chung, J. I. Jang, C. D. Malliakas, J. B. Ketterson and M. G. Kanatzidis, J. Am. Chem. Soc., 2010, 132, 384–389 CrossRef CAS PubMed; (b) H. Lin, L. Chen, L. J. Zhou and L. M. Wu, J. Am. Chem. Soc., 2013, 135, 12914–12921 CrossRef CAS PubMed.
- (a) A. C. Sutorik, J. Albritton-Thomas, T. Hogan, C. R. Kannewurf and M. G. Kanatzidis, Chem. Mater., 1996, 8, 751–761 CrossRef CAS; (b) G. H. Chan, C. Lee, D. Dai, M. H. Whangbo and J. A. Ibers, Inorg. Chem., 2008, 47, 1687–1692 CrossRef CAS PubMed; (c) H. J. Zhao, L. H. Li, L. M. Wu and L. Chen, Inorg. Chem., 2010, 49, 5811–5817 CrossRef CAS PubMed.
- H. Lin, L. H. Li and L. Chen, Inorg. Chem., 2012, 51, 4588–4596 CrossRef CAS PubMed.
- S. J. Kim, S. J. Park, H. S. Yun and J. W. Do, Inorg. Chem., 1996, 35, 5283–5289 CrossRef CAS.
- J. Y. Yao, B. Deng, D. E. Ellis and J. A. Ibers, J. Solid State Chem., 2005, 178, 41–46 CrossRef CAS PubMed.
- J. M. Babo and T. Scheid, Z. Anorg. Allg. Chem., 2008, 634, 1463–1465 CrossRef CAS.
- B. Deng, D. E. Ellis and J. A. Ibers, Inorg. Chem., 2002, 41, 5716–5720 CrossRef CAS PubMed.
- L. A. Koscielski and J. A. Ibers, Z. Anorg. Allg. Chem., 2012, 638, 2585–2593 CrossRef CAS.
- J. M. Babo and T. Schleid, Solid State Sci., 2010, 12, 238–245 CrossRef CAS PubMed.
- R. Patschke, P. Brazis, C. R. Kannewurf and M. G. Kanatzidis, Inorg. Chem., 1998, 37, 6562–6563 CrossRef CAS.
- CrystalClear, version 1.3.5, Rigaku Corp., The Woodlands, TX, 1999 Search PubMed.
- G. M. Sheldrick, SHELXTL, version 5.1, Bruker-AXS, Madison, WI, 1998 Search PubMed.
- G. Kortüm, Reflectance Spectroscopy, Springer-Verlag, New York, 1969 Search PubMed.
- (a) G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169–11186 CrossRef CAS; (b) J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter, 1992, 45, 13244–13249 CrossRef; (c) G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter, 1999, 59, 1758–1775 CrossRef CAS; (d) P. E. Blöchl, Phys. Rev. B: Condens. Matter, 1994, 50, 17953–17979 CrossRef; (e) P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter, 1994, 49, 16223–16233 CrossRef.
- (a) K. Iwasaki, H. Takizawa, K. Uheda, T. Endo and M. J. Shimada, Solid State Chem., 2001, 158, 61–67 CrossRef CAS; (b) K. Iwasaki, H. Takizawa, H. Yamane, S. Kubota, J. Takahashi, K. Uheda and T. Endo, Mater. Res. Bull., 2003, 38, 141–148 CrossRef CAS.
- K. Mitchell, F. Q. Huang, E. N. Caspi, A. D. McFarland, C. L. Haynes, R. C. Somers, J. D. Jorgensen, R. P. Van Duyne and J. A. Ibers, Inorg. Chem., 2004, 43, 1082–1089 CrossRef CAS PubMed.
- W. Bronger, H. Hardtdegen, M. Kanert, P. Mueller and D. Schmitz, Z. Anorg. Allg. Chem., 1996, 622, 313–318 CrossRef CAS.
- M. A. Pell, G. V. M. Vajenine and J. A. Ibers, J. Am. Chem. Soc., 1997, 119, 5186–5192 CrossRef CAS.
- J. R. Long, L. S. McCarty and R. H. Holm, J. Am. Chem. Soc., 1996, 118, 4603–4616 CrossRef CAS.
- (a) H. Schwer, E. Keller and V. Kramer, Z. Kristallogr., 1993, 204, 203–213 CrossRef CAS PubMed; (b) G. Krauss, E. Keller and V. Kraemer, Z. Kristallogr., 1996, 211, 188 CrossRef CAS.
- C. J. Oconnor, Prog. Inorg. Chem., 1982, 29, 203–283 CrossRef CAS.
- (a) A. Rohrbach, J. Hafner and G. Kresse, J. Phys.: Condens. Matter, 2003, 15, 979–996 CrossRef CAS; (b) H. B. Yahia, E. Gaudin, K. Boulahya, J. Darriet, W.-J. Son and M.-H. Whangbo, Inorg. Chem., 2010, 49, 8578–8582 CrossRef PubMed; (c) T. Chanier, M. Sargolzaei, I. Opahle, R. Hayn and K. Koepernik, Phys. Rev. B: Condens. Matter, 2006, 73, 134418 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: The cif file, experimental and theoretical methods, and additional tables and figures. CCDC 1044644–1044648. See DOI: 10.1039/c4qi00202d |
| This journal is © the Partner Organisations 2015 |