Influence of rare earth doping on the structural and electro-magnetic properties of SmFeAsO_0.7F_0.3 iron pnictide

Abstract

The effects of rare earth site doping on the structural, superconducting and magnetic properties of SmFeAsO_0.7F_0.3 iron pnictide are investigated. Gd³⁺ and Ce³⁺ ions are chosen by virtue of their position being on either side of Sm³⁺. Doping of both smaller (Gd³⁺) and larger (Ce³⁺) ions at the Sm³⁺ site increases the T_C up to 55 K. Doping with the smaller Gd³⁺ results in lattice contraction and thereby enhances T_C. It is interesting to observe that though Ce³⁺ doping in SmFeAsO_0.7F_0.3 exhibits an increase in lattice parameters, a substantial enhancement of T_C occurs. The enhancement in T_C due to increased charge carrier concentration is also confirmed using Hall Effect measurement. Apart from T_C enhancement, the simultaneous doping of both at oxygen and rare earth sites prominently increases the superconducting properties such as J_C, H_C1 and H_C2. The co-doped samples also exhibit better magnetic field dependence of J_C over the entire field of study. It is also observed that the Ce³⁺ doped sample shows higher J_C in the high field region due to its enhanced flux pinning properties.

---

Introduction

SmFeAsO_1−xF_x, superconductor belonging to the 1111 family of iron pnictides has received considerable attention in the field of superconductivity because of its very high upper critical field (H_C2) of the order of 100 T and a relatively high transition temperature (T_C).^1–4 Experiments were done rapidly to characterize the physical properties of this class of compounds and to explore different possibilities for further T_C enhancement.^5–7 New insights into the underlying physics of high-T_C superconductivity are also anticipated since the iron oxypnictides have some similarities to the cuprates with the simultaneous existence of a few significant dissimilarities too. The La1111 system behaves like MgB₂ in which thermal fluctuations of vortices do not significantly affect their behavior in the presence of strong magnetic fields to a large extent as it happens in the layered cuprates.⁸ However, the situation is different for the Sm1111 system having greater mass anisotropy and enhanced thermal fluctuations.⁹ Generally, the electronic band structure of the parent iron-based superconductors (REFeAsO, RE-rare earths) is semi-metallic, consisting of hole and electron Fermi surface pockets, separated by a (π, π) wave vector in momentum space.¹⁰ They have a layered crystal structure belonging to the tetragonal P4/nmm space group with alternating FeAs and REO layers in which conductivity occurs mainly in the FeAs layers while the REO layers act as charge reservoirs. Here the FeAs layer is negatively charged, and the REO layer is positively charged. The parent material shows a structural transition with temperature from the tetragonal to the orthorhombic phase and exhibits a spin density wave (SDW) order. Chemical doping in REFeAsO can suppress the structural transition and thereby SDW, leading to superconductivity. The carrier concentration in the FeAs layer increases by the substitution of F⁻ at the O²⁻ site or Th⁴⁺ at the RE³⁺ site and an increase in T_C is achieved by the creation of more carriers in the FeAs layer.^2,11 With doping the density of states of the system at the Fermi level was found to increase as the cell volume reduced, favoring the T_C enhancement. Both F⁻ for O²⁻ and Th⁴⁺ for RE³⁺ substitutions induce electrons as the charge carriers in the FeAs layer. Hole doping is another effective method to induce superconductivity in this material in which Sr²⁺ is substituted in place of the RE³⁺ site.¹² Oxygen deficiency also induces superconductivity; the crystal structure could be significantly modified compared with that of the parent compound, and T_C becomes maximum when the FeAs₄-lattices form a regular tetrahedron.¹³ Usually, in cuprate based superconductors any change made in the conducting layer (CuO layer) destroys superconductivity; however superconductivity is induced by doping in the FeAs layer of iron pnictides.¹⁴ In short, this system can sustain deliberately made changes in the conducting layer like doping at the Fe site and the creation of As vacancies.

Another key attraction of the 1111 family is the versatility of doping at different sites at the same time and thereby regulating the electronic properties of this system. Partial replacement of elements in the reservoir layer with those having different valencies or ionic radii causes lattice distortion and modification of crystalline as well as electronic structures. There are reports on doping at the rare earth site along with fluorine doping that improves or modifies the superconducting properties of iron pnictides.^7,15,16 Majority of the reports show that rare earth site doping was done with an element having a smaller ionic radius in order to obtain T_C enhancement. The higher T_C value is attributed to the increased internal chemical pressure from local lattice distortion induced by smaller-size dopants. In this paper, we have made an attempt to find the role of the ionic size of the dopant on the structural and superconducting properties of the superconductor by selectively choosing elements having smaller and larger ionic radii with respect to Sm³⁺. Herein, Gd³⁺ (93.5 pm) and Ce³⁺ (101 pm) were selected as dopants at the Sm³⁺ (95.8 pm) site in the SmFeAsO_0.7F_0.3 system. Sm_1−yRE_yFeAsO_0.7F_0.3 (RE = Gd, Ce) samples were prepared and their structural, as well as superconducting properties, were studied in detail.

Experimental

Polycrystalline samples of Sm_1−yRE_yFeAsO_0.7F_0.3 (RE = Gd, Ce) were prepared using a conventional solid state reaction method under ambient pressure. Powders of Sm, Fe, Fe₂O₃, and As were used as the starting materials (M/s Alfa Aesar, purity 99.9%). For rare earth site doping, pure metal powders of Gd and Ce were used. A nominal stoichiometric composition of SmFeAsO_0.7F_0.3 (Sm3), Sm_1−yGd_yFeAsO_0.7F_0.3 (y = 0.05, 0.10, 0.15, 0.20; named SmGd05, SmGd10, SmGd15, and SmGd20 respectively), Sm_1−yCe_yFeAsO_0.7F_0.3 (y = 0.05, 0.10, 0.15, 0.20; named SmCe05, SmCe10, SmCe15 and SmCe20 respectively) were chosen. The ingredients were stoichiometrically weighed and mixed thoroughly to form a homogeneous mixture. All chemical handlings were performed in an argon-filled glove box. The homogeneous mixture was compacted into rectangular pellets having dimensions of 15 × 5 × 2 mm, under a pressure of 500 MPa. The pellets were sealed inside evacuated quartz tubes and subjected to the following heating procedure. The samples were pre-processed at a temperature of 360 °C for 5 h. The pre-processed samples were again ground, pelletized, and sealed in evacuated quartz tubes and sintered at 850 °C for 30 h. In order to obtain dense pellets, the samples were again heat treated at a higher temperature of 1000 °C for 20 h. All the heating procedures were done in a programmable muffle furnace.

The phase identification of the samples was performed using an X-ray diffractometer (Philips X'Pert Pro) with CuKα radiation employing a proprietary high-speed detector and a monochromator at the diffracted beam side. Microstructural analysis of the samples was done using a scanning electron microscope (JEOL JSM 5600L). The compositional analysis of the samples was done using an energy-dispersive spectrometer attached to Nova Nano SEM 450. Resistivity versus temperature (ρ–T) measurement was carried out using a standard DC four probe method in a closed cycle cryocooler integrated cryostat (Janis Research Co., SHI SRDK-408 SW). The temperature dependence of AC susceptibility (χ–T) was measured using a closed cycle AC susceptometer (ARS-CS202S-DMX-19 SCC). DC magnetization measurements were carried out by using a Physical Property Measurement System (PPMS, Quantum Design). The ρ–T variation with applied magnetic fields and Hall Effect measurements were also carried out in a PPMS (Quantum Design DynaCool) using the four-probe method.

Results and discussion

The powder X-ray diffraction patterns of Gd and Ce doped samples after heat treatment show that the main phase formed in all the samples is SmFeAsO and their corresponding peaks are indexed on the basis of the tetragonal ZrCuSiAs-type structure with the space group P4/nmm (see Fig. S1†). In addition to the main phase, impurity phases of SmOF and FeAs are also present in all the samples. However, no secondary phases corresponding to Gd or Ce or their derivatives could be detected. The volume percentage of SmFeAsO, SmOF, and FeAs was estimated from the XRD data using the formula: vol% of phase X = (∑Integrated peak intensities of phase X)/(∑Integrated peak intensities of all phases), and the data is given in Table 1. The superconducting volume fraction is found to be about 90% or above for all the samples. Fig. 1(a) and (b) are enlarged representations of the XRD patterns around the main peak (102). The peak shows a shift in 2θ with doping. The (102) peak of Gd doped samples shifts towards the right, whereas that of Ce doped ones display a left shift with increasing doping content y. This is of course due to the RE³⁺ (Gd & Ce) doping at the Sm³⁺ site. The ionic radius of Gd³⁺ is smaller than that of Sm³⁺, but the ionic radius of Ce³⁺ is larger with respect to Sm³⁺. Doping with an element having smaller ionic radius usually gives a lattice parameter contraction, while doping with an element of larger ionic radius displays lattice expansion. Hence, the shift in the position of the peaks in the XRD pattern depicts the change of lattice parameters with Gd³⁺ and Ce³⁺ doping at the Sm³⁺ site. The substitution range of the dopants at the Sm³⁺ site in the SmFeAsO_0.7F_0.3 system was determined by measuring the change of lattice parameters with the nominal content, y. This is an accepted method for determining the extent of substitution due to which the lattice parameters increase or decrease linearly with increasing doping concentration and finally remains constant despite increasing dopant concentration.¹⁷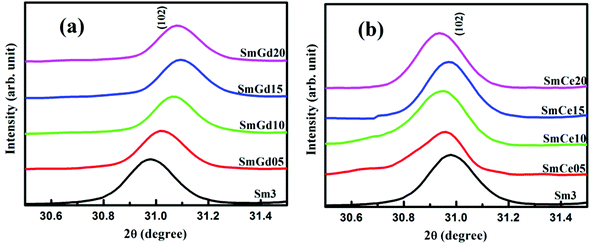

Fig. 1 Enlarged view of the main peak (102) of (a) Gd³⁺ doped and (b) Ce³⁺ doped samples with respect to Sm3.

Table 1 Quantitative phase and compositional analyses from XRD and EDX spectra

Sample name	Vol% of phases			Sm & Gd\Ce composition from EDAX				Lattice parameters (Å)		Density (g cm^−3)
	Pure	SmOF	FeAs	Sm		Gd\Ce		A	c
				Initial	Final	Initial	Final
Sm3	94.4	4.2	1.4	1.000	0.986	0.000	0.000	3.935(1)	8.486(2)	4.85
SmGd05	90.9	7.4	1.7	0.950	0.935	0.050	0.044	3.928(2)	8.480(1)	4.87
SmGd10	91.8	6.4	1.8	0.900	0.869	0.100	0.090	3.925(1)	8.475(1)	5.32
SmGd15	91.5	6.4	2.1	0.850	0.827	0.150	0.146	3.925(1)	8.467(1)	5.28
SmGd20	90.6	7.1	2.3	0.800	0.772	0.200	0.194	3.925(2)	8.468(2)	5.39
SmCe05	94.6	4.3	1.1	0.950	0.927	0.050	0.042	3.936(1)	8.492(2)	5.33
SmCe10	94.9	4.1	1.0	0.900	0.865	0.100	0.084	3.937(2)	8.497(1)	5.38
SmCe15	93.8	4.9	1.3	0.850	0.826	0.150	0.118	3.940(1)	8.498(2)	5.30
SmCe20	89.6	7.4	3.0	0.800	0.793	0.200	0.166	3.941(2)	8.499(1)	5.28

---

The lattice parameters a and c were calculated from Rietvield refined X-ray diffraction patterns and their variation with respect to doping concentration (y) is shown in Fig. 2(a) and (b). The refined lattice parameters obtained for the sample Sm3 (y = 0) are a = 3.935 Å and c = 8.486 Å. With Gd³⁺ doping, both a and c lattice parameters decrease systematically with nominal increase in the Gd content. For y = 0.15, both the lattice parameters reduce to a = 3.925 Å and b = 8.468 Å, but remain almost constant beyond y = 0.15. This suggests that the solubility limit of the Gd³⁺ ions is reached at y = 0.15 in the SmFeAsO_0.7F_0.3 system. Since the ionic size of Gd³⁺ is smaller than that of Sm³⁺, the above result confirms the successful substitution of Gd³⁺ at the Sm³⁺ site. However, Ce³⁺ doping at the Sm³⁺ site results in an elongation of both a and c lattice parameters. Lattice values increase with nominal increase in the y content up to y = 0.15 and then remains almost stagnant for y > 0.15. This is due to the larger ionic size of Ce³⁺ ions than that of Sm³⁺.

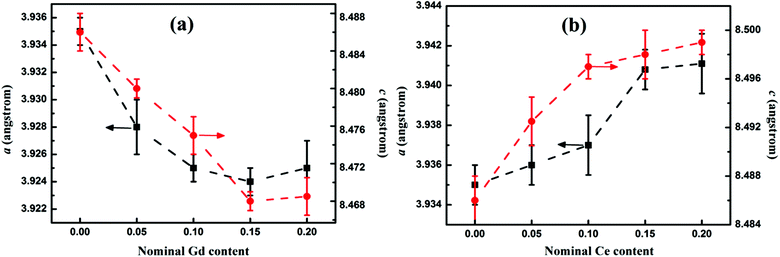Fig. 2 Variation of lattice parameters a and c of the samples Sm_1−yRE_yFeAsO_0.7F_0.3 (RE = Gd, Ce) with variation in y, (a) nominal Gd content and (b) nominal Ce content.

In order to determine the exact composition of the samples, we have performed EDX (Energy Dispersive X-ray) spot analysis on all the samples. Typical EDX patterns of Gd³⁺ and Ce³⁺ doped ones (SmGd10 and SmCe10) are shown in Fig. S2.† The C peak observed in the spectra is due to the carbon tape used for sample fixing on the SEM stub. The quantitative analysis shows that Fe, As, O and F amounts to a stoichiometry of around 1, 0.9, 0.7 and 0.2, respectively for all the samples. Though the quantification of light weight elements using EDX is not fully reliable, the observations clearly indicate the fluorine loss in all the samples. The doped samples contain the presence of Ce and Gd peaks in SmCe10 and SmGd10, respectively. In the EDX spectrum of SmGd10 an overlap of Sm and Gd exists since their energy levels are close enough. Nevertheless, the quantitative Sm and Gd/Ce composition of all the samples evaluated from EDX is given in Table 1. The Sm/RE ratio in all the samples is almost equal to the corresponding nominal value. The phase formation and effective doping of Ce/Gd in Sm1111 observed in XRD is thus confirmed using EDX.

Significant microstructural variation resulting from both Gd³⁺ and Ce³⁺ doping at the Sm site is observed from the SEM images of the samples. Fig. S3† shows the SEM images of the freshly fractured surfaces of the sample Sm3 and selected samples of Gd³⁺ (SmGd10 & SmGd20) and Ce³⁺ (SmCe10 & SmCe20) doped ones. All the samples exhibit a layered flaky morphology, a typical feature of iron pnictides. The pure sample, Sm3 exhibits a mix of layered flaky structure with well-defined edges and occasional granularity present near the voids. With rare earth site doping, these voids get reduced and the sample density increases. The densities of the samples were also calculated using Archimedes’ principle and the obtained values are included in Table 1. We can see that the co-doping in the Sm1111 system increases the density of the samples and that their values are getting closer to the theoretical density of iron pnictides.¹⁸ The layered grains are stacked randomly and hence the weak links present at the grain boundaries limit the transport current flow. With Ce³⁺ doping the surface microstructure changes from the layered flaky nature of pure Sm3 to a more granular (Fig. S3† SmCe10 and SmCe20) one. It is also observed that higher doping of Ce³⁺ degrades the microstructure (SmCe20 in Fig. S3†). The average grain sizes of the samples were also estimated statistically using software. The grain size of the samples Sm3, SmGd10 and SmGd20 is found to be almost the same and is around 3.5 μm. However, smaller grains having sizes of about 1.8 μm and 1.6 μm are obtained for SmCe10 and SmCe20, respectively.

Fig. 3 shows the resistivity versus temperature (ρ–T) plots of Sm_1−yRE_yFeAsO_0.7F_0.3 (RE = Gd, Ce) samples at zero magnetic field. The temperature at which resistivity falls sharply is taken as the T_C and the observed T_C values of all the samples are given in Table 2. All the samples show rather narrow transitions into the superconducting state at their respective transition temperatures and the sample Sm3 has a T_C at 46 K. But this value is lower than the highest T_C value (∼55 K) reported for the Sm1111 system elsewhere.^5,19 The difficulty in preventing or controlling the volatile loss of fluorine at higher processing temperature could be the main reason behind the reduction in T_C. However, in the present work all the samples i.e. a fluorine only doped sample and Ce and Gd co-doped samples were prepared using the same fluorine stoichiometry and all these were synthesized under identical conditions. Therefore, we used SmFeAsO_0.7F_0.3 as the reference sample. It is to be observed that due to the volatile loss of fluorine, the value of the F content in all the samples is almost identical and below the optimum level as observed from EDX. Interestingly, it is observed that both Gd³⁺ and Ce³⁺ doping with y = 0.1 increases the T_C from 46 to around 55 K. An enlarged view of the ρ–T plot near T_C is given in the inset of Fig. 3. A T_C of 54.6 K is obtained by Gd³⁺ substitution at the Sm³⁺ site (y = 0.1) and a T_C of 55.0 K for the Ce³⁺ (y = 0.1) substituted sample. The T_C value of the Gd³⁺ doped sample improves from 46 to 52.4 K for a stoichiometry of y = 0.05 and reaches a maximum at y = 0.1. Further doping of Gd³⁺ slightly reduces the T_C value and then remains almost constant irrespective of further increase in the dopant concentration. In the case of Ce³⁺ doping, maximum T_C is obtained for y = 0.1 and further doping reduces the T_C. It was observed that the over doping of Ce³⁺ considerably reduces the T_C. Therefore, in the present case the optimum doping concentration obtained for both Gd³⁺ and Ce³⁺ doping is found to be around y = 0.1.

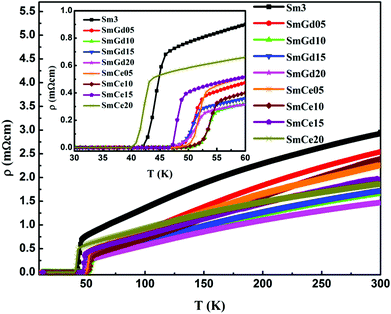Fig. 3 ρ–T plots of Sm3 (SmFeAsO_0.7F_0.3) as well as Gd³⁺ and Ce³⁺ doped samples; inset is an enlarged view around T_C.

Table 2 Different parameters observed for the samples from ρ–T and χ–T plots

Samples		Sm3	SmGd05	SmGd10	SmGd15	SmGd20	SmCe05	SmCe10	SmCe15	SmCe20
T C (K)	ρ–T	46.0	52.4	54.6	52.7	52.6	53.1	55.0	49.6	43.9
	χ–T	45.7	52.0	54.0	52.1	52.1	52.8	54.7	49.4	44.1
ρ 300 (mΩ cm)		2.9	2.5	1.7	1.7	1.5	2.3	2.4	1.9	1.8
RRR		3.4	6.2	6.2	5.4	5.3	5.1	6.1	3.9	2.8

---

Moreover, the normal state resistivity (ρ₃₀₀) of the sample Sm3 decreases with rare earth site doping and the resistivity of all samples show nearly linear behavior with temperatures down to a characteristic temperature and thereafter the resistivity drops more quickly down to T_C. The abrupt deviation from linearity in the ρ–T plot is due to the presence of a pseudogap, already reported in Sm-based iron pnictides.^20,21 Another observation is the suppression of this pseudo gap at optimum doping of both Ce and Gd. The residual resistivity ratio RRR (ρ₃₀₀/ρ₅₅) of the doped samples increased significantly up to the optimum doping level of y = 0.1 with respect to that of Sm3 (up to 6.2 from 3.4), indicating stronger impurity scattering in the rare earth doped ones. The ρ₃₀₀ and RRR values of all samples are given in Table 2.

In the case of Gd³⁺ doping, Sm³⁺ is replaced with a smaller ion which would create an internal chemical pressure in the system. Here, the substitution of a smaller Gd³⁺ ion in place of Sm³⁺ reduces both a and c values of the system and creates an isotropic lattice shrinkage. This triggers charge transfer from the charge reservoir layer (Sm₂O₂) into the conducting FeAs layer of the Sm1111 system.^22,23 Consequently, the T_C of the system increases with Gd doping, but only up to y = 0.1, beyond which T_C shows a decreasing tendency. This type of behavior was already reported in Y doped RE1111 systems.^16,22,24,25 Application of an external pressure into the system also exhibits a similar tendency if the sample is in the under doped region.^26,27 While the effect of pressure for the over doped iron pnictide compounds is different or even opposite, i.e. in over doped samples, monotonic decrease of T_C with pressure is expected.^28–30 However, in the present case, the F doped sample is in the under doped region and hence Gd³⁺ doping induces a positive chemical pressure on T_C, up to its optimum doping level.

Even though creation of an internal chemical pressure is regarded as an essentiality for the suppression of SDW instability and T_C enhancement, it is interesting to observe that Ce³⁺ doping in the multiband superconductor Sm1111 exhibits a lattice parameter increase and a substantial enhancement in T_C up to y = 0.1. It is to be noted that, unlike other rare earth elements, elemental Ce can attain a multiple valency of 3 and 4 or mixed valency depending on the surrounding environment at lower temperatures.³¹ The delocalized 4f electrons in cerium can fluctuate between two extreme valence states depending upon their local atomic configurations within the system. In the present case the structural modification created by the larger Ce³⁺ ion does not favor an increase in T_C but it is probably due to a change in valency from 3⁺ to 4⁺ at low temperatures that increases the charge density in the conducting layer. The possibility of variation of valency at lower temperatures could be the reason for the observed T_C enhancement. The observations conclude that, despite the difference in lattice parameter variation and origin of T_C enhancement, both Ce³⁺ and Gd³⁺ doped systems show a critical doping level of y = 0.1 and the maximum T_C achieved is around 55 K. Thus, the variation of T_C with the doping content i.e. dT_C/dy shows a sign reversal above y = 0.1. Doping of Ce³⁺ and Gd³⁺ ions can modify the Sm1111 system both structurally and in terms of density of states only up to a critical point above which the system gets distorted.

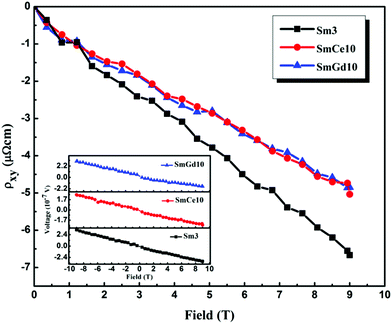
Although, Ce and Gd doping in the Sm1111 system have a different impact on the system, both of them eventually enhance the T_C through effective increase in carrier concentration. Hence, an assessment of the charge density of the optimally doped samples is highly essential. For this, we conducted Hall Effect measurements on selected samples (RE-free sample, Sm3 and optimally doped samples from RE-doped sets, SmGd10 and SmCe10). The measurements were done on rectangular pellets of uniform thickness and the transverse Hall-voltage was measured by connecting voltage leads at the middle of the pellets, exactly perpendicular to the line of the current leads and to the direction of the applied magnetic field. The magnetic field was applied in such a way that its direction is perpendicular to the plane of the rectangular pellet. In order to avoid the contribution from longitudinal resistance, the magnetic field was swept from 9 T to −9 T and then the Hall-voltage was estimated by subtracting the longitudinal part. The variation of transverse resistivity (ρ_xy) with the magnetic field at a fixed temperature of 100 K for the samples Sm3, SmCe10, and SmGd10 is shown in Fig. 4. The inset of Fig. 4 shows the measured voltage at 100 K by varying the magnetic field from 9 T to −9 T. Both Sm3 and RE-doped samples show negative Hall resistivity and also exhibit linear field dependence. From these linear ρ_xy–B plots, the Hall coefficient of the samples were calculated as R_H = ρ_xy/B. The R_H values of the samples are −7 × 10⁻⁹ m³ C⁻¹, −5.1 × 10⁻⁹ m³ C⁻¹, and −5.0 × 10⁻⁹ m³ C⁻¹ for Sm3, SmCe10, and SmGd10, respectively. The negative R_H values indicate that electrons are the major charge carriers in the samples.³² We can also see that this negative value of R_H decreases with RE doping, indicating the increase in the charge carrier density of the samples with both Gd and Ce doping at the Sm site. Moreover, the obtained R_H values for optimally doped samples are almost equal which shows that the charge carrier densities within the optimally doped samples are more or less the same and also higher than Sm3. The charge carrier densities for the samples Sm3, SmCe10, and SmGd10 (calculated from the equation n_e = 1/R_He) are 0.89 × 10²⁷ m⁻³, 1.23 × 10²⁷ m⁻³, and 1.25 × 10²⁷ m⁻³, respectively. Thus, substitution of both smaller and larger ions at the Sm site relatively improves the charge carrier density of the system and hence favors the T_C enhancement. The lattice shrinkage due to smaller isovalent Gd ions in Gd doped samples and the mixed valency nature of Ce in Ce doped ones assist the increase in charge density.

Fig. 4 Magnetic field dependence of Hall resistivity, ρ_xy of the samples Sm3, SmCe10 and SmGd10 measured at a temperature of 100 K. Inset shows the measured voltage at 100 K by varying the magnetic field from 9 to −9 T.

The real (χ′) and imaginary (χ′′) components of the AC susceptibility (at frequency, f = 208 Hz and AC field, H_ac = 4.94 × 10⁻⁴ T) as a function of the temperature have been investigated. Both χ′ and χ′′ are normalized with χ^′_max and χ^′′_peak, respectively. Fig. 5 shows the temperature versus χ′/χ^′_max and χ′′/χ^′′_peak of all the samples. All the samples exhibit diamagnetic transition in χ′ and the corresponding T_C values obtained are given in Table 2. Moreover, the χ′ of AC magnetic susceptibility is a measure of the energy stored in the sample due to the diamagnetic response of the screening current induced in the superconductor by the external magnetic field, whereas χ′′ is proportional to the energy loss due to the vortex motion. In the present study, the real part χ′ shows double step transition in all the samples. However, the double-stepping nature is not pronounced in the undoped sample and the sample SmCe20. A double step transition in the real part and its corresponding double peak in the imaginary part of AC susceptibility is a property of granular superconductors.³³ Corresponding to the lower temperature transition, the χ′′ plot shows a peak; although the peak corresponding to the higher temperature transition is not well resolved in Fig. 5. The observed double step nature of χ′, an indication of granular behavior of our samples, confirms the inherent property of iron pnictides.^34,35 In granular superconductors, screening current flows concurrently among the grains (intergrain current) and within the grains (intragrain current). Therefore, the output signal of AC measurement is a contribution of these two types of screening currents within the superconductor. Hence, the double step in χ′ of our samples can be also attributed to the existence of both intergrain and intragrain currents in the samples. It is also observed that the diamagnetic transition width gets broadened, and the depth of the first drop increases with an increase in doping up to the optimum doping level as shown in Fig. 5. The lowering of T_C due to Ce doping at y = 0.2 makes the nature and the position of the AC susceptibility curve for SmCe20 get closer to that of the undoped sample, resembling the reduction in T_C and revival of the pseudo gap in the resistivity data of SmCe20.

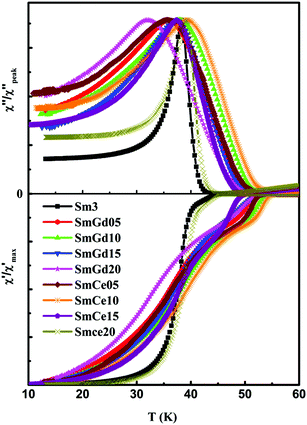Fig. 5 Normalized real (χ′) and imaginary (χ′′) part of AC susceptibility of Sm3 (SmFeAsO_0.7F_0.3) as well as Gd³⁺ and Ce³⁺ doped samples with frequency, f = 208 Hz and ac field, H_ac = 4.94 × 10⁻⁴ T.

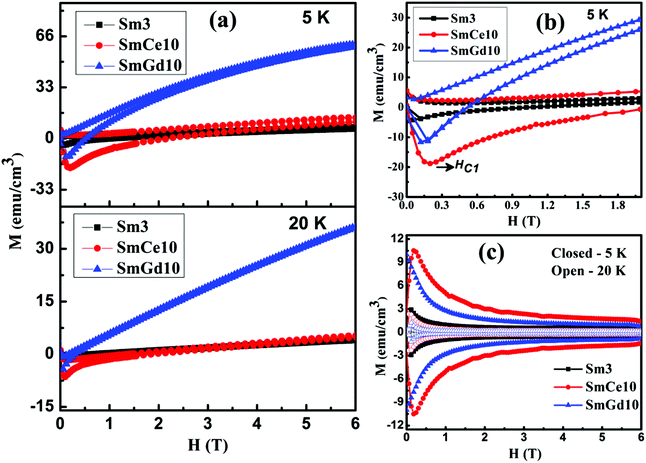
The dc magnetization of the sample was measured as a function of the applied magnetic field at different temperatures 5, 10, 20, 30, and 35 K. Fig. 6(a) shows the magnetization (M–H) loops of the sample Sm3 and the optimally doped samples (SmCe10 and SmGd10) at 5 and 20 K, with the applied magnetic fields up to 6 T. The obtained M–H curve is asymmetrical in nature, as already reported in RE1111 superconductors.³⁶ Application of an external magnetic field produces a negative magnetization inside the sample up to a particular field, and then the magnetization starts to increase and takes a positive value. The effect is evidently more pronounced for the Gd doped sample. The field at which magnetization starts to increase is taken as the lower critical field (H_C1) of the samples. An enlarged view of the M–H curve at 5 K around H_C1 is shown in Fig. 6(b). For the sample Sm3, H_C1 of 0.12 T is found at 5 K. Doping increases the H_C1 values, i.e., H_C1–0.2 T for SmCe10 and H_C1 ∼ 0.18 T for SmGd10. Here, the M–H curves can be treated as a superposition of both the superconducting contribution and a paramagnetic background. The paramagnetic contribution comes from the presence of RE³⁺ magnetic ions and magnetic impurity phases. It is also interesting to note that the paramagnetic background detected is very high in Gd³⁺ doped samples. This can be attributed to the relatively high paramagnetic moment of the Gd³⁺ ions (7.94μ_B for Gd³⁺, 2.4μ_B Ce³⁺ and 0.84μ_B for Sm³⁺). Reports on GdFeAsO_1−xF_x samples also reveal that a strong paramagnetic background in these samples arises due to the presence of Gd³⁺.³⁷ This paramagnetic background can be evaluated as a mean of the upper and lower hysteresis branch, M_P = (M⁺ + M⁻)/2, for each loop and this has been deducted from the experimentally obtained M–H curves.

Fig. 6 (a) M–H plots of the samples Sm3, SmCe10 and SmGd10 at temperatures 5 K and 20 K (b) an enlarged view of the plots around H_C1 and (c) the paramagnetic background subtracted hysteresis curves for the respective samples.

Fig. 6(c) shows the paramagnetic background subtracted hysteresis curves of the respective samples. At 5 K, the M–H curves of all three samples show a clear hysteresis loop. With increasing temperature, the width of the loop was found to decrease for all the samples. Rare earth site doping with both Ce³⁺ and Gd³⁺ considerably enhances the M–H loop width at 5 and 20 K. The maximum loop width is obtained for the sample SmCe10. Also, the maximum width of the background subtracted curve is found to be at a low magnetic field (around H_C1) and then the width reduces rapidly with increasing field and then demonstrates a field independent property. This typical behavior of granular superconductors is due to the weak-link nature of the grain boundaries, and its extreme sensitivity towards the magnetic field. However, at higher fields the width of the hysteresis curve remains almost constant up to the highest measured magnetic field of 6 T.

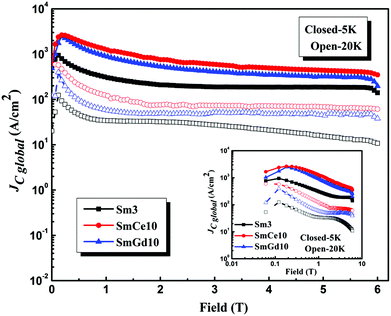
The critical current density (J_C) values estimated from the M–H loops at 5 K and 20 K of the samples Sm3, SmCe10 and SmGd10 are given in Fig. 7. The width of the M–H loop (ΔM) is due to the irreversible magnetization retained in the sample due to the flux pinning property of the superconductors. ΔM was calculated as M⁺ − M⁻; M⁺ and M⁻ are the magnetization produced in the increasing and decreasing branches. The numerical value of ΔM is proportional to the critical current density of the superconductor and the length scale of the current flow. Using the Bean critical state model,³⁸ we can calculate inter-grain/global J_C (J_C-global – current flowing through the entire sample) and intra-grain/local J_C (J_C-local – current flowing within the grains). J_C-global of the samples has been evaluated from the width of the M–H loop as J_C-global = 20ΔM/a(1 − a/3b); where a and b are the dimensions of the sample perpendicular to the applied magnetic field, a < b. Here ΔM is in emu cm⁻³, sample dimensions are in cm, and the obtained J_C is in A cm⁻². The sample Sm3 shows a J_C-global ∼ 0.9 × 10³ A cm⁻² in the low field region. However, J_C-global values of ∼2.5 × 10³ A cm⁻² are obtained for both the doped samples at around 0.18 T at 5 K. Though, these J_C values show a decreasing tendency with the field up to around 2 T, J_C remains constant (∼0.8 × 10³ A cm⁻² for SmCe10, ∼0.5 × 10³ A cm⁻² for SmGd10, and ∼0.2 × 10³ A cm⁻² for Sm3) with further increase in the magnetic field. These J_C values are distinctly better than those observed in randomly oriented polycrystalline cuprates, which are typically ∼100 A cm⁻².³⁹ Thus, the rare earth site doping in SmFeAsO_0.7F_0.3 considerably improves the J_C of the samples, in addition to the enhancement of T_C and H_C2 values. It is also found that J_C of the Ce³⁺ doped sample is higher than the Gd³⁺ doped one in the high field region; and its value is four times higher than the F only doped sample (Sm3). These observations suggest that the lattice defects created by the larger ion Ce³⁺ at the Sm³⁺ site in the SmFeAsO_0.7F_0.3 system act as stronger pinning centers than that created by smaller Gd³⁺ ions and thereby exhibit enhanced J_C (H) performance compared to the Gd doped sample. No obvious second peak in J_C-global–H is observed for the samples at 5 and 20 K. But, there exists reports revealing the second peaking in the Sm1111 samples at a temperature close to T_C. Therefore, for a close observation, a double logarithmic representation of J_C-global–H was plotted and is shown in the inset of Fig. 7. At 20 K, the F only doped sample, Sm3, depicted the second peak in the high field region. However, this is not clearly visible in the rare earth site doped samples even up to the highest magnetic field applied. This can be attributed to the very high H_C2 values of the rare earth doped samples as discussed in the succeeding section.

Fig. 7 Magnetic global J_C derived from the M–H plots for the samples Sm3, SmCe10 and SmGd10 at temperatures 5 K and 20 K. Inset shows the double logarithmic J_C-global–H plots showing the second peak effect.

The intra-grain J_C (J_C-local) was also calculated using the equation J_C-local = 30ΔM/r, where r is the grain size in cm. An average grain size of 3.5 μm for Sm3 and SmGd10 and 1.8 μm for SmCe10 was estimated from the SEM images. At 5 K, J_C-local of 3.5 × 10⁶ A cm⁻² was obtained for the Ce doped sample which is almost one order higher than the intra-grain J_C of Sm3 i.e. around 5.0 × 10⁵ A cm⁻². Ce³⁺ doping at the Sm site in Sm3 remarkably enhanced the J_C value within the grain over the entire magnetic field. Gd³⁺ doping in Sm3 also improved the J_C-local values, but to a lesser extent compared to the Ce³⁺ doped ones. A J_C-local of ∼1.3 × 10⁶ A cm⁻² was obtained for SmGd10. The microstructural analysis has already revealed that optimum doping of Ce³⁺ gives well-connected grains of a smaller size. In addition, the lattice mismatch between Ce³⁺ and Sm³⁺ is higher than that between Gd³⁺ and Sm³⁺. This in turn results in comparatively higher flux pinning in the SmCe10 sample than in SmGd10 at higher fields. The above reasons seem to be responsible for the better J_C–H behavior of SmCe10 over the entire field studied.

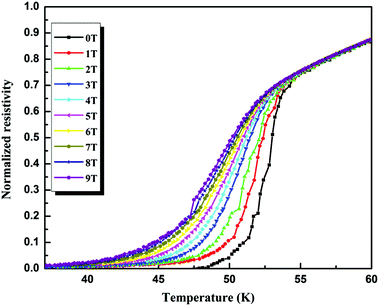
The H_C2 values of the samples Sm3, SmCe10 and SmGd10, have been also evaluated from the temperature dependence of their resistivity under varying magnetic fields. Fig. 8 shows the field dependent ρ–T plots for the sample SmCe10 with the magnetic fields varying from 0 to 9 T. The transition width broadens with the applied magnetic field in which there is a considerable reduction in the T_Coffset value with a slight decrease in T_Conset. This broadening was already reported in RE1111 pnictides and cuprate based superconductors and could be interpreted in terms of weak links or flux flow existing in the sample.^40,41 Weak link behavior of our samples has been revealed from their AC magnetic susceptibility measurements and discussed earlier. The magnetic field and temperature dependence of the resistivity value give information about the upper critical field, H_C2 and the irreversibility field, H_irr. The resistivity data was normalized with respect to the normal state resistivity at 65 K and then using the criteria of 90% and 10% of the normal state resistivity (ρ_n – resistivity value just above transition), both H_C2 and H_irr was estimated. H_C2 at zero temperatures for the samples is given by the Werthamer–Helfand–Hohenberg (WHH) formula H_C2(0) = 0.693 × (dH_C2/dT) × T_C.⁴² The slope dH_C2/dT was calculated from the temperature dependence plot of H_C2.

Fig. 8 ρ–T plots for the sample SmCe10 under the magnetic fields varying from 0–9 T.

Fig. 9 shows the H–T phase diagram i.e. the temperature dependence of both H_C2 (closed symbol) and H_irr (open symbol) of the samples Sm3, SmCe10 and SmGd10, derived from the ρ–T plots at different magnetic fields. The dH_C2/dT ∼ −5.4 T K⁻¹ for Sm3, dH_C2/dT ∼ −10.1 T K⁻¹ for SmCe10 and dH_C2/dT ∼ −9 T K⁻¹ for SmGd10 are obtained from the H–T phase diagram and the corresponding H_C2 (0) values are 170 T, 385 T and 340 T, respectively. Thus, a very high value of H_C2 was achieved by rare-earth site doping in the SmFeAsO_0.7F_0.3 system, especially for the Ce³⁺ doped system. The H_irr values were also estimated following the same WHH formula, from the slope of the H–T curves corresponding to 10% ρ_n. The H_irr values obtained for the samples Sm3, SmCe10, and SmGd10 are 34.7, 51.1, and 46.5 T, respectively. We can see that the irreversibility field of the samples SmCe10 and SmGd10 are rather high compared to that of Sm3. Therefore, it is evident that simultaneous doping at the oxygen and rare earth site increases the number of effective pinning centres in the form of lattice defects and substantially increases the critical fields of the Sm1111 system. The enhanced J_C (H) performance and very high upper critical fields in addition to the relatively high T_C around 55 K confirm the significant enhancement of superconducting properties by rare earth-site doping in the SmFeAsO_0.7F_0.3 system.

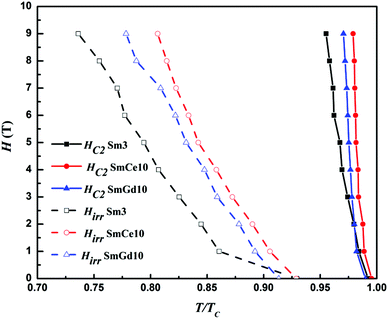Fig. 9 H–T phase diagram of the samples Sm3, SmCe10 and SmGd10; H_C2 and H_irr were determined from 90% and 10% points on the ρ–T plots at different magnetic fields.

Conclusions

In summary, rare-earth site doping in addition to F⁻ doping at the O²⁻ site has a significant impact on both structural and superconducting properties of SmFeAsO_0.7F_0.3. T_C increased up to 55 K for both Gd³⁺ and Ce³⁺ doped samples. Even though Ce and Gd doping have their own signature in T_C enhancement; both are found to increase the charge carrier concentration. Very high upper critical fields have also been obtained by rare earth site doping in SmFeAsO_0.7F_0.3. In addition, rare-earth site doping improves the critical current density of the samples throughout the entire range of the magnetic field studied. Enhanced flux pinning due to additional doping at the Sm³⁺ site is found to be responsible for the improved J_C (H) performance. However, the higher lattice mismatch in Ce doped samples is found to have better pinning capability than the Gd doped samples especially in the high field region.

Acknowledgements

J. B. Anooja, P. M. Aswathy and Neson Varghese acknowledge the Council for Scientific and Industrial Research (CSIR) for their research fellowships. The authors acknowledge the Department of Science & Technology (DST) and CSIR 12th Five Year Plan Project, “Sustainable technologies for the Utilization of Rare Earths (SURE),” (no. CSC0132) for financial support. We also thank Mr Ajeesh P. Paulose and Chithra H. Sharma for timely technical support.

References

1. Y. Kamihara, T. Watanabe, M. Hirano and H. Hosono, J. Am. Chem. Soc., 2008, 130, 3296.
2. X. H. Chen, T. Wu, G. Wu, R. H. Liu, H. Chen and D. F. Fang, Nature, 2008, 453, 761.
3. C. Senatore, R. Flükiger, M. Cantoni, G. Wu, R. H. Liu and X. H. Chen, Phys. Rev. B: Condens. Matter, 2008, 78, 054514.
4. P. M. Aswathy, J. B. Anooja, P. M. Sarun and U. Syamaprasad, Supercond. Sci. Technol., 2010, 23, 073001.
5. Z. A. Ren, W. Lu, J. Yang, W. Yi, X. L. Shen, Z. C. Li, G. C. Che, X. L. Dong, L. L. Sun, F. Zhou and Z. X. Zhao, Chin. Phys. Lett., 2008, 25, 2215.
6. Z. A. Ren, G. C. Che, X. L. Dong, J. Yang, W. Lu, W. Yi, X. L. Shen, Z. C. Li, L. L. Sun, F. Zhou and Z. X. Zhao, Europhys. Lett., 2008, 83, 17002.
7. Z. Wei, H. Li, W. L. Hong, Z. Lv, H. Wu, X. Guo and K. Q. Ruan, J. Supercond. Novel Magn., 2008, 21, 213.
8. G. Fuchs, S. L. Drechsler, N. Kozlova, G. Behr, A. Köhler, J. Werner, K. Nenkov, R. Klingeler, J. Hamann-Borrero, C. Hess, A. Kondrat, M. Grobosch, A. Narduzzo, M. Knupfer, J. Freudenberger, B. Büchner and L. Schultz, Phys. Rev. Lett., 2008, 101, 237003.
9. J. Jaroszynski, S. C. Riggs, F. Hunte, A. Gurevich, D. C. Larbalestier, G. S. Boebinger, F. F. Balakirev, A. Migliori, Z. A. Ren, W. Lu, J. Yang, X. L. Shen, X. L. Dong, Z. X. Zhao, R. Jin, A. S. Sefat, M. A. McGuire, B. C. Sales, D. K. Christen and D. Mandrus, Phys. Rev. B: Condens. Matter, 2008, 78, 064511.
10. I. I. Mazin, Nature, 2010, 464, 183.
11. N. D. Zhigadlo, S. Katrych, S. Weyeneth, R. Puzniak, P. J. W. Moll, Z. Bukowski, J. Karpinski, H. Keller and B. Batlogg, Phys. Rev. B: Condens. Matter, 2010, 82, 064517.
12. K. Kasperkiewicz, J. W. G. Bos, A. N. Fitch, K. Prassides and S. Margadonna, Chem. Commun., 2009, 707–709.
13. C. Lee, A. Iyo, H. Eisaki, H. Kito, M. T. Fernandezdiaz, T. Ito, K. Kihou, H. Matsuhata, M. Braden and K. Yamada, J. Phys. Soc. Jpn., 2008, 77, 083704.
14. V. P. S. Awana, P. Anand, A. Vajpayee, R. S. Meena, H. Kishan, M. Husain, R. Zeng, S. Yu, K. Yamaura and E. Takayama-Muromachi, J. Appl. Phys., 2010, 107, 09E146.
15. W. Yi, J. Yang, X. L. Shen, W. Lu, Z. C. Li, Z. A. Ren, G. C. Che, X. L. Dong, F. Zhou, L. L. Sun and Z. X. Zhao, Supercond. Sci. Technol., 2008, 21, 125022.
16. A. K. Ganguli, J. Prakash, S. J. Singh and S. Patnaik, Eur. Phys. J. B, 2010, 73, 177.
17. L. Vegard, Z. Phys., 1921, 5, 17.
18. Y. Ding, Y. Sun, J. C. Zhuang, L. J. Cui, Z. X. Shi, M. D. Sumption, M. Majoros, M. A. Susner, C. J. Kovacs, G. Z. Li, E. W. Collings and Z. A. Ren, Supercond. Sci. Technol., 2011, 24, 125012.
19. J. B. Anooja, P. M. Aswathy, P. M. Sarun and U. Syamaprasad, J. Alloys Compd., 2012, 514, 1.
20. A. L. Solov'ev and V. M. Dmitriev, Low Temp. Phys., 2009, 35, 169.
21. E. Arushanov, G. Fuchs, S. Levcenko, S. L. Drechsler, B. Holzapfel and L. Schultz, Supercond. Sci. Technol., 2011, 24, 105004.
22. M. Tropeano, C. Fanciulli, F. Canepa, M. R. Cimberle, C. Ferdeghini, G. Lamura, A. Martinelli, M. Putti, M. Vignolo and A. Palenzona, Phys. Rev. B: Condens. Matter, 2009, 79, 174523.
23. S. L. Shi, A. H. Fang, X. M. Xie, F. Q. Huang and M. H. Jiang, Chem. Mater., 2011, 23, 3039.
24. J. L. Yang, W. J. Ren, D. Li and Z. D. Zhang, J. Appl. Phys., 2011, 109, 07E154.
25. P. M. Shirage, K. Miyazawa, H. Kito, H. Eisaki and A. Iyo, Phys. Rev. B: Condens. Matter, 2008, 78, 172503.
26. W. Yi, C. Zhang, L. Sun, Z. Ren, W. Lu, X. Dong, Z. Li, G. Che, J. Yang, X. Shen, X. Dai, Z. Fang, F. Zhou and Z. Zhao, Europhys. Lett., 2008, 84, 67009.
27. A. S. Sefat, Rep. Prog. Phys., 2011, 74, 124502.
28. H. Takahashi, K. Igawa, K. Arii, Y. Kamihara, M. Hirano and H. Hosono, Nature, 2008, 453, 376.
29. Y. Takabayashi, M. T. McDonald, D. Papanikolaou, S. Margadonna, G. Wu, R. H. Liu, X. H. Chen and K. Prassides, J. Am. Chem. Soc., 2008, 130, 9242–9243.
30. W. Yi, L. Sun, Z. Ren, W. Lu, X. Dong, H. J. Zhang, X. Dai, Z. Fang, Z. Li, G. Che, J. Yang, X. Shen, F. Zhou and Z. Zhao, Europhys. Lett., 2008, 83, 57002.
31. A. Alam and D. D. Johnson, Phys. Rev. B: Condens. Matter, 2014, 89, 235126.
32. S. C. Riggs, R. D. McDonald, J. B. Kemper, Z. Stegen, G. S. Boebinger, F. F. Balakirev, Y. Kohama, A. Migliori, H. Chen, R. H. Liu and X. H. Chen, J. Phys.: Condens. Matter, 2009, 21, 412201.
33. H. Salamati and P. Kameli, J. Magn. Magn. Mater., 2004, 278, 237.
34. M. Polichetti, M. G. Adesso, D. Zola, J. L. Luo, G. F. Chen, Z. Li, N. L. Wang, C. Noce and S. Pace, Phys. Rev. B: Condens. Matter, 2008, 78, 224523.
35. G. Bonsignore, A. A. Gallitto, M. L. Vigni, J. L. Luo, G. F. Chen, N. L. Wang and D. V. Shovkun, J. Low Temp. Phys., 2011, 162, 40.
36. A. Yamamoto, A. A. Polyanskii, J. Jiang, F. Kametani, C. Tarantini, F. Hunte, J. Jaroszynski, E. E. Hellstrom, P. J. Lee, A. Gurevich, D. C. Larbalestier, Z. A. Ren, J. Yang, X. L. Dong, W. Lu and Z. X. Zhao, Supercond. Sci. Technol., 2008, 21, 095008.
37. Y. J. Cui, Y. L. Chen, C. H. Cheng, Y. Yang, Y. Zhang and Y. Zhao, J. Supercond. Novel Magn., 2010, 23, 625.
38. C. P. Bean, Phys. Rev. Lett., 1962, 8, 250.
39. J. M. Seuntjens and D. C. Larbalestier, J. Appl. Phys., 2007, 67, 1990.
40. Z. Gao, L. Wang, Y. Qi, D. Wang, X. Zhang, Y. Ma, H. Yang and H. Wen, Supercond. Sci. Technol., 2008, 21, 112001.
41. Y. Sun, Y. Ding, J. C. Zhuang, L. J. Cui, X. P. Yuan, Z. X. Shi and Z. A. Ren, Supercond. Sci. Technol., 2011, 24, 085011.
42. N. R. Werthamer, E. Helfand and P. C. Hohenberg, Phys. Rev., 1966, 147, 295.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5qi00047e

---