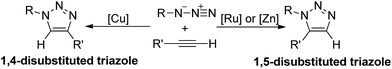Mechanism and selectivity for zinc-mediated cycloaddition of azides with alkynes: a computational study

Abstract

Density functional theory (DFT) method B3LYP with a dispersion term (B3LYP-D3BJ) has been used to clarify the regioselectivity of zinc mediated 1,3-dipolar cycloaddition of azides and alkynes. Computational results indicate that the dipolar cycloaddition takes place via a concerted five-membered-ring transition state, leading to a 1,5-disubstituted 1,2,3-triazole product, which is consistent with the experiment reported by Greaney's group. The coordination of imidazole ligand to zinc is reversible, and the regioselectivity is irrelevant to the coordination of imidazole ligand. Moreover, substituent effect of alkynes has also been studied. Finally, distortion–interaction analysis along the reaction pathways and frontier molecular orbital theory are used to explain the reactivity and 1,5-regioselectivity.

---

Introduction

1,3-Dipolar cycloadditions of azides and alkynes, which have been known for more than a century,¹ represent the most direct route to construct 1,2,3-triazoles,² and have been widely applied in biochemistry and material science.³ Many efforts have been made to promote the development of this type of reaction. During 1950s–1970s, Huisgen and co-workers systematically studied the uncatalytic thermal cycloadditions of azides and alkynes.⁴ In recent years, transition metal assisted 1,3-dipolar cycloadditions are emerged as a powerful strategy to synthesis 1,2,3-triazoles since the introduction of metal could improve the reactivity and control the regioselectivity.⁵ As shown in Scheme 1, when substituted alkynes and azides are employed as reactants, either 1,4- or 1,5-disubstituted 1,2,3-triazoles would be formed through 1,3-dipolar cycloaddition depending on what metal (Cu, Ru or Zn) is added.⁶

Scheme 1 Zinc-mediated azide–alkyne ligation to 1,5-disubstituted 1,2,3-triazoles.

The copper(I) catalyzed azide–alkyne cycloadditions (CuAAC) to selectively yield 1,4-disubstituted 1,2,3-triazoles, which is first reported by Meldal,^6b Fokin, and Sharpless,^6a individually, attract lots of attention due to the mild conditions, wide substrate scopes, and vast ranges of triazole application.⁷ Kinetic and mechanistic studies of CuAAC suggest that the active species contain two copper ions, one or two acetylenes, and one azide.⁸ Moreover, the π complexation of copper acetylide towards another copper ion also plays a critical role in positioning the substrates appropriately for the cycloaddition reaction, as well as activating the reacting acetylene towards nucleophilic attack by the azide.⁹

While Cu(I) catalysis has provided a reliable method for the construction of 1,4-disubstituted 1,2,3-triazoles,¹⁰ general methods for the synthesis of 1,5-disubstituted regioisomers are relatively scarce.¹¹ Fokin in collaboration with Jia^6a,6c reported some Ru(II)-catalyzed azide–alkyne cycloadditions (RuAAC) for the generation of 1,5-disubstituted 1,2,3-triazoles in moderate yields. Nonetheless, considerable limitations still exist in this approach, due to the strong base required, the utilization of alkalis¹² or magnesium acetylides,^10a,13 and the noble metal ruthenium.^6c–e

Recently, Greaney reported a zinc mediated 1,3-dipolar cycloaddition of azides and alkynes, which regioselectively generates 1,5-substituted 1,2,3-triazoles at room temperature.¹⁴ The unique regioselectivity obtained under mild condition draws our attention to investigate the detailed mechanism. In nowadays chemistry field, density functional theory (DFT) calculation, which has been extensively used for the mechanistic study of CuAAC and RuAAC,^6c,d,15,16 is regarded as a powerful tool to reveal the mechanism of 1,3-dipolar cycloadditions.¹⁷ Herein, we report our DFT calculations towards the mechanism and regioselectivity research of this Zn-mediated azide–alkyne cycloaddition, including frontier molecular orbital (FMO) theory¹⁸ and distortion–interaction energy analysis¹⁹ to provide interpretation for the regioselectivity.

Computational methods

All the DFT calculations were carried out with the Gaussian 09 series of programs.²⁰ DFT method B3LYP²¹ with a standard 6-311+G(d) basis set (SDD²² basis set for zinc atom) was used for geometry optimizations. Harmonic vibration frequency calculations were performed for all stationary points to confirm them as a local minima or transition structure and to derive the thermochemical corrections for the enthalpies and free energies. On the other hand, the addition of dispersion interaction into B3LYP functional could describe the long-range interactions better, thus an atom–atom additive damped empirical potential of the form –f(R)C₆/R⁶, which named B3LYP-D3BJ, was employed in our work to give more accurate energy information.²³ The solvent effects were considered by B3LYP-D3BJ method calculated single point energies with a standard 6-311+G(d) basis set (SDD basis set for zinc atom) on the gas-phase stationary points with a PCM solvation model.²⁴ Furthermore, the FMOs for some important intermediates were calculated using the B3LYP/6-311+G(d) level of theory.

Two kinds of free energies are given in the free energy profiles, i.e. the G(gas phase)_B3LYP and the G(THF)_B3LYP-D3BJ, which were obtained by eqn (1) and eqn (2), respectively. G_correction is the thermochemical corrections for the Gibbs free energies. E(gas phase)_B3LYP is the single point energy calculated at B3LYP/6-311+G(d) level in gas phase, and E(THF)_B3LYP-D3BJ is the single point energy calculated at B3LYP-D3BJ/6-311+G(d) level in THF based on gas phase stationary point.

G(gas phase)_B3LYP = E(gas phase)_B3LYP + G_correction (1)

G(THF)_B3LYP-D3BJ = E(THF)_B3LYP-D3BJ + G_correction (2)

In this work, the intrinsic reaction coordinates (IRCs)²⁵ of the transition states for zinc mediate dipolar cycloadditions between ethyl(phenylethynyl)zinc and azidobenzene were used to calculate the reaction pathway at the B3LYP/6-311+G(d) level of theory. The distortion energy (ΔE_dis) was set to the energy difference between the energy of distorted ethyl(phenylethynyl)zinc and azidobenzene parts along the reaction pathway and the energy of fully optimized ethyl(phenylethynyl)zinc and azidobenzene parts by single point energy calculations at the B3LYP/6-311+G(d) level of theory. The interaction energy (ΔE_int) was set to the energy difference between the single point energy of the geometry on the reaction coordinate and the energy of the relative distorted ethyl(phenylethynyl)zinc and azidobenzene parts. When the distortion, interaction, and total energies are plotted, the distance between the center of the two neutral nitrogen atoms in azidobenzene and the center of two reacting carbon atoms in ethyl(phenylethynyl)zinc is used to represent the reaction coordinate.

Results and discussion

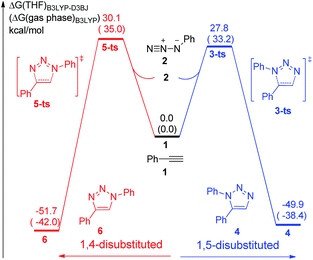
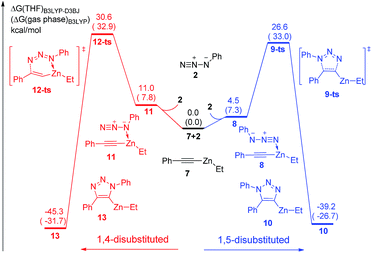
The uncatalytic 1,3-dipolar cycloadditions between azidobenzene and phenylacetylene are initially put forward. Computational results (Fig. 1) suggest that the activation free energy of corresponding transition state 5-ts is 30.1 kcal mol⁻¹, which is consistent with Fokin's result calculated at B3LYP/6-311G+(2d,2p) level of theory.^8b In another case, the barrier for the generation of 1,5-disubstituted 1,2,3-triazole via transition state 3-ts is 27.8 kcal mol⁻¹, which is 2.3 kcal mol⁻¹ lower compared with 1,4-disubstituted one.

Fig. 1 Free energy profiles for the uncatalytic cycloaddition of phenylacetylene and azidobenzene. The values given by kcal mol⁻¹ are the relative free energies calculated by B3LYP-D3BJ method in THF solvent. The values in parentheses are the free energies given by B3LYP in gas phase.

As shown in Fig. 2, ethyl(phenylethynyl)zinc 7, which could be easily formed from phenylacetylene and diethylzinc due to the higher acidity of phenylacetylene comparing with generated ethane, is chose as the reactant to study the reactivity of zinc mediated 1,3-dipolar cycloaddition. Coordination of 7 to the neutral nitrogen of azidobenzene 2 forms intermediate 8 with 4.5 kcal mol⁻¹ endothermic. The 1,3-dipolar cycloaddition to form 1,5-diphenyl-4-(ethyl)zinc-1,2,3-triazole 10 takes place irreversibly via a concerted transition state 9-ts with an overall activation free energy of 26.6 kcal mol⁻¹. The geometry information of transition state 9-ts is shown in Fig. 6. The two forming carbon–nitrogen bond lengths are 1.96 Å and 2.35 Å, respectively. The distance between nitrogen and zinc is 2.90 Å, which indicates none direct interaction between azidobenzene and zinc. In another case, coordination of the nucleophilic nitrogen atom of azidobenzene with 7 forms intermediate 11 with 11.0 kcal mol⁻¹ endothermic. The corresponding cycloaddition to form 1,4-regioisomer could occur via transition state 12-ts with an overall barrier of 30.6 kcal mol⁻¹. Intrinsic reaction coordinate (IRC) calculation of transition state 9-ts and 12-ts have proved it is the accurate transition state which connect the reactant and product. The nitrogen–zinc bond length of 2.22 Å in transition state 12-ts (Fig. 6) shows that when the neutral nitrogen–carbon bond is forming, the nucleophilic nitrogen still coordinates with zinc. The calculations indicate that when azidobenzene reacts with ethyl(phenylethynyl)zinc 7, the forming rate of 1,5-diphenyl-1,2,3-triazole is fast compared with the formation of 1,4-regiomer.

Fig. 2 Free energy profiles for the cycloaddition of ethyl(phenylethynyl)zinc and azidobenzene. The values given by kcal mol⁻¹ are the relative free energies calculated by B3LYP-D3BJ method in THF solvent. The values in parentheses are the free energies given by B3LYP in gas phase.

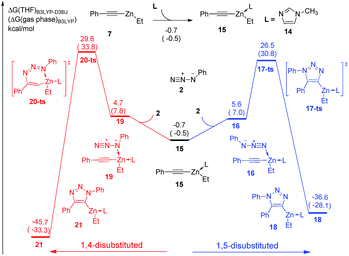
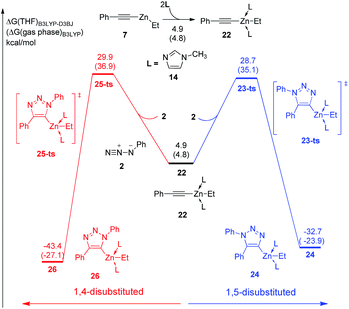
In the experiment, N-methylimidazole is added as a co-catalyst for zinc-mediated cycloaddition. Therefore, the ligand effects of N-methylimidazole towards reactivity and regioselectivity are considered theoretically. As shown in Fig. 3, The coordination of one molecular N-methylimidazole to ethyl(phenylethynyl)zinc 7 results in 0.7 kcal mol⁻¹ exothermic, and forms intermediate 15. Subsequently, intermediate 16 or 19 would be formed by the coordination of azidobenzene 2 with neutral or nucleophilic nitrogen atom with 6.3 kcal mol⁻¹ or 5.4 kcal mol⁻¹ endothermic, respectively. 1,5-Disubstituted product 18 could be formed via transition state 17-ts with a barrier of 26.5 kcal mol⁻¹. The relative free energy of transition 17-ts is 0.1 kcal mol⁻¹ lower than that of transition state 9-ts, which indicates that the cycloaddition for the formation of 1,5-diphenyl-1,2,3-triazole cannot be assisted by the coordination of one N-methylimidazole ligand. As contrast, the activation energy of transition state 20-ts for the formation of 1,4-disubstituted regioisomer 21 is 29.6 kcal mol⁻¹, which is 3.1 kcal mol⁻¹ higher comparing with that of transition state 17-ts. According to this data, the ratio of 1,5-substituted 1,2,3-triazole to 1,4-regioisomer should be 99 : 1. Therefore, the generation of 1,4-disubstituted regioisomer 21 is unfavorable, which is consistent with the experiment results. Theoretical calculations indicate that the regioselectivity is irrelevant to the coordination of N-methylimidazole ligand. The geometry information of transition state 20-ts is shown in Fig. 6. The nitrogen–zinc bond length of 2.39 Å in transition state 20-ts, which is 0.17 Å longer than the corresponding bond length in transition state 12-ts, indicates that the coordination of N-methylimidazole would weaken the interaction between zinc and azidobenzene in transition state.

Fig. 3 Free energy profiles for the cycloaddition of ethyl(phenylethynyl)zinc and azidobenzene with one N-methylimidazole ligand. The values given by kcal mol⁻¹ are the relative free energies calculated by B3LYP-D3BJ method in THF solvent. The values in parentheses are the free energies given by B3LYP in gas phase.

Moreover, two equivalent N-methylimidazole involved pathway was also calculated. As shown in Fig. 4, the coordination of second N-methylimidazole ligand is 5.6 kcal mol⁻¹ endothermic. Although the barrier of dipolar cycloaddition via transition state 23-ts is only 23.8 kcal mol⁻¹ from intermediate 22, the overall activation free energy for the formation of complex 24 is 29.4 kcal mol⁻¹, which is 2.2 kcal mol⁻¹ higher than that for transition state 17-ts. The activation free energy for the generation of relative 1,4-regioisomer with two ligands is 30.6 kcal mol⁻¹, which is 1.2 kcal mol⁻¹ higher than that for the formation of 1,5-disubstituted product due to the endothermic coordination of second ligand. Consequently, when dipolar cycloaddition of ethyl(phenylethynyl)zinc and azidobenzene to form 1,4- or 1,5-diphenyltriazole takes place, at most one N-methylimidazole ligand coordinates with zinc.

Fig. 4 Free energy profiles for the cycloaddition of ethyl(phenylethynyl)zinc and azidobenzene with two N-methylimidazole ligands. The values given by kcal mol⁻¹ are the relative free energies calculated by B3LYP-D3BJ method in THF solvent. The values in parentheses are the free energies given by B3LYP in gas phase.

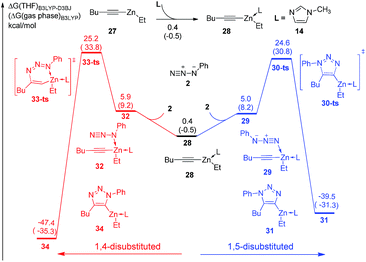
Substituent effects have also been considered in the theoretical study. As shown in Fig. 5, ethylhexynylzinc complex 27 is chosen to investigate the reactivity and regioselectivity of alkyl substituted alkynes instead of aryl substituent. The concerted [3 + 2] cycloaddition to form 1,5-disubstituted product 30 could take place via transition state 29-ts with an overall barrier of 24.6 kcal mol⁻¹. In another case, the barrier for the formation of 1,4-disubstituted product 34 via transition state 33-ts is 25.2 kcal mol⁻¹, which is 0.6 kcal mol⁻¹ higher than that for the formation of 1,5-regioisomer. The B3LYP-D3BJ calculations indicate that the reactivity of alkyl substituted alkynes is similar with aryl substituted substrate, while the regioselectivity of alkyl substituted alkynes is lower, which is consistent with experimental observations.

Fig. 5 Free energy profiles for the cycloaddition of ethylhexynylzinc and azidobenzene with one N-methylimidazole ligand. The values given by kcal mol⁻¹ are the relative free energies calculated by B3LYP-D3BJ method in THF solvent. The values in parentheses are the free energies given by B3LYP in gas phase.

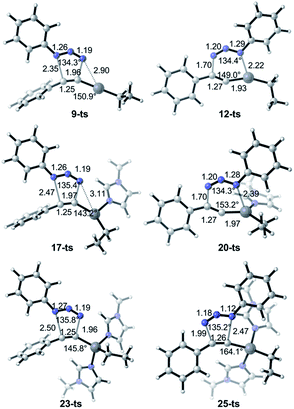Fig. 6 B3LYP optimized geometries of transition structures 9-ts, 12-ts, 17-ts, 20-ts, 23-ts and 25-ts. The values of bond length are given by Å.

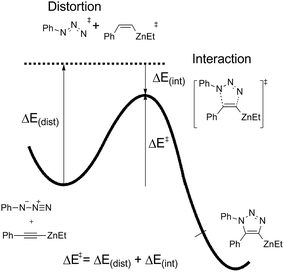
The distortion–interaction energy analysis, which is reported as a powerful model to explain reactivity trends for bimolecular reactions,²⁶ is employed to study this 1,3-dipolar cycloaddition. As shown in Fig. 7, the total activation energy (ΔE^‡) is decomposed into the sum of distortion energy (ΔE_dis) and interaction energy (ΔE_int) between distorted reactants.

Fig. 7 Relationship between the activation, distortion, and interaction energies.

Table 1 shows the distortion energies and interaction energies of the transition states 9-ts, 12-ts, 17-ts, 20-ts, 23-ts, and 25-ts. Comparing with transition states 9-ts and 12-ts, the distortion energy of transition state 12-ts is 11.0 kcal mol⁻¹ higher than that of transition state 9-ts, however the interaction energy of transition state 12-ts is 10.7 kcal mol⁻¹ lower due to the coordination of nucleophilic nitrogen atom with zinc. Therefore, the relative energy of transition state 12-ts is 2.3 kcal mol⁻¹ higher than that of transition state 9-ts. The coordination of one imidazole ligand decreases the binding energy of nitrogen with zinc in six-membered transition state, therefore the distortion energy of transition state 20-ts is 1.3 kcal mol⁻¹ lower than that of transition state 12-ts. Moreover, the distortion energy of transition state 17-ts is 1.9 kcal mol⁻¹ lower than that of 9-ts because of the stronger frontier molecular orbital interaction, which will be discussed later. Therefore, the overall activation energy of transition state 17-ts is 3.1 kcal mol⁻¹ lower than that of transition state 20-ts. Comparing with five-membered-ring type transition states 23-ts and 25-ts, the higher distortion energy of 25-ts leads to a higher activation energy.

Table 1 The distortion (ΔE_dis), interaction (ΔE_int), and reaction (ΔE^‡) energies of the 9-ts, 12-ts, 17-ts, 20-ts, 23-ts, and 25-ts transition states. ΔE_dis = ΔE_dis(azide) + ΔE_dis(alkyne); ΔE^‡ = ΔE_dis + ΔE_int. Values are given in kcal mol⁻¹

	ΔEdis	ΔEint	ΔE^‡	ΔΔG^‡
9-ts	29.9	−14.6	15.3	26.6
12-ts	40.9	−23.9	17.0	30.6
17-ts	28.0	−14.6	13.4	26.5
20-ts	39.6	−24.9	14.7	29.6
23-ts	25.7	−14.7	11.0	28.7
25-ts	29.6	−17.0	12.6	29.9

---

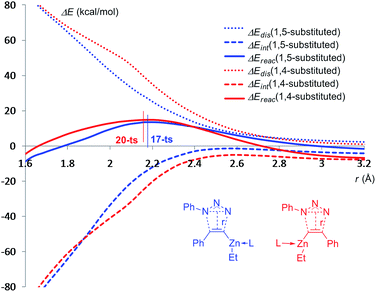
To further shed light on the regioselectivity for the cycloaddition of ethyl(phenylethynyl)zinc and azidobenzene with one imidazole ligand, the distortion and interaction energies along the reaction pathways for the formation of 1,5-disubstituted product 18 and the corresponding 1,4-regioisomer 21 have been calculated,²⁷ using the distances between dipole and dipolarophile as a reaction coordinate.²⁸ As shown in Fig. 8, as long as the distance between ethyl(phenylethynyl)zinc and azidobenzene are longer than 2.6 Å, the distortion energies for the two pathways are essentially the same. As the distance decreases below 2.6 Å, the distortion energy of the pathway for the formation of 1,4-disubstituted product climbs higher than for the formation of 1,5-regioisomer, because when the six-membered-ring transition state 20-ts is forming, ethyl(phenylethynyl)zinc part should be folded. For the formation of 1,4-disubstituted product 21, when the distance decreases below 2.1 Å, the six-membered-ring type geometry begins to transfer to five-membered-ring. Therefore, the gradient of distortion energy is decreased. Comparing with the red line and blue line, the relative energy of 20-ts is higher than that of 17-ts due to the higher distortion energy because of the stronger distortion of ethyl(phenylethynyl)zinc.

Fig. 8 Distortion, interaction, and total energies along the reaction pathways of the dipolar cycloadditions between ethyl(phenylethynyl)zinc and azidobenzene with one imidazole ligand. The solid lines are the reaction energies. The dotted lines are the distortion energies. The dashed lines are the interaction energies. The values given by kcal mol⁻¹ are the relative free energies calculated by B3LYP-D3BJ method in THF solvent.

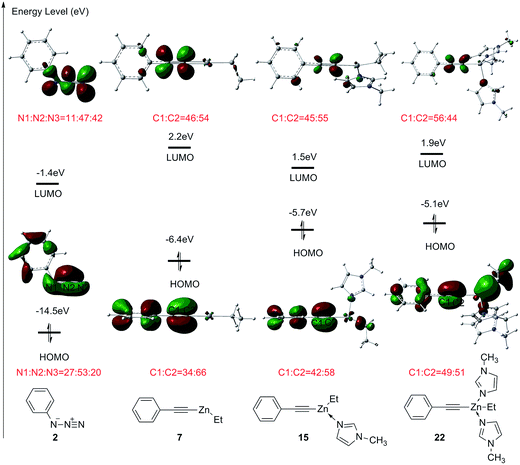
FMO theory is employed to further investigate the interaction between ethyl(phenylethynyl)zinc and azidobenzene.^17b,27a The molecular orbitals and orbital energies of dipole 2, and phenylethynylzinc 7, 15, and 22 are shown in Fig. 9. The energy levels of highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) for the ground state of azidobenzene 2 is −14.5 eV and −1.4 eV, respectively. The gap between the HOMO of phenylethynylzinc 7 and the LUMO of azidobenzene 2 is 7.3 eV lower than that between the HOMO of azidobenzene 2 and LUMO of phenylethynylzinc. Therefore, in the transition state of dipolar cycloaddition between ethyl(phenylethynyl)zinc and azidobenzene, the reactivity and regioselectivity are majorly depending on the orbital interaction between the HOMO of azidobenzene 2 and LUMO of phenylethynylzinc. When phenylethynylzinc 7 is coordinated with one or two imidazole ligands, the energy level of HOMO is increased due to the electron-donating effect of additional ligands, consequently, the reactivity is increased. However, the endothermic for the coordination of second imidazole leads to a higher overall barrier for this type reaction. The weight of the atomic orbitals in the ground state molecular orbitals also has been calculated to explain the selectivity. In azidobenzene 2, the weight of LUMO on N3 atom is higher than that on N1 atom. In one imidazole coordinated phenylethynylzinc 15, the weight of HOMO on C2 atom is higher than that on C1 atom. Therefore, when azidobenzene 2 reacts with phenylethynylzinc 15, 1,5-disubstituted 1,2,3-triazole is supposed to be the major product.

Fig. 9 Frontier molecular orbitals calculated for the model complex 2, 7, 15, and 22. The orbital energies have been provided in eV. The values for the proportions represent the weight of the atomic orbitals in the ground state molecular orbitals.

Conclusions

The DFT method B3LYP with a dispersion term (B3LYP-D3BJ) has been used to clarify the regioselectivity for the synthesis of 1,5-substituted 1,2,3-triazoles through zinc mediated 1,3-dipolar cycloaddition. Computational results suggest that only one N-methylimidazole ligand coordinates to the metal center during the reaction between ethyl(phenylethynyl)zinc and azidobenzene. 1,5-Substituted 1,2,3-triazole is formed through a five-membered-ring transition state with a lower activation free energy compared with the generation of 1,4-regioisomer via a six-membered-ring transition state. Moreover, substituent effect of alkynes has also been considered. B3LYP-D3BJ calculations show that alkyl substituted ethynylzinc owns the same reactivity as ethyl(phenylethynyl)zinc, while the regioselectivity is lower, however, B3LYP gives a higher regioselectivity, which is consistent with experimental observation. Beside, distortion–interaction analysis along the reaction pathways provides explanation for the reactivity and regioselectivity. The lower distortion energy in transition state leads to a lower activation energy for the generation of 1,5-substituted product. Furthermore, FMO analysis reveals the coordination of N-methylimidazole ligand towards zinc would increase the HOMO of ethyl(phenylethynyl)zinc, thereby improving the reactivity.

Acknowledgements

This work was supported by the National Science Foundation of China (Grants 21372266, and 51302327), and the Foundation of 100 Young Chongqing University (Project 0903005203191). We are also thankful for the project (no. 106112015CDJZR228806) supported by the Fundamental Research Funds for the Central Universities (Chongqing University).

Notes and references

1. A. Michael, J. Prakt. Chem., 1893, 48, 94.
2. (a) R. Huisgen, 1,3-Dipolar Cycloaddition Chemistry, ed. A. Padwa, Wiley, New York, 1984, pp. 1–176; (b) Synthetic Applications of 1,3 Dipolar Cycloaddition Chemistry toward Heterocycles and Natural Products, ed. A. Padwa and W. H. Pearson, Wiley, New York, 2002; (c) W. Lwowski, in 1,3-Dipolar Cycloaddition Chemistry, ed. A. Padwa, Wiley, New York, 1984, vol. 1, p. 559; (d) X.-Z. Cheng, W. Liu, Z.-D. Huang and C.-X. Kuang, Chin. Chem. Lett., 2003, 24, 764.
3. (a) J. P. Collman, N. K. Devaraj and C. E. D. Chidsey, Langmuir, 2004, 20, 1051; (b) A. E. Speers, G. C. Adam and B. F. Cravatt, J. Am. Chem. Soc., 2003, 125, 4686; (c) Q.-H. Li, Y. Ding and N.-W. Huang, Chin. Chem. Lett., 2014, 25, 1469.
4. (a) R. Huisgen, Proc. Chem. Soc., 1961, 357; (b) R. Huisgen, Angew. Chem., Int. Ed. Engl., 1963, 2, 565; (c) R. Huisgen, Angew. Chem., Int. Ed. Engl., 1963, 2, 633; (d) R. Huisgen, Angew. Chem., Int. Ed. Engl., 1968, 7, 321; (e) R. Huisgen, G. Mloston and E. Langhals, J. Am. Chem. Soc., 1986, 108, 6401.
5. (a) C. Girard, E. Önen, M. Aufort, S. Beauvière, E. Samson and J. Herscovici, Org. Lett., 2006, 8, 1689; (b) V. O. Rodionov, V. V. Fokin and M. G. Finn, Angew. Chem., 2005, 117, 2250 (Angew. Chem., Int. Ed., 2005, 44, 2210); (c) M. Hu, J. Li and S. Q. Yao, Org. Lett., 2008, 10, 5529; (d) C. Chowdhury, A. K. Sasmal and P. K. Dutta, Tetrahedron Lett., 2009, 50, 2678; (e) J. T. Fletcher, S. E. Walz and M. E. Keeney, Tetrahedron Lett., 2008, 49, 7030; (f) P. Zhong and S.-R. Guo, Chin. J. Chem., 2004, 22, 1183; (g) Q. Luo, G. Jia, J. Sun and Z. Lin, J. Org. Chem., 2014, 79, 11970–11980.
6. (a) V. V. Rostovtsev, L. G. Green, V. V. Fokin and K. B. Sharpless, Angew. Chem., Int. Ed., 2002, 41, 2596; (b) C. W. Tornøe, C. Christensen and M. Meldal, J. Org. Chem., 2002, 67, 3057; (c) L. Zhang, X. Chen, P. Xue, H. H. Y. Sun, I. D. Williams, K. B. Sharpless, V. V. Fokin and G. Jia, J. Am. Chem. Soc., 2005, 127, 15998; (d) B. C. Boren, S. Narayan, L. K. Rasmussen, L. Zhang, H. Zhao, Z. Lin, G. Jia and V. V. Fokin, J. Am. Chem. Soc., 2008, 130, 8923; (e) M. Lamberti, G. C. Fortman, A. Poater, J. Broggi, A. M. Z. Slawin, L. Cavallo and S. P. Nolan, Organometallics, 2012, 31, 756; (f) L.-J. Li, Y.-Q. Zhang, Y. Zhang, A.-L. Zhu and G.-S. Zhang, Chin. Chem. Lett., 2014, 25, 1161.
7. (a) G. C. Tron, T. Pirali, R. A. Billington, P. L. Canonico, G. Sorba and A. A. Genazzani, Med. Res. Rev., 2008, 28, 278; (b) J.-F. Lutz and Z. Zarafshani, Adv. Drug Delivery Rev., 2008, 60, 958; (c) J. E. Moses and A. D. Moorhouse, Chem. Soc. Rev., 2007, 36, 1249; (d) V. V. Fokin, ACS Chem. Biol., 2007, 2, 775; (e) J. A. Johnson, J. T. Koberstein, M. G. Finn and N. J. Turro, Macromol. Rapid Commun., 2008, 29, 1052; (f) M. Meldal and C. W. Tornøe, Chem. Rev., 2008, 108, 2952; (g) B. Lewandowski, G. De Bo, J. W. Ward, M. Papmeyer, S. Kuschel, M. J. Aldegunde, P. M. E. Gramlich, D. Heckmann, S. M. Goldup, D. M. D'Souza, A. E. Fernandes and D. A. Leigh, Science, 2013, 339, 189; (h) P. Thirumurugan, D. Matosiuk and K. Jozwiak, Chem. Rev., 2013, 113, 4905.
8. (a) M. Ahlquist and V. V. Fokin, Organometallics, 2007, 26, 4389; (b) F. Himo, T. Lovell, R. Hilgraf, V. V. Rostovtsev, L. Noodleman, K. B. Sharpless and V. V. Fokin, J. Am. Chem. Soc., 2005, 127, 210; (c) D. Cantillo, M. Ávalos, R. Babiano, P. Cintas, J. L. Jiménez and J. C. Palacios, Org. Biomol. Chem., 2011, 9, 2952.
9. (a) G. Pampaloni, R. Peloso, C. Graiff and A. Tiripicchio, Organometallics, 2005, 24, 819; (b) X. Yang and P. Knochel, Synlett, 2004, 13, 2303; (c) R. R. Conry, A. A. Tipton, W. S. Striejewske, E. Erkizia, M. A. Malwitz, A. Caffaratti and J. A. Natkin, Organometallics, 2004, 23, 5210; (d) J. M. Kok, B. W. Skelton and A. H. White, J. Cluster Sci., 2004, 15, 365.
10. (a) A. Krasiński, V. V. Fokin and K. B. Sharpless, Org. Lett., 2004, 6, 1237; (b) B.-Y. Lee, S. R. Park, H. B. Jeon and K. S. Kim, Tetrahedron Lett., 2006, 47, 5105; (c) I. Jlalia, H. Elamair, F. Meganem, J. Herscovici and C. Girard, Tetrahedron Lett., 2008, 49, 6756.
11. (a) D.-R. Hou, T.-C. Kuan, Y.-K. Li, R. Lee and K.-W. Huang, Tetrahedron, 2010, 66, 9415; (b) A. H. Yap and S. M. Weinreb, Tetrahedron Lett., 2006, 47, 3035; (c) M. M. Majireck and S. M. Weinreb, J. Org. Chem., 2006, 71, 8680; (d) J. R. Johansson, P. Lincoln, B. Nordén and N. Kann, J. Org. Chem., 2011, 76, 2355.
12. (a) S. W. Kwok, J. R. Fotsing, R. J. Fraser, V. O. Rodionov and V. V. Fokin, Org. Lett., 2010, 12, 4217; (b) M. E. Meza-Aviña, M. K. Patel, C. B. Lee, T. J. Dietz and M. P. Croatt, Org. Lett., 2011, 13, 2984; (c) L. Wu, Y. Chen, M. Tang, X. Song, G. Chen, X. Song and Q. Lin, Synlett, 2012, 23, 1529; (d) L. Hong, W. Lin, F. Zhang, R. Liu and X. Zhou, Chem. Commun., 2013, 49, 5589.
13. A. Akao, T. Tsuritani, S. Kii, K. Sato, N. Nonoyama, T. Mase and N. Yasuda, Synlett, 2007, 1, 31.
14. C. D. Smith and M. F. Greaney, Org. Lett., 2013, 15, 4826.
15. (a) M. Ahlquist and V. V. Fokin, Organometallics, 2007, 26, 4389; (b) B. F. Straub, Chem. Commun., 2007, 3868.
16. (a) L. K. Rasmussen, B. C. Boren and V. V. Fokin, Org. Lett., 2007, 9, 5337; (b) S. Oppilliart, G. Mousseau, L. Zhang, G. Jia, P. Thuéry, B. Rousseau and J.-C. Cintrat, Tetrahedron, 2007, 63, 8094.
17. (a) F. Risitano, G. Grassi, F. Foti, G. Bruno and A. Rotondo, Heterocycle, 2003, 60, 857; (b) D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10187; (c) H. Zhao, X. Li, X. Ran and W. Zhang, J. Mol. Struct.: THEOCHEM, 2004, 683, 207.
18. (a) K. Fukui, J. Org. Chem., 1971, 4, 57; (b) M. Burdisso, R. Gandolfi, S. Quartieri and A. Rastelli, Tetrahedron, 1987, 43, 159; (c) H. Y. Yoo and K. N. Houk, J. Am. Chem. Soc., 1997, 119, 2877.
19. (a) K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1976, 10, 325; (b) S. Nagase and K. Morokuma, J. Am. Chem. Soc., 1978, 100, 1666; (c) K. N. Houk, R. W. Gandour, R. W. Strozier, N. G. Rondan and L. A. Paquette, J. Am. Chem. Soc., 1979, 101, 6797; (d) R. D. J. Froese, J. M. Coxon, S. C. West and K. Morokuma, J. Org. Chem., 1997, 62, 6991; (e) N. Koga, T. Ozawa and K. Morokuma, J. Phys. Org. Chem., 1990, 3, 519; (f) J. M. Coxen, S. T. Grice, R. G. A. R. Maclagan and D. Q. McDonald, J. Org. Chem., 1990, 55, 3804; (g) J. M. Coxon, R. D. J. Rroese, B. Ganguly, A. P. Marchand and K. J. Morokuma, Synlett, 1999, 11, 1681; (h) M. Avalos, R. Babiano, J. L. Bravo, P. Cintas, J. Jim-enez, J. Palacios and M. A. Silva, J. Org. Chem., 2000, 65, 6613; (i) K. Geetha, T. C. Dinadayalane and G. N. Sastry, J. Phys. Org. Chem., 2003, 16, 298; (j) M. Manoharan and P. Venuvanalingam, J. Chem. Soc., Perkin Trans., 1997, 2, 1799; (k) K. Kavitha, M. Manoharan and P. Venuvanalingam, J. Org. Chem., 2005, 70, 2528; (l) K. Kavitha and P. Venuvanalingam, Int. J. Quantum Chem., 2005, 104, 67; (m) P. Blowers, L. Ford and R. Masel, J. Phys. Chem. A, 1998, 102, 9267.
20. M. J. Frisch, et al., Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2009. The full author list is shown in ESI†.
21. (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785.
22. (a) D. Liu, S. Tang, H. Yi, X. Qi, Y. Lan and A. Lei, Chem.–Eur. J., 2014, 20, 15605–15610; (b) O. Gutierrez, J. C. Tellis, D. N. Primer, G. A. Molander and M. C. Kozlowski, J. Am. Chem. Soc., 2015, 137, 4896.
23. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456.
24. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378.
25. (a) K. Fukui, Acc. Chem. Res., 1981, 14, 363; (b) H. P. Hratchian and H. B. Schlegel, in Theory and Applications of Computational Chemistry: The First 40 Years, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. Scuseria, Elsevier, Amsterdam, 2005, p. 195; (c) H. P. Hratchian and H. B. Schlegel, J. Chem. Phys., 2004, 120, 9918; (d) H. P. Hratchian and H. B. Schlegel, J. Chem. Theory Comput., 2005, 1, 61.
26. D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 10646.
27. (a) Y. Lan, S. E. Wheeler and K. N. Houk, J. Chem. Theory Comput., 2011, 7, 2104; (b) S. Liu, Y. Lei, X. Qi and Y. Lan, J. Phys. Chem., 2014, 118, 2638.
28. ESI†.

---

Footnotes

† Electronic supplementary information (ESI) available: Cartesian coordinates and energies of all reported structures and full authorship of Gaussian 09. See DOI: 10.1039/c5ra02703a

‡ Yingzi Li and Xiaotian Qi contributed equally to this work.

---