Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dielectric elastomers, with very high dielectric permittivity, based on silicone and ionic interpenetrating networks
Liyun Yu,
Frederikke Bahrt Madsen,
Søren Hvilsted and
Anne Ladegaard Skov*
Danish Polymer Centre, Department of Chemical and Biochemical Engineering, Technical University of Denmark, DTU, Søltofts Plads, Bldg. 227, 2800 Kgs. Lyngby, Denmark. E-mail: al@kt.dtu.dk
First published on 29th May 2015
Abstract
Dielectric elastomers (DEs), which represent an emerging actuator and generator technology, admittedly have many favourable properties, but their high driving voltages are one of the main obstacles to commercialisation. One way to reduce driving voltage is by increasing the ratio between dielectric permittivity and the Young's modulus of the elastomer. One system that potentially achieves this involves interpenetrating polymer networks (IPNs), based on commercial silicone elastomers and ionic networks from amino- and carboxylic acid-functional silicones. The applicability of these materials as DEs is demonstrated herein, and a number of many and important parameters, such as dielectric permittivity/loss, viscoelastic properties and dielectric breakdown strength, are investigated. Ionic and silicone elastomer IPNs are promising prospects for dielectric elastomer actuators, since very high permittivities are obtained while dielectric breakdown strength and Young's modulus are not compromised. These good overall properties stem from the softening effect and very high permittivity of ionic networks – as high as ε′ = 7500 at 0.1 Hz – while the silicone elastomer part of the IPN provides mechanical integrity as well as relatively high breakdown strength. All IPNs have higher dielectric losses than pure silicone elastomers, but when accounting for this factor, IPNs still exhibit satisfactory performance improvements.
Introduction
Dielectric elastomers (DEs) are based on an elastomer film sandwiched between thin and compliant electrodes. This emerging technology can be used for actuators,1 sensors2 and generators,3,4 due to its ability to expand and contract under an applied electric field, or to generate electrical energy when subjected to mechanical motion. The very high driving voltages which are necessary to activate the DE (usually in the order of several kVs) impose a number of limitations on the applicability of the technology, due to overly expensive electronics. Furthermore, handling precautions are generally necessary when dealing with high voltages. However, due to the possibility of introducing large strains – as opposed to e.g. piezoelectrics – the technology still holds great promise.5 Also, the dielectric elastomers have been shown versatile in a wide range of operational frequencies such that acceptable energy outputs can be achieved in as different applications a e.g. wave harvesting (0.01–0.1 Hz)6 and loudspeakers (frequencies higher than 1 kHz).7High-dielectric permittivity elastomers are required for improving the performance of many of the current devices based on DEs so that either reduced driving voltage or increased actuation at a given voltage can be obtained. The driving voltages of DEs are typically lowered by employing one of two methods, namely either – with the best effect – by reducing elastomer thickness (d) and/or – with less of an impact – by increasing the ratio between dielectric permittivity (ε′) and the Young's modulus (Y). For many elastomers it is difficult to proceed below the commonly encountered threshold thickness of ∼20 μm, due to processing issues such as the release of thin films from the curing substrate.8 Nevertheless, recent results in relation to thin film coating look promising as a technique for using thickness as an optimisation parameter.9
Prestretching of the elastomer film may be another method to greatly improve the important properties of the dielectric elastomer1 as well as suppress electro-mechanical instability.3,10 However, the effect of prestretching gradually disappears over time and therefore reliable products based entirely on this approach have not yet been realized. In this work we focus on materials without any need for prestretching.
Several approaches to increasing the dielectric permittivity of DEs have been investigated, including encapsulating conductive fillers,11 grafting dipoles12–15 and adding high-permittivity fillers.16–21 Many of these systems, however, fail to increase actuation performance (ε′/Y) or the maximum achievable level of actuation (ε′/YEB2, where EB is the dielectric breakdown strength), since the addition of hard additives, whether grafted or not, often increases the Young's modulus to the same extent as dielectric permittivity is increased; furthermore, breakdown strength may also be lowered significantly. Recently it was shown theoretically that a ten-fold enhancement of the electro-mechanical coupling could be achieved if a microstructural control over the hard fillers was imposed.22 Moreover, in order for an elastomer to be applicable as a DE, many other requirements have to be fulfilled, such as fast response times, high mechanical stability and very low conductivity.23 A novel soft silicone elastomer matrix based on chloropropyl-functional siloxane copolymers, however, looks promising with respect to overall DE properties.24
The focus of this work is to develop very high dielectric permittivity elastomers such that a decrease in electrical breakdown strength can be tolerated and an improvement in actuation performance is still obtained, by concentrating on increasing ε′/YEB2.
Recently, a novel class of polymers has been introduced, namely so-called “ionic networks”,25–27 which are based on macromolecular assembly through ionic interactions. These materials have been shown to possess extremely high dielectric permittivities, and in this work we explore the resulting properties of interpenetrating polymer networks (IPNs) based on silicone and siloxane-based ionic networks. IPNs are polymer networks consisting of two or more types of polymer that are cross-linked in situ, in order to produce interlaced networks. Due to stabilised bulk and surface morphology, which is created by the interlaced networks, IPNs often have different and superior properties compared to respective homopolymers.28,29 In addition, IPNs have previously been successfully applied as DEs, with the focus on materials in two different zero-stress states.30,31
In this work we exploit the favourable elastomer properties of silicone networks, which will provide the IPNs with high stability, fast response times and low viscous loss, and the high dielectric permittivity of ionic networks, which will provide the IPNs with a greater actuation response. We also investigate how different important DE properties, such as dielectric permittivity, dielectric loss, elastic modulus and dielectric breakdown strength, are affected by the concentration of ionic networks in IPNs and the type of silicone elastomer used.
Results and discussion
Dielectric interpenetrating elastomer networks were prepared according to Scheme 1. The networks were prepared by mixing carboxydecyl-terminated PDMS of either 1000 g mol−1 (DMS-B12) or 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 (DMS-B25) with amino-functional PDMS (AMS-162). Following the protonation of the amino groups, the components formed ionic bonds and thereby formed the ionic part of the interpenetrating silicone network. The ionic networks were mixed thereafter in a sequential way with various commercial silicone elastomer matrices, in order to elucidate the effect of the different formulations on the final dielectric and breakdown properties of the interpenetrating networks. The commercial two-component systems were respectively: RT625, an RTV silicone, and XLR630 and LR3043/30, both LSR silicones but with varying viscosities (XLR630 having the lowest viscosity). Furthermore, a number of samples were mixed with additional silica particles to reinforce systems which contained high concentrations of ionic networks.
000 g mol−1 (DMS-B25) with amino-functional PDMS (AMS-162). Following the protonation of the amino groups, the components formed ionic bonds and thereby formed the ionic part of the interpenetrating silicone network. The ionic networks were mixed thereafter in a sequential way with various commercial silicone elastomer matrices, in order to elucidate the effect of the different formulations on the final dielectric and breakdown properties of the interpenetrating networks. The commercial two-component systems were respectively: RT625, an RTV silicone, and XLR630 and LR3043/30, both LSR silicones but with varying viscosities (XLR630 having the lowest viscosity). Furthermore, a number of samples were mixed with additional silica particles to reinforce systems which contained high concentrations of ionic networks.
 | ||
| Scheme 1 Reaction scheme for the sequential formation of ionic and silicone interpenetrating polymer networks. | ||
Reference elastomer samples, made from pure PDMS (DMS-V35) and pure commercial and ionic networks, were also prepared. An overview of all the samples is shown in Table 1.
| # | Materials | Silicone [wt%] | Ionic network [wt%] | SiO2 [wt%] | |
|---|---|---|---|---|---|
| a The concentrations of SiO2 fillers in commercial silicones were estimated by TGA. | |||||
| 1 | Pure PDMS | PDMS V35 | 100 | 0 | 0 |
| 2 | Commercial siliconesa | RT625 | — | 0 | 27 |
| 3 | XLR630 | — | 0 | 37 | |
| 4 | LR3043/30 | — | 0 | 73 | |
| 5 | Ionic networks | AMS162 + B12 | 0 | 100 | 0 |
| 6 | (AMS162 + B12)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2 = 80 wt% SiO2 = 80 wt%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 wt% 20 wt% |
0 | 80 | 20 | |
| 7 | (AMS162 + B12)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2 = 70 wt% SiO2 = 70 wt%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 wt% 30 wt% |
0 | 70 | 30 | |
| 8 | Interpene-trating networks | XLR630![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (AMS162 + B12) = 70 wt% (AMS162 + B12) = 70 wt%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 wt% 30 wt% |
44.1 | 30 | 25.9 |
| 9 | RT625![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (AMS162 + B25) = 50 wt% (AMS162 + B25) = 50 wt%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 wt% 50 wt% |
36.5 | 50 | 13.5 | |
| 10 | RT625![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (AMS162 + B25) (AMS162 + B25)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2 = 50 wt% SiO2 = 50 wt%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 wt% 50 wt%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 wt% 10 wt% |
32.85 | 45 | 22.2 | |
| 11 | LR3043/30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (AMS162 + B12) = 70 wt% (AMS162 + B12) = 70 wt%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 wt% 30 wt% |
18.9 | 30 | 51.1 | |
| 12 | LR3043/30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (AMS162 + B12) = 50 wt% (AMS162 + B12) = 50 wt%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 wt% 50 wt% |
13.5 | 50 | 36.5 | |
| 13 | LR3043/30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (AMS162 + B12) = 30 wt% (AMS162 + B12) = 30 wt%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70 wt% 70 wt% |
8.1 | 70 | 21.9 | |
| 14 | LR3043/30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (AMS162 + B12) (AMS162 + B12)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2 = 30 wt% SiO2 = 30 wt%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70 wt% 70 wt%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 wt% 10 wt% |
7.29 | 63 | 29.7 | |
| 15 | LR3043/30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (AMS162 + B12) = 10 wt% (AMS162 + B12) = 10 wt%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 90 wt% 90 wt% |
2.7 | 90 | 7.3 | |
Dielectric properties
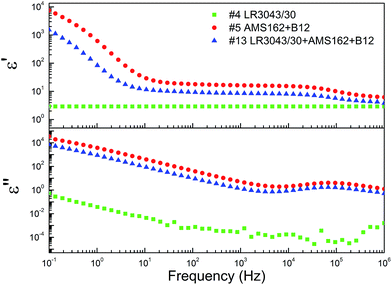
The effect of the concentration and type of commercial silicone system on the dielectric properties of the interpenetrating networks was determined by dielectric relaxation spectroscopy on film discs of approximately 0.5 to 1 mm in thickness. An example of a common dielectric spectrum is shown in Fig. 1.As evidenced in Fig. 1, both real (ε′) and imaginary (ε′′) parts of the dielectric permittivity vary significantly in relation to frequency. As a result of this typical behaviour we have chosen in the following to show data for two representative frequencies, namely 0.1 Hz and 1 MHz.
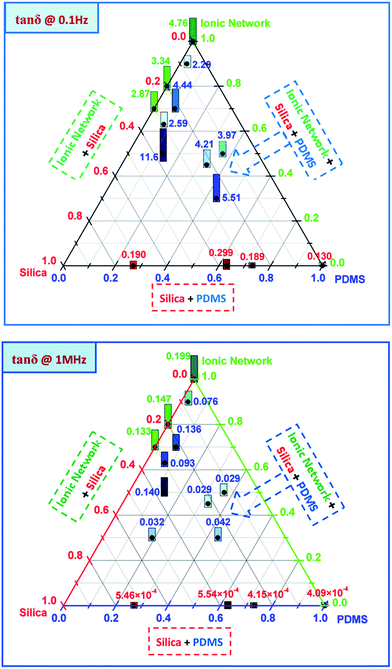
The resulting dielectric permittivities, as functions of composition at two different frequencies (0.1 Hz and 1 MHz), are shown as ternary plots in Fig. 2 and are summarised further in Table 2. Ternary plots were applied, as prepared samples comprise many variables. We chose the content of an ionic network, PDMS from a commercial elastomer and silica from a commercial elastomer+ added, respectively, as the variables. The values for different samples are represented by numbers as well as a bar indicating size. Commercial elastomers do not come with a list of contents, so the amounts of residue from the TGA measurements were used to measure the resulting silica content.
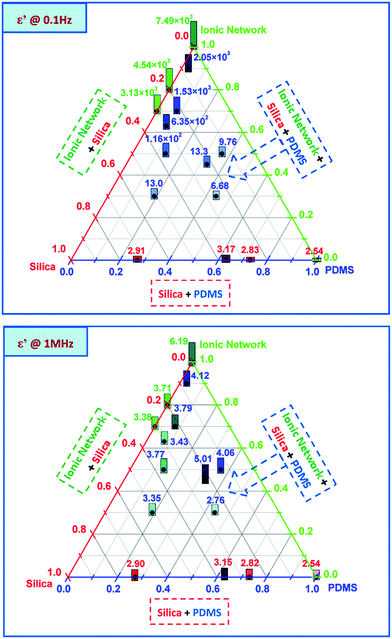 | ||
| Fig. 2 Dielectric permittivity as a function of the composition of interpenetrating ionic and silicone networks at 0.1 Hz and 1 MHz, respectively. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) at 0.1 Hz and 1 MHz, breakdown strengths (EB), Young's moduli and loss (tan
δ) at 0.1 Hz and 1 MHz, breakdown strengths (EB), Young's moduli and loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ), as well as the figure of merit calculations
δ), as well as the figure of merit calculations
| # | Breakdown strength | Dielectric properties | Viscoelastic properties | Figure of merit | Adjusted figure of merit | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EB [V μm−1] | ε′ | ε′ | tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ δ |
tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ δ |
Y = 3G′ [kPa] | tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ(rheo) δ(rheo) |
Fom (DEA) | Fom (DEA) | Fom (DEG) | Fom (DEG) | F*om (DEA) | F*om (DEA) | F*om (DEG) | F*om (DEG) | ||
| 0.1 Hz | 1 MHz | 0.1 Hz | 1 MHz | 0.01 Hz | 0.01 Hz | 0.1 Hz | 1 MHz | 0.1 Hz | 1 MHz | 0.1 Hz | 1 MHz | 0.1 Hz | 1 MHz | |||
| 1 | Pure PDMS | 40 | 2.5 | 2.5 | 0.130 | 4.1 × 10−4 | 64.3 | 0.06 | 0.25 | 0.25 | 0.19 | 0.19 | 0.33 | 0.25 | 0.20 | 0.19 |
| 2 | Commercial silicones | 87 | 2.8 | 2.8 | 0.189 | 4.2 × 10−4 | 84.4 | 0.03 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 3 | 120 | 3.2 | 3.2 | 0.299 | 5.5 × 10−4 | 227.2 | 0.04 | 0.79 | 0.79 | 2.13 | 2.13 | 0.72 | 0.79 | 1.95 | 2.12 | |
| 4 | 130 | 2.9 | 2.9 | 0.190 | 5.5 × 10−4 | 253.3 | 0.08 | 0.77 | 0.77 | 2.30 | 2.30 | 0.76 | 0.77 | 2.29 | 2.30 | |
| 5 | Ionic networks | 72 | 7.5 × 103 | 6.2 | 4.76 | 0.199 | 37.3 | 0.01 | 4107 | 3.41 | 1813 | 1.50 | 848 | 2.84 | 374 | 1.25 |
| 6 | 83 | 4.5 × 103 | 3.7 | 3.34 | 0.147 | 47.0 | 0.07 | 2620 | 2.15 | 1460 | 1.20 | 718 | 1.87 | 400 | 1.04 | |
| 7 | 101 | 3.1 × 103 | 3.4 | 2.87 | 0.133 | 124.2 | 1.74 | 1013 | 1.10 | 1491 | 1.62 | 311 | 0.97 | 458 | 1.43 | |
| 8 | Interpenetrating networks | 69 | 6.7 | 2.8 | 5.51 | 0.042 | 37.0 | 0.36 | 3.39 | 1.41 | 1.48 | 0.62 | 0.62 | 1.35 | 0.27 | 0.59 |
| 9 | 76 | 9.8 | 4.1 | 3.97 | 0.029 | 61.4 | 0.09 | 3.62 | 1.51 | 2.63 | 1.10 | 0.87 | 1.47 | 0.63 | 1.07 | |
| 10 | 82 | 13.3 | 5.0 | 4.21 | 0.029 | 70.5 | 0.12 | 5.00 | 1.89 | 4.17 | 1.58 | 1.14 | 1.84 | 0.95 | 1.53 | |
| 11 | 45 | 13.0 | 3.4 | 3.38 | 0.032 | 255.1 | 0.10 | 0.41 | 0.11 | 1.23 | 0.32 | 0.11 | 0.10 | 0.33 | 0.31 | |
| 12 | 78 | 1.7 × 102 | 3.8 | 11.6 | 0.140 | 113.7 | 0.08 | 24.0 | 0.80 | 33 | 1.07 | 2.31 | 0.70 | 3.12 | 0.94 | |
| 13 | 90 | 1.5 × 103 | 3.8 | 4.44 | 0.136 | 30.9 | 0.05 | 1579 | 3.93 | 579 | 1.44 | 345 | 3.46 | 126 | 1.27 | |
| 14 | 98 | 6.4 × 102 | 3.4 | 2.59 | 0.093 | 157.3 | 0.05 | 153 | 0.83 | 285 | 1.54 | 50.7 | 0.76 | 94.3 | 1.41 | |
| 15 | 87 | 2.1 × 103 | 4.1 | 2.3 | 0.076 | 30.5 | 0.03 | 2008 | 4.05 | 724 | 1.46 | 724 | 3.77 | 261 | 1.36 | |
As seen from the ternary plots in Fig. 2, pure PDMS networks (created from V35 and commercial silicones) have dielectric permittivities of approximately ε′ = 2.5–3.2 (red numbers), independent of frequency. Pure ionic networks, produced from carboxydecyl-terminated PDMS, amino-functional PDMS and different concentrations of reinforcing silica particles, display very high dielectric permittivities at a low frequency (as high as ε′ = 7.5 × 103 for the pure ionic network (green numbers)). At a higher frequency the pure ionic network also has higher dielectric permittivity than pure silicone (ε′ = 6.2), which corresponds to a two-fold increase compared to pure silicone.
The blue numbers in the ternary plots correspond to the measured dielectric permittivities of the interpenetrating ionic and silicone networks. As seen in Fig. 2, the dielectric permittivities of the interpenetrating networks are very high at low frequencies, ranging from ε′ = 6.7 to 2 × 103. At higher frequencies the highest dielectric permittivity of ε′ = 5 was obtained for a network with a 50% ionic network and a 50% silicone network (sample 10). Higher ionic network concentrations were shown to not necessarily induce higher dielectric permittivity at higher frequencies, while dielectric permittivity at low frequencies increases systematically in line with increasing ionic network concentrations.
The measured dielectric losses, represented as tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, at 0.1 Hz and 1 MHz, for the interpenetrating networks with different compositions are shown in Fig. 3 and summarised in Table 2.
δ, at 0.1 Hz and 1 MHz, for the interpenetrating networks with different compositions are shown in Fig. 3 and summarised in Table 2.
Tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ at 1 MHz for pure PDMS networks were very low, as seen by the red numbers at the bottom of Fig. 3. The highest dielectric loss at 1 MHz was obtained for a pure ionic network at a loss of approximately 0.2.
δ at 1 MHz for pure PDMS networks were very low, as seen by the red numbers at the bottom of Fig. 3. The highest dielectric loss at 1 MHz was obtained for a pure ionic network at a loss of approximately 0.2.
The tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ for the interpenetrating networks were all lower than this at this very frequency, and they are therefore within a suitable range for DEs. However, when the frequency was reduced, for example, to 0.1 Hz (Fig. 3, top figure), the situation changed entirely. At this frequency the tan
δ for the interpenetrating networks were all lower than this at this very frequency, and they are therefore within a suitable range for DEs. However, when the frequency was reduced, for example, to 0.1 Hz (Fig. 3, top figure), the situation changed entirely. At this frequency the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ for commercial silicone elastomers increased to ∼0.1–0.3, whereas the pure ionic network samples and the interpenetrating networks all had a tan
δ for commercial silicone elastomers increased to ∼0.1–0.3, whereas the pure ionic network samples and the interpenetrating networks all had a tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ which was >1. This means that at low frequencies dielectric losses are greater than dielectric permittivity contributions, thereby signifying that the materials in question start acting more like conductors than as capacitors.
δ which was >1. This means that at low frequencies dielectric losses are greater than dielectric permittivity contributions, thereby signifying that the materials in question start acting more like conductors than as capacitors.
Viscoelastic properties
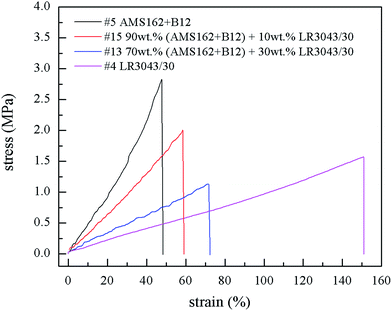
Firstly a few of the samples were investigated with respect to their ultimate elongations through stress–strain diagrams. Their behaviour is shown in Fig. 4.All four samples show linear behaviour until break which means that their Young's moduli are constant independent on the utilized strain.
The Young's moduli of the samples were determined through linear rheology due to the ease of this experimental technology which additionally directly provides information on the viscoelastic losses. Hereby the Young's modulus was calculated from the measured storage modulus, G′, since Y = 2(1 + ν)G, where G = G′(ω → 0), i.e. the initial shear modulus in finite elasticity. Due to the incompressibility of silicones (Poisson's ratio (ν) close to 0.5) the Young's modulus can be obtained as Y = 3G′, which describes frequency-independent elastic moduli up to a strain of approximately 15%. Furthermore, highly frequency-dependent viscous loss can be determined from the measured loss modulus, G′′, and it is usually referred to via the loss tangent, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ(rheo) = G′′/G′. The Young's moduli calculated from G′ at 0.01 Hz and tan
δ(rheo) = G′′/G′. The Young's moduli calculated from G′ at 0.01 Hz and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ(rheo) are shown in Table 2. For pure PDMS and the commercial silicones – as expected – the Young's moduli increased in line with increasing concentrations of reinforcing silica particles. The particles, therefore, greatly amplify the stiffness of the silicone networks. Furthermore, viscous losses, tan
δ(rheo) are shown in Table 2. For pure PDMS and the commercial silicones – as expected – the Young's moduli increased in line with increasing concentrations of reinforcing silica particles. The particles, therefore, greatly amplify the stiffness of the silicone networks. Furthermore, viscous losses, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ(rheo), were low for all of these samples, meaning that they were well cross-linked. The pure ionic network (sample 5) had by far the lowest Young's modulus and was therefore a lot softer than the silicone elastomers. tan
δ(rheo), were low for all of these samples, meaning that they were well cross-linked. The pure ionic network (sample 5) had by far the lowest Young's modulus and was therefore a lot softer than the silicone elastomers. tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ(rheo), however, was as low as for the silicone elastomers, thus implying that the ionic network was very well cross-linked. Upon adding silica particles (samples 6 and 7) the Young's modulus of the ionic networks increased, and at 30 wt% silica particles the ionic network became significantly stiffer. The tan
δ(rheo), however, was as low as for the silicone elastomers, thus implying that the ionic network was very well cross-linked. Upon adding silica particles (samples 6 and 7) the Young's modulus of the ionic networks increased, and at 30 wt% silica particles the ionic network became significantly stiffer. The tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ(rheo) for this sample was nevertheless high (>1), which indicates that the addition of high amounts of silica particles to the ionic networks to some extent hinders the cross-linking reaction. The Young's moduli of the interpenetrating networks varied depending on the type of commercial silicone elastomer used and the addition of silica particles. For the XLR630 elastomer the addition of 30 wt% ionic network decreased the Young's modulus significantly from 227 kPa to 37 kPa. Viscous loss, tan
δ(rheo) for this sample was nevertheless high (>1), which indicates that the addition of high amounts of silica particles to the ionic networks to some extent hinders the cross-linking reaction. The Young's moduli of the interpenetrating networks varied depending on the type of commercial silicone elastomer used and the addition of silica particles. For the XLR630 elastomer the addition of 30 wt% ionic network decreased the Young's modulus significantly from 227 kPa to 37 kPa. Viscous loss, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ(rheo), however, increased considerably, although it remained <1. The Young's modulus of the RT625 silicone elastomers only decreased from 84 kPa to 61 kPa after adding a 50 wt% ionic network (sample 9), and viscous loss remained low, indicating that the mechanical integrity of this sample was maintained. Adding silica particles to this elastomer (sample 10) increased the modulus somewhat to 70.5 kPa and also increased viscous loss ten-fold, thereby indicating increased damping behaviour. Again, this could be due to the silica particles hindering the cross-linking reaction of the ionic networks, due to uneven interactions between the silica particles and the two ionic network constituents' reactive groups, as one of them may be more prone to adhere to silica particles, which thus makes the network locally unstoichiometric. For the LR3043/30 silicone elastomer the addition of 30 wt% ionic network did not alter the Young's modulus, despite viscous loss, tan
δ(rheo), however, increased considerably, although it remained <1. The Young's modulus of the RT625 silicone elastomers only decreased from 84 kPa to 61 kPa after adding a 50 wt% ionic network (sample 9), and viscous loss remained low, indicating that the mechanical integrity of this sample was maintained. Adding silica particles to this elastomer (sample 10) increased the modulus somewhat to 70.5 kPa and also increased viscous loss ten-fold, thereby indicating increased damping behaviour. Again, this could be due to the silica particles hindering the cross-linking reaction of the ionic networks, due to uneven interactions between the silica particles and the two ionic network constituents' reactive groups, as one of them may be more prone to adhere to silica particles, which thus makes the network locally unstoichiometric. For the LR3043/30 silicone elastomer the addition of 30 wt% ionic network did not alter the Young's modulus, despite viscous loss, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ(rheo), being increased. Increasing the concentration of ionic network in this elastomer to 50 wt%, 70 wt% and 90 wt% decreased the Young's modulus significantly (from 253 kPa for pure LR3043/30 to 114 kPa, 30.9 kPa and 30.5 kPa for 50, 70 and 90 wt% ionic network, respectively). Common to all these samples was that viscous losses remained low, even at very high concentrations of ionic network. The addition of 10 wt% silica particles to an elastomer with a 70 wt% ionic network (sample 14) increased the Young's modulus significantly (from 30.9 kPa to 157 kPa) while still maintaining low viscous loss. The viscoelastic measurements indicate that the RT625 and LR3043/30 elastomers are more suitable for preparing ionic interpenetrating networks compared to XLR630, since they maintain low viscous losses after adding the ionic network. Furthermore, LR3043/30 can be used with reinforcing silica particles, without losses being compromised.
δ(rheo), being increased. Increasing the concentration of ionic network in this elastomer to 50 wt%, 70 wt% and 90 wt% decreased the Young's modulus significantly (from 253 kPa for pure LR3043/30 to 114 kPa, 30.9 kPa and 30.5 kPa for 50, 70 and 90 wt% ionic network, respectively). Common to all these samples was that viscous losses remained low, even at very high concentrations of ionic network. The addition of 10 wt% silica particles to an elastomer with a 70 wt% ionic network (sample 14) increased the Young's modulus significantly (from 30.9 kPa to 157 kPa) while still maintaining low viscous loss. The viscoelastic measurements indicate that the RT625 and LR3043/30 elastomers are more suitable for preparing ionic interpenetrating networks compared to XLR630, since they maintain low viscous losses after adding the ionic network. Furthermore, LR3043/30 can be used with reinforcing silica particles, without losses being compromised.
Dielectric breakdown strength
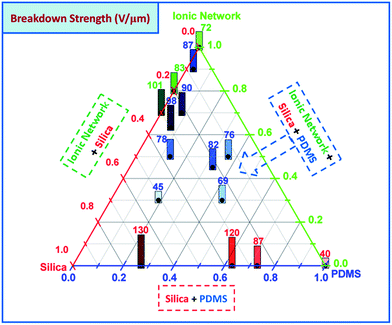
The measured dielectric breakdown strengths for the interpenetrating and pure networks are shown in Fig. 5.As seen in red numbers in the bottom right of Fig. 5, the breakdown strength of pure unreinforced PDMS is as low as 40 V μm−1. The dielectric breakdown strength then increases in line with increasing concentrations of silica particles, reaching 130 V μm−1 for LR3043/30. This is due to increasing stiffness, which has a significant influence on the breakdown strength of DEs, since increased stiffness supresses electromechanical instability.32 The breakdown strength of pure ionic networks also increases in line with increasing concentrations of silica particles, from 72 V μm−1 for a pure ionic network to 101 V μm−1 for a particle-filled network with 30 wt% silica. The breakdown strengths of the interpenetrating networks range from 45 V μm−1 to 90 V μm−1, and therefore in all cases they remain higher than for of a pure PDMS network. Surprisingly, breakdown strength does not necessarily increase in parallel with an increase in silica content, but it does exhibit more complex behaviour, perhaps again due to the particle–ionic network interactions.
Figure of merit
The equations for figures of merit (Fom), to assess elastomer performance as a dielectric elastomer actuator (DEA)33 and a dielectric elastomer generator (DEG),34 are defined as follows:
 | (1) |
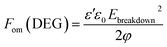 | (2) |
The relative figure of merit values for the actuation mode illustrate that at both 0.1 Hz and 1 MHz, samples 13 and 15, which are prepared with the commercial elastomer LR3043/30, show the highest overall improvement in predicted actuator properties. This is due to the relatively soft nature of these films, combined with increased dielectric permittivity. Furthermore, the pure ionic network without reinforcing silica (sample 5) also has a very high relative figure of merit at low frequencies, due to its very high dielectric permittivity at this particular frequency. This sample, however, has reduced dielectric breakdown strength. The predicted properties for a DEG at 0.1 Hz have improved the most for those samples prepared with a pure ionic network (samples 5–7). The interpenetrating networks prepared with LR3043/30 and a high concentration of ionic networks (samples 13–15) also show high gains in overall properties, due to the very high dielectric permittivities obtained at this frequency. At a higher frequency (1 MHz) the relative figures of merit – and thereby overall DEG properties – have increased to a lesser extent compared to the RT625 reference sample. Therefore, the most promising use of the ionic and interpenetrating networks, based on the figure of merit calculations, would be as DEAs or DEGs operated at low frequencies.
Due to the high dielectric losses recorded at low frequencies, a new figure of merit expression that takes into account these high losses is introduced:
 | (3) |
This correction factor is a general means of introducing losses as done for rheological measurements. This expression is reasonable, since the figure of merit should be coupled to the heat conduction of the DE element.37,38 tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ is in this way a measure of heat conduction from dielectric losses, as they are assumed to be more significant than viscoelastic losses. Viscoelastic losses of well-crosslinked silicone elastomers are usually far below 10%.39,40
δ is in this way a measure of heat conduction from dielectric losses, as they are assumed to be more significant than viscoelastic losses. Viscoelastic losses of well-crosslinked silicone elastomers are usually far below 10%.39,40
The results for these calculations are shown in Table 2. It is clear that for many of the samples the adjusted figure of merit is significantly lower than that for the non-corrected. Furthermore, some samples now have adjusted figures of merit that are <1, signifying that there is no actual improvement in overall properties compared to the RT625 reference material when dielectric losses are taken into consideration. Nevertheless, pure ionic networks and the interpenetrating networks prepared with LR3043/30 still have significant improvements at low frequencies. This signifies that these materials would still be of great use for DEAs and DEGs at low frequencies, due to their very high dielectric permittivities. It is still important to consider that when dielectric losses increase, the temperature of the DE under an applied voltage will also increase. Increased temperature will again increase the loss, and so a destructive loop may occur especially for stacked, thicker films.
For the elastomers to compete with the benchmark with respect to achievable strains, namely the acrylic-based double adhesive VHB 4910 by 3M,1 there is still some way to go but the elastomers within this study do not require prestrain and will thus provide a more reliable actuation over time. Further studies will elucidate the reliability and ageing effects in this type of elastomers.
However, by combining the ionic IPN elastomers with other recent synthesis strategies such as the chloropropyl-functional silicone system introduced by Madsen et al.24 either the ionic network could be side-chain substituted with chloropropyl groups or the commercial elastomer could be replaced by a chloropropyl-functionalised elastomer. In this way, lower losses and higher dielectric permittivities would probably be achievable.
Experimental
Materials and methods
The following were obtained from Gelest Inc: 6–7% aminopropylmethylsiloxane dimethylsiloxane copolymer AMS-162 (![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) w ≈4500 g mol−1), carboxydecyl terminated poly(dimethyl siloxane) DMS-B12 (
w ≈4500 g mol−1), carboxydecyl terminated poly(dimethyl siloxane) DMS-B12 (![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) w = 1000 g mol−1), DMS-B25 (
w = 1000 g mol−1), DMS-B25 (![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) w = 10
w = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1), vinyl-terminated PDMS (DMS-V35) (
000 g mol−1), vinyl-terminated PDMS (DMS-V35) (![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) w = 49
w = 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 g mol−1) and tetrakis(dimethylsiloxy)silane (tetra-functional cross-linker) (
500 g mol−1) and tetrakis(dimethylsiloxy)silane (tetra-functional cross-linker) (![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) w = 329 g mol−1). The commercial silicone elastomers ELASTOSIL® RT625, POWERSIL® XLR630 and ELASTOSIL® LR3043/30, which are two-component silicone rubbers, were acquired from Wacker Chemie AG. RT625 is a room-temperature vulcanisation rubber (RTV), for which the mixing ratio of parts A and B is 9
w = 329 g mol−1). The commercial silicone elastomers ELASTOSIL® RT625, POWERSIL® XLR630 and ELASTOSIL® LR3043/30, which are two-component silicone rubbers, were acquired from Wacker Chemie AG. RT625 is a room-temperature vulcanisation rubber (RTV), for which the mixing ratio of parts A and B is 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, while XLR630 and LR3043/30 are liquid silicone rubbers (LSRs), for which the mixing ratios of parts A and B are 1
1, while XLR630 and LR3043/30 are liquid silicone rubbers (LSRs), for which the mixing ratios of parts A and B are 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Platinum cyclovinylmethyl–siloxane complex catalyst (511) was supplied by Hanse Chemie AG, and silica particles (hexamethyldisilazane-treated amorphous silicon dioxide) were purchased from Fluorochem with an ultimate particle size of 20 nm and a surface area of 150–200 m2 g−1.
1. Platinum cyclovinylmethyl–siloxane complex catalyst (511) was supplied by Hanse Chemie AG, and silica particles (hexamethyldisilazane-treated amorphous silicon dioxide) were purchased from Fluorochem with an ultimate particle size of 20 nm and a surface area of 150–200 m2 g−1.
Dielectric relaxation spectroscopy (DRS) was performed on a Novocontrol Alpha-A high-performance frequency analyser (Novocontrol Technologies GmbH & Co. KG) operating in the frequency range 10−1 to 106 Hz at 23 °C. The sample diameters were 25 mm, while thicknesses were approximately 0.5–1.0 mm. Typical deviations in measurements were of the order of 5% estimated from 3 measurements on identical samples. Electrical breakdown tests were performed on an in-house-built device based on international standards (IEC 60243-1 (1998) and IEC 60243-2 (2001)). Film thicknesses were measured through the microscopy of cross-sectional cuts, and the distance between the spherical electrodes was set accordingly with a micrometre stage and gauge. An indentation of less than 5% of sample thickness was added, to ensure that the spheres were in contact with the sample. The polymer film was slid between the two spherical electrodes (radius of 20 mm), and the breakdown was measured at the point of contact, with a stepwise increasing voltage applied (50–100 V per step) at a rate of 0.5–1 steps per s. More details on the experimental setup can be found in Zakaria et al.41 Each sample was subjected to 12 breakdown measurements, and an average of these values was given as the breakdown strength of the sample. The sample thicknesses were approximately 40–100 μm. Typical standard deviations on breakdown strength measurements are of the order of ±2 V μm−1.
The initial silica concentration in the commercial silicone elastomers was evaluated through thermal gravimetric analysis (TGA) on a Q500 from TA Instruments, and measurements were carried out under a nitrogen atmosphere at a heating rate of 10 °C min−1, from room temperature to 900 °C. In silicone elastomers, which contain fillers, a large portion of the residue at 900 °C corresponds to the initial silica concentration, but not in a trivial way. The silica in the commercial formulations, however, was estimated based on the residual amount as found by TGA.
Linear viscoelastic (LVE) data for the films were measured using an ARES-G2 rheometer (TA Instruments) set to a controlled strain mode, with 1% strain and with frequency sweeps from 100 Hz to 0.01 Hz at ambient temperature using a parallel-plate geometry 25 mm in diameter. The LVE measurement was repeated once on the same sample.
The stress–strain curves of films were tested at RT by ARES-G2 rheometer using SER2 geometry. The sample of 20 mm length and 6 mm width was placed between two drums and initially separated by a distance of 12.7 mm. The test specimen was elongated uniaxially at steady Hencky strain rate of 0.01 (s−1) until sample failure at the middle part. Each composition was subjected to four tensile measurements which were then averaged. Typical standard deviations on rheological measurements are of the order of ±5%.
General procedure for elastomer synthesis
All ionic networks were prepared by mixing stoichiometric amounts of amino-functional PDMS (AMS-162) and carboxylic acid-functional PDMS (DMS-B12 or DMS-B25), using a Speedmixer (DAC 150FVZ, Hauschild Co.) for 2 minutes at 2000 rpm. Then the commercial two-component silicone mixtures were mixed into the above ionic networks, using a Speedmixer for 2 minutes at 2000 rpm. Finally, the silica fillers were mixed in, using the Speedmixer for 2 minutes at 2000 rpm for the filled samples.The stoichiometric imbalance (i.e. r) of pure PDMS reference, which is the ratio between the vinyl groups of the PDMS V35 and hydride groups of 4-functional cross-linker, was 1, and for this sample the concentration of platinum catalyst was 1.6 ppm. The mixture was combined using a Speedmixer for 2 minutes at 2000 rpm.
Uniform mixtures were cast with a film applicator (3540 bird, Elcometer) on a glass substrate and fully cured after 24 h at 100 °C. Table 1 provides an overview of all the prepared samples.
Conclusions
Ionic and silicone interpenetrating networks hold great promise for future use as dielectric elastomers, due to their very high dielectric permittivities and relatively high breakdown strengths. Based on figure of merit calculations, improved overall actuation properties could be obtained for IPNs prepared with LR3043/30 silicone elastomers as dielectric elastomer actuators, even when significant dielectric losses are taken into account. This is because the ionic part of the interpenetrating networks provides very high dielectric permittivity, while the silicone elastomer LR3043/30 provides great mechanical stability (low viscous losses) and furthermore high dielectric breakdown strength. This provides the interpenetrating networks with excellent overall dielectric elastomer actuator properties compared, for example, to similar silicone elastomers with conductive or metal oxide fillers, where increased dielectric permittivity is often matched with equally increased Young's moduli and/or decreased dielectric breakdown strengths.Acknowledgements
The authors would like to acknowledge financial support from InnovationsFonden, Denmark.Notes and references
- R. Pelrine, R. Kornbluh, Q. Pei and J. Joseph, Science, 2000, 287, 836–839 CrossRef CAS
.
- J. D. W. Madden, N. A. Vandesteeg, P. A. Anquetil, P. G. A. Madden, A. Takshi, R. Z. Pytel, S. R. Lafontaine, P. A. Wieringa and I. W. Hunter, IEEE J. Oceanic Eng., 2004, 29, 706–728 CrossRef
.
- Z. Suo, Acta Mech. Solida Sin., 2010, 23, 549–578 CrossRef
.
- J. Zhou, L. Jiang and R. Khayat, Soft Matter, 2015, 11, 2983–2992 RSC
.
- P. Brochu and Q. Pei, Macromol. Rapid Commun., 2010, 31, 10–36 CrossRef CAS PubMed
.
- S. Jin, A. Koh, C. Keplinger, T. Li, S. Bauer and Z. Suo, IEEE ASME Trans Mechatron., 2011, 16, 33–41 CrossRef
.
- R. Heydt, R. Kornbluh, J. Eckerle and R. Pelrine, Proc. SPIE, 2006, 6168, 61681M-1-8 Search PubMed
.
- S. Vudayagiri, M. D. Junker and A. L. Skov, Polym. J., 2013, 45, 871–878 CrossRef CAS PubMed
.
- B. Balakrisnan, S. Patil and E. Smela, J. Micromech. Microeng., 2009, 19, 047002 CrossRef
.
- N. Cohen and G. deBotton, Eur. J. Mech. Solid., 2014, 48, 48–59 CrossRef PubMed
.
- M. Molberg, D. Crespy, P. Rupper, F. Nüesch, J.-A. E. Månson, C. Löwe and D. M. Opris, Adv. Funct. Mater., 2010, 20, 3280–3291 CrossRef CAS PubMed
.
- B. Kussmaul, S. Risse, G. Kofod, R. Waché, M. Wegener, D. N. McCarthy, H. Krüger and R. Gerhard, Adv. Funct. Mater., 2011, 21, 4589–4594 CrossRef CAS PubMed
.
- F. B. Madsen, I. Dimitrov, A. E. Daugaard, S. Hvilsted and A. L. Skov, Polym. Chem., 2013, 4, 1700–1707 RSC
.
- F. B. Madsen, A. E. Daugaard, S. Hvilsted, M. Y. Benslimane and A. L. Skov, Smart Mater. Struct., 2013, 22, 104002 CrossRef
.
- F. B. Madsen, L. Yu, A. E. Daugaard, S. Hvilsted and A. L. Skov, Polymer, 2014, 55, 6212–6219 CrossRef CAS PubMed
.
- S. Vudayagiri, S. Zakaria, L. Yu, S. S. Hassouneh, M. Benslimane and A. L. Skov, Smart Mater. Struct., 2014, 23, 105017 CrossRef
.
- Y. Liu, L. Liu, Z. Zhang and J. Leng, Smart Mater. Struct., 2009, 18, 095024 CrossRef
.
- H. Liu, L. Zhang, D. Yang, Y. Yu, L. Yao and M. Tian, Soft Mater., 2013, 11, 363–370 CrossRef CAS PubMed
.
- H. Stoyanov, P. Brochu, X. Niu, E. D. Gaspera and Q. Pei, Appl. Phys. Lett., 2012, 100, 262902 CrossRef PubMed
.
- G. Ouyang, K. Wang and X. Y. Chen, J. Micromech. Microeng., 2012, 22, 074002 CrossRef
.
- G. Gallone, F. Galantini and F. Carpi, Polym. Int., 2010, 59, 400–406 CrossRef CAS PubMed
.
- A. Lewinstein, G. Uner, G. deBotton and S. Rudykh, Appl. Phys. Lett., 2013, 102, 151905 CrossRef PubMed
.
- P. Brochu and Q. Pei, Macromol. Rapid Commun., 2010, 31, 10–36 CrossRef CAS PubMed
.
- F. B. Madsen, L. Yu, A. E. Daugaard, S. Hvilsted and A. L. Skov, RSC Adv., 2015, 5, 10254–10259 RSC
.
- L. González, A. L. Skov and S. Hvilsted, J. Polym. Sci., Part A: Polym. Chem., 2013, 51, 1359–1371 CrossRef PubMed
.
- L. González, L. Yu, S. Hvilsted and A. L. Skov, RSC Adv., 2014, 4, 36117–36124 RSC
.
- M. A. Aboudzadeh, M. E. Muñoz, A. Santamaría, R. Marcilla and D. Mecerreyes, Macromol. Rapid Commun., 2012, 33, 314–318 CrossRef CAS PubMed
.
- L. H. Sperling, Polym. Adv. Technol., 1996, 7, 197–208 CrossRef CAS
.
- S. R. Batten and R. Robson, Angew. Chem., Int. Ed., 1998, 37, 1460–1494 CrossRef
.
- S. M. Ha, W. Yuan, Q. Pei, R. Pelrine and S. Stanford, Adv. Mater., 2006, 18, 887–891 CrossRef CAS PubMed
.
- P. Brochu, H. Stoyanov, X. Niu and Q. Pei, Smart Mater. Struct., 2013, 22, 055022 CrossRef
.
- M. Kollosche and G. Kofod, Appl. Phys. Lett., 2010, 96, 071904 CrossRef PubMed
.
- P. Sommer-Larsen and A. L. Larsen, Proc. SPIE, 2004, 5385, 68–77 CAS
.
- T. G. McKay, E. Calius and I. A. Anderson, Proc. SPIE, 2009, 7287, 72870P-1–72870P-10 Search PubMed
.
- A. Dorfman and R. W. Ogden, Acta Mech., 2005, 174, 167–183 CrossRef PubMed
.
- A. Dorfman and R. W. Ogden, Int. J. Eng. Sci., 2010, 48, 1–14 CrossRef PubMed
.
- S. Zakaria, P. H. F. Morshuis, M. Y. Benslimane, K. V. Gernaey and A. L. Skov, Proc. SPIE, 2014, 9056, 90562V Search PubMed
.
- J. Huang, S. Shian, R. M. Diebold, Z. Suo and D. R. Clarke, Appl. Phys. Lett., 2012, 101, 122905 CrossRef PubMed
.
- A. L. Larsen, K. Hansen, P. S. Larsen, O. Hassager, A. Bach, S. Ndoni and M. Jørgensen, Macromolecules, 2003, 36, 10063–10070 CrossRef CAS
.
- M. A. Villar and E. M. Valles, Macromolecules, 1996, 29, 4081–4089 CrossRef CAS
.
- S. B. Zakaria, P. H. F. Morshuis, B. M. Yahia, L. Yu and A. L. Skov, Smart Mater. Struct., 2015, 24, 055009 CrossRef
.
| This journal is © The Royal Society of Chemistry 2015 |