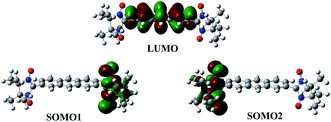
Role of the coupler to design organic magnetic molecules: LUMO plays an important role in magnetic exchange

Abstract

We have designed seven organic diradicals with polyacene couplers to show the effect of the configuration, aromaticity [estimated with the help of Nucleus Independent Chemical Shift (NICS(0) and NICS(I)), and Harmonic Oscillator Model of Aromaticity (HOMA)] and HOMO–LUMO gap of the couplers on the exchange coupling constant of the diradicals. It has been observed that the linear polyacenes are less aromatic compared to the corresponding angular ones. We have correlated aromaticity indexes NICS and HOMA to explain the change of aromaticity for structures having the same number of carbon and hydrogen atoms and rings. The diradicals with linear couplers manifest stronger exchange coupling constants compared to those with angular couplers. It has been found that the NICS value cannot adequately address the aromaticity of the polyacenes, whereas the HOMA value can reliably account for the observations. Here, we have found the HOMO–LUMO gap is the determining factor for the extent of the magnetic exchange coupling constant in the diradicals. It has been found that not only the energy value of the LUMO, but also its occupation number and spatial position, play an important role in magnetic exchange in diradicals. Thus, the role of the LUMO in magnetic exchange has been firmly established through this work. The magneto-structural correlation has also been studied to establish the mechanism of magnetic interaction.

---

Introduction

Organic radicals¹ have been widely studied due to their versatile applicability in the field of magnetism,² and for their superconductivity,³ spintronic properties,⁴ photomagnetic behaviour⁵ and so on. In organic diradicals, the nature and extent of the magnetic interaction largely depends on the coupler between the two radical centres.⁶ The effect of linear polyacene as coupler between two verdazyl radicals has been studied by Bhattacharya et al.^6b They have found that the longer linear polyacene couplers produce strong exchange coupling between the radicals due to the radicaloid nature of the larger polyacenes. It has also been noticed that the aromaticity of the coupler plays a very important role in determining the magnetic exchange coupling constant. It has been found that in the case of diradicals the spin density values on the connected atoms are important to determine the magnetic interaction.⁷ Barone et al., found that the bridges with delocalized π electrons contribute significantly to the coupling between two radical centers.⁸ Ko et al. studied the intramolecular magnetic coupling constant of different diradicals using a scaling factor approach.⁹ They found that the exchange coupling constant depends on the length of the coupler.

It is important to study the electronic structure and aromaticity of the linear and angular polyacenes as coupler before designing of magnetic molecules. Linear polyacenes become more reactive with an increase in the number of rings, so that the higher members cannot be characterized experimentally.^10,11 Major chemical reactions occur preferentially at the inner rings. The successive reduction in the gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) is another example of monotonic behaviour in the polyacene series.^12,13 When a linear polyacene is changed to a angular polyacene, the aromaticity of each of the rings is changed.

The molecular orbitals are crucial to understand the electronic structure of a molecule. In case of magnetic molecules, the singly occupied molecular orbitals (SOMOs) play an important role in magnetic interactions.^6c With the help of extended Hückel theory, Hoffmann¹⁴ suggested that if the energy difference is less than 1.5 eV between two consecutive SOMOs, then parallel orientation of spins occurs. Within the MO framework, one also needs to figure out the overlap between the SOMOs, for which the argumentation leading to Hund's rule is severely weakened.^15,16 At the B3LYP level with 6-31G(d,p) basis set, 4n π antiaromatic linear and angular polyheteroacenes have been investigated by Constantinides et al.¹⁷ where they found that for a SOMO splitting ΔE_SS >1.3 eV, a singlet ground state results with antiparallel orientation of spins. Zhang et al.¹⁸ have shown that critical value of ΔE_SS is different in different cases. Therefore, only SOMOs are not sufficient to describe the magnetic interaction in molecules. Therefore, it is necessary to study the role of other orbitals to find out the key factor to determine and understand the magnetic exchange.

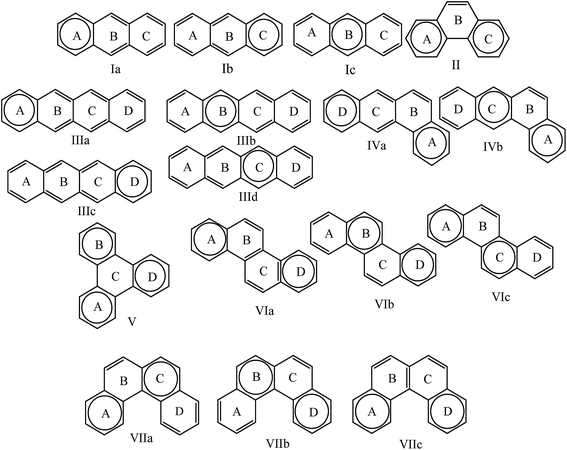
In this work we have designed seven diradicals with polyacene couplers to illustrate the effect of coupler to design magnetic molecules and the role of molecular orbitals (especially LUMO) in the exchange mechanism. We choose the polyacenes as couplers because these are the well-known aromatic systems, which have different isomers with different aromaticity. We have studied the nature of the change in aromaticity with the change in the structure (from linear to angular) of the polyacene couplers with same number of rings and atoms, namely, (A) (I) anthracene and (II) phenanthrene; (B) (III) tetracene, (IV) benzanthracene, (V) triphenylene, (VI) chrysene and (VII) benzophenanthrene (Fig. 1). The local aromaticity of individual rings in terms of HOMA, NICS(0) and NICS(I) have been studied. We have also compared the HOMO–LUMO gap of the linear and angular polyacenes to study their reactivity. Then we use these polyacene to design magnetic diradical molecules to correlate the magnetic property with the coupler's aromaticity and HOMO–LUMO gap. The itinerant exchange between two radical centres occurs through conjugated π electrons in the molecules. The exchange interactions are conventionally explained by the energy of SOMOs and their spatial distribution.⁶ Here, for the first time we discuss the role of LUMO in the intramolecular magnetic exchange. We have studied the exchange mechanism of the designed diradicals in the light of HOMO–LUMO gap and the spatial distribution of molecular orbitals as well. The closeness of LUMO and HOMO and the spatial position of LUMO play very important role in the exchange mechanism and hence in the value of the coupling constants.

Fig. 1 The polyacene compounds under study.

Theoretical details and computational methodology

The lack of unique definition and multidimensional nature of aromaticity leads to assign different indices to quantify aromaticity. These include different structural indices such as the harmonic oscillator model of aromaticity (HOMA) which can reliably explain the differences in aromaticity in complicated systems.¹⁹ The geometry based indices HOMA quantifies the decrease in aromaticity with an increase in the bond length alternation and bond elongation.²⁰ Beside HOMA, nucleus independent chemical shift (NICS) is another widely used index of aromaticity because of its simplicity and efficiency.^21–23 NICS can be used to identify aromaticity, non-aromaticity, and anti-aromaticity of a single ring system and individual rings in polycyclic systems (local aromaticity).

The Harmonic Oscillator Model of Aromaticity (HOMA) index^24–30 can be used to study the density of local aromaticity³⁰ in polyacene molecules. The HOMA index is one of the most reliable structural indices of local aromaticity. The HOMA index for each ring in a polycyclic aromatic hydrocarbon molecule is defined as:^24–29

where α and R are the constants characteristic of C–C bonds in a hydrocarbon π system, n is the number of π bonds, R_i is the observed or calculated length of the ith C–C bond in a given ring and the summation is made over all the π bonds. A large positive HOMA value indicates a larger degree of local aromaticity in the ring concerned. We adopted the values α = 257.7 and R₀ = 1.388 Å to calculate HOMA indices.³¹

The origin of magnetism in diradical is due to the exchange coupling between radical centers. We have estimated the magnetic exchange coupling constant of the designed diradicals. The magnetic exchange coupling constant can be calculated by the spin projected formulae given by Ginsberg,³² Noodleman,³³ and Davidson³⁴ (GND) as J^GND = (E_BS − E_T)/S_max² which is applicable only when the overlap between magnetic orbitals is low. On the other hand Yamaguchi formulae³⁵ within DFT framework; which is given by J^Y = (E_BS − E_T)/S_T² − S_BS², is applicable for both strong and weak overlap limit. For the calculation of magnetic exchange coupling constant (J), following our previous works³⁶ we employ the Yamaguchi equation and also the Noodleman's equation. In the above, J is the magnetic exchange coupling constant, the positive value of J indicates ferromagnetic coupling whereas negative value indicates antiferromagnetic coupling. E_BS is the energy of the BS state and E_T is that of the triplet state, whereas 〈S_T²〉 and 〈S_BS²〉 represents the average spin square values of triplet and BS states respectively.

All the molecular geometries have been optimized within unrestricted DFT framework using B3LYP/6-31+G(d,p), B3LYP/6-311++G(d,p) and BP86/6-311++G(d,p) combinations. Aromaticity index NICS of the bare couplers have been estimated by using UB3LYP/GIAO methodology³⁷ with 6-31+G(d) basis set. We have calculated the NICS values at the center of the rings [NICS(0)] and as the σ framework of C–C and C–H affects the π electrons and hence NICS is also calculated at 1 Å above the ring surface [NICS(I)] where the π electron density is known to be maximum. All the computations have been done using Gaussian09W quantum chemical package.³⁸

Results and discussion

Aromaticity of the polyacene coupler

The magnetic exchange coupling constant of the diradical depends on the aromaticity of the polyacene coupler.^6b In this study we have calculated the aromaticity index HOMA, NICS(0) and NICS(I) of different linear polyacenes and their corresponding angular isomers like anthracene (set A, I–II) and tetracene (set B, III–VII). The values of HOMA, NICS(0) and NICS(I) for individual rings and their averages and energy of the polyacenes are given in Table 1.

Table 1 The values of HOMA, NICS(0), NICS(I), total HOMA, average NICS, HOMO–LUMO gap (ΔE_HL) and energy of the coupler (B3LYP/6-31+G(d,p))

Coupler		Ring	A	B	C	D	Average(NICS)/total(HOMA)	ΔEHL (eV)	Energy (a.u.)
Set A	I	HOMA	0.60	0.68	0.60	—	0.69	3.55	−539.56432
		NICS(0)	−7.52	−11.19	−7.52	—	−8.74
		NICS(I)	−9.53	−12.55	−9.53	—	−10.54
	II	HOMA	0.84	0.42	0.84	—	0.72	4.67	−539.57253
		NICS(0)	−8.81	−5.50	−8.81	—	−7.71
		NICS(I)	−10.68	−7.97	−10.68	—	−9.78
Set B	III	HOMA	0.51	0.59	0.59	0.51	0.64	2.75	−693.20676
		NICS(0)	−6.73	−11.02	−11.02	−6.73	−8.88
		NICS(I)	−8.85	−12.39	−12.39	−8.85	−10.62
	IV	HOMA	0.72	0.25	0.87	0.68	0.66	3.72	−693.21982
		NICS(0)	−8.65	−3.59	−10.35	−8.32	−7.73
		NICS(I)	−10.51	−6.37	−12.0	−10.23	−9.78
	V	HOMA	0.88	0.88	0.03	0.88	0.71	4.84	−693.22077
		NICS(0)	−8.08	−7.81	−1.70	−8.03	−6.41
		NICS(I)	−10.09	−9.98	−4.89	−10.02	−8.75
	VI	HOMA	0.82	0.53	0.53	0.82	0.68	4.21	−693.22310
		NICS(0)	−8.64	−6.10	−6.09	−8.64	−7.37
		NICS(I)	−10.57	−8.44	−8.43	−10.57	−9.50
	VII	HOMA	0.76	0.30	0.30	0.76	0.55	4.21	−693.20686
		NICS(0)	−9.35	−6.73	−6.73	−9.35	−8.04
		NICS(I)	−10.92	−8.64	−8.64	−10.92	−9.78

---

Clar's rule states that the Kekulé resonance structure with the largest number of disjoint aromatic π sextets, i.e., benzene-like moieties, is the most important for the characterization of polycyclic aromatic hydrocarbons (PAHs).^10,11 Aromatic π sextets are defined as six π electrons localized in a single benzene-like ring separated from adjacent rings by formal C–C single bonds. Following this analogy, we explain the aromatic behaviour of the coupler considering the resonance structure having highest number of possible sextets at a time (Fig. 2). It is expected that the rings with a π sextet have higher local aromaticity. From Fig. 2 it may appear that for coupler I the π electrons can be delocalized over the three rings equally; i.e., all the rings should have equal aromaticity according to sextet theory. But we get the middle ring to be more aromatic than the side rings, which can be seen from the HOMA and NICS values (Table 1). This could be explained easily in the light of sextet migration theory given by of Klein and coworkers.^39,40 According to this theory when the sextet is in the middle of polyacene then it can migrate to both the sides of polyacene providing the middle ring more aromaticity. On the other hand phenanthrene which is an isomer of anthracene, contains two aromatic sextets in the terminals and these are localized and consequently the side rings have higher values of NICS and HOMA than the central one. It is never possible to have a sextet (to generate a ring current) in ring B in case of phenanthrene and consequently the NICS values are too low for ring B. Therefore, from the local aromaticity point of view HOMA and NICS correlate well with the sextet theory.

Fig. 2 Representation of seven poly aromatic hydrocarbons and their Clar structures with the corresponding ring labels. Clar's aromatic π sextets are indicated with circles.

Next we consider the tetracenes in a similar way. In case of polyacene III we see that the HOMA and NICS values of middle rings (B and C) are higher than that of sides. This can also be explained by the sextet migration theory as before. In case of polyacene IV the ring B has abruptly low HOMA and NICS values. If we look at the Clar structures of IV in Fig. 2, we can see that in ring B it is impossible to generate a sextet or ring current and hence, the low HOMA and NICS values in ring B is observed. For the same reason, ring C of polyacene V has low HOMA and NICS values. For polyacene VI and VII the middle rings are less aromatic than sides. From Fig. 2 it is obvious as sextet appears lesser number of times in ring B and C.

As the HOMA can be calculated for total molecule, we have compared the total aromaticity of the polyacenes with respect to total HOMA and average NICS. From Table 1 we can see that the total HOMA and average NICS predict opposite results. Therefore, we should justify which one is more appropriate in this case; the energy values of the polyacene can give us an insight. From Table 1 it is clear that the energy value of linear polyacene is higher than the angular one which suggests that the angular polyacene is more aromatic which is well correlated with HOMA values. The inadequacy of NICS to determine aromatic nature in some cases is also noted by other groups.⁴¹ Therefore, we have compared the total aromaticity of the polyacene by HOMA values. The reliability of HOMA index in this case is also supported another way that the HOMA is a geometry based aromaticity index and here also the polyacenes are geometrically different from one another. The total HOMA value of phenanthrene is higher than that of anthracene. This can be explained as anthracene contains one Clar sextet but phenanthrene contains two sextets at a time (Fig. 2). The total HOMA values of the angular polyacenes are higher than that of linear one except VII. The low HOMA value of polyacene VII is due to its cis and nonplanar structures (angle between two terminal rings is 18.4°). The high energy value of polyacene VII can also explain its low HOMA value as well. We have also calculated the HOMO–LUMO gap of the polyacene and find that the gap is greater for the angular polyacene than the corresponding linear polyacene; i.e., the linear polyacenes are more reactive. Therefore, we have seen that the linear polyacenes are less stable, less aromatic and highly reactive than the angular one. In the next sections we discuss how the aromaticity and stability of the polyacene couplers will affect the magnetic interaction in polyacene coupled diradicals.

Magnetic exchange coupling constant of the polyacene coupled diradicals

We have designed seven nitronyl nitroxide based diradicals (Fig. 3) coupled with above mentioned polyacenes (Fig. 1). The magnetic exchange coupling constant J (Table 3) has been determined by using Yamaguchi formulae³⁵ for all the diradicals. We have calculated the magnetic exchange coupling constant values with different density functionals and basis sets. Although, the values of coupling constant are different for different methods, but they follow the similar trend. From Table 2 we can see that the strong magnetic exchange coupling constant comes out for the linear coupler, whereas for corresponding angular coupler it is very weak, even if they have same number of carbon and hydrogen atoms and same number of rings. Only difference is in their arrangement. As the aromaticity of the linear and angular polyacenes are different consequently the coupling constant of the diradicals. Therefore, it is obvious that the aromaticity of the coupler directly affects the extent of magnetic coupling constant. We rely on HOMA values to analyze the effect of the aromaticity of the couplers on the magnetic coupling of the diradicals. We have found that the less aromatic linear coupler gives the high magnetic exchange coupling constant. The HOMO–LUMO gap of the coupler (Table 1) is less for linear polyacene than its angular analogue and the coupling constant is higher when the coupler is linear. Therefore, couplers with low HOMO–LUMO gap facilitate the strong magnetic coupling constant. The coupler VI and VII have the same HOMO–LUMO gap and comparable coupling constant. Thus, we can say that less aromatic coupler with low HOMO–LUMO gap will be the promising candidate to design diradical based organic magnets.

Fig. 3 The diradicals under study.

Table 2 Intramolecular exchange-coupling constant (J cm⁻¹) using different functionals and basis sets, for the diradicals (1–7)

Diradicals		B3LYP/6-31+G(d,p)		B3LYP/6-311++G(d,p)		BP86/6-311++G(d,p)		B3LYP/6-311+G(d,p) (ref. 43)
		J^Y (cm^−1)	J^GND (cm^−1)	J^Y (cm^−1)	J^GND (cm^−1)	J^Y (cm^−1)	J^GND (cm^−1)	J^Y (cm^−1)	J^GND (cm^−1)
A	1	47.33	48.28	44.80	46.09	7.68	7.68	13.44	13.52
	2	18.03	24.14	23.26	23.26	3.73	3.73	8.76	8.76
B	3	63.31	65.84	57.43	59.26	8.93	8.78	13.81	13.92
	4	17.38	17.56	17.43	17.56	2.79	2.79	—	—
	5	17.56	17.56	18.06	18.06	2.92	2.92	—	—
	6	13.16	13.16	11.67	11.67	1.80	1.80	—	—
	7	13.04	13.04	13.39	13.39	2.13	2.13	4.76	4.77

---

The SOMOs are mainly responsible for magnetic interaction in diradicals through itinerant exchange.^14–18 It has been said that the low SOMO–SOMO gap or degenerate SOMOs produce strong magnetic exchange coupling constant.¹⁴ Also the disjoint SOMOs favor the antiferromagnetic interaction in diradicals.⁶ The SOMO–SOMO energy gap and the HOMO–LUMO energy gap for the designed diradicals are listed in Table 3. From Table 3 we observe that for diradical 3 SOMO–SOMO gap is highest and J value is also maximum among the series. The diradical 7 has the degenerate SOMOs with weak exchange coupling constant. So, the SOMO–SOMO gap is not only the determining factor there must be some other reason. If we look at the HOMO–LUMO gap of the diradicals (Table 3) it is surprising that the HOMO–LUMO gap is lowest for diradical 1 and 3 for three and four member rings in the coupler. Now, we can say that there is an important role of LUMO to determine the extent of magnetic interaction of diradicals. This observation is also consistent with our previous result in ref. 42, where with decreasing HOMO–LUMO gap coupling constant increases. To ensure this analogy we are going to the next subsection to discuss this issue in details. Our calculated magnetic exchange coupling constant is also qualitatively consistent with the previous results calculated by Ali et al.⁴³ Our calculated magnetic exchange coupling constant is larger than that of ref. 43, this is because of basis set effect. In ref. 43 they have optimized the geometry with 6-311G(d,p) basis set and single point calculations have been done using 6-311+G(d,p) basis set, whereas we have optimized the geometry with 6-311++G(d,p) basis set. The BP86 functional produces very small value of magnetic exchange coupling constant compare to B3LYP. This anomalous behaviour of the BP86 functional arises because BP86 tends to over stabilize low-spin with respect to high-spin states.⁴⁴ Therefore, we recommend that the B3LYP is more suitable compare to BP86 for the calculation of magnetic exchange coupling constant.

Table 3 The energy difference between SOMOs (ΔE_SS) and HOMO–LUMO (ΔE_HL) using different functionals and basis sets for the diradicals

Diradical		B3LYP/6-31+G(d,p)		B3LYP/6-311++G(d,p)		BP86/6-311++G(d,p)
		ΔESS (eV)	ΔEHL (eV)	ΔESS (eV)	ΔEHL (eV)	ΔESS (eV)	ΔEHL (eV)
A	1	0.0	3.07	0.0	3.03	0.0	1.26
	2	0.02	3.43	0.02	3.41	0.02	1.64
B	3	0.18	2.61	0.18	2.59	0.0	1.0
	4	0.02	3.15	0.02	3.13	0.02	1.36
	5	0.02	3.41	0.02	3.39	0.01	1.64
	6	0.03	3.39	0.04	3.37	0.02	1.59
	7	0.0	3.30	0.0	3.28	0.0	1.51

---

Mechanism of magnetic interaction

Spatial distribution of molecular orbital is an important issue in magnetism, electronic transport etc.⁴⁵ The spatial distribution of the molecular orbitals of all the diradicals are presented in Fig. 4. According to Borden and co-workers^15,16 when the non-bonding molecular orbitals of a diradical have no atoms in common i.e., disjoint in nature, the diradical favour antiferromagnet ground state. The non disjoint SOMOs favour ferromagnetic ground state. From Fig. 4 we can see that SOMOs of diradicals 2, 4, 5 and 6 are disjoint and SOMOs of diradicals 1, 3 and 7 are nondisjoint although all the diradicals are ferromagnetic. Interestingly, we can see from the Fig. 4 that only the symmetric diradicals (1, 3 and 7) have nondisjoint SOMOs. We have computed the MOs with different functional and basis sets, in all the cases we find similar results. Therefore, as a consequence, the application of Borden's rule^15,16 is clearly violated for the disjoint diradicals 2, 4, 5 and 6 while is respect for the symmetric non-disjoint diradicals 1, 3 and 7. This is may be the failure of present day approximate density functionals or may be the Borden's analogy which is derived for alternate hydrocarbons does not fit for these diradicals because these diradicals are not strictly alternate hydrocarbons and follow different mechanism of interaction.

Fig. 4 Spatial distribution of molecular orbitals (the green and brown colour represents the different phase of the orbital coefficients), the iso value is 0.02 (B3LYP/6-311++G(d,p)).

Table 3 tells us that all the diradicals have low SOMO–SOMO energy gap except diradical 3. The diradical 7 has degenerate SOMOs. However, the magnetic exchange coupling constant of all the diradicals are very weak except for diradical 3. If we look into the spatial distribution of LUMOs we can see that LUMO resides in the middle of SOMOs except diradical 3. For diradical 3 SOMO2 and LUMO share the same spatial position in the molecule. In case of diradical 3 although the SOMO–SOMO gap is high but HOMO–LUMO gap is low and SOMO2 (HOMO) and LUMO share same spatial position. Therefore, it is easier to exchange the unpaired electrons of SOMOs through LUMO. That is the reason for strong exchange coupling constant of diradical 3. Thus, we can say that the itinerant exchange may occur through LUMO. To establish this correlation we have computed the electron occupation in LUMO (Table 4).

Table 4 Natural orbital occupation of the diradical in their triplet state

Diradical		B3LYP/6-31+G(d,p)	B3LYP/6-311++G(d,p)	BP86/6-311++G(d,p)
		LUMO	LUMO	LUMO
A	1	0.034	0.034	0.008
	2	0.029	0.029	0.007
B	3	0.042	0.041	0.009
	4	0.030	0.030	0.007
	5	0.028	0.029	0.007
	6	0.028	0.028	0.007
	7	0.029	0.029	0.007

---

From Table 4 we can see that the HOMO−2 has occupation less than 2 and LUMO, LUMO+1 have some occupation. Therefore, it can be believed that LUMO takes part in the exchange mechanism. Here, we can see that in case of diradicals 1 and 3, LUMO has the highest occupation in their respective series (A and B) and hence strong exchange coupling constant. Therefore, one can say that the itinerant exchange between two radical centers in diradicals occurs through LUMO (schematic representation Fig. 5). The LUMO mediated super exchange has also been reported by Browne et al. in case of CT complexes.⁴⁰

Fig. 5 Schematic representation of magnetic interaction via LUMO.

Magneto-structural correlation

We have studied the magneto-structural correlation of all the diradicals using B3LYP functional in combination with 6-311++G(d,p) basis set. We have done the single point calculations on the optimized geometry of the same level of theory. The calculated magnetic exchange coupling constant values with respect to the dihedral angle (ϕ) (Fig. 6) between radical and polyacene are presented in Fig. 7.

Fig. 6 Representation of the dihedral angle (ϕ) between the radical and the polyacene.

Fig. 7 Magneto-structural correlations developed by varying dihedral angle (ϕ) between the radical and the polyacene (B3LYP/6-311++G(d,p)).

It can be seen that the magnetic exchange coupling constant decreases with increasing dihedral angle. The coupling constant goes to zero after 70° dihedral angle (ϕ). In the optimized geometry the dihedral angle ϕ is in between 0° to 10° for all the diradicals. Therefore, we can say that the radicals and the polyacenes are in same plane. When we increase the dihedral angle, the radical and polyacene are in different planes.

The increasing dihedral angle between the radicals and polyacene increase the angle between the orbitals (HOMO and LUMO) which affects the coupling constant. At 90° dihedral angle the SOMOs and LUMO are in orthogonal position (Fig. 8). This orthogonality between SOMOs and LUMO leads to zero exchange coupling constant. Here the SOMOs are in same plane only the LUMO is out of plane. If there is no role of LUMO, then the coupling constant should not be changed. This observation confirms that the participation of LUMO in magnetic exchange.

Fig. 8 The molecular orbitals of the diradical 3 at 90° dihedral angle (ϕ) (B3LYP/6-311++G(d,p)).

The spin density plot (Fig. 9) suggests that with increasing dihedral angle spin polarization through bridge decreases and reach to zero spin density on the coupler at ϕ = 90°, which leads to zero magnetic exchange coupling constant. This observation is consistent with our previous results in ref. 39.

Fig. 9 The spin density plot of the diradical 3 at different radical–polyacene dihedral angle (ϕ).

Conclusions

In this work we study the effect of aromaticity of linear and their corresponding angular polyacenes on the magnetic exchange of polyacene coupled diradicals. We have seen that the linear polyacenes are less aromatic compared to the angular one. The variation of aromaticity of the polyacenes cannot be addressed by NICS but the HOMA values explain the aromatic nature precisely in these systems. HOMA being a geometry based index, naturally it can describe the aromaticity due to change in geometry in a better way. We have found that the less aromatic linear coupler with low HOMO–LUMO gap is appropriate for getting strong magnetic exchange coupling constant of designed diradicals. As the SOMO–SOMO energy gap cannot appropriately address the magnetic exchange coupling constant, we concentrate on the HOMO–LUMO gap of the diradicals which now can adequately explain the extent of magnetic exchange coupling constant. To illustrate the mechanism of itinerant exchange and to investigate the role of LUMO we plot the spatial distribution of MOs. We find that the position of LUMO in the diradical plays an important role in the extent and mechanism of magnetic interaction. If the SOMOs and LUMO cover the whole molecule and SOMOs and LUMO have the same special position, magnetic exchange is facilitated through LUMO. The occupation number of LUMO also suggests through LUMO magnetic exchange interaction in the diradicals. The proposed mechanism is also supported well by the magneto-structural correlation.

Acknowledgements

We are thankful to CSIR India for financial support. S. S. is further thankful to CSIR, India for senior research fellowship. Authors are also thankful to Anirban Panda for fruitful discussions.

References

1. O. Kahn, Molecular Magnetism, VCH, New York, 1993.
2. P. M. Lahti, Magnetic Properties of Organic Materials, Marcel Dekker, New York, 1999.
3. (a) H. Kobayashi, A. Kobayashi and P. Cassoux, Chem. Soc. Rev., 2000, 29, 325–333; (b) S. Uji, H. Shinagawa, T. Terashima, T. Yakabe, Y. Terai, M. Tokumoto, A. Kobayashi, H. Tanaka and H. Kobayashi, Nature, 2001, 410, 908–910.
4. (a) G. A. Prinz, Science, 1998, 282, 1660–1663; (b) E. G. Emberly and G. Kirczenow, Chem. Phys., 2002, 281, 311–324.
5. (a) K. Matsuda, M. Matsuo and M. Irie, J. Org. Chem., 2001, 66, 8799–8803; (b) N. Tanifuji, M. Irie and K. Matsuda, J. Am. Chem. Soc., 2005, 127, 13344–13353.
6. (a) D. Bhattacharya and A. Misra, J. Phys. Chem. A, 2009, 113, 5470–5475; (b) D. Bhattacharya, S. Shil, A. Misra and D. J. Klein, Theor. Chem. Acc., 2010, 127, 57–67; (c) D. Bhattacharya, S. Shil, A. Panda and A. Misra, J. Phys. Chem. A, 2010, 114, 11833–11841.
7. K. C. Ko, D. Cho and J. Y. Lee, J. Phys. Chem. A, 2012, 116, 6837–6844.
8. V. Barone, I. Cacelli and A. Ferretti, J. Chem. Phys., 2009, 130, 09436.
9. K. C. Ko, D. Cho and J. Y. Lee, J. Phys. Chem. A, 2013, 117, 3561–3568.
10. E. Clar, Polycyclic Hydrocarbons, Academic Press, London, UK, 1964, vol. I and II.
11. E. Clar, The Aromatic Sextet, Wiley, London, UK, 1972.
12. B. A. Hess Jr and L. J. Schaad, J. Am. Chem. Soc., 1971, 93, 2413–2416.
13. J. Aihara, J. Phys. Chem. A, 1999, 103, 7487–7495.
14. R. Hoffmann, G. D. Zeiss and G. W. Van Dine, J. Am. Chem. Soc., 1968, 90, 1485–1499.
15. W. T. Borden and E. R. Davidson, J. Am. Chem. Soc., 1977, 99, 4587–4594.
16. W. T. Borden and E. R. Davidson, Acc. Chem. Res., 1981, 14, 69–76.
17. C. P. Constantinides, P. A. Koutentis and J. Schatz, J. Am. Chem. Soc., 2004, 126, 16232–16241.
18. G. Zhang, S. Li and Y. Jiang, J. Phys. Chem. A, 2003, 107, 5573–5582.
19. T. M. Krygowski, J. E. Zachara and H. Szatylwicz, J. Org. Chem., 2004, 69, 7038–7043.
20. T. M. Krygowski and M. K. Cyrański, Chem. Rev., 2001, 101, 1385–1420.
21. Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v. R. Schleyer, Chem. Rev., 2005, 105, 3842–3888.
22. P. v. R. Schleyer, M. Manoharan, H. Jiao and F. Stahl, Org. Lett., 2001, 3, 3643–3646.
23. P. v. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. v. E. Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318.
24. J. Kruszewski and T. M. Krygowski, Tetrahedron Lett., 1972, 3839–3842.
25. T. M. Krygowski, A. Ciesielski, C. W. Bird and A. Kotschy, J. Chem. Inf. Comput. Sci., 1995, 35, 203–210.
26. T. M. Krygowski, M. Cyrański, A. Ciesielski, B. Świrska and P. Leszczyński, J. Chem. Inf. Comput. Sci., 1996, 36, 1135–1141.
27. M. K. Cyrański, B. T. Stepień and T. M. Krygowski, Tetrahedron, 2000, 56, 9663–9667.
28. T. M. Krygowski and M. K. Cyrański, Chem. Rev., 2001, 101, 1385–1419.
29. T. M. Krygowski and M. K. Cyrański, Phys. Chem. Chem. Phys., 2004, 6, 249–255.
30. A. Mohajeri and A. Ashrafi, Chem. Phys. Lett., 2008, 458, 378–383.
31. G. Portella, J. Poater, J. M. Bofill, P. Alemany and M. Solà, J. Org. Chem., 2005, 70, 2509–2521.
32. A. P. Ginsberg, J. Am. Chem. Soc., 1980, 102, 111–117.
33. (a) L. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743; (b) L. Noodleman and E. J. Baerends, J. Am. Chem. Soc., 1984, 106, 2316–2327; (c) L. Noodleman, C. Y. Peng, D. A. Case and J.-M. Mouesca, Coord. Chem. Rev., 1995, 144, 199–244.
34. L. Noodleman and E. R. Davidson, Chem. Phys., 1986, 109, 131–143.
35. (a) S. Paul and A. Misra, J. Mol. Struct.: THEOCHEM, 2009, 907, 35–40; (b) S. Paul and A. Misra, J. Mol. Struct.: THEOCHEM, 2009, 895, 156–160; (c) S. Paul and A. Misra, J. Phys. Chem. A, 2010, 114, 6641; (d) S. Paul and A. Misra, J. Chem. Theory Comput., 2012, 8, 843–853.
36. (a) K. Yamaguchi, Y. Takahara, T. Fueno and K. Nasu, Jpn. J. Appl. Phys., 1987, 26, L1362–L1364; (b) K. Yamaguchi, F. Jensen, A. Dorigo and K. N. Houk, Chem. Phys. Lett., 1988, 149, 537–542.
37. K. Wolinski, J. F. Hilton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260.
38. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Rothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Orokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, revision B.01, Gaussian, Inc., Wallingford, CT, 2010.
39. A. Misra, D. J. Klein and T. Morikawa, J. Phys. Chem. A, 2009, 113, 1151–1158.
40. A. Misra, T. G. Schmalz and D. J. Klein, J. Chem. Inf. Model., 2009, 49, 2670–2676.
41. M. Solà, F. Feixas, J. Oscar, C. Jiménez-Halla, E. Matito and J. Poater, Symmetry, 2010, 2, 1156–1179.
42. S. Shil and A. Misra, RSC Adv., 2013, 3, 14352–14362.
43. M. E. Ali and S. N. Datta, J. Phys. Chem. A, 2006, 110, 13232–13237.
44. K. Pierloot and S. Vancoillie, J. Chem. Phys., 2006, 125, 124303.
45. W. R. Browne, R. Hage and J. G. Vos, Coord. Chem. Rev., 2006, 250, 1653–1668.

---

Footnote

† Electronic supplementary information (ESI) available: The optimized coordinate of the couplers and diradicals. See DOI: 10.1039/c5ra16670e

---