 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A comprehensive test set of epoxidation rate constants for iron(IV)–oxo porphyrin cation radical complexes†
Mala A.
Sainna
a,
Suresh
Kumar
b,
Devesh
Kumar
*b,
Simonetta
Fornarini
*c,
Maria Elisa
Crestoni
*c and
Sam P.
de Visser
*a
aManchester Institute of Biotechnology and School of Chemical Engineering and Analytical Science, The University of Manchester, 131 Princess Street, Manchester M1 7DN, UK. E-mail: sam.devisser@manchester.ac.uk
bDepartment of Applied Physics, School for Physical Sciences, Babasaheb Bhimrao Ambedkar University, Vidya Vihar, Rai Bareilly Road, Lucknow 226 025, India. E-mail: dkclcre@yahoo.com
cDipartimento di Chimica e Tecnologie del Farmaco, Università di Roma “La Sapienza”, P.le A. Moro 5, 00185, Roma, Italy. E-mail: mariaelisa.crestoni@uniroma1.it; simonetta.fornarini@uniroma1.it
First published on 8th December 2014
Abstract
Cytochrome P450 enzymes are heme based monoxygenases that catalyse a range of oxygen atom transfer reactions with various substrates, including aliphatic and aromatic hydroxylation as well as epoxidation reactions. The active species is short-lived and difficult to trap and characterize experimentally, moreover, it reacts in a regioselective manner with substrates leading to aliphatic hydroxylation and epoxidation products, but the origin of this regioselectivity is poorly understood. We have synthesized a model complex and studied it with low-pressure Fourier transform-ion cyclotron resonance (FT-ICR) mass spectrometry (MS). A novel approach was devised using the reaction of [FeIII(TPFPP)]+ (TPFPP = meso-tetrakis(pentafluorophenyl)porphinato dianion) with iodosylbenzene as a terminal oxidant which leads to the production of ions corresponding to [FeIV(O)(TPFPP+˙)]+. This species was isolated in the gas-phase and studied in its reactivity with a variety of olefins. Product patterns and rate constants under Ideal Gas conditions were determined by FT-ICR MS. All substrates react with [FeIV(O)(TPFPP+˙)]+ by a more or less efficient oxygen atom transfer process. In addition, substrates with low ionization energies react by a charge-transfer channel, which enabled us to determine the electron affinity of [FeIV(O)(TPFPP+˙)]+ for the first time. Interestingly, no hydrogen atom abstraction pathways are observed for the reaction of [FeIV(O)(TPFPP+˙)]+ with prototypical olefins such as propene, cyclohexene and cyclohexadiene and also no kinetic isotope effect in the reaction rate is found, which suggests that the competition between epoxidation and hydroxylation – in the gas-phase – is in favour of substrate epoxidation. This notion further implies that P450 enzymes will need to adapt their substrate binding pocket, in order to enable favourable aliphatic hydroxylation over double bond epoxidation pathways. The MS studies yield a large test-set of experimental reaction rates of iron(IV)–oxo porphyrin cation radical complexes, so far unprecedented in the gas-phase, providing a benchmark for calibration studies using computational techniques. Preliminary computational results presented here confirm the observed trends excellently and rationalize the reactivities within the framework of thermochemical considerations and valence bond schemes.
Introduction
The cytochromes P450 are part of the body's natural defence mechanism in the liver and perform vital functions for human health that include the biodegradation of xenobiotic and drug molecules.1 Due to this broad chemical function the P450s can bind and activate a large range of substrates with varying shapes and sizes. Generally, the P450s act as monoxygenases, whereby they bind and utilize molecular oxygen via a heme centre and transfer one of the oxygen atoms of O2 to a substrate, while the second oxygen atom leaves the process as a water molecule. The P450s react with substrates activating aliphatic and aromatic hydroxylation, epoxidation and sulfoxidation reactions, but have also been reported to catalyse desaturation and N-dealkylation reactions.2 There are many different P450 isozymes and until early 2014 thousands of different structures had been characterized.3 All P450s share common features which include a catalytically active heme group with a central iron atom that is linked to the protein by the thiolate sulphur atom of a cysteinate side chain.4Fig. 1 displays the structure of a typical P450 active site, namely the one belonging to the CYP124 isozyme as taken from the 2WM4 protein databank (pdb) file.5 As shown in Fig. 1 the substrate (tyramine) is located in a cleft nearby the heme, the substrate binding pocket, which is in a tight orientation with stabilizing hydrogen bonding interactions by several residues. The vacant sixth coordination site of iron is the position where molecular oxygen will bind during the catalytic cycle. The process includes two reduction and two protonation steps to synthesize the active species of P450 called Compound I (Cpd I).6 Cpd I is highly reactive and therefore difficult to study experimentally, however, a few reports on its spectroscopic properties have appeared in the literature.7
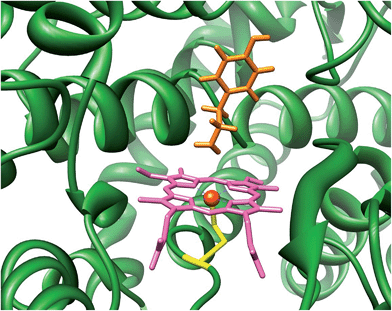 | ||
| Fig. 1 Active site of P450 as taken from the 2WM4 pdb file. Substrate tyramine is highlighted in orange. | ||
Due to the short lifetime of Cpd I, studying catalytic mechanisms and reaction rates of P450 catalysed reactions is challenging;8 therefore, many studies have focused on biomimetic iron–porphyrin complexes instead.9 These studies gave detailed insight into the effect of axial and equatorial ligands,10 but also on the local environment such as the substrate binding pocket. A particularly useful method to establish the properties and reactivity patterns of short-lived complexes, such as catalytic intermediates, is Fourier transform – ion cyclotron resonance (FT-ICR) mass spectrometry (MS).11 In FT-ICR MS, the charged species of interest (either positive or negative ion) is trapped in a collision cell for a specific time during which reactions with neutral gases can occur and be studied at the prevailing low pressure of the instrument. FT-ICR MS allows one to measure the ion distributions and fragmentation patterns at varying trapping time, thereby yielding insight into reactivities, and enabling one to calculate rate constants and thermochemical properties. In recent work, Crestoni, Fornarini and co-workers have succeeded in trapping and characterizing the Cpd I analogues of iron and manganese porphyrin complexes and studied their reactivity with a selection of substrates.12 Thus, the [MnV(O)(TPFPP)]+ complex (TPFPP = meso-tetrakis (pentafluorophenyl)porphinato dianion) was found to react with model substrates through oxygen atom transfer (OAT), electron transfer (ET), hydride transfer and ligand addition. However, no direct hydrogen atom transfer (HAT) with any tested substrate took place.
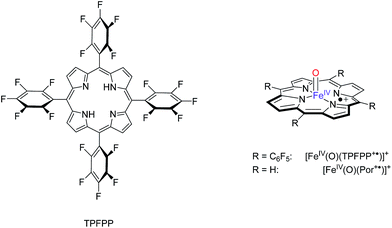
In order to find out what drives the OAT reaction of Cpd I with olefins, we decided to investigate the properties and reactivities of [FeIV(O)(Por+˙)]+ (Por = porphine dianion) and [FeIV(O)(TPFPP+˙)]+ with FT-ICR MS and with density functional theory (DFT) methods. These studies represent the first comprehensive – experimental and computational – study on olefin epoxidation by iron(IV)–oxo porphyrin cation radical models and allow correlations to be established between the OAT rate constant and the ionization energy (IE) of the olefin. These correlations are further supported and rationalized by computational modelling.
Methods
Materials
All chemicals used in the experiments, including (5,10,15,20-tetrakis(pentafluorophenyl)porphinato)iron(III) chloride, [FeIII(TPFPP)]Cl, were research grade products purchased from commercial sources and used as received. All the solvents were analytical grade. Ethylene, propylene, and E-2-butene were high purity gases from Matheson Gas Products Inc. Iodosylbenzene (C6H5IO) was prepared according to a published procedure and stored at −20 °C.13Instrumental
All experiments were run on a Bruker BioApex Fourier transform-ion cyclotron resonance (FT-ICR) mass spectrometer equipped with an Apollo I electrospray ionization source, a 4.7 T superconducting magnet, and a cylindrical infinity cell. Analyte solutions were continuously infused through a 50 μm internal diameter fused-silica capillary at a flow rate of 120 μL h−1 by a syringe pump and ions were accumulated in a radiofrequency-only hexapole ion guide for 0.8 s. The ion population, desolvated by a heated (380 K) N2 counter current drying gas, was pulsed into the ICR cell at room temperature (300 K), where the ion of interest was isolated by ion ejection procedures and allowed to react with the selected neutral reagent (L) admitted by a needle valve at stationary pressures in the range of 1.0–15 × 10−8 mbar. The pressure was measured with a cold-cathode sensor (IKR Pfeiffer Balzers S.p.A., Milan, Italy) calibrated by using the rate constant, kmethane = 1.1 × 10−9 cm3 s−1, for the reference reaction CH4+˙ + CH4 → CH5+ + CH3˙ and corrected for different response factors.14Pseudo-first order rate constants were obtained from the slope of the semi-logarithmic decrease of the parent ion abundance as a function of time and divided by the substrate concentration to determine the second-order rate constants (kexp) at 300 K. The reaction efficiencies (Φ) are percentages of the second-order rate constant with respect to the collision rate constant (kADO), i.e. Φ = kexp/kADO, calculated by the parametrized trajectory theory.15 These values and product ion branching ratios were found to be independent of the pressure of the neutral and of the additional presence of an inert bath gas, i.e. argon. The reproducibility of the kexp values was within 10%, while the error of the absolute rate constants is estimated to be ±30%.
Sample preparation
The [FeIV(O)(TPFPP+˙)]+ ion of interest was prepared by adding iodosylbenzene (0.5 mM) to [FeIII(TPFPP)]Cl (10 μM) in a CH3OH/CH2Cl2 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
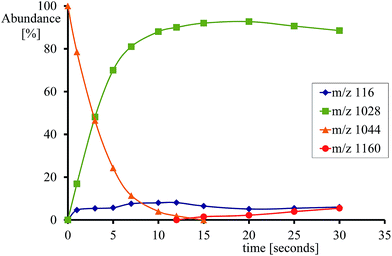
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) solvent mixture cooled at −40 °C. The so-formed [FeIV(O)(TPFPP+˙)]+ ion persisted at this temperature for about 1 h. The high-resolution electrospray ionization FT-ICR mass analysis shows the presence of ions [FeIV(O)(TPFPP+˙)]+ as a prominent cluster centered at m/z 1044, along with the resting form [FeIII(TPFPP)]+, characterized by the same isotopic pattern, and centered at m/z 1028.
1) solvent mixture cooled at −40 °C. The so-formed [FeIV(O)(TPFPP+˙)]+ ion persisted at this temperature for about 1 h. The high-resolution electrospray ionization FT-ICR mass analysis shows the presence of ions [FeIV(O)(TPFPP+˙)]+ as a prominent cluster centered at m/z 1044, along with the resting form [FeIII(TPFPP)]+, characterized by the same isotopic pattern, and centered at m/z 1028.
As already pointed out,16 the synthetic method yields a portion of an isomeric species, likely oxidized on the porphyrin ligand and ineffective in any OAT reaction to reductants. This OAT-unreactive fraction of the overall ion population at m/z 1044 has been identified as a four-coordinate iron(III) complex incorporating an O-atom on the porphyrin ligand, henceforth denoted as [FeIII(TPFPP-O)]+.16 Its relative amount has been evaluated exploiting the characteristic reaction with NO, displaying different paths from the two isomeric species. In fact, while [FeIII(TPFPP-O)]+ yields a ligand addition product, [FeIII(TPFPP-O)(NO)]+, the genuine iron(IV)–oxo complex [FeIV(O)(TPFPP+˙)]+ undergoes an OAT process by releasing [FeIII(TPFPP)]+.
Computation
All calculations discussed here utilize density functional theory (DFT) methods as implemented in the Jaguar and Gaussian-09 program packages.17 Two different models were investigated: (i) [FeIV(O)(Por+˙)]+ (A) that includes a porphyrin (Por) ring with all side-chains abbreviated to hydrogen atoms, and (ii) [FeIV(O)(TPFPP+˙)]+ (B), Scheme 1. Similar to previous work of ours in the field,18 we use the unrestricted hybrid density functional method UB3LYP19 as it was shown to reproduce the kinetics of metal(iv)–oxo oxidants well.20 Initial exploratory calculations employed a modest LANL2DZ basis set on iron and 6-31G on the rest of the atoms (basis set BS1)21 for geometry optimizations, analytical frequencies and geometry scans. These studies explored the potential energy surfaces involving reactants, intermediates and products on different spin states in detail and generated starting structures for the transition state optimizations. All local minima reported here had real frequencies only and the transition states were characterized by a single imaginary frequency for the correct mode. To improve the energetics of these structures we did single point calculations in the gas-phase with a triple-ζ quality basis set on iron (LACV3P+) and 6-311+G* on the rest of the atoms, basis set BS2. Subsequently, all geometries (local minima and transition states) were reoptimized at the UB3LYP/BS2 and UB3LYP-D3/BS2 levels of theory19,22 and characterized by an analytical frequency analysis. Barrier heights reported in this work were calculated relative to isolated reactants, although using reactant complexes instead only minor changes are observed (ESI†).The effect of solvent on the rate constants was tested through single point calculations using the self-consistent reactant field model as implemented in Gaussian with a dielectric constant representing chloroform (ε = 4.7113).
Ionization energies and bond dissociation energy (BDEOH) values were calculated as before23 and represent adiabatic values for reaction 1 and 2, respectively and report UB3LYP/BS2//UB3LYP/BS1 energies including ZPE and dispersion corrections.
| A → A+˙ + e− + IEA | (1) |
| [FeIV(OH)(Por)]+ → [FeIV(O)(Por+˙)]+ + H˙ + BDEOH | (2) |
Results
Gas phase reactivity with FT-ICR MS
The thus generated, naked five-coordinate species proves to be resistant with respect to any unimolecular dissociation process (kdiss ≤ 0.001 s−1). However, when the ion-molecule reactivity of the ion cluster at m/z 1044 is examined through the addition of NO into the FT-ICR cell, two reaction products are observed: (i) a major fraction of ions reacts by OAT and forms [FeIII(TPFPP)]+ and NO2 as the likely neutral product, (ii) a significant percentage of the starting ions undergo a ligand addition reaction to give a product with m/z 1074.
The product formed in the latter pathway has been sampled by collision induced dissociation (CID), and displays the loss of NO as unique fragmentation channel thus suggesting that NO has become part of the complex as intact ligand at a formerly vacant axial position. Note here that ligand addition is typical for the reactivity of tetracoordinate [FeIII(TPFPP)]+ ions.12a This finding provides circumstantial evidence for an ion population of the same elemental composition as [FeIV(O)(TPFPP+˙)]+, that may correspond to an isomeric structure oxidized on the porphyrin ligand, designated as [FeIII(TPFPP-O)]+.
The chemical titration reaction with NO is a way to resolve the isomeric distribution of electrosprayed ions at m/z 1044 and allowed us to establish the relative amount of [FeIV(O)(TPFPP+˙)]+ in each experiment, which is consistently found to be equal to or larger than 60% of the total ion population at m/z 1044.
| Substrate | IEa | k exp | k ADO | Φ | HT | CT | OAT | Add |
|---|---|---|---|---|---|---|---|---|
| a Ionization energies (IE, eV) are from ref. 24. N/A stands for not available. b Second-order rate constants (kexp) in units of 10−10 cm3 molecule−1 s−1 are measured at a temperature of 300 K in the FT-ICR cell. The estimated error in kexp is ±30%, although the internal consistency of the data is within ±10%. c Collision rate constants (kADO) evaluated with the parameterized trajectory theory. d Reaction efficiency (%), Φ = kexp/kADO × 100. e The reaction with cyclohexene-d10 gave a rate constant within experimental error of that for cyclohexene-h10. f The IE for α-pinene is 8.07 eV. | ||||||||
| Ethene | 10.51 | 8.5 × 10−5 | 8.5 | 1 × 10−3 | — | — | 100 | — |
| Propene | 9.73 | 7.6 × 10−3 | 9.45 | 0.080 | — | — | 100 | — |
| 1-Butene | 9.55 | 0.029 | 9.6 | 0.30 | — | — | 100 | — |
| E-2-Butene | 9.10 | 0.080 | 10.8 | 0.74 | — | — | 100 | — |
| 2,3-Dimethyl-1-butene | 9.07 | 0.145 | 9.5 | 1.5 | — | — | 100 | — |
| Cyclohexenee | 8.95 | 0.194–0.291 | 9.7 | 2–3 | — | — | 75 | 25 |
| 1,4-Cyclohexadiene | 8.82 | 0.511 | 9.29 | 5.5 | — | — | 90 | 10 |
| 2-Methoxy-1-propene | 8.64 | 0.819 | 10.5 | 7.8 | — | — | 100 | — |
| 1,3-Pentadiene | 8.60 | 0.826 | 9.6 | 8.6 | — | — | 100 | — |
| Styrene | 8.46 | 1.40 | 9.26 | 15 | — | — | 100 | — |
| 1,3-Cyclohexadiene | 8.25 | 1.58 | 9.29 | 17 | — | — | 100 | — |
| trans-β-Methylstyrene | 8.1–8.2 | 2.97 | 11.9 | 25 | 4 | — | 96 | — |
| Indene | 8.14 | 3.18 | 8.6 | 37 | 2 | 12 | 86 | — |
| β-Pinenef | N/A | 4.32–4.7 | 9.4 | 46–50 | — | — | 100 | — |
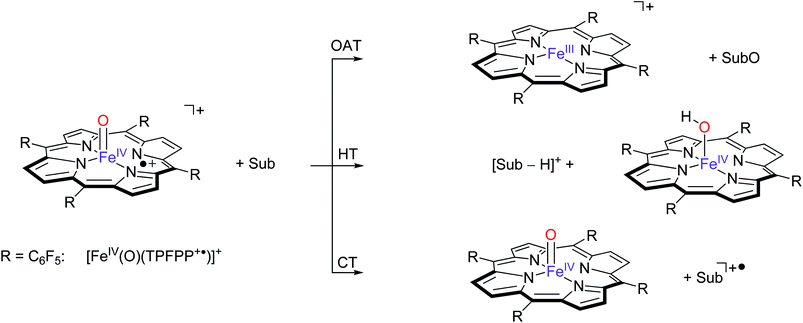 | ||
| Scheme 3 Pathways observed for the reaction of [FeIV(O)(TPFPP+˙)]+ ions (R = C6F5) with selected substrates (Sub) as studied with FT-ICR MS. | ||
These three pathways lead to different product ions in the recorded spectra: (i) [FeIII(TPFPP)]+ ions are the products of the OAT channel; (ii) ions at m/z corresponding to [Sub-H]+ are obtained from the HT processes; (iii) ions corresponding to Sub+˙ arise from a CT reaction. Interestingly, no evidence of hydrogen atom abstraction (HAT) is observed with any of the selected olefins listed in Table 1. In the case of two substrates, cyclohexene and 1,4-cyclohexadiene, molecular addition (Add) to the complex is also observed, leading to an ion with m/z value formally corresponding to [Fe(O)(TPFPP)(Sub)]+. It is possible that these addition complexes are products from a hydrogen atom abstraction reaction but currently this cannot be established from the product ions. However, experiments with fully deuterated cyclohexene (cyclohexene-d10) versus that of cyclohexene-h10 gave a rate constant ratio kH/kD very close to 1. Reactions starting with an initial hydrogen atom abstraction reaction normally encounter a large kinetic isotope effect (KIE = kH/kD) of well greater than 1, hence these KIE experiments implicate that no rate determining hydrogen atom abstraction takes place here.
Because the selected ions at m/z 1044 comprise isomeric species as described in the previous paragraph, it is important to mention that in all experiments with the selected substrates (olefins and unsaturated hydrocarbons) an unreactive fraction is observed in a corresponding relative amount as the species yielding the NO addition product in the probe reaction with nitric oxide. This species has been assigned the features of a porphyrin-oxidized complex and its contribution to the experiments has been thoroughly subtracted, an operation allowed by the distinctly different (un)reactivity of the two isomeric complexes [FeIV(O)(TPFPP+˙)]+ and [FeIII(TPFPP-O)]+. Henceforth, the implication of this species will not be further discussed.
Fig. 2 gives an example of the time dependence of the relative ion abundance of reactant and product ions as a function of time for the reaction of [FeIV(O)(TPFPP+˙)]+ with indene. In general, the ion abundance of [FeIV(O)(TPFPP+˙)]+ follows an exponential decay as a function of time, as illustrated by its reaction with indene in Fig. 2. The pseudo-first order decay of the reactant ion abundance as a function of time was then converted into a bimolecular rate constant, kexp, which was normalized by the respective collision rate constant (kADO) to give the relative efficiency (Φ = kexp/kADO × 100).15 The gas phase reactivity of [FeIV(O)(TPFPP+˙)]+ spans a wide range of reaction efficiencies, with values varying from 0.001% to 0.08% for terminal olefins, like ethene and propene, up to ca. 50% for electron-rich monoterpenes.
With most substrates a clean OAT conversion from reactants to products is observed without production of by-products and the time dependence shows a pattern like that displayed in Fig. 2. In the case of cyclohexene, about 25% addition occurs with the formation of an ion formally corresponding to [Fe(TPFPP)(c-C6H10)O]+. The formation of a long-lived complex with this substrate suggests that, within the metal coordination sphere, the olefin is activated to form an O-containing species endowed with appreciable affinity for the metal. Ligand binding to iron porphyrin complexes has been found to correlate with the gas phase basicity of the ligand.25 It may thus be inferred that the olefin has turned into a more basic species, either an epoxide by O-addition across the double bond or an alcohol by allylic C–H bond activation. The nature of the adduct complex has been further probed and confirmed by low-energy CID, and reveals the formation of the reduced species [FeIII(TPFPP)]+ through the release of SubO. The so-formed complex from the reaction of [FeIV(O)(TPFPP+˙)]+ with the olefin substrate may then be depicted as [FeIII(TPFPP)(SubO)]+. Similar product complexes have been observed previously from other substrates through oxygen atom-acceptor properties such as sulphides, amines, and phosphorus containing complexes.12a,16
In addition, substrates with low ionization potential are found to react via hydride transfer (trans-β-methylstyrene, and indene) and/or charge transfer reactions (indene) as side-reactions. We examined whether a charge-transfer (CT) reaction occurs between [FeIV(O)(TPFPP+˙)]+ and sampled substrates. As in FT-ICR MS only exothermic reactions are able to occur due to the low number of collisions in the gas, the data in Table 1 show that the charge-transfer reaction is exothermic with indene as a substrate (eqn (3)), but endothermic with other substrates. Thus, the enthalpy change for the charge-transfer between [FeIV(O)(TPFPP+˙)]+ and indene should be equal to the difference between the ionization energy of the substrate and the electron affinity (EA) of [FeIV(O)(TPFPP+˙)]+. Since, no charge-transfer reaction occurs with substrates with an ionization energy above 8.2 eV (Table 1), this implies that the EA of gaseous [FeIV(O)(TPFPP+˙)]+ ions must be lower than 8.2 eV. Previous FT-ICR MS studies predicted a lower limit of 7.5 eV for the EA of [FeIV(O)(TPFPP+˙)]+,16 which is in good general agreement with the data in Table 1. DFT calculations on [FeIV(O)(Por+˙)X] with different axial ligands X have yielded electron affinities of 3.06 eV for X = SH−, whereas values of 6.41 and 6.12 eV are found for systems with an imidazole or tyrosinate axial ligand, respectively.26 Clearly, removal of the axial ligand is expected to raise the EA of the iron(IV)–oxo porphyrin cation radical substantially with respect to axially ligated systems due to the loss of interaction between the a2u molecular orbital with axial ligand orbitals, vide infra.
| [FeIV(O)(TPFPP+˙)]+ + indene → [FeIV(O)(TPFPP)] + indene+˙ | (3) |
| ΔHEq3 = IEindene − EA[FeIV(O)(TPFPP+)] < 0 kcal mol−1 | (4) |
Interestingly, although cytochrome P450 isozymes react with typical olefins, such as propene, cyclohexene and Z- and E-butene, to give a mixture of epoxide and enol products, actually the precise product distributions depend on the specific P450 isozyme.27 Clearly, the substrate binding pocket and substrate orientation within the enzyme play a key role in determining the regioselectivity of the enzymatic reaction. In fact, enzymes manage to control the regioselectivity of substrate activation probably by binding the substrate under a specific orientation, which raises the epoxidation barriers and/or lowers the hydrogen atom abstraction barriers. Unfortunately, the FT-ICR MS results are unable to unequivocally distinguish hydroxylation products from epoxidation products as both have the same mass and are released as neutral molecules. As such, the experiments do not provide direct evidence supporting olefin epoxidation over a C–H activation channel in the reactions of [FeIV(O)(TPFPP+˙)]+ with the selected olefins. However, we are able to show indirect evidence, vide infra. Computational studies on the regioselectivity of propene epoxidation versus hydroxylation by [FeIV(O)(Por+˙)(SH)] gave lower epoxidation barriers in the gas-phase reaction,28 but solvent and environmental effects reversed the ordering. The computational studies from ref. 28, therefore, confirm the experimental trends in Table 1. This finding underlines the benchmark role played by a mechanistic study in the gas phase.
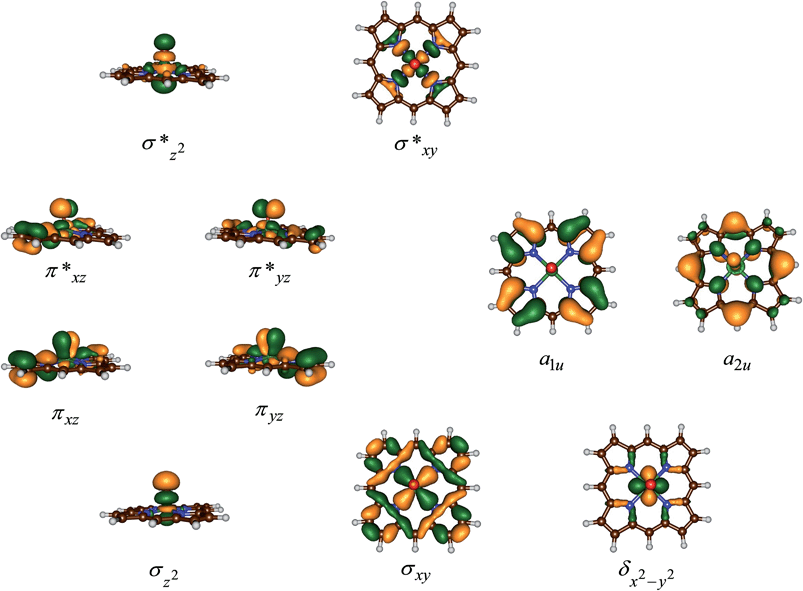
Fig. 3 displays the high-lying occupied and low-lying virtual orbitals of 4,2A; the orbitals for 4,2B look very similar. These orbitals are dominated by the interactions of the metal 3d orbitals with its ligands and several π-type porphyrin orbitals. Lowest in energy are a pair of σ-type orbitals (σz2 and σxy): σz2 represents the σ-interactions of the 3dz2 orbital on iron with the 2pz orbital on oxygen, whereas the σxy gives the interactions of the 3dxy orbital on iron with 2px,y orbitals on the four nitrogen atoms of the porphyrin ligand. The antibonding combinations of these two orbitals (σ*z2 and σ*xy) are high in energy and virtual. Also doubly occupied is the δx2−y2 orbital, which is a lone-pair orbital located in the plane of the porphyrin ring. Finally, the interaction of the metal 3dxz/3dyz with the 2px/2py on the oxygen atom leads to a pair of πxz/πyz and a pair of π*xz/π*yz set of orbitals. The σz2, σxy, πxz and πyz bonding orbitals are doubly occupied and low-lying in all calculations reported here. In addition to the metal-type orbitals there are also two porphyrin-type π-orbitals that in D4h symmetry have the labels a1u and a2u. With a thiolate as axial ligand the a2u orbital strongly mixes with a 3pz orbital on sulphur and hence is destabilized in energy,29 which strongly affects the electron affinity of the oxidant and consequently is responsible for its push-effect.30
The set of orbitals displayed in Fig. 3 is occupied with 15 electrons and as several of these orbitals are close in energy there are a number of possibilities to distribute the electrons over the orbitals. In addition, states can also be found in various spin states ranging from doublet to quartet and sextet, where we identify the spin state with a superscript in front of the electronic state label. Thus, the electronic state labelled as 4A2u has an overall quartet spin state and singly occupied a2u molecular orbital with overall electronic configuration: σz22 σxy2 πxz2 πyz2 δx2−y22 π*xz1 π*yz1 a1u2 a2u1 or in short [core] δx2−y22 π*xz1 π*yz1 a1u2 a2u1. Similarly, we calculated the doublet spin state (2A2u state), where the unpaired electron in the a2u orbital is antiferromagnetically coupled to the unpaired electrons in the two π* orbitals: 2A2u = [core] δx2−y22 π*xz↑ π*yz↑ a1u2 a2u↓.
Previous studies with either imidazole, acetonitrile or thiolate as axial ligand,29,31 showed the 4,2A2u states to be close in energy and well below alternative states. However, this was due to considerable mixing of the a2u orbital with the axial ligand orbitals, which obviously is not possible in our chemical system that lacks an axial ligand. However, in an isolated porphyrin macrocycle, the a1u and a2u orbitals are degenerate;32 therefore, we decided to investigate a range of possible electronic states for the pentacoordinated iron(IV)–oxo porphyrin cation radical system, [FeIV(O)(Por+˙)]+. Firstly, we tested the stability of the 4,2A2u states and the alternative 4,2A1u states with [core] δx2−y22 π*xz1 π*yz1 a1u1 a2u2 orbital occupation. In addition, we attempted to generate models with the iron in oxidation state iron(V), i.e.2Πxz state with occupation [core] δx2−y22 π*xz1 a1u2 a2u2, or the iron in oxidation state iron(III), i.e. the 4A state with orbital occupation [core] δx2−y22 π*xz2 π*yz1 a1u1 a2u1 and the 6Σxy,III state with [core] δx2−y22 π*xz1 π*yz1 σ*xy1 a1u1 a2u1 occupation. However, all our attempts to calculate iron(III) or iron(V) states failed and converged back to lower lying solutions with four electrons on the metal in a formal iron(IV) oxidation state, hence the 2Πxz, 4A and 6Σxy,III states are high in energy and inaccessible to our chemical system.
Table 2 summarizes relative energies of optimized geometries of the various electronic spin states as calculated with different DFT methods for 2,4,6A. As follows from Table 2 all calculations of A give a 2A1u ground state that is nearly degenerate with the corresponding quartet spin state. In general, calculations done at UB3LYP/BS2 and UB3LYP-D3/BS2 give almost identical spin state orderings and relative energies, which shows that dispersion is not a critical component for these chemical structures. Nevertheless, the 4,2A2u and 4,2A1u states are close in energy and all four states could have a finite lifetime.
| State | Configuration | A | A | A |
|---|---|---|---|---|
| ΔE + ZPE | ΔE + ZPE | ΔE + ZPE | ||
| a Relative energies in kcal mol−1 with respect to the 2A1u state, ND stands for not determined. b Energies obtained at UB3LYP/BS2//UB3LYP/BS1 level of theory. c Energies and geometries calculated at UB3LYP/BS2 level of theory. d Energies and geometries calculated at UB3LYP-D3/BS2 level of theory. | ||||
| 2A1u | δ2 π*xz↑ π*yz↑ a1u↓ | 0.00 | 0.00 | 0.00 |
| 4A1u | δ2 π*xz↑ π*yz↑ a1u↑ | 0.71 | 0.19 | 0.21 |
| 2A2u | δ2 π*xz↑ π*yz↑ a2u↓ | 1.65 | 3.75 | 3.80 |
| 4A2u | δ2 π*xz↑ π*yz↑ a2u↑ | 1.25 | 3.42 | 3.47 |
| 6A2u | δ↑ π*xz↑ π*yz↑ σ*xy↑ a2u↑ | 9.25 | 18.68 | 19.38 |
| 4Δxy | δ↑ π*xz↑ π*yz↑ σ*xy↑ a1u↓ | 9.69 | ND | ND |
| 4Δzz | δ↑ π*xz↑ π*yz↑ σ*z2↑ a2u↓ | 19.53 | ND | ND |
Optimized geometries of the 4,2A2u and 4,2A1u states are given in Fig. 4. Geometrically, no dramatic changes in bond lengths are obtained between the three optimization techniques. A small basis set gives slightly longer Fe–O distances than those found with a triple-ζ basis set. The effect of dispersion is negligible on the optimized geometries: UB3LYP/BS2 and UB3LYP-D3/BS2 give virtually the same chemical structures. Addition of meso-substituents to the porphyrin ring such as pentafluorophenyl groups is not expected to dramatically change key bond lengths in the optimized geometries and relative energies of individual spin states.33 Thus, recent work of the Goldberg group showed that meso-substituted manganese–oxo porphyrinoid complexes retained the spin state ordering and converged to a closed-shell singlet manganese(V)–oxo state in all cases.33a
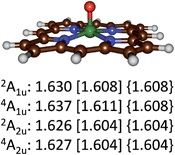 | ||
| Fig. 4 Optimized geometries of the 4,2A2u and 4,2A1u states of 4,2A as calculated with UB3LYP/BS1 [UB3LYP/BS2] {UB3LYP-D3/BS2} with Fe–O bond lengths in angstroms. | ||
The calculations on the low-lying 4,2A2u and 4,2A1u states reported in Table 2 and Fig. 4 show that geometrically there are very little differences between these states, but the spin state ordering and relative energies are sensitive to the method and basis set. Recent complete active site (CASSCF) and restricted active site (RASSCF) calculations of Pierloot and co-workers34 calculated the 4,2A2u and 4,2A1u states of A within 1 kcal mol−1 of each other with a small preference for the A1u states. However, they also located two low-lying iron(V) states, which we were unable to characterize and for which no experimental evidence exist. Unfortunately, our chemical systems (in particular structure B) are too large to attempt calculations using the CASSCF and RASSCF methods; therefore, we decided to continue with UB3LYP instead.
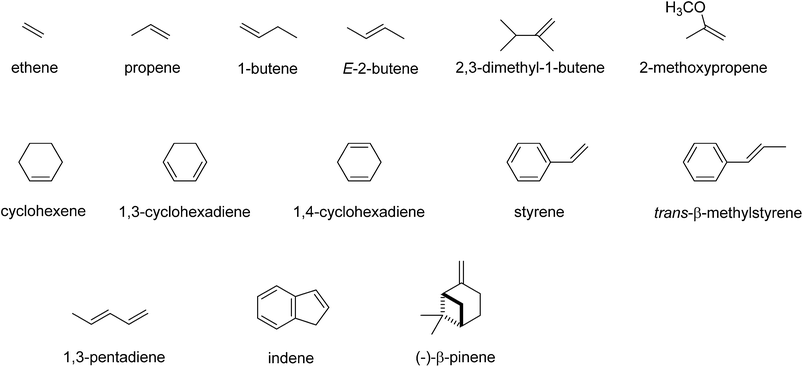
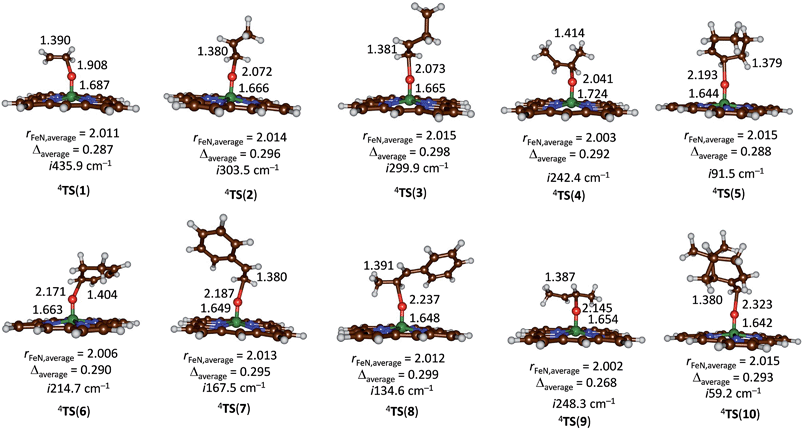
Subsequently, we investigated the substrate epoxidation by [FeIV(O)(Por+˙)]+, i.e.4A. We find the lowest lying barriers to proceed from the 4A2u state and will focus on those in the following. Previous studies on the epoxidation of olefins by [FeIV(O)(Por+˙)(L)] with L = NCCH3 or Cl− showed that the same trends in reactivity are observed when the Por ligand is replaced by TPFPP,35 hence the smaller model was used in this study. We investigated substrate epoxidation with a range of olefins: ethene (1), propene (2), 1-butene (3), E-2-butene (4), cyclohexene (5), 1,3-cyclohexadiene (6), styrene (7), trans-β-methylstyrene (8), Z-2-butene (9) and 2-pinene (10). For all substrates we calculated the full potential energy profile from reactants to epoxide products, see ESI,† but for space restrictions we will focus on the rate determining C–O bond formation transition states (TSCO) only. All reactions are concerted with a single C–O activation barrier leading to epoxide product complexes PE. This is unusual as previous calculations on substrate epoxidation by Cpd I models gave a stepwise mechanism via a radical intermediate that via a ring-closure barrier was separated from epoxide product complexes.36 The orientation of the substrate and the strong displacement of the metal from the porphyrin plane are the likely reason for the fact that radical intermediates are saddlepoints here. Thus, the ring-closure barrier on the quartet spin state surface involves an electron transfer from substrate into σ*z2. The latter orbital in iron–porphyrin complexes with axial ligand, e.g. thiolate, contains a strong contribution from axial ligand orbitals (3pz) and therefore is high in energy. Since our particular system lacks an axial ligand, the σ*z2 orbital is considerably lower in energy and as a consequence the lifetime of the radical intermediate is reduced and the reaction to form products is now concerted.
Fig. 5 gives the optimized geometries of the C–O activation transition states (TSCO) for all substrates. Generally, the transition states occur early with a long C–O distance and relatively short Fe–O distance that has not dramatically changed from what it was in the iron(IV)–oxo porphyrin cation radical state. As expected the metal is considerably displaced from the plane through the four nitrogen atoms of the porphyrin ring by as much as 0.268–0.299 Å. These transition states bear resemblance to substrate epoxidation barriers calculated previously for P450 Cpd I reactions with olefins.36 Electronically, all transition states are accomplished by single electron transfer from the substrate into the a2u orbital and the formation of an [FeIV(OSub)(TPFPP)]+ transition state with orbital occupation [core] δx2−y22 π*xz1 π*yz1 a1u2 a2u2ϕSub1 with ϕSub a radical on the substrate group.
Discussion
The present work gives a detailed and extensive overview on the reactivity of iron(IV)–oxo porphyrin cation radical systems with a test-set of olefins. We determined rate constants and measured product ion distributions in the gas phase using FT-ICR MS. This comprehensive set of transition metal containing reactivities is unique and will enable computation to benchmark and calibrate its methods effectively. This is particularly important for transition metal complexes, such as iron(IV)-oxo species, where the reproducibility of the computational (DFT) methods sometimes varies strongly depending on the density functional method used, the basis set, environmental perturbations, dispersion effects etc.37 In this work, we supplemented the experimental studies with a series of preliminary DFT calculations for two reasons: (i) to validate and calibrate computational methods against experiment; (ii) to establish the physicochemical properties that influence the rate constant of the chemical reaction.Let us first start with a comparison of the experimental and computational reaction rates. As FT-ICR MS experiments are being performed at very low pressures, these experimental conditions are close to Ideal Gas conditions with very few molecular collisions per second. In the kinetic study of ion-molecule reactions in the gas phase one needs to consider that thermal equilibration of the reacting system with the environment is in general not granted. On the contrary, when small species react at low pressures, the absence of thermalizing collisions leads to non-equilibrium energy distributions. In the absence of solvation, the double-well potential model first proposed by Brauman in 1977 to account for the kinetic behaviour of displacement reactions by anionic nucleophiles predicts that the energy of the intermediate and transition state must lie below the energy of the combined reactants.38 Because at low pressure the intermediates cannot be stabilized by unreactive collisions, determining the transition state energy is less straightforward than in solution. However, the kinetics results presently reported deal with a relatively large reactant ion that effectively establishes thermal equilibrium with the environment through coupling with the background radiation field allowed by the several low frequency infrared modes of the iron(IV)–oxo macrocyclic ligand complex. This condition is responsible, for example, for the consistency between the kinetics of NO ligand addition to iron(II/III) porphyrin complexes and the equilibrium data independently established through equilibrium measurements.25 Because of these considerations, the notion can be adopted that the presently investigated systems are in prevailing thermal equilibrium with the environment and reaction kinetics can be interpreted within the framework of transition state theory. Consequently, reaction rates represent bimolecular reactions and as such they should compare to computationally determined reaction rates well.
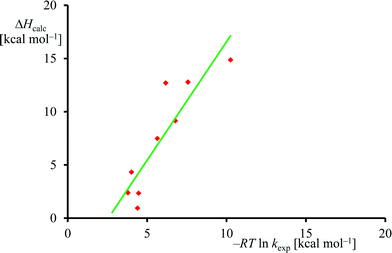
The experimental rate constants (Table 1) were converted into free energy units via −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kexp, with R the gas constant and T the temperature, using transition state theory and plotted against the calculated enthalpy of activation for the same substrates, see Fig. 6. Although only a limited computational study is reported here, when we calculate the deviation between experiment and theory for each data point, we find an average difference between experiment and theory of 1.5 kcal mol−1 with a standard deviation of 3.4 kcal mol−1. As such, the DFT methods used here reproduce the trends obtained from experimental enthalpies of activation well and the linearity and reproducibility of the calculations is well within the typical error reported for DFT calculations using this method of about 5 kcal mol−1.39 There is, however, a large systematic error as well as a relatively large standard deviation that require further studies. Note that the experimental data in Fig. 6 refers to free energies of activation, whereas the computational results are enthalpy changes instead. The systematic error between experiment and theory contains entropic corrections to the energy.
kexp, with R the gas constant and T the temperature, using transition state theory and plotted against the calculated enthalpy of activation for the same substrates, see Fig. 6. Although only a limited computational study is reported here, when we calculate the deviation between experiment and theory for each data point, we find an average difference between experiment and theory of 1.5 kcal mol−1 with a standard deviation of 3.4 kcal mol−1. As such, the DFT methods used here reproduce the trends obtained from experimental enthalpies of activation well and the linearity and reproducibility of the calculations is well within the typical error reported for DFT calculations using this method of about 5 kcal mol−1.39 There is, however, a large systematic error as well as a relatively large standard deviation that require further studies. Note that the experimental data in Fig. 6 refers to free energies of activation, whereas the computational results are enthalpy changes instead. The systematic error between experiment and theory contains entropic corrections to the energy.
Subsequently, we investigated the origin of the rate constant, and in particular, the physical and chemical properties of the substrate and oxidant that determine the reaction mechanism and the enthalpy of activation of an epoxidation reaction. Previous studies on heteroatom oxidation and double bond epoxidation by P450 enzymes implicated a correlation between the natural logarithm of the rate constant with the ionization energy of the substrate.12d,e,28,40 To find out whether the data in Table 1 follow these trends as well, we plot RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kexpversus experimentally known ionization energies,24 in Fig. 7. The set of data shown in Table 1 and Fig. 7 gives a linear correlation between the natural logarithm of the rate constant and the ionization energy of the substrate with an R2 = 0.96. Fig. 7b displays the correlation between the DFT calculated enthalpy of activation of the reaction of [FeIV(O)(Por+˙)]+ with olefins. In agreement with the experimental trends given in part (a) of Fig. 7 also the computational trends link the natural logarithm of the rate constant to the ionization energy of the substrate. Clearly, the key physicochemical property that drives the reaction mechanism and affects the rate constant of substrate epoxidation by iron(IV)–oxo porphyrin cation radical complexes is the ionization energy of the substrate.
kexpversus experimentally known ionization energies,24 in Fig. 7. The set of data shown in Table 1 and Fig. 7 gives a linear correlation between the natural logarithm of the rate constant and the ionization energy of the substrate with an R2 = 0.96. Fig. 7b displays the correlation between the DFT calculated enthalpy of activation of the reaction of [FeIV(O)(Por+˙)]+ with olefins. In agreement with the experimental trends given in part (a) of Fig. 7 also the computational trends link the natural logarithm of the rate constant to the ionization energy of the substrate. Clearly, the key physicochemical property that drives the reaction mechanism and affects the rate constant of substrate epoxidation by iron(IV)–oxo porphyrin cation radical complexes is the ionization energy of the substrate.
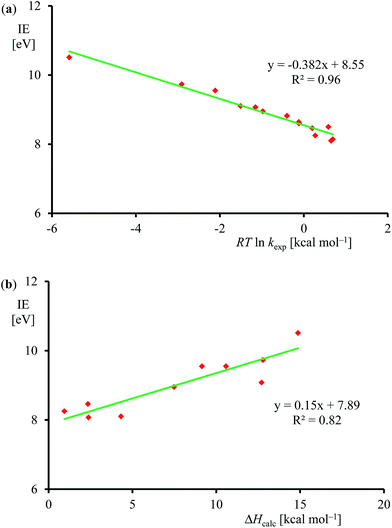 | ||
Fig. 7 (a) Correlation between experimentally determined RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kexp (for raw data, see Table 1) versus known ionization energies (IE). (b) Correlation between calculated epoxidation activation enthalpy (in kcal mol−1) and experimental ionization energy for the substrates in Fig. 5. kexp (for raw data, see Table 1) versus known ionization energies (IE). (b) Correlation between calculated epoxidation activation enthalpy (in kcal mol−1) and experimental ionization energy for the substrates in Fig. 5. | ||
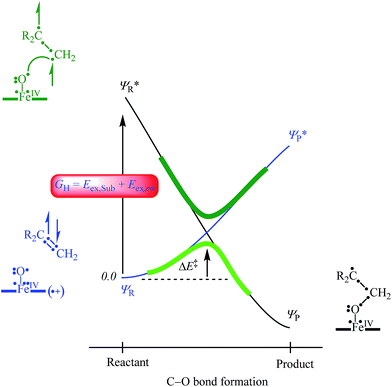
In order to explain the experimental and computational trends in the reaction mechanisms, we devised a valence bond (VB) curve crossing diagram, which is schematically depicted in Fig. 8. This diagram starts bottom left with the reactant configuration of [FeIV(O)(TPFPP+˙)]+ in electronic configuration πxz2 πyz2 δx2−y22 π*xz1 π*yz1 a2u1. The π and π* electrons along the FeO bond are identified with dots in the VB diagram and due to occupation of πxz2 π*xz1 there are three dots on the left-hand-side of the Fe–O bond. In addition, there are three electrons in the πyz and π*yz orbitals, which are identified with the other three dots on the right-hand-side of the Fe–O bond. Furthermore, the oxidant has a radical on the porphyrin ring for single occupation of the a2u molecular orbital. The substrate double bond is also highlighted with four electrons spread out over the interaction. Upon approach of the substrate on the iron(IV)–oxo species a radical intermediate is formed that has a single bond between the oxygen and carbon atoms and a doubly occupied a2u orbital.
In VB theory the electronic configuration in the reactant complex (ΨR) connects to an excited state in the product geometry (Ψ*P) as shown with the blue line in Fig. 8. At the same time the product electronic configuration (ΨP) connects to an excited state in the reactant geometry (Ψ*R), black line in Fig. 8. These two VB curves cross and lead to an avoided crossing and a transition state for the C–O bond formation with barrier ΔE‡. The barrier height is linearly proportional to the curve crossing energy, which in its own right is a fraction of the excitation energy (GH) from the reactant wave function to the product wave function in the geometry of the reactants, i.e. for ΨR → Ψ*R. The difference in VB structures for ΨR and Ψ*R thereby should give a reflection of the key electron transfer/migrations upon product formation. Moreover, based on the excitation energy, the factors that determine the barrier height can be predicted.
An analysis of the differences between the reactant and product wave functions in the reactant geometry reveals the following information: First of all, a comparison of the VB structures of ΨR and Ψ*R shows that the electrons in the π-bond of the olefin are singlet paired in the ground state and triplet coupled in the excited state, hence the excitation energy GH includes the π–π* electron excitation in the substrate, Eex,Sub. Generally, the first ionization potential of an olefin corresponds to the removal of an electron from a π-orbital, and, hence, is proportional to the π–π* excitation energy. Indeed, our experimentally and computationally determined barrier heights correlate linearly with the ionization energy of the olefin, and therefore support the VB model.
One of the electrons originating from the π-bond of the olefin forms a bond with the π*xz electron along the FeO bond, to create the C–O bonding pair of electrons. This means that the πxz/π*xz pair of orbitals during the reaction splits back into individual atomic orbitals namely 3dxz(Fe) and 2px(O). The 2px(O) electron pairs with the electron from the substrate, while one of the electrons of the 3dxz(Fe) orbital is transferred into the a2u orbital through internal excitation/rehybridization of the oxidant, Eex,ox. The promotion gap, GH, therefore, will be proportional to the π–π* excitation in the substrate and the 3dxz to a2u electron transfer in the oxidant: GH = Eex,Sub + Eex,ox. Obviously, since the ionization energy represents the energy to remove an electron from a π-type orbital of an olefin, this will imply a linear correlation between the first excited state and the ionization energy of the substrate.28 The VB diagram, therefore, confirms a linear correlation between the ionization energy of the substrate and the C–O bond formation enthalpy of activation as shown above.
Although, the oxygen atom transfer reaction between [FeIV(O)(TPFPP+˙)]+ and an olefin could lead to either epoxide or hydroxylated products, unfortunately the FT-ICR MS experiments cannot distinguish the two. Thus, several substrates in Scheme 2 and Table 1 contain aliphatic groups that in a reaction with an iron(IV)–oxo group can be converted into an alcohol. A correlation between the rate constant of oxygen atom transfer and the ionization energy, Fig. 7a, of the olefin provides indirect experimental evidence that all reactions lead to epoxidation products. In fact, hydrogen atom abstraction reactions should not correlate with the ionization potential of the substrate, but were shown to be proportional to the strength of the C–H bond of the substrate that is formed.12e,40 To test that the rate constants do not correlate with the bond dissociation energy (BDECH) of the C–H bond of the substrate that is broken, we plot in Fig. 9 calculated BDECH and barrier heights of selected olefins, namely propene, Z-2-butene, E-2-butene, cyclohexene and 1,3-cyclohexadiene. As can be seen from Fig. 9, no correlation between BDECH and barrier height exists, and, therefore, hydrogen atom abstraction is not the rate determining step in the reaction mechanism. Further evidence that hydrogen atom abstraction reactions can be ruled out here comes from kinetic isotope effect (KIE) studies. We measured the rate constant of oxygen atom transfer with cyclohexene and cyclohexene-d10 and determined a KIE = kH/kD ∼1 (Table 1). Consequently, the oxygen atom transfer is unlikely to proceed with an initial hydrogen atom abstraction and double bond epoxidation will be the dominant pathway.
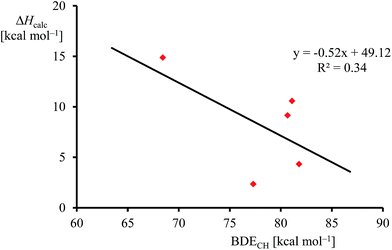 | ||
| Fig. 9 Correlation between calculated epoxidation activation enthalpy (in kcal mol−1) and BDECH for the substrates. | ||
The experimental trends, therefore, provide the first indirect experimental evidence that in the gas-phase the regioselectivity of double bond epoxidation versus aliphatic hydroxylation will be in favour of the epoxidation pathway. This implies that in enzymatic systems, such as the cytochromes P450, the shape and size of the substrate binding pocket will influence the regioselectivity of hydroxylation over epoxidation and can change the natural preference away from epoxidation.
Finally, the calculations presented in this work obviously refer to gas-phase results and hence correlate well with gas-phase mass spectrometric data. In order to further establish that the work can be extrapolated to solution phase, we did a series of single point calculations using the polarized continuum model with a dielectric constant of ε = 4.7 to mimic a solution. The obtained correlation between solvent corrected free energies of activation of epoxidation reactions by [FeIV(O)(Por+˙)]+ is plotted against the solvent corrected ionization energy of all substrates in Fig. S1, ESI.† Even in solvent, the linear trend in the correlation between free energy of activation and ionization energy is retained, therefore, we expect to be able to extrapolate our results to the solution phase as well.
Conclusions
In this work we report a comprehensive combined mass spectrometric and computational study on substrate epoxidation by iron(IV)–oxo porphyrin cation radical complexes in the gas phase. We present a novel method to synthesize [FeIV(O)(TPFPP+˙)]+ in the gas phase at low pressure. Furthermore, we report a large set of experimentally derived rate constants and product distributions. All olefins undergo oxygen atom transfer, whereas compounds with low ionization energy also give a certain degree of hydride transfer and charge transfer reactions. Our experimentally determined reaction rates correlate linearly with the ionization potential of the substrate and show that the electron transfer from substrate to oxidant is rate determining. A thorough computational survey has confirmed the suggested mechanism and provides a rationale for the observed trend in the rate constants. Moreover, the work highlights a regioselective epoxidation over hydroxylation in the gas phase.Acknowledgements
MAS thanks the Petroleum Technology Development Fund for a studentship. The National Service of Computational Chemistry Software (NSCCS) is thanked for providing valuable cpu time to SdV. DK acknowledges the Department of Science and Technology (New Delhi) for a Ramanujan Fellowship. MEC and SF thank the Università degli Studi di Roma La Sapienza for support.Notes and references
-
(a) M. Sono, M. P. Roach, E. D. Coulter and J. H. Dawson, Chem. Rev., 1996, 96, 2841 CrossRef CAS PubMed
; (b) J. T. Groves, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 3569 CrossRef CAS PubMed
; (c) Cytochrome P450: Structure, Mechanism and Biochemistry, ed. P. R. Ortiz de Montellano, Kluwer Academic/Plenum Publishers, New York, 3rd edn, 2004 Search PubMed
; (d) I. G. Denisov, T. M. Makris, S. G. Sligar and I. Schlichting, Chem. Rev., 2005, 105, 2253 CrossRef CAS PubMed
; (e) Handbook of Porphyrin Science, ed. K. M. Kadish, K. M. Smith and R. Guilard, World Scientific, New Jersey, 2010 Search PubMed
; (f) P. R. Ortiz de Montellano, Chem. Rev., 2010, 110, 932 CrossRef CAS PubMed
; (g) E. O'Reilly, V. Koehler, S. Flitsch and N. Turner, Chem. Commun., 2011, 47, 2490 RSC
; (h) G. Grogan, Curr. Opin. Chem. Biol., 2011, 15, 241 CrossRef CAS PubMed
.
-
(a)
J. T. Groves, Models and Mechanisms of Cytochrome P450 Action, in Cytochrome P450: Structure, Mechanism and Biochemistry, ed. P. R. Ortiz de Montellano, Kluwer Academic/Plenum Publishers, New York, 3rd edn, 2005, ch. 1, pp. 1–44 Search PubMed
; (b) Y. Watanabe, H. Nakajima and T. Ueno, Acc. Chem. Res., 2007, 40, 554 CrossRef CAS PubMed
.
- D. R. Nelson, Methods Mol. Biol., 2006, 320, 1 CAS
.
-
(a) T. L. Poulos, B. C. Finzel, I. C. Gunsalus, G. C. Wagner and J. Kraut, J. Biol. Chem., 1985, 260, 6122 Search PubMed
; (b) T. L. Poulos, B. C. Finzel and A. J. Howard, Biochemistry, 1986, 25, 5314 CrossRef CAS
.
- J. B. Johnston, P. M. Kells, L. M. Podust and P. R. Ortiz de Montellano, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 20687 CrossRef CAS PubMed
.
-
(a) B. Meunier, S. P. de Visser and S. Shaik, Chem. Rev., 2004, 104, 3947 CrossRef CAS PubMed
; (b) Iron-containing enzymes: Versatile catalysts of hydroxylation reaction in nature, ed. S. P. de Visser and D. Kumar, RSC Publishing, Cambridge, UK, 2011 Search PubMed
.
- J. Rittle and M. T. Green, Science, 2010, 330, 9337 CrossRef PubMed
.
-
(a) K. Auclair, Z. Hu, D. M. Little, P. R. Ortiz de Montellano and J. T. Groves, J. Am. Chem. Soc., 2002, 124, 6020 CrossRef CAS PubMed
; (b) P. Lafite, F. André, D. C. Zeldin, P. M. Dansette and D. Mansuy, Biochemistry, 2007, 46, 10237 CrossRef CAS PubMed
; (c) T. S. Dowers, D. A. Rock, D. A. Rock and J. P. Jones, J. Am. Chem. Soc., 2004, 126, 8868 CrossRef CAS PubMed
; (d) H. L. R. Cooper and J. T. Groves, Arch. Biochem. Biophys., 2011, 507, 111 CrossRef CAS PubMed
; (e) K. M. Roberts and J. P. Jones, Chem.–Eur. J., 2010, 16, 8096 CrossRef CAS PubMed
.
- See, e.g.,
(a) J. T. Groves and R. S. Myers, J. Am. Chem. Soc., 1983, 105, 5791 CrossRef CAS
; (b) J. T. Groves and Y. Watanabe, J. Am. Chem. Soc., 1986, 108, 507 CrossRef CAS PubMed
; (c) D. Ostović and T. C. Bruice, J. Am. Chem. Soc., 1989, 111, 6511 CrossRef
; (d) J. T. Groves, Z. Gross and M. K. Stern, Inorg. Chem., 1994, 33, 5065 CrossRef CAS
; (e) N. Stephenson and A. T. Bell, Inorg. Chem., 2006, 45, 2758 CrossRef CAS PubMed
; (f) N. Hessenauer-Ilicheva, A. Franke, D. Meyer, W.-D. Woggon and R. van Eldik, J. Am. Chem. Soc., 2007, 129, 12473 CrossRef CAS PubMed
; (g) R. Mas-Balleste and L. Que Jr, J. Am. Chem. Soc., 2007, 129, 15964 CrossRef CAS PubMed
; (h) P. Comba and G. Rajaraman, Inorg. Chem., 2008, 47, 78 CrossRef CAS PubMed
; (i) P. C. A. Bruijnincx, I. L. C. Buurmans, S. Gosiewska, M. A. H. Moelands, M. Lutz, A. L. Spek, G. van Koten and R. J. M. Klein Gebbink, Chem.–Eur. J., 2008, 14, 1228 CrossRef CAS PubMed
; (j) J. F. Hull, E. L. O. Sauer, C. D. Incarvito, J. W. Faller, G. W. Brudvig and R. H. Crabtree, Inorg. Chem., 2009, 48, 488 CrossRef CAS PubMed
; (k) A. McGown, W. D. Kerber, H. Fujii and D. P. Goldberg, J. Am. Chem. Soc., 2009, 131, 8040 CrossRef CAS PubMed
; (l) A. Company, Y. Feng, M. Güell, X. Ribas, J. M. Luis, L. Que Jr and M. Costas, Chem.–Eur. J., 2009, 15, 3359 CrossRef CAS PubMed
; (m) A. Franke, M. Wolak and R. van Eldik, Chem.–Eur. J., 2009, 15, 10182 CrossRef CAS PubMed
; (n) N. Hessenauer-Ilicheva, A. Franke, M. Wolak, T. Higuchi and R. van Eldik, Chem.–Eur. J., 2009, 15, 12447 CrossRef CAS PubMed
.
-
(a) Z. Gross and S. Nimri, Inorg. Chem., 1994, 33, 1731 CrossRef CAS
; (b) Z. Gross, J. Biol. Inorg. Chem., 1996, 1, 368 CrossRef CAS
; (c) K. Czarnecki, S. Nimri, Z. Gross, L. M. Proniewicz and J. R. Kincaid, J. Am. Chem. Soc., 1996, 118, 2929 CrossRef CAS
.
-
(a) A. G. Marshall, C. L. Hendrickson and G. S. Jackson, Mass Spectrom. Rev., 1998, 17, 1 CrossRef CAS
; (b) J. Roithová and D. Schröder, Chem. Rev., 2010, 110, 1170 CrossRef PubMed
; (c) N. M. M. Nibbering, Mass Spectrom. Rev., 2006, 25, 962 CrossRef CAS PubMed
.
-
(a) M. E. Crestoni and S. Fornarini, Inorg. Chem., 2005, 44, 5379 CrossRef CAS PubMed
; (b) M. E. Crestoni and S. Fornarini, Inorg. Chem., 2007, 46, 9018 CrossRef CAS PubMed
; (c) M. E. Crestoni, S. Fornarini, F. Lanucara, J. J. Warren and J. M. Mayer, J. Am. Chem. Soc., 2010, 132, 4336 CrossRef CAS PubMed
; (d) M. E. Crestoni, S. Fornarini and F. Lanucara, Chem.–Eur. J., 2009, 15, 7863 CrossRef CAS PubMed
; (e) F. Lanucara and M. E. Crestoni, Chem.–Eur. J., 2011, 17, 12092 CrossRef CAS PubMed
.
-
H. Saltzman and J. G. Sharefkin, Organic Syntheses, Wiley, New York, 1973, vol. 5, p. 658, Collect Search PubMed
.
-
(a)
M. Meot-Ner, in Gas Phase Ion Chemistry, ed. M. T. Bowers, Academic Press, New York, 1979, vol. 1 Search PubMed
; (b) J. E. Bartmess and R. M. Georgiadis, Vacuum, 1983, 33, 149 CrossRef CAS
.
- T. Su and W. J. Chesnavich, J. Chem. Phys., 1982, 76, 5183 CrossRef CAS PubMed
.
- B. Chiavarino, R. Cipollini, M. E. Crestoni, S. Fornarini, F. Lanucara and A. Lapi, J. Am. Chem. Soc., 2008, 130, 3208 CrossRef CAS PubMed
.
-
(a)
Schrodinger, Jaguar, version 7.9, LLC, New York, NY, 2011 Search PubMed
; (b) M. J. Frisch, Gaussian 09, revision D.01, Gaussian, Inc., Wallingford, CT, 2004 Search PubMed
.
-
(a) R. Latifi, M. A. Sainna, E. V. Rybak-Akimova and S. P. de Visser, Chem.–Eur. J., 2013, 19, 4058 CrossRef CAS PubMed
; (b) M. G. Quesne, R. Latifi, L. E. Gonzalez-Ovalle, D. Kumar and S. P. de Visser, Chem.–Eur. J., 2014, 20, 435 CrossRef CAS PubMed
.
-
(a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS PubMed
; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS
.
-
(a) A. K. Vardhaman, C. V. Sastri, D. Kumar and S. P. de Visser, Chem. Commun., 2011, 47, 11044 RSC
; (b) A. K. Vardhaman, P. Barman, S. Kumar, C. V. Sastri, D. Kumar and S. P. de Visser, Angew. Chem., Int. Ed., 2013, 52, 12288 CrossRef CAS PubMed
; (c) S. Kumar, A. S. Faponle, P. Barman, A. K. Vardhaman, C. V. Sastri, D. Kumar and S. P. de Visser, J. Am. Chem. Soc., 2014, 136, 17102 CrossRef CAS PubMed
.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270 CrossRef CAS PubMed
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- S. P. de Visser, J. Am. Chem. Soc., 2010, 132, 1087 CrossRef CAS PubMed
.
- S. G. Lias, J. E. Bartmess, J. F. Liebman, J. L. Holmes, R. D. Levin and W. G. Mallard, in Ion Energetics Data in NIST Chemistry WebBook, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg, MD, 20899, http://webbook.nist.gov, NIST Standard Reference Database Number 69, retrieved in September 2014 Search PubMed.
- F. Angelelli, B. Chiavarino, M. E. Crestoni and S. Fornarini, J. Am. Soc. Mass Spectrom., 2005, 16, 589 CrossRef CAS PubMed
.
- S. P. de Visser, Inorg. Chem., 2006, 45, 9551 CrossRef CAS PubMed
.
-
(a) R. E. White, J. T. Groves and G. A. McClusky, Acta Biol. Med. Ger., 1979, 38, 475 CAS
; (b) R. T. Ruettinger and A. J. Fulco, J. Biol. Chem., 1981, 256, 5728 CAS
; (c) J. T. Groves and D. V. Subramanian, J. Am. Chem. Soc., 1984, 106, 2177 CrossRef CAS
; (d) J. T. Groves, G. E. Avaria-Neisser, K. M. Fish, M. Imachi and R. L. Kuczkowski, J. Am. Chem. Soc., 1986, 108, 3837 CrossRef CAS
; (e) J. F. Bartoli, O. Brigaud, P. Battioni and D. Mansuy, J. Chem. Soc., Chem. Commun., 1991, 440 RSC
; (f) T. Ohno, N. Suzuki, T. Dokoh, Y. Urano, K. Kikuchi, M. Hirobe, T. Higuchi and T. Nagano, J. Inorg. Biochem., 2000, 82, 123 CrossRef CAS
; (g) S. Yoshioka, S. Takahashi, K. Ishimori and I. Morishima, J. Inorg. Biochem., 2000, 81, 141 CrossRef CAS
.
- S. P. de Visser, F. Ogliaro, P. K. Sharma and S. Shaik, J. Am. Chem. Soc., 2002, 124, 11809 CrossRef CAS PubMed
.
-
(a) M. T. Green, J. Am. Chem. Soc., 1999, 121, 7939 CrossRef CAS
; (b) F. Ogliaro, S. P. de Visser, S. Cohen, J. Kaneti and S. Shaik, ChemBioChem, 2001, 11, 848 CrossRef
.
- J. H. Dawson, R. H. Holm, J. R. Trudell, G. Barth, R. E. Linder, E. Bunnenberg, C. Djerassi and S. C. Tang, J. Am. Chem. Soc., 1976, 98, 3707 CrossRef CAS
.
-
(a) S. P. de Visser, S. Shaik, P. K. Sharma, D. Kumar and W. Thiel, J. Am. Chem. Soc., 2003, 125, 15779 CrossRef CAS PubMed
; (b) T. Kamachi and K. Yoshizawa, J. Am. Chem. Soc., 2003, 125, 4652 CrossRef CAS PubMed
; (c) C. M. Bathelt, J. Zurek, A. J. Mulholland and J. N. Harvey, J. Am. Chem. Soc., 2005, 127, 12900 CrossRef CAS PubMed
; (d) S. P. de Visser, J. Phys. Chem. A, 2005, 109, 11050 CrossRef CAS PubMed
; (e) S. P. de Visser, L. Tahsini and W. Nam, Chem.–Eur. J., 2009, 15, 5577 CrossRef CAS PubMed
; (f) R. Lonsdale, J. Oláh, A. J. Mulholland and J. N. Harvey, J. Am. Chem. Soc., 2011, 133, 15464 CrossRef CAS PubMed
; (g) H. Isobe, S. Yamanaka, M. Okumura, K. Yamaguchi and J. Shimada, J. Phys. Chem. B, 2011, 115, 10730 CrossRef CAS PubMed
.
- A. Ghosh, Acc. Chem. Res., 1998, 31, 189 CrossRef CAS
.
-
(a) H. M. Neu, M. G. Quesne, T. Yang, K. A. Prokop-Prigge, K. M. Lancaster, J. Donohoe, S. DeBeer, S. P. de Visser and D. P. Goldberg, Chem.–Eur. J., 2014, 20, 14584 CrossRef CAS PubMed
; (b) F. Lanucara, B. Chiavarino, M. E. Crestoni, D. Scuderi, R. K. Sinha, P. Maitre and S. Fornarini, Inorg. Chem., 2011, 50, 4445 CrossRef CAS PubMed
.
- M. Radoń, E. Broclawic and K. Pierloot, J. Chem. Theory Comput., 2011, 7, 898 CrossRef
.
-
(a) D. Kumar, L. Tahsini, S. P. de Visser, H. Y. Kang, S. J. Kim and W. Nam, J. Phys. Chem. A, 2009, 113, 11713 CrossRef CAS PubMed
; (b) D. Kumar, R. Latifi, S. Kumar, E. V. Rybak-Akimova, M. A. Sainna and S. P. de Visser, Inorg. Chem., 2013, 52, 7968 CrossRef CAS PubMed
.
-
(a) S. P. de Visser, F. Ogliaro, N. Harris and S. Shaik, J. Am. Chem. Soc., 2001, 123, 3037 CrossRef CAS PubMed
; (b) S. P. de Visser, F. Ogliaro and S. Shaik, Angew. Chem., Int. Ed., 2001, 40, 2871 CrossRef CAS
; (c) S. P. de Visser, F. Ogliaro, P. K. Sharma and S. Shaik, Angew. Chem., Int. Ed., 2002, 41, 1947 CrossRef CAS
; (d) D. Kumar, B. Karamzadeh, G. N. Sastry and S. P. de Visser, J. Am. Chem. Soc., 2010, 132, 7656 CrossRef CAS PubMed
; (e) D. Kumar, S. P. de Visser and S. Shaik, Chem.–Eur. J., 2005, 11, 2825 CrossRef CAS PubMed
.
- See, e.g.,
(a) A. Ghosh and P. R. Taylor, Curr. Opin. Chem. Biol., 2003, 7, 113 CrossRef CAS
; (b) M. Swart, A. R. Groenhof, A. W. Ehlers and K. Lammertsma, J. Phys. Chem. A, 2004, 108, 5479 CrossRef CAS
; (c) S. P. de Visser, M. G. Quesne, B. Martin, P. Comba and U. Ryde, Chem. Commun., 2014, 50, 262 RSC
.
- M. L. Chabinyc, S. L. Craig, C. K. Regan and J. I. Brauman, Science, 1998, 279, 1882 CrossRef CAS
.
-
(a) Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157 CrossRef CAS PubMed
; (b) T. Schwabe and S. Grimme, Acc. Chem. Res., 2008, 41, 569 CrossRef CAS PubMed
; (c) T. Weymuth, E. P. A. Couzijn, P. Chen and M. Reiher, J. Chem. Theory Comput., 2014, 10, 3092 CrossRef CAS
.
- Y. Watanabe, T. Iyanagi and S. Oae, Tetrahedron Lett., 1980, 21, 3685 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the computational results, including Tables with group spin densities, charges, absolute and relative energies as well as structures and Cartesian coordinates is provided. See DOI: 10.1039/c4sc02717e |
| This journal is © The Royal Society of Chemistry 2015 |

![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2) by [FeIV(O)(TPFPP+˙)]+. Valence electrons are identified with a dot and lines (curved and straight) in the VB structures represent bonds.
CH2) by [FeIV(O)(TPFPP+˙)]+. Valence electrons are identified with a dot and lines (curved and straight) in the VB structures represent bonds.