Open Access Article
Open Access ArticleMolecular mapping of poly(methyl methacrylate) super-helix stereocomplexes†
Andrew Joseph
Christofferson‡
a,
George
Yiapanis§‡
a,
Jing Ming
Ren
b,
Greg Guanghua
Qiao
b,
Kotaro
Satoh
c,
Masami
Kamigaito
c and
Irene
Yarovsky
*a
aSchool of Aerospace, Mechanical and Manufacturing Engineering, RMIT University, GPO Box 2476, VIC 3001, Australia. E-mail: irene.yarovsky@rmit.edu.au
bDepartment of Chemical and Biomolecular Engineering, University of Melbourne, Melbourne, VIC 3010, Australia
cDepartment of Applied Chemistry, Nagoya University, Chikusa-ku, Nagoya 464-8603, Japan
First published on 1st December 2014
Abstract
In this study, by using X-ray powder diffraction profiles as blueprints, we successfully mapped the most probable molecular-level structural arrangement of the PMMA super-helix stereocomplexes through molecular dynamic simulations. Molecular-level resolution of the PMMA triple-helix supramolecule was not previously achievable by experimental methods. After constructing molecular models of stereo-regular complexes composed of linear it- and st-PMMAs, our all-atom molecular dynamics simulations identified the stereocomplex structure that best reproduces experimental diffraction profiles and thermodynamic properties as a double helix of isotactic (it-)PMMA with a helical pitch of 1.8 nm and 9 units per turn surrounded by a single helix of syndiotactic (st-)PMMA with an average helical pitch of 0.9 nm and 20 units per turn. The it-/st- complexing stoichiometry in the PMMA triple-helix is therefore 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20. This presents the first all-atom model of the it-/st-PMMA triple-helix stereocomplex that accurately fits experimental X-ray diffraction profiles. In addition, the simulation results revealed the outer st-PMMA helix of the PMMA stereocomplex has a fiber diameter of at least 1.85 nm and adopts a non-ideal helical geometry. Furthermore, through dynamic simulations, surprising new sights into the effect of the structural configuration of the PMMA stereocomplex (i.e., helical pitch and direction, and tilt angle) on the physical properties of their crystal structures were obtained. Those crystal properties include X-ray diffraction profile, packing density, chain–chain spacing, chain width and cohesive energy density.
20. This presents the first all-atom model of the it-/st-PMMA triple-helix stereocomplex that accurately fits experimental X-ray diffraction profiles. In addition, the simulation results revealed the outer st-PMMA helix of the PMMA stereocomplex has a fiber diameter of at least 1.85 nm and adopts a non-ideal helical geometry. Furthermore, through dynamic simulations, surprising new sights into the effect of the structural configuration of the PMMA stereocomplex (i.e., helical pitch and direction, and tilt angle) on the physical properties of their crystal structures were obtained. Those crystal properties include X-ray diffraction profile, packing density, chain–chain spacing, chain width and cohesive energy density.
Introduction
Naturally occurring helical supramolecular assemblies, such as RNA, DNA and some protein sequences, regulate essential biological activities in living organisms. For example, the double helical structure of DNA is a determining factor in the storage, transmission and translation of genetic information, while the helical structure of collagen provides great tensile strength for tissue support.1 Emerging technologies in polymer synthesis and developments in biomimicry have led to an increasing interest in synthetic polymers which are able to form helical structures. The ultimate goal of the research and development of artificial helical systems is to create advanced nanomaterials that mimic or replicate exquisite functions of their natural analogues.2,3One of the most intriguing synthetic super-helix is perhaps the poly(methyl methacrylate) (PMMA) stereocomplex, as multiple-strand synthetic helices are very rare. The unique supramolecular architecture provides the PMMA stereocomplex with useful properties for a number of potential applications in life science and nanotechnology. For instance, PMMA stereocomplex formation has been exploited as an assembly mode for the fabrication of ultrathin films,4,5 nanoparticles,6,7 network and gel formations,8 as well as fibers9 and dialysis membranes.10 Moreover, other interesting and remarkable characteristics of PMMA stereocomplexes that have been explored, include stereospecific polymerization-templating,5 molecular recognition capability11,12 and helix-sense stereo-complexation.6
The structures of PMMA stereocomplexes have been studied since the 1950s, but to date, the exact structural arrangements of PMMA stereocomplexes at the molecular level still remain elusive.
In complexing solvents such as acetonitrile or acetone, isotactic PMMA (it-PMMA) can self-aggregate to form a double-stranded helix with definitive crystalline characteristics.13,14 Its aggregation depends strongly on the degree of stereoregularity, the nature of the solvent and on temperature.15 Many attempts were made to elucidate the crystal structure using X-ray diffraction analysis, but due to the amorphous nature of the supramolecular assembly, conflicting results were obtained. For many years, the consensus based on X-ray results16–18 and early molecular models was that the it-PMMA structure consisted of two 101 helices (10 repeating MMA units per turn) of it-PMMA chains intertwined to form a double helix in the crystal with a helical pitch of 2.1 nm.
In addition to the double helix, it-PMMA can be combined with syndiotactic PMMA (st-PMMA) to form a stereocomplex.13,19,20 With an it![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) st complexing ratio (monomer ratio in the stereoregular region of the polymer) of 1
st complexing ratio (monomer ratio in the stereoregular region of the polymer) of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2,21 Schomaker and Challa proposed a model based on X-ray fiber diffraction of a 91 double-stranded helix of it-PMMA and st-PMMA in a 1
2,21 Schomaker and Challa proposed a model based on X-ray fiber diffraction of a 91 double-stranded helix of it-PMMA and st-PMMA in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 monomer ratio.22 While X-ray fiber diffraction gave a fiber identity period of 1.84 nm,22,23 consistent with a 91 helix, due to the poor quality of the diffraction patterns resulting from an inherently disordered structure a quantitative analysis was not possible and the proposed model was recommended as a starting point for further investigations. Interestingly, the authors found that stereocomplexes of atactic and isotactic PMMA gave fiber X-ray diffraction patterns with the main characteristics of the it-/st-PMMA stereocomplex diffraction pattern still present, suggesting that the degree of tacticity of the st-PMMA is not critical to stereocomplexation.22
2 monomer ratio.22 While X-ray fiber diffraction gave a fiber identity period of 1.84 nm,22,23 consistent with a 91 helix, due to the poor quality of the diffraction patterns resulting from an inherently disordered structure a quantitative analysis was not possible and the proposed model was recommended as a starting point for further investigations. Interestingly, the authors found that stereocomplexes of atactic and isotactic PMMA gave fiber X-ray diffraction patterns with the main characteristics of the it-/st-PMMA stereocomplex diffraction pattern still present, suggesting that the degree of tacticity of the st-PMMA is not critical to stereocomplexation.22
More recently, the introduction of the Langmuir–Blodgett technique coupled with atomic force microscopy (AFM) analysis has enabled the direct observation of the it-/st-PMMA stereocomplex.24,25 Based on their observations, Yashima and colleagues proposed a model of a 91 it-PMMA double-stranded helix with a helical pitch of 1.84 nm surrounded by a single helix of 181 st-PMMA with a helical pitch of 0.92 nm. These early works demonstrated that the exact arrangement of the supramolecular complex proved difficult to resolve based upon experimental methods.
In this work, we discovered that by using the X-ray diffraction profiles of the PMMA stereocomplex crystals as blueprints, the most probable molecular-level arrangements of the PMMA super-helix stereocomplexes can be successfully mapped through molecular dynamic (MD) simulations. Due to stereo-association being dominated by non-covalent interactions, MD simulation provides a unique method for resolving structural features of it-/st-PMMA crystals and this becomes the only way to obtain an all-atom structural model compatible with X-ray diffraction results. More specifically, we constructed models of it-PMMA and st-PMMA crystals comprising double-stranded helices of it-PMMA and single-stranded st-PMMA with varying helical pitch and direction in excellent agreement with experimentally obtained diffraction data. Our results show that an average of 20 PMMA repeating units are required to form one helix turn for the st-PMMA in the triple-helix stereocomplex structure and this is distinguished from any previously reported results. Through MD simulation, other than mapping the structural features of the PMMA stereocomplexes, we obtained new insights into the effect of helical pitch and helix direction on the molecular structure and stability of it- and st-PMMA crystals by analyzing the following properties: X-ray diffraction profiles, density, chain–chain spacing, chain width, and cohesive energy density.
Methods
Synthesis of it-PMMA, st-PMMA, and it-/st-PMMA stereocomplexes
The it-PMMA was synthesized by anionic polymerization according to previously published procedures,26 and full details of the synthesis and characterization may be found elsewhere.27 The general procedure employed for the synthesis of it-PMMA was as follows: the initiator solution (Grignard reagent, t-C4H9MgBr, [t-C4H9MgBr] = 286 mM in diethyl ether, 0.39 mL) was added to anhydrous toluene (5.4 mL) in a Schlenk tube at −78 °C under Ar. Methyl methacrylate (MMA) was then added slowly (1.2 mL in 5 min) causing the mixture to turn orange. The polymerization solution was kept at −78 °C for 126 h, and then anhydrous methanol (1 mL) was added to the Schlenk flask to quench the reaction. The reaction solution was diluted with toluene (20 mL), washed with 1 M HCl (20 mL × 3) and distilled water (20 mL × 3), dried over anhydrous magnesium sulphate (MgSO4), filtered and precipitated into hexane to afford the it-PMMA (it-L10k) as a white powder, 0.95 g (85%); GPC: Mn = 10.3 kDa, Mw/Mn = 1.12; 1H NMR: mm/mr/rr (%) = 93/3/4; DSC: Tg = 53.6 °C and Tm = 137.5 °C.The procedure for synthesis of st-PMMA was adopted from previously published literature with modifications,28–30 and the full details may be found elsewhere.27 In brief, copper(I) bromide (CuBr, 36.0 mg, 0.25 mmol) and copper(II) bromide (CuBr2, 5.6 mg, 0.025 mmol) were added to a dry round-bottom flask equipped with a 3-way stopcock in a glovebox, followed by addition (under dry N2) of 1,1,1,3,3,3-hexafluoro-2-phenyl-2-propanol (PhC(CF3)2OH, 8.4 mL), MMA (2.7 mL, 25.2 mmol), 2,2′-bipyridyl (bpy, 495 mM in toluene, 1.0 mL) and prop-2-ynyl 2-bromo-2-methylpropanoate (PgBr, 503 mM in toluene, 0.50 mL). The reaction was conducted at 0 °C with samples taken periodically under N2. The polymerization was terminated after 11 h by cooling the reaction to −78 °C. A sample was extracted for 1H NMR spectroscopic analysis, and the remaining product was diluted with ethyl acetate (EtOAc, 200 mL), washed with 1 M HCl (100 mL × 2), then distilled water (150 mL × 2). The extracted product was collected, concentrated and then precipitated in hexane, followed by drying in vacuo to afford the st-PMMA (st-L4k) as a white solid, 0.88 g (87.8%); 1H NMR: MMA conversion = 33% (theoretical Mn = 3.5 kDa); GPC: Mn = 4.2 kDa, Mw/Mn = 1.34; 13C NMR: mm/mr/rr (%) = 2/26/72; DSC: Tg = 98.6 °C and Tm = 99.5 °C.
The general procedure employed for the synthesis of the PMMA stereocomplex was as follows:31 the st-PMMA (10 mg) and it-PMMA (10 mg) precursors were separately dissolved in an acetonitrile/water mixture (MeCN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O = 9
H2O = 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) at concentrations of 2 mg mL−1 and combined to an it
1) at concentrations of 2 mg mL−1 and combined to an it![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) st molar ratio of 1
st molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. The solutions were left to stand at room temperature for 24 h. After removing the solvent in vacuo, the st-L4k/it-L10k stereocomplexes were dried under reduced vacuum (0.05 mmHg) for 24 h before DSC and XRD analysis; Tm = 126.4 °C.32
2. The solutions were left to stand at room temperature for 24 h. After removing the solvent in vacuo, the st-L4k/it-L10k stereocomplexes were dried under reduced vacuum (0.05 mmHg) for 24 h before DSC and XRD analysis; Tm = 126.4 °C.32
Experimental X-ray scattering
The X-ray measurements were performed on a Rigaku R-AXIS IV detector system equipped with a Rigaku FR-E rotating-anode generator and confocal mirror monochromated CuKα radiation (0.15418 nm) focused through a 0.5 mm pinhole collimator, which was supplied at 45 kV voltage and 45 mA current, equipped with a flat imaging plate having a specimen-to-plate distance of 200.0 mm. The dried powders were placed in a borosilicate glass capillary tube, and their X-ray diffractograms were taken at ambient temperatures (20–25 °C) from the edge-view position.Construction of PMMA molecular models
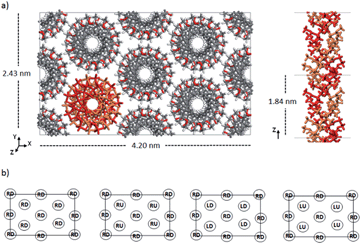
Double-stranded helices of 101 and 91 it-PMMA (10 units per turn and 9 units per turn, respectively) were constructed based on reported bond lengths, bond angles and internal rotation angles.16,24 Crystal models were assembled by arranging eight identical double-stranded helices in a hexagonal packing mode within a periodically replicated orthorhombic unit cell (Fig. 1a). The fiber axes of the chains were oriented in the z-direction and to eliminate the terminal melting propensity of finite polymeric chains, each it-PMMA fragment was connected to its periodic image in the z-direction, mimicking an infinite PMMA crystal (Fig. 1a). Each cell displayed initial dimensions of 4.20 and 2.43 nm in the x- and y-directions respectively, and varied in length along the z-direction depending on the helical pitch of the chains; 2.10 and 1.84 nm for the 101 and 91 it-PMMA crystals respectively. We examined structural perturbations associated with the handedness (right or left) and orientation (down/down or up/down) of the helices by considering four packing motifs (Fig. 1b).Single-stranded helices of 181 st-PMMA with a helical pitch of 0.92 nm were constructed based on reported bond lengths, bond angles and internal rotation angles from the proposed Yashima model for the triple helix stereocomplex.24 Similar to the it-PMMA, the fiber axes of the chains were oriented in the z-direction and each st-PMMA fragment was connected to its periodic image in the z-direction, mimicking an infinite PMMA crystal (Fig. 2). For this model (91-it-/181-st-PMMA) only the Right Down packing motif was employed. In order to more closely reproduce the experimental stereocomplex synthesized in this work, additional st-PMMA fragments of 40 PMMA units were constructed, labeled 40mer-st, corresponding to the l-st-PMMA (st-L4k) fragments. Each cell contained two it-PMMA double helices surrounded by a single st-PMMA helix of the same sense and direction in a hexagonal packing arrangement with initial cell dimensions of 3.98 and 2.36 nm in the x- and y-directions. The length along the z-direction depended on the helical pitch of the it-PMMA double helix; 2.10 and 1.84 nm for the 101-it/40mer-st and 91-it/40mer-st models respectively. For the 101-it/40mer-st model only the Rright Ddown packing motif was employed, while for the 91-it/40mer-st model all four packing motifs (Fig. 1b) were employed.
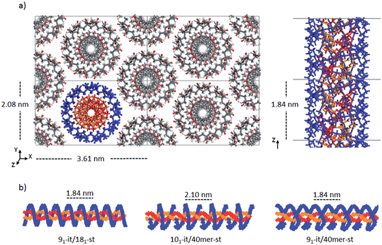 | ||
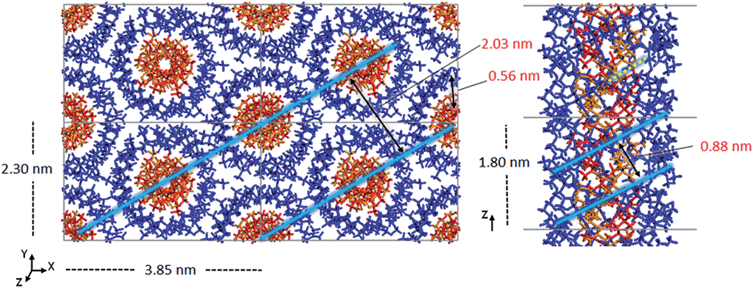
| Fig. 2 a) Initial model crystal structure of the 91-it-/181-st-PMMA stereocomplex, (b) schematic representations of the three triple helix stereocomplex systems. | ||
Computational method
Simulations were carried out using the LAMMPS33 software distributed by Sandia National Laboratories. Analysis was performed using the Materials Studio 6.1 (ref. 34) software. The potential energy was calculated using the PCFF force field35,36 which has been shown to reproduce structural and thermodynamic properties of condensed phase polymeric systems well.37–40 Short-range non-bonded interactions were calculated using the atom-based summation method, with a cutoff radius of 15.5 Å. A long-range tail correction was applied for van der Waals interactions larger than the cut-off radius. The PPPM (particle–particle–particle–mesh) method41 was applied for long-range Coulomb interactions.For all models, we initially performed energy minimization with unit cell dimensions fixed and a force convergence criterion of 0.01 kcal mol−1 Å−1. Subsequently, we undertook molecular dynamics (MD) simulations in the NPT ensemble (constant number of particles, pressure and temperature) for a total of 40 ns. For the it-/st-PMMA stereocomplex simulations, atom coordinates of the it-PMMA were fixed for the first 20 ns, followed by 20 ns of simulation with all coordinates varying. The temperature and pressure were maintained at 298 K and 1 atm respectively using the Nose-Hoover thermostat and barostat.42,43 A time step of 1 fs was implemented, with atomic coordinates and thermodynamic quantities recorded every 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps. The models were considered equilibrated when the energy and density attained a steady value (standard deviation within 1%). The geometry of the equilibrated models was optimized by energy minimization with a force convergence criterion of 0.001 kcal mol−1 Å−1 and the optimized structures were used for analysis of density, structural parameters, cohesive energy density and calculated X-ray diffraction profiles.
000 steps. The models were considered equilibrated when the energy and density attained a steady value (standard deviation within 1%). The geometry of the equilibrated models was optimized by energy minimization with a force convergence criterion of 0.001 kcal mol−1 Å−1 and the optimized structures were used for analysis of density, structural parameters, cohesive energy density and calculated X-ray diffraction profiles.
Results and discussion
The it-PMMA double helix structure
Fig. 3 presents the X-ray scattering plots of it-PMMA crystals obtained from the simulations and the XRD experiments. The simulated plots display similar features to those obtained from powder diffraction experiments, with the 91 it-PMMA model showing the most consistent agreement with experiment compared to the 101 it-PMMA model.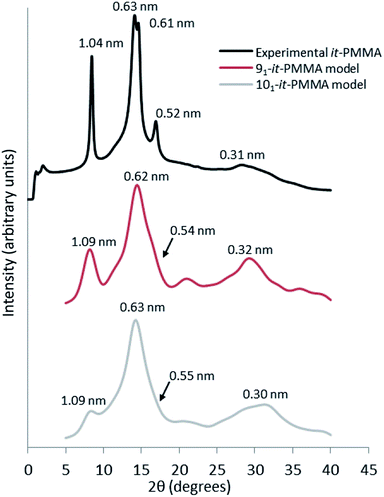 | ||
| Fig. 3 Wide angle X-ray scattering profiles obtained from powder diffraction experiments and molecular dynamics simulations for the it-PMMA double helix in the Right Down packing motif. | ||
The experimental peak at 1.04 nm, which arises from the chain–chain spacing in the x- and xy-directions (see Fig. 4), is reproduced by both the 91 and 101 models, but the former generates a greater peak intensity. The peak at 0.60–0.63 nm is likely associated with the chain–chain spacing in the y-direction and the pitch spacing along the fiber axis. The pitch spacing can be calculated from the helical pitch multiplied by the cosine of the tilt angle, where the tilt angle for an ideal helix is the helix diameter multiplied by π and divided by the helical pitch.44 For a calculated tilt angle of 54° and helical pitch of 1.81 nm for the 91 double helix, the pitch spacing equals 0.73 nm. For the 101 double helix model, the tilt angle is closer to 50° and the pitch spacing is 0.80 nm. Based on these values we can conclude that while the peak is associated with the pitch spacing, it does not directly correspond to it.
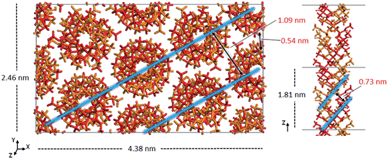 | ||
| Fig. 4 Model of the optimized crystal structure of 91 it-PMMA in the Right Down packing motif. The chain–chain spacing (left) and pitch spacing (right) are shown in light blue. | ||
The peak at 0.52 nm arises primarily due to reflections from the x-plane. Finally, the peak at 0.31 nm corresponds to the inter-monomer spacing along the axis of the helix. Fig. 3 shows that for the 91 it-PMMA model this particular peak is positioned just below 30°, in line with the experimental X-ray diffraction data, while for the 101 it-PMMA model the peak is positioned just above 30°.
We should note here that the peak intensities reflect contributions from various crystallographic planes, which makes it difficult to precisely determine the exact contribution to each peak. In general, however, we see an excellent agreement between the simulated and experimentally obtained diffraction patterns validating our models.
Table 1 summarizes the simulated model properties and compares them with the experimental values available. For both the 91 and 101 double helixes, densities ranged from 1.220 to 1.255 g cm−3, comparing well to an experimental density of 1.23 g cm−3.45 To compare the relative thermodynamic stability of the model structures we calculated the cohesive energy density which is equal to the internal energy divided by the molar volume of a system, and describes the amount of energy required to remove a unit volume of molecules from their neighbors to infinite separation.47
| Description | Packing motif | Density (g cm−3) | Helical pitch (nm) | Cohesive energy density (J cm−3) |
|---|---|---|---|---|
| a Experimental cohesive energy density of PMMA with unspecified tacticity.46 | ||||
| Experiment | — | 1.23 (ref. 45) | 1.84 (91)24 | 361a |
| 2.10 (101)16 | ||||
| 91 it-PMMA | RD | 1.235 ± 0.007 | 1.80 ± 0.01 | 385 ± 12 |
| RD/RU | 1.240 ± 0.014 | 1.79 ± 0.01 | 281 ± 12 | |
| RD/LD | 1.220 ± 0.001 | 1.81 ± 0.01 | 221 ± 1 | |
| RD/LU | 1.240 ± 0.028 | 1.80 ± 0.03 | 285 ± 4 | |
| 101 it-PMMA | RD | 1.225 ± 0.007 | 2.01 ± 0.09 | 302 ± 3 |
| RD/RU | 1.215 ± 0.007 | 1.95 ± 0.15 | 281 ± 1 | |
| RD/LD | 1.235 ± 0.021 | 2.05 ± 0.01 | 227 ± 36 | |
| RD/LU | 1.255 ± 0.007 | 2.06 ± 0.01 | 271 ± 22 | |
The 91 it-PMMA exhibits a larger cohesive energy density than the 101 it-PMMA in every case, with the Right Down 91 model at 385 ± 12 J cm−3 compared to 302 ± 3 J cm−3 for the 101. Interestingly, there was a range in cohesive energy density values for both the 91 and 101 models, with the Right Down packing motif providing the largest values for both models, although there appear to be no obvious trends between cohesive energy density and other properties, including structural parameters, density, and the experimental X-ray diffraction profiles for the different packing motifs.
In summary, based on the analyses of X-ray diffraction data, density, structural parameters and cohesive energy densities, the model that best agrees with the experimental data is a 91 it-PMMA double helix with a helical pitch of 1.80 ± 0.01 nm, a tilt angle of 54°, and a pitch spacing of 0.73 nm.
Structure of the it-/st-PMMA stereocomplex
For the simulated it-/st-PMMA stereocomplex models, we can assign the experimental X-ray diffraction peaks as follows. The peak at 2.08 nm (Fig. 5) is associated with the spacing between the triple helices in the x- and xy-planes. The peak at 0.78 nm is associated with the helical pitch of the st-PMMA, but does not directly correspond to it. The experimental peaks at 0.63 and 0.58 nm arise from multiple contributions, with the peak at 0.63 likely associated with the helical pitch of the it-PMMA, as well as spacings in the x- and y-planes. Similar to the it-PMMA models, the peak at 0.31 nm is associated with inter-monomer spacing. These three peaks were reproduced reasonably well by all models, and demonstrate that the it-PMMA double helix retains its structure when complexed with st-PMMA.It can be seen from Fig. 5 that the 91-it/181-st stereocomplex model (infinite st-PMMA with 18 units per turn complexed with infinite it-PMMA with 9 units per turn) failed to reproduce the experimental X-ray diffraction data. Most notably the experimentally observed peak of 2.08 nm is shifted to a shorter d-spacing of 1.86 nm. This suggests that the chain width of this model is too narrow, resulting in a crystal that is overly compact. This is further supported by a density of 1.240 ± 0.001 g cm−3 calculated for this structure compared to the experimental density of 1.215 g cm−3.45 In addition, this model fails to reproduce the helical pitch of the st-PMMA, with a value of 0.97 ± 0.016 nm for the model, compared to the experimentally measured value of 0.92 ± 0.02 nm.24 This is reflected by a shift in the associated peak d-spacing to 0.89 nm, compared to the experimental peak at 0.78 nm.
Previous ab initio calculations6 suggested that the helical pitch ratio for it-PMMA and st-PMMA is not exactly 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Based on this, we constructed models of infinite it-PMMA with 40-unit st-PMMA fragments (40mer-st) which is in line with the size of the st-PMMA fragments used in our X-ray diffraction experiments. These 40mer-st fragments exhibited an average helical pitch of 20 MMA units, with gaps of approximately 1–2 units between fragments in the z-direction.
1. Based on this, we constructed models of infinite it-PMMA with 40-unit st-PMMA fragments (40mer-st) which is in line with the size of the st-PMMA fragments used in our X-ray diffraction experiments. These 40mer-st fragments exhibited an average helical pitch of 20 MMA units, with gaps of approximately 1–2 units between fragments in the z-direction.
While the 101 it-PMMA complexed with 40-unit st-PMMA model (101-it-/40mer-st) maintains the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 it
2 it![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) st complexing ratio, the model fails to reproduce the experimental helical pitch and experimental X-ray diffraction peak at 0.78 nm. Similar to the infinite triple helix model (91-it/181-st), this peak is shifted to the left, associated with an increased pitch spacing. The density of this model was found to be 1.185 ± 0.007 g cm−3, well below the experimental value.
st complexing ratio, the model fails to reproduce the experimental helical pitch and experimental X-ray diffraction peak at 0.78 nm. Similar to the infinite triple helix model (91-it/181-st), this peak is shifted to the left, associated with an increased pitch spacing. The density of this model was found to be 1.185 ± 0.007 g cm−3, well below the experimental value.
Fig. 5 demonstrates that the 91 it-PMMA complex with 40-unit st-PMMA fragment model (91-it/40mer-st) exhibits the best agreement with experimental X-ray diffraction profiles. The density range of 1.200–1.215 g cm−3 for the four packing motifs is also in a good agreement with experiment, and the cohesive energy density range for this model is 387–399 J cm−3, compared to values of 362 ± 18 J cm−3 and 287 ± 9 J cm−3 for the 101-it/40mer-st and 91-it/181-st models, respectively (Table 2).
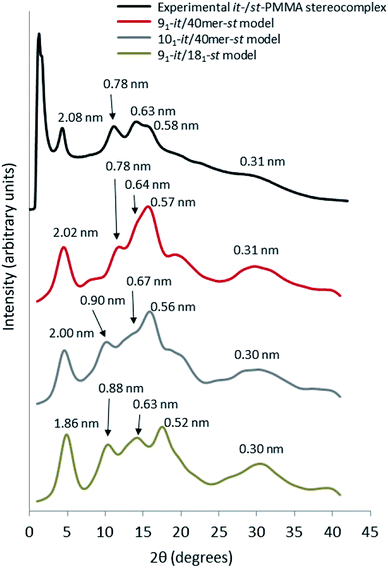 | ||
| Fig. 5 Wide angle X-ray scattering data obtained from powder diffraction experiments and molecular dynamic simulation for the it-/st-PMMA stereocomplex in the Right Down packing motif. | ||
| Description | Packing motif | Density (g cm−3) | Helical pitch st-PMMA (nm) | Cohesive energy density (J cm−3) | Chain width (nm) | Sum of differencesa (nm) |
|---|---|---|---|---|---|---|
| a Sum of differences refers to the sum of the numerical value differences between the peak positions of the simulated structures and the experimental X-ray diffraction. Thus, a smaller value indicates a better agreement with experiment. b Experimental cohesive energy density of PMMA with unspecified tacticity.46 | ||||||
| Experiment | — | 1.215 (ref. 45) | 0.92 ± 0.02 (ref. 24) | 361b | ||
| 91-it/181-st | RD | 1.240 ± 0.001 | 0.97 ± 0.016 | 287 ± 9 | 1.68 ± 0.018 | 0.39 |
| 101-it/40mer-st | RD | 1.185 ± 0.007 | 0.96 ± 0.007 | 362 ± 18 | 1.84 ± 0.007 | 0.27 |
| 91-it/40mer-st | RD | 1.215 ± 0.007 | 0.90 ± 0.004 | 398 ± 2 | 1.85 ± 0.001 | 0.08 |
| 91-it/40mer-st | RD/RU | 1.210 ± 0.001 | 0.89 ± 0.006 | 399 ± 1 | 1.85 ± 0.001 | 0.16 |
| 91-it/40mer-st | RD/LD | 1.200 ± 0.001 | 0.90 ± 0.004 | 387 ± 1 | 1.86 ± 0.011 | 0.17 |
| 91-it/40mer-st | RD/LU | 1.210 ± 0.001 | 0.90 ± 0.008 | 398 ± 2 | 1.84 ± 0.010 | 0.17 |
Unlike the it-PMMA structures, there was little difference in density, cohesive energy density, or X-ray diffraction for the different packing motifs of the stereocomplex (Table 2). The average st-PMMA helical pitch of this model is 0.90 ± 0.005 nm, in good agreement with the AFM measurements of 0.92 ± 0.02,24 with approximately 20 MMA units per turn. While this results in an it![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) st complexing ratio of 9
st complexing ratio of 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20, it is important to note that the established it
20, it is important to note that the established it![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) st stoichiometric ratio of 1
st stoichiometric ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 is merely the best mixing ratio for complexation, and different mixing ratios still result in the same final stereocomplex.21 Additionally, the it-PMMA helical pitch of ∼1.80 nm is in good agreement with the fiber X-ray diffraction experiments that show a fiber identity period of 1.84 nm.22,23 The optimized structure of the 91-it/40mer-st model is shown in Fig. 6.
2 is merely the best mixing ratio for complexation, and different mixing ratios still result in the same final stereocomplex.21 Additionally, the it-PMMA helical pitch of ∼1.80 nm is in good agreement with the fiber X-ray diffraction experiments that show a fiber identity period of 1.84 nm.22,23 The optimized structure of the 91-it/40mer-st model is shown in Fig. 6.
When Yashima and colleagues proposed the triple helix model, they also proposed a quadruple helix model that could correspond to their AFM results with two strands of st-PMMA wrapped around an it-PMMA double helix.24 We constructed models of the quadruple helix with 40-unit st-PMMA and both 91 and 101 it-PMMA (Fig. S1, ESI†), but the X-ray diffraction profiles and calculated densities of these models were in a lesser agreement with experiment (Fig. S2, Table S1, ESI†). While both the triple helix and quadruple helix models can in principle satisfy the AFM results as well as explain the observed weakness of the first-layer-line reflection (corresponding to a spacing of 1.84 nm) of the fiber X-ray diffraction,22,24 only the triple helix model fully reproduces the experimental density and powder X-ray diffraction profile.
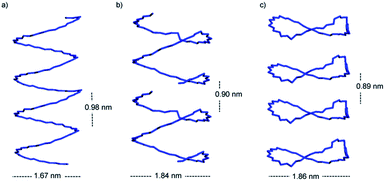
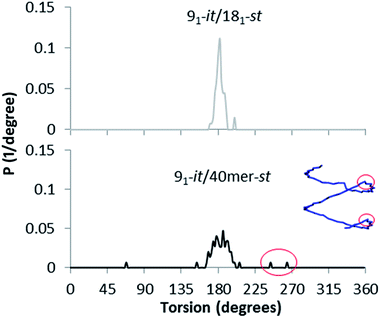
Interestingly, the st-PMMA helix of the 91-it/40mer-st model exhibits a distinct deviation from ideal helical geometry, not seen in either the 101-it/40mer-st or 91-it/181-st models (Fig. 7). This non-ideal helical geometry is characterized by a broader distribution in backbone internal angles and torsions, as well as a small number of torsions evenly distributed approximately every 20 monomer units (2 per turn) of the st-PMMA chain that deviate widely from the standard values of around 180° for an ideal helix comprising 18 units per turn (Fig. 8). Notably, this non-ideal geometry is required to reproduce the experimental X-ray diffraction peak at 0.78 nm, and is similar to the geometry found in the recently discovered and characterized stereocomplex of a cyclic form of 18-unit st-PMMA with linear double helix it-PMMA27 (Fig. 7c), which also exhibits an X-ray diffraction peak at 0.78 nm. The cyclic triple helix stereocomplex also has a similar fiber diameter to that of the 91-it/40mer-st model (the linker unit of the cyclic st-PMMA corresponds to roughly two MMA units) and a corresponding X-ray diffraction peak at 2.08 nm.
To further examine the PMMA stereocomplexation ratio, we constructed models of 36-unit st-PMMA fragments with infinite 91-it-PMMA double helices (91-it/36mer-st). While these systems maintained the 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 it- to st-PMMA monomer ratio of the Yashima model, the resulting structure had a density of 1.16 g cm−3; far below the predicted value. Interestingly, the overall structure resembled the non-ideal helical geometry of 91-it/40mer-st model, but with wide gaps between the st-PMMA fragments.
18 it- to st-PMMA monomer ratio of the Yashima model, the resulting structure had a density of 1.16 g cm−3; far below the predicted value. Interestingly, the overall structure resembled the non-ideal helical geometry of 91-it/40mer-st model, but with wide gaps between the st-PMMA fragments.
We noted that the gap between successive st-PMMA fragments in the 91-it/40mer-st model roughly corresponds to two MMA units. We thus constructed models of infinite st-PMMA with 21 units per turn. This 91-it/211-st model exhibited a similar structure and X-ray diffraction profile to the 91-it/40mer-st model, but had a cohesive energy density of 245 ± 21 J cm−3; far smaller than the predicted value. This further emphasizes that the helical pitch ratio cannot be exactly 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (i.e. the st-PMMA cannot complete exactly two full turns in the distance required for the it-PMMA to complete one full turn).
1 (i.e. the st-PMMA cannot complete exactly two full turns in the distance required for the it-PMMA to complete one full turn).
In order to gain a better understanding of the interactions driving the stability of the supramolecular assembly, we determined the st![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) it contact area and total free volume of the 91-it/40mer-st and 91-it/181-st models. Our results show that both models exhibit similar free volume (approximately 10% of the total volume) and st
it contact area and total free volume of the 91-it/40mer-st and 91-it/181-st models. Our results show that both models exhibit similar free volume (approximately 10% of the total volume) and st![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) it contact area (approximately 35–36% of the total st-PMMA surface area is in contact with it-PMMA for both models). This suggests that the observed differences in thermodynamic and structural properties are not due to differences in the packing of the stereocomplexes. A decomposition of the cohesive energy density for the two models reveals that in particular the electrostatic interactions between the st- and it-PMMA of the 91-it/181-st model are strongly unfavorable. Because the it- and st-PMMA have different helical pitches, a deviation from ideal helical geometry is necessary to maximize the non-bond interactions as seen in the 91-it/40mer-st model.
it contact area (approximately 35–36% of the total st-PMMA surface area is in contact with it-PMMA for both models). This suggests that the observed differences in thermodynamic and structural properties are not due to differences in the packing of the stereocomplexes. A decomposition of the cohesive energy density for the two models reveals that in particular the electrostatic interactions between the st- and it-PMMA of the 91-it/181-st model are strongly unfavorable. Because the it- and st-PMMA have different helical pitches, a deviation from ideal helical geometry is necessary to maximize the non-bond interactions as seen in the 91-it/40mer-st model.
Conclusions
By using the X-ray diffraction profiles as blueprints, through MD simulation we have successfully mapped the most likely configuration of it-PMMA stereocomplex, which is a 91 double helix with a helical pitch of 1.8 nm and a tilt angle of 54°. For the it-/st-PMMA triple-helix stereocomplex, the most likely configuration was determined to be a 91 it-PMMA double helix with a helical pitch of 1.85 nm surrounded by a single helix of st-PMMA with an average helical pitch of approximately 0.9 nm, and approximately 20 units per turn. Additionally, we found that the outer st-PMMA helix must have a fiber diameter of at least 1.8 nm and a non-ideal helical geometry to reach agreement with the experimental density and X-ray diffraction profile. A 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 it- to st-PMMA complexing ratio cannot simultaneously reproduce the structural features and the correct density. These results enabled us to suggest an all-atom model of the linear it-/st-PMMA triple helix stereocomplex that accurately reproduces experimental X-ray diffraction profiles for the first time.
2 it- to st-PMMA complexing ratio cannot simultaneously reproduce the structural features and the correct density. These results enabled us to suggest an all-atom model of the linear it-/st-PMMA triple helix stereocomplex that accurately reproduces experimental X-ray diffraction profiles for the first time.
The molecular dynamics simulations described in this study provide a vital tool to resolve molecular-level arrangement of complex molecular structures, when experimental means are inadequate. Furthermore, the reported molecular mapping technique is expected to have a wide scope of applications in macro(supra)molecular chemistry, including design and synthesis, structural characterization and property simulation.
Acknowledgements
We acknowledge the generous allocation of high performance computational resources from the Australian National Computational Infrastructure (NCI), the Western Australian computational facility (iVEC), the Victorian Partnership for Advanced Computing (VPAC) and the Victorian Life Sciences Computational Initiative (VLSCI). We thank Dr Qiao Sun for helpful comments on the manuscript. We also thank the reviewers for their comments and suggestions.Notes and references
- R. D. Harkness, Biol. Rev., 1961, 36, 399–455 CrossRef CAS PubMed.
- K. Matyjaszewski, Science, 2011, 333, 1104–1105 CrossRef CAS PubMed.
- F. S. Bates, M. A. Hillmyer, T. P. Lodge, C. M. Bates, K. T. Delaney and G. H. Fredrickson, Science, 2012, 336, 434–440 CrossRef CAS PubMed.
- T. Serizawa, K.-i. Hamada, T. Kitayama, N. Fujimoto, K. Hatada and M. Akashi, J. Am. Chem. Soc., 2000, 122, 1891–1899 CrossRef CAS.
- T. Serizawa, K.-i. Hamada and M. Akashi, Nature, 2004, 429, 52–55 CrossRef CAS PubMed.
- T. Kawauchi, A. Kitaura, J. Kumaki, H. Kusanagi and E. Yashima, J. Am. Chem. Soc., 2008, 130, 11889–11891 CrossRef CAS PubMed.
- T. Kawauchi, J. Kumaki, A. Kitaura, K. Okoshi, H. Kusanagi, K. Kobayashi, T. Sugai, H. Shinohara and E. Yashima, Angew. Chem., Int. Ed., 2008, 120, 525–529 CrossRef.
- T. Kawauchi, J. Kumaki and E. Yashima, J. Am. Chem. Soc., 2006, 128, 10560–10567 CrossRef CAS PubMed.
- M. Crne, J. O. Park and M. Srinivasarao, Macromolecules, 2009, 42, 4353–4355 CrossRef CAS.
- C. Ronco, Polymethylmethacrylate: a flexible membrane for a tailored dialysis/volume, Karger, Basel; New York, 1999 Search PubMed.
- T. Serizawa, T. Sawada and T. Kitayama, Angew. Chem., Int. Ed., 2007, 119, 737–740 CrossRef.
- T. Serizawa, T. Sawada, H. Matsuno, T. Matsubara and T. Sato, J. Am. Chem. Soc., 2005, 127, 13780–13781 CrossRef CAS PubMed.
- K. Könnecke and G. Rehage, Colloid Polym. Sci., 1981, 259, 1062–1069 Search PubMed.
- J. Spěváček and B. Schneider, Adv. Colloid Interface Sci., 1987, 27, 81–150 CrossRef.
- S. Bistac and J. Schultz, Macromol. Chem. Phys., 1997, 198, 531–535 CrossRef CAS.
- H. Kusanagi, Y. Chatani and H. Tadokoro, Polymer, 1994, 35, 2028–2039 CrossRef CAS.
- F. Bosscher, G. Tenbrinke, A. Eshuis and G. Challa, Macromolecules, 1982, 15, 1364–1368 CrossRef CAS.
- H. Kusanagi, H. Tadokoro and Y. Chatani, Macromolecules, 1976, 9, 531–532 CrossRef CAS.
- T. G. Fox, B. S. Garrett, W. E. Goode, S. Gratch, J. F. Kincaid, A. Spell and J. D. Stroupe, J. Am. Chem. Soc., 1958, 80, 1768–1769 CrossRef CAS.
- A. Y. Koshevnik, M. M. Kusakov, N. M. Lubman, L. I. Mekenitskaya, O. V. Orlova, A. A. Pasynskaya, E. A. Razumovskaya and L. M. Shul'pina, Polym. Sci. U.S.S.R., 1970, 12, 2384–2390 CrossRef.
- E. J. Vorenkamp, F. Bosscher and G. Challa, Polymer, 1979, 20, 59–64 CrossRef CAS.
- E. Schomaker and G. Challa, Macromolecules, 1989, 22, 3337–3341 CrossRef CAS.
- F. Bosscher, G. Ten Brinke and G. Challa, Macromolecules, 1982, 15, 1442–1444 CrossRef CAS.
- J. Kumaki, T. Kawauchi, K. Okoshi, H. Kusanagi and E. Yashima, Angew. Chem., Int. Ed., 2007, 46, 5348–5351 CrossRef CAS PubMed.
- J. Kumaki, T. Kawauchi, K. Ute, T. Kitayama and E. Yashima, J. Am. Chem. Soc., 2008, 130, 6373–6380 CrossRef CAS PubMed.
- K. Hatada, K. Ute, K. Tanaka, T. Kitayama and Y. Okamoto, Polym. J., 1985, 17, 977–980 CrossRef CAS.
- J. M. Ren, K. Satoh, T. K. Goh, A. Blencowe, K. Nagai, K. Ishitake, A. J. Christofferson, G. Yiapanis, I. Yarovsky, M. Kamigaito and G. G. Qiao, Angew. Chem., Int. Ed., 2014, 53, 459–464 CrossRef CAS.
- T. Shibata, K. Satoh, M. Kamigaito and Y. Okamoto, J. Polym. Sci., Part A: Polym. Chem., 2006, 44, 3609–3615 CrossRef CAS.
- Y. Miura, T. Satoh, A. Narumi, O. Nishizawa, Y. Okamoto and T. Kakuchi, J. Polym. Sci., Part A: Polym. Chem., 2006, 44, 1436–1446 CrossRef CAS.
- Y. Miura, T. Satoh, A. Narumi, O. Nishizawa, Y. Okamoto and T. Kakuchi, Macromolecules, 2005, 38, 1041–1043 CrossRef CAS.
- T. K. Goh, J. F. Tan, S. N. Guntari, K. Satoh, A. Blencowe, M. Kamigaito and G. G. Qiao, Angew. Chem., Int. Ed., 2009, 48, 8707–8711 CrossRef CAS PubMed.
- The melting temperature of PMMA stereocomplex is lower than expected due to the low tacticity and molecular weight of st-PMMA. Stereocomplexes made from low molecular weight polymers generally have low thermal stabilities. For a review on this matter, please refer to: J. Spěváček and B. Schneider, Adv. Colloid Interface Sci., 1987, 27, 81–150 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- Materials Studio 6.1, Accelrys Software Inc, San Diego, CA, USA, 2012 Search PubMed.
- PCFF is distributed along with Accelrys' software package Materials Studio. More information may be found on the Accelrys website http://www.accelrys.com.
- H. Sun, S. J. Mumby, J. R. Maple and A. T. Hagler, J. Am. Chem. Soc., 1994, 116, 2978–2987 CrossRef CAS.
- S. Chunsrivirot and B. L. Trout, Langmuir, 2011, 27, 6910–6919 CrossRef CAS PubMed.
- C. De Leener, E. Hennebicq, J.-C. Sancho-Garcia and D. Beljonne, J. Phys. Chem. B, 2009, 113, 1311–1322 CrossRef CAS PubMed.
- I. Díaz, E. Díez, J. Camacho, S. León and G. Ovejero, Fluid Phase Equilib., 2013, 337, 6–10 CrossRef PubMed.
- G. Yiapanis, A. J. Christofferson, M. Plazzer, M. Weir, E. L. Prime, G. G. Qiao, D. H. Solomon and I. Yarovsky, Langmuir, 2013, 29, 14451–14459 CrossRef CAS PubMed.
- R. W. Hockney and J. W. Eastwood, Computer Simulation Using Particles, Adam Hilger, New York, 1989 Search PubMed.
- S. Nose, J. Chem. Phys., 1984, 81, 511–519 CrossRef CAS PubMed.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef.
- J. Ramos and T. Lazaridis, Protein Sci., 2011, 20, 1845–1855 CrossRef CAS PubMed.
- K. E. Min and D. R. Paul, J. Polym. Sci., Part B: Polym. Phys., 1988, 26, 1021–1033 CrossRef CAS.
- H. J. Vandenburg, A. A. Clifford, K. D. Bartle, R. E. Carlson, J. Carroll and I. D. Newton, Analyst, 1999, 124, 1707–1710 RSC.
- B. B. Sauer and G. T. Dee, Macromolecules, 2002, 35, 7024–7030 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4sc02971b |
| ‡ A.C. and G.Y. contributed equally. |
| § Current address: IBM Research Australia, 5/204 Lygon St, Melbourne, Victoria 3001, Australia. |
| This journal is © The Royal Society of Chemistry 2015 |