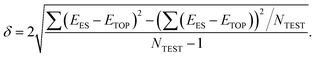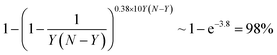Open Access Article
Open Access ArticleHow to determine accurate chemical ordering in several nanometer large bimetallic crystallites from electronic structure calculations†
Sergey M.
Kozlov
a,
Gábor
Kovács
a,
Riccardo
Ferrando
b and
Konstantin M.
Neyman
 *ac
*ac
aDepartament de Química Física and Institut de Química Teòrica i Computacional (IQTCUB), Universitat de Barcelona, c/Martí i Franquès 1, 08028 Barcelona, Spain
bDipartimento di Fisica and CNR-IMEM, via Dodecaneso 33, 16146 Genova, Italy
cInstitució Catalana de Recerca i Estudis Avançats (ICREA), 08010 Barcelona, Spain. E-mail: konstantin.neyman@icrea.cat
First published on 2nd April 2015
Abstract
Chemical and physical properties of binary metallic nanoparticles (nanoalloys) are to a great extent defined by their chemical ordering, i.e. the pattern in which atoms of the two elements are located in a given crystal lattice. The reliable determination of the lowest-energy chemical ordering is a challenge that impedes in-depth studies of several-nm large bimetallic particles. We propose a method to efficiently optimize the chemical ordering based solely on results of electronic structure (density functional) calculations. We show that the accuracy of this method is practically the same as the accuracy of the underlying quantum mechanical approach. This method, due to its simplicity, immediately reveals why one or another chemical ordering is preferred and unravels the nature of the binding within the nanoparticles. For instance, our results provide very intuitive understanding of why gold and silver segregate on low-coordinated sites in Pd70Au70 and Pd70Ag70 particles, while Pd70Cu70 exhibits matryoshka-like structure and Pd70Zn70 features Zn and Pd atoms arranged in layers. To illustrate the power of the new method we optimized the chemical ordering in much larger Pd732Au731, Pd732Ag731, Pd732Cu731, and Pd732Zn731 nanocrystals, whose size ∼4.4 nm is common for catalytic applications.
Introduction
Nanoparticles (NPs) composed of atoms of more than one metal are often referred to as nanoalloys. They represent a lively research subject, thanks to their usage in catalysis, magnetism, optics, nanomedicine, etc.1 Properties of nanoalloys strongly depend not only on their geometric structure and size, but also on the composition. The latter makes nanoalloys much more tunable for tailored applications compared to monometallic particles.Size and composition are to a significant extent determined by preparation conditions. At the same time the geometric structure of bimetallic NPs is affected by the relative thermodynamic stability of conceivable atomic arrangements of the two components with more stable structures being easier to obtain. Computational search for the geometric structure and shape that yield the lowest energy for a given NP size and composition is a part of the so-called global optimization problem.2,3 Although numerous techniques have been developed to treat this extremely difficult problem, even nowadays global optimization of only relatively small clusters is feasible.
Another part of the global optimization problem is the search for the lowest-energy chemical ordering, that is, the location of atoms of different elements within a given geometric structure. Chemical ordering governs such NP properties as surface composition and electronic structure, which are crucial for surface reactivity and heterogeneous catalysis.4 A rich variety of chemical ordering patterns can be found in nanoalloys: from ordered phases and solid solutions through core–shell and multishell arrangements to phase-separated quasi-Janus particles. As a rule, strong heteroatomic bonds and charge transfer between atoms of various metals tend to favor well-mixed structures, while big differences in atomic sizes and surface energies of the metals facilitate surface segregation.2 Despite the fact that recent advances in electron microscopy techniques have allowed the visualization of individual atoms in bimetallic NPs, it is still hard to derive three-dimensional chemical ordering solely based on experimental data. Therefore, predicting the most thermodynamically stable chemical ordering theoretically is of great importance.
This task is extremely difficult, because the number of possible inequivalent arrangements of atoms of different types within a given geometric structure (i.e. the number of the so-called homotops) is enormously big.2 For instance, for a binary alloy particle consisting of N atoms, AYBN−Y, the total number of homotops is N!/Y!(N − Y!), which for Y = N/2 is approximately 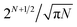 (including structures equivalent by symmetry). This renders the complete exploration of the homotop landscape unfeasible already for NPs of a few dozens of atoms. At the same time, NPs that are relevant to chemical experiments and practical applications very often contain from several hundred to several thousand atoms.
(including structures equivalent by symmetry). This renders the complete exploration of the homotop landscape unfeasible already for NPs of a few dozens of atoms. At the same time, NPs that are relevant to chemical experiments and practical applications very often contain from several hundred to several thousand atoms.
In order to deal with this formidable problem, intelligent search algorithms combined with reliable energetic models are indispensable. Efficient search algorithms that can explore the low-energy part of the homotop landscape have been developed recently.5–8 However, these algorithms can be used in the relevant size range only within simplified energetic models,9,10 since ab initio search procedures are by far too tedious. Nowadays, state-of-the-art ab initio searches are still limited to alloy clusters with a few dozens of atoms,3 despite that much bigger NPs can be routinely calculated by density functional theory methods (DFT).11–14
Simplified approaches to calculate energy of particles comprise atomistic interaction potentials and lattice models. Reliable interatomic potentials are now available for some phase-separating systems15–19 and for certain systems making solid solutions,20,21 while their accuracy is often limited when dealing with systems forming ordered phases.22 Generally speaking, the reliability of atomistic approaches for nanostructured materials is system-dependent and cannot be predicted a priori. Rather, it needs to be examined for each case against higher-level calculations. Furthermore, lattice models depend on a set of energetic parameters that are often fitted on bulk or surface quantities obtained by experiments or ab initio calculations by ad hoc procedures.23–25
Here we propose a general and systematic method for developing lattice models that aims at transferring ab initio or DFT level of accuracy to NP sizes that are relevant to experiments and practical applications. This method is based on the analysis of energy related to topological degrees of freedom, ETOP, which is reminiscent of model Hamiltonians in the Ising model26 or the cluster expansion method.27 Topological degrees of freedom used in this work take into account (1) the formation of heteroatomic bonds, (2) the different coordination of atoms in different positions of a NP, and (3) the possible tetragonal distortion in L10 alloys. The parameters in the energy expression for each NP size and composition are derived by a rigorous fitting procedure based on energies, EES, from a limited set of density functional (electronic structure) calculations for NPs of the same size and composition. The inherently physical origin of the fitted parameters allows one to directly rationalize the nature of binding in the considered alloys. The accuracy and precision of the employed approach were assessed and found to be sufficient to obtain realistic models.
Herein, the chemical ordering in Pd70X70 NPs of fcc structure for X = Au, Ag, Cu and tetragonal L10 structure for X = Zn has been optimized employing the proposed method.‡ Note that unsupported transition metal NPs of this size were shown to be representative models for catalytic studies.28–30 In order to ensure finding the lowest-energy homotops, we used a multiple exchange algorithm, which allowed us to overcome very big energy barriers in the configurational space of certain NPs. In principle, one would expect bulk segregation of Pd in all these structures, since Pd has the highest surface energy among the considered metals.31,32 Nevertheless, only for Pd–Au and Pd–Ag we found high stability of the segregated structures, while Pd–Cu and Pd–Zn exhibited more complex morphologies. We also performed the fitting of topological energies for Pd79–YAuY and Pd140−YAuY and found that the ETOP expressions depend much less on the NP size than on the composition. This observation allowed us to apply the topological expressions obtained for Pd70X70 NPs (X = Au, Ag, Cu and Zn) to the optimization of the chemical ordering in the respective 4.4 nm big Pd732X731 NPs, illustrating the power of the proposed approach.
Note that the proposed energy expressions are extendable to account for other contributions, due to e.g. NP–support or NP–adsorbate interactions. This makes the presented method very promising for studies of bimetallic NPs with experimentally accessible sizes in experimentally relevant conditions.
Results and discussion
Methodology: optimization of chemical ordering in nanoalloys
The idea of topological energies was inspired by the observation that in bimetallic NPs AYBN−Y atoms of one element often prefer to occupy interior sites in the most stable structures, while atoms of the other element tend to stay at low-coordinated surface sites.2,33 The formation of heteroatomic bonds and layered structures during the alloying process is also known to be important. To quantify these trends we considered the following form of topological energies, ETOP, that depend only on the mutual positions of atoms of types A and B within a predetermined lattice,| ETOP = E0 + εA–BBONDNA–BBOND + εACORNERNACORNER + εAEDGENAEDGE + εATERRACENATERRACE + εLAYERNLAYER. | (1) |
Here, E0 is a constant (for a given particle AYBN−Y) required to minimize the offset between ETOP and energies of the electronic structure calculations, EES; NA–BBOND – number of heteroatomic bonds (nearest-neighbor A–B pairs of atoms) in the considered structure; NACORNER, NAEDGE and NATERRACE numbers of atoms of type A on corners, edges and terraces, respectively. Other parameters, such as NA–ABOND, NB–BBOND or NBCORNER, NBEDGE, and NBTERRACE as well as NAINTERIOR depend linearly on the employed parameters for a given NP size and composition. Thus, they were not included in the ETOP expression. The term 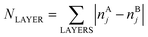 accounts for possible atomic arrangements in monometallic layers and concomitant tetragonal distortion of nanoparticle’s lattice. nAj and nBj are the numbers of atoms A and atoms B, respectively, in layer j of a NP and the sum is taken over all layers. |nAj − nBj| is maximal for layers composed entirely of atoms A or B and is close to zero for layers composed of both atoms in equal proportions.
accounts for possible atomic arrangements in monometallic layers and concomitant tetragonal distortion of nanoparticle’s lattice. nAj and nBj are the numbers of atoms A and atoms B, respectively, in layer j of a NP and the sum is taken over all layers. |nAj − nBj| is maximal for layers composed entirely of atoms A or B and is close to zero for layers composed of both atoms in equal proportions.
In eqn (1)εi are energetic parameters associated with each degree of freedom Ni considered in the topological energy. They will be referred to as descriptors. In contrast to parameters in many empirical methods, each descriptor εi has a clear physical meaning. For instance, εA–BBOND is related to the energy gain caused by the mixing of two metals. For example, the formation (mixing) energy of ordered L10 A0.5B0.5 bulk alloy from separated bulk A and bulk B is 4εA–BBOND per atom, since in this alloy each atom forms 8 heteroatomic bonds and each bond connects two atoms. In turn, εACORNER is the energy required for or gained from the exchange of an atom of type A on the corner with an atom of type B in the NP interior (given that the number of heteroatomic bonds remains constant). εLAYER is a descriptor associated with the formation of layers in (tetragonally distorted) L10 structure; the latter is favored when εLAYER < 0. Note that for Au–Pd, Ag–Pd and Cu–Pd alloys εLAYER values were calculated to be zero within statistical accuracy. Hence, the term 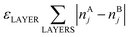 was neglected for description of these materials, which did not affect the accuracy of the ETOP expression. The model Hamiltonian that leads to the topological energy expression (1) for bimetallic nanocrystals with fcc structure is presented in the ESI.†
was neglected for description of these materials, which did not affect the accuracy of the ETOP expression. The model Hamiltonian that leads to the topological energy expression (1) for bimetallic nanocrystals with fcc structure is presented in the ESI.†
For each nanocrystal with a given shape, size and composition, an individual topological energy expression is tailored via fitting the descriptors εi to the DFT total energy EES values of various homotops of this particular NP (obtained via local geometry optimization at DFT level). This way of fitting leads to a rather high accuracy of this approach compared to e.g. interatomic potentials despite the more complex structure of the latter with many more fitting parameters. Naturally, this way of fitting leads to different topological expressions for nanoparticles of different shape, size and composition. However, since each of these descriptors εi determines certain interactions, changes in their values from system to system directly reflect the underlying changes in material properties.
In this work we calculated DFT energies EES of 28 to 127 homotops to fit ETOP for every considered NP shape and composition via multiple linear regression.34 When several structures with the same set of Ni were present in the fitting set, only the structure with the lowest EES was taken for the fitting. The electronic structure calculations of EES for NFIT NP structures required for the fitting is the most computationally demanding part of the method. Therefore, one should aim to keep the number of DFT calculations at a minimum. Nevertheless, we have to point out that insufficient size of the fitting set would lead to overfitting and poor statistical accuracy of the obtained descriptors εi. The accuracy can be estimated as 95% confidence intervals via the bootstrap method.35 This method was applied since it seamlessly takes into account that εi are not independent statistical quantities and may strongly correlate with each other. In practice, descriptors that significantly contribute to ETOP have rather small inaccuracies, while those not crucial for the fitting are determined less accurately. Note that the inaccuracy of the descriptors does not reflect the inaccuracy of the energy expression as a whole.
The precision of the topological expressions themselves was estimated as twice the residual standard deviation (RSD) δ between EES and ETOP energies for a set of NTEST ≥ 10 structures not included in the fitting procedure
According to this definition, (relative) ETOP values are within δ from the respective (relative) EES values with >95% probability. In turn, the accuracy (trueness) of the topological energies, ΔE, was estimated as the energy difference between the lowest-energy structure according to the ES calculations and the global minimum structure within the topological energy optimization. Since many homotops yield the same ETOP value but somewhat different EES, the energy difference ΔE was calculated by the topological expression to avoid any arbitrariness.
Once descriptors in eqn (1) for a given system are determined, one may use this formula to perform optimization of the chemical ordering within the predetermined lattice. In this work, we carried out Monte-Carlo simulations with only one kind of moves – simultaneous exchange of n random atoms of element A with n random atoms of element B. The number of atoms to be exchanged was chosen randomly with the probability p(n) ∼ n−3/2, which yields the probability of single exchange moves for big NPs around 1/ζ(3/2) ∼ 38%, where ζ is the Riemann zeta function. This method makes it possible to overcome very big energy barriers that exist, e.g. in the configurational space of Pd–Zn NPs (see the respective discussion in Pd–Zn section).
The temperature in a Monte-Carlo simulation was chosen in such a way that a system spends <50% of time in the lowest-energy configuration. A configuration of AYBN−Y NP was considered a global minimum, if a move from it to a lower energy structure failed after 10Y(N − Y) multiple exchange moves. This means that we applied every possible one of Y(N − Y) single exchange moves for the global minimum search with probability of
The code that performs Monte-Carlo simulations was written in a way that whenever it finds a structure with lower energy than the previously calculated ones, the geometry is recorded. Out of these structures, NTEST structures with the lowest ETOP energies were calculated by the chosen ES technique, and their ES energies were used to estimate the precision of the topological energy approach employed in the Monte-Carlo simulation. Thus, the test sets included rather diverse low-energy structures ranging from the predicted global minimum to structures located ∼NTEST multiple exchange moves far from it in the configurational space. If we wanted to improve the precision δ of the ETOP estimated using this test set, then the test set was added to the fitting set and new descriptors were obtained. As a result of the global optimization with the new energy expression, a new test set was generated in the fashion described above and the precision of the new ETOP expression was estimated on the new test set, which had not yet been included in the fitting.
Such way of fitting allows for a better description of low-energy structures (prevailing in the fitting set). It suits the purpose of global optimization focusing on finding the structure with the lowest possible energy. In the cases where calculated high-energy structures are qualitatively different from low-energy homotops, one may consider deliberately removing high-energy structures from the fitting in order to further improve the description of low-energy structures. One of such cases could be alloys of metals with considerably different atomic sizes, where high-energy and low-energy homotops may have notably different geometric structures due to the mechanical stress and concomitant relaxation.
The Monte-Carlo scheme also allows one to estimate thermal energy associated with the Boltzmann population of different homotops for a given NP structure. Thermal energies calculated in such a way (with fixed atomic positions) are used only to inspect the magnitude of chemical disorder at finite temperature and to put precision δ of the proposed approach into perspective. Other contributions to the thermal energy may be much bigger and, thus, more important. Nevertheless, they are not relevant to the analysis performed herein.
In the present work we applied the just outlined method to the optimization of chemical ordering in PdAu, PdAg and PdCu NPs with fcc lattices as well as in PdZn NPs with tetragonally distorted L10 lattice. It is important to emphasize that having slightly modified topological energy expression and/or electronic structure calculations one may apply the proposed method to a variety of materials, crystalline structures and reaction conditions. For instance, one may substitute εATERRACENATERRACE in (1) by εA{111}NA{111} and εA{100}NA{100} to account separately for segregation on {111} and {100} facets in NPs of certain shapes. Similar modifications can be done to distinguish different kinds of edges and corners. To account for NP–support interactions one may add the term εAINTERFACENAINTERFACE to eqn (1) to describe support-induced segregation on the interface. In order to account for the reaction atmosphere there is no need to change the ETOP expression at all: it is sufficient to consider the presence of adsorbates in the respective electronic structure calculations. Extension of the method to handle arrays of heterometallic NPs (e.g. like the monometallic arrays36) is also straightforward.
Pd–Au
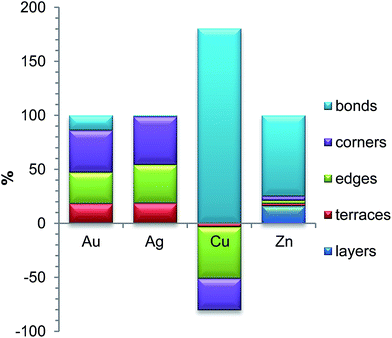
Alloys of Au and Pd have been intensively studied37,38 due to their numerous actual and potential applications in heterogeneous catalysis. They include H2O2 synthesis,39 CH4 conversion to methanol,40 C–C coupling,41 oxygen reduction reaction,42 and various hydrogenation43 and oxidation44,45 reactions. According to theoretical predictions the Au-shell Pd-core structure is the most thermodynamically favorable for Pd–Au NPs,46 while a rich variety of Pd–Au NP structures has been detected experimentally.47–49 It is important to note that the surface composition of Pd–Au systems may be altered by adsorbates such as CO and that even single Au or Pd atoms or dimers on the surface may significantly affect the overall catalytic performance of the system.50–53According to our analysis, the most significant contributions to the ETOP (here and in the following discussion E0 is subtracted from ETOP) for Pd70Au70 NP come from stabilization of Au atoms on low-coordinated sites (Table 1). The lower coordination number of the site, the bigger is the energy gain: 200 meV for 9-coordinated terrace atoms of Au, 301 meV for 7-coordinated edge atoms, and 404 meV for 6-coordinated corner atoms. The respective contributions to the global minimum energy calculated with the ETOP are 18%, 29% and 39% (Fig. 1). The energy of a Pd–Au bond is calculated by ETOP to be only ∼13 meV; however, due to the large number of the heteroatomic bonds their contribution to the energy is sizeable, 14%.
| X | Au | Ag | Cu | Zn |
|---|---|---|---|---|
| a 95% confidence intervals of εi are also given, e.g. −13+4−6 means that the interval is −19 to −9. | ||||
| ε Pd–XBOND | −13+4−6 | −1+2−2 | −26+5−5 | −160+52−40 |
| ε XCORNER | −404+76−72 | −361+50−68 | 95+36−33 | −251+316−342 |
| ε XEDGE | −301+52−77 | −289+78−129 | 147+46−45 | −205+280−243 |
| ε XTERRACE | −200+52−64 | −163+43−64 | 183+42−40 | −90+231−234 |
| ε LAYER | — | — | — | −105+29−38 |
| N FIT | 32 | 53 | 127 | 28 |
| δ | 115 | 150 | 360 | 348 |
| ΔE | 26 | 29 | 171 | 0 |
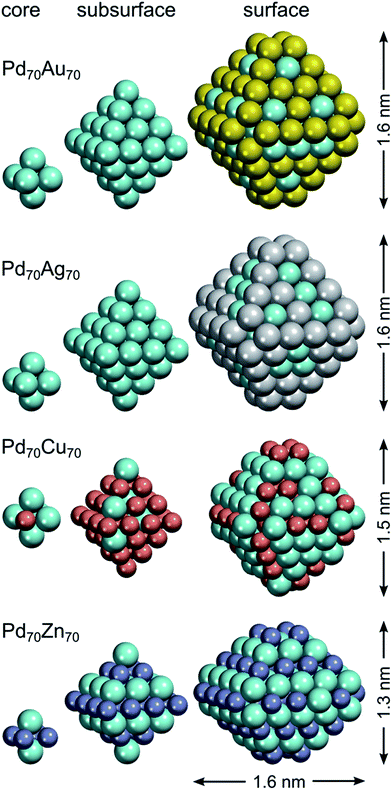
The chemical ordering of the lowest-energy homotop found for Pd70Au70 nicely reflects the magnitude of different terms in the topological energy expression (see Fig. 2). There, Au atoms occupy all the most energetically stable corner and edge positions and the remaining Au atoms are in surface terrace positions. The configuration of Au atoms on terraces may vary from facet to facet tending to maximize the number of Pd–Au bonds. Note, however, that in the lowest-energy structure found by DFT there is only 260 heteroatomic bonds, while in the global minimum according to ETOP it is 262 (Table 2). This finding reflects the expected presence of other minor contributions (of the order of δ = 115 meV) to the EES that are not accounted for by the ETOP, eqn (1).
| X | N Pd–XBOND | N XCORNER | N XEDGE | N XTERRACE | N XSUBSURFACE | N XCORE | N X–X | N Pd–X | N Pd–Pd | |
|---|---|---|---|---|---|---|---|---|---|---|
a For NPs with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 composition, the average coordination number of X by Pd equals the average coordination number of Pd by X.
b The same structure yields both the lowest EES and ETOP for Pd70Zn70; in this structure 1 composition, the average coordination number of X by Pd equals the average coordination number of Pd by X.
b The same structure yields both the lowest EES and ETOP for Pd70Zn70; in this structure 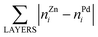 equals to 136. equals to 136.
|
||||||||||
| Au | ES | 260 | 24 | 24 | 22 | 0 | 0 | 3.57 | 3.71 | 7.17 |
| TOP | 262 | 24 | 24 | 22 | 0 | 0 | ||||
| Ag | ES | 234 | 24 | 24 | 22 | 0 | 0 | 3.94 | 3.34 | 7.54 |
| TOP | 262 | 24 | 24 | 22 | 0 | 0 | ||||
| Cu | ES | 358 | 16 | 17 | 1 | 35 | 1 | 4.20 | 5.11 | 3.69 |
| TOP | 382 | 12 | 14 | 8 | 34 | 2 | ||||
| Znb | ES = TOP | 422 | 16 | 14 | 16 | 20 | 4 | 2.57 | 6.03 | 3.54 |
Pd–Ag
Pd–Ag alloys are studied mostly because of their potential applications as hydrogenation,54–57 fuel cell58 and other catalysts,59–61 sensors62 and biosensors.63 Similarly to Pd–Au NPs, theoretical studies8,64 predict Pd-core/Ag-shell structure of Pd–Ag NPs and surface segregation of Ag was also observed experimentally.56,57,60 Interestingly, several experimental studies report homogeneous Pd–Ag alloys59,62,65 or even Pd-shell/Ag-core structures.58 It was also found that the surface segregation may be affected by the presence of adsorbates such as atomic H.57,66We have found interactions in Pd70Ag70 to be quite similar to those in Pd70Au70: the lower the coordination number of a site, the more energy is gained when it is occupied by an Ag atom. The most prominent contributions to the topological energy ETOP come from Ag atoms on corners (45%), edges (36%) and terraces (18%) (Fig. 1). The energy of Pd–Ag bonds is calculated to be essentially zero (−1 ± 2 meV); thus, their contribution to ETOP does not exceed 1%.
In line with the topological energy expression for PdAg, the structure of Pd70Ag70 with the lowest EES has all corner and edge positions occupied by silver atoms. The remaining Ag atoms are located on terraces, whereas the NP interior is composed of solely Pd (Fig. 2). The number of heteroatomic bonds in this structure is only 234, i.e. significantly less than 262 in the global minimum for the respective ETOP. The reason for this difference is the negligible energy associated with NPd–AgBOND, which probably compares in magnitude with other contributions to the EES, not accounted for by the ETOP.
Pd–Cu
A lot of scientific effort has been devoted to Pd–Cu alloys since they catalyze oxygen reduction reaction,67,68 O-enhanced water–gas shift reaction (when supported on ceria),69,70 formic acid oxidation,71 water denitrification72–74 and several hydrogenation reactions.55,75,76 Early interatomic potential studies revealed two competing effects governing the structure of Pd–Cu NPs: the tendency to maximize the number of heteroatomic bonds and the tendency of Pd77 or Cu78 to segregate on the surface. In some studies the enrichment of the surface by Cu or Pd was found to depend on their concentration.79 In those studies the most energetically stable NP structures also featured higher concentration of surface Cu atoms on corner and edge sites rather than on terrace sites. Experimentally Pd–Cu NPs with Cu-rich surfaces72,80 and well mixed ordered or disordered Pd–Cu alloys71,75,81 were characterized. Note that CO-induced surface segregation of Pd was documented for Pd–Cu.80We consider chemical ordering in Pd–Cu with fcc structure since for NPs of few nm it is more stable than bcc structure observed in Pd–Cu bulk.78,82 The energetic stability of Pd–Cu NPs comes mainly from the energy of heteroatomic bonds, which is twice of that in Pd–Au NPs (Table 1). Unlike the cases of Pd–Au and Pd–Ag, Cu prefers to stay inside the NP, whereas the surface of Pd70Cu70 is enriched by Pd. The reason is that Pd atoms are bigger than Cu atoms and, therefore, tend to segregate on the surface, where a part of the elastic stress is relieved.77 Note, however, that the employed density functional (as well as other local and gradient-corrected functionals) also favors Pd segregation on the surface, since it predicts the surface energy of Pd(111) to be slightly smaller than the surface energy of Cu(111) in disagreement with experiments.32,109 Curiously, the order of stability of Cu in different positions, interior > corner > edge > terrace, does not correlate with the coordination number of Cu in these sites. Since descriptors corresponding to Cu atoms on corner, edge and terrace positions are positive (reflecting that these positions are unstable for Cu with respect to interior ones), their destabilizing contributions to the ETOP of the global minimum are −29, −47 and −3%, respectively. Hence, to counteract that the contribution of the heteroatomic bonds to ETOP formally exceeds 100%.
The descriptor value for Pd–Cu bonds, −26+5−5 meV per bond, corresponds to the binding energy of −104+20−20 meV per atom in (fcc or bcc) Pd–Cu bulk, which agrees with the experimental value of −114 meV per atom for the bcc alloy.83
The homotop with the lowest EES of the Pd70Cu70 NP exhibits matryoshka-like (also called onion- or multishell-like) arrangement with Pd-rich surface shell, Cu-rich subsurface shell and Pd-rich core. This chemical ordering allows the formation of 358 heteroatomic bonds, while the number of Cu atoms is kept low on the surface, especially on terraces. The structure of the global minimum according to the ETOP features even more heteroatomic bonds, 382, more Cu atoms on terraces and less Cu on edges and corners.
Pd–Zn
Bimetallic Pd–Zn is actively studied84–86 (often in the form of surface alloys87–89) because of its catalytic activity in (reverse) water–gas shift90–92 and hydrogenation reactions93 as well as potential application as selective and highly stable94,95 catalysts for methanol steam reforming.96–98 However, the employment of Pd–Zn catalysts is complicated by the significant dependence of their properties on the Zn–Pd ratio,91,99 NP size92 and the composition of the subsurface region.98 Further complications come from strong dependence of the structure and composition of Pd–Zn systems on environmental conditions.85,89,100Both bulk and nanoparticulate Pd–Zn are known to have tetragonally distorted L10 crystal structure101,102 without pronounced surface segregation of any component.87,94 Experimental interatomic distances in a distorted fcc-like bulk lattice of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PdZn are Zn–Zn = Pd–Pd = 289 pm and Pd–Zn = 222 pm.102 There, Pd and Zn atoms form monometallic layers and the distances between adjacent atoms in different layers are shorter than those within the same layer. The clear propensity of Pd70Zn70 NPs to build alternating Pd and Zn layers normal to one of the [001], [010] or [001] directions (equivalent in the fcc lattice) accompanied by NP compression along this direction is revealed by DFT calculations and topological ordering optimizations (Fig. 2). Energy of such compression is properly taken into account by the term εLAYERNLAYER in eqn (1). It noticeably increases the ETOP precision for Pd70Zn70 from 1294 meV to 348 meV (the accuracy ΔE is 0, even when this term is neglected in the ETOP expression). For alloys that do not tend to form layered structures, the term εLAYERNLAYER does not improve the ETOP precision or may be even somewhat detrimental due to overfitting. For instance, for Pd70Cu70 excluding that contribution from ETOP increases precision of the latter by 16%.
1 PdZn are Zn–Zn = Pd–Pd = 289 pm and Pd–Zn = 222 pm.102 There, Pd and Zn atoms form monometallic layers and the distances between adjacent atoms in different layers are shorter than those within the same layer. The clear propensity of Pd70Zn70 NPs to build alternating Pd and Zn layers normal to one of the [001], [010] or [001] directions (equivalent in the fcc lattice) accompanied by NP compression along this direction is revealed by DFT calculations and topological ordering optimizations (Fig. 2). Energy of such compression is properly taken into account by the term εLAYERNLAYER in eqn (1). It noticeably increases the ETOP precision for Pd70Zn70 from 1294 meV to 348 meV (the accuracy ΔE is 0, even when this term is neglected in the ETOP expression). For alloys that do not tend to form layered structures, the term εLAYERNLAYER does not improve the ETOP precision or may be even somewhat detrimental due to overfitting. For instance, for Pd70Cu70 excluding that contribution from ETOP increases precision of the latter by 16%.
Heteroatomic bonds in Pd–Zn NPs are found to be an order of magnitude stronger than those in the other investigated alloys. This difference reflects the fact that composites of Au, Ag, Cu with Pd are alloys of d-elements, while Zn is an sp-element. Strong heteroatomic Pd–Zn bonds of polar character (the charge separation is estimated to range from Pd−0.2Zn+0.2 to Pd−0.4Zn+0.4)11,102 result in the prevalence of ordered structures of Pd–Zn in the phase diagram.85 On the contrary, alloys of d-elements are more prone to exhibit more random crystal structures, where the number of heteroatomic bonds is not maximal. Hence, Pd–Zn is better classified as an intermetallic compound rather than a bimetallic alloy.103
In line with these considerations, the dominant ETOP contribution for Pd70Zn70 is given by Pd–Zn bonds. The descriptor εPd–ZnBOND = −160+52−40 meV yields the alloy formation energy of −640+208−160 meV per atom, in agreement with the measured value of −520 meV per atom.104 Hence, heteroatomic bonds define 75% of the ETOP of the global minimum, while the rest comes mostly from the energy associated with the formation of the layered structure (16%). Despite that the energies of Zn atoms on low-coordinated sites are only slightly smaller than the respective energies of Ag atoms in Pd70Ag70, their overall contribution is rather small (9%) compared to that of Pd–Zn bonds. Since the relative energies of Pd70Zn70 NPs do not strongly depend on the number of low-coordinated Zn atoms (compared to other characteristics), it is hard to accurately fit the respective descriptors. Therefore, the formal statistical inaccuracy of εZnCORNER, εZnEDGE and εZnTERRACE exceeds 100%. Yet, this does not seem to affect the overall accuracy of the proposed approach, because these descriptors appear to be less important for the description of Pd–Zn NPs. To examine how sensitive the chemical ordering in the obtained global minimum is to the statistical inaccuracy of the descriptors for Pd70Zn70 (Table 1), its chemical ordering was re-optimized with 10 other sets of descriptors. These sets were generated by fixing each one of the 5 descriptors at the lowest or the highest value of its 95% confidence interval and re-fitting all other descriptors using the same homotops as the training set. Despite substantial variations of descriptors produced in such a way, global optimizations with all these 10 sets yielded the homotop with the same Ni characteristics as in the homotop presented in Fig. 2 and Table 2.
The structures with the lowest EES and ETOP are the same for Pd70Zn70 NPs due to the high accuracy of the topological energy expression. They feature the maximum possible number of heteroatomic bonds, 422, for the A70B70 NP of the considered shape. The NLAYER value is also the maximum possible, 136, for this particular stoichiometry and shape. As already mentioned, the energies of Zn atoms on the low-coordinated sites are of minor importance for the determination of the most stable Pd70Zn70 homotops. Hence, the amounts of Zn atoms on various types of low-coordinated sites have intermediate values. All in all, the most energetically stable homotop exhibits the layered L10 structure, similar to PdZn bulk. Nevertheless, this structure also exposes Pd atoms on Zn-composed edges, due to the slight excess of Pd for the formation of perfect layered structure. Unlike monolayer thick Pd–Zn films on Pd(111),89 no zigzag-like structures are seen on {111} facets of Zn70Pd70 particles.
Note that for Pd70Zn70 NP one could construct a homotop apparently very similar to the obtained global minimum by exchanging all Zn atoms with all Pd atoms at once. This homotop has the same number of heteroatomic bonds and the same layered structure as the global minimum, but fewer Zn atoms on corners and edges and more Zn atoms on terraces. Therefore, its EES (ETOP) is 1765 meV (1389 meV) higher than that of the global minimum displayed in Fig. 2. Despite the apparent similarity, for the simulation code this homotop looks absolutely different compared to the global minimum structure, since the position of every atom has changed. The transition from one homotop to another via exchange of one random Zn atom with a random Pd atom at a time would go through the configurations with rather small amount of Pd–Zn bonds and, therefore, very high relative energy. In practice, it was impossible to overcome the transition state between these two homotops via single exchange moves even at Monte-Carlo simulation temperatures as high as 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. However, the transformation between the discussed homotop and the global minimum does not pose any difficulty when multiple exchange moves are applied, that is, n random atoms are exchanged at a time (see Methodology). This illustrates the efficiency of the employed computational scheme, which we believe is sufficient to ensure that the lowest-energy structures from the Monte-Carlo simulations are indeed the global minima within the studied topological framework.
000 K. However, the transformation between the discussed homotop and the global minimum does not pose any difficulty when multiple exchange moves are applied, that is, n random atoms are exchanged at a time (see Methodology). This illustrates the efficiency of the employed computational scheme, which we believe is sufficient to ensure that the lowest-energy structures from the Monte-Carlo simulations are indeed the global minima within the studied topological framework.
Thermal energies
Naturally, a system in thermodynamic equilibrium adopts exclusively its global minimum configuration only at zero Kelvin, while at any finite temperature the presence of other homotops is possible with a probability determined by the Boltzmann factor. The configurational space of Pd70Au70, Pd70Ag70 and Pd70Cu70 NPs features many homotops different from the global minima only by the number of heteroatomic bonds. The energies of these homotops are just slightly higher than the energies of the corresponding global minima and hence the population of these homotop states is notable even at relatively low temperatures. Consequently, these homotops can contribute to the thermal energy.It is very instructive to compare the thermal energy accumulated by chemical (dis-)ordering to the precision δ of the topological expressions (Table 1). For example, the Pd70Au70 NP obtains (homotopic) thermal energy of 115 meV already at ∼140 K (that is, at this temperature the average energy of the system in our Monte-Carlo simulations is 115 meV above the energy of the global minimum). Therefore, despite that the structure of Pd70Au70 with the lowest found EES (Fig. 2) may not yet be the global minimum for the chosen ES computational scheme, it is certainly feasible at 140 K and may serve as a representative model for the NP at this and higher temperatures. In a similar way one gets that the considered lowest-energy structure of the Pd70Ag70 is a representative homotop at ∼360 K, while for Pd70Cu70 this temperature is ∼220 K.
Unlike the aforementioned three nanoalloys, PdZn features strong heteroatomic bonds with εPd–ZnBOND of 160 meV. Thus, there are not many low-energy homotops around the global minimum. In fact, the second most stable structure has the energy ETOP ∼ 205 meV higher than the global minimum. Therefore, below 500 K essentially the global minimum structure alone is present in the thermodynamic ensemble. Much higher temperatures are required to populate less stable homotop states, so the (homotopic) thermal energy reaches the precision of the topological expression, 348 meV, only at ∼1300 K. Thus, this high temperature is related mostly to the propensity of Pd–Zn to form regular nanostructures and to avoid any disorder, rather than to the low precision of the ETOP for this system. Note that Zn evaporates from Pd–Zn surface alloys at temperatures above 800 K.105 Therefore, it is safe to assume a very small degree of disorder in experimental samples of Pd–Zn close to the thermodynamic equilibrium.
Mixing energies
Another way to quantify the binding strength of the metals A and B in AYBN−Y NPs is by means of their mixing energy (per atom):| EMIX = [NE(AYBN−Y) − YE(AN) − (N − Y)E(BN)]/N2, |
The mixing energies (per atom) of the homotops with the lowest energy EES, calculated using the respective topological expression and DFT are presented in Table 3 (see also Table S1†). The magnitudes of ES mixing energies are found to be ∼110 meV for Pd–Au, Pd–Ag and Pd–Cu NPs, while for Pd–Zn it is almost 500 meV. The magnitudes of EMIXTOP energies resemble the respective EMIXES values, except the case of Pd–Ag, for which EMIXTOP is almost twice smaller than EMIXES. The reason is that the topological energy expression for Pd–Ag assigns almost zero energy to the heteroatomic Pd–Ag bonds and consequently predicts their essentially vanishing contribution to the mixing energy. In the rather similar Pd70Au70 NP heteroatomic bonds are responsible for 30% of the mixing energy calculated using ETOP, which can explain the 33% difference between EMIXTOP for Pd–Au and Pd–Ag.
| NP | Pd70Au70 | Pd70Ag70 | Pd70Cu70 | Pd70Zn70 |
|---|---|---|---|---|
| a The 95% confidence intervals for EMIXES were calculated as δ divided by the number of atoms in the NP; the 95% confidence intervals for EMIXTOP were calculated with the bootstrap analysis. | ||||
| E MIXES | −109+1−1 | −108+1−1 | −119+3−3 | −498+2−2 |
| E MIXTOP | −82+15−15 | −55+10−10 | −89+14−13 | −484+100−135 |
Dependency of descriptors on the composition and the size of nanoparticles
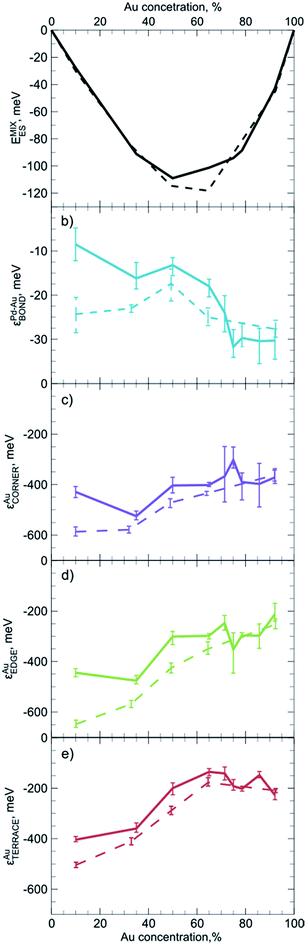
For practical purposes it is very important to know if descriptors obtained for one system can also be used to represent a slightly different system. For instance, one may wonder if descriptors calculated for smaller NPs yield reasonable results when applied to bigger species, for which ES calculations are unfeasible. To evaluate the dependency of descriptors on the size and the composition of NPs we constructed ETOP expressions and performed optimization of chemical ordering in PdYAu79−Y (Y = 6, 28, 40, 53, 71) and PdYAu140−Y (Y = 11, 20, 30, 35, 40, 49, 70, 91, 126) NPs. The results are summarized in Fig. 3, where the error bars represent 60% confidence intervals of the εi calculated via the bootstrap analysis. Note that if such confidence intervals for two εi values do not overlap, the probability that these descriptors are not different is less than ((1 − 0.6)/2)2 = 4%.The first observation is that the descriptors (and the mixing energies) significantly depend on the composition of the NPs. That is, the binding in Pd-rich Pd–Au NPs is quite different from that in Au-rich NPs. The latter feature stronger heteroatomic bonds, but less stable gold atoms on surface sites compared to Pd-rich NPs. These differences are probably related to the gradual changes in the electronic structure and average interatomic distances in the NPs with growing Au content. In most cases quantitative changes of the descriptors do not cause qualitative changes in the NP ordering. The only exception is that at very low Au concentrations Au atoms seem to prefer to occupy edges rather than corners of the Pd–Au NPs. This effect is more pronounced for PdYAu79−Y than for PdYAu140−Y NPs. The change in the relative stability of corner and edge positions for Au is reflected in the structure of the respective global minima.
A similar phenomenon was mentioned in a previous study of PdYAu79−Y NPs.33 Nevertheless, Pd–Au NPs prepared by galvanic displacement expose Au atoms on corners rather than on edges.49 However, according to our calculations corners are the most stable positions for Au only at moderate and high Au concentrations. The inconsistency between the presented and experimental results may also be due to kinetic limitations in the experimental setup or deficiencies of the employed exchange–correlation density functional.
One notices a rather limited dependency of the descriptors εi and the mixing energies per atom on the NP size. Especially at high Au concentrations, differences between εi values for PdYAu79−Y and PdYAu140−Y are barely visible and they are often within the statistical accuracy of the calculations. However, at lower Au content the binding was found to be slightly stronger in the smaller NPs. In numerous cases it was shown that many observables of NPs bigger than 1.5 nm already depend rather smoothly on their size and start to converge to a certain value.29,30,106 Hence, it is probable that the descriptors calculated for PdYAu140−Y as well as for other Pd70X70 NPs may serve as a reasonable approximation for descriptors of bigger NPs or, at least, they will lead to qualitatively correct chemical ordering, when applied to bigger NPs. At the same time, descriptors may not work satisfactorily for very small bimetallic clusters, where the quantum nature of interatomic interaction is expected to be notable. Our findings suggest that it is more important to use descriptors tailored for appropriate particle composition than for its exact size.
One may ask, to what extent applications of the present topological method can be limited to such high-symmetry “magic” shapes of bimetallic crystallites, as truncated octahedral ones discussed so far. To address this question we optimized the chemical ordering in a fcc NP Pd61Au61 of just C3v symmetry (see ESI†) with a shape reminiscent of typical shapes of supported Pd NPs.28 The individual topological descriptors, the overall picture of interactions as well as the chemical ordering in Pd61Au61 are very similar to those of the highly symmetric truncated octahedral NP Pd70Au70. The accuracy ΔE and precision δ values of the ETOP expressions for Pd61Au61 and Pd70Au70 are also very close. These findings strongly suggest that the method is applicable to reliably describe chemical ordering also in nanocrystallites with rather unsymmetrical shapes.
Extrapolation to the 4.4 nm large nanoparticles
Benefiting from the rather moderate dependency of descriptors on NP size, we can apply the descriptors calculated for Pd70X70 NPs to bigger ∼4.4 nm Pd732X731 NPs as an illustrative example (see Fig. 4). The shape of these NPs is chosen to mimic the shape of Pd70X70 NPs, i.e. featuring small {100} facets composed of only four atoms. To simulate NPs with bigger {100} facets one would need to calculate the descriptor for X atoms on {100} terraces, which are absent in our M140 models. Mind that using the proposed ETOP expression we were able to perform efficient simulations of such ∼4.4 nm NPs with the speed of >107 Monte-Carlo steps per hour on one Intel 2.66 GHz processor. | ||
| Fig. 4 Structures of Pd732X731 (X = Au, Ag, Cu and Zn) NPs with optimized chemical ordering. Pd atoms are displayed as cyan spheres; elements X – as spheres of other colors. | ||
Both Pd732Au731 and Pd732Ag731 NPs have surfaces covered by Au and Ag, respectively. In turn, their subsurface shells are composed mostly of Pd atoms and only two Au or three Ag atoms, which allows the maximization of the number of heteroatomic bonds. Consequently, the cores of the NPs have stoichiometries of Pd332Au157 and Pd333Ag156. In order to maximize the number of heteroatomic bonds these Pd0.68X0.32 cores also develop L10-like structure with partially formed layers of Au or Ag in Pd. The structure of the Pd–Cu NPs is more complicated due to two competing tendencies: maximization of NPd–CuBOND and bulk segregation of Cu. As a result, the surface shell has a stoichiometry of Pd412Cu160 and exhibits abundant Cu monomers as well as occasionally present Cu dimers on terraces and edges. Each corner of the NP has two Cu atoms on the opposite vertices of the small {100} facet. The subsurface shell of the NP is enriched in Cu (stoichiometry Pd87Cu315). Finally, the NP core has almost 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry, Pd233Cu256, and again features layer-like structure. As for the global minimum of Pd732Zn731, quite expectedly, it has almost a bulk-cut structure similarly to the Pd70Zn70 case.
1 stoichiometry, Pd233Cu256, and again features layer-like structure. As for the global minimum of Pd732Zn731, quite expectedly, it has almost a bulk-cut structure similarly to the Pd70Zn70 case.
Conclusions
We propose a method to optimize chemical ordering in bimetallic NPs using an energy expression related to topological degrees of freedom, ETOP. This expression depends on the topology of bonds between the atoms composing the NP, but not on the explicit coordinates of these atoms. Using this approach we optimized the chemical ordering in truncated octahedral PdYAu79−Y and PdYAu140−Y NPs as well as in Pd70Ag70 and Pd70Cu70 NPs with fcc lattices and Pd70Zn70 with L10 lattice; the chemical ordering in the fcc nanocrystal Pd61Au61 with a less symmetric shape has been also determined. We emphasize that this approach can be applied to bimetallics of any given lattice type, up to the point, when the structure becomes strongly disordered, e.g. at higher temperatures or in conceivable cases of particularly big irregular lattice distortions for some combinations of metals.§For every NP size and composition descriptors in the ETOP expression were fitted to the energies of more than 20 NP structures obtained via density functional calculations. The precision of the topological description tailored in such a way (i.e. their ability to predict results of the electronic structure calculations) was 115–360 meV for Pd70X70 NPs (X = Au, Ag, Cu and Zn) and the accuracy of the ETOP was at least twice better. For the Pd–Au, Pd–Ag, and Pd–Cu NPs the precision of the topological approach is comparable to the thermal energy associated with the population of low-energy homotops at temperatures of 140–360 K. Therefore, even if some of the lowest-energy homotops found here are not exactly the lowest-energy ones (according to electronic structure calculations), they are representative homotops at very moderate temperatures.
A very useful advantage of the proposed approach is that the descriptors εi in the ETOP expression have a clear physical meaning, e.g. the energy of heteroatomic bonds or the relative energy of X atoms on terrace, edge or corner positions of the NP (interior positions being the reference). Thus, the overall binding energy is inherently a sum of contributions from particular structural features. In turn, changes of these contributions from system to system reflect changes in their properties. Analyzing the structure of the topological energy expression we were able to get valuable insights into the binding in Pd–Au, Pd–Ag, Pd–Cu and Pd–Zn nanoalloys. Note that available experimental formation energies of bulk 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PdCu and PdZn agree well with the descriptor values εPd–XBOND of heteroatomic bonds for Pd70Cu70 and Pd70Zn70 NPs, respectively. The analysis of descriptors for PdYAu79−Y and PdYAu140−Y NPs showed a notable dependency on the composition of the NPs, but much smaller dependency on their size. This allows one to use descriptors based on electronic structure calculations of relatively small NPs of e.g. 140 atoms to optimize chemical ordering in bigger species formed of thousands of atoms. Hence, we applied our method to describe the chemical ordering in large Pd732X731 (X = Au, Ag, Cu and Zn) NPs, which are beyond the scale of conventional density functional calculations.
1 PdCu and PdZn agree well with the descriptor values εPd–XBOND of heteroatomic bonds for Pd70Cu70 and Pd70Zn70 NPs, respectively. The analysis of descriptors for PdYAu79−Y and PdYAu140−Y NPs showed a notable dependency on the composition of the NPs, but much smaller dependency on their size. This allows one to use descriptors based on electronic structure calculations of relatively small NPs of e.g. 140 atoms to optimize chemical ordering in bigger species formed of thousands of atoms. Hence, we applied our method to describe the chemical ordering in large Pd732X731 (X = Au, Ag, Cu and Zn) NPs, which are beyond the scale of conventional density functional calculations.
The optimization of Pd–Au and Pd–Ag NPs with ETOP yields Au and Ag atoms preferentially occupying positions with lower coordination numbers. The energy gain due to the formation of heteroatomic bonds is rather small for these materials and plays a secondary role in the determination of the NP ordering. On the contrary, the energy of heteroatomic bonds is the driving force for the alloying of Cu and Pd. In this case, the stability of Cu atoms is the highest inside the NP and the lowest on NP terraces. These two effects lead to the matryoshka-like structure of the lowest-energy Pd70Cu70 homotop, which has the surface shell enriched with Pd, the subsurface region enriched with Cu and the core composed mostly of Pd.
Unlike bimetallic Pd–Au, Pd–Ag and Pd–Cu alloys formed by d-elements, the binding in intermetallic Pd–Zn involves the interaction of a noble d-metal with an sp-element. The result is a much higher energy gain due to the formation of Pd–Zn bonds and a much higher (in magnitude) mixing energy of Pd–Zn NPs compared to other considered nanoalloys. The preferential occupation of any particular type of sites by Zn atoms is much less important for the NP structure and energy in this case. The structure of the most energetically stable homotop is very close to the cut from bulk Pd–Zn with L10 crystal structure. Just like the bulk, it features alternating Pd and Zn layers and tetragonal distortion. The term in the ETOP expression related to the formation of such a layered structure turned out to be responsible for 16% of the binding in Pd–Zn NPs.
The proposed method for the optimization of the chemical ordering in bimetallic particles paves the way to atomistic studies of several nanometer big bimetallic crystallites with known lattice structure. Fortunately, the latter can be determined by contemporary experimental techniques. Notably, the present new approach may be straightforwardly augmented for applications to heterometallic nanocrystals on a support or in a reaction atmosphere.
Methods
Electronic structure calculations were performed with the periodic plane-wave code VASP.107 We used the PBE108 exchange–correlation functional found to be one of the most appropriate common functionals for the description of transition metals.109,110 The interaction between valence and core electrons was treated within the projector augmented wave approach. To moderate computational expenditures we carried out calculations with the 250–280 eV energy cut-off of plane-wave basis sets, which yielded results very close to those obtained with the cut-off 415 eV (Table S1†). The one-electron levels were smeared by 0.1 eV using the first-order method of Methfessel and Paxton;111 finally, converged energies were extrapolated to the zero smearing. Calculations were performed only at the Γ-point in the reciprocal space. All atoms were allowed to move (relax) during the geometry optimization until forces on them became less than 0.2 eV nm−1. The minimal separation between NPs exceeded 0.7 nm, at which the interaction between adjacent NPs was found to be negligible.28,36Acknowledgements
This study was supported by the European Commission (FP7-NMP.2012.1.1-1 project ChipCAT, Ref. 310191 and COST Actions MP0903 and CM0904), the Spanish MINECO (grant CTQ2012-34969) and the Generalitat de Catalunya (projects 2014SGR97 and XRQTC). Financial support from the Spanish MEDU is gratefully acknowledged by SMK (FPU grant AP2009-3379). The authors thank the Red Española de Supercomputación for provided computer resources and technical assistance.Notes and references
- F. Calvo, Nanoalloys from Fundamentals to Emergent Applications, Elsevier, Amsterdam, 2013 Search PubMed.
- R. Ferrando, J. Jellinek and R. L. Johnston, Chem. Rev., 2008, 108, 845–910 CrossRef CAS PubMed.
- S. Heiles and R. L. Johnston, Int. J. Quantum Chem., 2013, 113, 2091–2109 CrossRef CAS PubMed.
- D. Wang, H. L. Xin, R. Hovden, H. Wang, Y. Yu, D. A. Muller, F. J. DiSalvo and H. D. Abruña, Nat. Mater., 2013, 12, 81–87 CrossRef CAS PubMed.
- D. Bochicchio and R. Ferrando, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 165435 CrossRef.
- D. Schebarchov and D. J. Wales, J. Chem. Phys., 2013, 139, 221101 CrossRef CAS PubMed.
- F. Calvo, Faraday Discuss., 2008, 138, 75–88 RSC.
- G. G. Rondina and J. L. F. Da Silva, J. Chem. Inf. Model., 2013, 53, 2282–2298 CrossRef CAS PubMed.
- R. Marchal, A. Genest, S. Krüger and N. Rösch, J. Phys. Chem. C, 2013, 117, 21810–21822 CAS.
- F. Calvo and C. Mottet, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 035409 CrossRef.
- K. M. Neyman, R. Sahnoun, C. Inntam, S. Hengrasmee and N. Rösch, J. Phys. Chem. B, 2004, 108, 5424–5430 CrossRef CAS.
- S. M. Kozlov, G. F. Cabeza and K. M. Neyman, Chem. Phys. Lett., 2011, 506, 92–97 CrossRef CAS PubMed.
- J. Kleis, J. Greeley, N. A. Romero, V. A. Morozov, H. Falsig, A. H. Larsen, J. Lu, J. J. Mortensen, M. Dułak, K. S. Thygesen, J. K. Nørskov and K. W. Jacobsen, Catal. Lett., 2011, 141, 1067–1071 CrossRef CAS.
- G. Barcaro, A. Fortunelli, M. Polak and L. Rubinovich, Nano Lett., 2011, 11, 1766–1769 CrossRef CAS PubMed.
- M. Alcantara Ortigoza and T. S. Rahman, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 195404 CrossRef.
- M. Molayem, V. G. Grigoryan and M. Springborg, J. Phys. Chem. C, 2011, 115, 7179–7192 CAS.
- D. Bochicchio and R. Ferrando, Nano Lett., 2010, 10, 4211–4216 CrossRef CAS PubMed.
- K. Laasonen, D. Bochicchio, E. Panizon and R. Ferrando, J. Phys. Chem. C, 2013, 117, 26405–26413 CAS.
- Y. Wang and M. Hou, J. Phys. Chem. C, 2012, 116, 10814–10818 CAS.
- L. O. Paz-Borbón, R. L. Johnston, G. Barcaro and A. Fortunelli, J. Phys. Chem. C, 2007, 111, 2936–2941 Search PubMed.
- F. R. Negreiros, Z. Kuntova, G. Barcaro, G. Rossi and A. Fortunelli, J. Chem. Phys., 2010, 132, 234703 CrossRef PubMed.
- G. Barcaro, R. Ferrando, A. Fortunelli and G. Rossi, J. Phys. Chem. Lett., 2010, 1, 111–115 CrossRef CAS.
- M. Polak and L. Rubinovich, Phys. Chem. Chem. Phys., 2014, 16, 1569–1575 RSC.
- M. Mueller, P. Erhart and K. Albe, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 155412 CrossRef.
- F. Lequien, J. Creuze, F. Berthier, I. Braems and B. Legrand, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 075414 CrossRef.
- K. Binder and E. Luijten, Phys. Rep., 2001, 344, 179–253 CrossRef CAS.
- G. L. W. Hart, V. Blum, M. J. Walorski and A. Zunger, Nat. Mater., 2005, 4, 391–394 CrossRef CAS PubMed.
- S. M. Kozlov, H. A. Aleksandrov, J. Goniakowski and K. M. Neyman, J. Chem. Phys., 2013, 139, 084701 CrossRef PubMed.
- S. M. Kozlov, H. A. Aleksandrov and K. M. Neyman, J. Phys. Chem. C, 2014, 118, 15242–15250 CAS.
- S. M. Kozlov and K. M. Neyman, Top. Catal., 2013, 56, 867–873 CrossRef CAS PubMed.
- L. Vitos, A. V. Ruban, H. L. Skriver and J. Kollár, Surf. Sci., 1998, 411, 186–202 CrossRef CAS.
- F. R. de Boer, R. Boom, W. C. M. Mattens, A. R. Miedema and A. K. Niessen, Cohesion in Metals, North-Holland, Amsterdam, 1988 Search PubMed.
- I. V. Yudanov and K. M. Neyman, Phys. Chem. Chem. Phys., 2010, 12, 5094–5100 RSC.
- P. Wessa, Free Statistics Software, version 1.1.23-r7, Office for Research Development and Education, 2014, http://www.wessa.net/ Search PubMed.
- A. C. Davison and D. V. Hinkley, Bootstrap Methods and their Application, Cambridge University Press, Cambridge, 1997 Search PubMed.
- F. Viñes, F. Illas and K. M. Neyman, Angew. Chem., Int. Ed., 2007, 46, 7094–7097 CrossRef PubMed.
- A. Wang, X. Y. Liu, C.-Y. Mou and T. Zhang, J. Catal., 2013, 308, 258–271 CrossRef CAS PubMed.
- G. J. Hutchings and C. J. Kiely, Acc. Chem. Res., 2013, 46, 1759–1772 CrossRef CAS PubMed.
- J. K. Edwards, B. Solsona, E. N. N, A. F. Carley, A. A. Herzing, C. J. Kiely and G. J. Hutchings, Science, 2009, 323, 1037–1041 CrossRef CAS PubMed.
- M. H. Ab Rahim, M. M. Forde, R. L. Jenkins, C. Hammond, Q. He, N. Dimitratos, J. A. Lopez-Sanchez, A. F. Carley, S. H. Taylor, D. J. Willock, D. M. Murphy, C. J. Kiely and G. J. Hutchings, Angew. Chem., Int. Ed., 2013, 52, 1280–1284 CrossRef CAS PubMed.
- R. Nath Dhital, S. Karanjit, C. Kamonsatikul and H. Sakurai, J. Am. Chem. Soc., 2012, 134, 20250–20253 CrossRef PubMed.
- M. Nie, P. K. Shen and Z. Wei, J. Power Sources, 2007, 167, 69–73 CrossRef CAS PubMed.
- N. E. Kolli, L. Delannoy and C. Louis, J. Catal., 2013, 297, 79–92 CrossRef CAS PubMed.
- M. Nie, H. Tang, Z. Wei, S. P. Jiang and P. K. Shen, Electrochem. Commun., 2007, 9, 2375–2379 CrossRef CAS PubMed.
- D. I. Enache, J. K. Edwards, P. Landon, B. Solsona-Espriu, A. F. Carley, A. A. Herzing, M. Watanabe, C. J. Kiely, D. W. Knight and G. J. Hutchings, Science, 2006, 311, 362–365 CrossRef CAS PubMed.
- L. O. Paz-Borbón, R. L. Johnston, G. Barcaro and A. Fortunelli, J. Chem. Phys., 2008, 128, 134517 CrossRef PubMed.
- R. C. Tiruvalam, J. C. Pritchard, N. Dimitratos, J. A. Lopez-Sanchez, J. K. Edwards, A. F. Carley, G. J. Hutchings and C. J. Kiely, Faraday Discuss., 2011, 152, 63–86 RSC.
- A. Bruma, R. Ismail, L. O. Paz-Borbón, H. Arslan, G. Barcaro, A. Fortunelli, Z. Y. Li and R. L. Johnston, Nanoscale, 2013, 5, 646–652 RSC.
- H. Zhang, T. Watanabe, M. Okumura, M. Haruta and N. Toshima, Nat. Mater., 2012, 11, 49–52 CrossRef PubMed.
- J. Zhang and A. N. Alexandrova, J. Phys. Chem. Lett., 2013, 4, 2250–2255 CrossRef CAS.
- F. Gao, Y. Wang and D. W. Goodman, J. Phys. Chem. C, 2010, 114, 4036–4043 CAS.
- P. Han, S. Axnanda, I. Lyubinetsky and D. W. Goodman, J. Am. Chem. Soc., 2007, 129, 14355–14361 CrossRef CAS PubMed.
- F. Gao, Y. Wang and D. W. Goodman, J. Phys. Chem. C, 2009, 113, 14993–15000 CAS.
- Q. Zhang, J. Li, X. Liu and Q. Zhu, Appl. Catal., A, 2000, 197, 221–228 CrossRef CAS.
- S. K. Kim, J. H. Lee, I. Y. Ahn, W.-J. Kim and S. H. Moon, Appl. Catal., A, 2011, 401, 12–19 CrossRef CAS PubMed.
- A. Pachulski, R. Schödel and P. Claus, Appl. Catal., A, 2011, 400, 14–24 CrossRef CAS PubMed.
- A. Yarulin, I. Yuranov, F. Cárdenas-Lizana, D. T. L. Alexander and L. Kiwi-Minsker, Appl. Catal., A, 2014, 478, 186–193 CrossRef CAS PubMed.
- K. Tedsree, T. Li, S. Jones, C. W. A. Chan, K. M. K. Yu, P. A. J. Bagot, E. A. Marquis, G. D. W. Smith and S. C. E. Tsang, Nat. Nanotechnol., 2011, 6, 302–307 CrossRef CAS PubMed.
- Y. Lu and W. Chen, ACS Catal., 2012, 2, 84–90 CrossRef CAS.
- H. Rong, S. Cai, Z. Niu and Y. Li, ACS Catal., 2013, 3, 1560–1563 CrossRef CAS.
- L. Li, M. Chen, G. Huang, N. Yang, L. Zhang, H. Wang, Y. Liu, W. Wang and J. A. Gao, J. Power Sources, 2014, 263, 13–21 CrossRef CAS PubMed.
- Q. Wang, J. Zheng and H. Zhang, J. Electroanal. Chem., 2012, 674, 1–6 CrossRef CAS PubMed.
- H. Wang, Y. Zhang, H. Li, B. Du, H. Ma, D. Wu and Q. Wei, Biosens. Bioelectron., 2013, 49, 14–19 CrossRef CAS PubMed.
- F. R. Negreiros, G. Barcaro, Z. Kuntová, G. Rossi, R. Ferrando and A. Fortunelli, Surf. Sci., 2011, 605, 483–488 CrossRef CAS PubMed.
- W. He, X. Wu, J. Liu, W. Zhou, X. Hu and S. Xie, Chem. Mater., 2010, 22, 2988–2994 CrossRef CAS.
- S. González, K. M. Neyman, S. Shaikhutdinov, H.-J. Freund and F. Illas, J. Phys. Chem. C, 2007, 111, 6852–6856 Search PubMed.
- F. Fouda-Onana, S. Bah and O. Savadogo, J. Electroanal. Chem., 2009, 636, 1–9 CrossRef CAS PubMed.
- L. Zhang and G. Henkelman, J. Phys. Chem. C, 2012, 116, 20860–20865 CAS.
- J. Kugai, J. T. Miller, N. Guo and C. Song, Appl. Catal., B, 2011, 105, 306–316 CrossRef CAS PubMed.
- J. Kugai, J. T. Miller, N. Guo and C. Song, J. Catal., 2011, 277, 46–53 CrossRef CAS PubMed.
- L. Lu, L. Shen, Y. Shi, T. Chen, G. Jiang, C. Ge, Y. Tang, Y. Chen and T. Lu, Electrochim. Acta, 2012, 85, 187–194 CrossRef CAS PubMed.
- U. Matatov-Meytal and M. Sheintuch, Catal. Commun., 2009, 10, 1137–1141 CrossRef CAS PubMed.
- O. S. G. P. Soares, J. J. M. Órfão and M. F. R. Pereira, Appl. Catal., B, 2009, 91, 441–448 CrossRef CAS PubMed.
- Q. Zhang, L. Ding, H. Cui, J. Zhai, Z. Wei and Q. Li, Appl. Surf. Sci., 2014, 308, 113–120 CrossRef CAS PubMed.
- M. Friedrich, S. A. Villaseca, L. Szentmiklósi, D. Teschner and M. Armbrüster, Materials, 2013, 6, 2958–2977 CrossRef CAS PubMed.
- G. Kyriakou, M. B. Boucher, A. D. Jewell, E. A. Lewis, T. J. Lawton, A. E. Baber, H. L. Tierney, M. Flytzani-Stephanopoulos and E. C. H. Sykes, Science, 2012, 335, 1209–1211 CrossRef CAS PubMed.
- J. M. Montejano-Carrizales, M. P. Iniguez and J. A. Alonso, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16649–16658 CrossRef CAS.
- L. Zhu, K. S. Liang, B. Zhang, J. S. Bradley and A. E. DePristo, J. Catal., 1997, 167, 412–416 CrossRef CAS.
- L. Yang, Philos. Mag. A, 2000, 80, 1879–1888 CAS.
- J. S. Bradley, E. W. Hill, B. Chaudret and A. Duteil, Langmuir, 1995, 11, 693–695 CrossRef CAS.
- M. Friedrich and M. Armbrüster, Chem. Mater., 2009, 21, 5886–5891 CrossRef CAS.
- V. Shah and L. Yang, Philos. Mag. A, 1999, 79, 2025–2049 CAS.
- R. Hultgren, P. D. Desai, D. T. Hawkins, M. Gleiser and K. Kelley, Selected Values of Thermodynamic Properties of Binary Alloys, American Society for Metals, Russell Township, 1973 Search PubMed.
- K. Föttinger, Catal. Today, 2013, 208, 106–112 CrossRef PubMed.
- M. Armbrüster, M. Behrens, K. Föttinger, M. Friedrich, É. Gaudry, S. K. Matam and H. R. Sharma, Catal. Rev., 2013, 55, 289–367 Search PubMed.
- S. M. Kozlov, H. A. Aleksandrov, L. V. Moskaleva, M. Bäumer and K. M. Neyman, in Comprehensive Inorganic Chemistry, ed. J. Reedijk and K. Poeppelmeier, Elsevier, Amsterdam, 2nd edn, 2013, vol. 7, Surface Inorganic Chemistry and Heterogeneous Catalysis, ed. R. Schlögl and J. W. Niemantsverdriet, pp. 475–503 Search PubMed.
- Z.-X. Chen, K. M. Neyman and N. Rösch, Surf. Sci., 2004, 548, 291–300 CrossRef CAS PubMed.
- A. Bayer, K. Flechtner, R. Denecke, H.-P. Steinrück, K. M. Neyman and N. Rösch, Surf. Sci., 2006, 600, 78–94 CrossRef CAS PubMed.
- C. Weilach, S. M. Kozlov, H. H. Holzapfel, K. Föttinger, K. M. Neyman and G. Rupprechter, J. Phys. Chem. C, 2012, 116, 18768–18778 CAS.
- R. A. Dagle, A. Platon, D. R. Palo, A. K. Datye, J. M. Vohs and Y. Wang, Appl. Catal., A, 2008, 342, 63–68 CrossRef CAS PubMed.
- L. Bollmann, J. L. Ratts, A. M. Joshi, W. D. Williams, J. Pazmino, Y. V. Joshi, J. T. Miller, A. J. Kropf, W. N. Delgass and F. H. Ribeiro, J. Catal., 2008, 257, 43–54 CrossRef CAS PubMed.
- V. Lebarbier, R. Dagle, A. Datye and Y. Wang, Appl. Catal., A, 2010, 379, 3–6 CrossRef CAS PubMed.
- M. W. Tew, H. Emerich and J. A. van Bokhoven, J. Phys. Chem. C, 2011, 115, 8457–8465 CAS.
- T. Conant, A. M. Karim, V. Lebarbier, Y. Wang, F. Girgsdies and A. Datye, J. Catal., 2008, 257, 64–70 CrossRef CAS PubMed.
- Q. Zhang and R. J. Farrauto, Appl. Catal., A, 2011, 395, 64–70 CrossRef CAS PubMed.
- N. Iwasa, S. Masuda, N. Ogawa and N. Takezawa, Appl. Catal., A, 1995, 125, 145–157 CrossRef CAS.
- N. Iwasa and N. Takezawa, Top. Catal., 2003, 22, 215–216 CrossRef CAS.
- C. Rameshan, W. Stadlmayr, C. Weilach, S. Penner, H. Lorenz, M. Hävecker, R. Blume, T. Rocha, D. Teschner, A. Knop-Gericke, R. Schlögl, N. Memmel, D. Zemlyanov, G. Rupprechter and B. Klötzer, Angew. Chem., Int. Ed., 2010, 49, 3224–3227 CrossRef CAS PubMed.
- M. Friedrich, D. Teschner, A. Knop-Gericke and M. Armbrüster, J. Catal., 2012, 285, 41–47 CrossRef CAS PubMed.
- K. Föttinger, J. A. van Bokhoven, M. Nachtegaal and G. Rupprechter, J. Phys. Chem. Lett., 2011, 2, 428–433 CrossRef.
- S. Penner, B. Jenewein, H. Gabasch, B. Klötzer, A. Knop-Gericke, R. Schlögl and K. Hayek, J. Catal., 2006, 241, 14–19 CrossRef CAS PubMed.
- M. Friedrich, A. Ormeci, Y. Grin and M. Armbrüster, Z. Anorg. Allg. Chem., 2010, 636, 1735–1739 CrossRef CAS PubMed.
- Some researchers find the notation Zn–Pd (with the positively charged atom mentioned first) to be more appropriate than Pd–Zn.
- S. Kou and Y. A. Chang, Acta Metall., 1975, 23, 1185–1190 CrossRef CAS.
- H. Gabasch, A. Knop-Gericke, R. Schlögl, S. Penner, B. Jenewein, K. Hayek and B. Klötzer, J. Phys. Chem. B, 2006, 110, 11391–11398 CrossRef CAS PubMed.
- A. Roldán, F. Viñes, F. Illas, J. M. Ricart and K. M. Neyman, Theor. Chem. Acc., 2008, 120, 565–573 CrossRef.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- P. Janthon, S. M. Kozlov, F. Viñes, J. Limtrakul and F. Illas, J. Chem. Theory Comput., 2013, 9, 1631–1640 CrossRef CAS.
- P. Janthon, S. A. Luo, S. M. Kozlov, F. Viñes, J. Limtrakul, D. G. Truhlar and F. Illas, J. Chem. Theory Comput., 2014, 10, 3832–3839 CrossRef CAS.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS.
- G. Kovács, S. M. Kozlov, I. Matolínová, M. Vorokhta, V. Matolín and K. M. Neyman, Phys. Chem. Chem. Phys., 2015, 17 10.1039/C5CP01070E.
Footnotes |
| † Electronic supplementary information (ESI) available: (1) Derivation of a model Hamiltonian yielding the topological energy expression for nanoparticles with fcc lattices. (2) Data on the sensitivity of calculated density functional energies on the quality of the employed plane-wave basis sets. (3) Evaluation of the method performance for less symmetric bimetallic nanocrystallites. See DOI: 10.1039/c4sc03321c |
| ‡ For the sake of brevity, we refer to the optimization of chemical ordering within a fixed NP lattice as global optimization and to the ordering that yields the lowest energy within this lattice as the global minimum. |
| § Note added in proof: Recently the present method has been used to determine chemical ordering of Pt-Co nanoparticles prepared by magnetron sputtering.112 There, applicability of the method to accurately describe chemical ordering of magnetic alloy particles composed of metals with notably different atomic radii was demonstrated. |
| This journal is © The Royal Society of Chemistry 2015 |