Revealing the thermodynamic driving force for ligand-based reductions in quinoids; conceptual rules for designing redox active and non-innocent ligands

Abstract

Metal and ligand-based reductions have been modeled in octahedral ruthenium complexes revealing metal–ligand interactions as the profound driving force for the redox-active behaviour of orthoquinoid-type ligands. Through an extensive investigation of redox-active ligands we revealed the most critical factors that facilitate or suppress redox-activity of ligands in metal complexes, from which basic rules for designing non-innocent/redox-active ligands can be put forward. These rules also allow rational redox-leveling, i.e. the moderation of redox potentials of ligand-centred electron transfer processes, potentially leading to catalysts with low overpotential in multielectron activation processes.

---

Introduction

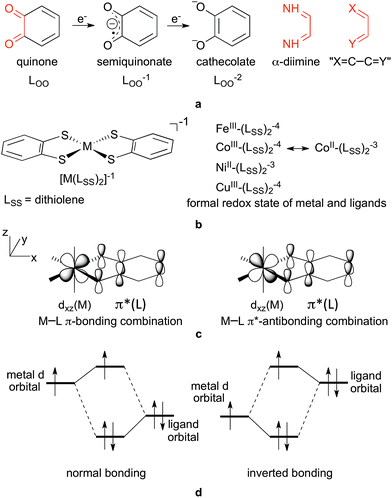
The potential for realizing the dreams of activating and converting abundant but inert molecules, such as N₂, CH₄, H₂O and CO₂, into energy carriers and other valuable compounds has contributed to the renewed interest in ligand redox non-innocence.^1,2 To this end, such ligands are used either to promote ligand-centred catalysis³ or to facilitate first row transition metal-based multi-electron reactions,⁴ where non-innocent ligands serve as electron reservoirs. Very diverse ligands can behave non-innocently depending on a variety of conditions⁵ and, accordingly, there are no clear structural criteria for exhibiting non-innocence.

Orthoquinoid ligands, such as benzoquinone (Fig. 1a), and also α-dicarbonyl derivatives, such as α-diimine (Fig. 1a), both containing the same fundamental X=C–C=Y (where X and Y are O, S and NH, Fig. 1a) coordinating functionality, however, show redox-active behaviour very often: the two-electron redox series analogous to the quinone(0) → semiquinonate(−1) → cathecolate(−2) (Fig. 1a) is typically easily accessible in the various metal complexes containing these ligands.^5–8 Accordingly, complexes containing these ligands have attracted significant attention and have been investigated by means of, amongst others, X-ray absorption spectroscopy, resonance Raman, EPR, magnetic circular dichroism, and also computational techniques.^9–33 For example, the thorough and systematic studies of Wieghardt and Neese and co-workers on homoleptic bis(dithiolene) complexes, [M(L_SS)₂]^z, (z = −2, −1, 0, M = Fe, Co, Ni, Pd, Pt, Cu, Au)^9–16 (Fig. 1b) analysed and clarified the complicated electronic structures of these complexes in the light of their observed physicochemical properties. Considerable further understanding was provided in the long-standing research of Lever on substituted benzoquinonediimine (L_NN), benzoquinone (L_OO) and aminophenol (L_NO) ruthenium complexes of general formula [(acac)₂RuL_XY]^+z and [(bpy)₂RuL_XY]^+z.^17–25 In these types of compounds, structural parameters such as the ligand C–C and C–N bond lengths have been used as indicators for non-innocence and in the assignment of the oxidation state of benzoquinone derivatives in various complexes.^9,26–30 On the other hand, cases are also known and discussed where this interpretation fails, for example in highly delocalized systems³¹ or quinone derivatives^10,11,15,32 with sulphur donor atoms, i.e. benzene-1,2-dithiolene, which will be denoted generically as L_SS in this work. Also, in Ru complexes the ligand oxidation state has been a matter of debate for a while due to some inconsistencies in the structural and spectral predictions;³³ Remenyi and Kaupp however convincingly demonstrated both pure Ru^III–L⁰ and mixed Ru^II–L⁰ ↔ Ru^III–L⁻¹ and Ru^II–L⁻¹ ↔ Ru^III–L⁻² states in the different oxidation states of the complex.³³

Fig. 1 (a) Two-electron redox series of quinone to cathecolate, α-diimine, and the common X=C–C=Y structural motif highlighted in red; (b) general structure of square-planar bis-dithiolene complexes ([M(L_SS)₂]⁻¹) and the assigned formal oxidation state of the metal and ligands for Fe, Co, Ni and Cu derivatives; (c) π-type interactions between the metal d_π-orbital (d_xz) and the redox-active orbital of quinoids, the magnitude of mixing of these metal- and ligand-based orbitals determines non-innocence; (d) normal and inverted bonding for a two-orbital-three-electron case, e.g. orbitals in (c) with three electrons.

Orthoquinoid derivatives were also amongst the first ligand scaffolds to demonstrate the applicability of non-innocent ligands as electron reservoirs to induce noble-metal reactivity in base metals. In several landmark studies^34,35 Heyduk demonstrated that zirconium could mimic two-electron reactivity cooperating with quinoid-like redox-active ligands. For example, Zr^IV complexes (THF)₂Zr(L_NO)₂ ^36,37 and (THF)₂Zr(L_NN)₂ ^38,39 undergo oxidative addition when exposed to halogens X₂ (X = Cl, Br, I) to form the corresponding (bis)halide derivatives Zr(L)₂X₂. Having a d⁰ configuration Zr^IV cannot provide the electrons needed for these processes and, thus, in these transitions, each redox-active ligand, either L_NN or L_NO, provides one electron to facilitate the overall two-electron activation of molecular X₂. Another spectacular example is the carbon–carbon bond-forming reductive elimination of biphenyl from the [Zr^IVPh₂(L_NO)₂]²⁻ dianion,^37,40 initiated upon two-electron oxidation of the redox active L_NO ligands. As of now, this electron-borrowing strategy with ligand involvement in the redox process has become one of the pillars of cooperative catalysis.⁴¹ For instance, recently, R–X bond activating oxidative addition was realized with a Co^III-(bis)amidophenolate (L_NO) complex,⁴² without changing the d-electron configuration of the central metal ion.

From these exemplary studies, it is clearly seen that static non-innocence, i.e. the ambiguity in metal vs. ligand oxidation states, is due to the strong mixing of ligand orbitals with metal orbitals.²¹ Especially for quinoid ligands, it is the mixing of the redox-active LUMO π* orbital of the ligand with the appropriate d_π metal orbital, as shown in Fig. 1c for an ideal octahedral complex. To get an idea of the magnitude of non-innocence of ligands, Lever thoroughly investigated the spatial distribution of the most relevant molecular orbitals describing σ-, π- and δ-interactions in various [(acac)₂RuL_NN]⁰ and [(bpy)₂RuL_NN]⁺² complexes.^18,21,23,43 The deducted magnitudes for non-innocence based on the π-interaction were in good accordance with other measures, such as various bond orders in the ligand, the net charge of the ligand, π-backdonation, and could even be correlated with redox properties of the central metal and the ligand as well.²¹

The chemically intuitive concept that the relative energy of interacting metal and ligand orbitals predominantly determines the level of orbital mixing and binding mode was clearly illustrated by Neese and Wieghardt for the isoelectronic [Fe(L_SS)₂]⁻² and [Co(L_SS)₂]⁻¹ systems.⁹ The higher effective nuclear charge of cobalt in the valence region lowers the energy of metal orbitals and brings them closer to the deeper lying ligand π-orbitals, resulting in stronger mixing. For metals with an even higher effective charge (Cu), the orbital energies of the metal orbitals are below those of the ligand orbitals and an inverted bonding situation⁴⁴ arises as shown in Fig. 1d, typically discussed for unpaired electron situations⁴⁵ where the distribution of radical character between the metal and ligand plays a role in determining the principal characteristics of the complex.

The above mentioned studies are extremely useful to clarify and interpret the bonding situations in complexes containing non-innocent ligands, i.e. for static non-innocence (ambiguity in oxidation states); however, they miss the very spirit of the redox-activity of benzoquinone related ligands, which is a very important feature considering its possible application in cooperative catalysis.⁴¹

The important question remains: why is the common X=C–C=Y structural motif (Fig. 1a, red), especially when fused with a benzo ring, so optimal for accepting electrons when bound to a metal? The answer to this question is still lacking in spite of the deep understanding of static non-innocent behaviour of these ligands. Nevertheless, one might initially argue, for example, that this structure is so effective because its relevant π-orbital mixes with the metal d_π, i.e. it exhibits static non-innocence. On the contrary, mixing of these orbitals actually increases the energy of the redox-active antibonding combination (LUMO), at least in a first order approximation, and thus the complex would be less likely to accept electrons, as was clearly demonstrated by the negative shift in redox potentials with increasing non-innocence.²¹ Another answer might attribute redox-activity to a superior electron delocalization in the extended π-system of the ligand upon reduction, as suggested by a delocalized LUMO. However, it was recently shown for organic molecules with delocalized π-systems that the shape of the LUMO does not even qualitatively resemble the electron density build-up when an electron is added to the system⁴⁶ implying that deducting spatial information about the redox event from the shape of the LUMO is ambiguous. Also, the low lying LUMO of 3,5-di-tert-butyl-1,2-benzoquinone (L_OO^tBu) allows the first electron reduction of the free ligand at −0.955 V,^47,48 whereas it undergoes the same reduction in metal complexes at much more positive potentials, e.g. at −0.01 V in (bpy)₂Ru(L_OO^tBu)⁴⁹ indicating that the coordination to a metal critically eases ligand-centred reductions and should thus play an essential part in the explanation of the redox active behaviour.

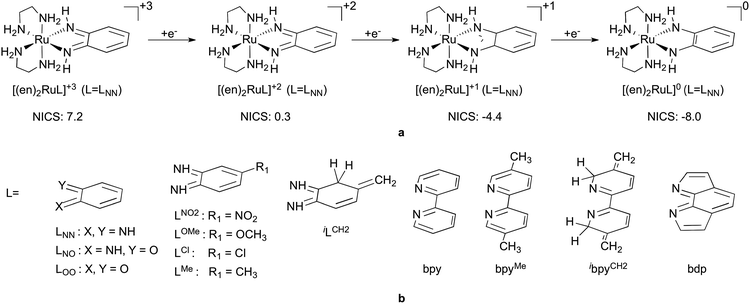
In this study, we provide a conceptual understanding for the redox active behaviour of orthoquinoid related ligands using an in-depth, extensive and systematic computational investigation of octahedral ruthenium complexes shown in Fig. 2. We believe that this systematic large-scale computational study is the first step towards simple and predictive rules for designing redox non-innocent ligands and controlling the redox potential of ligand-based reductions. Our study reveals that the major thermodynamic driving force for ligand-based reduction mainly originates from important M–L ligand interactions that critically stabilize the M–L^−1/−2 configurations upon ligand-centred reduction. We put our new findings into context with available experimental findings resolving some discrepancies within them, and, based on our findings, we also propose a new ligand frame that shows superior electron accepting capacity.

Fig. 2 (a) The four state redox series investigated for octahedral ruthenium complexes containing one non-innocent ligand, L, and two spectator 1,2-diaminoethane (en) ligands and NICS values computed for the six-membered carbon ring of L_NN; (b) redox active ligands investigated.

Results and discussion

In the first part of this contribution we introduce our hypothesis to account for the high affinity of the X=C–C=Y structural motif to accept electrons, especially when bound to a metal. Convincing support for this will be provided through an in-depth analysis on a selected redox series [(en)₂RuL_NN]^+3/+2/+1/0, depicted in Fig. 2a, octahedral complexes with two innocent en ligands and a bidentate non-innocent ligand L_NN. In the second part we discuss how and why various factors, such as ring fusion, contact atom, substitution, etc., influence the redox properties of ligands, demonstrated via a systematic investigation of redox properties of a more extensive set of complexes (Fig. 2b).

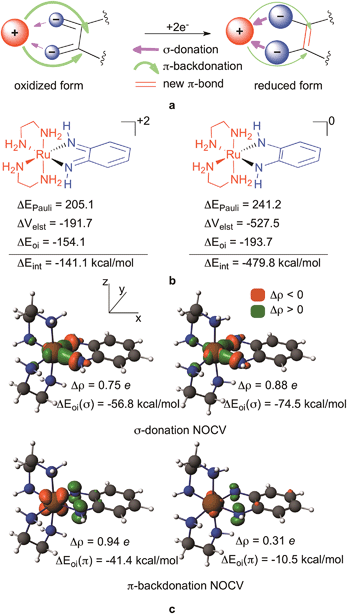
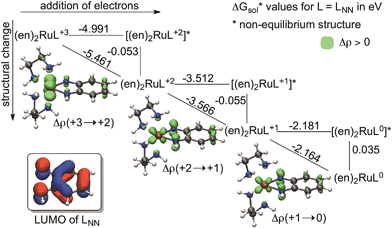
Fig. 3a summarizes the key elements of our theory for the rationalization of the redox active behaviour of orthoquinoids: the key point is that instead of being delocalized, the incoming electrons accumulate on the contact atoms of the ligand (as indicated by the bigger blue circles in Fig. 3a) resulting in a considerably enhanced electrostatic interaction with the positive metal centre, accompanied by a much better σ-donation from the contact atoms to the metal (purple arrow) in the reduced species. Another simultaneously occurring effect of the reduction is the diminishing π-backdonation from the metal to the ligand (green arrow). We will now provide detailed evidence for this unexpected ligand behaviour upon reduction. The fundamental finding that fosters our idea is the change of the electron density upon reduction plotted in 3D⁵⁰ (Fig. 4). These figures also provide a clear visual representation of redox non-innocent behaviour in transition metal complexes when the ligand actively participates together with the metal in the reduction process of the complex, as they actually enable the identification of the regions where the density is accumulated in the reduction processes. Accordingly, Fig. 4 clearly shows that the electron is predominantly accumulated on the metal, namely on the d_yz orbital, for [(en)₂RuL_NN]⁺³ to [(en)₂RuL_NN]⁺², in line with a Ru^III to Ru^II transition. For formal ligand-based transitions, i.e. going from [(en)₂RuL_NN]⁺² to [(en)₂RuL_NN]⁺¹ and to [(en)₂RuL_NN]⁰, the electron density increases on the metal but mostly on the contact atoms of the ligand. The delocalization to backbone of the ligand is much less apparent than could perhaps be expected on the basis of the shape of the redox active LUMO (Fig. 4).

Fig. 3 (a) Explanation for the M–L interaction driven ligand reduction; (b) energy decomposition analysis for the M–L interaction in [(en)₂RuL_NN]⁺² (left) and [(en)₂RuL_NN]⁰ (right); and (c) NOCV orbitals representing σ-donation and π-backdonation for [(en)₂RuL_NN]⁺² (left) and [(en)₂RuL_NN]⁰ (right).

Fig. 4 Theoretical square scheme for the [(en)₂RuL_NN]^+3/+2/+1/0 redox series with the corresponding electron density change and the LUMO of L_NN.

Understanding why the electron density is accumulating locally on the contact atoms upon reduction provides the key for the high electron affinity of the X=C–C=Y structural pattern when attached to a metal centre. As can be seen in Fig. 3a, significantly better M–L interactions compared to the case where the electron(s) is delocalized to the ligand backbone are encountered. First, electrostatic interactions between the metal and the ligand significantly increase upon accumulation of electrons on the contact atoms. Second, the contact atoms become better σ-donors resulting in stronger dative interactions with the metal.

On the whole, these two effects considerably stabilize the reduced form and thus give rise to a relatively easy ligand-based reduction of the complex. It should, however, be noted that this does not exclude a low-lying LUMO as one of the prerequisites (see later) of redox active behaviour, but it emphasizes the two-state (oxidized and reduced forms) nature of redox-activity and the crucial difference in M–L interactions in these two states. In other words, until static non-innocence can be seen as a one-state phenomenon, i.e. the ambiguity of oxidation states of constituting metal and ligands is characteristic of a given redox state of the complex, the redox activity of ligands is a two-state phenomenon determined by the stabilization mechanisms in both the oxidized and reduced forms of the complex as, for example, implied in Fig. 3a.

A Ziegler–Rauk energy decomposition analysis^51–55 (Fig. 3b) that decomposes the interaction energy (ΔE_int) between the ligand L_NN^0/−2 and the metal based fragment (en)₂Ru⁺² to steric (ΔE_Pauli), electrostatic (ΔV_elst) and orbital (ΔE_oi) interactions^51–54,56 clearly supports the hypothesis outlined in Fig. 3a. As Fig. 3b shows, the interaction energy between the ligand and the metal becomes considerably more attractive, and thus stabilizing, by −338 kcal mol⁻¹ (−14.7 eV!) upon two-electron reduction of the ligand. Much of this stabilization results from the increased electrostatic attraction, which is −192 kcal mol⁻¹ for [(en)₂RuL_NN]⁺² and −528 kcal mol⁻¹ for [(en)₂RuL_NN]⁰. Admittedly, orbital interaction also becomes slightly more attractive in the reduced form, whereas destabilizing steric repulsion between the ligand and the metal also increases (Fig. 3b) upon reduction.

Using the recent Natural Orbitals for Chemical Valence (NOCV)^57–61 technique, the orbital interaction contributions can be associated with electron density reorganizations upon complex formation representing the dominant σ-donation and π-backdonation (Fig. 3c). In these NOCV orbitals density accumulations (Δρ) and depletions upon complex formation⁶² are symbolized by green and orange lobes, respectively. Accordingly, the top figures in Fig. 3c represent σ-donation from the contact atom's lone pairs to the metal d-orbital (d_xy) whereas the bottom ones identify charge flow from the metal to the ligand in the π-subspace. As hypothesised, donation from the lone pairs to the d_xy increases notably upon reduction (by 0.13 e and ∼20 kcal mol⁻¹), whereas backdonation from the metal d_xz to the π* ligand diminishes by 0.63 e and 31 kcal mol⁻¹ upon reduction in line with the concept in Fig. 3a.

It is important to note that with our analysis, we do not imply that the backbone of the ligand is completely unimportant in the reduction process. There is a recombination of electrons in the tethering carbon chain formally resulting in a new π-bond upon two-electron reduction as also shown in Fig. 3a (purple). Also, in line with earlier reports,⁴³ undoubtedly, the redox-active LUMO becomes populated upon reduction; however it does not only induce a well-recognized structural change, shortening of the C–C bond and lengthening of the C–N ones – as discussed above, but it also reshapes the lower lying molecular orbitals. As a result, reduction actually induces an accumulation of electrons at the electronegative contact atoms, which have the stabilizing effects discussed for Fig. 3, and a recombination of electrons in the tethering backbone. The general consequence of this theory is that various ligands of X=(CR)_n=Y type, with electronegative X and Y contact atoms and an unsaturated tethering fragment, should likely exhibit non-innocent behaviour and redox-activity when bound to a metal. Also, this rationalization helps to understand why gold, silver and copper remain in oxidation state +3 in [Cu(L_SS)₂]⁻¹, [Ag(L_SS)₂]⁻¹ and [Au(L_SS)₂]⁻¹ (see also Fig. 1b); superior M–L bindings account for the observed L_SS⁻²–Au^III–L_SS⁻² formal oxidation state assignment, whereas, in contrast, effective charge arguments should lead to a L_SS⁻¹–Ag^I–L_SS⁻¹ formal assignment.

As mentioned above, the reduction/oxidation of α-diimine and quinone related ligands triggers a characteristic geometry change: shortening of the C–C bond and elongation of the C–X and C–Y ones of X=C–C=Y upon reduction, in line with the bonding and antibonding characteristics of the LUMO along these bonds, respectively. This is a well-documented manifestation, which is even used to estimate the magnitude of redox non-innocence.^9,26–30 To our best knowledge, however, the energetic contribution of this effect to the redox-activity of ligands as well the importance of structural flexibility in redox active behaviour have not been assessed so far.

To quantify the contribution of this geometrical change to the reduction process we computed so-called theoretical square schemes introduced by Baik, Schauer and Ziegler⁶³ and used them to analyse the origin of the potential-inversion phenomena of various systems.^64,65 As Fig. 4 shows, a theoretical square scheme separates the reduction process into electron attachment (horizontal) and structural relaxation (vertical) steps. This analysis for [(en)₂RuL_NN]^+3/+2/+1/0 (Fig. 4) indicates a negligible contribution from the geometry change (∼0.06 eV) to the overall reduction (2.2 eV to 5.5 eV) in the case of benzoquinonidiimine in (en)₂RuL_NN. This finding implies that structural flexibility is not a prerequisite of ligand redox-activity in line with the occurrence of “hidden-noninnocence”,^66,67 where non-innocent behaviour does not manifest in any characteristic structural change of the ligand. As a result, the electron attachment process dominates the overall energetics of ligand-based reductions and this is to a large extent predetermined by the electron affinity of the complex, as implied by a correlation between measured potentials and calculated electron affinities for subsets of molecules.⁶⁸

From a pragmatic point of view, one might say that the electron affinity of these complexes depends on the intrinsic electron affinity of the ligand and on the discussed change in the metal–ligand interaction in the case of ligand based electron additions. While the machinery of changing M–L interactions upon reduction is thoroughly discussed above, we still need to account for the intrinsic electron affinity of the ligand.⁶⁹ A high intrinsic electron affinity can be linked to a low-lying LUMO in general; for organic molecules, even good correlations between LUMO energies and computed/measured electron affinities have been demonstrated.⁷⁰ Thus, an intrinsically low-lying LUMO makes a ligand a good candidate to behave redox-actively in the presence of an appropriate metal. However, whether a ligand with a low-lying LUMO does indeed become redox active in a complex depends strongly on its binding to the metal and its ability to undergo the described critical change upon reduction.

The above analysis provides a simple understanding for the superb redox activity of orthoquinoid and α-diimine derivatives, and, moreover, for many other redox non-innocent ligands based on the X=CR–CR=Y scaffold, such as L_ONO⁷¹ and L_ONNO⁷² in Fig. 5 and more recent scaffolds.^73–75 It is even potentially applicable to ligands with longer unsaturated tethering chains, such nacnac or acac (Fig. 5).

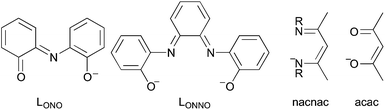Fig. 5 Arbitrary selection of redox active ligands, for which the same mechanisms presumably operate as for orthoquinoid derivatives.

Nevertheless, to derive useful guidelines for redox-active ligand design we needed to expand our study to a representative set of complexes, where we introduced various perturbations to influence the intrinsic electron affinity of the ligand and/or the M–L interactions. Thus, using the redox series of general formula [(en)₂RuL]^+3/+2/+1/0 and various redox-active ligands (L) in Fig. 2b we determined and quantified the most relevant ligand related factors that control the thermodynamics of ligand-based reductions, such as the electronegativity of the contact atoms, substitution, and nonaromatic-to-aromatic and aromatic-to-nonaromatic transitions.⁷⁶Table 1 lists the redox potentials (E⁰vs. Fc/Fc⁺) for the three-electron redox series of octahedral ruthenium complexes with one redox active ligand (L) and two spectator 1,2-diaminoethane (en) ligands, computed using the assessed protocol described in the ESI.† The +3 to +2 transition corresponds to a formal metal-centred Ru^III to Ru^II reduction, whereas +2 to +1 and +1 to 0 transitions formally represent gradual one-electron reduction of the redox-active L ligand.

Table 1 Reduction potentials vs. Fc/Fc⁺, E⁰, in volts, computed in acetonitrile

[(en)2RuL]^n	+3 → +2	+2 → +1	+1 → 0
LNN	0.54	−1.26	−2.70
LNO	0.85	−0.77	−2.48
LOO	1.04	−0.20	−2.02
L^NO2	0.85	−0.75	−2.15
L^OMe	0.43	−1.42	−2.76
L^Cl	0.63	−1.13	−2.59
L^Me	0.45	−1.35	−2.73
^iL^CH2	0.31	−1.80	−3.07
bpy	0.31	−2.08	−3.19
bpy^Me	0.24	−2.25	−3.34
^ibpy^CH2	0.36	−1.49	−2.65
bdp	0.50	−0.28	−1.60

---

Based on Sanderson's geometric mean postulate⁷⁷ on the electronegativity of molecules and on Mülliken's definition of electronegativity,⁷⁸ the electron affinity of molecules is directly related to the electronegativity of the constituent atoms: the higher the electronegativity of the atoms, the higher the electron affinity of the molecule. Replacing the NH contact functionalities in L_NN with more electronegative oxygen atoms in L_NO and L_OO we indeed found that ligand-based reductions became easier by about 0.5 V per NH to O substitution (+2 to +1 and +1 to 0 transitions in Table 1), which can be explained on the basis of the higher electronegativity of oxygen vs. nitrogen. This finding agrees quantitatively with experimental data for analogous [(bpy)₂RuL_NN]^+2/+1 and [(bpy)₂RuL_OO]^+2/+1 transitions differing in redox potentials by 0.99 V.^79,80 In addition, since oxygen is a worse electron donor than nitrogen in NH, the metal centre becomes more electron deficient and the metal-based reduction (+3 → +2) also gets easier by about 0.3 V when going from L_NN to L_NO and to L_OO.

Functionalization is another effective way of altering the redox activity of ligands. Since substitution affects the energy of the redox active orbital(s), it is expected to directly influence the energetics of ligand-based reductions. Accordingly, we altered the parent L_NN ligand at the C4 position with electron withdrawing (NO₂, Cl) and donating (OMe, CH₃) substituents (Fig. 2b). As could be expected, modulation of the π-subspace has a larger effect than that of the σ-subspace. Namely, π-withdrawing (NO₂) groups facilitate ligand-centred electron transfer by about ∼0.5 V (compare L_NN with L^NO₂), whereas π-donating (OMe) groups decrease the redox potential for L^0/−1 and L^−1/−2 transitions by ∼0.1 V on average. Ligand-based redox processes are less sensitive (less than 0.1 V) to inductive effects, as in the case of L^Me and L^Cl. These values, including the shifts for the Ru^III/II transitions, are also in quantitative agreement with experimental observations for C4 substituted benzoquinonediimine in (acac)₂RuL_NN systems.²¹

In addition, it is critical to realize that the benzo-C₆ ring of these ligands undergoes a formal antiaromatic-to-aromatic (4e⁻ to 6e⁻) transition (Fig. 2) upon two-electron reduction. To the best of our knowledge not much attention has been devoted to this aspect; however, if it is indeed so, such a transition could ease the reduction process by approximately 1.3 V, based on an estimation of the aromatic stabilization of benzene of ∼30 kcal mol⁻¹. First, we probed the aromaticity of the ring in the ligand through a magnetic criterion, the so-called Nucleus Independent Chemical Shift (NICS)^81,82 values in the centre of the benzo-C₆ ring, as well as 1 Å above the centre, called NICS(1), both being established measures of aromaticity. Herein NICS values are discussed only for the parent (en)₂RuL_NN^+3/+2/+1/0 series, also given in Fig. 2a, because very similar trends could be deducted for the related structures investigated. The NICS values of 7.2, 0.3, −4.4 and −8.0 along the [(en)₂RuL_NN]^+3/+2/+1/0 series clearly indicate a gradual aromatization of the C₆ ring fragment upon reduction and a diatropic ring-current of strength similar to benzene⁸³ in the most reduced form [(en)₂RuL_NN]⁰.

Moreover, the energetic stabilization through the aromatization in the various reduction steps in benzoquinonediimine was probed through the ‘isomerization method’^84,85 of Schleyer (L^Mevs.ⁱL^CH₂). The isomerization method is on the comparison of two constitutional isomers differing only in the presence and absence of ring delocalization, thus, probing the so-called aromatic stabilization energy (ASE). In our ligand set L^Me and ⁱL^CH₂ are constitutional isomers and exhibit the same length of delocalization; however, ring-currents are present in L^Me, and absent in ⁱL^CH₂ due to the saturated sp³ carbon in the ring. Instead of directly comparing the energies of these isomeric species in various oxidation states we rather compare the redox potentials of the various steps to reveal the effect of build-up of aromaticity during the reduction of (en)₂RuL^Me. The contribution of cyclic delocalization, i.e. aromaticity, to the redox potential is 0.14 V, 0.45 V and 0.34 V in the consecutive redox steps of the [(en)₂RuL^Me]^+3/+2/+1/0 series, respectively. The resulting effect of 0.93 V for this nonaromatic-to-aromatic transition significantly eases ligand-centred reductions of benzo-fused ligands and agrees in magnitude with the expected value of about 30 kcal mol⁻¹, the aromatic stabilization of benzene.⁸⁶ This nonaromatic-to-aromatic transition augments the above discussed redox-active behaviour of the X=C–C=Y binding motif and, as such, these results provide strong support to Caulton's intuitive proposal that the six-membered ring “merely alters redox potentials, but makes no fundamental change”.⁷

In the light of these findings it is easy to understand why the bpy ligand, which exhibits the same optimal N=C–C=N motif augmented with a much larger delocalized backbone than benzoquinonediimine (L_NN), does not tend to accept electrons easily:⁷⁹ reduction of bpy to bpy⁻¹ and to bpy⁻² induces a loss of aromatic stabilization of the ligand that suppress ligand redox activity. The intrinsically aromatic (6e⁻) pyridine rings of bpy become nonaromatic and thus less stable upon one- and two-electron reduction. To assess the contribution of this effect to the redox properties of bpy we used an isomerization method analogous to that introduced for the benzoquinonediimine derivative above: bpy^Me, i.e. the (bis)methyl derivative of bpy (Fig. 2b) is aromatic in the oxidized form and expected to lose aromatic stabilization upon reduction, whereas no cyclic delocalization of any kind can develop in the structural isomer ⁱbpy^CH₂. Accordingly, we expect that it is much easier to reduce ⁱbpy^CH₂ than bpy^Me, since the former is not destabilized by any aromatic-to-nonaromatic transition upon reduction as opposed to bpy^Me. Comparison of the redox potentials for these two derivatives indicates that the penalty for the aromatic-to-nonaromatic transition in bpy is as much as 0.7 V (bpy^Mevs.ⁱbpy^CH₂) for both bpy/bpy⁻¹ and bpy⁻¹/bpy⁻² transitions. The emphasized nonaromatic-to-aromatic transition in L_NN and aromatic-to-nonaromatic transition in bpy actually reveal the experimentally observed differences in the redox-activity of benzoquinonediimine and bipyridine and, also, it provides quantitative support to Caulton's hypothesis that “an aromatic system makes reduction (where aromaticity is interrupted) more energetically costly”.⁷

Finally, to test the predictive power of our rules we ‘designed’ a hitherto unknown benzodipyrrole ligand (bdp, Fig. 2b), which contains three nonaromatic rings that synchronously become aromatic upon two-electron reduction. We find that the first electron reduction of bdp indeed is very feasible (Table 1), taking place at −0.28 V, i.e. at a 1 V more positive potential than the easily reducible benzoquininediimine (L_NN) ligand. The second electron reduction of bdp also takes place at a very positive potential compared to the other studied ligands indicating that the anticipated synchronous nonaromatic-to-aromatic transitions indeed significantly ease ligand-centred electron transfers. Finally, such a positive shift in the first ligand reduction for bdp results in a potential separation of only 0.78 V for the formally Ru^III/II and bdp^0/−1 transitions showing that the derived simple rules might be applicable in efficient redox-leveling (moderating redox potentials) to avoid high activation overpotential in multielectron transitions.

Conclusions

This work provides new conceptual understanding for metal–ligand interaction-governed redox-active behaviour of quinoid derivatives and, more generally, redox-active ligands containing the X=C–C=Y structural motif, where X and Y are electronegative contact atoms, such as N, O or S (see e.g.Fig. 2 and 5). A central finding is that the electron density accumulates predominantly on the contact atoms upon reduction, whereas delocalization to the carbon-based backbone of the ligand is not as apparent as expected based on the spatial distribution of the redox active LUMO. This finding implies that electrostatic interaction and σ-donation are critically more stabilizing in the reduced form than in the oxidized form of the complexes, unambiguously supported by energy decomposition and NOCV analyses in the various oxidation states. Thus, the change in M–L bonding upon reduction is a key thermodynamic driving force for facilitating ligand-centered electron transfers. Another important factor, though not a prerequisite according to our findings, is an intrinsically low-lying ligand LUMO orbital, which might manifest, depending also on the metal–ligand binding mode, in an easy ligand-centred reduction. Through an extensive investigation we demonstrated that the redox potential of ligand-based reductions can be further tuned by changing the contact atoms, with substitution affecting the π-subspace and using transitions of increasing aromaticity upon reduction. As demonstrated for bipyridine (bpy), aromatic-to-nonaromatic transitions significantly suppress redox-activity (by 0.7 V for bpy); thus for designing efficient redox active ligands one should avoid aromatic systems. Subsequently, the recipe for reducing non-innocent ligands is to use electronegative contact atoms tethered with a delocalized chain to avoid unstable localized radicals upon reduction, but to exclude aromatic frames that drastically reduce the electron accepting capacity when undergoing aromatic-to-nonaromatic transitions.

Acknowledgements

FDP and PG wish to acknowledge the VUB for a Strategic Research Program. BP thanks FWO (1279414N) and the OTKA-Hungarian Research Fund (HUMAN_MB08-1-2011-0018) for the financial support.

References

1. O. R. Luca and R. H. Crabtree, Chem. Soc. Rev., 2013, 42, 1440–1459.
2. V. Lyaskovskyy and B. de Bruin, ACS Catal., 2012, 2, 270–279.
3. W. I. Dzik, J. I. Van der Vlugt, J. N. H. Reek and B. de Bruin, Angew. Chem., Int. Ed., 2011, 50, 3356–3358.
4. P. J. Chirik and K. Wieghardt, Science, 2010, 327, 794–795.
5. W. Kaim and B. Schwederski, Coord. Chem. Rev., 2010, 254, 1580–1588.
6. M. D. Ward and J. A. McCleverty, J. Chem. Soc., Dalton Trans., 2002, 275–288.
7. K. G. Caulton, Eur. J. Inorg. Chem., 2012, 435–443.
8. W. Kaim, Eur. J. Inorg. Chem., 2012, 343–348.
9. K. Ray, T. Petrenko, K. Wieghardt and F. Neese, Dalton Trans., 2007, 1552–1566.
10. K. Ray, A. Begum, T. Weyhermüller, S. Piligkos, J. Van Slageren, F. Neese and K. Wieghardt, J. Am. Chem. Soc., 2005, 127, 4403–4415.
11. K. Ray, E. Bill, T. Weyhermüller and K. Wieghardt, J. Am. Chem. Soc., 2005, 127, 5641–5654.
12. S. Sproules and K. Wieghardt, Coord. Chem. Rev., 2010, 254, 1358–1382.
13. K. Ray, T. Weyhermüller, A. Goossens, M. W. J. Crajé and K. Wieghardt, Inorg. Chem., 2003, 42, 4082–4087.
14. K. Ray, T. Weyhermüller, F. Neese and K. Wieghardt, Inorg. Chem., 2005, 44, 5345–5360.
15. T. Petrenko, K. Ray, K. E. Wieghardt and F. Neese, J. Am. Chem. Soc., 2006, 128, 4422–4436.
16. S. Sproules and K. Wieghardt, Coord. Chem. Rev., 2011, 255, 837–860.
17. M. Haga, E. S. Dodsworth and A. B. P. Lever, Inorg. Chem., 1986, 25, 447–453.
18. R. A. Metcalfe and A. B. P. Lever, Inorg. Chem., 1997, 36, 4762–4771.
19. R. Santana da Silva, S. I. Gorelsky, E. S. Dodsworth, E. Tfouni and A. B. P. Lever, J. Chem. Soc., Dalton Trans., 2000, 4078–4088.
20. P. R. Auburn, E. S. Dodsworth, M. Haga, W. Liu, W. A. Nevin and A. B. P. Lever, Inorg. Chem., 1991, 30, 3502–3512.
21. A. B. P. Lever, Coord. Chem. Rev., 2010, 254, 1397–1405.
22. S. I. Gorelsky, E. S. Dodsworth, A. B. P. Lever and A. A. Vlcek, Coord. Chem. Rev., 1998, 174, 469–494.
23. A. B. P. Lever and S. I. Gorelsky, Coord. Chem. Rev., 2000, 208, 153–167.
24. A. B. P. Lever, H. Masui, R. A. Metcalfe, D. J. Stufkens, E. S. Dodsworth and P. R. Auburn, Coord. Chem. Rev., 1993, 125, 317–331.
25. S. I. Gorelsky, A. B. P. Lever and M. Ebadi, Coord. Chem. Rev., 2002, 230, 97–105.
26. P. Chaudhuri, C. N. Verani, E. Bill, E. Bothe, T. Weyhermüller and K. Wieghardt, J. Am. Chem. Soc., 2001, 123, 2213–2223.
27. H. Chun, C. N. Verani, P. Chaudhuri, E. Bothe, E. Bill, T. Weyhermüller and K. Wieghardt, Inorg. Chem., 2001, 40, 4157–4166.
28. X. Sun, H. Chun, K. Hildenbrand, E. Bothe, T. Weyhermüller, F. Neese and K. Wieghardt, Inorg. Chem., 2002, 41, 4295–4303.
29. D. Herebian, E. Bothe, F. Neese, T. Weyhermüller and K. Wieghardt, J. Am. Chem. Soc., 2003, 125, 9116–9128.
30. D. Herebian, E. Bothe, E. Bill, T. Weyhermüller and K. Wieghardt, J. Am. Chem. Soc., 2001, 123, 10012–10023.
31. E. Bill, E. Bothe, P. Chaudhuri, K. Chlopek, D. Herebian, S. Kokatam, K. Ray, T. Weyhermüller, F. Neese and K. Wieghardt, Chem.–Eur. J., 2005, 11, 204–224.
32. R. Kapre, K. Ray, I. Sylvestre, T. Weyhermüller, S. DeBeer George, F. Neese and K. Wieghardt, Inorg. Chem., 2006, 45, 3499–3509.
33. C. Remenyi and M. Kaupp, J. Am. Chem. Soc., 2005, 127, 11399–11413.
34. K. J. Blackmore, N. Lal, J. W. Ziller and A. F. Heyduk, J. Am. Chem. Soc., 2008, 130, 2728–2729.
35. F. Lu, R. A. Zarkesh and A. F. Heyduk, Eur. J. Inorg. Chem., 2012, 467–470.
36. K. J. Blackmore, J. W. Ziller and A. F. Heyduk, Inorg. Chem., 2005, 44, 5559–5561.
37. L_NO = 2,4-di-tert-butyl-6-tert-butylamidophenolate.
38. L_NN = N,N′-bis(neo-pentyl)-orthophenylenediamide.
39. N. A. Ketterer, H. Fan, K. J. Blackmore, X. Yang, J. W. Ziller, M.-H. Baik and A. F. Heyduk, J. Am. Chem. Soc., 2008, 130, 4364–4374.
40. M. R. Haneline and A. F. Heyduk, J. Am. Chem. Soc., 2006, 128, 8410–8411.
41. J. I. Van der Vlugt, Eur. J. Inorg. Chem., 2012, 363–375.
42. A. L. Smith, K. I. Hardcastle and J. D. Soper, J. Am. Chem. Soc., 2010, 132, 14358–14360.
43. D. Kalinina, C. Dares, H. Kaluarachchi, P. G. Potvin and A. B. P. Lever, Inorg. Chem., 2008, 47, 10110–10126.
44. J. Li, L. Noodleman and D. A. Case, ed. E. I. Solomon and A. B. P. Lever, Electronic Structure Calculations: Density Functional Methods with Application to Transition Metal Complexes, Wiley, New York, 1999, vol. I, pp. 661–724.
45. R. K. Szilagyi, B. S. Lim, T. Glaser, R. H. Holm, B. Hedman, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 2003, 125, 9158–9169.
46. F. Zielinski, V. Tognetti and L. Joubert, Chem. Phys. Lett., 2012, 527, 67–72.
47. All redox potentials in this paper are given with reference to the Fc/Fc⁺ couple.
48. M. W. Lehmann and D. H. Evans, J. Electroanal. Chem., 2001, 500, 12–20.
49. M. Haga, K. Isobe, S. R. Boone and C. G. Pierpont, Inorg. Chem., 1990, 29, 3795–3799.
50. See the ESI† for details.
51. T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10.
52. T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1558–1565.
53. T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1755–1759.
54. F. M. Bickelhaupt and E. J. Baerends, Rev. Comput. Chem., 2000, 15, 1–86.
55. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
56. B. Pinter, T. Fievez, F. M. Bickelhaupt, P. Geerlings and F. De Proft, Phys. Chem. Chem. Phys., 2012, 14, 9846–9854.
57. M. Mitoraj and A. Michalak, Organometallics, 2007, 26, 6576–6580.
58. M. Mitoraj and A. Michalak, J. Mol. Model., 2007, 13, 347–355.
59. M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975.
60. M. Mitoraj, M. Parafiniuk, M. Srebro, M. Handzlik, A. Buczek and A. Michalak, J. Mol. Model., 2011, 17, 2337–2352.
61. R. Kurczab, M. P. Mitoraj, A. Michalak and T. Ziegler, J. Phys. Chem. A, 2010, 114, 8581–8590.
62. For other applications of NOCV orbitals see e.g. B. Pinter, V. Van Speybroeck, M. Waroquier, P. Geerlings and F. De Proft, Phys. Chem. Chem. Phys., 2013, 15, 17354–17365.
63. M.-H. Baik, T. Ziegler and C. K. Schauer, J. Am. Chem. Soc., 2000, 122, 9143–9154.
64. R. L. Lord, F. A. Schultz and M.-H. Baik, Inorg. Chem., 2010, 49, 4611–4619.
65. R. L. Lord, C. K. Schauer, F. A. Schultz and M.-H. Baik, J. Am. Chem. Soc., 2011, 133, 18234–18242.
66. M. M. Khusniyarov, E. Bill, T. Weyhermüller, E. Bothe and K. Wieghardt, Angew. Chem., Int. Ed., 2011, 50, 1652–1655.
67. L. K. Blusch, K. E. Craigo, V. Martin-Diaconescu, A. B. McQuarters, E. Bill, S. Dechert, S. DeBeer, N. Lehnert and F. Meyer, J. Am. Chem. Soc., 2013, 135, 13892–13899.
68. S. B. Bateni, K. R. England, A. T. Galatti, H. Kaur, V. A. Mendiola, A. R. Mitchell, M. H. Vu, B. F. Gherman and J. A. Miranda, Beilstein J. Org. Chem., 2009, 5, 82.
69. Within the fragment-based approach that we followed for the Ziegler–Rauk energy decomposition analysis (e.g.Fig. 3) a low-lying LUMO manifests in a small electronic preparation penalty, denoted typically as ΔE_strain, when forming L_NN⁻¹ and L_NN⁻² from L_NN. A detailed analysis of this relationship for an extensive set of molecules is beyond the scope of this conceptual study and will be published elsewhere.
70. C.-G. Zhan, J. A. Nichols and D. A. Dixon, J. Phys. Chem. A, 2003, 107, 4184–4195.
71. P. Chaudhuri, M. Hess, J. Müller, K. Hildenbrand, E. Bill, T. Weyhermüller and K. Wieghardt, J. Am. Chem. Soc., 1999, 121, 9599–9610.
72. P. Chaudhuri, M. Hess, U. Flörke and K. Wieghardt, Angew. Chem., Int. Ed., 1998, 37, 2217–2220.
73. D. L. J. Broere, L. L. Metz, B. de Bruin, J. N. H. Reek, M. A. Siegler and J. I. Van der Vlugt, Angew. Chem., Int. Ed., 2015, 54, 1516–1520.
74. S. Ghosh and M.-H. Baik, Chem.–Eur. J., 2015, 21, 1780–1789.
75. B. de Bruin, E. Bill, E. Bothe, T. Weyhermüller and K. Wieghardt, Inorg. Chem., 2000, 39, 2936–2947.
76. Metallacycle aromaticity, i.e. stabilization originating from the cyclic delocalization in the M–X=C–C=Y five-member ring, has been also assumed to contribute to the stabilization of related complexes. Via a well-constructed homodesmic reaction (see e.g. K. K. Baldridge and M. S. Gordon, J. Am. Chem. Soc., 1988, 110, 4204–4208 ). We quantified this stabilization to be relatively small, about 5.6 kcal mol⁻¹ in the most affected [(en)₂RuL_NN]⁺² form, and to change by about 0.3 eV along the entire redox series of [(en)₂RuL_NN]^+3/+2/+1/0. Due to its insignificant contribution and the rather technical nature of the characterization method we do not discuss these findings in this study, but will present them elsewhere.
77. R. T. Sanderson, Chemical Bonds and Bond Energy, Academic Press, New York, 1976.
78. R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840.
79. H. Masui, A. B. P. Lever and E. S. Dodsworth, Inorg. Chem., 1993, 32, 258–267.
80. M. Ebadi and A. B. P. Lever, Inorg. Chem., 1999, 38, 467–474.
81. P. v. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. v. E. Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318.
82. Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v. R. Schleyer, Chem. Rev., 2005, 105, 3842–3888.
83. For comparison, the NICS value of benzene is −8.4 at the same level of theory.
84. C. S. Wannere, D. Moran, N. L. Allinger, B. A. Hess, L. J. Schaad and P. v. R. Schleyer, Org. Lett., 2003, 5, 2983–2986.
85. P. v. R. Schleyer and F. Pühlhofer, Org. Lett., 2002, 4, 2873–2876.
86. I. Fernandez, G. Frenking and G. Merino, Chem. Soc. Rev., 2015 10.1039/c5cs00004a.

---

Footnote

† Electronic supplementary information (ESI) available: Computational protocols and equilibrium structures. See DOI: 10.1039/c5sc01140j

---