Open Access Article
Open Access ArticleOvercoming aggregation in indium salen catalysts for isoselective lactide polymerization†
D. C.
Aluthge
,
J. M.
Ahn
and
P.
Mehrkhodavandi
*
Department of Chemistry, University of British Columbia, 2036 Main Mall, Vancouver, BC V6T 1Z1, Canada. E-mail: mehr@chem.ubc.ca
First published on 6th July 2015
Abstract
A methodology for controlling aggregation in highly active and isoselective indium catalysts for the ring opening polymerization of racemic lactide is reported. A series of racemic and enantiopure dinuclear indium ethoxide complexes bearing salen ligands [(ONNOR)InOEt]2 (R = Br, Me, admantyl, cumyl, t-Bu) were synthesized and fully characterized. Mononuclear analogues (ONNOR)InOCH2Pyr (R = Br, t-Bu, SiPh3) were synthesized by controlling aggregation with the use of chelating 2-pyridinemethoxide functionality. The nuclearity of metal complexes was confirmed using PGSE NMR spectroscopy. Detailed kinetic studies show a clear initiation period for these dinuclear catalysts, which is lacking in their mononuclear analogues. The polymerization behavior of analogous dinuclear and mononuclear compounds is identical and consistent with a mononuclear propagating species. The isotacticity of the resulting polymers was investigated using direct integration and peak deconvolution methodologies and the two were compared.
Introduction
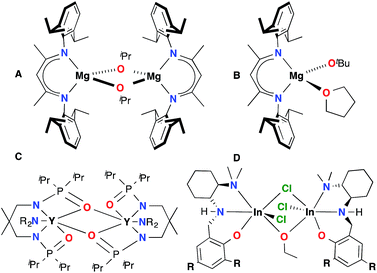
Poly (lactic acid) (PLA) is a biodegradable polyester1 with increasing impact in emerging markets2 and numerous commercial3 and cutting edge scientific4 applications. Attempts to extend this range of applications have focused on improving PLA macro-5 and microstructure.6 A major challenge in the field is the ring opening polymerization (ROP) of a mixture of lactide isomers to yield PLA with controlled mechanical properties. A benchmark study in this field is the site selective polymerization of racemic lactide (rac-LA) to form isotactic PLA. Although organo-7 and metal catalysts6 ranging the entire periodic table8 have been evaluated for this reaction, only a few have generated highly isotactic PLA material.9 Trivalent metals supported by salen10 and phosphasalen11 type ligands have been particularly successful. While aluminum catalysts have been prevalent in the literature,6a recent work by our group12 and others9f,h,13 shows that indium complexes have the potential to be more reactive and functional group tolerant than their aluminum analogues.The majority of ROP catalysts are comprised of a chelate-supported Lewis acidic metal centre with an alkoxide initiator built in or generated in situ via alcoholysis.1 Due to the electrophilicity of the metal centres and the bridging ability of the alkoxide ligands, aggregation is observed in many of these systems.13h,l,14 While aggregation can be beneficial in some cases,15 in others it can lead to poor control over catalyst speciation and reactivity, as well as polymer macro- and microstructure (Chart 1).16 For example, dinuclear isopropoxide bridged β-diiminate magnesium complex A16d is not selective for the polymerization of rac-LA, while the mononuclear analogue B17 is highly heteroselective. Aggregation impacts polymerization processes by generating competing active species, as observed for complex C.16f In our asymmetrically-bridged indium systems D, any disturbance of catalyst nuclearity leads to loss of stereoselectivity and complicates isolation of discrete complexes.18 Similar studies on the role of steric effects on catalyst selectivity of aluminum salen complexes show that these trends are not entirely predictable.10n While the issue of aggregation persists in the literature, to the best of our knowledge no broadly applicable strategy has been put forward to overcome this challenge.
Aggregation phenomena are especially important for complexes bearing trivalent indium complexes due to their Lewis acidity and large ionic radii.12b In a recent communication, we reported a dinuclear indium salen alkoxide complex which is a highly active and isoselective catalyst for the ring-opening polymerization of racemic lactide at room temperature.12a Herein, we report our full investigations into the structure reactivity relationships of these catalysts, the aggregation phenomena we encountered, and the general strategy we developed to overcome aggregation in this system. We also investigate the isoselectivity of these systems in detail and discuss two different methods of quantifying Pm values for isotactic PLA. Finally, we discuss the nature of the propagating species and evaluate the efficacy of salen supports for indium complexes.
Results and discussion
Synthesis and characterization of complexes
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH resonances. In the corresponding 13C{1H} spectra, the N
CH resonances. In the corresponding 13C{1H} spectra, the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH resonances appear at >160 ppm.
CH resonances appear at >160 ppm.
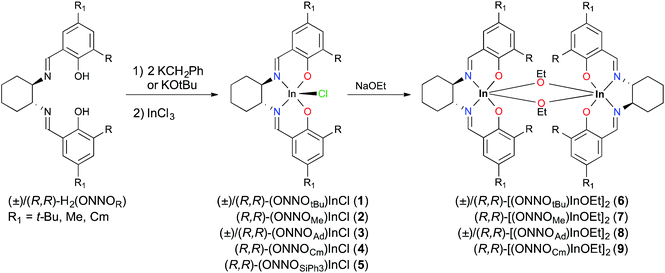
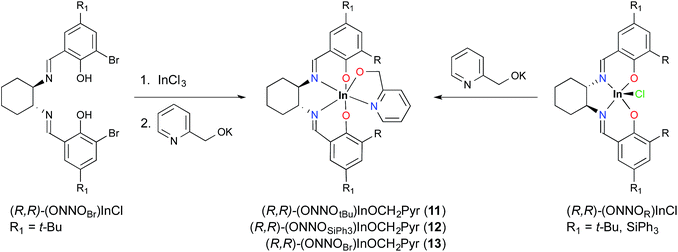
Metallation reactions are ligand dependent and can be carried out via two routes. The first is deprotonation of the proligands followed by salt metathesis with an appropriate indium trihalide compound, as reported for (±)/(R,R)-1 previously.12a Deprotonation of (±)/(R,R)-H2(ONNOR) with two equiv. of KCH2Ph or KOt-Bu, followed by addition of one equiv. of InCl3, yields the respective racemic or enantiopure indium chloride derivatives (±)/(R,R)-(ONNOR)InCl (R = t-Bu 1, Me 2, Ad 3, Cm 4, SiPh35) (Scheme 1). However, similar reactions with (R,R)-H2(ONNOBr) form intractable mixtures, necessitating a different synthetic route towards alkoxide complexes as described later in this work. The 1H NMR spectra of complexes (±)/(R,R)-1–5 show two singlet resonances corresponding to the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH group between 8 and 9 ppm, indicative of the loss of the C2 rotational axis of the ligand after metallation. The 1H NMR spectra of the racemic complexes are identical to their enantiopure analogues (Fig. S5–S12†).
CH group between 8 and 9 ppm, indicative of the loss of the C2 rotational axis of the ligand after metallation. The 1H NMR spectra of the racemic complexes are identical to their enantiopure analogues (Fig. S5–S12†).
The solid state structures of (±)-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12a and (±)-3 (Fig. S39†), determined by single crystal X-ray crystallography, contain five-coordinate indium centers with unremarkable distorted square pyramidal geometries. In contrast, the structure of (R,R)-2·CH3CN, obtained in acetonitrile, has a distorted octahedral geometry with an acetonitrile molecule coordinating to the indium trans to the chloride (Fig. S40†). The In–Cl distance in (R,R)-2·CH3CN (Å) is longer than the In–Cl bond distances in either (±)-1 or (±)-3 (2.470(1), 2.371(2) and 2.3704(7) Å for 2·CH3CN, 1, and 3 respectively) and can be attributed to the trans influence from the coordinating acetonitrile.
12a and (±)-3 (Fig. S39†), determined by single crystal X-ray crystallography, contain five-coordinate indium centers with unremarkable distorted square pyramidal geometries. In contrast, the structure of (R,R)-2·CH3CN, obtained in acetonitrile, has a distorted octahedral geometry with an acetonitrile molecule coordinating to the indium trans to the chloride (Fig. S40†). The In–Cl distance in (R,R)-2·CH3CN (Å) is longer than the In–Cl bond distances in either (±)-1 or (±)-3 (2.470(1), 2.371(2) and 2.3704(7) Å for 2·CH3CN, 1, and 3 respectively) and can be attributed to the trans influence from the coordinating acetonitrile.
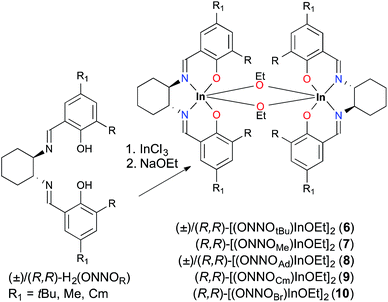
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH resonances, similar to those observed for the (ONNOR)InCl complexes. Compounds (R,R)-6–8 contain two diastereotopic multiplet resonances for the –OCH2CH3 protons between 3 and 4 ppm, while in the spectrum of (R,R)-9, perhaps as a result of the increased steric hinderance, these methylene protons appear as a quartet at 3.51 ppm (Fig. S13–S18†).
NH resonances, similar to those observed for the (ONNOR)InCl complexes. Compounds (R,R)-6–8 contain two diastereotopic multiplet resonances for the –OCH2CH3 protons between 3 and 4 ppm, while in the spectrum of (R,R)-9, perhaps as a result of the increased steric hinderance, these methylene protons appear as a quartet at 3.51 ppm (Fig. S13–S18†).
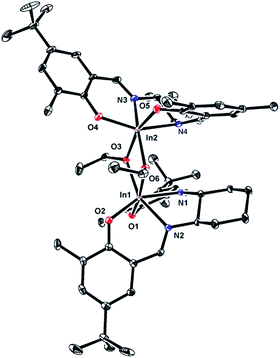
The solid state molecular structure of (R,R)-7, determined by single crystal X-ray crystallography, is analogous to that of complex (±)-6 (Fig. 1).12a Both complexes are dimeric, with distorted octahedral geometries around the indium centres and comparable bond lengths and angles. A notable difference between the structures of 6 and 7 is the distortion in the salen ligand despite the rigid cyclohexyl backbone. While 6-coordinate dimeric [(salen)Al(OR)]2 complexes are known,20 the most common coordination number for salen aluminum alkoxide complexes is five.10o,21 In contrast, the larger ionic radius of In(III) often renders indium alkoxide complexes prone to aggregation and formation of dimeric [(κ4-ligand)In(OR)]2 complexes such as those reported by us12b and others.13l,21,22
Replacement of the ethoxide group with a coordinating alkoxide, namely pyridin-2-ylmethoxide, solves this problem. This approach affords an indium–alkoxide bond where the pyridine moiety can occupy the final coordination site to form a stable six-coordinate metal center. Complexes (R,R)-11 and (R,R)-12 can be prepared using the salt metathesis route by treating (R,R)-1 and (R,R)-5, respectively, with potassium pyridin-2-ylmethoxide, KOCH2Pyr (Scheme 3). The ortho-bromo complex can be accessed in a one-pot synthesis by treating H2(ONNOBr) with InCl3 and excess KOCH2Pyr (Scheme 3). In contrast to (R,R)-11 and (R,R)-13, the bulkier complex (R,R)-12 is more challenging to obtain in pure form, with minor impurities (∼5–10%) observed by 1H NMR spectroscopy after repeated purification attempts (Fig. S26†).
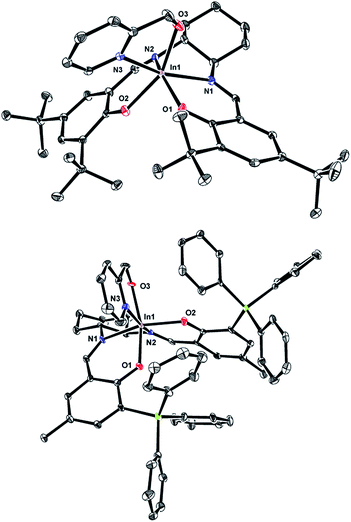
Single crystals of (R,R)-11 and (R,R)-12 can be obtained by slow evaporation from hexanes. The solid state structures of these mononuclear complexes show distorted octahedral indium centers supported by a chelating pyridyl moiety (Fig. 2). Comparison of the In–N bond distances of (R,R)-11 shows that the In–NPyr bond distance of 2.296(2) Å is longer than the two In–NImine bond distances (2.228(2) and 2.258(2) Å). In contrast, for (R,R)-12 the In–N bond distances have similar values, with In–NPyr and the two In–NImine being 2.242(7), 2.233(7), and 2.234(6) Å, respectively. The shorter In–NPyr bond for (R,R)-12 indicates stronger coordination of the pyridyl moiety. The C–Si bond distances (1.862(8)–1.874(8) Å) between the salicylaldehyde moiety and the –SiPh3 groups are considerably longer than the analogous C–C bond distances in (R,R)-11 (1.548(3)–1.539(3) Å), indicating that the steric bulk lies further away from the indium centre in (R,R)-12 compared to (R,R)-11.
The solution structures of these compounds correspond to those in the solid state. The 1H NMR spectra of (R,R)-11 and (R,R)-13 show singlets corresponding to the methylene resonances of pyridin-2-ylmethoxide at 5.03 and 4.77 ppm, respectively (Fig. S22–S27†). However in (R,R)-12, with the bulkier –SiPh3 groups, the methylene protons appear as two diastereotopic resonances at 4.59–4.54 and 4.05–4.01 ppm. This suggests fluxional behaviour of the pyridine moiety in (R,R)-11 and (R,R)-13, which is hindered in 12. Variable temperature 1H NMR spectra (CDCl3) of (R,R)-11 show the room temperature singlet at 5.03 ppm resolving into two diastereotopic resonances at −20 °C (Fig. S31†).
| Compound | D t (× 10−10 m2 s−1) | r H | r X-ray | |
|---|---|---|---|---|
| a D t was determined using PGSE NMR spectroscopy with tetrakis(trimethylsilyl)silane (TMSS) as an internal standard. [Compound] = 4.5 mM samples were prepared in 0.94 mM TMSS solution in CD2Cl2. Dt is calculated from slopes of plots of In(I/I0) vs. γ2δ2G2[Δ − (δ/3)] × 10−10 (m2 s−1). b Calculated from Dt values using a modified Stokes–Einstein equation (see ESI). c Calculated, where solid-state data is available, from the crystal structure unit cell volume (V) as well as the number of the compound of interest (n) occupying the unit cell assuming spherical shape (3V/4πn)1/3. | ||||
| 1 | H2(ONNOtBu)24 | 9.5(3) | 6.1 | 5.9 |
| 2 | (ONNOtBu)InCl (±)-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12a 12a |
9.1(2) | 6.4 | 5.9 |
| 3 | (ONNOBr)InOCH2Pyr (R,R)-13 | 8.6(5) | 6.6 | — |
| 4 | (ONNOtBu)InOCH2Pyr (R,R)-11 | 8.5(2) | 6.7 | 6.2 |
| 5 | [(ONNOBr)InOEt]2 (R,R)-10 | 6.9(4) | 8.1 | — |
| 6 | [(ONNOMe)InOEt]2 (R,R)-7 | 7.0(4) | 8.0 | 7.8 |
| 7 | [(ONNOtBu)InOEt]2 (±)-6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12a 12a |
6.5(5) | 8.5 | 8.3 |
| 8 | [(ONNOAd)InOEt]2 (R,R)-8 | 6.3(5) | 8.8 | — |
| 9 | [(ONNOCm)InOEt]2 (R,R)-9 | 6.0(4) | 9.2 | — |
The alkoxide-bridged dimers have different stabilities in solution, which can affect their reactivity with lactide. The 1H NMR spectrum of (R,R)-6 in THF-d8 shows no indication of dissociation. When (R,R)-6 is stirred in refluxing pyridine for 16 h no changes in the complex are observed in the 1H NMR spectrum (Fig. S29†). However, a similar reaction in neat ethyl acetate shows that ∼20% of the compound is converted to other products (Fig. S30†). This suggests that while the dinuclear ethoxide complex is stable in solution, it can dissociate in the presence of esters like ethyl acetate and lactide.
The relative stability of these complexes can be investigated further by using crossover experiments between the t-butyl substituted complex, (R,R)-6, and the adamantyl, and bromo-substituted analogues (R,R)-8 and (R,R)-10, respectively. Notably, the (R,R)-6/(R,R)-8 pair with bulkier ortho substituents shows almost complete crossover in 10 min (Fig. S32†) while the (R,R)-6/(R,R)-10 pair shows no evidence of a crossover product in this period and only minor crossover after 16 h (Fig. S33†). This suggests that [(ONNOBr)In(OEt)]2 is less prone to dissociation than the bulkier analogues.
Lactide polymerization studies
| Catalysta |
M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) I I |
Time (h) | Convb (%) | M ntheo (kDa) | M nGPC (kDa) | Đ | P m | P m | |
|---|---|---|---|---|---|---|---|---|---|
| a In CH2Cl2 at 25 °C, [catalyst] ≈ 1 mM. b Conversions were determined by 1H NMR spectroscopy. Mntheo = molecular weight of chain-end + 144 g mol−1 × 200 × conversion. c In THF (2 mg mL−1) and molecular weights were determined by GPC-LLS (flow rate = 0.5 mL min−1). Universal calibration was carried out with polystyrene standards, laser light scattering detector data, and concentration detector. Each experiment is duplicated to ensure precision. d Calculated according to Method A, using the relative integrals of rmr and rmm resonances (see ESI). e Calculated using Method B after performing peak deconvolution to integrate all five peaks in the methine region of 1H{1H}NMR spectra (see ESI). | |||||||||
| 1 | [(ONNOtBu)InOEt]2 (R,R)-6 | 200 | 1 | 99 | 28.5 | 34.9 | 1.39 | 0.76 | 0.85 |
| 2 | [(ONNOtBu)InOEt]2 (R,R)-6 | 600 | 4 | 99 | 85.5 | 89.5 | 1.52 | 0.75 | — |
| 3 | [(ONNOAd)InOEt]2 (R,R)-8 | 200 | 1 | 98 | 28.2 | 36.3 | 1.42 | 0.77 | 0.80 |
| 4 | [(ONNOAd)InOEt]2 (R,R)-8 | 500 | 2 | 99 | 71.3 | 69.4 | 1.33 | 0.74 | — |
| 5 | [(ONNOCm)InOEt]2 (R,R)-9 | 200 | 2 | 97 | 27.9 | 27.9 | 1.56 | 0.73 | — |
| 6 | [(ONNOCm)InOEt]2 (R,R)-9 | 500 | 5 | 98 | 70.6 | 79.0 | 1.42 | 0.72 | 0.80 |
| 7 | [(ONNOBr)InOEt]2 (R,R)-10 | 200 | 2 | 97 | 27.9 | 52.9 | 1.15 | 0.55 | — |
| 8 | [(ONNOBr)InOEt]2 (R,R)-10 | 500 | 5 | 99 | 71.3 | 97.0 | 1.35 | 0.57 | 0.70 |
| 9 | [(ONNOMe)InOEt]2 (R,R)-7 | 200 | 2 | 98 | 28.2 | 47.5 | 1.19 | 0.60 | — |
| 10 | [(ONNOMe)InOEt]2 (R,R)-7 | 500 | 5 | 99 | 71.3 | 91.7 | 1.29 | 0.62 | 0.71 |
| 11 | (ONNOtBu)InOCH2Pyr (R,R)-11 | 200 | 1 | 98 | 28.5 | 36.7 | 1.27 | 0.74 | 0.78 |
| 12 | (ONNOtBu)InOCH2Pyr (R,R)-11 | 600 | 4 | 97 | 83.5 | 86.1 | 1.37 | 0.75 | — |
| 13 | (ONNOBr)InOCH2Pyr (R,R)-13 | 200 | 0.5 | 98 | 28.2 | 35.8 | 1.15 | 0.59 | 0.69 |
| 14 | (ONNOBr)InOCH2Pyr (R,R)-13 | 500 | 0.5 | 98 | 70.6 | 70.4 | 1.25 | 0.56 | — |
| 15 | (ONNOSiPh3)InOCH2Pyr (R,R)-12 | 200 | 16 | 75 | — | — | — | 0.73 | — |
| 16 | (ONNOSiPh3)InOCH2Pyr (R,R)-12 | 200 | 24 | 93 | 26.8 | 36.7 | 1.30 | 0.75 | — |
The catalysts in this family are isoselective. The Pm values can be calculated by substituting integrations of tetrad sequences, determined using 1H{1H} NMR spectroscopy (Fig. S44–S50†). The tacticity of PLA is calculated using a set of equations derived using a Bernoullian statistical model.16d,25 While the use of these equations in the direct interpretation of integrations of 1H{1H} NMR spectra of PLA is well established,26 other reports use the subtly different methodology of peak deconvolution for calculating tacticity.9m,10s,11,26a,27 This issue has arisen partly due to the fact that with most commonly available NMR instruments, the mmr, mmm, mrm resonances overlap and cannot be integrated separately. Hence, calculation of Pm values can be based on the integration of rmr and rmm resonances in the majority of systems where perfectly isotactic PLA is not formed and stereoerrors are present (Method A) (see ESI†).
The accuracy of the Pm values calculated using deconvoluted spectra depends on the accuracy and the applicability of the deconvolution algorithm and spectral resolution. We encountered the limitations of this methodology in our systems. Inspection of the results in Table 2 shows that the deconvolution methodology has inflated the Pm values. In particular, inspection of entries 1 and 3 shows that catalysts 6 and 8 have nearly identical Pm values generated from Method A, while they have significantly different values from Method B. The discrepancy widens when comparing entries 3 and 5, with identical values for Method B and significantly different values for Method A.
Another inconsistency arises from the relationship between Pm and Pr values in this methodology. The most general form of the equations uses Pm and Pr as two independent variables, requiring the use of at least two different equations to calculate the tacticity.16d,25 However, in order to apply method B the relationship Pm = 1 − Pr must be true. In this case, these equations are reduced to expressions containing a single variable Pm values for each of the five resonances are calculated and averaged to give the final Pm value of the polymer.26a This derivation, however, is only valid for a system with exclusive site control where a single statistical event does not impact the other, not for those where both site and chain-end control may be operative such as the system under investigation here.25
While we acknowledge that there is no ideal way to calculate tacticities based on these equations due to the non-ideal behaviour of natural systems, we conclude that a comparison of Pm values obtained using the two different methods of calculation is precarious. We do not claim one method to be superior to the other; however, any comparison of literature Pm values must be carried out with consistency and transparency. In particular, Method B does not account well for systems where chain end control may be a significant contributor to selectivity such as ours.
Polymer melting point is a stronger arbiter of isotacticity in PLA. In our systems, the polymers generated from rac-LA with most stereoselective catalysts, (R,R)-6 and (R,R)-8, are amorphous (Tg ∼ 55 °C) (Fig. S37 and S38†). In comparison, Williams et al. have reported polymers with similar Pm values obtained using peak deconvolution methodology which are crystalline and have Tm values > 170 °C. Clearly, a comparison of the two systems using only the Pm values obtained using peak deconvolution is insufficient.11
A comparison of the selectivities listed in Table 2 using Method A shows that a decrease in ligand steric hinderance correlates to decreased Pm values, while increasing the steric bulk of the ligands does not result in appreciable increase in Pm values above ∼0.75. A similar observation was made by Carpentier et al. in a series of aluminum salen catalysts with a chiral diphenyl ethylene backbone for lactide polymerization, where changing the ortho substituent from t-butyl group to a methyl functionality decreased the isoselectivity from Pm ∼0.9 to ∼0.8.10s This suggests that, although the ortho substituents of the salicylaldehyde moieties play a key role in imparting stereoselectivity, the mechanism for control of selectivity may be more nuanced.
The differences in ligand steric bulk have a significant impact on rates of propagation. The cumyl-substituted complex (R,R)-9 requires longer reaction times for reaching full conversion than adamantyl substituted (R,R)-8 under the same reaction conditions. This may be due to a more sterically congested ligand environment, which hinders the approach of lactide to the metal centre. In situ monitoring of catalysts (R,R)-8 and (R,R)-9 shows first order rates for the ring opening polymerization of L-, D-, and rac-LA similar to those observed for (R,R)-6 (Fig. S52†). The plot for (R,R)-8 shows a brief initiation period followed by linear propagation, while for (R,R)-9 the initiation period is not observable. Both catalysts polymerize L-LA more rapidly than D-LA, with kL-LA/kD-LA values of 4 and 6, respectively, for (R,R)-8 and (R,R)-9 (Table 3, entries 1, 2 and 4, 5).
| Catalysta | Mb | k obs (× 10−4 s−1) | |
|---|---|---|---|
| a All reactions were carried out with 200 equiv. of monomer (M) in CD2Cl2 at 25 °C and followed to 90% conversion by 1H NMR spectroscopy. a[Catalyst] = 0.0011 M, b[M] = 0.45 M. | |||
| 1 | [(ONNOAd)InOEt]2 (R,R)-8 | D-LA | 9.4(2) |
| 2 | [(ONNOAd)InOEt]2 (R,R)-8 | L-LA | 38(8) |
| 3 | [(ONNOAd)InOEt]2 (R,R)-8 | rac-LA | 9.4(2) |
| 4 | [(ONNOCm)InOEt]2 (R,R)-9 | D-LA | 2.4(5) |
| 5 | [(ONNOCm)InOEt]2 (R,R)-9 | L-LA | 14(3) |
| 6 | [(ONNOCm)InOEt]2 (R,R)-9 | rac-LA | 2.7(5) |
| 7 | (ONNOtBu)InOCH2Pyr (R,R)-11 | D-LA | 6.1(12) |
| 8 | (ONNOtBu)InOCH2Pyr (R,R)-11 | L-LA | 29(6) |
| 9 | (ONNOtBu)InOCH2Pyr (R,R)-11 | rac-LA | 6.9(14) |
| 10 | (ONNOBr)InOCH2Pyr (R,R)-13 | D-LA | 53(11) |
| 11 | (ONNOBr)InOCH2Pyr (R,R)-13 | L-LA | 52(10) |
| 12 | (ONNOBr)InOCH2Pyr (R,R)-13 | rac-LA | 62(12) |
Aside from the loss of isotactic bias discussed earlier, a closer examination of the polymerization behaviour of [(ONNOBr)InOEt]2 (R,R)-10 and [(ONNOMe)InOEt]2 (R,R)-7 can elucidate the impact of decreased steric bulk on reaction rates (Table 2, entries 7–10). Counter-intuitively, both (R,R)-10 and (R,R)-7 polymerize 200 equiv. of rac-LA in double the time required for the bulkier (R,R)-6 under identical conditions. Furthermore, catalysts 7 and 10 are unique in the series for generating polymers with higher than expected molecular weights at low monomer loading (Table 2, entries 7 and 9).
In situ monitoring of catalysts (R,R)-7 and (R,R)-10 shows that the rates of polymerization of rac-LA for these catalysts do not have a first order dependence on lactide concentration (Fig. S53†). First order plots for the polymerization of L-, D- and rac-LA with both catalysts show long initiation periods (>1 h) compared to (R,R)-6, with (R,R)-10. This is consistent with the higher than expected molecular weights of the polymers. While first order rate constants cannot be calculated due to the curved nature of the plots, a qualitative assessment of the plots asserts that (R,R)-10 does not show a marked preference for one enantiomer of lactide over the other. This is consistent with the essentially atactic nature of the polymers generated (Pm ∼ 0.55). Complex (R,R)-7, which generates PLA with modest isotacticity (Pm ∼ 0.60), shows a higher rate for the polymerization of L-LA. These observations, in conjunction with the much shorter initiation periods observed for the bulkier complexes (R,R)-6, (R,R)-8, and (R,R)-9, suggest that the bulkier complexes undergo more facile initiation.
Polymerization data for [(ONNOtBu)In(OEt)]2 (R,R)-612a and (ONNOtBu)InOCH2Pyr (R,R)-11 are nearly identical (Table 2, entries 1, 2 and 11, 12). Both complexes show living behaviour for polymerization of rac-LA (Fig. S36†). Polymers generated with both systems are isotactically enriched, with Pm values of ∼0.75. The MALDI–TOF spectra of PLA oligomers made with both catalysts show peaks corresponding to [H(C3H4O)n(OZ)H]+ (Z = OEt or OCH2Pyr) separated by m/z ∼ 72, which indicates extensive transesterification (Fig. S34 and S35). The kobs values and kL-LA/kD-LA ratios (both 5) are consistent for (R,R)-6 and (R,R)-11 having the same propagating species (Fig. S54a†).
The only difference between complexes 6 and 11 is in the slight initiation period observed for 6, which is not observed for 11 (Fig. S52a and S54a†). This distinction is magnified for the less bulky complexes (ONNOBr)InOCH2Pyr (R,R)-13 and [(ONNOBr)InOEt]2 (R,R)-10. Mononuclear complex (R,R)-13 lacks the prolonged initiation period of its dinuclear analogue completely (Fig. S54b†) and is more active than any of the indium salen catalysts investigated in the series (Table 3, entries 10–12). Unlike (R,R)-10, the molecular weights of polymers made with (R,R)-13 at low lactide loadings match the expected values closely (Table 2, entries 7 and 13), which is consistent with the lack of initiation period. Complexes (R,R)-10 and 13 show no preference for either enantiomer of lactide and the polymers generated with both catalysts are essentially atactic; indicating that the initiation period does not affect overall selectivity (Table 2, entries 13 and 14).
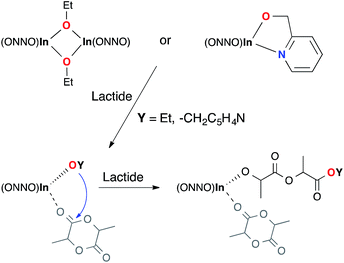
We propose a mechanism where in the initiation step, dinuclear complexes dissociate in the presence of lactide to form mononuclear propagating species (Scheme 4). The equilibria between the monomeric and dimeric forms of the catalysts are dictated by the steric bulk of the ligand substituents. The initiation periods are longer for the less bulky dinuclear complexes 7 and 10 in comparison to complexes 6 and 8. The bulkier cumyl-substituted dimer 9 does not have an observable initiation period. When mononuclear catalysts 11 and 13 are used, the initiation periods are also not observable, confirming that the initiation period is caused by the monomer–dimer equilibrium and that the active species are mononuclear.
Once aggregation is eliminated, the propagation rates for the mononuclear catalysts are entirely dependent on the ligand steric environment. The sterically bulky complex (ONNOSiPh3)InOCH2Pyr (R,R)-12 is the least active catalyst in this series of compounds and achieves >90% conversion in 24 hours (Table 2, entries 15 and 16). In contrast, (ONNOBr)InOCH2Pyr (R,R)-13, with the lowest steric bulk, has the highest reaction rate. This disparity can be attributed to the bulky ortho-phenolate groups hindering the reactivity of the monomer with the metal center. The decrease in rate does not affect selectivity; catalyst (R,R)-12 generates isotactic PLA with Pm ∼ 0.75.
The similarity in the isoselectivity of complexes 11 and 12 can be explained by examining the structures of the mononuclear complexes, as these are the propagating species (Fig. 2). It is clear that the coordination environment around the indium centres is flexible, and instead of generating a C2 symmetric axis, the ligand creates a C1 symmetric steric environment that prevents steric control of lactide coordination to the indium centres. In contrast, isoselective indium catalysts bearing tridentate half salen ligands (Chart 1D) remain dinuclear during propagation, highlighting the ligand-dependence of nuclearity in these indium based catalysts.
Conclusions
We investigated the structure/activity relationship for a series of dinuclear and mononuclear indium salen complexes. We showed that these complexes are excellent catalysts for the isoselective polymerization of racemic lactide.28 In particular, we developed a generally applicable methodology for preventing aggregation in these systems by using a coordinating alkoxide, pyridin-2-ylmethoxide.29 These mononuclear catalysts showed no initiation period and allowed us to determine that, unlike their tridentate counterparts, the propagating species for tetradentate indium salen complexes is mononuclear.Although these clearly-defined mononuclear indium complexes allowed us to explore the effects of ligand substituents with a range of steric bulk on isoselective polymerization of lactide, we determined that the large ionic radius of indium allows for a great deal of flexibility in the structure and creates a ceiling for isoselective polymerization of racemic lactide. Our future efforts will be aimed at developing a new generation of ligand supports for indium.
Acknowledgements
PM gratefully acknowledges financial support from NSERC Strategic Grant and from Green Centre Canada.Notes and references
- O. Dechy-Cabaret, B. Martin-Vaca and D. Bourissou, Chem. Rev., 2004, 104, 6147–6176 CrossRef CAS PubMed.
- M. McCoy, Chem. Eng. News, 2014, 92, 14 Search PubMed.
- G. Q. Chen and M. K. Patel, Chem. Rev., 2012, 112, 2082–2099 CrossRef CAS PubMed.
- C.-F. Cheng, H.-Y. Hsueh, C.-H. Lai, C.-J. Pan, B.-J. Hwang, C.-C. Hu and R. M. Ho, NPG Asia Mater., 2015, 7, e170 CrossRef CAS.
- (a) S. Corneillie and M. Smet, Polym. Chem., 2015, 6, 850–867 RSC; (b) M. Y. Xiong, D. K. Schneiderman, F. S. Bates, M. A. Hillmyer and K. C. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 8357–8362 CrossRef CAS PubMed; (c) M. A. Hillmyer and W. B. Tolman, Acc. Chem. Res., 2014, 47, 2390–2396 CrossRef CAS PubMed; (d) A. L. Holmberg, K. H. Reno, R. P. Wool and T. H. Epps, Soft Matter, 2014, 10, 7405–7424 RSC; (e) R. Roux, C. Ladaviere, A. Montembault and T. Delair, Mater. Sci. Eng., C, 2013, 33, 997–1007 CrossRef CAS PubMed; (f) K. Kataoka, A. Harada and Y. Nagasaki, Adv. Drug Delivery Rev., 2012, 64, 37–48 CrossRef; (g) J. K. Oh, Soft Matter, 2011, 7, 5096–5108 RSC; (h) H. Z. Liu and J. W. Zhang, J. Polym. Sci., Part B: Polym. Phys., 2011, 49, 1051–1083 CrossRef CAS.
- (a) P. J. Dijkstra, H. Z. Du and J. Feijen, Polym. Chem., 2011, 2, 520–527 RSC; (b) J. C. Buffet and J. Okuda, Polym. Chem., 2011, 2, 2758–2763 RSC; (c) C. M. Thomas, Chem. Soc. Rev., 2010, 39, 165–173 RSC; (d) M. J. Stanford and A. P. Dove, Chem. Soc. Rev., 2010, 39, 486–494 RSC; (e) K. Fukushima and Y. Kimura, Polym. Int., 2006, 55, 626–642 CrossRef CAS.
- (a) H. A. Brown and R. M. Waymouth, Acc. Chem. Res., 2013, 46, 2585–2596 CrossRef CAS PubMed; (b) N. E. Kamber, W. Jeong, R. M. Waymouth, R. C. Pratt, B. G. G. Lohmeijer and J. L. Hedrick, Chem. Rev., 2007, 107, 5813–5840 CrossRef CAS PubMed.
- (a) A. K. Sutar, T. Maharana, S. Dutta, C. T. Chen and C. C. Lin, Chem. Soc. Rev., 2010, 39, 1724–1746 RSC; (b) C. A. Wheaton, P. G. Hayes and B. J. Ireland, Dalton Trans., 2009, 4832–4846 RSC; (c) H. R. Kricheldorf, Chem. Rev., 2009, 109, 5579–5594 CrossRef CAS PubMed; (d) T. Chivers and J. Konu, Comments Inorg. Chem., 2009, 30, 131–176 CrossRef CAS.
- (a) A. Stopper, J. Okuda and M. Kol, Macromolecules, 2012, 45, 698–704 CrossRef CAS; (b) R. Heck, E. Schulz, J. Collin and J. F. Carpentier, J. Mol. Catal. A: Chem., 2007, 268, 163–168 CrossRef CAS; (c) P. L. Arnold, J. C. Buffet, R. Blaudeck, S. Sujecki and C. Wilson, Chem.–Eur. J., 2009, 15, 8241–8250 CrossRef CAS PubMed; (d) P. L. Arnold, J. C. Buffet, R. P. Blaudeck, S. Sujecki, A. J. Blake and C. Wilson, Angew. Chem., Int. Ed., 2008, 47, 6033–6036 CrossRef CAS PubMed; (e) A. Otero, J. Fernandez-Baeza, A. Lara-Sanchez, C. Alonso-Moreno, I. Marquez-Segovia, L. F. Sanchez-Barba and A. M. Rodriguez, Angew. Chem., Int. Ed., 2009, 48, 2176–2179 CrossRef CAS PubMed; (f) M. Normand, E. Kirillov, T. Roisnel and J. F. Carpentier, Organometallics, 2012, 31, 1448–1457 CrossRef CAS; (g) F. Drouin, T. J. J. Whitehorne and F. Schaper, Dalton Trans., 2011, 40, 1396–1400 RSC; (h) J.-C. Buffet, J. Okuda and P. L. Arnold, Inorg. Chem., 2010, 49, 419–426 CrossRef CAS PubMed; (i) A. Buchard, D. R. Carbery, M. G. Davidson, P. K. Ivanova, B. J. Jeffery, G. I. Kociok-Kohn and J. P. Lowe, Angew. Chem., Int. Ed., 2014, 53, 13858–13861 CrossRef CAS PubMed; (j) A. P. Dove, H. B. Li, R. C. Pratt, B. G. G. Lohmeijer, D. A. Culkin, R. M. Waymouth and J. L. Hedrick, Chem. Commun., 2006, 2881–2883 RSC; (k) L. Zhang, F. Nederberg, R. C. Pratt, R. M. Waymouth, J. L. Hedrick and C. G. Wade, Macromolecules, 2007, 40, 4154–4158 CrossRef CAS; (l) H. L. Chen, S. Dutta, P. Y. Huang and C. C. Lin, Organometallics, 2012, 31, 2016–2025 CrossRef CAS; (m) H. B. Wang, Y. Yang and H. Y. Ma, Macromolecules, 2014, 47, 7750–7764 CrossRef CAS; (n) Isotacticity can be quantified by the probability of meso linkages (Pm) in the polymer. A completely isotactic polymer would have Pm = 1.
- (a) G. Montaudo, M. S. Montaudo, C. Puglisi, F. Samperi, N. Spassky, A. LeBorgne and M. Wisniewski, Macromolecules, 1996, 29, 6461–6465 CrossRef CAS; (b) N. Spassky, M. Wisniewski, C. Pluta and A. LeBorgne, Macromol. Chem. Phys., 1996, 197, 2627–2637 CrossRef CAS; (c) T. M. Ovitt and G. W. Coates, J. Polym. Sci., Part A: Polym. Chem., 2000, 38, 4686–4692 CrossRef CAS; (d) D. Jhurry, A. Bhaw-Luximon and N. Spassky, Macromol. Symp., 2001, 175, 67–79 CrossRef CAS; (e) Z. Y. Zhong, P. J. Dijkstra and J. Feijen, Angew. Chem., Int. Ed., 2002, 41, 4510–4513 CrossRef CAS; (f) Z. Y. Zhong, P. J. Dijkstra and J. Feijen, J. Am. Chem. Soc., 2003, 125, 11291–11298 CrossRef CAS PubMed; (g) Z. H. Tang, X. S. Chen, X. Pang, Y. K. Yang, X. F. Zhang and X. B. Jing, Biomacromolecules, 2004, 5, 965–970 CrossRef CAS PubMed; (h) Z. H. Tang, X. S. Chen, Y. K. Yang, X. Pang, J. R. Sun, X. F. Zhang and X. B. Jing, J. Polym. Sci., Part A: Polym. Chem., 2004, 42, 5974–5982 CrossRef CAS; (i) N. Nomura, R. Ishii, M. Akakura and K. Aoi, J. Am. Chem. Soc., 2002, 124, 5938–5939 CrossRef CAS PubMed; (j) R. Ishii, N. Nomura and T. Kondo, Polym. J., 2004, 36, 261–264 CrossRef CAS; (k) N. Nomura, R. Ishii, Y. Yamamoto and T. Kondo, Chem.–Eur. J., 2007, 13, 4433–4451 CrossRef CAS PubMed; (l) N. Nomura, A. Akita, R. Ishii and M. Mizuno, J. Am. Chem. Soc., 2010, 132, 1750–1751 CrossRef CAS PubMed; (m) P. Hormnirun, E. L. Marshall, V. C. Gibson, A. J. P. White and D. J. Williams, J. Am. Chem. Soc., 2004, 126, 2688–2689 CrossRef CAS PubMed; (n) P. Hormnirun, E. L. Marshall, V. C. Gibson, R. I. Pugh and A. J. P. White, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15343–15348 CrossRef CAS PubMed; (o) M. H. Chisholm, N. J. Patmore and Z. P. Zhou, Chem. Commun., 2005, 127–129 RSC; (p) M. H. Chisholm, J. C. Gallucci, K. T. Quisenberry and Z. P. Zhou, Inorg. Chem., 2008, 47, 2613–2624 CrossRef CAS PubMed; (q) H. Z. Du, A. H. Velders, P. J. Dijkstra, J. R. Sun, Z. Y. Zhong, X. S. Chen and J. Feijen, Chem.–Eur. J., 2009, 15, 9836–9845 CrossRef CAS PubMed; (r) H. Z. Du, A. H. Velders, P. J. Dijkstra, Z. Y. Zhong, X. S. Chen and J. Feijen, Macromolecules, 2009, 42, 1058–1066 CrossRef CAS; (s) N. Maudoux, T. Roisnel, V. Dorcet, J. F. Carpentier and Y. Sarazin, Chem.–Eur. J., 2014, 20, 6131–6147 CrossRef CAS PubMed; (t) A. Pilone, K. Press, I. Goldberg, M. Kol, M. Mazzeo and M. Lamberti, J. Am. Chem. Soc., 2014, 136, 2940–2943 CrossRef CAS PubMed.
- (a) C. Bakewell, T. P. A. Cao, N. Long, X. F. Le Goff, A. Auffrant and C. K. Williams, J. Am. Chem. Soc., 2012, 134, 20577–20580 CrossRef CAS PubMed; (b) C. Bakewell, A. J. P. White, N. J. Long and C. K. Williams, Angew. Chem., Int. Ed., 2014, 53, 9226–9230 CrossRef CAS PubMed.
- (a) D. C. Aluthge, B. O. Patrick and P. Mehrkhodavandi, Chem. Commun., 2013, 49, 4295–4297 RSC; (b) D. C. Aluthge, E. X. Yan, J. M. Ahn and P. Mehrkhodavandi, Inorg. Chem., 2014, 53, 6828–6836 CrossRef CAS PubMed.
- (a) S. M. Quan and P. L. Diaconescu, Chem. Commun., 2015, 51, 9643–9646 RSC; (b) S. Ghosh, R. R. Gowda, R. Jagan and D. Chakraborty, Dalton Trans., 2015, 44, 10410–10422 RSC; (c) M. Normand, V. Dorcet, E. Kirillov and J. F. Carpentier, Organometallics, 2013, 32, 1694–1709 CrossRef CAS; (d) A. Kapelski and J. Okuda, J. Polym. Sci., Part A: Polym. Chem., 2013, 51, 4983–4991 CrossRef CAS; (e) L. E. N. Allan, G. G. Briand, A. Decken, J. D. Marks, M. P. Shaver and R. G. Wareham, J. Organomet. Chem., 2013, 736, 55–62 CrossRef CAS; (f) E. M. Broderick, N. Guo, C. S. Vogel, C. Xu, J. Sutter, J. T. Miller, K. Meyer, P. Mehrkhodavandi and P. L. Diaconescu, J. Am. Chem. Soc., 2011, 133, 9278–9281 CrossRef CAS PubMed; (g) M. Bompart, J. Vergnaud, H. Strub and J. F. Carpentier, Polym. Chem., 2011, 2, 1638–1640 RSC; (h) M. P. Blake, A. D. Schwarz and P. Mountford, Organometallics, 2011, 30, 1202–1214 CrossRef CAS; (i) A. Pietrangelo, S. C. Knight, A. K. Gupta, L. J. Yao, M. A. Hillmyer and W. B. Tolman, J. Am. Chem. Soc., 2010, 132, 11649–11657 CrossRef CAS PubMed; (j) M. G. Hu, M. Wang, P. L. Zhang, L. Wang, F. J. Zhu and L. C. Sun, Inorg. Chem. Commun., 2010, 13, 968–971 CrossRef CAS; (k) A. Pietrangelo, M. A. Hillmyer and W. B. Tolman, Chem. Commun., 2009, 2736–2737 RSC; (l) I. Peckermann, A. Kapelski, T. P. Spaniol and J. Okuda, Inorg. Chem., 2009, 48, 5526–5534 CrossRef CAS PubMed.
- S. Dagorne, M. Normand, E. Kirillov and J. F. Carpentier, Coord. Chem. Rev., 2013, 257, 1869–1886 CrossRef CAS.
- (a) A. F. Douglas, B. O. Patrick and P. Mehrkhodavandi, Angew. Chem., Int. Ed., 2008, 47, 2290–2293 CrossRef CAS PubMed; (b) C. Xu, I. Yu and P. Mehrkhodavandi, Chem. Commun., 2012, 48, 6806–6808 RSC; (c) I. Yu, A. Acosta-Ramirez and P. Mehrkhodavandi, J. Am. Chem. Soc., 2012, 134, 12758–12773 CrossRef CAS PubMed; (d) D. C. Aluthge, C. L. Xu, N. Othman, N. Noroozi, S. G. Hatzikiriakos and P. Mehrkhodavandi, Macromolecules, 2013, 46, 3965–3974 CrossRef CAS; (e) J. Fang, I. Yu, P. Mehrkhodavandi and L. Maron, Organometallics, 2013, 32, 6950–6956 CrossRef CAS.
- (a) B. J. O'Keefe, L. E. Breyfogle, M. A. Hillmyer and W. B. Tolman, J. Am. Chem. Soc., 2002, 124, 4384–4393 CrossRef; (b) B. J. O'Keefe, S. M. Monnier, M. A. Hillmyer and W. B. Tolman, J. Am. Chem. Soc., 2001, 123, 339–340 CrossRef; (c) C. K. Williams, L. E. Breyfogle, S. K. Choi, W. Nam, V. G. Young, M. A. Hillmyer and W. B. Tolman, J. Am. Chem. Soc., 2003, 125, 11350–11359 CrossRef CAS PubMed; (d) B. M. Chamberlain, M. Cheng, D. R. Moore, T. M. Ovitt, E. B. Lobkovsky and G. W. Coates, J. Am. Chem. Soc., 2001, 123, 3229–3238 CrossRef CAS PubMed; (e) C. K. Williams, N. R. Brooks, M. A. Hillmyer and W. B. Tolman, Chem. Commun., 2002, 2132–2133 RSC; (f) R. H. Platel, L. M. Hodgson, A. J. P. White and C. K. Williams, Organometallics, 2007, 26, 4955–4963 CrossRef CAS; (g) H. Y. Ma, T. P. Spaniol and J. Okuda, Angew. Chem., Int. Ed., 2006, 45, 7818–7821 CrossRef PubMed; (h) A. Duda and S. Penczek, Makromol. Chem., Macromol. Symp., 1991, 47, 127–140 CrossRef CAS.
- M. H. Chisholm, J. Gallucci and K. Phomphrai, Inorg. Chem., 2002, 41, 2785–2794 CrossRef CAS PubMed.
- (a) K. M. Osten, I. Yu, I. R. Duffy, P. O. Lagaditis, J. C. C. Yu, C. J. Wallis and P. Mehrkhodavandi, Dalton Trans., 2012, 41, 8123–8134 RSC; (b) K. M. Osten, D. C. Aluthge, B. O. Patrick and P. Mehrkhodavandi, Inorg. Chem., 2014, 53, 9897–9906 CrossRef CAS PubMed; (c) K. M. Osten, D. C. Aluthge and P. Mehrkhodavandi, Dalton Trans., 2015, 44, 6126–6139 RSC.
- (a) E. N. Jacobsen, W. Zhang and M. L. Guler, J. Am. Chem. Soc., 1991, 113, 6703–6704 CrossRef CAS; (b) X. Q. Yao, M. Qiu, W. R. Lu, H. L. Chen and Z. Zheng, Tetrahedron: Asymmetry, 2001, 12, 197–204 CrossRef CAS; (c) V. Rudzevich, D. Schollmeyer, D. Braekers, J. F. Desreux, R. Diss, G. Wipff and V. Bohmer, J. Org. Chem., 2005, 70, 6027–6033 CrossRef CAS PubMed; (d) C. T. Cohen, C. M. Thomas, K. L. Peretti, E. B. Lobkovsky and G. W. Coates, Dalton Trans., 2006, 237–249 RSC.
- (a) D. A. Atwood, J. A. Jegier and D. Rutherford, Inorg. Chem., 1996, 35, 63–70 CrossRef CAS PubMed; (b) T. M. Ovitt and G. W. Coates, J. Am. Chem. Soc., 2002, 124, 1316–1326 CrossRef CAS PubMed.
- D. A. Atwood and M. J. Harvey, Chem. Rev., 2001, 101, 37–52 CrossRef CAS PubMed.
- (a) D. A. Atwood, J. A. Jegier and D. Rutherford, Bull. Chem. Soc. Jpn., 1997, 70, 2093–2100 CrossRef CAS; (b) M. S. Hill and D. A. Atwood, Main Group Chem., 1998, 2, 191–202 CrossRef CAS.
- The 1H NMR spectra of incomplete reactions, after the addition of NaOEt show resonances corresponding to the respective characterized (ONNOR)InCl complexes, indicating their synthesis as an intermediate species (Fig. S28†).
- J. W. Yoon, T. S. Yoon and W. Shin, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1997, 53, 1685–1687 Search PubMed.
- F. A. Bovey and P. A. Mirau, NMR of Polymers, Academic Press, San Diego, 1996 Search PubMed.
- (a) J. Coudane, C. Ustariz-Peyret, G. Schwach and M. Vert, J. Polym. Sci., Part A: Polym. Chem., 1997, 35, 1651–1658 CrossRef CAS; (b) M. T. Zell, B. E. Padden, A. J. Paterick, K. A. M. Thakur, R. T. Kean, M. A. Hillmyer and E. J. Munson, Macromolecules, 2002, 35, 7700–7707 CrossRef CAS.
- (a) H. R. Kricheldorf, C. Boettcher and K. U. Tonnes, Polymer, 1992, 33, 2817–2824 CrossRef CAS; (b) A. M. Goldys and D. J. Dixon, Macromolecules, 2014, 47, 1277–1284 CrossRef CAS; (c) T. R. Jensen, L. E. Breyfogle, M. A. Hillmyer and W. B. Tolman, Chem. Commun., 2004, 2504–2505 RSC.
- P. Mehrkhodavandi, D. C. Aluthge, T. J. Clark, B. Mariampillai and Y. Yan, Ca. Pat., PCT/CA2013/050191, 2013.
- P. Mehrkhodavandi and D. C. Aluthge, Ca. Pat., PCT/CA2015/050601, 2014.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental section, full characterization of compounds in solution and in the solid state, polymerization and polymer analysis, details of reactivity, tacticity determination, DSC, PGSE studies, in situ polymerization studies. CCDC 1062730–1062733 and 1062738. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5sc01584g |
| This journal is © The Royal Society of Chemistry 2015 |