Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Excitonic splittings in molecular dimers: why static ab initio calculations cannot match them
Philipp
Ottiger
a,
Horst
Köppel
b and
Samuel
Leutwyler
 *a
*a
aDept. für Chemie und Biochemie, Freiestrasse 3, CH-3012 Bern, Switzerland. E-mail: leutwyler@iac.unibe.ch; Fax: +41 31 631 3940; Tel: +41 31 631 4479
bPhysikalisch-Chemisches Institut, Universität Heidelberg, Im Neuenheimer Feld 229, D-69120 Heidelberg, Germany
First published on 26th August 2015
Abstract
After decades of research on molecular excitons, only few molecular dimers are available on which exciton and vibronic coupling theories can be rigorously tested. In centrosymmetric H-bonded dimers consisting of identical (hetero)aromatic chromophores, the monomer electronic transition dipole moment vectors subtract or add, yielding S0 → S1 and S0 → S2 transitions that are symmetry-forbidden or -allowed, respectively. Symmetry breaking by 12C/13C or H/D isotopic substitution renders the forbidden transition weakly allowed. The excitonic coupling (Davydov splitting) can then be measured between the S0 → S1 and S0 → S2 vibrationless bands. We discuss the mass-specific excitonic spectra of five H-bonded dimers that are supersonically cooled to a few K and investigated using two-color resonant two-photon ionization spectroscopy. The excitonic splittings Δcalc predicted by ab initio methods are 5–25 times larger than the experimental excitonic splittings Δexp. The purely electronic ab initio splittings need to be reduced (“quenched”), reflecting the coupling of the electronic transition to the optically active vibrations of the monomers. The so-called quenching factors Γ < 1 can be determined from experiment (Γexp) and/or calculation (Γcalc). The vibronically quenched splittings Γ·Δcalc are found to nicely reproduce the experimental exciton splittings.
1 Introduction
Molecular excitons are collective excited states that are important for the function of a wide range of biological and chemical multichromophoric systems. These involve weakly interacting ultraviolet (UV) or visible chromophores with distinctly non-additive excited-state properties. Molecular excitons occur in molecular crystals, conjugated polymers with aromatic side groups, photosynthetic light-harvesting antenna systems, photosynthetic reaction centers and nucleic acids.1–11 In all of these systems, the excitonic interactions have a significant impact on the electronic structure and functions. Depending on the strength of the intermolecular electronic interactions one observes time-independent spectroscopic phenomena such as line splittings or band splittings, or alternatively time-dependent photophysical effects such as long-range energy transfer, as succinctly summarized by Förster,12 see Table 1.| Coupling Strength | Quant.-mech. Treatment | Electronic States | Experimental Effects |
|---|---|---|---|
| Strong | Stationary | Delocalized | Separated band systems |
| Weak | Stationary | Partially local. | Band splittings, intensities |
| Very weak | Time-depdt. | Localized | Excitation transfer (FRET) |
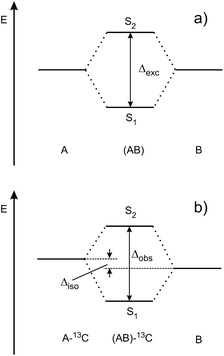
Excitonic coupling in molecular dimers and larger aggregates has been theoretically studied since the late 1950s,13–24 but only few experimental investigations have rigorously tested the predictions of exciton coupling theories. In the following, we discuss vibronically resolved ultraviolet UV spectra of symmetric molecular homo-dimers that are formed, rotationally and vibrationally cooled to a few degrees K and isolated in supersonic jets. These dimers consist of identical chromophores denoted A and B. If the A·B dimer structure is centrosymmetric (Ci or C2h) and the monomers are exchanged by an inversion î, the electronic transition-dipole moment vectors of the local S0 → S1 transitions of A and B combine exactly parallel or antiparallel. Of the resulting dimer S0 → S1 and S0 → S2 transitions, one is electric-dipole forbidden, while the other is symmetry-allowed. However, minimal symmetry perturbations such as 12C/13C- or H/D isotopic substitution lift the symmetry restrictions of the forbidden transition sufficiently to render both transitions allowed.25–30 The excitonic interaction (coupling) between A and B can then be measured as the Davydov splitting energy Δexc = 2VAB between the S0 → S1 and S0 → S2 vibrationless transitions, where VAB is the excitonic coupling matrix element.16
By combining laser vibronic spectroscopy with mass-specific (i.e. H/D or 12C/13C isotope-specific) detection, the excitonic splittings of different isotopic species can be measured. These provide strict benchmarks for the predictions of exciton and vibronic coupling theories. Current improvements of these theories31–34 can be tested and will provide a deeper understanding of excitonic interactions in dimers and larger multichromophoric systems.
In a symmetric molecular dimer A·B, the monomer S0 → S1 excitations are simultaneously subject to two interactions, (i) the exchange of the electronic excitation energy that tends to distribute the excitation uniformly over A and B and (ii) the electronic–vibrational coupling which tends to localize the excitation on either one of the monomers by linking it to a vibrational displacement. The “weak” and “strong” dimer vibronic coupling cases were defined in the 1960s in terms of the relative size of the excitonic and vibronic couplings.13–15,17 A first model treatment of linear vibronic coupling of two electronic states in a symmetric dimer was undertaken by Witkowski and Moffitt15 and by Fulton and Gouterman18,19 50 years ago; these concepts were later extended by other workers.20–24
2 Excitonic splitting: basic features
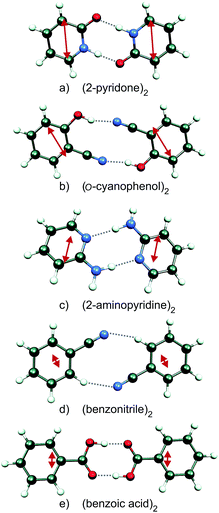
We have investigated the C2h- or C2-symmetric doubly H-bonded homodimers (2-pyridone)2, (o-cyanophenol)2, (2-aminopyridine)2, (benzonitrile)2 and (benzoic acid)2 shown in Fig. 1. The close-lying H-bond donor/acceptor groups of the monomers lead to rigid self-dimers with well-defined distances and orientations between the monomer electronic transition dipole moment vectors![[small mu, Greek, vector]](https://www.rsc.org/images/entities/b_i_char_e0e9.gif) A,
A, ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/b_i_char_e0e9.gif) B. For (2-pyridone)2, (benzonitrile)2 and (benzoic acid)2, the ground- and excited-state gas-phase structures have been determined by laser high-resolution spectroscopy.35–38 The infrared and UV spectra of the o-cyanophenol dimer, the m-cyanophenol dimer and the mixed o-cyanophenol-m-cyanophenol dimer have been investigated at vibronic resolution by Lahmani, Zehnacker and co-workers,39,40 and similarly for the anthranilic acid (2-amino-benzoic acid) dimer by Levy, Zwier and co-workers.41 We also note several theoretical and spectroscopic studies of the stacked anisole dimer,42–44 although stacked dimers are outside the scope of this short review.
B. For (2-pyridone)2, (benzonitrile)2 and (benzoic acid)2, the ground- and excited-state gas-phase structures have been determined by laser high-resolution spectroscopy.35–38 The infrared and UV spectra of the o-cyanophenol dimer, the m-cyanophenol dimer and the mixed o-cyanophenol-m-cyanophenol dimer have been investigated at vibronic resolution by Lahmani, Zehnacker and co-workers,39,40 and similarly for the anthranilic acid (2-amino-benzoic acid) dimer by Levy, Zwier and co-workers.41 We also note several theoretical and spectroscopic studies of the stacked anisole dimer,42–44 although stacked dimers are outside the scope of this short review.
Since the S0 → S1 excitation of the monomers is in-plane ππ*, the excitonic interaction in the dimer is dominated by the respective transition-dipole moment vectors, which combine in parallel or antiparallel manner, giving rise to the S0 → S1 and S0 → S2 excitations of the dimer, see Fig. 1 and 2. In the C2h dimers, one transition is Ag → Ag and is strictly electric-dipole forbidden, while the other transition is Ag → Bu, is allowed and is also experimentally observed. However, even a single 12C/13C- or H/D-isotopic substitution lead to sufficiently large deviations from inversion-symmetry as to render the Ag → Ag transition weakly allowed and observable. Mass-selective detection of the 13C-isotopomer spectra of the dimers in Fig. 1, which exhibit 10–15% of the intensity of the all 12C-isotopomers due to the natural 13C content, in combination with UV/UV holeburning techniques allow to record isotopomer-specific cold gas-phase absorption spectra.
Fig. 3 shows the spectroscopically observed splittings between the S0 → S1 and S0 → S2 transitions of the 13C-dimers in Fig. 1. As indicated in Fig. 2, the 12C/13C substitution renders the monomers unequal, hence an additional isotopic splitting Δiso arises from the isotope-induced differences of zero-point vibrational energies of the S0 and S1 states of the monomer. This results in small changes of the S0 → S1 excitation energies of the chromophores in the 13C-dimer. As a consequence the observed S1/S2 splitting Δobs is slightly larger than the purely excitonic splitting, cf.Fig. 2(b). In second order perturbation theory, the 12C/13C or H/D isotopic shift Δiso and the excitonic splitting Δexc combine as
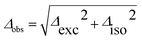 | (1) |
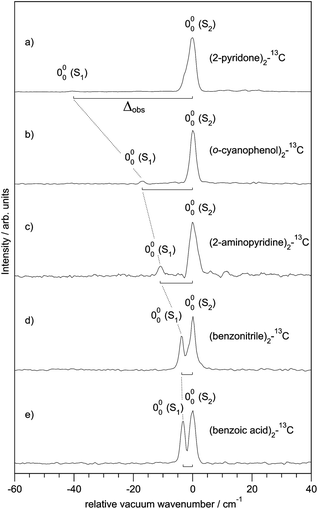 | ||
| Fig. 3 Experimentally observed splittings Δobs between the S1 and S2 electronic origins of the 13C-isotopomers of the doubly H-bonded dimers in Fig. 1. | ||
Thus the experimentally observed splittings of the singly 13C- or D-substituted dimers are upper limits to Δexc. Given a sufficiently large set of isotopomers with different Δiso contributions, the purely excitonic interaction Δexc can then be determined to within 0.5–1 cm−1.26–30
3 Experimental techniques
The dimers in Fig. 1 were produced in pulsed supersonic jets using neon carrier gas, resulting in isolated and vibrationally cold (Tvib ∼ 5 K) complexes.26,28–30 The skimmed molecular beam was spatially and temporally overlapped with an excitation and an ionization laser in the source of a time-of-flight mass spectrometer. By scanning the excitation laser wavelength, the dimers were excited from their S0 vibrational ground state to the vibrational levels of the electronic excited state and from there subsequently ionized by the ionization laser at fixed wavelength, according to a two-color resonant two-photon ionization scheme (2C-R2PI). Recording the ion current at different mass channels in dependence of the excitation wavelength yields mass selective absorption spectra of the complexes. The use of UV/UV depletion and holeburning techniques, where the ground state population of a specific isomer is depleted with an additional laser that precedes the excitation laser temporally, allows to record spectra that are both mass and isomer specific.25–304 Experimental vs. calculated splittings
A number of excited-state quantum-chemical investigations have studied the S1, S2 and higher Sn state energies of symmetric molecular dimers. Many of these have focused on face-to-face stacked dimers such as (benzene)2,45 stacked nucleobases,46–50 and the anisole dimer.42 Our calculations of the excitonic splittings of the H-bonded dimers in Fig. 1 using ab initio methods at the CC2/aug-cc-pVTZ level at the symmetric ground-state geometries gave vertical excitonic splittings Δvert between 1100 cm−1 and 10 cm−1, see column 2 of Table 2. Very similar splitting energies are obtained by calculating the transition-dipole ↔ transition-dipole interaction between the CC2/aug-cc-pVTZ calculated transition-dipole moments of the two monomers (column 3 of Table 2).12,16 In contrast, the corresponding observed S1/S2 splittings of the 13C-isotopomers Δobs are between 44 cm−1 and 0.9 cm−1 or 5–25 times smaller (column 5 of Table 2).26–30 In case of (2-pyridone)2, (o-cyanophenol)2 and (2-aminopyridine)2, the contribution of the 13C isotopic shift Δiso to the observed splitting is negligible, thus for these dimers Δobs = Δexp, see columns 4 and 5 of Table 2.26,28 In contrast, for (benzonitrile)2 and (benzoic acid)2, the contribution of Δiso is non-negligible and the excitonic splitting Δexp was deduced from experimental data on several isotopomers.29,30| Δ vert | Dipole–dipole | Δ obs (Fig. 3) | Δ exp | |
|---|---|---|---|---|
| (2-Pyridone)2 | 1125 | 745 | 43.5 | 43.5 |
| (o-Cyanophenol)2 | 309 | 299 | 16.4 | 16.4 |
| (2-Aminopyridine)2 | 416 | 362 | 11.5 | 11.5 |
| (Benzonitrile)2 | 10 | 14 | 3.9 | 2.1 |
| (Benzoic acid)2 | 11 | 22 | 3.4 | 0.9 |
All excited-state ab initio calculations of the S1–S2 energy gap, be they vertical or adiabatic, yield excitonic splittings that are systematically larger than the experimental ones. This is not due to an insufficiency of the calculations, but arises from the degeneracy of the two electronic states in symmetric homodimers (or near-degeneracy in the isotopically substituted dimers). In this situation, the Born–Oppenheimer (frozen-nuclei) approximation used in the ab initio calculations leads to electronic splittings that cannot reproduce the experimental ones. The latter are vibronic (vibrational–electronic) quantities that include the effects of all 3N − 6 intra- and intermolecular vibrations of the dimer on the excitonic interaction between the two electronic states. This vibronic coupling significantly reduces or quenches the gap between the two lowest vibronic states, relative to the energy gap between the Born–Oppenheimer calculated S1/S2 state energies.18–24,28 After explicitly taking this quenching by the vibronic coupling into account, correlated excited-state wave function methods as CC2 are sufficient to obtain accurate results for H-bonded dimers.
5 Linear vibronic coupling model for excitonic systems
5.1 Hamiltonian and potential energy surfaces
A model for the excitonic coupling of two electronically excited states coupled to a single vibrational mode was introduced by Fulton and Gouterman (FG)18,19 and numerically solved in 1964.19 The dimer electronic ground state is written as a Hartree product of wave functions ϕ0 on A and B| Ψ0 = ϕA0·ϕB0 | (2) |
Electronic excitation of A or B results in the excited electronic states (where q and Q refer to electronic and nuclear coordinates)
| ΨAexc(q; Q0) = ϕAexc(qA; QA)·ϕB0(qB; QB) | (3) |
| ΨBexc(q; Q0) = ϕA0(qA; QA)·ϕBexc(qB; QB) | (4) |
Since the Born–Oppenheimer approximation is no longer applicable due to the degeneracy of these excited states, they used as a basis for the vibronic wave function
| Ψ(q; Q0) = α(Q)·ΨAexc(q; Q0) + β(Q)·ΨBexc(q; Q0) | (5) |
The parameters α, β depend on the vibrational coordinate Q and are determined by solving the vibronic Hamiltonian (6) where VAB represents the excitonic interaction between A and B:
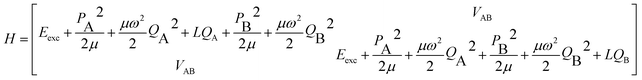 | (6) |
The FG model considers one intramolecular vibration per monomer, which is assumed to be totally-symmetric in the monomer point group. It is represented by a harmonic-oscillator potential 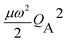 (i = A, B), for which only linear coupling occurs upon electronic excitation, that is, with a horizontal shift LQi along the coordinate Qi, but with no change of the reduced mass μ or frequency ω. For derivatives of benzene, an intramolecular vibration that typically shows considerable vibronic coupling is the in-plane (a′) deformation vibration ν6a, as discussed for 2-aminopyridine.26 The diagonals of eqn (6) are then transformed to a symmetrized vibrational basis corresponding to the symmetric and antisymmetric combinations of this monomer vibration.
(i = A, B), for which only linear coupling occurs upon electronic excitation, that is, with a horizontal shift LQi along the coordinate Qi, but with no change of the reduced mass μ or frequency ω. For derivatives of benzene, an intramolecular vibration that typically shows considerable vibronic coupling is the in-plane (a′) deformation vibration ν6a, as discussed for 2-aminopyridine.26 The diagonals of eqn (6) are then transformed to a symmetrized vibrational basis corresponding to the symmetric and antisymmetric combinations of this monomer vibration.
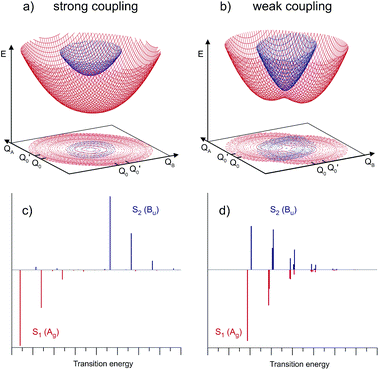
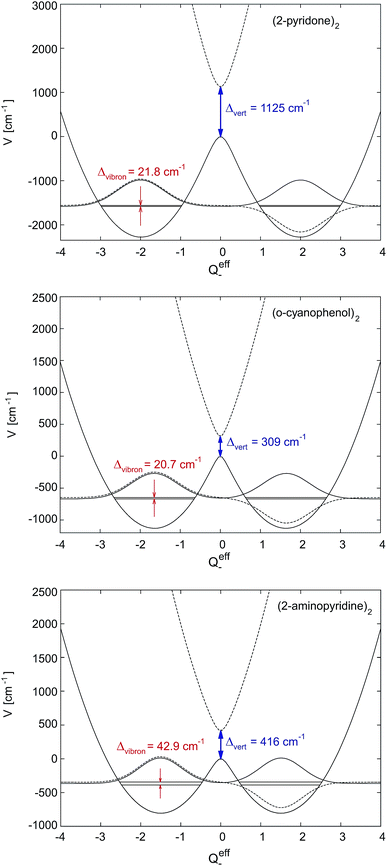
Depending on the strength of the excitonic interaction VAB between the monomers and the strength of the coupling LQi to the vibrational mode, the dimer can be classified as strong- or weak-coupling case.13–15,17 The corresponding potentials and resulting vibronic spectra are shown in Fig. 4. Note that in the use of FG, the coupling strength refers to the strength of the electronic interaction, not to the coupling to vibrational modes. In the case of electronic (excitonic) coupling that is strong relative to the vibrational coupling 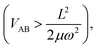 the S1 and S2 states of the complex remain largely independent, resulting in well-separated band systems for both states, see Table 1, line 1. Note that the frequency of the antisymmetric vibration in the dimer is lower than ω in the lower (red-shifted) state and higher than ω in the higher-energy (blue-shifted) state. In case of weak excitonic coupling, the S1 and S2 states interact considerably, resulting in a double-minimum potential along the antisymmetric direction in the S1 state, see Fig. 4(b). The vibronic band systems of the two S1 and S2 states overlap strongly, giving rise to band splittings and band intensity effects, cf.Table 1, line 2.
the S1 and S2 states of the complex remain largely independent, resulting in well-separated band systems for both states, see Table 1, line 1. Note that the frequency of the antisymmetric vibration in the dimer is lower than ω in the lower (red-shifted) state and higher than ω in the higher-energy (blue-shifted) state. In case of weak excitonic coupling, the S1 and S2 states interact considerably, resulting in a double-minimum potential along the antisymmetric direction in the S1 state, see Fig. 4(b). The vibronic band systems of the two S1 and S2 states overlap strongly, giving rise to band splittings and band intensity effects, cf.Table 1, line 2.
The excitonic coupling of all the H-bonded molecular dimers in Fig. 1 correspond to the weak-coupling case. For the intramolecular vibrations, experimental data confirms the theoretical prediction of band splitting. Interestingly, band splittings are also observed for the intermolecular vibrational modes of the dimer, resulting in complex band patterns.25–33 Although the FG model is based on the treatment of intramolecular vibrations, it could be parameterized to reproduce the band splittings and patterns resulting from antisymmetric intermolecular vibrations.26,51 This, however, is a purely phenomenological approach; recent multimode vibronic coupling52 calculations including both intra- and inter molecular vibrational modes on an equal footing are able to reproduce both the inter- and intramolecular vibronic band patterns for (o-cyanophenol)2.33
5.2 Vibrational quenching
In weak-coupling dimers, the vibronic coupling not only leads to complicated vibronic band patterns, but also to a considerable reduction of the electronic excitonic splitting Δexc. From the above model and assuming VAB to be small, the energy levels are obtained by first-order perturbation theory as:12,28Ev′± = Ev′ ± VAB〈![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) Av′|χA0〉〈 Av′|χA0〉〈![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) Bv′|χB0〉 Bv′|χB0〉 | (7) |
Since the vibrational overlap integrals for monomers A and B are identical, the spacing between a given pair of excitonically split vibronic bands is
Δvibron = 2VAB|〈![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) v′|χ0〉|2 v′|χ0〉|2 | (8) |
This means that the purely electronic excitonic splitting 2VAB is reduced by the (dimensionless) Franck–Condon factor (FCF), which is always smaller than unity. When specializing to the splitting between the S1/S2 state electronic origins, we obtain the quenching factor Γ
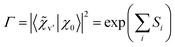 | (9) |
| Δ vert | Γ calc | Δ calcvibron | Δ exp | |
|---|---|---|---|---|
| (2-Pyridone)2 | 1125 | 0.019 | 21.4 | 43.5 |
| (o-Cyanophenol)2 | 309 | 0.067 | 20.7 | 16.4 |
| (2-Aminopyridine)2 | 416 | 0.102 | 42.2 | 11.5 |
| (Benzonitrile)2 | 10 | 0.228 | 2.3 | 2.1 |
| (Benzoic acid)2 | 11 | 0.189 | 2.1 | 0.9 |
6 Band intensities
6.1 S1/S2 origin band intensities
As discussed above, the Ag → Ag transition is forbidden in exactly centrosymmetric dimers, and for the dimers in Fig. 1 the S0 → S1 band is not observed. The excited state wave functions corresponding to the S1 and S2 states can be written as:12,29,53Ψ+ = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α·ϕAexcϕB0 + sin α·ϕAexcϕB0 + sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α·ϕA0ϕBexc α·ϕA0ϕBexc | (10) |
Ψ− = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α·ϕAexcϕB0 − cos α·ϕAexcϕB0 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α·ϕA0ϕBexc α·ϕA0ϕBexc | (11) |
| tan(2α) = |Δexc|/(|EA*B − EAB*|). | (12) |
For the symmetric homodimers EA*B and EAB* are degenerate, giving α = π/4, and the coupled exciton states are completely delocalized over both monomers. For slightly asymmetric dimers such as the 13C-isotopomers, the excitation energy difference between the isotopically substituted monomer and the non-substituted all-12C-monomer results in a partial localization of the S1 and S2 excited state wave functions on A or B. Given the electronic oscillator strength of the monomer, fel,mono, the relative electronic oscillator strengths of the S0 → S1 and S2 dimer are29
fel,dimer+ = (1 + 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α·sin α·sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α)fel,mono α)fel,mono | (13) |
fel,dimer− = (1 − 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α·sin α·sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α)fel,mono α)fel,mono | (14) |
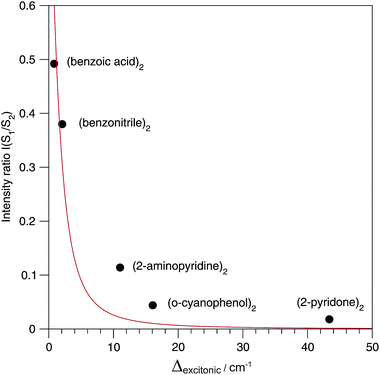
The relative S1/S2 band intensity depends on the excitonic splitting Δexp and the isotopic shift between the origins of A and B, Δiso = EA* − EB*. In Fig. 5, the intensity ratios I(S2)/I(S1) of the S0 → S1 and S0 → S2 origin bands of the 13C-isotopomers of the five dimers are plotted as a function of the excitonic splitting Δexp. These experimental intensity ratios are compared to the ratio of oscillator strengths calculated with eqn (13) and (14). Using the same 12C/13C isotopic shift Δiso = 3.3 cm−1 (as determined experimentally for (benzoic acid)2 and (benzonitrile)228,30) for all dimers, the intensity ratio is very nicely predicted by eqn (13) and (14). The deviation for (2-aminopyridine)2 is expected due to its non-planar C2-symmetric S0 state geometry, where the absence of inversion symmetry induces finite intensity of the S0 → S1 origin of the all-12C dimer.
6.2 Delocalization and exciton hopping in the excited state
For all the symmetric dimers studied, the symmetry lowering by 12C/13C isotope substitution results in the appearance of the S0 → S1 electronic origin. Its intensity relative to the S0 → S2 origin increases with decreasing splitting between the S1 and S2 origins, as the result of the decrease of the excitonic splitting Δexc relative to Δiso, see Fig. 2(b). Given the excitonic splittings Δexc in Table 2, eqn (1) shows that the observed S1/S2 splitting Δobs is dominated by Δiso for the (benzonitrile)2 and (benzoic acid)2 dimers, which have small monomer S0 → S1 transition dipole moments. In this limit, the excitonic states become localized on the isotopically distinct A or B moieties, as is clearly visible in Fig. 3(d and e). In both cases, the S1 electronic 000 band is almost fully localized on the 13C-monomer while the S2 000 band is localized on the all-12C-monomer. These observations confirm the interpretation of full delocalization of the dimer excited states over both chromophores in case of the symmetric dimers without isotope substitution.In earlier spectroscopic studies of the symmetric dimers (benzoic acid)2,36,38 (benzonitrile)2,37,54 (o-cyanophenol)2,39,40,55 and (anthranilic acid)2,41 the authors repeatedly discussed whether the excited state is localized or delocalized. Based on the observation of non-totally symmetric vibrational bands in the supersonic jet electronic spectra,39,40,55 on the analysis of the excited-state IR NH-stretch bands of (anthranilic acid)2,41 and on the slightly asymmetric structure of (benzoic acid)236,38 and (benzonitrile)2,37,54 derived from the rotationally resolved vibronic laser spectra, the electronic excitation was postulated to be localized on one of the monomers. This argument is unconvincing, since one then expects the appearance of a second electronic origin with similar intensity that is localized on the other moiety. However, no such second electronic origin was identified in any of the discussed complexes.36–41,55 In contrast, our recent work has revealed the appearance of the second 000 band of (benzoic acid)2, (benzonitrile)2 and (o-cyanophenol)2 if the C2h symmetry is lowered to CS by isotopic substitution, with concomitant localization of the electronic excitations.29,30,33
As discussed in Section 5.2, the appearance of non-totally symmetric vibronic excitations is fully compatible with delocalized excitonic states, since the vibronic coupling in weak-coupling systems results in the appearance of additional bands, as shown in Section 5. The asymmetric dimer geometry that is implied by the two S1-state minima along the asymmetric vibrational mode Q− for the weak-coupling case in Fig. 4(b) do not contradict the interpretation of the excitonic excitation as being delocalized. Instead, considering the total effect of vibronic coupling to the totally symmetric monomer modes, this is expected, since the delocalized excited state wave functions of both the S1 and S2 states have the highest probability density close to the two equivalent minima of the double minimum potential (note that the levels corresponding to the vibronic S1 and S2 origins are both located in the lower (double-minimum) potential in Fig. 6). Thus the most probable geometry of (benzoic acid)2 and (benzonitrile)2 in their S1 and S2 excited states should be slightly asymmetric, in agreement with the structures determined by high-resolution laser measurements of the 000 bands.36–38,54
In a semiclassical picture, the excitation can be considered to be hopping between the A and B chromophores, with a resonance transfer rate12
| kAB = 4|sin(2α)||VAB|/h | (15) |
For the 13C- and D-substituted dimers the difference in excitation energy between the two inequivalent chromophores EA*B − EAB* results in an increase of the hopping time. The hopping times for the symmetric (benzoic acid)2 and (benzonitrile)2 have been determined as texc = kAB−1 = 17.7 and 8.0 ps.29,30 This means that the symmetric homodimers are not only electronically symmetric, but that the vibrational asymmetry along the antisymmetric coordinates is averaged out on this timescale. The hopping times for the corresponding 13C-(benzoic acid)2 and 13C-(benzonitrile)2 increase significantly to 124 ps and 15 ps, respectively.
7 Adiabatic description and effective mode approximation
7.1 One-dimensional effective mode description
The above interpretation (Sec. 5.1) of the quenched exciton splitting is based on perturbation theory using the locally excited states of the monomers as zero-order states (they are degenerate for symmetry-equivalent monomers, as is always assumed in this section). These electronic states are an example of diabatic states as they are not eigenstates of the electronic Hamiltonian of the dimer. As an alternative, Kopec et al. have formulated an approach explaining the quenching of the excitonic splitting in molecular dimers based on adiabatic electronic states and potential energy surfaces (PES).32 The adiabatic PES are defined as the eigenvalues of the fixed-nuclei part of the Hamiltonian (6), i.e. dropping the nuclear kinetic energy part, and are best written as functions of the symmetric and antisymmetric linear combinations of the monomeric coordinates QA and QB. In dimensionless form they read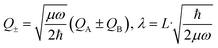 | (16) |
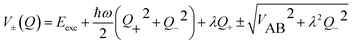 | (17) |
For the relevant case of weak excitonic coupling the lower surface V− has a double-minimum shape (see below) with a stabilization energy Estab (or, equivalently, energy barrier at Q = 0 separating the two equivalent distorted minima) of
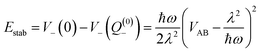 | (18) |
The displacement along the asymmetric mode at the distorted minima reads
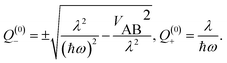 | (19) |
The above expressions can be readily generalized for the ubiquitous case of several vibronically active modes.32 Rather than giving lengthy equations we just note that the following quantities appearing in the above expressions for the stabilization energy and asymmetric distortion are to be replaced as follows:
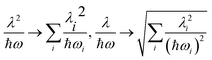 | (20) |
This leads to an elegant construction of an effective antisymmetric vibrational mode, which allows to visualize the total effect of all relevant modes in a single dimension. The latter is defined by requiring that the distortion and stabilization energy for this single mode correctly reproduce that of the full multi-mode system as given by eqn 18–20. It leads to frequency Ω and coupling constant Λ of the effective mode defined as in eqn (20) where the arrows are replaced by equal signs.
7.2 Nonadiabatic tunneling interpretation
Fig. 6 shows the symmetric-dimer S1- and S2-state effective mode potentials, with the quenched vibronic splitting Δvibron and the purely electronic splitting Δvert for two representative cases. It illustrates the above discussed discrepancy between the ab initio calculated and the experimentally observed excitonic splittings. Indeed, the ab initio methods yield rather accurate results for the purely electronic S1–S2 energy gap but this splitting is not observable in any excitonic molecular dimer. The actual vibronic S1 and S2 origins correspond to the energy levels indicated, on which, due to weak coupling, two strongly overlapping vibrational band structures would build up.The quenched vibronic energy splittings given in the figure have been obtained by numerically diagonalizing the FG Hamiltonian with the effective mode parameters obtained as described above and the same underlying multi-mode coupling constants as used in the perturbation theoretical approach of Sec. 5.1. The effective mode results of Fig. 6 can thus be directly compared with the corresponding entries in the column 4 of Table 3. The excellent agreement between the two approaches should be noted and mutually confirms the reliability of the different approximations.
The double minimum-shape of the lower adiabatic PES V− suggests an interpretation of the quenched excitonic splitting as originating from quantum tunneling on V−. It should however be born in mind that the calculated splitting results from a coupled-surface vibronic computation and includes the influence of the upper PES V+ on the tunneling motion. To explicitly reveal this, we have recomputed the effective-mode excitonic splitting as pure tunneling splitting on V− by suppressing the nonadiabatic coupling to V+.32 This results in splittings about 3–6 times larger than those given in Fig. 6. The quenched splittings are thus due to nonadiabatic tunneling between the two conformations where the excitation rests primarily on one of the two monomers. We emphasize that the energy gap of the interacting states is always kept fixed at the ab initio value Δvert indicated, for example, in Fig. 6. Therefore the nonadiabatic coupling effects are not subject to the ambiguity discussed in ref. 56. Nevertheless, in a genuine multimode treatment some deviations may arise.
Recent methodological developments in our groups57 have given a very simple closed-form expression which accurately reproduces the exciton splitting due to nonadiabatic tunneling. To this end the perturbation theoretical approach of Sec. 5.2 is applied to the localized ground state vibrational wave functions of the left and right potential wells of V−(Qeff−) as depicted in Fig. 6. The latter wells, and the ground state vibrational wave functions, are taken to be harmonic. Due to the very construction of the effective mode (see end of Sec. 7.1), the stabilization energy as well as total distortion of the many-mode problem is captured exactly by the effective mode. In the limit of vanishing excitonic splitting Δvert the vibrational overlap, and hence the vibrational quenching, of Sec. 5.2 are thus exactly recovered. For small finite splitting Δvert the vibrational ground state wave functions can be easily computed in the harmonic limit. The only effect of nonzero Δvert(=2VAB) is a small decrease of Q(0)− in eqn (19) compared to the case VAB = 0. The vibrational overlap is thus slightly increased, the quenching slightly decreased and the quenched excitonic splitting again slightly increased in this approach compared to the earlier version of Sec. 5.2. In practice the differences are very minor, amounting to only 1 cm−1 or less, and the quenched excitonic splittings Δvibron lie in the same range as in Table 3 and Fig. 6. Thus, the combined effects of the effective mode and nonadiabatic tunneling are incorporated in this modified perturbation-theoretical approach.
8 Conclusions
The investigation of the rigid C2h or C2 symmetric H-bonded dimers (2-pyridone)2, (o-cyanophenol)2, (2-aminopyridine)2, (benzonitrile)2 and (benzoic acid)2 by species- and isotope-selective laser spectroscopic methods have revealed that the symmetric dimers exhibit only a single vibronic band system, which is typically the S0 → S2 excitation, due to symmetry selection rules. However, even minimal symmetry breaking by replacing a single 12C atom by a 13C atom reveals the existence of the close-lying S0 → S1 band system. The energy difference between the S1 and S2 000 bands corresponds to the excitonic splitting in these dimers.The observed excitonic splittings Δexp are typically 5–25 times smaller than the energy gaps between the S1 and S2 states that are calculated vertically at the ground-state minimum geometry. The large difference between the calculated and experimental splittings results from vibronic coupling between the two degenerate electronic states, and can be considered a consequence of the Born–Oppenheimer approximation that is inherent to the ab initio calculations.
The vibronic coupling model introduced by Witkowski15 in 1960 and subsequently extended and solved by Fulton and Gouterman18,19 includes two electronic states that are coupled to a pair of vibrations of the dimer (one per monomer). The FG model can be adapted to reproduce the observed band structure and splitting for one pair of vibrations at a time, although its application to intermonomer degrees of freedom was not anticipated by FG and is purely phenomenological.26,51 The development of a one-dimensional effective mode vibronic coupling description32 projects the multidimensional couplings of all vibrational modes of the dimers onto a single antisymmetric vibrational coordinate, thereby giving valuable insights into the S1/S2 potential shapes, vibronic quenching behavior and interpretation of the excited-state geometry of the dimers.28–30,32
The experimental excitonic splittings in these dimers are then obtained by correcting the large excitonic splittings predicted by the Born–Oppenheimer-based ab initio calculations by the vibronic quenching factor Γ, which can be obtained from the experimental or calculated S0 ↔ S1 spectra of the respective monomer moieties. From a perturbation-theoretical point of view, Γ can be viewed as arising from the product of the excited-state vibrational displacements (Huang–Rhys factors) along the optically active vibrations of the monomer, thereby fragmenting the ab initio calculated electronic oscillator strength fel into the much smaller vibronic oscillator strengths of the vibronic fundamental excitations, fvibron ≪ fel.27,28,32 The smaller fvibron give rise to proportionally smaller excitonic splittings between the respective pairs of vibronic transitions of the dimer.27 In the five dimers discussed here, Γ = 0.03–0.25.
Recent multimode vibronic coupling calculations were able to reproduce the observed band patterns in the spectrum of (o-cyanophenol)2,33 and explain the excitonic splittings not only of the intramolecular, but also of the intermolecular vibrations. Related methods for the interpretation of vibronic coupling in a single molecule containing two weakly coupled chromophores have been developed by Slipchenko and co-workers,31,34 and have been applied to the vibronic spectra of diphenylmethane and several of its derivatives.58–60
Future challenges will involve the exploration of excitonic couplings in dimers that are more strongly asymmetrized than by 12C/13C-substitution. Examples are asymmetrization by H/D isotopic exchange or by chemically attaching a methyl group to one of the chromophores.51 More extreme cases are excitonic dimers that do not fulfill the requirement of inversion symmetry, such as the paradigmatic T-shaped aromatic dimers (benzene)2,61–65 and (naphthalene)2,66 in which the A and B monomers are symmetry-inequivalent.
Acknowledgements
The authors are indebted to S. Kopec for useful discussions and for a careful reading of the manuscript. H. Köppel thanks the Deutsche Forschungsgemeinschaft for financial support (grant number KO 945/17-1). P. Ottiger and S. Leutwyler thank the Swiss National Science Foundation for financial support via grants 200020-32540 and 200020-152816.References
- Y. C. Cheng and G. Fleming, Annu. Rev. Phys. Chem., 2009, 60, 241–262 CrossRef CAS PubMed.
- V. I. Novoderezhkin and R. van Grondelle, Phys. Chem. Chem. Phys., 2010, 12, 7352–7365 RSC.
- G. D. Scholes, G. R. Fleming, A. Olaya-Castro and R. van Grondelle, Nat. Chem., 2011, 3, 763–774 CrossRef CAS PubMed.
- F. Fassioli, R. Dinshaw, P. C. Arpin and G. D. Scholes, J. R. Soc., Interface, 2014, 11, 20130901 CrossRef PubMed.
- J. Strümpfer and K. Schulten, J. Chem. Phys., 2012, 137, 065101 CrossRef PubMed.
- J. L. Bredas, D. Beljonne, V. Coropceanu and J. Cornil, Chem. Rev., 2004, 104, 4971–5003 CrossRef CAS PubMed.
- F. C. Spano, Annu. Rev. Phys. Chem., 2006, 57, 217–243 CrossRef CAS PubMed.
- G. D. Scholes and G. Rumbles, Nat. Mater., 2006, 5, 683–696 CrossRef CAS PubMed.
- B. Bouvier, T. Gustavsson, D. Markovitsi and P. Millié, Chem. Phys., 2002, 275, 75–92 CrossRef CAS.
- D. Markovitsi, D. Onidas, T. Gustavsson, F. Talbot and E. Lazzarotto, J. Am. Chem. Soc., 2005, 127, 17130–17131 CrossRef CAS PubMed.
- C. T. Middleton, K. de La Harpe, C. Su, Y. K. Law, C. E. Crespo-Hernandez and B. Kohler, Annu. Rev. Phys. Chem., 2009, 60, 217–239 CrossRef CAS PubMed.
- T. Förster, Modern Quantum Chemistry, Academic Press, New York, 1965, ch. III, p. 93 Search PubMed.
- W. T. Simpson and D. L. Peterson, J. Chem. Phys., 1957, 26, 588–593 CrossRef CAS.
- D. S. McClure, Can. J. Chem., 1958, 36, 59–71 CrossRef CAS.
- A. Witkowski and W. Moffitt, J. Chem. Phys., 1960, 33, 872–875 CrossRef CAS.
- A. S. Davydov, Theory of Molecular Excitons, McGraw-Hill, New York, 1962 Search PubMed.
- R. E. Merrifield, Rad. Res., 1963, 20, 154–158 CrossRef.
- R. L. Fulton and M. Gouterman, J. Chem. Phys., 1961, 35, 1059–1071 CrossRef CAS.
- R. L. Fulton and M. Gouterman, J. Chem. Phys., 1964, 41, 2280–2286 CrossRef CAS.
- A. R. Gregory, W. H. Henneker, W. Siebrand and M. Z. Zgierski, J. Chem. Phys., 1976, 65, 2071 CrossRef CAS.
- R. Gregory, W. H. Henneker, W. Siebrand and M. Z. Zgierski, J. Chem. Phys., 1977, 67, 3175–3180 CrossRef.
- R. Friesner and R. Silbey, J. Chem. Phys., 1981, 74, 1166–1174 CrossRef CAS.
- R. Friesner and R. Silbey, J. Chem. Phys., 1981, 75, 3925–3936 CrossRef CAS.
- M. Andrzejak and P. Petelenz, Chem. Phys., 2007, 335, 155–163 CrossRef CAS.
- A. Müller, F. Talbot and S. Leutwyler, J. Chem. Phys., 2002, 116, 2836–2847 CrossRef.
- P. Ottiger, S. Leutwyler and H. Köppel, J. Chem. Phys., 2009, 131, 204308 CrossRef PubMed.
- P. Ottiger and S. Leutwyler, Chimia, 2011, 65, 228–230 CrossRef CAS PubMed.
- P. Ottiger, S. Leutwyler and H. Köppel, J. Chem. Phys., 2012, 136, 174308 CrossRef PubMed.
- P. Ottiger and S. Leutwyler, J. Chem. Phys., 2012, 137, 204303 CrossRef PubMed.
- F. A. Balmer, P. Ottiger and S. Leutwyler, J. Phys. Chem. A, 2014, 118, 11253–11261 CrossRef CAS PubMed.
- B. Nebgen, F. L. Emmert and L. V. Slipchenko, J. Chem. Phys., 2012, 137, 084112 CrossRef PubMed.
- S. Kopec, P. Ottiger, S. Leutwyler and H. Köppel, J. Chem. Phys., 2012, 137, 184312 CrossRef PubMed.
- S. Kopec, P. Ottiger, S. Leutwyler and H. Köppel, J. Chem. Phys., 2015, 142, 084308 CrossRef PubMed.
- B. Nebgen and L. V. Slipchenko, J. Chem. Phys., 2014, 141, 134119 CrossRef PubMed.
- A. Held and D. Pratt, J. Chem. Phys., 1992, 96, 4869–4876 CrossRef CAS.
- K. Remmers, W. L. Meerts and I. Ozier, J. Chem. Phys., 2000, 112, 10890–10894 CrossRef CAS.
- M. Schmitt, M. Böhm, C. Ratzer, S. Siegert, M. van Beek and W. L. Meerts, J. Mol. Struct., 2006, 795, 234–241 CrossRef CAS.
- I. Kalkman, C. Vu, M. Schmitt and W. L. Meerts, ChemPhysChem, 2008, 9, 1788–1797 CrossRef CAS PubMed.
- F. Lahmani, M. Broquier and A. Zehnacker-Rentien, Chem. Phys. Lett., 2002, 354, 337–348 CrossRef CAS.
- K. L. Barbu-Debus, M. Broquier, F. Lahmani and A. Zehnacker-Rentien, Mol. Phys., 2005, 103, 1655–1662 CrossRef.
- C. A. Southern, D. H. Levy, J. A. Stearns, G. M. Florio, A. Longarte and T. S. Zwier, J. Phys. Chem. A, 2004, 108, 4599 CrossRef CAS.
- G. Pietraperzia, M. Pasquini, N. Schiccheri, G. Piani, M. Becucci, E. Castellucci, M. Biczysko, J. Bloino and V. Barone, J. Phys. Chem. A, 2009, 113, 14343–14351 CrossRef CAS PubMed.
- N. Schiccheri, M. Pasquini, G. Piani, G. Pietraperzia, M. Becucci, M. Biczysko, J. Bloino and V. Barone, Phys. Chem. Chem. Phys., 2010, 12, 13547–13554 RSC.
- M. Pasquini, G. Pietraperzia, G. Piani and M. Becucci, J. Mol. Struct., 2011, 993, 491–494 CrossRef CAS.
- K. Diri and A. I. Krylov, J. Phys. Chem. A, 2012, 116, 653–662 CrossRef CAS PubMed.
- J. M. Jean and K. B. Hall, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 37–41 CrossRef CAS.
- G. Olaso-Gonzalez, D. Roca-Sanjuan, L. Serrano-Andrés and M. Merchan, J. Chem. Phys., 2006, 125, 231102 CrossRef PubMed.
- G. Olaso-Gonzalez, M. Merchan and L. Serrano-Andrés, J. Am. Chem. Soc., 2008, 130, 10768–10779 CrossRef PubMed.
- G. Olaso-Gonzalez, M. Merchan and L. Serrano-Andrés, J. Am. Chem. Soc., 2009, 131, 4368–4377 CrossRef CAS PubMed.
- C. R. Kozak, K. A. Kistler, Z. Lu and S. Matsika, J. Phys. Chem. B, 2010, 114, 1674–1683 CrossRef CAS PubMed.
- C. G. Heid, P. Ottiger, R. Leist and S. Leutwyler, J. Chem. Phys., 2011, 135, 154311 CrossRef PubMed.
- H. Köppel, W. Domcke and L. S. Cederbaum, Adv. Chem. Phys., 1984, 57, 59–246 CrossRef.
- Y. Maréchal and A. Witkowski, J. Chem. Phys., 1968, 48, 3697–3705 CrossRef.
- D. R. Borst, D. W. Pratt and M. Schäfer, Phys. Chem. Chem. Phys., 2007, 9, 4563–4571 RSC.
- N. Seurre, K. L. Barbu-Debus, F. Lahmani, A. Zehnacker-Rentien and J. Sepiol, Chem. Phys., 2003, 295, 21–33 CrossRef CAS.
- J. F. Stanton, J. Chem. Phys., 2010, 133, 174309 CrossRef PubMed.
- H. Köppel and S. Kopec, unpublished.
- N. R. Pillsbury, C. W. Muller, W. L. Meerts, D. F. Plusquellic and T. S. Zwier, J. Phys. Chem. A, 2009, 113, 5000–5012 CrossRef CAS PubMed.
- C. P. Rodrigo, C. W. Müller, N. R. Pillsbury, W. H. James, D. Plusquellic and T. S. Zwier, J. Chem. Phys., 2011, 134, 164312 CrossRef PubMed.
- E. G. Buchanan, P. S. Walsh, D. F. Plusquellic and T. S. Zwier, J. Chem. Phys., 2013, 138, 204313 CrossRef PubMed.
- J. B. Hopkins, D. E. Powers and R. E. Smalley, J. Phys. Chem., 1981, 85, 3739–3742 CrossRef CAS.
- K. O. Börnsen, H. L. Selzle and E. W. Schlag, Z. Naturforsch. Teil A, 1984, 39, 1255–1258 Search PubMed.
- K. O. Börnsen, H. Selzle and E. Schlag, J. Chem. Phys., 1986, 85, 1726–1732 CrossRef.
- B. F. Henson, G. V. Hartland, V. A. Venturo and P. M. Felker, J. Chem. Phys., 1992, 97, 2189–2208 CrossRef CAS.
- V. Venturo and P. M. Felker, J. Chem. Phys., 1993, 99, 748–751 CrossRef CAS.
- J. A. Wessel and J. A. Syage, J. Phys. Chem., 1990, 94, 737–747 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2015 |