Multiangle dynamic light scattering for the improvement of multimodal particle size distribution measurements
M.
Naiim
a,
A.
Boualem
b,
C.
Ferre
*a,
M.
Jabloun
b,
A.
Jalocha
a and
P.
Ravier
b
aCILAS, 8 Avenue Buffon, CS 16319, 45063 Orléans, Cedex 2, France. E-mail: cferre@cilas.com; Fax: +33 2 38 64 59 48; Tel: +33 2 38 64 41 17
bUniv. Orléans, PRISME, 45067 Orléans, France
First published on 28th October 2014
Abstract
Dynamic Light Scattering (DLS) is a widely used technique for measuring the size distributions of nano- and micro-particles dispersed in a liquid. The principle is based on the analysis of the temporal fluctuations of light scattered by the particles at a given scattering angle. However, single-angle DLS measurements may lack resolution and robustness, particularly for multimodal and/or polydisperse samples. Multi-angle Dynamic Light Scattering (MDLS) provides more robust, reproducible and accurate Particle Size Distributions (PSDs) than single-angle DLS. In this paper, a novel inversion method based on Bayesian inference is proposed for the estimation of the number PSD from MDLS measurements. The efficiency and robustness of this method is demonstrated through simulated and real data.
1 Introduction
Dynamic Light Scattering (DLS) is commonly used for sizing sub-micrometric particles dispersed in a dilute suspension.1 The multi-scattering effect, which appears if the sample is too concentrated, may be treated by the cross correlation method.2 DLS has numerous advantages: it is non-invasive, fast, and provides an absolute estimate of particle size. Experimentally, a cuvette containing the sample is irradiated by a polarized laser beam which leads to a scattering signal in all directions, depending on the particle size. The Brownian motion of the particles induces temporal variations of the scattered intensity recorded at a given angle. The time Auto-Correlation Function (ACF) of the intensity signal is analyzed to obtain the Particle Size Distribution (PSD).As the properties of nanoparticles are influenced by their size, the estimation of the PSD is an important issue in their characterization. This information is helpful for the study of their impact on environment and health.3 Measuring the PSD of a complex sample with a good resolution is essential in many applications as protein characterization, quality of blood platelet determination, and process control of nanoparticles growth.4,5 It is also important for determining the relative fractions of a mixture to improve its properties.6
The inversion of DLS data is known as an ill-posed mathematical problem since the solution is not unique, and a small amount of noise present in the measured data can lead to large variations in the estimated PSD. Several algorithms, such as the Cumulants method,7 CONTIN,8 non-negative least squares9 or the maximum entropy method,10 are usually used to retrieve the PSD from DLS data. In general, satisfying results are achieved for monomodal samples or multimodal samples having populations with comparable intensity contributions and spaced by at least a factor 2 in diameter. However, due to the low information content of the time ACF acquired at a single angle, these methods do not give reliable results for more complex samples.11 Indeed, the intensity scattered by a particle strongly depends on its size and on the scattering angle. Recovering the exact composition of the sample from single-angle DLS measurements can thus be difficult if the intensity scattered by one population predominates.
Multiangle Dynamic Light Scattering (MDLS) allows getting more information about the studied sample by combining the DLS data acquired at several angles. Former studies have demonstrated that MDLS provides more robust, reproducible and accurate PSD than single-angle DLS, particularly for polydisperse and/or multimodal samples.11–13 New data analysis methods have to be developed to optimize the results obtained by MDLS.
In the present work, we propose a Bayesian method for the estimation of the number PSD from MDLS measurements. The Bayesian approach is innovative and very promising in terms of repeatability and robustness.14 Clementi et al.15 proposed a Bayesian approach for MDLS measurements analysis. The first step consists in calculating the Z-average diameters (harmonic intensity averaged particle diameter) for each scattering angle by the method of Cumulants. The PSD is then estimated by applying Bayesian inference to the Z-average diameters. However, the estimation errors on the Z-average diameters propagate for complex samples and can lead to large errors on the PSD. To overcome this issue, we propose to directly estimate the PSD from the autocorrelation functions.
Basic theoretical principles on DLS and the new Bayesian method are presented in section 2. Section 3 provides insights into the results obtained when the innovative numerical method is applied to simulated and experimental data, as well as comparisons with usual procedures.8,15
2 Theory
2.1 Dynamic light scattering
Estimating the PSD from single-angle DLS data consists in inverting the normalized electric field ACF, g(1)(τ). g(1)(τ) is related to the measured normalized intensity ACF, g(2)(τ), by the Siegert relation:16| g(2)(τ) = 1 + β|g(1)(τ)|2, | (1) |
For a monomodal and monodisperse sample, the electric field ACF is a single exponential decay:
| g(1)(τ) = e−Γτ, | (2) |
| Γ = Dsq2 | (3) |
The magnitude of the scattering vector is given by:
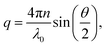 | (4) |
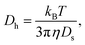 | (5) |
Polydisperse or/and multimodal samples are composed of populations with different diameters. Each of them gives a contribution similar to a monomodal distribution, and the electric field autocorrelation function can be represented by an integral over the intensity-weighted distribution of decay rates, G(Γ):1
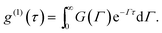 | (6) |
After inversion of the electric field ACF, g(1)(τ), the intensity-weighted PSD is deduced from G(Γ). Mie theory can then be applied to convert the intensity distribution to a volume or number distribution.17
MDLS consists in doing DLS measurements at several scattering angles, and to solve the whole equations system.
2.2 Proposed Bayesian inversion method
The aim of our work is to improve the multimodal number-weighted PSD (NPSD) estimation from MDLS measurements using a Bayesian method. Contrarily to the method proposed by Clementi et al.,15 we propose to directly apply the Bayesian inference to the MDLS measurements (time ACF), and not to the Z-average diameters. In this way, the effect of error propagation will be drastically limited. The proposed method is a free-form model, i.e. no assumption is made about the NPSD shape. The diameter range and the number of points of the solution are specified by the user.The Bayesian inference approach is a statistical inversion method. It allows taking into account available a priori information as well as model and measurements uncertainties. In this approach, the quantities involved in the mathematical model are represented as random variables with joint probability distributions. The solution of the inverse problem is summarized in a probability distribution, called posterior distribution, when all prior knowledge has been incorporated. Contrarily to deterministic methods, which only provide a reasonable estimate of the quantity of interest, various different estimates can be calculated from the posterior probability distribution in statistical approaches. Furthermore, statistical methods are much more appropriated than deterministic ones for solving ill-posed problems. Indeed, a regularization parameter is often used in deterministic methods in order to obtain a smooth solution to the problem. On the contrary, the Bayesian inference approach averages all the solutions consistent with the data, leading to more robust results.14
In practical applications, the posterior probability density function can be very complex and/or highly multivariate. In such cases, Markov Chain Monte Carlo (MCMC) methods are typically used to draw samples from the posterior probability density function of interest. Then, the inference about the parameters of interest is made from the drawn samples.
The mathematical development of the proposed Bayesian inversion method is detailed in ref. 18. Here is a brief description. The discrete NPSD f(Dh) is estimated, for a set of particle diameters (Dh,1, …, Dh,N), from the MDLS data acquired at different angles {θr, r = 1, …, R}. For each angle θr, the intensity ACF is measured at discrete time delays {τm, m = 1, …, Mr}. The proposed statistical model for the measured intensity ACFs, 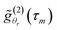 , is expressed by:
, is expressed by:
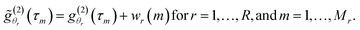 | (7) |
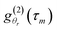 is the noise-free intensity ACF at the angle θr and wr(m) is an additive noise assumed to be normally distributed with zero mean and variance σ2r at the angle θr.
is the noise-free intensity ACF at the angle θr and wr(m) is an additive noise assumed to be normally distributed with zero mean and variance σ2r at the angle θr.
We note ![[f with combining low line]](https://www.rsc.org/images/entities/i_char_0066_0332.gif) = [f(Dh,1), …, f(Dh,N)]T,
= [f(Dh,1), …, f(Dh,N)]T, 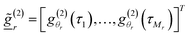 for r = 1, …, R and
for r = 1, …, R and 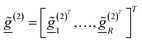 . T denotes the transpose operator.
. T denotes the transpose operator.
Using the Bayes formula, the joint posterior probability distribution of the NPSD vector and the noise variances given the MDLS data can be expressed by:
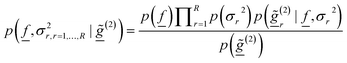 | (8) |
![[f with combining low line]](https://www.rsc.org/images/entities/i_char_0066_0332.gif) ) and p(σ2r) express the available prior information about the NPSD and the noise variance respectively.
) and p(σ2r) express the available prior information about the NPSD and the noise variance respectively. 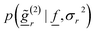 is the likelihood function (i.e., the conditional probability density function of the measured DLS data at the angle θr given a NPSD vector
is the likelihood function (i.e., the conditional probability density function of the measured DLS data at the angle θr given a NPSD vector ![[f with combining low line]](https://www.rsc.org/images/entities/i_char_0066_0332.gif) and a variance σ2r). The used prior densities and the expression of the likelihood function are detailed in ref. 18.
and a variance σ2r). The used prior densities and the expression of the likelihood function are detailed in ref. 18.
As result of marginalisation step with respect to the noise variances, the posterior probability density function of interest (i.e. of the NPSD vector ![[f with combining low line]](https://www.rsc.org/images/entities/i_char_0066_0332.gif) given the measured MDLS data) is given by:
given the measured MDLS data) is given by:
 | (9) |
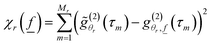 .
.
The posterior probability density function of interest is sampled using a MCMC Metropolis-within-Gibbs sampler. The NPSD is estimated from the generated Markov chain by the minimum mean square error (MMSE) estimator.
3 Application to simulated and real data
The numerical analysis for inverting MDLS data is first validated through simulated data. It is then tested on different experimental cases. For all tests, the polystyrene latex particles are dispersed in water at 25 °C (refractive index n = 1.33, viscosity η = 0.89 cP). The light source is a vertically-polarized laser diode of wavelength λ0 = 638 nm.3.1 Simulations
To simulate MDLS data, an arbitrary PSD is first defined. The noise-free normalized intensity ACFs at different angles are then calculated using the mathematical model described in section 2.2. An additive Gaussian noise is finally added to the data.The arbitrary chosen PSD is a trimodal mixture of latex particles represented by a combination of 3 Gaussian distributions with mean diameters D1 = 400 nm, D2 = 600 nm and D3 = 1019 nm, and respective standard deviations σ1 = 7 nm, σ2 = 10 nm and σ3 = 10 nm. The relative number fractions of each mode are respectively 73%, 20% and 7%. Autocorrelations functions were simulated at 13 angles between 60 and 120°, with a step of 5° between each angle. An additive noise of 10−3 amplitude is added to the ACFs.
3.2 Experimental data
Experiments were carried out using the Nano DS Particle Size Analyzer from CILAS. In this system, the sample is contained in a square-shaped scattering cell. The scattered light is collected by a single-mode optical fiber mounted on a goniometer arm, and connected to a photomultiplier.Dilute suspensions of polystyrene standard spheres (NIST traceable particle size standards, Thermo Scientific) were used for experimental studies. Sample 1 is a bimodal mixture of 102 nm and 596 nm particles, with relative number fractions of 99.7% and 0.3%, respectively. Sample 2 is the trimodal mixture used for simulations. Both samples were measured at angles between 60 and 120°. The angular step was 10° for sample 1, and 5° for sample 2. For each sample, 5 measurements of 10 min duration were realized at each angle.
3.3 Results
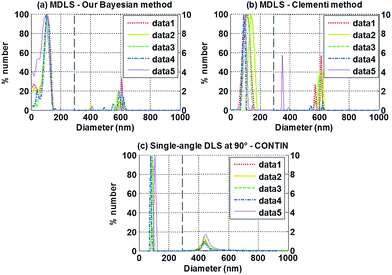
Fig. 1 compares the results obtained with our method and that of Clementi15 on the simulated data. These results clearly show that the NPSD assessed with our method is the closest one to the expected NPSD. The 3 peaks at 400 nm, 600 nm and 1019 nm are well resolved with a very good accuracy. Their relative number fractions are respectively 74%, 19% and 7%. On the contrary, the method of Clementi does not clearly resolve the 3 peaks.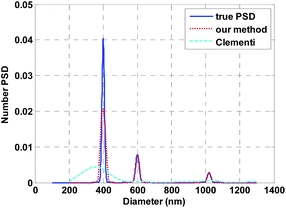 | ||
| Fig. 1 Comparison of the results obtained with our method and the method of Clementi on the simulated data. | ||
More details about the validation of our method on simulated data and other examples can be found elsewhere.18
Fig. 2(a) shows the NPSDs obtained with our algorithm from the experimental data measured for sample 1. Both peaks around 100 nm and 600 nm are well resolved with a good accuracy (less than 6% error on the position of the peaks), and with relative fractions consistent with those expected. Compared to the results obtained with the method of Clementi15 from the same MDLS data (Fig. 2(b)), our method shows better repeatability and accuracy. Fig. 2(c) gives the results obtained for the same sample by single-angle analysis at 90° with the CONTIN algorithm. In this case, single-angle analysis also permits to resolve both populations. However, the error on the position of the peak at 600 nm is greater than 20%. As one can notice from Fig. 2(a), the proposed method has some limitations for particles of diameter of about 100 nm or lower. This problem, which is also mentioned in other MDLS studies,11,12,15 is due to the fact that the light scattered by such small particles shows little angular variations.
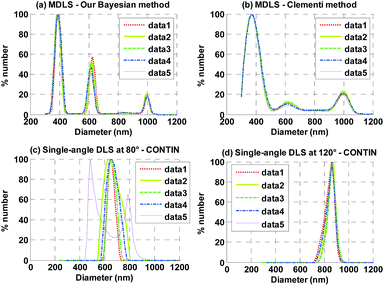
Results obtained for sample 2 with our method (a), the method of Clementi (b), and by single-angle DLS at 80° (c) and 120° (d) with the CONTIN algorithm are given in Fig. 3. Our method resolves successfully the 3 peaks around 400 nm, 600 nm and 1019 nm, with accuracy better than 5% and a good repeatability. The relative number fractions measured for the 3 peaks are respectively 60%, 27% and 13%. The measured number fractions of the peaks at 600 nm and 1019 nm are slightly greater than those expected, whereas the 400 nm number fraction is underestimated. However, the estimated NPSD is very close to that expected.
As shown in Fig. 3(b), the 3 peaks are also retrieved by the inversion method of Clementi, but with a lower precision than with our method.
As expected, CONTIN is unable to resolve the 3 peaks of the distribution of sample 2, because the different populations are spaced by less than a factor 2 in diameter. The PSD calculated by CONTIN possesses only one peak, whose position varies as a function of the scattering angle. For the quantities mixed to the preparation of sample 2, Mie theory predicts that the 3 populations scatter almost the same amount of light around 80°, whereas the intensity scattered by the particles of 1019 nm predominates around 120°. The mean diameter of the estimated distribution at 80° is thus close to the mean of the mixed diameters (Fig. 3(c)). As shown in Fig. 3(d), it is closer to 1019 nm at 120°.
These results clearly show the advantage of MDLS for the analysis of complex samples having 2 or more closely spaced modes. Furthermore, the comparison of our results to those obtained with the Clementi method15 seems to confirm the reduction of error propagation by applying directly the Bayesian method to the ACFs. The NPSDs calculated with the proposed approach show better resolution, repeatability and agreement with the expected distributions.
4 Conclusions
For complex unknown samples containing several populations, single-angle DLS can hardly give reliable results because the chosen angle may be inappropriate to detect all the present populations. MDLS, combined with a powerful inversion method to analyze simultaneously all the available data, is a very useful technique to overcome this issue. The efficiency of the proposed method has been demonstrated through experimental and simulated examples. Our technique is able to resolve peaks spaced by less than a factor 2 in diameter, with a better accuracy compared to other developed MDLS algorithms. This new method has been successfully tested on data acquired with the Nano DS from CILAS. This robust approach combined with a multi-angle instrument is efficient to characterize complex samples that cannot be measured by DLS instruments nowadays.Acknowledgements
We would like to thank the FUI program, the Région Centre and Orléans Innovation Network for their financial support through the Nano+ project.References
- R. Xu, Particle characterization: light scattering methods, Kluwer Academic Publishers, Dordrecht, the Netherlands, 2000 Search PubMed.
- P. N. Pusey, Suppression of multiple scattering by photon cross-correlation techniques, Curr. Opin. Colloid Interface Sci., 1999, 4(3), 177–185 CrossRef CAS.
- T. Provder, Challenges in particle size distribution measurement past, present and for the 21st century, Prog. Org. Coat., 1997, 32, 143–153 CrossRef CAS.
- F. Bensebaa, Nanoparticle Technologies: from Lab to Market, Elsevier, 2013 Search PubMed.
- H. Li, J. Addai-Mensah, J. C. Thomas and A. R. Gerson, The crystallization mechanism of Al(OH)3 from sodium aluminate solutions, J. Cryst. Growth, 2005, 279, 508–520 CrossRef CAS PubMed.
- T. Jiang and C. F. Zukoski, Rheology of high density glass of binary colloidal mixtures in unentangled polymer melts, Soft Matter, 2013, 9, 3117 RSC.
- D. E. Koppel, Analysis of macromolecular polydispersity in intensity correlation spectroscopy: the method of cumulants, J. Chem. Phys., 1972, 57, 4814–4820 CrossRef CAS PubMed.
- S. W. Provencher, A constrained regularization method for inverting data represented by linear algebraic or integral equations, Comput. Phys. Commun., 1982, 27, 213–227 CrossRef.
- I. D. Morrison, E. F. Grabowski and C. A. Herb, Improved techniques for particle size determination by quasi-elastic light scattering, Langmuir, 1985, 1, 496–501 CrossRef CAS.
- A. K. Livesey, P. Licinio and M. Delaye, Maximum entropy analysis of quasielastic light scattering from colloidal dispersions, J. Chem. Phys., 1986, 84, 5102–5107 CrossRef CAS PubMed.
- G. Bryant and J. C. Thomas, Improved particle size distribution measurements using multiangle dynamic light scattering, Langmuir, 1995, 11, 2480–2485 CrossRef CAS.
- G. Bryant, C. Abeynayake and J. C. Thomas, Improved particle size distribution measurements using multiangle dynamic light scattering. 2. Refinements and applications, Langmuir, 1996, 12, 6224–6228 CrossRef CAS.
- P. G. Cummins and E. J. Staples, Particle size distributions determined by a multiangle analysis of photon correlation spectroscopy data, Langmuir, 1987, 3, 1109–1113 CrossRef CAS.
- D. Watzenig, Bayesian inference for inverse problems – statistical inversion, Elektrotechnik & Informationstechnik, 2007, 124, 240–247 Search PubMed.
- L. A. Clementi, J. R. Vega, L. M. Gugliotta and H. R. B. Orlande, A Bayesian inversion method for estimating the particle size distribution of latexes from multiangle dynamic light scattering measurements, Chemom. Intell. Lab. Syst., 2011, 107, 165–173 CrossRef CAS PubMed.
- International Standard ISO 22412, Particle size analysis – dynamic light scattering (DLS), 2008.
- H. C. van de Hulst, Light scattering by small particles, John Wiley & Sons, New York, 1957 Search PubMed.
- A. Boualem, M. Jabloun, P. Ravier, M. Naiim and A. Jalocha, An improved Bayesian inversion method for the estimation of multimodal particle size distributions using multiangle Dynamic Light Scattering measurements, Statistical Signal Processing (SSP), 2014 IEEE Workshop on, pp. 360–363, June 29 2014–July 2 2014 Search PubMed.
| This journal is © The Royal Society of Chemistry 2015 |