Surface patterns in drying films of silica colloidal dispersions
F.
Boulogne†
*,
F.
Giorgiutti-Dauphiné
and
L.
Pauchard
UPMC Univ Paris 06, Univ Paris-Sud, CNRS, F-91405. Lab FAST, Bat 502, Campus Univ, Orsay, F-91405, France. E-mail: boulogne@fast.u-psud.fr; Fax: +33-1-69-15-80-60; Tel: +33-1-69-15-80-46
First published on 5th November 2014
Abstract
We report an experimental study on the drying of silica colloidal dispersions. Here we focus on surface instability occurring in a drying paste phase before crack formation which affects the final film quality. Observations at macroscopic and microscopic scales reveal the occurrence of instability, and the morphology of the film surface. Furthermore, we show that the addition of adsorbing polymers on silica particles can be used to suppress the instability under particular conditions of molecular weight and concentration. We relate this suppression to the increase of the paste elastic modulus.
1. Introduction
Patterns arising in soft materials such as elastomers, gels and biological tissues have been receiving growing attention.1 The understanding and control of the underlying instabilities are crucial for technological applications (microelectronics, microfluidics), for biological systems (wrinkling of human skin or drying fruit2) and for medical applications where gels are used as biological scaffolds for tissues or organs. In addition, various patterns which affect the surface of films have been reported in the literature. One of the most studied patterns concerns wrinkles observed when a hard skin, sitting on a soft layer, is compressed. Beyond a critical strain, it results in a periodic sinusoidal deformation of the interface3–6 for which the periodicity has been derived theoretically.2,7 When the strain is further increased, a secondary instability occurs leading to a wrinkle-to-fold transition;8,9 this results in a localization of the deformation.10 Under a biaxial compressive stress, it has been shown that a repetitive wrinkle-to-fold transition produces a hierarchical network of folds.11,12 These patterns are observed in various systems such as glassy polymers,3,13 polyethylene sheets2 or foams.14 Another group of patterns arises in soft layers supported by rigid substrates.1 Under compressive stresses, an instability often called creasing is manifested by localized and sharp structures at the free surface. These are commonly observed in elastomers,15,16 and hydrogels,17 or in the situation of a rising dough in a bowl.18 Despite similarities in their morphologies, origins of folds and creases are strongly different. Whereas folds are a secondary instability of wrinkles, creases are a direct deformation of a flat film (creases are also known as sulci19,20). Moreover drying films can produce characteristic crack patterns as they are dried21,22. The drying-induced cracks can invade the surface and propagate simultaneously into the volume of the medium with evaporation of the solvent, resulting in the division of the plane into polygonal domains.In this paper, we experimentally investigate patterns displayed at the surface of drying films of silica nanoparticles in an aqueous solvent. We discuss the occurrence of these patterns, and we examine their main features using different imaging techniques and rheological measurements. Moreover, the polymer/silica interaction is usually used to tune the mechanical properties of composite films. Consequently, we propose here a method to suppress these structures by adding adsorbing polymers to the silica nanoparticles.
2. Experimental
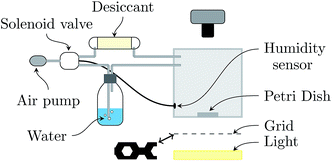
2.1. Controlled drying conditions
Experiments consist in drying a colloidal suspension in a circular glass Petri dish (inner diameter 2R = 5.6 cm) placed in a chamber which has controlled temperature (22 ± 2 °C) and relative humidity (RH = 50 ± 2%).23 The setup is sketched in Fig. 1. The top and bottom walls of the chamber are transparent for visualization by transmitted light. The bottom wall is carefully adjusted horizontally prior to each experiment. Since the sample contrast is very low, the Schlieren technique24 is used: a honeycomb grid is positioned between the bottom wall and an extended light source. A camera (Nikon D300), located at the top of the chamber, records a photograph each minute.In the following, mi varies in the range 1 to 9 g, resulting in an initial thickness hi varying in the range from ≃0.3 to 2.5 mm.
2.2. Colloidal dispersions
We used three aqueous dispersions of silica colloidal particles: Ludox SM-30, HS-40 and TM-50, commercially available from Sigma-Aldrich. The pH is in the range of 9–10, and so the particle surface bears a high negative charge density.26 SM-30 is used without treatment, while HS-40 and TM-50 are diluted using pure water (MilliQ quality, resistivity: 18 MΩ cm) at pH 9.5 by addition of NaOH. A weight ratio of 90/10 (HS-40/water) and 75/25 (TM-50/water) are chosen to obtain similar initial volume fractions. In the following, SM (unmodified), HS and TM designate these dispersions; their main properties are reported in Table 1.| Silica | Diameter 2a (nm) | ϕ 0 | ρ (kg m−3) | pH |
|---|---|---|---|---|
| SM | 10 | 0.15 | 1180 | 9.9 |
| HS | 16 | 0.19 | 1250 | 9.8 |
| TM | 26 | 0.20 | 1260 | 9.2 |
The effect of polymer chains on TM particles is investigated using polyethylene oxide (PEO) or alternatively polyvinylpyrrolidone (PVP). Indeed, a high affinity for silica surfaces is known for PEO and PVP resulting in adsorption on silica particles. To simplify the notations, polymers are denoted as Pi. Different molecular weights are studied (Pi: 300 Da, P1: 600 Da, P2: 3350 Da, P3: 6000 Da, P4: 35 kDa, P5: 600 kDa and P6: 8 mDa) for PEO and P7: 40 kDa for PVP. Polymers were purchased from Sigma-Aldrich and were dissolved in pure water at pH 9.5. This solution, with a weight concentration of polymers denoted as Cp is used for the dilution of TM-50. As a result, the final polymer concentration in the TM dispersion is Cp/4.
The adsorption of polymers on silica particles has been largely studied in the literature.27–30 In particular, it has been shown, from adsorption isotherms, that silica particles are totally covered with polymers for concentrations above 1 mg m−2 for PEO27 and PVP.31 In our experiments, the polymer concentrations do not exceed ≲0.01 mg m−2, which is much lower than the covering concentration. In this concentration range, polymers adsorb on particles to form necklaces;29 the dispersed state is stable since the interactions between necklaces are repulsive.32
2.3. Visualisation techniques
Observations are done at a macroscopic scale with an optical transmission microscope (DM2500 Leica) .At a microscopic scale, the surface profile is investigated using an Atomic Force Microscope (AFM, Vicco) in tapping mode on dried TM samples (scanning area is 80 × 80 μm2) prepared with an initial weight mi = 6 g. To complete these measurements at the onset of the propagation, an optical profiler is used (Taylor Hobson, 10×, working distance 7 mm). This contact-less method allows us to measure the surface profile of consolidating materials with a typical surface area of 1.6 × 1.6 mm2.
3. Results
3.1. Macroscopic observations
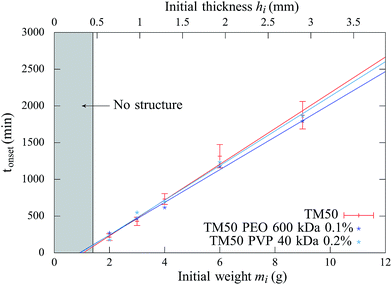
In addition, above this critical initial weight, the onset time tonset needed to observe the structure growth, is measured for dispersions of different initial weights deposited in the container, ranging from 1 to 9 g. The results are reported in Fig. 3 and show that the onset time increases linearly with the initial weight.
Similar experiments have been carried out with other samples and the results are summarized in Table 2. For SM and HS samples, no structure appears at the film surface, independent of the investigated range of film thicknesses.
| Sample | SM | HS | TM | TM + (P0, P1, P2, P3) | TM + (P4, P5, P6, P7) | |
|---|---|---|---|---|---|---|
| ∀Cp | C p < Ccp | C p > Ccp | ||||
| Observation | ∀h, no pattern | ∀h, no pattern | Patterns if h > hc | Patterns if h > hc | Patterns if h > hc | ∀h, no pattern |
Consequently, we studied the addition of adsorbing polymers only on TM samples. For a sample of initial weight mi = 3 g deposited in the container (hi = 1 mm), using PEO with molecular weights larger than 6 kDa, the formation of the structures is suppressed above a critical concentration Ccp = 0.13% (within an uncertainty of 0.03% for P3 and 0.01% for P4, P5 and P6). Thus, the weight amount of polymers necessary to suppress the structures is found to be independent of the molecular weight (for Mw ≥ 6 kDa). However, for shorter polymer chains (Mw < 6 kDa), and for concentrations up to Cp = 0.6%, the structures still form.
Moreover, addition of PVP (40 kDa) to TM particles results in suppression of the structures for Ccp(PVP) = 0.33 ± 0.03%. We notice that the molecular weight of a polymer unit for PEO MPEOw = 44 g mol−1 and for PVP MPVPw = 111 g mol−1:
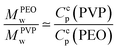 | (1) |
As a result, the structures are suppressed for a critical number of polymer units (160 ± 10 units per colloidal particle, i.e. 7.6 ± 0.6 μg m−2). We checked that the drying kinetics are not affected by the addition of polymers by weight measurements.23
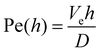 ,34 where h is the film thickness, Ve is the evaporation rate and D is the diffusion coefficient. The evaporation rate is found to be equal to Ve ≃ 1 × 10−8 m s−1 under the same drying conditions.23 The diffusion coefficient is deduced from the Stokes–Einstein relationship D = kBT/(6πηsa), where ηs = 1 mPa s is the solvent viscosity. From thicknesses lying in the range [0.4, 2.9] mm, the Péclet number is between 0.2 and 1.8. The value close to 1 does not allow us to distinguish between skin formation or consolidation in the bulk.
,34 where h is the film thickness, Ve is the evaporation rate and D is the diffusion coefficient. The evaporation rate is found to be equal to Ve ≃ 1 × 10−8 m s−1 under the same drying conditions.23 The diffusion coefficient is deduced from the Stokes–Einstein relationship D = kBT/(6πηsa), where ηs = 1 mPa s is the solvent viscosity. From thicknesses lying in the range [0.4, 2.9] mm, the Péclet number is between 0.2 and 1.8. The value close to 1 does not allow us to distinguish between skin formation or consolidation in the bulk.
However, to determine the state of the material, we gently collected a fraction of the material located at the surface of our samples (e.g. TM sample, mi = 9 g, typically 1/4th of the paste thickness); the sample was operated during the propagation of structures and before the apparition of cracks. We measured a volume fraction of ϕ = 38 ± 2% which is compatible with an elastic material (ϕ > 0.35) of non-aggregated particles (ϕ < 0.61);35 this material, deposited in a test tube filled thereafter with deionized water, can be redispersed after shaking.
3.2. Visualisation
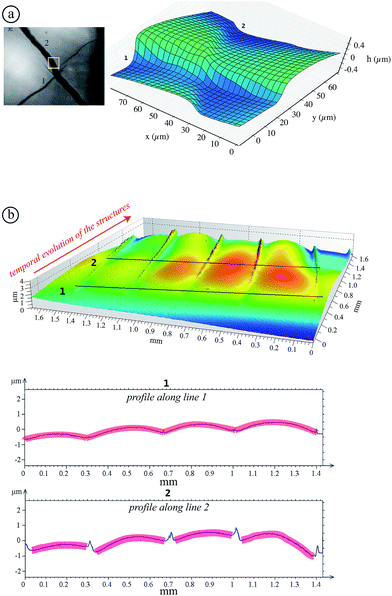
As shown in previous pictures, the structures exhibit an isotropic pattern in the center of the sample. However, while structures propagate in a thickness gradient naturally imposed by the meniscus at the edge of the container, they become preferentially oriented radially and ortho-radially (Fig. 5(b)).
A meniscus at the edge of the container extends over few times the capillary length scale 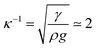 mm (γ is the surface tension of water). At the final stage, we obtain isotropic patterns (Fig. 5(a)) in a region covering 40% of the total surface area which corresponds to the flat film area.
mm (γ is the surface tension of water). At the final stage, we obtain isotropic patterns (Fig. 5(a)) in a region covering 40% of the total surface area which corresponds to the flat film area.
Moreover, in the case of experiments carried out with SM and HS samples for mi ∈ [2, 12] g, no structure can be observed. This statement is also confirmed using AFM, and optical profiler images.
Finally, measurements using AFM and optical profiler techniques reveal the absence of structures in TM with polymers above Ccp as in the case of observations using optical microscopy. Note that polymer addition below Ccp leads to a lower structure height. For instance, addition of PEO (600 kDa, Cp = 0.1%) decreases the maximum height to 1 μm (mi = 6 g).
3.3. Rheology
In the following the rheological properties of pastes are investigated at the onset of structure formation. In order to compare the elastic moduli of different silica pastes, measurements are performed at a well-defined consolidation time: the onset time for TM films and the same consolidation time for other systems. Samples are prepared using the same protocol: the initial weights range from 7 to 9 g. We collect surface samples corresponding to 4/5th of the film thickness in the center of the container. A part is used for a dried extract in order to deduce the volume fraction ϕ. The paste elastic modulus is measured using a rheometer (Anton Paar MCR501) in the plate–plate geometry (diameter: 24.93 mm) with a solvent trap. The gap is adjusted between 0.3 and 0.7 mm according to the amount of paste used for the measurement. Small oscillatory shear flow tests are performed with an amplitude of 0.2%, and a frequency sweep from 100 Hz to 1 Hz for 200 s per point. Under these conditions, the elastic modulus G′(ω) does not vary significantly with the frequency (relative variations lower than 10%) and the deformation amplitude up to a few percent above which the elastic modulus decreases. The average value is denoted by G0 in the following.In this way, five samples are considered: SM, HS and TM dispersions and binary mixtures of TM and PEO (600 kDa) at Cp = 0.2% and Cp = 0.4%. For TM samples (without polymers), since structures appear at ϕ = 38 ± 2%, we selected other samples (where no structures are developed) with a similar volume fraction. The results are shown in Fig. 7. Our results on the HS sample are consistent with values available in the literature.37 Note that, for all studied samples, the loss modulus (G′′(ω)) appears to be at least one order of magnitude lower than G0. For pure dispersions, the elastic modulus decreases nearly one order of magnitude when the mean particle size varies from 10 to 26 nm. In contrast, the addition of a small amount of PEO adsorbing on TM particles results in the increase of the paste elastic modulus.
4. Discussion
Our observations concerning the dynamics of formation and the characteristics of the pattern show that the structures observed here can be scarcely related to wrinkles. Indeed, wrinkles are periodic deformations of the interface5 whereas our patterns are clearly localized.Folds, described as a secondary instability arising from wrinkles,8 present strong similarities such as the localization of the deformation and the subdivision of domains and crossing patterns.11 However, the observation of wrinkles is expected but it has never been observed in our systems. Moreover, wrinkles and folds result from the deformation of skin in contact with a softer material whereas at the onset of the structure formation, the film seems to behave like a homogeneous paste phase.
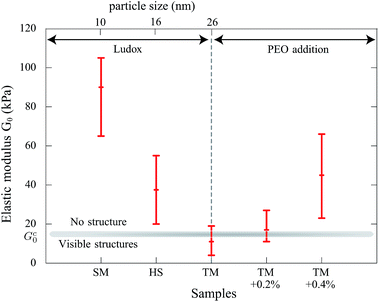
Observations at the onset of patterning (top graph of Fig. 6(b)) suggest some morphological similarities with crease patterns of swelling elastomers reported in the literature16 while the mechanism is different. The observed arches evolve to a “saw-tooth roof shape” as shown by AFM measurements (Fig. 6(a)). This transition is illustrated in the bottom graph of Fig. 6(b) where the onset of the lost of symmetry can be seen. Indeed, this transition may be attributed to the fact that colloidal pastes are able to change their microstructures. A possible explanation of the symmetry breakage from the onset of the instability to the final state can be that any further strain energy is dissipated in the shear of the material (creep flow).
The second question addressed in this paper concerns the absence of structures for SM and HS particles, as well as the suppression by the addition of adsorbing polymers.
The mechanical properties of pastes depend on the colloidal dispersion or the concentration of additional polymers. The strain in the paste phase at the onset time can deduce the elastic modulus. Indeed, assuming that the internal stress during the drying process comes from the flux of water through the porous matrix made by silica particles, the greatest stress occurs at the drying surface where the pore pressure is larger.38 There, the stress σ scales as follows:
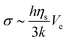 | (2) |
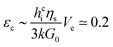 | (3) |
Measurements show that above a critical elastic modulus, structures are suppressed. This critical value is estimated by Gc0 = 15 ± 5 kPa from Fig. 7. Indeed, for pastes exhibiting larger elastic moduli, shrinkage induced by the drying is withstood by the paste network leading to a low strain. Further shrinkage is frustrated by adhesion of the paste onto the substrate and results in tensile stress and crack formation. However, for pastes exhibiting lower elastic moduli, the strain is larger leading to possible surface corrugations. eqn (3) also suggest that Gc0 should depend on the film thickness if εc does not. From our observations, we cannot conclude on a dependence of Gc0 with the film thickness because near the threshold, the presence or absence of structures is difficult to be stated. Indeed, the structure density decreases with the film thickness as shown in the inset of Fig. 3.
In the case of pure colloidal dispersions (SM, HS, and TM), the particle size affects the elastic modulus (Fig. 7), consequently the permeability. Indeed, fitting the elastic moduli as a function of the particle size with a power law, G0 ∝ ap, leads to values p ∈ [−1, −3]. The inaccuracy comes from the large error bars and the little number of available samples. Taking into account the particle size dependency in the permeability with the Carman–Kozeny model, the deformation varies as ε ∝ a−(p+2). A power coefficient p lower than −2 would be consistent with our observations on the suppression effect. We can also note that our description assumes that changing Ludox only results in varying particle size. It is worth noting that other parameters may have effects, such as polydispersity (see ref. 25 (p. 324) for measurements) which can modify the permeability.39
Finally, we also observed that patterns are hierarchical (Fig. 2) which introduces different lengthscales. The final pattern settles after 250 minutes in the given example. This suggests that the refinement is related to the consolidation of the material that can be analyzed by the increase of the elastic modulus in time which increases the stress in the material.
5. Conclusion
In this paper, we report experimental observations on surface instabilities during the drying of silica colloidal dispersions. These patterns grow if films are thicker than a critical thickness and that the onset time increases linearly with the initial film thickness and is concomitant with a paste phase sitting on the substrate. Measurements using microscopy techniques highlight the surface corrugations resulting first in arches that evolves to a saw tooth roof shape. We also provide a method to prevent these patterns by the addition of a small amount of polymers which increases the material elastic modulus. From this technique, we estimated a critical elastic modulus for structure formation.As a perspective, it would be interesting to refine the description of the evolution from arches to the saw-tooth roof shape which is attributed to a creep flow caused by the nature of the material. Thus, a competition between the creasing instability and the creep flow may exist in the selection of the final characteristic distance separating structures. In particular, in a future study, the evolution of structures could be related to the characteristics (onset time and final size) of the different generations in order to establish a criterion for the distance between structures and to precise the influence of loss of symmetry on the development of instability. Further theoretical developments might focus on similarities and differences of surface instabilities in visco-elasto-plastic materials compared to visco-elastic gels.
Acknowledgements
The authors thank the Triangle de la Physique for the rheometer (Anton Paar, MCR 501) and A. Aubertin for designing the experimental setup. We are grateful to B. Cabane, J.-P. Hulin, G. Gauthier and C. Quilliet for fruitful discussions and A. Chennevière, C. Poulard and F. Restagno for guidance and for sharing their AFM and optical profiler.References
- X. Li, D. Ballerini and W. Shen, Biomicrofluidics, 2012, 6, 011301 CrossRef PubMed.
- E. Cerda and L. Mahadevan, Phys. Rev. Lett., 2003, 90, 074302 CrossRef CAS.
- K. Huraux, T. Narita, B. Bresson, C. Fretigny and F. Lequeux, Soft Matter, 2012, 8, 8075–8081 RSC.
- Y. Xuan, X. Guo, Y. Cui, C. Yuan, H. Ge, B. Cui and Y. Chen, Soft Matter, 2012, 8, 9603–9609 RSC.
- Y.-C. Chen and A. Crosby, Soft Matter, 2013, 9, 43–47 RSC.
- J. Genzer and J. Groenewold, Soft Matter, 2006, 2, 310–323 RSC.
- J. Groenewold, Phys. A, 2001, 298, 32–45 CrossRef.
- F. Brau, P. Damman, H. Diamant and T. Witten, Soft Matter, 2013, 9, 8177–8186 RSC.
- F. Brau, H. Vandeparre, A. Sabbah, C. Poulard, A. Boudaoud and P. Damman, Nat. Phys., 2011, 7, 56–60 CrossRef CAS.
- L. Pocivavsek, R. Dellsy, A. Kern, S. Johnson, B. Lin, K. Lee and E. Cerda, Science, 2008, 320, 912–916 CrossRef CAS PubMed.
- P. Kim, M. Abkarian and H. Stone, Nat. Mater., 2011, 10, 952–957 CrossRef CAS PubMed.
- P. Reis, Nat. Mater., 2011, 10, 907–909 CrossRef CAS PubMed.
- Y. Ebata, A. Croll and A. Crosby, Soft Matter, 2012, 8, 9086–9091 RSC.
- P. Reis, F. Corson, A. Boudaoud and B. Roman, Phys. Rev. Lett., 2009, 103, 045501 CrossRef CAS.
- W. Hong, X. Zhao and Z. Suo, Appl. Phys. Lett., 2009, 95, 111901–111903 CrossRef PubMed.
- S. Cai, D. Chen, Z. Suo and R. Hayward, Soft Matter, 2012, 8, 1301–1304 RSC.
- V. Trujillo, J. Kim and R. Hayward, Soft Matter, 2008, 4, 564–569 RSC.
- S. Cai, K. Bertoldi, H. Wang and Z. Suo, Soft Matter, 2010, 6, 5770–5777 RSC.
- E. Hohlfeld and L. Mahadevan, Phys. Rev. Lett., 2011, 106, 105702 CrossRef.
- T. Tallinen, J. Biggins and L. Mahadevan, Phys. Rev. Lett., 2013, 110, 024302 CrossRef CAS.
- P. Xu, A. Mujumdar and B. Yu, Drying Technol., 2009, 27, 636–652 CrossRef.
- A. Routh, Rep. Prog. Phys., 2013, 76, 046603 CrossRef PubMed.
- F. Boulogne, F. Giorgiutti-Dauphiné and L. Pauchard, Oil Gas Sci. Technol. – Rev. IFP Energies nouvelles, 2013, 69, 397–404 CrossRef PubMed.
- L. Weinstein, Eur. Phys. J. Spec. Top., 2010, 182, 65–95 CrossRef.
- H. Bergna, The Colloid Chemistry of Silica, American Chemical Society, 1994 Search PubMed.
- R. Iler, The Chemistry of Silica: Solubility, Polymerization, Colloid and Surface Properties and Biochemistry of Silica, Wiley-Interscience, 1979 Search PubMed.
- F. Lafuma, K. Wong and B. Cabane, J. Colloid Interface Sci., 1991, 143, 9–21 CrossRef CAS.
- Y. Otsubo, Langmuir, 1990, 6, 114–118 CrossRef CAS.
- K. Wong, P. Lixon, F. Lafuma, P. Lindner, O. Charriol and B. Cabane, J. Colloid Interface Sci., 1992, 153, 55–72 CrossRef CAS.
- S. Parida, S. Dash, S. Patel and B. Mishra, Adv. Colloid Interface Sci., 2006, 121, 77–110 CrossRef CAS PubMed.
- P. Ilekti, Ph.D. thesis, Université Pierre et Marie Curie, 2000.
- B. Cabane, K. Wong, P. Lindner and F. Lafuma, J. Rheol., 1997, 41, 531–547 CrossRef CAS.
- N. Bassou and Y. Rharbi, Langmuir, 2009, 25, 624–632 CrossRef CAS PubMed.
- A. Routh and W. Russel, AIChE J., 1998, 44, 2088–2098 CrossRef CAS.
- F. Boulogne, L. Pauchard, F. Giorgiutti-Dauphiné, R. Botet, R. Schweins, M. Sztucki, J. Li, B. Cabane and L. Goehring, EPL, 2014, 105, 38005 CrossRef.
- C. Parneix, P. Vandoolaeghe, V. Nikolayev, D. Quéré, J. Li and B. Cabane, Phys. Rev. Lett., 2010, 105, 266103 CrossRef CAS.
- E. Di Giuseppe, A. Davaille, E. Mittelstaedt and M. François, Rheol. Acta, 2012, 51, 451–465 CrossRef CAS.
- C. Brinker and G. Scherer, Sol–Gel Science: the Physics and Chemistry of Sol–Gel Processing, Academic Press, 1990 Search PubMed.
- G. Scherer and R. Swiatek, J. Non-Cryst. Solids, 1989, 113, 119–129 CrossRef CAS.
Footnote |
| † Now at: Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA. |
| This journal is © The Royal Society of Chemistry 2015 |


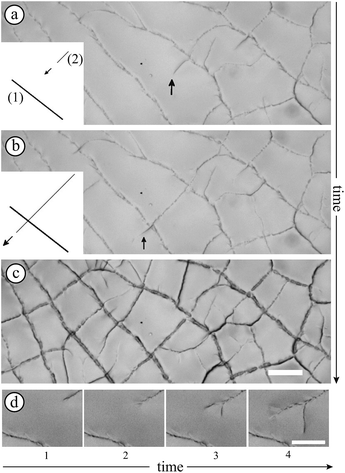

![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0072_20d1.gif) designates the radial direction.). The scale bars represent 100 μm.
designates the radial direction.). The scale bars represent 100 μm.