Solvent vapour mediated spontaneous healing of self-organized defects of liquid crystal films†
Bolleddu
Ravi
a,
Rabibrata
Mukherjee
b and
Dipankar
Bandyopadhyay
*ac
aDepartment of Chemical Engineering, Indian Institute of Technology Guwahati, India. E-mail: dipban@iitg.ernet.in
bInstability & Soft Patterning Laboratory, Department of Chemical Engineering, IIT Kharagpur, 721302, India
cCentre for Nanotechnology, Indian Institute of Technology Guwahati, India
First published on 24th October 2014
Abstract
Ultrathin liquid crystal films showed a nematic to isotropic transition when exposed to solvent vapour for a short duration while a reverse isotropic to nematic transition was observed when the film was isolated from the solvent exposure. The phase transitions were associated with the appearance and fading of surface patterns as the solvent molecules diffused into and out of the film matrix, resulting in the destruction or restoration of the orientational order. A long-time solvent vapour exposure caused the dewetting of the film on the surface, which was demonstrated by the formation of holes and their growth in size with the progress of time. Even at this stage, withdrawal of the solvent exposure produced an array of nematic fingers, which nearly self-healed the dewetted holes. The change in contact angle due to the phase transition coupled with the imbalance of osmotic pressure across the contact line due to the differential rate of solvent evaporation from the film and the hole helped the fingers to grow towards the centre of the hole. The appearance of the fingers upon withdrawal of the solvent exposure and their disappearance upon exposure to solvent were also found to be a nearly reversible process. These findings could significantly contribute to the development of vapour sensors and self-healing surfaces using liquid crystal thin films.
Introduction
Liquid surfaces have the remarkable ability to heal defects seamlessly because of their inability to withstand even a trivial amount of external force. In comparison, although solids can easily resist external stresses owing to their inherent elastic stiffness, surface defects can be permanent because of the presence of the finite yield stress for failure. Thus, the major challenge is to develop functional materials, which can endure external stresses together with defect healing properties. Such materials find important applications in tissue engineering, self-healing and scratch resistant coatings, and pressure sensitive adhesives, among many others.1–9 Of particular interest here are liquid crystalline materials in which the solid like orientational order of the molecules helps to withstand the external stresses to some extent, whereas the liquid like fluidity brings in the capacity to self-heal the defects. In this article, we experimentally demonstrate that the self-organized defects originating from the instabilities of an ultrathin (<100 nm) liquid crystal (LC) film can indeed be spontaneously healed with the periodic exposure and withdrawal of solvent vapour.It is well known that ultrathin polymer films rupture spontaneously and dewet following the spinodal pathway in which thermal or mechanical fluctuations on the film-surface grow to form holes under the influence of destabilizing van der Waals forces.10–15 A film can also rupture due to the nucleation of holes over topographic or chemical surface defects due to lateral wettability gradients.16–18 In both mechanisms, the holes grow with time and coalesce to produce the Voronoi tessellation of polymer ribbons, which at a later stage deplete into droplets due to the Rayleigh–Plateau instability. The inherently random dewetted structures find important technological applications when long-range ordering is achieved by guiding the evolution through the substrates with periodic physicochemical patterns.19–22
In contrast to isotropic liquid polymer films, the dewetting of ultrathin LC films is considerably different.15,23–32 When an ultrathin LC film is thermally annealed to the nematic to isotropic (N–I) phase transition temperature (TP), periodic undulations appear on the surface of the film signifying the destruction of the orientational nematic order of the LC molecules.15,27 The N–I phase transition results in an isotropic LC film, which is demonstrated by the disappearance of the surface undulations. At this stage, instead of heating the film to a higher temperature, if the isotropic LC film is cooled steadily below TP, a reverse isotropic to nematic (I–N) phase transition is observed. The I–N transition is also associated with the appearance and subsequent fading of undulations on the surface of an unbroken film, as the orientational order of the molecules is restored. The N–I and I–N transitions with periodic heating and cooling around TP are nearly a reversible process.27 On the other hand, following the N–I transition, if the isotropic film is heated beyond TP, the film dewets and holes appear randomly on the surface.15,23,27 Previous studies argued that the long-range Lifschitz–van der Waals interaction,15,23–26 pseudo-Casimir force based director fluctuations28,29 and the textures of the LC film surface27 could be the different reasons for these instabilities. Surprisingly, until now the instabilities of LC films have always been explored solely in the thermal annealing route. The effects of solvent vapour annealing,33 a method extensively adopted to cause the dewetting of thin polymer films, has never been investigated in the context of LC thin films.
In the present work, we show room temperature N–I and I–N phase transitions in thin LC films after periodic solvent vapour exposure and withdrawal. Similar to the thermal annealing route,27 the solvent vapour induced N–I and I–N transitions were marked by the appearance and fading of surface undulations. The transitions were found to be a quasi-reversible process as the cycles of the N–I and I–N transitions could be performed repeatedly through periodic solvent exposure and withdrawal. The experiments confirmed that in LC films, solvent exposure could act as an analogue to thermal annealing in ambient conditions. Importantly, a long-time solvent exposure beyond the N–I transition led to the dewetting of the film with the appearance and growth of holes. Remarkably, at this stage, withdrawal of the solvent exposure produced an array of branched nematic fingers, which nearly self-healed the dewetted zones. Even at this stage, the formation of the nematic fingers upon withdrawal of the solvent contact and disappearance of the nematic fingers through solvent annealing were found to have quasi-reversible characteristics, as these events could be performed periodically for many cycles.
Results and discussion
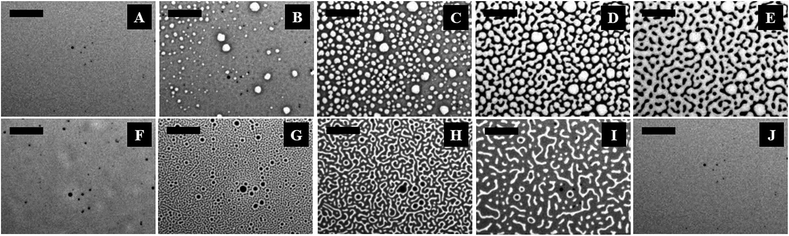
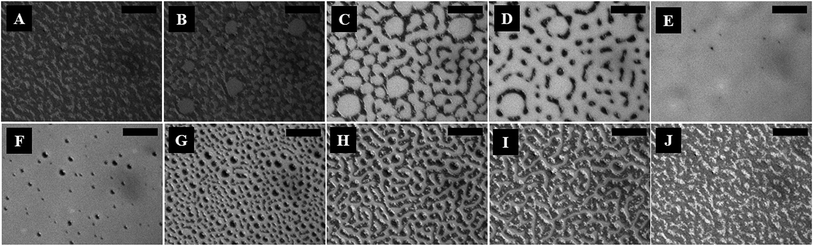
Fig. 1 (and the ESI video 1†) shows a cycle of the forward N–I phase transition upon solvent vapour annealing (images A–F) and the reverse I–N phase transition (and the ESI video 2†) upon removal of the solvent exposure (images F–J). Images 1A and 1B show that the initially flat surface of the nematic film deformed and that circular spots appeared due to the adsorption of the solvent molecules when the solvent source was introduced into the experimental chamber. The spots grew with time as more solvent molecules penetrated into the film surface (image 1C) and subsequently, the circular spots expanded and coalesced to form bi-continuous structures (image 1D). It may be noted here that, in the experimental chamber, the solvent vapour source was introduced from one of the sides of the sample, which caused the solvent vapour to diffuse across the sample from the side where the source was placed to the other side. Thus, as time progressed, the solvent diffused from left to right, which has been captured in the ESI video 1.† Further, the time t = 0 s reported in the figure caption represents the frame marginally before the first spot of solvent nucleated on the film. The accumulation of the solvent molecules on the surface and their subsequent diffusion into the bulk of the film resulted in the gradual destruction of the nematic orientational order of the LC molecules, leading to the N–I transition. The completion of the N–I transition was demonstrated by the disappearance of the surface features, resulting in a flat isotropic film (image 1F). Images 1F and 1G represent a sequence where the solvent vapour sources were removed from the film chamber following the N–I transition. This triggered a reverse I–N transition, as shown in the images 1F–1J and the ESI video 2.† The removal of the solvent exposure led to an outward diffusion of the solvent molecules from the film matrix to the surroundings. Consequently, the extent of swelling of the film reduced, which in turn restored the nematic ordering within the film, resulting in the I–N phase transformation. This backward I–N transition was also associated with the appearance and fading of an intermediate surface roughness. Image 1J shows a nearly flat nematic thin film after completion of the I–N transition. Interestingly, the N–I and I–N transitions upon periodic exposure and removal of the solvent were found to be a quasi-reversible process as the cycle could be repeated for several times, which was observed in the case of thermal annealing.27The polarizing microscope images (A–E) in Fig. 2 (and the ESI video 3†) confirm that the surface texture of the nematic film progressively disappeared during the N–I phase transition, as the solvent molecules started aggregating on the film surface. The images (A–E) in Fig. 2 confirm that the lighter circular spots in the images (A–E) of Fig. 1 were indeed the local nucleation of the solvent molecules. The floating solvent molecules near the nematic–air interface enforced a grey rather than black colouration to the isotropic phase under polarization microscopy. The images (F–J) in Fig. 2 (and the ESI video 3†) show that the surface texture of the nematic film was progressively restored when the solvent vapour source was removed from the chamber and the I–N phase transition took place as the solvent molecules evaporated out of the film matrix. The images (F–J) in Fig. 2 confirm that the dark spots in the images (F–J) of Fig. 1 were the reappearance of the nematic phase as the solvent molecules evaporated out of the film matrix.
It may be noted here that, during the N–I transition, when the solvent molecules adsorbed on the surface and progressively diffused into the film, the system was always away from equilibrium due to the difference in chemical potential inside the film. However, a long-time exposure of the solvent on the film helped in reaching equilibrium at the isotropic state, after the film surface became homogeneous. Similarly, for the I–N transition the film was again out of equilibrium when the solvent molecules started evaporating from the film matrix. A long-time evaporation of the solvent molecules from the film led to a nematic film with a flat surface under equilibrium conditions. Importantly, when a nematic film was annealed through solvent vapour exposure to its phase transition point, the system tried to achieve two different types of equilibrium. While the coexistence of the solvent molecules with the nematic and isotropic phases created a difference in chemical potential across the film, the molecular rearrangements due to the elastic (viscous) response of the nematic (isotropic) phase tried to establish a mechanical equilibrium inside the film. A few previous works30,31 on the thermal annealing of nematic films have shown that thermal and mechanical equilibriums could be attained during phase transitions when the temperature was kept constantly near TP. These studies showed that if the temperature (T) was kept constant (TU > T > TL) amid the upper (TU) and lower (TL) bound of temperatures between which the patterns appeared and disappeared on the surface of the film, a thermal as well as a mechanical equilibrium could be attained. In such a situation, the patterns that appeared during the phase transition could be retained for a longer duration. In order to understand the typical experimental time scales for the chemical and mechanical equilibriums for the system under consideration, we performed similar experiments keeping the partial pressure of the solvent vapour nearly constant. The partial pressure on the film was maintained at a constant value by manually adjusting the loss of vapour through the experimental chamber with respect to the amount of solvent evaporated from the source. The ESI videos 4 and 5† show the morphological evolution of nematic films with two different film thicknesses (h = 47.3 ± 1.2 nm and h = 64.4 ± 0.55 nm) when the partial pressure of the solvent vapour surrounding it was kept nearly constant. The videos suggest that the patterns that appeared during phase transition could be retained for a longer duration when the partial pressure was nearly constant. Further, the characteristic time for the molecular rearrangement to attain the mechanical equilibrium was observed to be rather larger for the thinner film. In comparison, for the thicker film, the evolution to attain the mechanical equilibrium was observed to be much faster. Remarkably again, thermal and solvent vapour annealing showed very similar behaviours in this regard.
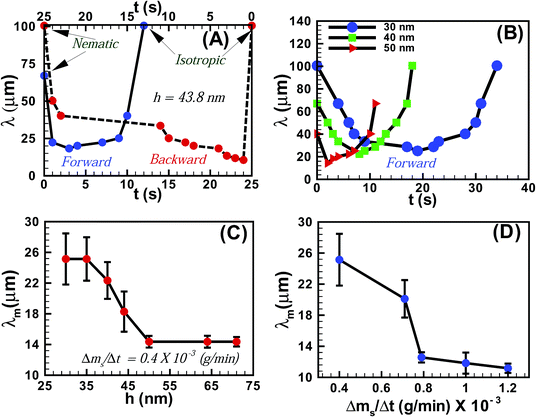
Fig. 3A shows the variation of the average periodicity of the surface features (λ) with time (t) during the N–I and I–N transitions for the film shown in Fig. 1 (film thickness h = 43.8 ± 0.9 nm). It may be noted here that the time t = 0 s represents the frame when the initial lighter spots of the solvent molecules nucleated on the film. During the initial stages of the N–I transition λ decreased with the progressive increase in the number of solvent molecules adsorbed on the film-surface. The trend continued until the surface was nearly saturated with the solvent molecules and λ attained a minimum value (λm). Beyond this point the features progressively disappeared (increase in λ) as the solvent molecules gradually diffused into the film matrix and the film became isotropic. The I–N transition upon removing solvent vapour exposure was also initiated with a reduction in λ until a minimum was attained, which demonstrated the outward diffusion of the solvent molecules from the film matrix. As the solvent molecules completely diffused out of the film, λ increased until a nearly flat nematic film surface emerged. The plot also highlights the existence of some hysteresis in terms of λ and t between the forward (N–I) and the backward (I–N) transitions, due to the differential rates of solvent intake on the film surface and diffusion of the solvent molecules within the film surface. Fig. 3B shows the variation of λ with t during the forward N–I transition at different values of h. The figure suggests that the transition took less time with increasing h. The observation was somewhat counter intuitive because the solvent molecules would require longer time to diffuse deeper into a thicker film to cause the N–I transition. The possible reason could be that the order of the LC molecules at the free-surface is less (more) constrained in a thicker (thinner) film because of their larger (smaller) distance from the strongly anchored LC molecules on the substrate.34 Previous studies demonstrated that the 5CB molecules form dimers in the bulk of the film,23,35,36 while at the nematic–substrate (nematic–air) interface the 5CB molecules show a planar (homeotropic) orientation.23,30,35–39 Thus, a less (more) constrained nematic–air interface allowed faster (slower) kinetics of the nematic to isotropic transition or vice versa for the thicker (thinner) films. The ESI videos 4 and 5† also demonstrate that the molecular rearrangements could be much faster for the thicker films, which could also speed up the kinetics of the process. We further investigated the variation of λm with h, which is shown in Fig. 3C. The plots suggest that for h < 50 nm, λm progressively decreased with increasing h. However, λm became nearly independent of h for thicker films (h > 50 nm). These observations suggest that beyond hC ∼50 nm the number density of the nucleation sites for the solvent molecules on the film surface become independent of h. The rate of solvent vapour evaporation (Δms/Δt) into the experimental chamber also influenced λm. Fig. 3D shows that λm progressively decreased with an increasing rate of solvent evaporation from the source, which led to a faster penetration of the solvent molecules inside the film. This particular aspect of the solvent vapour annealing of LC films was also similar to the thermal annealing of LC films where λm is known to change with the rate of heating.27
Fig. 4 (and the ESI video 6†) shows the dewetting and subsequent hole-healing of a nematic film upon prolonged solvent exposure beyond the stage of the N–I transition and thereafter the removal of the solvent exposure. Previous studies showed that a 5CB film is completely wettable on a Si surface in the nematic phase while the isotropic 5CB film is only partially wettable on a Si wafer.36Fig. 4A shows that long-time (697 s) solvent exposure led to the dewetting of a 5CB film with the formation of a hole surrounded by a thick rim. The pathway appeared identical to the thermal dewetting of a polymeric film when annealed beyond the glass transition temperature. It may be noted here that while the thermal annealing destroyed the orientational order of the LC from the bottom substrate, the solvent annealing did the same through the LC–air interface. Further, solvent vapour induced dewetting of a polymer thin film leads to permanent holes and features, which remain unaltered even after withdrawing the sample from solvent vapour exposure. In comparison, for the nematic films, the morphology of the holes was found to change when the solvent sources were withdrawn from the chamber.
Fig. 4B shows the morphology of the hole after 61 s of the solvent source withdrawal. The key features observed were: (i) contact line around the hole becomes unstable with the appearance of periodic wavy patterns; (ii) surface pattern on the film surface demonstrating an I–N transition in the other part of the film, as observed previously in Fig. 1G and H; and (iii) the drop or thread like residuals of the films start spreading on the hole. The appearance and disappearance of surface patterns implied that progressively the nematic order was restored inside the film as solvent molecules started diffusing out of the film matrix. Since the 5CB film is completely wettable on a silicon surface in the nematic state,36 spreading with a change in contact angle was observed in Fig. 4B in place of the droplets or threads on the hole in Fig. 4A. The evaporation across the contact line changed the contact angle as the isotropic film was progressively converted into a nematic film with time and the contact line motion towards the centre of the hole was set in. In regular circumstances, the nematic film was expected to uniformly spread on the entire hole to fully cover it. However, the differential rate of solvent evaporation from the film, hole–rim, contact line, and dewetted zone was very closely coupled with the change in contact angle, as the isotropic film was gradually converted into a nematic film. Thus, during the I–N transition, Fig. 4B and C show the appearance of a contact-line instability in the form of nematic fingers around the hole once the contact line motion set in. With the progress of time, the differential rate of solvent evaporation from the film, hole–rim, contact line, and hole created an imbalance of the osmotic pressure across the contact line which in conjugation with the change in contact angle stimulated the contact line motion.
Fig. 4C (808 s after withdrawal of solvent source) and 4D (2071 s after withdrawal of solvent source) suggest that the change in contact angle and the osmotic pressure imbalance across the contact line helped the nematic fingers to grow towards the centre of the hole. Fig. 4D shows that the fingers stretched along the contact line almost all the way until the ruptured hole is nearly healed up. It may be noted here that if the solvent exposure was reintroduced at any stage of the hole-healing process, the fingers disappeared following an N–I transition and the film again started dewetting the surface, which clearly emphasized the quasi-reversible nature of the solvent vapour induced dewetting of the LC thin film. The hole-healing through the nematic fingers upon removal of the solvent exposure and dewetting of the film through hole-growth upon solvent exposure could also be repeated for many cycles, which are shown in the ESI video 7.† The ESI video 8† shows that when there are multiple holes on a dewetted film the fingering instability could again self-heal almost the entire dewetted zone upon removal of the solvent exposure.
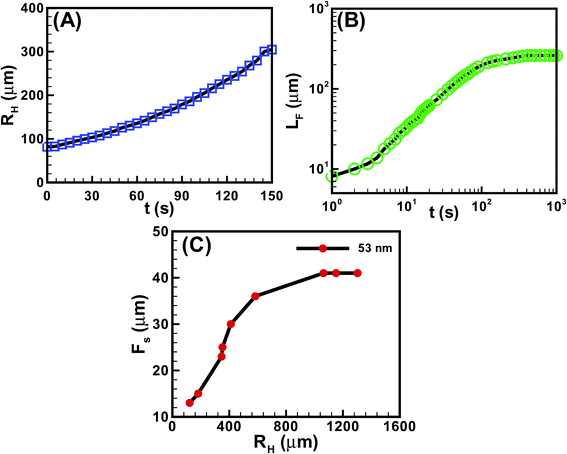
Fig. 5 shows the kinetics of hole and finger growth during solvent vapour annealing and removal of solvent vapour exposure. Fig. 5A and B show the variations of the hole diameter (RH) during hole-growth and average length of the fingers (LF) during hole-healing with time (t). The kinetics of hole-growth were observed to be much faster than the hole-healing process. The plots also suggest that the isotropic holes grew almost linearly with time during dewetting, whereas the hole-healing took place in three distinct phases. The initial slower regime corresponds to the development of the instability along the contact line while the film underwent the I–N transition. The subsequent faster regime corresponds to the growth of the nematic fingers towards the hole-centre because of the change in contact angle and osmotic pressure imbalance across the contact line. Towards the end, the healing process became exceedingly sluggish because of the reduction in the driving force owing to the lack of solvent inside the film matrix and hole. Fig. 5C shows that the periodicity of the fingers (FS) was much smaller when the hole-radius (RH) was smaller. However, FS initially increased and then saturated to a constant value with increasing RH.
Experimental
In the experiments, 5CB (4-n-pentyl-4′-cyanobiphenyl) nematic LC (99.99% pure, Sigma Aldrich, TP ∼33.5 ± 0.5 °C) was used without any further processing. The films were spin coated from a solution of 5CB, either in toluene or in n-hexane (HPLC grade, Merck) on square (∼1 cm × ∼1 cm) and thoroughly cleaned pieces of silicon wafer (<100>, Boron doped P type, resistivity 0.01–0.02 Ω cm). The coated samples were kept under vacuum at ambient conditions (25 ± 1.0 °C) for about 10 minutes to remove any excess residual solvent. The 5CB film is nematic at room temperature, 25 °C, although it can show the isotropic liquid with an increase in temperature beyond TP ∼33.5 ± 0.5 °C. The dipole moment associated with the –CN group of the 5CB molecules enables them to form dimers in the bulk of the film of length 25 Å with their polar head facing each other while the length of a single 5CB molecule is 18.7 Å.23,35,36 On a thoroughly cleaned Si wafer with a few nanometers of native oxide layer, the 5CB molecules show a planar or quasi-planar anchoring molecular arrangement at the Si–nematic interface.23,30,35–39 In comparison, the molecular arrangement is homeotropic at the nematic–air free surface.23,30,35–39 The 5CB completely wets a Si surface to form a film in the nematic phase while the isotropic 5CB film is only partially wettable on the Si wafer.36,40The thicknesses of the films were measured using an Imaging Ellipsometer (single wavelength, nanofilm_ep3-sw, Accurion Gmbh., Gottingen). Fig. S1A in the ESI† shows the variations of film thickness (h) with the concentration of 5CB in the two solvents. The phase transition and dewetting of the 5CB films were carried out by exposing the films to solvent vapour. For this purpose, the spin casted 5CB films were initially placed in a closed chamber with a glass cover and subsequently a container containing a fixed quantity (100 μl) of the solvent was introduced inside the chamber. The solvent molecules diffused into the film and reduced the TP of the nematic film to the ambient temperature. The experimental chamber was mounted on the stage of an optical microscope (Leica DM 2500M) where in situ observations were made with a CCD camera using white light in reflection mode. The rate of evaporation in the chamber could be controlled by introducing multiple solvent sources, each having a fixed volume of 100 μl. The average rate of evaporation of the solvent vapour in the chamber was measured by performing a control experiment on a microbalance and calculating the ratio of the mass evaporated (Δms) over a specific amount of time (Δt). Fig. S1B in the ESI† shows the rate of evaporation (Δms/Δt) from the sources. Fig. S1C† in the supplementary section compares the thickness of the films having a homogeneous surface before and after the N–I or I–N transitions. The figure suggests that the film swelled during the N–I transition due to the diffusive penetration of solvent molecules into the film matrix. Based on the elipsometric measurement of roughness, Fig. S1D in the ESI† shows that the surface roughness reached a maximum value during the N–I phase transition, before dropping to a very low value after the phase transition was complete. The figure also confirms that the film did not dewet during the phase transition because the amplitudes of the undulations were much lower than the initial thickness of the film. The variation in roughness of the films (R) during N–I and I–N transitions were quantified using the roughness tool from the ellipsometric images.
The wavelength (λ) of the instability features were obtained from the image analysis of the optical micrographs using the open source software imageJ. Initially the micrograph was loaded and the image was converted to the 8-bit format. Following this, the pixels were calibrated with a scale bar. In order to obtain the average spacing of the patterns the ‘analyze/plot profile’ option of the software was used for a selected area or length. The reciprocal of the number of cycles appeared per unit length was reported as the average spacing between the structures.
Conclusions
The article reports quasi-reversible N–I and I–N phase transitions of an ultrathin nematic film at room temperature upon solvent annealing and de-annealing. The transitions were accompanied by the appearance and fading of surface patterns as the solvent destroyed (restored) the orientational order while diffusing into (out of) the film. The experiments confirmed that solvent exposure could act as an analogue to thermal annealing in ambient conditions. A prolonged solvent vapour annealing led to the dewetting of the nematic film following the N–I transition. During this stage, removing the solvent exposure led to an exciting fingering instability at the contact line, surrounding the dewetted zones. The change in contact angle due to phase transition coupled with the imbalance of osmotic pressure due to the differential rate of solvent evaporation across the contact line helped the fingers to grow towards the centre of the hole. The fingers grew with time to attain structures with significantly high aspect-ratio and branching patterns, which nearly self-healed the dewetted zones. Interestingly, even at this stage, the growth of the fingers could be arrested and dewetting could be resumed by introducing solvent vapour exposure. The formation of the nematic fingers upon withdrawal of the solvent exposure and the removal of the fingers through the dewetting of the films upon solvent vapour annealing were found to be a quasi-reversible process. The characteristics of the fingering instability observed for the nematic ultrathin films in the present study were very different from the same originated due to the osmotic pressure imbalance during the spreading of a droplet loaded with surfactants.41,42 The results reported here show the potential for future developments of futuristic vapour sensors and self-healing coatings using LC thin films.Acknowledgements
The authors (B.R. and D.B.) acknowledge the support of the DST, India through its fast-track scheme, SR/FTP/ETA-091/2009, and FIST grant SR/FST/ETII-028/2010. Useful contributions from Kartick Mondal are also gratefully acknowledged.Notes and references
- P. G. de Gennes, Rev. Mod. Phys., 1985, 57, 827–863 CrossRef CAS.
- A. Oron, S. H. Davis and S. G. Bankoff, Rev. Mod. Phys., 1997, 69, 931–980 CrossRef CAS.
- R. V. Craster and O. K. Matar, Rev. Mod. Phys., 2009, 81, 1131–1198 CrossRef CAS.
- R. Mukherjee, S. Das, A. Das, S. K. Sharma, A. K. Raychaudhuri and A. Sharma, ACS Nano, 2010, 4, 3709–3724 CrossRef CAS PubMed.
- D. Gentili, G. Foschi, F. Valle, M. Cavallini and F. Biscarini, Chem. Soc. Rev., 2012, 41, 4430–4443 RSC.
- C. J. Van Oss, M. K. Chaudhury and R. J. Good, Chem. Rev., 1988, 88, 927–941 CrossRef CAS.
- E. Ruckenstein and R. K. Jain, J. Chem. Soc., Faraday Trans. 2, 1974, 70, 132–147 RSC.
- S. J. Woltman, G. D. Jay and G. P. Crawford, Nat. Mater., 2007, 6, 929–938 CrossRef CAS PubMed.
- E. Gering and C. T. Atkinson, J. Parasitol., 2004, 90, 879–881 CrossRef PubMed.
- A. Sharma and R. Khanna, Phys. Rev. Lett., 1998, 81, 3463–3466 CrossRef CAS.
- A. Sharma, Eur. Phys. J. E, 2003, 12, 397–408 CrossRef CAS PubMed.
- G. Reiter, Phys. Rev. Lett., 1992, 68, 75–78 CrossRef CAS.
- R. Xie, A. Karim, J. F. Douglas, C. C. Han and R. A. Weiss, Phys. Rev. Lett., 1998, 81, 1251–1254 CrossRef CAS.
- R. Seemann, S. Herminghaus and K. Jacobs, Phys. Rev. Lett., 2001, 86, 5534–5537 CrossRef CAS.
- S. Herminghaus, K. Jacobs, K. Mecke, J. Bischof, A. Fery, M. Ibn-Elhaj and S. Schlagowski, Science, 1998, 282, 916–919 CrossRef.
- R. Konnur, K. Kargupta and A. Sharma, Phys. Rev. Lett., 2000, 84, 931–934 CrossRef CAS.
- U. Thiele, M. G. Velarde and K. Neuffer, Phys. Rev. Lett., 2001, 87, 016104 CrossRef CAS.
- K. Kargupta and A. Sharma, Phys. Rev. Lett., 2001, 86, 4536–4539 CrossRef CAS.
- A. Sehgal, V. Ferreiro, J. F. Douglas, E. J. Amis and A. Karim, Langmuir, 2002, 18, 7041–7048 CrossRef CAS.
- A. Sehgal, D. Bandyopadhyay, K. Kargupta, A. Sharma and A. Karim, Soft Matter, 2012, 8, 10394–10402 RSC.
- R. Mukherjee, D. Bandyopadhyay and A. Sharma, Soft Matter, 2008, 4, 2086–2097 RSC.
- S. Roy and R. Mukherjee, ACS Appl. Mater. Interfaces, 2012, 4, 5375–5385 CAS.
- F. Vandenbrouck, M. P. Valignat and A. M. Cazabat, Phys. Rev. Lett., 1999, 82, 2693–2696 CrossRef CAS.
- S. Sankararaman and S. Ramaswamy, Phys. Rev. Lett., 2009, 102, 118107 CrossRef.
- S. Chandrasekhar, Liq. Cryst., Cambridge University Press, Cambridge, England, 1992 Search PubMed.
- P. G. de Gennes and J. Prost, Phys. Liq. Cryst., Oxford, Clarendon, 1993 Search PubMed.
- S. Schlagowski, K. Jacobs and S. Herminghaus, Europhys. Lett., 2002, 57, 519 CrossRef CAS.
- A. Ajdari, L. Peliti and J. Prost, Phys. Rev. Lett., 1991, 66, 1481–1484 CrossRef.
- P. Ziherl, R. Podgornik and S. Žumer, Phys. Rev. Lett., 2000, 84, 1228–1231 CrossRef CAS.
- D. van Effenterre, R. Ober, M. P. Valignat and A. M. Cazabat, Phys. Rev. Lett., 2001, 87, 125701 CrossRef CAS.
- D. van Effenterre, M. P. Valignat and D. Roux, Europhys. Lett., 2003, 62, 526 CrossRef CAS.
- R. Garcia, E. Subashi and M. Fukuto, Phys. Rev. Lett., 2008, 100, 197801 CrossRef CAS.
- S. H. Lee, P. J. Yoo, S. J. Kwon and H. H. Lee, J. Chem. Phys., 2004, 121, 4346–4351 CrossRef CAS PubMed.
- M. Ruths and B. Zappone, Langmuir, 2012, 28, 8371–8383 CrossRef CAS PubMed.
- M. P. Valignat, S. Villette, J. Li, R. Barberi, R. Bartolino, E. Dubois-Violette and A. M. Cazabat, Phys. Rev. Lett., 1996, 77, 1994–1997 CrossRef CAS.
- F. Vandenbrouck, S. Bardon, M. P. Valignat and A. M. Cazabat, Phys. Rev. Lett., 1998, 81, 610–613 CrossRef CAS.
- A. J. leadbetter, R. M. Richardson and C. N. Colling, J. Phys. Colloq., 1975, 36, C1 CrossRef.
- H. Kasten and G. Strobl, J. Chem. Phys., 1995, 103, 6768–6774 CrossRef CAS PubMed.
- A. M. Cazabat, U. Delabre, C. Richard and Y. Yip Cheung Sang, Adv. Colloid Interface Sci., 2011, 168, 29–39 CrossRef CAS PubMed.
- C. Poulard and A. M. Cazabat, Langmuir, 2005, 21, 6270–6276 CrossRef CAS PubMed.
- S. M. Troian, X. L. Wu and S. A. Safran, Phys. Rev. Lett., 1989, 62, 1496–1499 CrossRef CAS.
- S. M. Troian, E. Herbolzheimer and S. A. Safran, Phys. Rev. Lett., 1990, 65, 333–336 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The supporting videos 1–8 discussed in the manuscript, the brief descriptions on the supporting videos, and supporting figures are uploaded as supporting material. See DOI: 10.1039/c4sm02111h |
| This journal is © The Royal Society of Chemistry 2015 |