Structural and mechanical properties of cardiolipin lipid bilayers determined using neutron spin echo, small angle neutron and X-ray scattering, and molecular dynamics simulations

Abstract

The detailed structural and mechanical properties of a tetraoleoyl cardiolipin (TOCL) bilayer were determined using neutron spin echo (NSE) spectroscopy, small angle neutron and X-ray scattering (SANS and SAXS, respectively), and molecular dynamics (MD) simulations. We used MD simulations to develop a scattering density profile (SDP) model, which was then utilized to jointly refine SANS and SAXS data. In addition to commonly reported lipid bilayer structural parameters, component distributions were obtained, including the volume probability, electron density and neutron scattering length density. Of note, the distance between electron density maxima D_HH (39.4 Å) and the hydrocarbon chain thickness 2D_C (29.1 Å) of TOCL bilayers were both found to be larger than the corresponding values for dioleoyl phosphatidylcholine (DOPC) bilayers. Conversely, TOCL bilayers have a smaller overall bilayer thickness D_B (36.7 Å), primarily due to their smaller headgroup volume per phosphate. SDP analysis yielded a lipid area of 129.8 Ų, indicating that the cross-sectional area per oleoyl chain in TOCL bilayers (i.e., 32.5 Ų) is smaller than that for DOPC bilayers. Multiple sets of MD simulations were performed with the lipid area constrained at different values. The calculated surface tension versus lipid area resulted in a lateral area compressibility modulus K_A of 342 mN m⁻¹, which is slightly larger compared to DOPC bilayers. Model free comparison to experimental scattering data revealed the best simulated TOCL bilayer from which detailed molecular interactions were determined. Specifically, Na⁺ cations were found to interact most strongly with the glycerol hydroxyl linkage, followed by the phosphate and backbone carbonyl oxygens. Inter- and intra-lipid interactions were facilitated by hydrogen bonding between the glycerol hydroxyl and phosphate oxygen, but not with the backbone carbonyl. Finally, analysis of the intermediate scattering functions from NSE spectroscopy measurements of TOCL bilayers yielded a bending modulus K_C of 1.06 × 10⁻¹⁹ J, which was larger than that observed in DOPC bilayers. Our results show the physicochemical properties of cardiolin bilayers that may be important in explaining their functionality in the inner mitochondrial membrane.

---

1. Introduction

Cardiolipin (CL) lipids are a group of anionic phospholipids that are found predominantly in the inner mitochondrial membrane (IMM) of eukaryotic cells,¹ and in the plasma membranes of certain bacteria.² Unlike common phospholipids, CL is composed of two phosphate moieties, each attached to two hydrocarbon chains via a glycerol backbone. CL's peculiar structure restricts phosphate mobility, reduces headgroup area, and promotes the tendency for forming non-lamellar phases.^2,3 CL plays an important role in the IMM of eukaryotes, including: (1) supporting the activation of mitochondrial related enzymes; (2) disrupting⁴ or promoting⁵ supramolecular organization; and (3) increasing mitochondria membrane electronegativity which leads to programmed cell death.^6,7 In addition, defects in CL remodeling can cause detrimental diseases such as Barth syndrome.⁸ More details about the physiological importance of CL can be found in recent review articles.^2,9–11

To understand CL's functionality, elucidating its detailed physicochemical properties through the use of model CL bilayers is essential. To date, only a handful of experimental results detailing the structure and organization of CL bilayers exist, including reports about headgroup orientation, thermotropic phase behavior, and the lamellar/non-lamellar phase transition (see review article² and the references therein). Both coarse-grained and atomistic molecular dynamics (MD) simulation studies of CL bilayers have been carried out.^12–20 However, the lack of experimental data needed for comparison has hampered the development of CL force fields. In the present study we used different contrast small angle neutron and X-ray scattering (SANS and SAXS, respectively), neutron spin echo (NSE) spectroscopy, and all-atom MD simulations to characterize the structural and mechanical properties of a fluid phase tetraoleoyl cardiolipin (TOCL) bilayer. Specifically, we developed a scattering density profile (SDP) model to jointly refine SANS and SAXS data. Bilayer structural parameters were then determined from SDP model analysis, along with component distributions, including volume probability (vP), one-dimensional electron density (ED) and neutron scattering length density (NSLD). We also performed five sets of area-constrained MD simulations. Model free comparison to experimental scattering data revealed the best simulated bilayer, from which detailed atomic interactions and the area compressibility modulus K_A were determined. We also calculated the bending modulus K_C of TOLC bilayers by analyzing the intermediate scattering functions from NSE measurements using a Zilman–Granek (ZG) model.²¹

2. Materials and methods

2.1 Small angle neutron and X-ray scattering

Synthetic TOCL lipid (sodium salt) was purchased from Avanti Polar Lipids (Alabaster, AL) and used as received. The molecular volume of TOCL was determined using an Anton-Paar DMA5000 vibrating tube density meter (Graz, Austria).²² For SANS experiments (Oak Ridge national Laboratory), 50 nm sized unilamellar vesicles (ULVs) were prepared by mixing 30 mg of TOCL lipid powder with 1.0 ml D₂O water, followed by freeze–thaw cycling. The lipid dispersion was extruded using an Avanti mini-extruder. The resulting ULV solution was aliquoted into three microcentrifuge tubes, and diluted to different neutron external contrast conditions (i.e., 100, 70 and 50% D₂O). The final lipid concentration was about 10 mg ml⁻¹. ULVs for SAXS experiments (Cornell High Energy Synchrotron Source) were prepared in a similar manner, but using H₂O water instead. All scattering experiments were performed at 30 °C. Details regarding sample preparation, experimental procedures and data reduction can be found in ref. 23–26.

2.2 Neutron spin echo spectroscopy

50 nm sized ULVs suspended in 100% D₂O were prepared as described for the small angle scattering experiments. NSE spectroscopy measurements were performed at the Spallation Neutron Source (SNS), Oak Ridge National Laboratory. SNS is a time-of-flight neutron source, and two ranges of wavelengths (5–8 Å and 8–11 Å) were used to cover a range of Fourier time τ from 30 ps to 82 ns, and a q-range from 0.05 to 0.16 Å⁻¹. ULVs taken up in 3 mm thick Hellma quartz cells were placed in a temperature-controlled sample holder. Graphite foil was used to determine the instrumental resolution, and pure D₂O water was used for background subtraction. The collected data were binned to yield four q-values per scattering angle, resulting in a total of 16 q-values. For a given q, the final output from the NSE measurement is the intermediate scattering function, S(q, τ)/S(q, 0). The bilayer bending modulus K_C can be calculated from the intermediate scattering function using the ZG model:²¹

S(q, τ)/S(q, 0) = exp{−[Γ(q)τ]^2/3}, (1)

where Γ(q) is the relaxation rate describing the decay property of the intermediate scattering function:

Γ(q) = 0.025ε(k_BT/K_C)^1/2(k_BT/η)q³, (2)

where k_BT is the thermal energy, ε approaches unity at K_C ≫ k_BT, which is satisfied by typical lipid bilayers,²⁷ and η is the viscosity of the aqueous solution. Since Γ(q) is linearly related to q³, the bilayer bending modulus K_C can be determined by measuring the intermediate scattering function at several q values.

2.3 Molecular dynamics simulations

Initial coordinates for a TOCL bilayer made up of 100 lipids were generated by Packmol.²⁸ Lipid hydrogen atoms were explicitly included (all-atom model), in addition to 5778 water molecules and counterions to neutralize the system. MD simulations were performed using NAMD 2.9 (ref. 29) and the CHARMM 36 lipid force field.^30,31 Periodic boundary conditions were applied. For each system, atomic coordinates were first minimized using the conjugated gradient algorithm for 5000 steps, followed by 2 ns of equilibration in a constant particle number, pressure, and temperature (NPT) ensemble. Equilibrium was determined by monitoring the system's area per lipid and the root-mean-square deviation (RMSD). In all simulations, the van der Waals (vdW) interactions were truncated via a potential-based switching function used by X-PLOR. Starting from a switching distance of 10.5 Å, the vdW potential was brought smoothly to 0 at the cutoff distance of 12 Å. Electrostatic interactions were treated using the particle-mesh Ewald (PME) method with a 1.0 Å grid spacing.^32,33 The r-RESPA multiple-time-step method³⁴ was employed with a 2 fs time step for bonded, and 2 and 4 fs time steps for short-range non-bonded and long-range electrostatic interactions, respectively. The bonds between hydrogen and other atoms were constrained using the SHAKE algorithm.³⁵

We first simulated the TOCL bilayer using the NPT ensemble for 50 ns. Langevin dynamics were used to maintain a constant temperature of 303 K, while the Nosé-Hoover Langevin-piston algorithm^36,37 was used to maintain a constant pressure of 1 bar. The z-axis was allowed to expand and contract independently of the x–y plane (semi-isotropic pressure coupling). The resulting lipid area was 122.5 Ų. This simulation was used to guide the development of an SDP model for subsequent analysis of SAXS and SANS data. An additional five sets of constant particle number, area, normal pressure and temperature (NAP_nT) simulations were performed, where the average area per lipid was constrained to 127.2, 129.2, 131.2, 133.2 or 135.2 Ų, while the z-axis was allowed to expand and contract in order to maintain a constant P_n. Starting configurations for these simulations were selected snapshots from the NPT trajectory, with lipid areas close to their target values. The production run length for each of these simulations was between 101 and 132 ns. Only the final 50 ns of each trajectory were used for data analysis. For each of the area-constrained simulations, the surface tension γ was calculated from the difference between the normal and lateral components of the pressure tensor.^38,39

The CHARMM-GUI Membrane Builder⁴⁰ was used to generate coordinates for a dioleoyl phosphatidylcholine (DOPC) bilayer containing a total of 244 lipids. The entire system contained 14 408 water molecules. Simulations of DOPC followed the same procedures as those outlined for TOCL bilayers. The DOPC bilayer was first simulated using the NPT ensemble for 40 ns. The resulting lipid area was 67.5 Ų. Subsequently, five additional sets of NAP_nT simulations were performed where the average lipid area was constrained to 63.4, 65.4, 67.4, 69.4 or 71.4 Ų. The production run length for each of these simulations was between 86 and 93 ns. All simulations were conducted on the Hopper supercomputer located at the National Energy Research Scientific Computing Center (NERSC).

3. Results and discussion

3.1 Constructing SDP model

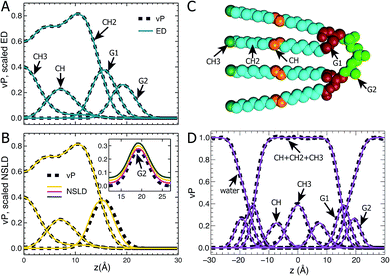
Following our previous studies of phosphatidylcholine (PC),^23,41 phosphatidylglycerol (PG),^25,42 and phosphatidylserine (PS)²⁶ bilayers, the SANS and SAXS data for TOCL ULVs were analyzed using the SDP model shown in Fig. 1A. The four oleoyl chains of TOCL were parsed into three components, depending on the number of hydrogens associated with each carbon atom, namely, the terminal methyl (CH₃), methylene (CH₂) and unsaturated methine (CH) groups. The amphiphilic headgroup was parsed into the backbone carbonyl (G1), and a G2 group which is comprised of the two phosphates and the glycerol hydroxyl linkage. The reason for not separating the phosphate and glycerol linkage is because of their positional overlap, as indicated by our MD simulations. This complicates the determination of component volumes for the phosphate and glycerol linkage from MD simulations.⁴³ On the other hand, our previous studies of PG and PS lipids indicate that both two-Gaussian (2G) and three-Gaussian (3G) headgroup models yield similar lipid bilayer structures.^25,26,42 Based on these observations, we decided to use the 2G headgroup model to jointly refine the SANS and SAXS data.

Fig. 1 TOCL bilayer component distributions. Atom number density distributions, obtained from area-constrained MD simulations of A = 131.2 Ų were used to calculate component vP, ED and NSLD profiles. (A) Comparison between component vPs (dark dashed lines) and their scaled ED distributions (solid cyan lines). (B) Comparison between component vPs (dashed lines) and their scaled NSLDs (yellow solid lines). Due to hydrogen exchange with water, the NSLD of G2 is dependent on D₂O concentration. The inset in (B) shows the comparison between G2's vP and its three NSLDs at 100% (magenta), 70% (yellow) and 50% (green) D₂O concentrations – the NSLDs were shifted vertically for clarity. (C) Parsing a TOCL lipid into five components. The hydrocarbon chain is parsed into the terminal methyl (CH3, forest), methylene (CH2, cyan), and unsaturated methine (CH, orange) groups, while the hydrogroup is parsed into the glycerol-carbonyl backbone (G1, firebrick), and the phosphate and glycerol linkage (G2, green). (D) Component vPs calculated from simulations (dark dashed lines) are fitted by analytical functions (solid lines). See the main text for more details.

The SDP model is based on the concept that the bilayer's component ED and NSLD can be described by its volume probability vP. However, this is not always the case, as was previously demonstrated by a study of DOPC bilayers.⁴¹ The overall vP of the phosphate and choline moieties does not coincide with the overall ED and NSLD. This therefore necessitates separating the choline and phosphate into two components.⁴¹ To check whether the proposed SDP model (Fig. 1) is suitable for the TOCL bilayer, we show component vP together with the corresponding ED (Fig. 1B) and NSLD (Fig. 1C) distributions. For each component, good overlap is observed between its vP and the scaled ED (Fig. 1B) – the scaling factor is the ratio of the component volume and the component electron number. This indicates that each component's ED can be well represented by its vP.

For components in the hydrocarbon chain region (i.e., CH3, CH2 and CH), good overlap is obtained between their vPs and the corresponding NSLDs (Fig. 1C). However, some discrepancy was observed between G1's vP and its NSLD. Such a discrepancy also exists in the SDP models for PC, PG and PS bilayers.^25,26,41 On the other hand, the difference is smaller than the typical positional uncertainties (∼0.5 Å) obtained from SDP model analysis. Therefore, we adopted the same grouping method for G1, as was used previously. For the G2 component, the glycerol linkage contains a hydroxyl which undergoes hydrogen exchange with the water solvent, making G2's NSLD dependent on D₂O concentration.^26,44 The inset to Fig. 1C compares G2's vP and its NSLDs at the three D₂O concentrations used in our SANS measurements. It is clear that G2's vP overlays with the three sets of NSLDs, lending support for the G2 grouping used.

The grouping of atoms shown in Fig. 1C enables component vPs, and consequently their EDs and NSLDs, to be represented by analytical functions (Fig. 1D). Specifically, four Gaussian functions are used to describe components CH3, CH, G1 and G2; the summation of CH, CH2 and CH3 in the hydrocarbon chain region is represented by a symmetrical error function; and the water vP is obtained by subtracting the lipid's vP from unity.^25,26,41 It is clear that component vPs can be well represented by these analytical functions. The goal of SDP model analysis is to determine a set of parameters describing these analytical functions by minimizing the difference between model form factors calculated from these analytical functions, and the experimental SANS and SAXS data.²⁶

3.2 SDP analysis

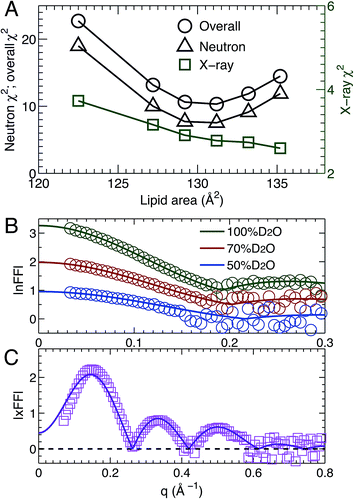
Using the described SDP model we simultaneously fit three sets of different contrast SANS data and one set of SAXS data. The best fitting results are shown in Fig. 2. It is clear that the model form factors (solid lines in Fig. 2A and B) agree very well with the experimental data (open symbols). The corresponding component EDs (Fig. 2C) and NSLDs (Fig. 2D) were calculated from the vPs in Fig. 2E. Based on parameters describing the analytical functions representing component vPs, the structural properties of the TOCL bilayer are determined. They include the overall bilayer thickness D_B, the bilayer hydrocarbon chain thickness 2D_C, the distance between electron density maxima D_HH, and the lipid area A. It should be noted that D_B is given by the Gibbs dividing surface, which divides the water distribution into two equal parts (Fig. 2E). 2D_C is defined by the full width of the error function, which is comprised of the CH, CH2 and CH3 components (Fig. 2E). A is related to either D_B or 2D_C through volumetric information, that is A = D_B/2V_L (V_L is the lipid volume) or A = (V_L − V_HL)/D_C (V_HL is the headgroup volume).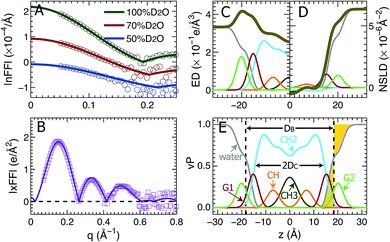

Fig. 2 Simultaneously refining different contrast SANS and SAXS data using the SDP model. (A) Neutron form factors at three external D₂O concentrations – data are shifted vertically for clarity. (B) X-ray form factor. (C) and (D) are the component ED and NSLD distributions of one bilayer leaflet. (E) Component vPs obtained from best fits to the data. They are used to calculate the EDs and NSLDs in (C) and (D), respectively. The overall bilayer thickness D_B is defined by the Gibbs dividing surface (vertical dashed line), and the hydrocarbon chain thickness 2D_C is represented by the full width of the error function describing the sum of the CH3, CH2 and CH components. Color scheme is the same as in Fig. 1.

Table 1 contains several important TOCL bilayer structural parameters, which were calculated from the best SDP fit shown in Fig. 2. The total lipid volume V_L, which was obtained from density measurements, and the lipid headgroup volume V_HL were fixed during data analysis. A value of 490 ų for V_HL was used, which was estimated from MD simulations of the TOCL bilayer and a tetramyristoyl cardiolipin (TMCL) bilayer (data not shown). This value is slightly smaller than a recently reported headgroup volume of 506.8 ų for TMCL.⁴⁵ To assess the effect of V_HL on bilayer structure, we performed additional SDP analysis by varying V_HL by ±10%. The resultant lipid area A changed by only 0.2%, a difference which is negligible compared to the 2% upper bound limit in uncertainty associated with SDP analysis. Note that the small effect of V_HL on lipid bilayer structure using SDP analysis was also observed for a PS bilayer.²⁶

Table 1 Structural parameters for TOCL bilayers calculated from area-constrained MD simulations (A = 131.2 Ų) and from SDP model analysis. Also displayed are the corresponding parameters for a DOPC bilayer obtained using a similar SDP model analysis⁴¹

	TOCL (MD)	TOCL (SDP)	DOPC (SDP)
V L (Å^3)	2400	2380	1303
V HL (Å^3)	493	490	331
D B (Å)	36.6	36.7	38.7
D HH (Å)	37.4	39.4	36.7
2DC (Å)	29.1	29.1	28.8
A (Å^2)	131.2	129.8	67.4

---

Table 1 also lists structural parameters of a TOCL bilayer calculated from MD simulations with the average lipid area constrained to 131.2 Ų, and a DOPC bilayer which was determined using a similar SDP analysis.⁴¹ For the TOCL bilayer, MD simulations and SDP analysis yielded similar overall bilayer and hydrocarbon chain thicknesses. This is understandable since the simulation was performed at a lipid area (i.e., 131.2 Ų) close to that obtained from SDP analysis (i.e., 129.8 Ų) – the simulation also generated a lipid volume close to the experimental value. The largest discrepancy resides in the distance between the electron density maxima D_HH. SDP analysis suggested a D_HH that is 2.0 Å larger than what simulation predicted. This difference may explain the discrepancies between the simulation and experimental form factors in the following section.

Since DOPC contains two oleyol chains and TOCL contains four oleoyl chains, it is interesting to compare their bilayer structures. The last two columns in Table 1 show that the average cross-sectional area of the oleoyl chain in TOCL (32.5 Ų) is smaller than for DOPC (33.7 Ų). This is consistent with TOCL's larger hydrocarbon chain thickness, assuming the same molecular volume for the oleoyl chains in TOCL and DOPC bilayers. The larger 2D_C for TOCL also explains its larger D_HH, which is primarily determined from the position of the electron dense phosphate group. On the other hand, TOCL exhibits a smaller overall bilayer thickness D_B than DOPC. This is mainly due to TOCL's smaller volume for each phosphate moiety, when compared to DOPC (i.e., 245 ų for TOCL versus 331 ų for DOPC). It is noteworthy that the larger D_HH for the tetraoleoyl TOCL, compared to the dioleoyl DOPC, is consistent with a recent study which compared the structures of dimyristoyl PC (DMPC) and tetramyristoyl PC (TMCL) bilayers.⁴⁵

3.3 Model-free evaluation of simulated bilayers

MD simulations are useful in revealing detailed molecular features within a lipid bilayer, assuming that the simulated bilayer is able to reproduce experimental observations. One way to validate simulations is to use a model free comparison between form factors calculated from simulated bilayers and the experimental ones shown in Fig. 2.^25,26,46 Such comparisons were performed for the six sets of simulations with different lipid areas. The goodness of the comparison is given by χ², which describes the difference between the simulation and experimental form factors.^25,26,46Fig. 3A shows χ² for individual neutron and X-ray form factors, and the overall χ² which sums the neutron and X-ray χ². Because there are three sets of neutron data, but only one X-ray data set, the neutron χ² is larger than the X-ray χ². In addition, the neutron χ² is U-shaped, while the χ² for X-rays decreases continuously with increasing lipid area. The overall χ² behavior resembles that of the neutron χ². The smallest overall χ² was obtained near the lipid area predicted by SDP analysis. Fig. 3B and C show the detailed comparison between the best simulated bilayer with the smallest χ² (i.e., A = 131.2 Ų) and the experimental form factors. It is clear that good agreement is obtained for the neutron data. However, noticeable differences are observed in the case of the X-ray form factor, especially in the region of the first lobe. This indicates that further improvements to the force fields describing CL bilayers are needed.

Fig. 3 Direct comparison between simulation and experimental form factors. (A) The agreement between experimental scattering data and bilayers simulated at different lipid areas is characterized by the χ². The neutron and overall χ² are represented by the left axis, and the X-ray χ² by the right axis. The neutron χ² is U-shaped, while the one for X-rays decreases monotonically. The neutron χ² reaches its minimum near 131.2 Ų. (B) and (C) show comparisons for the best simulated bilayer with A = 131.2 Ų (solid lines) and the different contrast SANS and SAXS data (symbols).

3.4 Lipid bilayer area compressibility K_A

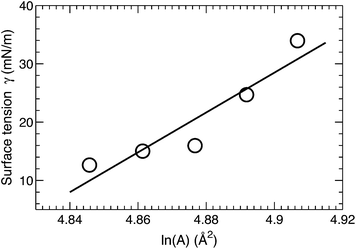
A surface tension γ was applied in order to constrain the average lipid area to a desired value. The magnitude of γ needed to displace the lipid area by a constant value is quantified by the lateral area compressibility modulus K_A, which can be calculated from K_A = ∂γ/∂(ln A).⁴⁶ For the five area-constrained simulations, the surface tensions and the corresponding lipid areas are shown in Fig. 4. A linear fit to the data resulted in a K_A of 342 mN m⁻¹. This value is smaller than that reported by two earlier simulations, which calculated K_A by quantifying lipid area fluctuations.^12,18 The larger values from these simulations may be attributed to their smaller lipid areas, which can in turn suppress lateral area fluctuations. As a control, we also simulated a DOPC bilayer at different lipid areas. The calculated K_A is 320 mN m⁻¹ (data not shown), which is close to the 321 mN m⁻¹ obtained using the fluctuation expression, but greater than the 277 mN m⁻¹ value calculated by the surface tension versus lipid area relationship.⁴⁷ Our slightly larger K_A for the tetraoleoyl TOCL bilayer, compared to the dioleoyl DOPC bilayer, implies that the glycerol linkage sterically hinders the two phosphate moieties, thus making it difficult for TOCL's four chains to compress against each other.^2,3 On the other hand, the difference is small, implying that the restriction is not pronounced. This is consistent with the not too different chain cross-sectional areas for TOCL and DOPC bilayers shown in Section 3.2.

Fig. 4 Applied surface tension γ as a function of the logarithm of the lipid area in area-constrained MD simulations. The linear fit to the data results in a lateral area compressibility modulus K_A of 342 mN m⁻¹ for TOCL bilayers.

Based on the polymer brush model,²⁷ the bilayer bending modulus K_C is related to the area compressibility modulus by K_A = 24 K_C/(2D_C)². Substituting K_A (obtained from our surface tension calculation) and the hydrocarbon chain thickness 2D_C (obtained from SDP analysis), the predicted K_C turns out to be 1.2 × 10⁻¹⁹ J. We will compare this value to the bending modulus obtained from NSE analysis in Section 3.6.

3.5 Molecular interactions inferred from the “best” simulated bilayer

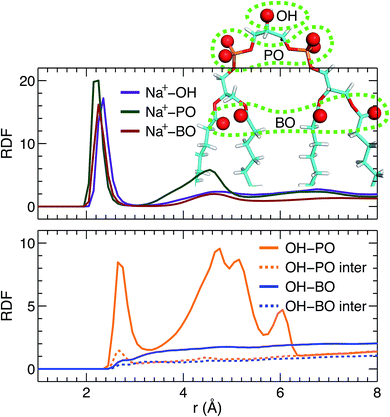
Direct comparison without any model intervening between the simulation and experimental form factors indicates that the simulated bilayer with an average lipid area of 131.2 Ų agrees best with the experimental data. Here we show Na⁺ cation-lipid and lipid–lipid interactions based on the best simulated bilayer by calculating volume-averaged radial distribution functions (RDFs). We first calculated the RDF for Na⁺ ions with respect to three types of lipid oxygen atoms, namely, the hydroxyl oxygen of the terminal glycerol linkage (OH), the four phosphate non-ether oxygens (PO), and the four backbone carbonyl oxygens (BO). The results are shown in Fig. 5A. Well-resolved peaks are identified near 2.3 Å for all oxygens. Moreover, based on the magnitude of the RDF peaks, and the fact that there is only one OH, but four oxygens for the PO and BO groups, the Na⁺ ions interact most strongly with the glycerol linkage OH. Surprisingly, Na⁺ ions interact similarly with the phosphate PO and the backbone BO. This observation is very different from our previous study of a PS bilayer, where Na⁺ ions interacted weakly with the backbone carbonyl oxygen.²⁶ One explanation for this is that the smaller headgroup per phosphate in TOCL provides less coverage for the backbone oxygens, exposing them to water and Na⁺ ions.⁴⁸ The presence of strong interactions between cations and CL headgroups is consistent with other simulations.¹⁹

Fig. 5 RDFs within a TOCL bilayer. (A) RDFs between Na⁺ ions and three types of lipid oxygens, namely, glycerol hydroxyl oxygen (OH), phosphate non-ether oxygen (PO), and backbone carbonyl oxygen (BO). (B) Lipid–lipid RDFs between OH and PO, and between OH and BO. The dashed lines represent inter-lipid RDFs, while the solid lines include both intra- and inter-lipid RDFs.

In addition to ion–lipid interactions, we also explored the role of lipid–lipid interactions in mediating TOCL bilayer organization. RDFs between the glycerol linkage OH, and the phosphate PO and the backbone carbonyl BO are shown in Fig. 5B. The dashed lines are the calculated inter-lipid pairs, while the solid lines include both the inter- and intra-lipid pairs. It is clear that OH interacts with PO by forming hydrogen bonds, as indicated by the RDF peaks near 2.7 Å. Moreover, intra-lipid hydrogen bonding is preferred over inter-lipid. This may be related to the lipid's bulky tetra-chain configuration which impairs the inter-lipid association between the OH and PO groups in adjacent lipids. For the RDF between OH and PO, additional broad peaks were observed at larger distances, which likely reflect the presence of inter-lipid interactions. For interactions between OH and BO, no discernable RDF peaks were identified, indicating no preferred interactions between the pair. This is primarily due to the restricted motion of the glycerol OH,⁴⁸ making it difficult for OH to approach the backbone BO which resides at the interface between the headgroup and the hydrocarbon chains. Our inter- and intra-lipid hydrogen bonding between the glycerol OH and phosphate PO is consistent with earlier simulations.^14,18 This observation is also supported by Fourier transform infrared (FTIR) spectroscopy measurements.⁴⁹ The authors remarked that the hydrogen bonding within CL headgroups provides a structural framework that may be important for conducting protons in the IMM. Hydrogen bonding is also in-line with the speculated role of CL as a proton trap for oxidative phosphorylation.⁵⁰ It is interesting to note that our recent study of a PS bilayer revealed similar inter-lipid hydrogen-bonding interactions.²⁶ It is conceivable then that the observed lipid–lipid interactions, which are weak or absent in neutral PC lipid bilayers, may be important for the specific functions played by these minority lipids.

3.6 Neutron spin echo spectroscopy and bilayer bending modulus

NSE spectroscopy is a powerful technique capable of studying dynamical properties of soft materials through the so-called intermediate scattering function. For example, NSE has been successfully applied in determining the bending moduli K_C of various model membrane systems, such as vesicles composed of pure lipids with different hydrocarbon chain composition,⁵¹ lipids with and without cholesterol,⁵² lipids with an antimicrobial peptide,⁵³ and oriented multibilayers,⁵⁴ to name a few.

As described in the Materials and Methods, by changing the scattering angle and the wavelength band, the intermediate scattering function S(q, τ)/S(q, 0) is obtained at discrete q values as a function of Fourier time τ. An example of the normalized intermediate scattering functions at six scattering vectors is shown in Fig. 6A. Using eqn (1) the data points at each q were fitted by a stretched exponential decay curve (solid lines). It is clear that the intermediate scattering functions are well modeled by the stretched exponential decay over the entire Fourier time regime. This indicates that the obtained NSE signal is dominated by membrane fluctuations in the q range studied. Moreover, the relaxation rate Γ(q) increases with q. This is shown in Fig. 6B, where Γ(q) is plotted as a function of q³. A linear fit to the data results in a slope b of 7.1 ± 0.2 ų ns⁻¹. Based on the ZG model (eqn (2)), b is related to the bilayer's bending modulus K_C. Taking the viscosity η of D₂O to be 0.9759 cP at 30 °C,⁵⁵ and the coefficient ε to be one (i.e., K_C ≫ k_BT), the calculated K_C is 9.5 × 10⁻¹⁹ J with an uncertainty of σ(K_C) = 2 K_Cσ(b)/b = 5.4 × 10⁻²⁰ J. This K_C is much larger than that of a typical lipid bilayer.²⁷ The abnormally large K_C derived from the ZG model has been attributed by neglecting local dissipation within the bilayer.^51–53,56 To compensate for the dissipation, an effective viscosity η_eff, which is three times that of the bulk solvent viscosity, was introduced.^51,53 One explanation for the altered viscosity is that the properties of water near the bilayer interface could be modified by molecular interactions (e.g., hydrogen bonding and electrostatic interactions) formed between the amphiphilic lipids and the interfacial water molecules. On the other hand, the choice of η_eff was mainly geared to reconciling differences between NSE results and those from other experimental approaches.^51,57 Substituting η_eff into eqn (2), the new bending modulus becomes: K_C = (1.06 ± 0.06) × 10⁻¹⁹ J. This value is close to the prediction in Section 3.4, which was calculated from the simulation-derived area compressibility modulus K_A and a polymer brush model.

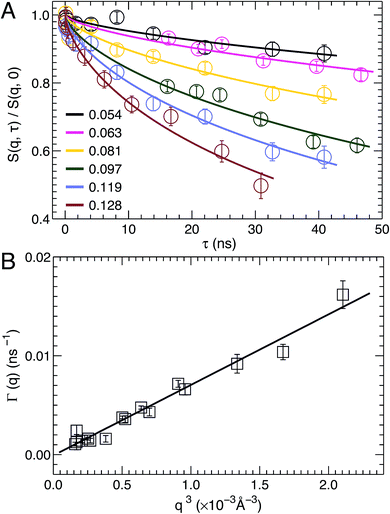Fig. 6 (A) Stretched exponential decays of NSE intermediate scattering functions S(q, τ)/S(q, 0) at selected scattering vectors q. For each curve, the corresponding q is shown in the figure legend. Analytical fits using eqn (1) are shown as solid lines. (B) The relaxation rate Γ(q) obeys the universal scaling law, Γ(q) ∼ q³. This is confirmed by a linear fit (solid line) to the data, which has a slope b of 7.1 ± 0.2 ų ns⁻¹.

In addition to scaling the solvent viscosity, the dissipation within a lipid bilayer can also be accounted for by considering that when a bilayer is bent, one monolayer is stretched and the other is compressed.⁵⁸ This leads to an inter-monolayer friction which damps the fluctuation in the density difference between the coupled monolayers.⁵⁸ The effective bending modulus K_Ceff from NSE measurements (eqn (2)) is then contributed by the usual hydrodynamically damped bending mode and the slipping mode damped by inter-monolayer friction:^56,58K_Ceff = K_C + d²K_A, where d is the distance between the monolayer neutral plane (no compression or stretching) and the bilayer center.^56,58,59 The physical basis of the substitution has been discussed by Watson and Brown.⁵⁶ Using the polymer brush model mentioned above,²⁷ we have K_Ceff = K_C [1 + 24(d/2D_C)²]. The difficulty associated with this method is how to determine the location of the neutral plane. Since DOPC and TOCL bilayers have a similar hydrocarbon chain thickness (Table 1), we assume the neutral plane is located similarly in the two bilayers, namely at d = 16.4 Å.⁵³ This results in K_C = (1.10 ± 0.06) × 10⁻¹⁹ J, which is in good agreement with the value obtained from scaling the solvent viscosity.

Recently, DMPC and TMCL bilayers were compared using X-ray diffuse scattering.⁴⁵ The authors reported that the bending modulus K_C for TMCL bilayers is about 50% larger than that of DMPC. For DOPC, the reported K_C ranges from 7.6 × 10⁻²⁰ J (ref. 60) to 8.5 × 10⁻²⁰ J (ref. 27), depending on the experimental technique used. Our calculated K_C for TOCL bilayers, using the ZG model and an effective viscosity, is 29–45% larger compared to previously reported K_C for DOPC bilayers. X-ray diffuse scattering also predicted a K_C of 7.5 × 10⁻²⁰ J for the TMCL bilayer,⁴⁵ a value smaller than that of the TOCL bilayer. The same trend is observed when comparing the two-chain PC lipid bilayers, that is the K_C of DMPC is smaller than that of DOPC.²⁷

4. Conclusions

In the present study we used scattering experiments and MD simulations to study the various structural and mechanical properties of a TOCL bilayer. In particular, an SDP model was developed based on MD simulations to jointly refine different contrast SANS and SAXS data. This resulted in detailed component vP, ED and NSLD profiles, as well as lipid bilayer structural parameters. The hydrocarbon chain thickness 2D_C and the distance between electron density maxima D_HH were found to be larger than those of the corresponding DOPC bilayer, while TOCL's overall bilayer thickness D_B is smaller, primarily due to its smaller headgroup volume per phosphate. The cross-sectional area per oleoyl chain is also smaller for the TOCL bilayer, compared to DOPC. Area stretching moduli K_A for TOCL and DOPC bilayers were determined by simulating at different lipid areas. It was found that the K_A for TOCL (342 mN m⁻¹) is slightly larger than that for DOPC (320 mN m⁻¹). By directly comparing simulation and experimental form factors, we identified the best simulated bilayer from which detailed atomic interactions within a TOCL bilayer were determined. We found that Na⁺ cations interact most strongly with the glycerol hydroxyl linkage, followed by the phosphate and backbone carbonyl oxygens. The glycerol hydroxyl also forms intra- and inter-lipid hydrogen bonds with the phosphate oxygen, but not with the backbone carbonyl oxygen. The bending modulus K_C of TOCL bilayers was determined using NSE spectroscopy measurements and the ZG model. Compared to DOPC bilayers, K_C was found to be larger for TOCL. We believe that the physicochemical properties of a TOCL bilayer reported here may be important for elucidating the functionality of cardiolipin lipids in the IMM.

Abbreviations

TOCL	Tetraoleoyl cardiolipin
NSE	Neutron spin echo
DOPC	Dioleoyl phosphatidylcholine
CL	Cardiolipin
TMCL	Tetramyristoyl cardiolipin
DMPC	Dimyristoyl phosphatidylcholine
PC	Phosphatidylcholine
PG	Phosphatidylglycerol
PS	Phosphatidylserine
IMM	Inner mitochondrial membrane
SANS	Small angle neutron scattering
SAXS	Small angle X-ray scattering
MD	Molecular dynamics
SDP	Scattering density profile
vP	Volume probability
ED	Electron density
NSLD	Neutron scattering length density
ZG model	Zilman–Granek model
ULV	Unilamellar vesicle
SNS	Spallation neutron source
RDF	Radial distribution function

Acknowledgements

Part of the research conducted at ORNL's High Flux Isotope Reactor (IPTS 7168) and Spallation Neutron Source (IPTS 5975 and IPTS 6192) was sponsored by the Scientific User Facilities Division, Office of Basic Energy Sciences, US Department of Energy. CHESS is supported by the NSF & NIH/NIGMS via NSF award DMR-1332208. Part of the computation used the resources of the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the U.S. Department of Energy under Contract no. DE-AC02-05CH11231. J. Katsaras is supported through the Scientific User Facilities Division of the DOE Office of Basic Energy Sciences (BES), and from the Laboratory Directed Research and Development Program of Oak Ridge National Laboratory (ORNL), managed by UT-Battelle, LLC, for the U.S. Department of Energy (DOE) under contract no. DE-AC05-00OR2275. J. Pan is supported by a startup fund from the University of South Florida.

References

1. G. van Meer, D. R. Voelker and G. W. Feigenson, Nat. Rev. Mol. Cell Biol., 2008, 9, 112–124.
2. R. N. A. H. Lewis and R. N. McElhaney, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 2069–2079.
3. P. R. Allegrini, G. Pluschke and J. Seelig, Biochemistry, 1984, 23, 6452–6458.
4. V. Betaneli, E. P. Petrov and P. Schwille, Biophys. J., 2012, 102, 523–531.
5. D. Acehan, A. Malhotra, Y. Xu, M. D. Ren, D. L. Stokes and M. Schlame, Biophys. J., 2011, 100, 2184–2192.
6. B. Heit, T. Yeung and S. Grinstein, Am. J. Physiol., 2011, 300, C33–C41.
7. M. Crimi and M. Degli Esposti, Biochim. Biophys. Acta, Mol. Cell Res., 2011, 1813, 551–557.
8. A. J. Chicco and G. C. Sparagna, Am. J. Physiol.: Cell Physiol., 2007, 292, C33–C44.
9. Z. T. Schug and E. Gottlieb, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 2022–2031.
10. S. M. Claypool, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 2059–2068.
11. M. Schlame and M. D. Ren, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 2080–2083.
12. M. Dahlberg and A. Maliniak, J. Phys. Chem. B, 2008, 112, 11655–11663.
13. S. Poyry, T. Rog, M. Karttunen and I. Vattulainen, J. Phys. Chem. B, 2009, 113, 15513–15521.
14. T. Rog, H. Martinez-Seara, N. Munck, M. Oresic, M. Karttunen and I. Vattulainen, J. Phys. Chem. B, 2009, 113, 3413–3422.
15. M. Dahlberg and A. Maliniak, J. Chem. Theory Comput., 2010, 6, 1638–1649.
16. M. A. Kiebish, R. Bell, K. Yang, T. Phan, Z. D. Zhao, W. Ames, T. N. Seyfried, R. W. Gross, J. H. Chuang and X. L. Han, J. Lipid Res., 2010, 51, 2153–2170.
17. N. Khalifat, J. B. Fournier, M. I. Angelova and N. Puff, Biochim. Biophys. Acta, Biomembr., 2011, 1808, 2724–2733.
18. D. Aguayo, F. D. Gonzalez-Nilo and C. Chipot, J. Chem. Theory Comput., 2012, 8, 1765–1773.
19. T. Lemmin, C. Bovigny, D. Lancon and M. Dal Peraro, J. Chem. Theory Comput., 2013, 9, 670–678.
20. S. Poyry, O. Cramariuc, P. A. Postila, K. Kaszuba, M. Sarewicz, A. Osyczka, I. Vattulainen and T. Rog, Biochim. Biophys. Acta, Bioenerg., 2013, 1827, 769–778.
21. A. G. Zilman and R. Granek, Phys. Rev. Lett., 1996, 77, 4788–4791.
22. J. J. Pan, X. L. Cheng, F. A. Heberle, B. Mostofian, N. Kucerka, P. Drazba and J. Katsaras, J. Phys. Chem. B, 2012, 116, 14829–14838.
23. N. Kučerka, M. P. Nieh and J. Katsaras, Biochim. Biophys. Acta, Biomembr., 2011, 1808, 2761–2771.
24. F. A. Heberle, J. J. Pan, R. F. Standaert, P. Drazba, N. Kucerka and J. Katsaras, Eur. Biophys. J., 2012, 41, 875–890.
25. N. Kučerka, B. W. Holland, C. G. Gray, B. Tomberli and J. Katsaras, J. Phys. Chem. B, 2012, 116, 232–239.
26. J. J. Pan, X. L. Cheng, L. Monticelli, F. A. Heberle, N. Kucerka, D. P. Tieleman and J. Katsaras, Soft Matter, 2014, 10, 3716–3725.
27. W. Rawicz, K. C. Olbrich, T. McIntosh, D. Needham and E. Evans, Biophys. J., 2000, 79, 328–339.
28. L. Martinez, R. Andrade, E. G. Birgin and J. M. Martinez, J. Comput. Chem., 2009, 30, 2157–2164.
29. J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802.
30. J. B. Klauda, R. M. Venable, J. A. Freites, J. W. O'Connor, D. J. Tobias, C. Mondragon-Ramirez, I. Vorobyov, A. D. MacKerell and R. W. Pastor, J. Phys. Chem. B, 2010, 114, 7830–7843.
31. S. E. Feller, D. X. Yin, R. W. Pastor and A. D. MacKerell, Biophys. J., 1997, 73, 2269–2279.
32. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
33. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
34. M. Tuckerman, B. J. Berne and G. J. Martyna, J. Chem. Phys., 1992, 97, 1990–2001.
35. J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
36. G. J. Martyna, D. J. Tobias and M. L. Klein, J. Chem. Phys., 1994, 101, 4177–4189.
37. S. E. Feller, Y. H. Zhang, R. W. Pastor and B. R. Brooks, J. Chem. Phys., 1995, 103, 4613–4621.
38. J. Sonne, F. Y. Hansen and G. H. Peters, J. Chem. Phys., 2005, 122, 124903.
39. O. Berger, O. Edholm and F. Jahnig, Biophys. J., 1997, 72, 2002–2013.
40. S. Jo, J. B. Lim, J. B. Klauda and W. Im, Biophys. J., 2009, 97, 50–58.
41. N. Kučerka, J. F. Nagle, J. N. Sachs, S. E. Feller, J. Pencer, A. Jackson and J. Katsaras, Biophys. J., 2008, 95, 2356–2367.
42. J. J. Pan, F. A. Heberle, S. Tristram-Nagle, M. Szymanski, M. Koepfinger, J. Katsaras and N. Kucerka, Biochim. Biophys. Acta, Biomembr., 2012, 1818, 2135–2148.
43. H. I. Petrache, S. E. Feller and J. F. Nagle, Biophys. J., 1997, 72, 2237–2242.
44. J. Pan, D. Marquardt, F. A. Heberle, N. Kucerka and J. Katsaras, Biochim. Biophys. Acta, Biomembr., 2014, 1838, 2966–2969.
45. A. L. Boscia, B. W. Treece, D. Mohammadyani, J. Klein-Seetharaman, A. R. Braun, T. A. Wassenaar, B. Klosgen and S. Tristram-Nagle, Chem. Phys. Lipids, 2014, 178, 1–10.
46. Q. Waheed and O. Edholm, Biophys. J., 2009, 97, 2754–2760.
47. A. R. Braun, J. N. Sachs and J. F. Nagle, J. Phys. Chem. B, 2013, 117, 5065–5072.
48. R. N. Lewis, D. Zweytick, G. Pabst, K. Lohner and R. N. McElhaney, Biophys. J., 2007, 92, 3166–3177.
49. W. Hubner, H. H. Mantsch and M. Kates, Biochim. Biophys. Acta, 1991, 1066, 166–174.
50. T. H. Haiens and N. A. Dencher, Febs Lett., 2002, 528, 35–39.
51. Z. Yi, M. Nagao and D. P. Bossev, J. Phys.: Condens. Matter, 2009, 21, 155104.
52. L. R. Arriaga, I. Lopez-Montero, F. Monroy, G. Orts-Gil, B. Farago and T. Hellweg, Biophys. J., 2009, 96, 3629–3637.
53. J. H. Lee, S. M. Choi, C. Doe, A. Faraone, P. A. Pincus and S. R. Kline, Phys. Rev. Lett., 2010, 105, 038101.
54. M. C. Rheinstadter, W. Haussler and T. Salditt, Phys. Rev. Lett., 2006, 97, 048103.
55. C. H. Cho, J. Urquidi, S. Singh and G. W. Robinson, J. Phys. Chem. B, 1999, 103, 1991–1994.
56. M. C. Watson and F. L. H. Brown, Biophys. J., 2010, 98, L9–L11.
57. S. Komura, T. Takeda, Y. Kawabata, S. K. Ghosh, H. Seto and M. Nagao, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 041402.
58. U. Seifert and S. A. Langer, Europhys. Lett., 1993, 23, 71–76.
59. E. Evans and A. Yeung, Chem. Phys. Lipids, 1994, 73, 39–56.
60. J. Pan, S. Tristram-Nagle, N. Kucerka and J. F. Nagle, Biophys. J., 2008, 94, 117–124.

---