Cytosine-functionalized polyurethane foam and its use as a sorbent for the determination of gold in geological samples†
Dingshuai
Xue
*a,
Hongyue
Wang
a,
Yanhong
Liu
a,
Ping
Shen
a and
Jiefang
Sun
b
aKey Laboratory of Mineral Resources, Institute of Geology & Geophysics, Chinese Academy of Sciences, P.O. Box 9825, Beijing 100029, China. E-mail: xuedingshuai@mail.iggcas.ac.cn; Fax: +86-10-62010846; Tel: +86-10-82998487
bState Key Laboratory of Environmental Chemistry and Ecotoxicology, Research Center for Eco-Environmental Sciences, Chinese Academy of Sciences, P. O. Box 2871, Beijing 100085, China. E-mail: sunjf2001@163.com
First published on 13th November 2015
Abstract
A solid phase extraction procedure was developed for the separation and preconcentration of trace amounts of Au(III) in geological samples by using a polyurethane foam column modified with cytosine. The influence of the flow rate of the sample solution, the pH effect, eluent type, sorption capacity, and presence of matrix ions on the solid phase extraction procedure was investigated. The analytical results for international gold reference materials measured by this new method were in close agreement with those obtained by other well-established methods and values. Under the optimum conditions, the detection limit (3σ, n = 6) for the analyte was 6 ng L−1, with an enrichment factor of 480. The equilibrium data were best represented by the Langmuir isotherm model, showing pseudo-first-order kinetics. The maximum adsorption capacity of Au(III) on the adsorbent was 98.9 mg g−1.
Introduction
Gold is one of the most important noble metals in the modern world due to its wide variety of applications in industry, medicine, and global economy.1 The demand for gold and other noble metals is growing with modernization. However, gold occurs in very low concentrations in the Earth's crust.2 Even though the sensitivity of modern instrumentation has increased enormously over the decades, direct analysis of gold in real samples is still very difficult owing to its very low abundance and instrumental interferences caused by matrix elements. Gold is a chalcophile element, which is distributed heterogeneously in silicates and tends to concentrate in sulfides and alloy phases in the mantle. It is usually called the “nugget effect”. Preconcentration is an important step in the determination of traces of gold in geological materials.3Different techniques are available for the preconcentration of gold, including the classical fire assay method using various collectors,4 precipitation and coprecipitation techniques,5 extraction processes,6 and sorption approach.7 The classical fire assay method is used for routine laboratory analyses that can accommodate a large sample mass (15–30 g) which reduces the nugget effect, but in general procedural blanks are relatively high. In addition, the fire assay procedure is quite tedious and time-consuming.8 Compared to liquid–liquid extraction and coprecipitation, the use of solid phase extraction (SPE) is more advantageous due to its high enrichment capability, ease of separation, and ability to sync with different instrumental techniques.
In recent years, complexing sorbents and ion exchangers have been widely used for noble metal preconcentration.9 Some newly designed materials such as bonded-phase silica sorbents,10 polymeric sorbents,11 biosorbents,12 and carbon-based sorbents have been proposed and are of significant interest.13 In terms of gold mineral analysis, activated carbon and polyurethane foam (PUF) are the most practical and commonly used adsorbing materials. AC has a large specific surface area and good selectivity to Au, but the small size of AC causes high pressure in the SPE cartridge, while PUF combines the advantages of high efficiency, low cost, easy handling, and easy storage.
Bowen first used PUF as an absorbent material for the sorption and recovery of inorganic and organic compounds from aqueous solutions.14 Then, PUF was used by Braun to separate and recover gold.15,16 These studies aroused wide interest, and PUF has been extensively studied.17,18 However, two main problems have necessitated the need for the preparation of a functionalized PUF: (1) the lack of selectivity of PUFs, and (2) low sorption capacity. To date, modified PUFs have exhibited higher adsorption capacities and selectivity capacities than untreated PUFs, thus allowing wider application of modified PUFs.19 Functionalized PUFs have been used as excellent sorbents with good stability, high capacity, and good flexibility.20,21 Also, functionalized PUFs have been shown to facilitate relatively fast separations with good enrichment capacities.22,23
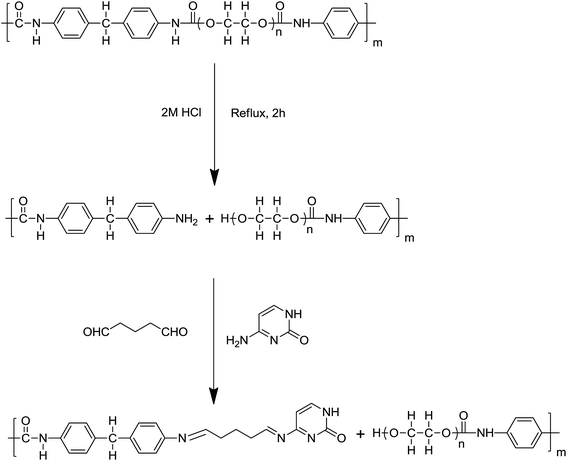
In the present work, PUF was acid hydrolyzed to produce PUF-NH2, and it was then further modified with the chelating ligand cytosine (Cyt) through a linking arm to form Cyt-functionalized PUF (PUF-Cyt). Cytosine is a kind of natural product obtained easily and exhibits satisfactory immobilization on PUF and also acts as a good ligand for metal ions due to the presence of heteroatoms (N, O). PUF-Cyt was used as the sorbent for the separation and preconcentration of gold in geological samples. The new sorbent showed high selectivity, sensitivity, and adsorption capacity for the solid phase extraction of Au(III). Several factors influenced the performance of PUF-Cyt. These factors, including the solution acidity, adsorption capacity of the adsorbent, effect of other metal ions, and recovery behavior, were systematically studied and optimized. The proposed method was applied to the determination of trace amounts of gold in geological samples.
Experimental
Reagents and materials
All solvents were reagent grade or better. Ultrapure water with a resistivity of 18.2 MΩ cm−1 was obtained from a Milli-Q water purification system. Concentrated HNO3 (65–68%, w/w), HCl (36–38%, w/w), and HF (40%, w/w) were ultrapure grade (BV-III, Beijing Institute of Chemical Reagent, Beijing, China). Suprapure H2O2 (30%, m m−1; Merck, Darmstadt, Germany) was used for acid digestion. Glutaraldehyde (25 wt%, Sigma-Aldrich, Germany) and cytosine (Sinopharm, China) were used to prepare PUF-Cyt. The standard stock solution for Au(III) was obtained from Merck (Darmstadt, Germany). Working standard solutions were prepared by appropriate dilution of the commercial stock solution. Commercial PUF (a polyether of open-cell type, ca. 100% open cell, JX-1) was purchased from Jixiang Sponge Co., Ltd in Yangzhou, China.Instrumentation
An iCAP 7400 ICP-OES (Thermo, USA) with a concentric nebulizer and a cinnabar spray chamber was employed for the determination of all metal ions. The wavelength of Au was selected as 242.795 nm and the optimum operation conditions are summarized in Table S1.† Infrared spectra were recorded on a Nicolet Nexus 6700 FTIR apparatus (Thermo Scientific, USA), and were used to confirm the structure of PUF and PUF-Cyt. Elemental analysis was carried out using a universal CHNOS elemental analyzer Vario EL III (Elementar Analysensysteme GmbH, Germany). The column process was performed using a BT101F peristaltic pump (Lead Fluid Technology Co., Ltd, Baoding, China). A THZ-C-1 horizontal shaking bath (Taicang Instrument Factory, Jiangsu, China) was used in batch procedures. The pH value was measured using a pHS-3G digital pH meter (Lei Ci Device Works, Shanghai, China). A model L550 centrifuge (Xiangyi Centrifugal Machine Equipment Co., Ltd, Changsha, China) and Milli-Q-purified water apparatus (Millipore Co., Bedford, MA, USA) were used in a variety of tests. A muffle furnace (SX2-4-10) was obtained from the Great Wall Furnace Company, China. Round-bottom Savillex PFA screw-cap capsules (180 mL; Savillex Corporation, Eden Prairie, MN, USA) were used for sample digestion experiments.Synthesis of PUF-Cyt
Commercial PUF (2.0 g) was crushed using a mincing machine, and then boiled in a 2 mol L−1 HCl solution for 2 h to generate the maximum number of free amino groups. Amine derivatives of PUF (PUF-NH2) were obtained, and then washed with water four times. The product was collected and dried under vacuum at 25 °C. Finally, 1.9 g of dry PUF-NH2 was obtained. Cyt was immobilized on PUF-NH2 using the bifunctional reagent glutaraldehyde as a linking arm to form an imine. Then, 2 mL of 25% aqueous glutaraldehyde solution was diluted to 100 mL with a phosphate buffer (pH 7). Purified PUF-NH2 (1.0 g) was immersed in this solution and stirred at room temperature in an argon atmosphere for 1 h. Finally, 0.1 g of Cyt dissolved in 60 mL of phosphate buffer (pH 7) was added to the reaction system under an argon flow. The reaction was allowed to continue with stirring for about 5 h at room temperature under an argon atmosphere. The solution was then stored for 2 days at room temperature. Finally, the product was filtered and washed with water, and then dried under vacuum at 25 °C. Subsequently, PUF-Cyt was smashed by a food-processing blender and sieved. Particles between 100 and 200 μm were used for adsorption studies. The scheme for the synthesis of PUF-Cyt used in this study is shown in Fig. 1. The estimated mass fraction of Cyt in PUF-Cyt was 8.7% (please see details in the ESI†).Sample preparation
Ten gram samples were used to reduce the risk of erratic results due to the presence of native gold particles, known as the nugget effect. The digestion was carried out using a slightly modified aqua regia procedure described in the literature.24 Approximately 10 g of finely powdered sample (200 mesh) was placed in a porcelain crucible (100 mL) and heated at 650 °C for 1 h in a muffle furnace with the door half open. The sample was then transferred into a 180 mL Savillex PFA vessel. Next, 40 mL of 50% aqua regia was added to the Savillex PFA vessel and the mixture was heated on an electric hot plate (150 °C) until the mixture evaporated to a moist residue. This procedure was repeated with 20 mL of 50% aqua regia. After digestion with aqua regia, 15 mL of HF + 10 mL of HNO3 was added slowly to avoid violent boiling due to the exothermic reaction. The solutions were then evaporated to dryness on a hot plate to remove silicates. After diluting with the desired concentration of HCl for the extraction of the analyte, the sample was transferred to a 100 mL volumetric flask and diluted up to the mark with the same concentration of HCl. After ∼30 min, the solids settled to the bottom of the flask. Then, 25 mL of the resulting clear solution was used for the sorption and preconcentration of gold in geological samples. The above sample treating procedure is a general one which would be slightly different for different rock types. For example, the sample mass can reduce to 5 g for soil and ultramafic rocks; for Ni–Cu sulphide samples, which have relatively low nugget effects, it would be reduced to 2 g. The corresponding acid consumption should reduce in proportion to the sample mass. But for ultramafic rocks that contain refractory minerals (olivine, spinel, etc.), further processing is required. After the dissolution of silicate minerals in mixtures of hydrofluoric acid and nitric acid, 10 mL of HCl and additional H2O2 (3 mL) were added. Then, the vessel was capped and heated at 180 °C in an electric oven for 2 h. The vessel was opened and evaporated to a moist residue on an electric hot plate. Finally, the sample was diluted to the volume with the procedures mentioned above.Batch procedure
A series of standards or sample solutions containing Au(III) were transferred into a 50 mL grinding mouth Erlenmeyer flask with a matching stopper. The pH of each solution was adjusted to 1 with 0.1 mol L−1 HCl and 0.1 mol L−1 NH3·H2O. The volume was then adjusted to 10 mL with ultrapure water. PUF-Cyt (0.05 g) was added and the mixture was shaken vigorously for 30 min using a mechanical reciprocating shaker to attain equilibrium. The adsorbent was then separated. The amount of the metal ions remaining in the aqueous solution was measured by inductively coupled plasma optical emission spectrometry (ICP-OES). The amount of the metal ions extracted with the foam was calculated by difference. The amount of Au(III) retained at equilibrium (capacity of adsorbent, Qe, mg g−1) on the tested solid adsorbent was calculated using eqn (1).| Qe = (C0 − C)V/m | (1) |
Column procedure
PUF-Cyt (0.25 g) was packed in a PP column (83 mm × 15.6 mm ID) blocked with frits at the inlet and outlet of the column. The bottom of the column was connected via a pump tubing to a peristaltic pump to control the flow rate. Before use, 0.25 mol L−1 HCl and deionized water were successively passed through the column in order to clean and neutralize it. Portions of aqueous standard or sample solutions of Au(III) (25 mL) adjusted to pH 1 with 0.1 mol L−1 HCl and 0.1 mol L−1 NH3·H2O were passed through the column at a flow rate of 4 mL min−1. Afterwards, the analyte retained on the column was eluted with 5.0 mL of 1% (m/v) thiourea in 0.1 mol L−1 HCl. The effluent or eluted solution containing the target analyte was analyzed by ICP-OES. Blank samples were subjected to the same procedure. All values obtained were corrected by subtracting the values of the procedural blank.Results and discussion
Characterization of PUF-Cyt
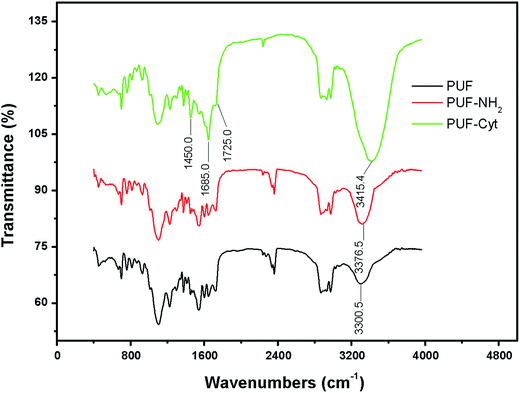
FTIR spectra were obtained for PUF, PUF-NH2 and PUF-Cyt to determine the presence of Cyt on PUF. The FTIR spectra for these samples are illustrated in Fig. 2. Comparing the IR spectra of PUF, PUF-NH2 and PUF-Cyt, the broad band at 3300.5 cm−1 assigned to νN–H and νO–H for PUF was shifted to 3376.5 cm−1 for PUF-NH2 and 3415.4 cm−1 for PUF-Cyt, with significant increase in the peak areas, because the number of amino groups increased significantly for PUF-NH2 and the number of secondary amines (N–H bond) in Cyt increased for PUF-Cyt. The spectrum of PUF-Cyt shows additional peaks at 1685 cm−1 for the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond and 1725 cm−1 for the C
N bond and 1725 cm−1 for the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond of the cytosine moiety. The peak at ≈1450−1 in the FTIR-spectrum of PUF-Cyt is attributed to the vibration of the –CH– bond in the cytosine moiety.
O bond of the cytosine moiety. The peak at ≈1450−1 in the FTIR-spectrum of PUF-Cyt is attributed to the vibration of the –CH– bond in the cytosine moiety.
Scanning electron microscopy (SEM) imaging was performed on an AURIGA Compact FIB-SEM. The SEM image (Fig. S1a and b†) at magnification 117 showed a ruptured structure of PUF-Cyt formed by the breakage of chemical bonds during hydrolysis.
The pH of the zero point-of-charge (pHZPC) was measured according to the method proposed by Noh.25 A series of flasks containing 25 mL of the sample solution were adjusted to pH values ranging from 1 to 13 by adding HCl or NaOH. PUF-Cyt (0.1 g) was added to each of these pH-adjusted solutions. After 24 h, the final pH (pHf) of each solution was measured. The difference between the initial and final pH values (ΔpH = pHf − pHi) was plotted against pHi. pHZPC is the pH at which pHi = pHf. The pHZPC values for PUF and PUF-Cyt were determined from these plots and found to be 7.2 and 7.5, respectively (Fig. S2†). Using these data, it was found that the surface sites of PUF-Cyt were positively charged at pH values lower than 7.5, and became negatively charged at pH values greater than 7.5 (Table 1).
| Property | PUF | PUF-NH2 | PUF-Cyt |
|---|---|---|---|
| Elemental analysis C, H, N, S and O (%) | 65.3, 8.4, 6.7, 0.5 and 19.1 | 64.6, 8.6, 7.8, 0.5 and 18.5 | 64.3, 8.7, 7.6, 0.5 and 18.9 |
| Color | White | Faint yellow | Brown |
| pHZPC | 7.2 | 4.2 | 7.5 |
| Density (kg m−3) | 13.8 | 18.3 | 21.5 |
Elemental analysis of PUF-Cyt showed that the hydrogen (8.7%) and nitrogen (7.6%) contents of the samples increased, whereas the amount of carbon (64.3%) decreased compared with that of PUF (Table 2). This result likely occurred because Cyt contains more nitrogen. The amount of cytosine modified on the PUF was calculated by difference; the details are provided in the ESI.† Consequently, these experimental results suggest that PUF was successfully modified by Cyt.
| Pseudo-first-order model | k 1 (min−1) | R 2 |
| 3.162 | 0.988 | |
| Pseudo-second-order model | k 2 (g mg−1 min−1) | R 2 |
| 0.642 | 0.970 | |
| Intraparticle diffusion model | K i (mg g−1 min−0.5) | R 2 |
| 2.029 | 0.941 |
Effect of pH on the adsorption of Au(III)
The acidity of a solution is one of the most important factors affecting the adsorption process, and has two effects on metal adsorption. First, protons in acid solutions can protonate the binding sites of chelating molecules. Second, hydroxide in basic solutions may complex and precipitate metals.26 Therefore, the pH of a sample solution is a vital parameter for quantitative adsorption and recovery of analytes using the SPE technique. In this experiment, the effect of pH and sample acidity on the degree of sorption of Au(III) and base metals was evaluated through the batch procedure. The effect of solution acidity on the degree of sorption was investigated over the pH range of 0.6–5 (Fig. 3). Maximum Au(III) recoveries occurred in the pH range of 0.6–2. In HCl, the main chemical form of the Au(III) ion in aqueous solution is AuCl4−, which has a high formation constant (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β4 = 31.05).27 The chloro-anionic species can be adsorbed by protonated –CH
β4 = 31.05).27 The chloro-anionic species can be adsorbed by protonated –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– (imine) groups on PUF-Cyt, forming ion-pair complexes. Therefore, electrostatic interactions are very effective in the adsorption of AuCl4− (Fig. S3†). According to the hard/soft acid/base theory,28 a chelating sorbent with N or O donor atoms can strongly bind noble metals. In acidic solutions, according to the results obtained in this work, the mechanism for adsorbing gold on PUF-Cyt involves an ion chelation process with the aid of electrostatic interactions. In addition, 10 mL of 1.0 μg mL−1 of base metal cation solutions, such as Fe(III), Co(II), Ni(II), Cu(II), Pb(II), Zn(II), Cr(III), Cd(II), and Ru(IV), were also investigated by equilibrating with 50 mg of sorbent, as was done for the experiments at pH 1. The degree of sorption for the base metal cations was generally low at high acidity and increased with increasing pH. Therefore, we selected pH 1 as the enrichment acidity for subsequent studies in order to eliminate the adsorption of other base metal ions that may be present in the samples.
N– (imine) groups on PUF-Cyt, forming ion-pair complexes. Therefore, electrostatic interactions are very effective in the adsorption of AuCl4− (Fig. S3†). According to the hard/soft acid/base theory,28 a chelating sorbent with N or O donor atoms can strongly bind noble metals. In acidic solutions, according to the results obtained in this work, the mechanism for adsorbing gold on PUF-Cyt involves an ion chelation process with the aid of electrostatic interactions. In addition, 10 mL of 1.0 μg mL−1 of base metal cation solutions, such as Fe(III), Co(II), Ni(II), Cu(II), Pb(II), Zn(II), Cr(III), Cd(II), and Ru(IV), were also investigated by equilibrating with 50 mg of sorbent, as was done for the experiments at pH 1. The degree of sorption for the base metal cations was generally low at high acidity and increased with increasing pH. Therefore, we selected pH 1 as the enrichment acidity for subsequent studies in order to eliminate the adsorption of other base metal ions that may be present in the samples.
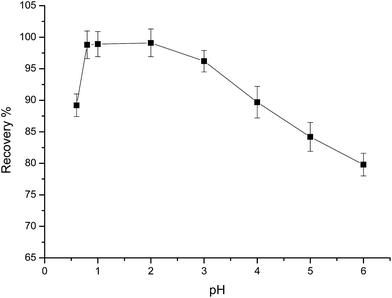 | ||
| Fig. 3 Effect of pH on the adsorption of 1.0 μg mL−1 Au(III). Other conditions: 50 mg PUF-Cyt, shaking time 30 min, temperature 25 °C (n = 3). | ||
Effect of shaking time and adsorption kinetics
The effect of shaking time on the adsorption of Au(III) was studied by the batch procedure. Different shaking times ranging from 0.2 to 30 min were tested to determine the percent extraction of Au(III) by PUF-Cyt (Fig. 4).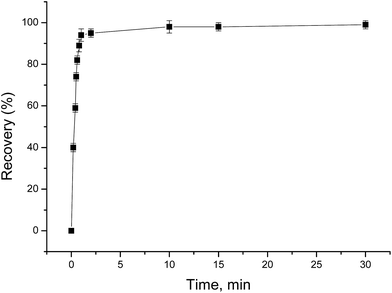 | ||
| Fig. 4 Effect of shaking time on the adsorption of 1.0 μg mL−1 Au(III). Other conditions: 50 mg PUF-Cyt, pH 1.0, temperature 25 °C (n = 3). | ||
From the graph shown in Fig. 4, it is evident that the adsorption of Au(III) was greater than 95% during the first min. After 1 min, however, the rate of adsorption of Au(III) reduced considerably. The amount of the adsorbed Au(III) increased with increasing contact time and reached a maximum at 30 min. Therefore, 30 min was selected as the adsorption equilibrium time. This fast initial sorption is probably due to the high affinity between gold ions and amino groups on the sorbent.
In order to investigate the mechanism of the adsorption process and obtain characteristic constants of adsorption, kinetic models were exploited to analyze the experimental data. Models for pseudo-first-order, pseudo-second-order, and intraparticle diffusion were used to test the experimental data. The data were fitted into each of these three models (Fig. S4†). Eqn (2)–(4) show the equations of the three kinetic models.
Pseudo-first-order kinetic model:
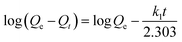 | (2) |
Pseudo-second-order kinetic model:
| t/Qt = 1/k2Q2e + t/Qe | (3) |
Intraparticle diffusion kinetic model:
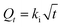 | (4) |
The regression coefficients and rate constants k1, k2, and ki for these three kinetic models are listed in Table 2. As can be seen in Table 2, the values of regression coefficients (R2, 0.988) for the pseudo-first-order rate equation are higher than those of the pseudo-second-order rate equation (R2, 0.970), suggesting that the pseudo-first-order rate equation best represents the adsorption system. It is clear from Fig. S4c† that the linear portion of the plot did not pass through the origin. Such a situation may suggest that the reaction is multilinear, indicating that two or more steps took place during adsorption.29 Recall that the adsorption of Au(III) was found to be rapid initially, but then became slow and stagnated with time, and Au(III) was slowly transported into the pores and retained in the micropores.
Effect of the initial concentration of Au(III) ions on the adsorption isotherm
The influence of the initial Au(III) concentration on the adsorption capacity of PUF-Cyt was investigated.As shown in Fig. 5, the amount of Au(III) ions adsorbed per unit mass of PUF-Cyt increased initially, and then reached a plateau. This result showed that the initial Au(III) concentration provided a driving force to overcome the mass transfer resistance between the adsorption medium and the adsorbent. Higher ion concentrations increase the mass transfer driving force and enhance the collision probability between metal ions and the adsorbent.30 The capacity study was adopted from the report of Maquieira et al.31 A breakthrough curve was obtained by plotting the concentration (μg mL−1) versus the micrograms of Au(III) adsorbed per gram of PUF-Cyt. From the breakthrough curve, the maximum adsorption capacity of PUF-Cyt for Au(III) was determined to be 98.8 mg g−1 at 298 K. The adsorption isotherm is critical in optimizing the use of the adsorbent, since it can be used to assess the adsorption capacity of the adsorbent and describe how the adsorbate interacts with the adsorbent. For interpreting the adsorption experimental data, the Langmuir,32 Freundlich,33 and Dubinin–Radushkevich (D–R)34 isotherm models were applied. Eqn (5) gives the expression of the Langmuir model.
| Ce/Qe = Ce/Qmax + 1/KQmax | (5) |
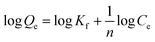 | (6) |
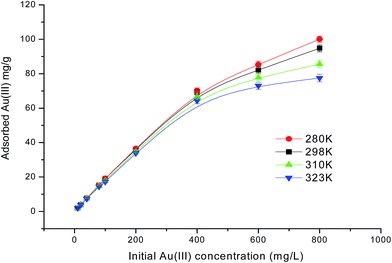 | ||
| Fig. 5 Effect of the initial concentration of Au(III) ions on PUF-Cyt at various temperatures. Other conditions: 50 mg PUF-Cyt, pH 1.0, shaking time 30 min (n = 3). | ||
The values of n and Kf were calculated from the slope and intercept of the plot of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Qeversus log
Qeversus log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce. The calculated values of the Langmuir and Freundlich equations' parameters are given in Table 3. As can be seen, the Langmuir model (Fig. S5a†) exhibited higher values of regression coefficients than those obtained from the Freundlich model (Fig. S5b†). The theoretical Qmax value (96.90 mg g−1, 298 K) obtained from the Langmuir model was close to the experimental values (98.8 mg g−1). The R2 values for the Langmuir isotherm model are greater than 0.988. Thus, the Langmuir model is found to better describe the adsorption isotherm and the sorption behavior of Au(III) onto PUF-Cyt is considered to be representative of sorption onto a monolayer. Additionally, both Qmax and k decreased with increasing temperature, indicating that the bonding between heavy metals and the active sites of the adsorbent weakened at higher temperatures, and that the adsorption process is exothermic.
Ce. The calculated values of the Langmuir and Freundlich equations' parameters are given in Table 3. As can be seen, the Langmuir model (Fig. S5a†) exhibited higher values of regression coefficients than those obtained from the Freundlich model (Fig. S5b†). The theoretical Qmax value (96.90 mg g−1, 298 K) obtained from the Langmuir model was close to the experimental values (98.8 mg g−1). The R2 values for the Langmuir isotherm model are greater than 0.988. Thus, the Langmuir model is found to better describe the adsorption isotherm and the sorption behavior of Au(III) onto PUF-Cyt is considered to be representative of sorption onto a monolayer. Additionally, both Qmax and k decreased with increasing temperature, indicating that the bonding between heavy metals and the active sites of the adsorbent weakened at higher temperatures, and that the adsorption process is exothermic.
| Adsorption isotherms | Isotherm constants | Temperature (K) | |||
|---|---|---|---|---|---|
| 280 | 298 | 310 | 323 | ||
| Langmuir isotherm constants | Q max (mg g−1) | 101.94 | 96.90 | 90.25 | 80.45 |
| K (L mg−1) | 0.05810 | 0.05562 | 0.03865 | 0.03321 | |
| R 2 | 0.9884 | 0.9908 | 0.9908 | 0.9898 | |
| R L | 0.0211–0.6325 | 0.0220–0.6426 | 0.0313–0.7212 | 0.0363–0.7507 | |
| Freundlich isotherm constants | K f (mg g−1) (L mg−1)1/n | 7.810 | 7.107 | 5.542 | 4.754 |
| n | 2.028 | 2.003 | 1.958 | 1.960 | |
| R 2 | 0.9799 | 0.9723 | 0.9777 | 0.9693 | |
| Dubinin–Radushkevich isotherm constants | Q D–R (mg g−1) | 3.458 | 3.469 | 3.300 | 3.211 |
| β × 10−2 (mol2 J−2) | −8.709 | −10.498 | −10.12 | −7.729 | |
| E | 2.396 | 2.182 | 2.223 | 2.543 | |
| R 2 | 0.5208 | 0.5565 | 0.4231 | 0.3711 | |
The dimensionless constant, RL, was used to evaluate whether the influence of the adsorption isotherm was favorable or unfavorable, which is referred to as the separation factor, defined by the following equation:
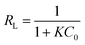 | (7) |
The RL values (illustrated in Table 3) were between 0 and 1, suggesting that the adsorption was favorable. The Langmuir and Freundlich isotherms could not be used to evaluate the physical and chemical characteristics of adsorption. Therefore, the equilibrium data were also analyzed by the Dubinin–Radushkevich isotherm (D–R isotherm) to determine whether the adsorption processes were physical or chemical. The linearized D–R equation has the following form:
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Qe = ln Qe = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QD–R − βε2 QD–R − βε2 | (8) |
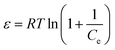 | (9) |
Sorption energy E (kJ mol−1) gives information about the adsorption mechanism, whether it is physical or chemical. If the magnitude of E is between 8 and 16 kJ mol−1, the sorption process follows chemical ion exchange. The sorption mechanism is physical when E < 8 kJ mol−1. This relationship is represented by eqn (10).
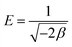 | (10) |
All the parameters calculated are presented in Table 3. The value of the correlation coefficient (0.557) indicated that the D–R isotherm (Fig. S5c†) is a poor fit to the adsorption process. The values of QD–R are not high enough to indicate the adsorption capacity, whereas the values of the apparent energy of adsorption depict the physical adsorption process. Therefore, the D–R isotherm did not give a good fit to the adsorption process.
A comparison of the maximum adsorption capacities of PUF-Cyt for Au(III) plus other adsorbents reported in the literature is given in Table 4. Compared with other alternative adsorbents, it was apparent that PUF-Cyt had higher adsorption capacities than other types of PUF adsorbents and most of the other adsorbents. The results indicated that PUF-Cyt exhibited good adsorption efficiency and it is a promising adsorption material for the analysis of Au(III).
| Sorbent | Reagent used | EFa | Capacity (mg g−1) | LOD (μg L−1) | LOQ (μg L−1) | Ref. |
|---|---|---|---|---|---|---|
| a EF: enrichment factor. | ||||||
| IEPUF | Polysiloxane | — | 5.29 | 0.01 (FAAS) | 0.033 | 35 |
| PUF-NH2 | HCl | 125 | 41.4 | — | — | 36 |
| LPPF | HCl, NaNO2 | 450 | 70.5 | 0.0033 (UV-vis) | 0.011 | 37 |
| Attapulgite | Triocarbohydrazide | 150 | 66.7 | 0.32 (ICP-OES) | — | 38 |
| Amberlite XAD-200 | Diethyldithiocarbamate | 200 | 12.3 | 16.6 (FAAS) | 36.5 | 39 |
| Activated carbon | 1-Amino-2-naphthol-4-sulfonate | 200 | 32.3 | 0.26 (ICP-OES) | — | 40 |
| Silica gel | Nanometer TiO2 | 50 | 3.56 | 0.21 (FAAS) | — | 41 |
| Carbon nanotubes | N,N′-Bis(2-hydroxybenzylidene)-2,2′(aminophenylthio)ethane | 250 | 75 | 0.03 (FAAS) | — | 42 |
| Cellulose fiber | Taurine | — | 34.5 | — | — | 43 |
| Chitosan | 4-Amino-4′-nitroazobenzene | — | 69.93 | 0.01 (FAAS) | — | 44 |
| Alumina | Polyethyleneimine ion-exchange polymer | 460 | 6 | 0.0262 (FAAS) | — | 45 |
| PUF-Cyt | Cytosine | 480 | 98.8 | 0.006 (ICP-OES) | 0.02 | Present work |
Adsorption thermodynamics
The thermodynamic parameters for the sorption of Au(III) were calculated using van't Hoff equations (eqn (11) and (12)).ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = ΔS0/R − ΔH0/RT K = ΔS0/R − ΔH0/RT | (11) |
| ΔG0 = ΔH0 − TΔS0 | (12) |
The values of ΔH and ΔS0 can be calculated from the slope and intercept of the plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K versus 1/T, respectively (Fig. S6†). The thermodynamic parameters are summarized in Table 5. The negative value of ΔH0 (−8.59 kJ mol− 1) indicates that the sorption process of Au(III) is an exothermic chemisorption. Hence, the amount of Au(III) adsorbed at equilibrium must decrease with increasing temperature. The negative ΔS0 (−3.30 J mol−1 K−1) indicates a decreased randomness at the solid–liquid interface during the sorption of Au(III). The negative values of ΔG0 indicate that the adsorption process is feasible and spontaneous with a high preference for Au(III) on PUF-Cyt.
K versus 1/T, respectively (Fig. S6†). The thermodynamic parameters are summarized in Table 5. The negative value of ΔH0 (−8.59 kJ mol− 1) indicates that the sorption process of Au(III) is an exothermic chemisorption. Hence, the amount of Au(III) adsorbed at equilibrium must decrease with increasing temperature. The negative ΔS0 (−3.30 J mol−1 K−1) indicates a decreased randomness at the solid–liquid interface during the sorption of Au(III). The negative values of ΔG0 indicate that the adsorption process is feasible and spontaneous with a high preference for Au(III) on PUF-Cyt.
| Temperature (K) | ΔG0 (kJ mol−1) | ΔH0 (kJ mol−1) | ΔS0 (J mol−1 K−1) |
|---|---|---|---|
| 280 | −7.66 | −8.59 | −3.30 |
| 298 | −7.60 | ||
| 310 | −7.56 | ||
| 323 | −7.52 |
Effect of sample flow rate, sample volume, and enrichment factor
The effect of the sample flow rate on the recovery of Au(III) was investigated by passing 25 mL of the sample solution through the column at a rate of 1.0–8.0 mL min−1. Flow rates in the range of 1.0–4.0 mL min−1 exerted no significant effect on the recovery of Au(III), whereas flow rates greater than 4.0 mL min−1 decreased the recovery percentage (Fig. 6). Hence, all subsequent experiments were conducted at a flow rate of 4.0 mL min−1.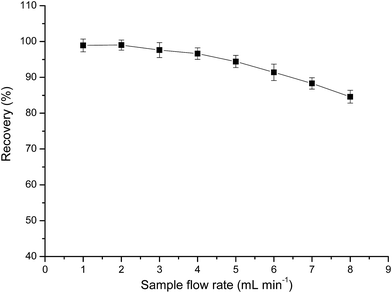 | ||
| Fig. 6 Effect of sample flow rate on the recovery (%) of Au. Other conditions: 0.25 g PUF-Cyt; pH 1.0; concentration of Au(III): 1.0 μg mL−1. | ||
In order to obtain reliable analytical results and a high concentration factor, it is important to achieve satisfactory recovery of the analyte from large volumes of sample solutions. Hence, the effect of sample volume on the retention of analyte was investigated by passing 100–3200 mL of sample solutions containing 20.0 μg of Au(III) through the PUF-Cyt column, and subjecting them to the procedure discussed in this paper. The results indicated that Au(III) ions were recovered in high quantities when the sample volume was less than 2400 mL. After elution with 5 mL of the eluent, an enrichment factor of 480 was achieved. These results were excellent when compared with those obtained by using other materials for the preconcentration of gold (Fig. 7).
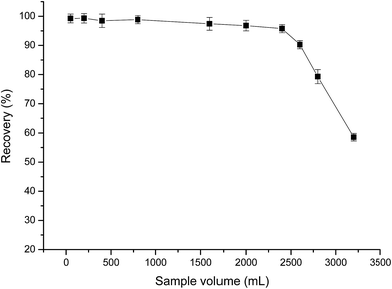 | ||
| Fig. 7 Effect of sample volume on the recovery of Au(III). Other conditions: Au, 20.0 μg; sample flow rate, 4.0 mL min−1; 0.25 g PUF-Cyt; pH 1.0 (n = 3). | ||
Optimization of elution conditions
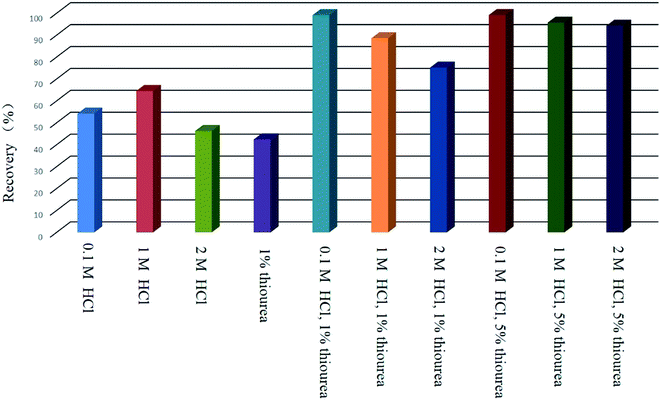
Quantitative desorption of gold can be achieved if an eluent is used to decompose the ion-pair complexes formed on the sorbent surface. The effects of various eluting agents such as HCl and H2NCSNH2 were examined. It was found that adding small amounts of thiourea as a chelating reagent in 0.1 mol L−1 HCl helped elute gold from the adsorbent. Hence, thiourea combined with 0.1 mol L−1 HCl was employed and the effect of different concentrations of thiourea was investigated for the elution of Au. The experimental results (Fig. 8) indicated that high recovery (>95%) was obtained with 1% (m/v) thiourea. The eluent solution consisting of 1% (m/v) thiourea in 0.1 mol L−1 HCl was able to completely remove the analyte. Thiourea develops a positive charge in hydrochloric acid, thus favoring complex formation with gold–chloro complexes. In addition, gold has a higher affinity for S than N. Therefore, thiourea with 0.1 mol L−1 HCl was used in the experiment. It was found that 5.0 mL of this elution solution was sufficient to quantitatively recover the analyte. Hence, 5.0 mL was selected as the eluent volume for subsequent experiments. Effluents were collected separately and analyzed by ICP-OES. Higher concentrations of thiourea (5% (m/v)) were also effective for desorbing the analytes; however, high concentrations of thiourea interfere with analyses done using ICP-OES.Effect of matrix ions
Matrix effects are important in the analysis of gold in real samples. A binary mixture (25 mL) containing 25 μg of Au(III) and interfering cations such as Na+, K+, Ca2+, Mg2+, Al3+, Fe3+, Co2+, Ni2+, Cu2+, Pb2+, Zn2+, Mn2+, Cr3+, Cl−, and NO32− was investigated to assess method selectivity under the optimal conditions described previously. Solutions for testing anions were prepared by dissolving their corresponding sodium salts in water, whereas cation interferences were prepared using their nitrates. The results showed that none of these ions induced a remarkable influence on the assay. The tolerance limit of coexisting ions causing recoveries of the examined elements was set to <90%, which is shown in Table 6.| Coexisting ions | Concentration (μg mL−1) | Recovery of gold (%) |
|---|---|---|
| Na+ | 1000 | 96.40 |
| K+ | 1000 | 97.92 |
| Cl− | 1000 | 99.03 |
| Ca2+ | 600 | 96.41 |
| Mg2+ | 600 | 97.12 |
| NO32− | 600 | 97.58 |
| Al3+ | 300 | 96.33 |
| Fe3+ | 300 | 95.24 |
| Co2+ | 100 | 95.98 |
| Ni2+ | 100 | 96.46 |
| Cu2+ | 100 | 97.66 |
| Pb2+ | 100 | 95.65 |
| Zn2+ | 100 | 95.72 |
| Mn2+ | 100 | 94.93 |
| Cr3+ | 100 | 98.27 |
| Sn2+ | 100 | 98.64 |
| Tl+ | 100 | 97.22 |
| Pt4+ | 100 | 95.76 |
| Pd2+ | 100 | 96.11 |
| Te4+ | 100 | 95.87 |
| Sb3+ | 100 | 95.14 |
Analytical performance
In order to assess the applicability of this method to real samples, separation and recovery of gold in geological samples were attempted. The accuracy of the method was verified by determining Au in WMS-1a, MA-2c (International Standard Reference Materials; CANMET, Hamilton, Canada), and GAu-14, GAu-16, GAu-18 (certified reference material; Beijing, China), which were either developed especially for the task of gold analysis or are well known and commonly used reference materials for major and trace element analysis. Certified values and standard deviations of reference values were obtained from the database available at the CANMET internet website, http://www.nrcan.gc.ca/mining-materials/certified-reference-materials/8001/. The proposed values for GAu-14, GAu-16, and GAu-18 were obtained from Yan et al.46 The results, listed in Table 7, are in good agreement with the certified values. The details on the certified reference materials of WMS-1a, MA-2c, GAu 14, GAu 16, GAu 18 are listed in Table S2.†| Sample | Found (μg g−1) | Certified value (μg g−1) |
|---|---|---|
| GAu-14 (ng g−1) | 104 ± 6.0 | 100.0 ± 3.0 |
| GAu-16 | 1.11 ± 0.06 | 1.09 ± 0.03 |
| WMS-1a | 0.32 ± 0.02 | 0.30 ± 0.02 |
| MA-2c | 3.00 ± 0.11 | 3.02 ± 0.06 |
The reliability of our method was checked by spiking experiments with tap water, sea water, and GAu-18. The results are shown in Table 8. The recovery of the spiked samples was satisfactory, and, hence, the presented procedure indicates that the reliability of PUF-Cyt for the determination of Au in geological samples is acceptable.
Under optimized conditions, a calibration curve (Fig. S7†) was constructed in the linear range of 0.05–10 μg mL−1 with a correlation factor of 0.9998 (Y = 10.6684X + 0.2762). Based on the definition of the International Union of Pure and Applied Chemistry, the detection limit was calculated as the concentration of analyte that corresponds to three times the standard deviation of eight replicate measurements of the procedural blank sample using the entire sample treatment process (LOD = 3σ, where σ is the standard deviation of blank determination).47 Using this procedure, the detection limit for gold was determined to be 0.006 μg L−1 and the limit of quantitation (LOQ = 10σ) for gold was 0.02 μg L−1.
Conclusions
A novel adsorbent was prepared based on the modification of PUF with a Cyt ligand. The kinetics and thermodynamics of the gold ion sorption on PUF-Cyt were studied. A negative ΔS value and exothermic enthalpy value indicated moderately strong affinity of Au(III) for the modified sorbent. The sorption mechanism of gold ions on PUF-Cyt may proceed via chelation and ion association. The selectivity and recovery of PUF-Cyt for the extraction and preconcentration of gold ions from geological samples were also investigated. The procedure offers a useful and reliable enrichment technique for the preconcentration of Au(III) with acceptable accuracy and precision. The optimal conditions for preconcentration were investigated systematically. This method represents high tolerance limits for potential matrix ions, satisfactory reproducibility, and relatively high sorption capacity. The detection limit and enrichment factor were better than most of the previously reported methods (Table 4).Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (no. 41403021 and 21207142) and Open Research Foundation of the Key Laboratory of Mineral Resources, Institute of Geology and Geophysics, Chinese Academy of Sciences (no. 12).References
- M. F. Guerra and T. Calligaro, Meas. Sci. Technol., 2003, 14, 1527–1537 CrossRef CAS.
- C. W. Corti and R. J. Holliday, Gold Bull., 2004, 37, 20–26 CrossRef CAS.
- K. Pyrzynska, Anal. Chim. Acta, 2012, 741, 9–14 CrossRef CAS PubMed.
- M. Resano, E. García-Ruiz, M. A. Belarra, F. Vanhaecke and K. S. McIntosh, Trends Anal. Chem., 2007, 26, 385–395 CrossRef CAS.
- M. Gros, J. P. Lorand and A. Luguet, Chem. Geol., 2002, 185, 179–190 CrossRef CAS.
- F. H. Chormann, M. J. Spencer, W. B. Lyons and P. A. Mayewski, Chem. Geol., 1985, 53, 25–30 CrossRef CAS.
- O. B. Mokhodoeva, G. V. Myasoedova and I. V. Kubrakova, J. Anal. Chem., 2007, 62, 607–622 CrossRef CAS.
- M. Resano, E. García-Ruiz, M. A. Belarra, F. Vanhaecke and K. S. McIntosh, Trends Anal. Chem., 2007, 26, 385–395 CrossRef CAS.
- V. Camel, Spectrochim. Acta, Part B, 2003, 58, 1177–1233 CrossRef.
- M. L. Kim and M. B. Tudino, Talanta, 2010, 82, 923–930 CrossRef CAS PubMed.
- A. M. Donia, A. A. Atia and K. Z. Elwakeel, Sep. Purif. Technol., 2005, 42, 111–116 CrossRef CAS.
- Y. C. Chang and D. H. Chen, Gold Bull., 2006, 39, 98–102 CrossRef CAS.
- L. Zhang, Z. Li, X. Du and X. Chang, Microchim. Acta, 2011, 174, 391–398 CrossRef CAS.
- H. J. M. Bowen, J. Chem. Soc. A, 1970, 1082–1085 RSC.
- T. Braun and A. B. Farag, Anal. Chim. Acta, 1973, 65, 115–126 CrossRef CAS.
- T. Braun and A. B. Farag, Anal. Chim. Acta, 1973, 66, 419–426 CrossRef CAS.
- T. Braun, M. N. Abbas, A. Elek and L. Bakos, J. Radioanal. Chem., 1981, 67, 359–366 CrossRef CAS.
- A. S. Bashammakh, S. O. Bahhafi, F. M. Al-Shareef and M. S. El-Shahawi, Anal. Sci., 2009, 25, 413–418 CrossRef CAS PubMed.
- V. A. Lemos, M. S. Santos, E. S. Santos, M. J. S. Santos, W. N. L. dos Santos, A. S. Souza, D. S. de Jesus, C. F. das Virgens, M. S. Carvalho and N. Oleszczuk, Spectrochim. Acta, Part B, 2007, 62, 4–12 CrossRef.
- M. F. El-shahat, E. A. Moawed and M. A. A. Zaid, Talanta, 2003, 59, 851–866 CrossRef CAS PubMed.
- M. F. El-Shahat, E. A. Moawed and A. B. Farag, Talanta, 2007, 71, 236–241 CrossRef CAS PubMed.
- E. A. Moawed, N. Burham and M. F. El-Shahat, J. Assoc. Arab Univ. Basic Appl. Sci., 2013, 14, 60–66 Search PubMed.
- E. A. Moawed, I. Ishaq, A. Abdul-Rahman and M. F. El-Shahat, Talanta, 2014, 121, 113–121 CrossRef CAS PubMed.
- G. Chakrapani, P. L. Mahanta, D. S. R. Murty and B. Gomathy, Talanta, 2001, 53, 1139–1147 CrossRef CAS PubMed.
- J. S. Noh and J. A. Schwarz, J. Colloid Interface Sci., 1989, 130, 157–164 CrossRef CAS.
- R. Liu and P. Liang, Anal. Chim. Acta, 2007, 604, 114–118 CrossRef CAS PubMed.
- A. E. Sillen and M. Martell, Stability Constants of Metal-ion Complexes, Special Publication No. 17, The Chemical Society, London, 2nd edn, 1964 Search PubMed.
- R. G. Pearson, J. Am. Chem. Soc., 1963, 85, 3533–3539 CrossRef CAS.
- G. McKay, J. Chem. Technol. Biotechnol., 1983, 33, 196–204 CrossRef.
- S. R. Bai and T. E. Abraham, J. Sci. Ind. Res., 1998, 57, 806–816 Search PubMed.
- A. Maquieira, H. A. M. Elmahadi and R. Puchades, Anal. Chem., 1994, 66, 3632–3638 CrossRef CAS.
- I. Langmuir, J. Am. Chem. Soc., 1918, 40, 1361–1403 CrossRef CAS.
- H. Freundlich, Colloid and Capillary Chemistry, Methuen, London, 1936, vol. 397 Search PubMed.
- M. M. Dubinin and L. V. Radushkevich, Proc. Acad. Sci. USSR, Phys. Chem. Sect., 1947, 331 Search PubMed.
- A. B. Farag, M. H. Soliman, O. S. Abdel-Rasoul and M. S. El-Shahawi, Anal. Chim. Acta, 2007, 601, 218–229 CrossRef CAS PubMed.
- E. A. Moawed, Chromatographia, 2007, 67, 77–78 Search PubMed.
- E. A. Moawed and M. F. El-Shahat, Anal. Chim. Acta, 2013, 788, 200–207 CrossRef CAS PubMed.
- L. Zhang, Z. Li, Z. Hu and X. Chang, Spectrochim. Acta, Part A, 2011, 79, 1234–1239 CrossRef CAS PubMed.
- H. B. Sentruk, A. Gundogdu, V. N. Bulut, C. Duran, M. Soylak, L. Elci and M. Tufekci, J. Hazard. Mater., 2007, 149, 317–323 CrossRef PubMed.
- L. Zhang, Z. Li, X. Du and X. Chang, Microchim. Acta, 2011, 174, 391–398 CrossRef CAS.
- R. Liu and P. Liang, Anal. Chim. Acta, 2007, 604, 114–118 CrossRef CAS PubMed.
- T. Shamspur and A. Mostafavi, J. Hazard. Mater., 2009, 168, 1548–1553 CrossRef CAS PubMed.
- A. D. Dwivedi, S. P. Dubeya, S. Hokkanen, R. N. Fallah and M. Sillanpää, Chem. Eng. J., 2014, 255, 97–106 CrossRef CAS.
- H. Wang, C. Bao, F. Li, X. Kong and J. Xu, Microchim. Acta, 2009, 168, 99–105 CrossRef.
- D. Afzali, Z. Daliri and M. A. Taher, Arabian J. Chem., 2014, 7, 770–774 CrossRef CAS.
- M. Yan, C. Wang, Q. Cao, T. Gu and Q. Chi, Geostand. Newsl., 1995, 19, 125–133 CrossRef CAS.
- G. L. Long and J. D. Winefordner, Anal. Chem., 1983, 52, 712A Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ay01737h |
| This journal is © The Royal Society of Chemistry 2016 |