Proton transfer in acetylacetone and its α-halo derivatives
Fatemeh
Dolati
a,
Sayyed Faramarz
Tayyari
*a,
Mohammad
Vakili
a and
Yan Alexander
Wang
*b
aChemistry Department, Ferdowsi University of Mashhad, Mashhad, Iran. E-mail: tayyari@ferdowsi.um.ac.ir
bDepartment of Chemistry, University of British Columbia, Vancouver, BC V6T 1Z1, Canada. E-mail: yawang@chem.ubc.ca
First published on 18th November 2015
Abstract
A two-dimensional potential energy surface was utilized to treat the proton transfer in acetylacetone (AA) and its α-halo derivatives: α-fluoro-(FAA), α-chloro-(ClAA), and α-bromo-acetylacetone (BrAA). This potential energy function, which couples O–H stretching and in-plane bending vibrations, was acquired through ab initio calculations for a fixed skeleton geometry. The resulting potential energy surfaces were then used to calculate the proton tunneling frequencies and proton transfer barrier heights. The barrier heights (the energy difference between the saddle point and the minima) calculated at the MP2/6-31G(2d,p) level of theory for proton transfers in AA, FAA, ClAA, and BrAA are 7.2, 9.4, 6.3, and 5.9 kcal mol−1, respectively. The theoretically predicted proton transfer barrier heights exhibit excellent linear correlations with geometrical, electronic structural, and topological parameters evaluated by the atoms-in-molecule (AIM) and natural bond orbital (NBO) analyses.
1. Introduction
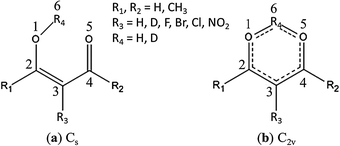
β-Diketones constitute a class of organic compounds that have at least one α-hydrogen atom enable them to undergo keto–enol tautomerization. The cis-enol forms of β-diketones (Fig. 1) are stabilized by an intramolecular hydrogen bond (IHB), whose strength is further enhanced by π-electron delocalization in the chelated ring.1 This effect was named by Gilli et al.1 as the resonance assisted hydrogen bond.The IHB is the main factor for the high content of the enols in most β-diketone samples. In the case of symmetric β-diketones (i.e., R1 = R2, R4 = H or D in Fig. 1), there should be two possibilities for the IHB proton movement in the cis-enols. The IHB proton may be localized in the mid-point between the two O atoms (O1 and O5), with a symmetric single-minimum potential function (Fig. 1b), or being near one of the two O atoms, with a symmetric double-minimum potential function (Fig. 1a). The IHB proton transfer in the enol form of β-diketones has been extensively investigated from both experimental2–21 and theoretical22–34 points of view.
Among the two simplest members of this class of compounds, malonaldehyde (R1 = R2 = R3 = R4 = H in Fig. 1) and acetylacetone (R1 = R2 = CH3, R3 = R4 = H in Fig. 1), acetylacetone (AA) offers more intriguing interplay between the IHB proton transfer and the conformations of the two terminal methyl groups. Take the ground state of the Cs conformation of AA (Fig. 1a) for example, the methyl group (R1) on the O1–H6 side is in the gauche position with respect to the sp3 O1 atom whereas the methyl group (R2) on the C4![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O5 side is in the eclipsed position with respect to the sp2 O5 atom. During the H6 transfer through the IHB setup (Fig. 1b), these two methyl groups must simultaneously rotate into an identical eclipsed position through a C2v structure (Fig. 1b) to achieve the minimum energy. Based on such an understanding, Rios and Rodríguez investigated the IHB proton transfer in AA and obtained a double minimum potential function with a barrier height of about 7 kcal mol−1.22 On the other hand, ab initio calculations performed by Matanović et al. concluded a barrier of only half the height, 3.4 kcal mol−1, for the IHB proton transfer in AA.23 Previous attempt to observe the tunneling frequency for AA in the gas, liquid, or solid states was not successful.9,10 It becomes desirable to appreciate whether such a discrepancy can be attributed to an asymmetric structure due to different conformations of the two terminal methyl groups in the AA molecule during the IHB proton transfer.
O5 side is in the eclipsed position with respect to the sp2 O5 atom. During the H6 transfer through the IHB setup (Fig. 1b), these two methyl groups must simultaneously rotate into an identical eclipsed position through a C2v structure (Fig. 1b) to achieve the minimum energy. Based on such an understanding, Rios and Rodríguez investigated the IHB proton transfer in AA and obtained a double minimum potential function with a barrier height of about 7 kcal mol−1.22 On the other hand, ab initio calculations performed by Matanović et al. concluded a barrier of only half the height, 3.4 kcal mol−1, for the IHB proton transfer in AA.23 Previous attempt to observe the tunneling frequency for AA in the gas, liquid, or solid states was not successful.9,10 It becomes desirable to appreciate whether such a discrepancy can be attributed to an asymmetric structure due to different conformations of the two terminal methyl groups in the AA molecule during the IHB proton transfer.
The structure and the IHB of AA have been subjected to many theoretical26–33 and experimental9–23 investigations, but the most stable form between the C2v and Cs structures (Fig. 1) still remain unresolved. An early electron diffraction (ED)15 and a later microwave investigation21 have identified the C2v structure to be the dominant enol form of AA. However, many other investigations based on neutron12 and X-ray crystallography,13,14 liquid NMR,19 gas phase ED,17,20 and vibrational spectroscopy9–11 supported the Cs structure to be the dominate enol form of AA in the gas, liquid, and solid phases, in agreement with the results of almost all theoretical studies.26–33
For the simpler malonaldehyde (MA) system, experimental2–5 and theoretical studies24 all established that the IHB proton transfer follows a symmetric double-minimum potential with a proton tunneling frequency of about 22 cm−1. Tayyari et al.24 applied two-dimensional symmetric double minimum potential for the hydrogen transfer in the bent IHB system and correctly obtained the proton tunneling frequencies of MA24 and α-nitro-malonaldehyde (NO2-MA).25 Such a model was also successfully applied to the IHB of 6-hydroxy-2-formylfulvene,34 a nearly linear hydrogen bonded system.
Based on our previous success on the MA system, we aimed our investigation at the bent IHB system in AA and its α-halo derivatives by applying a similar two-dimensional potential surface for the IHB proton transfer processes. The obtained proton tunneling frequency and potential barrier height in AA were compared with those in α-fluoro (FAA), α-chloro (ClAA), and α-bromo (BrAA) derivatives to shed light on the nature of the IHB and to resolve any inconsistent results previously reported for such systems. The nature of IHBs in these systems was further examined by natural bond orbital (NBO) and atoms-in-molecules (AIM) analyses.
2. Computational procedure
All ab initio calculations in this work were performed using the Gaussian 09W Package.35 Since MP236,37 was already demonstrated to produce superior theoretical results,24 we have thus employed it again for this study. However, the 6-31G(d,p) basis set, which was employed in previous work, is not capable of modeling the IHB of the BrAA system involving the Br atom (for more details in Section 3.1 below). The geometry optimizations were thus performed at the MP2 level of theory using two larger basis sets, 6-31G(2d,p) and 6-31G(df,p), with two different enhanced polarization schemes instead. To evaluate the validity of theoretical results, similar calculations were also performed on MA and NO2-MA for comparison purpose.To explore the two-dimensional proton transfer potential surface, the O1–H6 distance in AA and its α-halo derivatives was varied from 0.90 to 1.18 Å (in steps of 0.01 Å) and the ∠O1–H6⋯O5 angle was scanned from 0° to 28° (in steps of 2°); the corresponding energies were calculated with all other geometrical parameters fixed at their optimized equilibrium values of the ground state. More specifically, to estimate the energy difference between the gauche and eclipsed conformations during proton movement, the ∠O1–H6⋯O5 angle was subsequently optimized while the O1–H6 distance was increased from 0.90 to 1.30 Å (in steps of 0.05 Å) with all other structural parameters frozen at their equilibrium positions. This scan gives the minimum potential energy in the two-dimensional (constrained) potential surface along the path from the minima to the saddle point. Such a scheme has been successfully applied before for a wide range of IHB systems with excellent agreement with experimental results.24,25,34
The calculated potential energy surfaces were then fitted to the following anharmonic two-dimensional potential function:
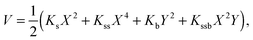 | (1) |
The barrier heights were calculated as follows. At the minimum positions of the IHB proton transfer process, Xm and Ym, we have
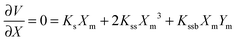 | (2) |
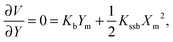 | (3) |
| Xm2 = −2KbYm/Kssb | (4) |
| Ym = KsKssb/(4KssKb − Kssb2). | (5) |
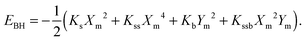 | (6) |
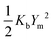 ,
,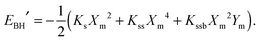 | (7) |
For the purpose of brevity, the readers are directed to our previous publications24,25,34 for full explanation on the detailed procedure of obtaining the energy levels and tunneling frequencies.
The nature of the IHBs within AA and its α-halo derivatives can also been studied by the AIM theory,38 because the electronic density at the bond critical point (CP), ρc(r), and its Laplacian, ∇2ρc(r), are useful parameters for the estimation of the relative strength of hydrogen bonding.39 According to Espinosa and Molins,40 hydrogen bond strength (EHB) is equal to one-half of the local potential energy density Vρ(r) at the hydrogen bond CP:
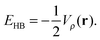 | (8) |
3. Results and discussion
3.1. Potential surfaces
Among the theoretical results of selected potential energy surfaces and structural parameters, proton transfer barrier heights, and proton tunneling frequencies depicted in Table 1, the magnitudes of the proton transfer barrier heights, EBH and EBH′, directly signify the strength of the IHB: the lower the proton transfer barriers, the easier the proton transfer, and thus the stronger the IHB.| Compound | R O1⋯O5 (Å) | R O1–H6 (Å) | R O5⋯H6 (Å) | ∠O1–H6⋯O5 (degrees) | |Xm| (Å) | Y m (Å) | E BH (kcal mol−1) | E BH′ (kcal mol−1) | ν t (cm−1) |
|---|---|---|---|---|---|---|---|---|---|
| a E BH and EBH′ are proton transfer barrier heights measured at the saddle point and at the midpoint of O1 and O5 atoms from the energy minima, respectively. Xm and Ym are the minimum positions for the IHB proton transfer process on the potential energy surface. b The first value of the tunneling splitting frequency is for the normal molecule (with all 1H isotopes) and the second frequency is for its deuterated analogous (R3 = R4 = D in Fig. 1). | |||||||||
| 6-31G(2d,p) | |||||||||
| BrAA | 2.5261 | 1.0021 | 1.5958 | 150.8 | 0.3127 | 0.1157 | 5.91 | 7.83 | 121/22 |
| ClAA | 2.5363 | 1.0008 | 1.6073 | 150.5 | 0.3190 | 0.1190 | 6.27 | 8.31 | 101/16 |
| AA | 2.5586 | 0.9986 | 1.6342 | 150.5 | 0.3335 | 0.1258 | 7.18 | 9.47 | 65/8.2 |
| FAA | 2.6108 | 0.9914 | 1.6914 | 148.9 | 0.3673 | 0.1448 | 9.36 | 12.44 | 20/1.5 |
| MA | 2.5918 | 0.9948 | 1.6783 | 148.6 | 0.3663 | 0.1462 | 8.67 | 11.78 | 25/2.0 |
| NO2-MA | 2.5703 | 0.9988 | 1.6660 | 148.2 | 0.3513 | 0.1325 | 7.73 | 10.33 | 40/4.0 |
| 6-31G(df,p) | |||||||||
| BrAA | 2.5124 | 1.0043 | 1.5879 | 150.7 | 0.3113 | 0.1177 | 5.65 | 7.66 | 131/24 |
| ClAA | 2.5169 | 1.0029 | 1.5954 | 150.4 | 0.3130 | 0.1189 | 6.18 | 8.21 | 114/19 |
| AA | 2.5458 | 0.9999 | 1.6293 | 150.2 | 0.3309 | 0.1276 | 7.28 | 9.62 | 66/8.4 |
| FAA | 2.5933 | 0.9915 | 1.6971 | 148.3 | 0.3704 | 0.1556 | 9.38 | 12.83 | 19/1.3 |
| MA | 2.5794 | 0.9947 | 1.6812 | 148.1 | 0.3600 | 0.1455 | 8.72 | 11.85 | 27/2.3 |
| NO2-MA | 2.5661 | 0.9991 | 1.6603 | 147.7 | 0.3482 | 0.1373 | 7.95 | 10.67 | 42/4.2 |
First, the positive values of EBH and EBH′ clearly verify that the Cs structure (Fig. 1a) is the ground state for AA and its α-halo derivatives, consistent to nearly all previous experimental and theoretical conclusions,9–14,17,19,20,26–33 except for only two experiments.15,21
Second, calculations with the 6-31G(d,p) basis set predicted a weaker IHB in BrAA than in ClAA, which is opposite to the results with the 6-31G(2d,p) and 6-31G(df,p) basis sets. In a well-established NMR experiment,41 the chemical shifts of the enolated proton in ClAA and BrAA were observed at 15.35 and 15.75 ppm, respectively, suggesting the IHB in BrAA to be considerably stronger than that in ClAA. We thus conclude that the 6-31G(d,p) basis set has some deficiency in modeling the BrAA and ClAA systems.
On the other hand, calculations with the two other better basis sets, 6-31G(2d,p) and 6-31G(df,p), produced very similar results for the proton transfer barrier heights and proton tunneling frequencies (see Table 1). This result demonstrates that a higher level of polarization in the Pople's basis set, e.g., (2d,p) and (df,p), is critical for generating reliable results but offers very little difference once the basis-set enhancement in polarization goes beyond the (d,p) level.
Furthermore, we can rely on the experimental data to gauge the quality of our theoretical results. For MA and its deuterated analogous D2MA (R3 = R4 = D in Fig. 1), the observed proton tunneling frequencies of the benchmark systems are 21.58 and 2.88 cm−1,5 respectively. The corresponding values for NO2-MA and its deuterated analogue are 35 ± 15 and 3.00 ± 0.02 cm−1,7 respectively. In all such cases, our theoretical predictions agree very well with the available experimental data,5,7 although the computational results based on the 6-31G(2d,p) basis set are slightly better than those of the 6-31G(df,p) basis set. Thereby, we will proceed forthcoming discussions mainly based on the MP2/6-31G(2d,p) results (especially in the presentation of Fig. 2–4).
According to our calculations with the 6-31G(2d,p) basis set, the predicted proton transfer barrier heights, EBH, for AA, BrAA, ClAA, FAA, NO2-MA, and MA are about 7.2, 5.9, 6.3, 9.4, 7.7, and 8.7 kcal mol−1, respectively. The proton tunneling frequencies for AA and its partially deuterated partner, D2AA, are estimated to be around 65 and 8 cm−1, respectively. In comparison, our calculated barrier height for AA is in excellent agreement with that predicated by Rios and Rodríguez,22 but is twice the magnitude of that indicated by Matanović et al.23 Given that our modeling yields highly consistent results to previous extensive experimental and theoretical studies on MA and its derivatives,5,7,24,25 we thus have confidence in our theoretically predicted IHB proton transfer barrier heights for AA and D2AA.
Naturally, one might envision that the transition state of the IHB proton transfer process resembles the C2v structure shown in Fig. 1b. We hence searched for such a C2v transition state for MA and D2MA with all other geometrical parameters fully relaxed. Eventually, we indeed identified the C2v “transition state” but unfortunately with much lower barrier heights: EBH = 3.7 kcal mol−1 and EBH′ = 6.1 kcal mol−1, very similar to the situation in AA encountered by Matanović et al. previously.23 Moreover, with such small barriers, the proton tunneling frequencies for MA and D2MA were predicted to be over 120 and 25 cm−1, respectively, nearly 6 and 9 times bigger than the experimental values, 21.58 and 2.88 cm−1.5 Obviously, the IHB proton tunneling is an early, sudden quantum process without going through the classical C2v transition state. Such an understanding lends strong support to our two-dimensional potential energy surface model for the IHB proton transfer process, in which we only scanned the O1–H6 distance and the ∠O1–H6⋯O5 angle and kept all other geometrical parameters fixed at their optimized equilibrium values.
3.2. Structural parameters
Selected structural parameters intimately related to the IHBs of AA, FAA, ClAA, BrAA, MA, and NO2-MA are also collected in Table 1. Our theoretical results with both basis sets clearly show that the O1⋯O5 and O5⋯H6 distances follow the trend: FAA > MA > NO2-MA > AA > ClAA > BrAA, exactly in an inverse correlation with the O1–H6 distance and the IHB strength as being consistently predicted by the proton transfer barrier heights, EBH and EBH′.In comparison with MA, the two methyl groups in AA exert extra steric and electron-donating effects that strengthen the IHB in AA. Likewise, in ClAA and BrAA, the repulsion between the H atoms of the methyl groups and the lone pairs of electrons in the halogen atoms in turn increases the steric tension between the two methyl groups and the lone pairs of electrons on the O1 and O5 atoms. As a result, both ClAA and BrAA possess a stronger IHB than AA does.
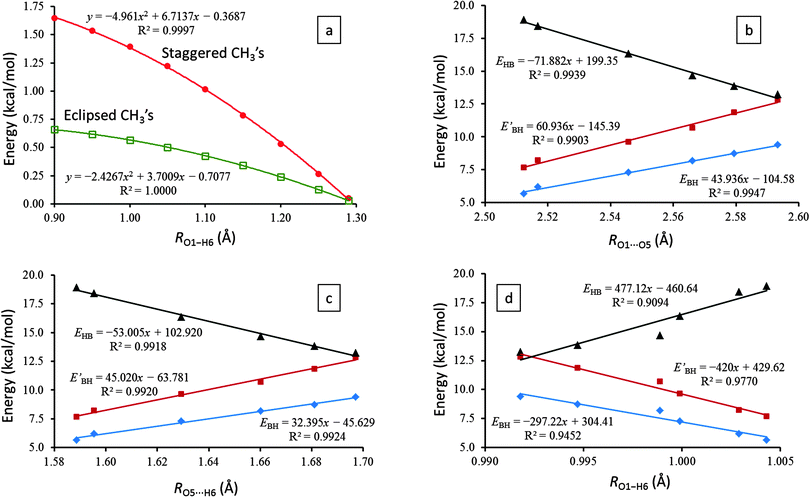
To investigate the influence of the relative conformations of the two terminal methyl groups in AA on its IHB proton transfer process, we rotated both methyl groups into either staggered or eclipsed orientation to both O1 and O5 atoms. For these two conformations, we subsequently scanned the O1–H6 distance from 0.90 to 1.30 Å (to reach the C2v transition state) and optimized the corresponding ∠O1–H6⋯O5 angle (among all structural parameters). From their energies (measured from the asymmetric ground state) plotted in Fig. 2a, we immediately found that for all points lead to the C2v transition state, any rotation of the two terminal methyl groups away from the asymmetric ground state must pay a penalty of higher energy.
More specifically, simultaneously staggered methyl groups agitate the electron structure much more than concurrently eclipsed methyl groups do. As the system approaches the C2v transition state, the energy differences are smoothly shrinking to zero. Only at the C2v transition state, the energy gaps between all different conformations of the two terminal methyl groups vanish completely: the methyl groups can rotate freely. In combination with Section 3.2, we therefore can draw a convincing conclusion that our two-dimensional potential energy surface, despite its simplicity, is adequate in modeling the IHB proton tunneling process even without incorporating the rotations of the two terminal methyl groups in the formulation explicitly.
Fig. 2b–d exhibit excellent linear correlations between the IHB proton transfer barrier heights, EBH and EBH′, and the essential geometrical parameters of the IHB systems, the O1⋯O5, O5⋯H6, and O1–H6 distances. Such results suggest that the proton transfer barrier heights, EBH and EBH′, can be utilized for the characterization of the bent IHB systems, at least for the six molecules studied herein.
Additionally, the linear correlations shown in Fig. 2b predict that the proton transfer barrier will disappear when RO1⋯O5 contracts to 2.38 Å, which corresponds to a hydrogen bond strength EHB ≈ 28 kcal mol−1 (see Section 3.4 for more details on EHB). Consistent results can also be derived from the linear correlations of EHB with RO5⋯H6 (Fig. 2c) and with RO1–H6 (Fig. 2d).
3.3. NBO analysis
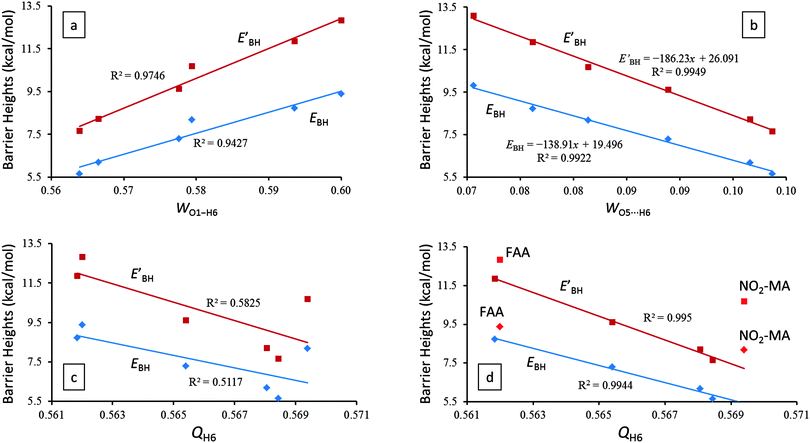
The Wiberg bond orders42 of the O1–H6, O5⋯H6, and O1⋯O5 atom pairs and the natural charges on the H6, O1, and O5 three atoms predominantly involved in the IHB for AA and its derivatives are listed in Table 2. Not surprisingly, the trend of the predicted proton transfer barrier heights (thus the opposite trend of the IHB strength) indeed correlates positively with the O1–H6 bond order (Fig. 3a) and negatively with the O5⋯H6 bond order (Fig. 3b). These results are consistent with the theoretical results discussed in Sections 3.1 and 3.2.| Compound | W O5⋯H6 | W O1–H6 | W O1⋯O5 | Q O1 | Q O5 | Q H6 |
|---|---|---|---|---|---|---|
| 6-31G(2d,p) | ||||||
| BrAA | 0.0945 | 0.5645 | 0.0328 | −0.7307 | −0.7628 | 0.5692 |
| ClAA | 0.0912 | 0.5684 | 0.0324 | −0.7224 | −0.7632 | 0.5687 |
| AA | 0.0857 | 0.5775 | 0.0303 | −0.7312 | −0.7794 | 0.5661 |
| FAA | 0.0698 | 0.5969 | 0.0287 | −0.7124 | −0.7702 | 0.5632 |
| MA | 0.0756 | 0.5914 | 0.0310 | −0.7150 | −0.7676 | 0.5628 |
| NO2-MA | 0.0797 | 0.5784 | 0.0287 | −0.6902 | −0.7349 | 0.5700 |
| 6-31G(df,p) | ||||||
| BrAA | 0.0987 | 0.5639 | 0.0336 | −0.7388 | −0.7737 | 0.5684 |
| ClAA | 0.0966 | 0.5665 | 0.0334 | −0.7380 | −0.7738 | 0.5681 |
| AA | 0.0889 | 0.5776 | 0.0310 | −0.7458 | −0.7892 | 0.5654 |
| FAA | 0.0706 | 0.6003 | 0.0289 | −0.7275 | −0.7804 | 0.5620 |
| MA | 0.0762 | 0.5936 | 0.0311 | −0.7239 | −0.7735 | 0.5618 |
| NO2-MA | 0.0814 | 0.5794 | 0.0289 | −0.7003 | −0.7408 | 0.5694 |
Qualitatively, we expect that an increased IHB strength should enlarge the partial charge on O1, reduce the partial charges on O5 and H6, and increase the O1⋯O5 bond order. However, our theoretical results assembled in Table 2 reveal that the O1⋯O5 bond order and the charges on O1, O5, and H6 are much less successful in quantifying the relative order of the IHB strength among the six molecules investigated here. Compared with the excellent correlations between the proton transfer barrier heights, EBH and EBH′, and the O1–H6 (Fig. 3a) and O5⋯H6 (Fig. 3b) bond orders, there exists a very weak correlation between the barrier heights and the natural charge on the enol proton H6, QH6 (Fig. 3c). However, if the QH6 data points of FAA and NO2-MA are excluded from the linear fitting, the quality of the correlation between the barrier heights and QH6 becomes greatly improved (Fig. 3d). Evidently, the extremely electronegative F atom in FAA and NO2 group in NO2-MA abnormally withdraw too much electron cloud from the H6 atom and diminish the usefulness of utilizing QH6 to ascertain the relative strength of the IHBs.
3.4. AIM analysis
To further assess the IHB character, the topology of the electron density calculated at the MP2/6-31G(2d,p) and MP2/6-31G(df,p) levels of theory was diagnosed by the AIM analysis.40 According to the AIM theory, the structural elements constituted a molecule are identified at the critical points of the electron density distribution, ρc(r): atoms corresponding to local maxima, bonds and rings to saddle points, and cages to local minima. The sign of the Laplacian, ∇2, of the electron density at a bond critical point implies whether the charge is concentrated, as in covalent bonds ∇2ρc(r) < 0, or depleted, as in ionic and hydrogen bonds ∇2ρc(r) > 0. Thus, the AIM theory provides another analytical tool for describing the nature of the IHBs in AA and its derivatives.At the hydrogen bond critical point, the calculated total electronic density, ρc(r), the corresponding Laplacian, ∇2ρc(r), the hydrogen bond strength, EHB, the (negative) potential electron energy density, −Vρ(r), the kinetic electron energy density, Gρ(r), and their ratio (GVR), −Gρ(r)/Vρ(r), are displayed in Table 3. It is illuminating to know that for all six molecules studied in this work, their GVR values at the hydrogen bond critical points are less than one, unveiling a partially covalent character of the IHBs.43
| Compound | ρ c(r) | ∇2ρc(r) | G ρ (r) | −Vρ(r) | GVR | E HB |
|---|---|---|---|---|---|---|
| a ρ c(r) in e Å−5, ∇2ρc(r) in e Å−3, EHB in kcal mol−1. | ||||||
| 6-31G(2d,p) | ||||||
| BrAA | 0.0617 | 0.1713 | 0.0408 | 0.0450 | 0.867 | 18.31 |
| ClAA | 0.0601 | 0.1681 | 0.0396 | 0.0433 | 0.874 | 17.61 |
| AA | 0.0565 | 0.1594 | 0.0455 | 0.0513 | 0.889 | 16.08 |
| FAA | 0.0494 | 0.1434 | 0.0491 | 0.0561 | 0.914 | 13.58 |
| MA | 0.0509 | 0.1466 | 0.0506 | 0.0584 | 0.907 | 14.11 |
| NO2-MA | 0.0524 | 0.1483 | 0.0417 | 0.0464 | 0.900 | 14.55 |
| 6-31G(df,p) | ||||||
| BrAA | 0.0632 | 0.1635 | 0.0506 | 0.0603 | 0.839 | 18.91 |
| ClAA | 0.0620 | 0.1624 | 0.0496 | 0.0587 | 0.846 | 18.40 |
| AA | 0.0572 | 0.1536 | 0.0452 | 0.0520 | 0.869 | 16.32 |
| FAA | 0.0485 | 0.1379 | 0.0383 | 0.0421 | 0.910 | 13.21 |
| MA | 0.0503 | 0.1410 | 0.0397 | 0.0441 | 0.900 | 13.83 |
| NO2-MA | 0.0529 | 0.1442 | 0.0414 | 0.0467 | 0.886 | 14.65 |
Also, in agreement with the above discussions in Sections 3.1–3.3, EHB estimated by the AIM analysis does indeed manifest strong linear correlations with the key geometrical parameters (i.e., RO1⋯O5, RO5⋯H6, and RO1–H6) and the proton transfer barrier heights (i.e., EBH and EBH′) of the IHB systems (Fig. 2).
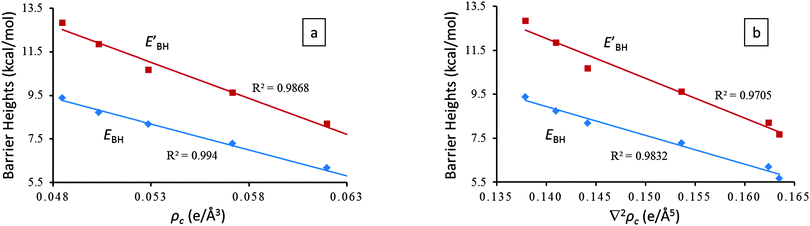
Given the fact that the proton transfer barrier heights, EBH and EBH′, possess excellent linear correlations with EHB (Fig. 2) and the AIM topological parameters (Fig. 4), ρc(r) and ∇2ρc(r), we therefore conclude that EBH and EBH′ are accurate indicators of hydrogen bond strength for symmetric resonance assisted hydrogen bond systems.
4. Conclusion
The geometries of AA, its α-halo derivatives, MA and NO2-MA were optimized at the MP2 level of theory with 6-31G(df,p) and 6-31G(2d,p) basis sets. Based on these calculations, two-dimensional symmetric double minimum potential energy surfaces were obtained for the bent IHB systems of the six molecules. The proton transfer barrier heights, EBH and EBH′, of these IHB systems were predicted to be within the ranges of 5.6–9.4 and 7.6–12.8 kcal mol−1, respectively. The proton transfer barrier heights, EBH and EBH′, demonstrate excellent linear correlations with geometrical and AIM topological parameters. Computational results confirm that EBH and EBH′ are effective descriptors for the IHBs within the symmetric hydrogen bonded systems.Acknowledgements
Y. A. W. thanks the Natural Sciences and Engineering Research Council (NSERC) of Canada for financial support. The authors would like to thank Ms Mansoureh Keikhaei for her help in drawing the potential surface diagrams.References
- G. Gilli, F. Belluci, V. Ferretti and V. Bertolesi, J. Am. Chem. Soc., 1989, 111, 1023–1028 CrossRef CAS.
- W. F. Rowe, R. W. Duerst and E. B. Wilson, J. Am. Chem. Soc., 1976, 98, 4021 CrossRef CAS.
- S. L. Baughcum, R. W. Duerst, W. F. Rowe, Z. Smith and E. B. Wilson, J. Am. Chem. Soc., 1981, 103, 6296 CrossRef CAS.
- S. L. Baughcum, Z. Smith, E. B. Wilson and R. W. Duerst, J. Am. Chem. Soc., 1984, 106, 2260 CrossRef CAS.
- P. Turner, S. L. Baughcum, S. L. Coy and Z. Smith, J. Am. Chem. Soc., 1984, 106, 2265 CrossRef CAS.
- N. D. Sanders, J. Mol. Spectrosc., 1981, 86, 27 CrossRef CAS.
- W. Caminati, J. Chem. Soc., Faraday Trans. 2, 1982, 78, 825 RSC.
- S. F. Tayyari and F. Milani-Nejad, Spectrochim. Acta, Part A, 1998, 54, 255 CrossRef.
- S. F. Tayyari, T. Zeegers-Huyskens and J. L. Wood, Spectrochim. Acta, Part A, 1979, 35, 1289 CrossRef.
- S. F. Tayyari, PhD thesis, London University, 1978.
- S. F. Tayyari and F. Milani-Nejad, Spectrochim. Acta, Part A, 1998, 56, 2679 CrossRef.
- M. R. Johnson, N. H. Jones, A. Geis, A. J. Horsewill and H. P. Trommsdorff, J. Chem. Phys., 2002, 116, 5694 CrossRef CAS.
- A. Camerman, D. Mastropaolo and N. Camerman, J. Am. Chem. Soc., 1983, 105, 1584 CrossRef CAS.
- R. Boese, M. Y. Antipin, D. Bläser and K. A. Lyssenko, J. Phys. Chem. B, 1998, 102, 8654 CrossRef CAS.
- A. H. Lowrey, C. George, P. D'Antonio and J. Karle, J. Am. Chem. Soc., 1971, 93, 6399 CrossRef CAS.
- A. L. Andreassen and S. H. Bauer, J. Mol. Struct., 1972, 12, 381 CrossRef CAS.
- K. Iijima, A. Ohnogi and S. Shibata, J. Mol. Struct., 1987, 156, 111 CrossRef CAS.
- R. K. Harris and R. C. Rao, Org. Magn. Reson., 1983, 21, 580 CrossRef CAS.
- W. Egan, G. Gunnarsson, T. E. Bull and S. Forsen, J. Am. Chem. Soc., 1977, 99, 4568 CrossRef CAS.
- R. Srinivasa, J. S. Feenstra, S. T. Park, S. Xu and A. H. Zewail, J. Am. Chem. Soc., 2004, 126, 2266 CrossRef PubMed.
- W. Caminati and J.-U. Grabow, J. Am. Chem. Soc., 2006, 128, 854 CrossRef CAS PubMed.
- M. A. Rios and J. Rodríguez, THEOCHEM, 1990, 204, 137 CrossRef.
- I. Matanović, N. Došlić and Z. Mihalić, Chem. Phys., 2004, 306, 201 CrossRef.
- S. F. Tayyari, M. Zahedi, F. Tayyari and F. Milani-Nejad, THEOCHEM, 2003, 637, 171 CrossRef CAS.
- S. F. Tayyari, M. Zahedi-Tabrizi, H. Azizi-Toopkanloo, S. S. Hepperle and Y. A. Wang, Chem. Phys., 2010, 368, 62 CrossRef CAS.
- N. S. Hush, M. K. Livett, J. B. Peel and G. D. Willett, Aust. J. Chem., 1987, 40, 599 CrossRef CAS.
- J. J. Dannenberg and R. Rios, J. Phys. Chem., 1994, 98, 6714 CrossRef CAS.
- T. Ishida, F. Hirata and S. Kato, J. Chem. Phys., 1999, 110, 3938 CrossRef CAS.
- S. H. Bauer and C. F. Wilcox, Chem. Phys. Lett., 1997, 279, 122 CrossRef CAS.
- O. A. Sharafeddin, K. Hinsen, T. Carrington Jr. and B. Roux, J. Comput. Chem., 1997, 18, 1760 CrossRef CAS.
- J. Mavri and J. Grdadolnik, J. Phys. Chem. A, 2001, 105, 2039 CrossRef CAS.
- S. J. Grabowski, J. Phys. Org. Chem., 2003, 16, 797 CrossRef CAS.
- V. B. Delchev, H. Mikosch and G. S. Nikolov, Monatsh. Chem., 2001, 132, 339 CrossRef CAS.
- S. F. Tayyari, M. Zahedi-Tabrizi, H. Rahemi, H. A. Mirshahi, J. S. Emampour, M. Rajabi and F. Milani-Nejad, THEOCHEM, 2005, 730, 17–21 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- R. F. W. Bader, Atoms in Molecules. A Quantum Theory, Oxford University Press, New York, 1990 Search PubMed.
- E. Espinosa, M. Souhassou, H. Lachekar and C. Lecomte, Acta Crystallogr., Sect. B: Struct. Sci., 1999, 55, 563 CrossRef , and references cited therein.
- E. Espinosa and E. Molins, J. Chem. Phys., 2000, 113, 5686 CrossRef CAS.
- J. L. Burdett and M. T. Rogers, J. Am. Chem. Soc., 1964, 86, 2105 CrossRef CAS.
- K. W. Wiberg, Tetrahedron, 1968, 24, 1083 CrossRef CAS.
- B. A. Shainyan, N. N. Chipanina, T. N. Aksamentova, L. P. Oznobikhina, G. N. Rosentsveig and I. B. Rosentsveig, Tetrahedron, 2010, 66, 8551 CrossRef CAS.
| This journal is © the Owner Societies 2016 |