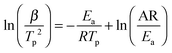View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/C5CP04257G (Paper) Phys. Chem. Chem. Phys., 2016, 18, 244-251

Synthesis, structure and the dehydrogenation mechanism of calcium amidoborane hydrazinates†

Zhao Li ab, Teng He *a, Guotao Wu a, Weidong Chen ab, Yong Shen Chua c, Jianping Guo b, Dong Xie a, Xiaohua Ju a and Ping Chen *ad
aDalian National Laboratory for Clean Energy, Dalian Institute of Chemical Physics, Chinese Academy of Sciences, 457, Zhongshan Road, Dalian, 116023, China. E-mail: heteng@dicp.ac.cn; pchen@dicp.ac.cn
bUniversity of the Chinese Academy of Sciences, Beijing 100049, China
cSchool of Chemical Sciences, Universiti Sains Malaysia, 11800, Pulau Pinang, Malaysia
dState Key Laboratory of Catalysis, Dalian Institute of Chemical Physics, Chinese Academy of Sciences, 457, Zhongshan Road, Dalian, 116023, China

Received 21st July 2015 , Accepted 5th November 2015

First published on 5th November 2015

Abstract

The calcium amidoborane hydrazinates, Ca(NH2BH3)2·nN2H4, were firstly synthesized by reacting different molar ratios of Ca(NH2BH3)2 and N2H4. In particular, Ca(NH2BH3)2 and N2H4 with a molar ratio of 1[thin space (1/6-em)]:[thin space (1/6-em)]2 crystallizes into the orthorhombic symmetry P212121 space group with the lattice parameters of a = 6.6239(4) Å, b = 13.7932(6) Å, c = 4.7909(2) Å. The dehydrogenations of calcium amidoborane hydrazinates are two-step reactions, exhibiting superior dehydrogenation properties compared with those of pristine Ca(NH2BH3)2. For Ca(NH2BH3)2–1/2N2H4, approximately 4.6 equiv. hydrogen (or 7.9 wt% hydrogen) can be released at 150 °C. Kinetic analysis shows that the activation energies for the two steps of hydrogen desorption from Ca(NH2BH3)2·2N2H4 are much lower than those of pristine Ca(NH2BH3)2, suggesting an improvement in the dehydrogenation kinetics of Ca(NH2BH3)2 after coordinating with N2H4. Isotopic labeling results show that the driving force for the dehydrogenation of calcium amidoborane hydrazinates is the combination mechanism of protonic hydrogen and hydridic hydrogen (Hδ+ and Hδ−). In addition, initial H2 release from calcium amidoborane hydrazinates originates from the interaction of [–BH3] and N2H4, rather than [–BH3] and [–NH2] (in [–NH2BH3]).

1. Introduction

Due to the increasingly serious global energy crisis, searching and utilizing efficient alternative energy sources are inevitable, among which hydrogen can be viewed as a clean and promising energy carrier.1–3 However, the lack of efficient hydrogen storage materials on board is one of the most difficult challenges for the coming “hydrogen economy”. In the past decade, much effort has been made to synthesise ammonia borane (AB, NH3BH3), which has a high hydrogen capacity (ca. 19.6 wt%) and moderate dehydrogenation properties.4–6 However, its drawbacks such as a severe dehydrogenation kinetic barrier, the emission of poisonous by-products and sample foaming limit its direct application.7,8 To solve these problems, one of the most important options is to replace H in the [–NH3] group from AB with metals forming metal amidoborane (MAB), which is implemented by reacting AB with metal hydrides including LiH,9 NaH,9 KH,10 CaH2,11,12 MgH2,13 SrH2.14 Besides MABs derived from AB-hydride interactions, metal amidoborane ammoniates can be obtained through the interactions of amides,15 imides or nitrides16 with AB. Alternatively, a straight-forward method, which is the absorption of stoichiometric NH3 by metal amidoboranes, can also give rise to metal amidoborane ammoniates. The ligand of NH3 in metal amidoborane ammoniates not only improves the hydrogen capacity, but also moderates the dehydrogenation kinetics. For instance, although Ca(NH2BH3)2·2NH3 desorbs NH3 in an open system forming Ca(NH2BH3)2, it releases H2 directly in a close system at 150 °C.17,18 Other metal amidoborane ammoniates, such as LiNH2BH3·NH3, can reversibly desorb/adsorb NH3 at room temperature. However, the decomposition of LiNH2BH3·NH3 can produce 3.0 equiv. H2 under ammonia at low temperature.19 The examples above have revealed that the cation properties including electronegativity, charge and ionic radius may significantly affect its coordination capability to a ligand, which will alter the activity of the ligand and further lead to different dehydrogenation performance.20 For example, Li+ and Mg2+ have a similar ionic radius but Mg bears more positive charges and thus executes stronger coordination with NH3. As a result, Mg(NH2BH3)2·NH3 releases H2 rather than NH3 under dynamic Ar flow different from those of LiNH2BH3·NH3.21 In addition, coordination strength is affected by the number of ligands attaching to the metal center as well. Mg(NH2BH3)2·3NH3 releases NH3 and H2 under dynamic flow, whereas Mg(NH2BH3)2·NH3 prefers to give off only H2 under the same conditions.22 In general, the ligand, like ammonia, plays a vital role not only in stabilizing amidoboranes and increasing the hydrogen capacity, but also in altering the dehydrogenation behavior. Therefore, it is of great interest to explore other ligands with high hydrogen content and optimize the dehydrogenation properties of metal amidoboranes.

Recently, hydrazine (NH2NH2) has attracted much attention in hydrogen production. Hydrazine hydrate can release hydrogen at room temperature with the presence of catalysts.23,24 Since there is lone pair electrons on N, hydrazine can coordinate with [–BH3] forming hydrazine borane (N2H4BH3) which shows improved dehydrogenation properties after being modified by metal hydrides (NaH, LiH and KH etc.).25–27 Additionally, hydrazine can be used as the reductants to regenerate spent fuels of AB and lithium amidoborane to their original state in liquid ammonia, achieving a complete hydrogen cycle.28,29 Considering the combination of protonic Hδ+ and hydridic Hδ− to form hydrogen, hydrazine with Hδ+ can coordinate with Hδ− containing compounds and modify their dehydrogenation properties. Recently, several borohydride hydrazinates were synthesized and the improved dehydrogenation kinetics with different dehydrogenation routes have been demonstrated.30,31 Similarly, hydrazinate of lithium amidoborane (LiNH2BH3·NH2NH2) has also been synthesized. Although it exhibited improved dehydrogenation properties as compared with pristine LiNH2BH3,32 the underlying dehydrogenation mechanism was not well understood. Since the interaction of cations and ligands can obviously affect the properties, much effort should be made to synthesize other amidoborane hydrazinates, which alter the hydrogen storage performances. In the present study, we have successfully prepared calcium amidoborane hydrazinates (Ca(NH2BH3)2·nN2H4), with Ca(NH2BH3)2·2N2H4 exhibiting a new compound crystallizing in an orthorhombic cell with the space group of P21212 and the lattice parameters of a = 6.6239(4) Å, b = 13.7932(6) Å, c = 4.7909(2) Å. Improved dehydrogenation properties were reported as compared with pristine Ca(NH2BH3)2. More importantly, an isotope-labelling method was employed to investigate its dehydrogenation mechanism.

2. Experimental section

2.1 Sample preparation

Ca powders (99%, Alfa Aesar), (NH4)2CO3 (99%, Acros), NaBH4 (98%, Aldrich), NaBD4 (98%, Aldrich) and D2O (99%, Aldrich) were used without further purification. NH3BH3 was homemade by the metathesis of (NH4)2CO3 and NaBH4 through ball-milling according to R1. NaBH4 and pre-ball milled (NH4)2CO3 were dissolved into tetrahydrofuran (THF) with a 2[thin space (1/6-em)]:[thin space (1/6-em)]1 molar ratio and ball-milled for 4 h at 40 °C. Then the filtrate was concentrated under vacuum to obtain AB.33 NH3BD3 was prepared by the same procedure but with NaBD4 instead of NaBH4. ND3BH3 was synthesized by repeating dissolution of AB in D2O and evaporation under vacuum at room temperature three times.34 Ca(NH2)2 was prepared by the reaction of Ca powder and liquid NH3 (R2). Ca(NH2BH3)2 was made by dissolving the mixture of NH3BH3 and Ca(NH2)2 in THF according to R3. The solvent was then removed via rotor evaporation under reduced pressure, yielding powdery Ca(NH2BH3)2. Similarly, Ca(NH2BD3)2 was synthesized via the same methods but with NH3BD3 instead of NH3BH3. Ca(ND2BH3)2 was synthesized by using the deuterium complexes like ND3BH3 and Ca(ND2)2 according to R4.
 
(NH4)2CO3 + 2NaBH4 → 2NH3BH3 + Na2CO3 + 2H2(R1)
 
Ca + 2NH3 → Ca(NH2)2 + H2(R2)
 
Ca(NH2)2 + 2NH3BH3 → Ca(NH2BH3)2 + 2NH3(R3)
 
Ca(ND2)2 + 2ND3BH3 → Ca(ND2BH3)2 + 2ND3(R4)
All experiments were performed under strictly anaerobic and anhydrous conditions in the MBRAUN glovebox filled with purified argon. To synthesize calcium amidoborane hydrazinate samples with ratios of 1/0.5, 1/1, 1/2, 1/3, around 300 mg Ca(NH2BH3)2 and calculated hydrazine were placed separately into a sealed bottle at room temperature. Due to the vapour pressure, hydrazine can automatically absorb into Ca(NH2BH3)2 overnight. The samples were then ball milled on a Retsch PM 400 planetary mill at 150 rpm under an inert atmosphere for 2 h.

2.2 Dehydrogenation and characterization

To examine the new structures and the mechanism of hydrogen evolution from the Ca(NH2BH3)2·nN2H4 system, the samples before and after dehydrogenation were characterized by Fourier transform infrared (FTIR), X-ray diffraction (XRD), solid-state 11B magic angle spinning nuclear magnetic resonance (MAS NMR). FTIR spectra were recorded using a Varian 3100 FTIR spectrometer at room temperature. XRD data were collected on a PANalytical X'pert diffractometer equipped with Cu Kα radiation (40 kV and 40 mA). NMR experiments were implemented at room temperature on a Bruke AVANCE 500 MHz NMR spectrometer (11.7 T). All of those solid samples were spun at 10 kHz with a 4 mm ZrO2 rotor in diameter, in which the powders were fully loaded. In a homemade temperature programmed desorption (TPD) system combined with a mass spectrometer (MS, Hiden HPR-20), a dynamic flow mode was applied, in which purified argon was used as a carrier gas and the heating rate was set to be 2 °C min−1. Volumetric release experiments were performed on a homemade Sieverts-type apparatus to quantify the hydrogen evolution. A 50–60 mg sample was heated to a given temperature at a ramping rate of 2 °C min−1.

2.3 First-principles calculation method

First-principles calculations were performed using the Vienna ab initio simulation package (VASP), which is based on DFT and the pseudopotential plane wave method.35,36 The projector aug-mented wave (PAW) potentials were used with a cut-off energy of 500 eV.37 The generalized gradient approximation (GGA) due to Perdew and Wang (GGA-PW91) was used to treat the electronic exchange–correlation energy.38 According to their lattice constants, different k-point meshes generated by the Monkhorst–Pack method were selected. In geometry optimizations, experimental atomic positions and cell parameters were used as starting models for the relaxations. Full ionic and volumetric relaxations were carried out until the self-consistency was achieved within a tolerance of the total energy of 0.01 meV and atomic forces of 0.01 eV Å−1.

3. Results and discussion

3.1 Syntheses and structures

The as-prepared calcium amidoborane hydrazinates were examined by XRD as shown in Fig. S1 (ESI†). As the amount of hydrazine absorbed on Ca(NH2BH3)2 increases, the phase of Ca(NH2BH3)2 disappears gradually, accompanied by the appearance of new phases. From FTIR in Fig. S2 (ESI†), Ca(NH2BH3)2–nN2H4 (n = 1/2, 1, 2) samples exhibit different spectra to that of Ca(NH2BH3)2. The B–H stretching bands ranging from 2150 to 2270 cm−1 in Ca(NH2BH3)2–nN2H4 show a red shift compared with that of Ca(NH2BH3)2, indicating the weakened B–H bonds. However, the N–H vibration bands of Ca(NH2BH3)2·nN2H4 split into several peaks due to the complicated coordination environments. From 11B MAS NMR results in Fig. S3 (ESI†), the chemical shift at −17.9 ppm that belongs to sp3 hybridized [–BH3] in Ca(NH2BH3)2 shifts to −24.3 ppm as hydrazine increases gradually, indicating the change of the B environment and the formation of new species. The high field shift to −24.3 ppm of Ca(NH2BH3)2·nN2H4 indicates that a higher electron density surrounds B compared with pristine Ca(NH2BH3)2,17 which may be attributed to the electron donation of N2H4 when it coordinates with Ca(NH2BH3)2 and results in elongated B–H bonds.

To explore and solve the crystal structures of calcium amidoborane hydrazinates, the XRD pattern and the Rietveld fits of newly synthesized Ca(NH2BH3)2·2N2H4 are shown in Fig. 1. The crystal structure is then partially solved by using direct space methods under this space group. Due to the uncertainty of H positions, first-principles molecular dynamics simulated annealing are then performed to confirm the Ca(NH2BH3)2 and NH2NH2 configuration with the lowest energy. Rietveld structural refinement on the optimal structural candidate is performed using the GSAS package on the XRD data. The Ca(NH2BH3)2 and NH2NH2 are kept as rigid bodies with common refined bond lengths and bond angles constrained as reasonable values due to the inadequate number of observations. One Ca(NH2BH3)2 and one NH2NH2 group together with lattice parameters are refined, yielding the agreement factors of Rwp = 5.95%, Rp = 4.45%.


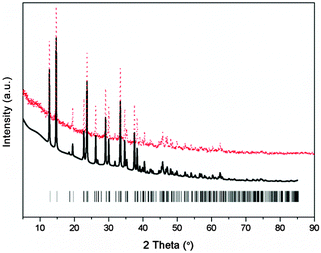image file: c5cp04257g-f1.tif
Fig. 1 Experimental (dots), fitted (line) XRD profiles of Ca(NH2BH3)2·2N2H4 at 298 K (Cu Kα radiation). Vertical bars indicate the calculated positions of Bragg peaks of Ca(NH2BH3)2·2N2H4.

The new sets of diffraction peaks emerging in Ca(NH2BH3)2·2N2H4 can be well indexed by an orthorhombic P21212 space group with a = 6.6239(4) Å, b = 13.7932(6) Å, c = 4.7909(2) Å. The crystal structure of Ca(NH2BH3)2·2N2H4 and the local coordination of Ca2+ cations are shown in Fig. 2. And the interatomic distances in Ca(NH2BH3)2·2N2H4 as compared with pristine Ca(NH2BH3)2 and pristine hydrazine can be found in Table 1. Each Ca2+ coordinates with two [NH2BH3]− groups and four NH2NH2 groups, leading to a distorted octahedral environment, which is preferred in the commonly observed Ca(VI) complex hydrides, e.g., Ca(NH2)2,39 CaNH,40 and Ca(BH4)2.41


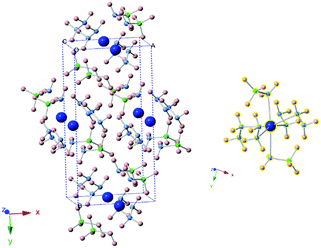image file: c5cp04257g-f2.tif
Fig. 2 (left) Crystal structure of Ca(NH2BH3)2·2N2H4. Calcium is represented by blue spheres, boron by green spheres, nitrogen by purple spheres, hydrogen by pink spheres. (right) Coordination environment of Ca2+. Each Ca2+ coordinates with four N2H4 groups and two [BH2NH3−] groups.
Table 1 Interatomic distances (Å) in Ca(NH2BH3)2·2N2H4 compared with pristine Ca(NH2BH3)2 and hydrazine at room temperature
(Å) Ca(NH2BH3)2·2N2H4 Ca(NH2BH3)2 NH2NH2
Ca–N bonds 2.486 (Ca–[NH2BH3]) 2.466 —
2.563–2.579 (Ca–[NH2NH2])
N–H bonds 1.022 ([NH2BH3]) 1.020 1.021
1.025–1.030 (NH2NH2)
B–N bonds 1.558 1.546 —
B–H bonds 1.242–1.246 1.230–1.250 —
N–N bonds 1.452 — 1.449

The distances between Ca2+ and N in the adjacent NH2NH2 are 2.563 and 2.579 Å, similar to the Ca–N distances in the coordinate bond, such as Ca(BH4)2·2N2H4 (2.540 Å).31 At the same time, Ca2+ directly bonds with two NH2BH3− ions giving the closest Ca–N distance of 2.486 Å, similar to Ca–N distances in ionic bonds, such as Ca(NH2BH3)2·2NH3 (2.521 Å)17 and Ca(NH2)2 (2.411–2.573 Å).39 Since the coordination of NH2NH2 to Ca(NH2BH3)2 is through the donation of a lone pair electron, Ca2+ will bear higher electron density than that in pristine Ca(NH2BH3)2, resulting in the elongated Ca–N distance (Ca–[NH2BH3]) in Ca(NH2BH3)2·2N2H4 as shown in Table 1. Similarly, due to the lower electron density of N, N–H (in NH2NH2 ligand) distances in Ca(NH2BH3)2·2N2H4 are longer than that of pristine hydrazine, indicating the activation of the N–H bond in hydrazinate. Furthermore, each N atom in one hydrazine molecule is coordinated by a Ca2+ from the opposite direction, which may lead to the elongated distance between N–N. Moreover, the B–H and N–H bond distances in the amidoborane anion, NH2BH3−, have lengthened, agreeing with FTIR and NMR results. From the crystal structure, it was found that Hδ+ (in NH2NH2 or NH2BH3) has a short distance with its neighbouring Hδ− in [–BH3], ranging from 2.00–2.37 Å (less than 2.4 Å), which indicates the establishment of a dihydrogen bonding network. Such an interaction of the oppositely charged Hδ+ (in NH2NH2 and NH2) and Hδ– (in BH3−) may consequently contribute to the elongated N–H and B–H bonds in Ca(NH2BH3)2·2N2H4. It is reported that the dihydrogen bonding network in ammonia borane is primarily responsible for the stability of the molecular crystal at room temperature.5 The dihydrogen bonding network and the ionic/electrostatic interactions between Ca and NH2BH3/N2H4 ligands in Ca(NH2BH3)2·2N2H4 are thus responsible for the structural stabilization and are likely to have positive impacts on their dehydrogenation. Although Ca(NH2BH3)2–3N2H4 also shows new diffraction peaks in XRD patterns, the structure was not resolved due to poor crystallinity.

3.2 Dehydrogenation of Ca(NH2BH3)2·nN2H4 (n = 1/2, 1, 2)

TPD-MS measurement is employed to investigate the dehydrogenation properties of Ca(NH2BH3)2·nN2H4 compared with the pristine Ca(NH2BH3)2. As shown in Fig. 3, pristine Ca(NH2BH3)2 releases hydrogen with a broad peak centered at around 150 °C identical to that reported in the literature.17 Obviously, the decomposition of Ca(NH2BH3)2·nN2H4 (n = 1/2, 1, 2) can be viewed as a two-step process: the first dehydrogenation process occurs in the temperature range of 100–125 °C and the second is between 160–185 °C. It is known that the number of ligands coordinating with the metal center contributes to the different decomposition behaviours. Similarly, the more the ligands coordinate with a metal center, the easier they would be detached.20 However, a different phenomenon is observed in the case of Ca(NH2BH3)2·nN2H4. The signal of ligand N2H4 is undetectable during TPD-MS experiments, indicating that the coordinated N2H4 prefers to react with Ca(NH2BH3)2 instead of self-detachment. For the Ca(NH2BH3)2·2N2H4 sample mentioned above (Fig. 3d), it starts to release hydrogen at around 98 °C with a peak centered at 118 °C, accompanied by the evolution of NH3 in the first step. The evolution of NH3 should be attributed to the excess of N from N2H4 in the system which results in the side reaction (i.e., deammonization) that occurs simultaneously with dehydrogenation. Therefore, in order to suppress the ammonia evolution, the content of hydrazine is reduced to 1[thin space (1/6-em)]:[thin space (1/6-em)]1 (Ca(NH2BH3)2[thin space (1/6-em)]:[thin space (1/6-em)]N2H4) (Fig. 3c). It can be found that the first dehydrogenation peak of Ca(NH2BH3)2–N2H4 centered at 113 °C is still accompanied by a trace mount of ammonia. Further decreasing the amount of N2H4 to 0.5 resulted in no NH3 release (Fig. 3b). This is likely due to the complete conversion of H+ in N2H4 to H2 when an equal amount of Hδ+ and Hδ− coexists in the sample. It was reported that the decomposition of hydrazine follows two competitive routes (R5 and R6) giving rise to H2 and N2 or N2 and NH3 under mild conditions even with the presence of noble or noble metal-like catalysts.23,24 However, no N2 can be observed during the dehydrogenation/decomposition of Ca(NH2BH3)2·nN2H4. Therefore, the evolution of NH3 during the decomposition of Ca(NH2BH3)2·nN2H4 (n = 1/2, 1, 2) is not from the self-decomposition of hydrazine, which means that hydrogen is derived from the interaction of Ca(NH2BH3)2 and hydrazine.
 
NH2NH2 → N2 + 2H2(R5)
 
3NH2NH2 → N2 + 4NH3(R6)
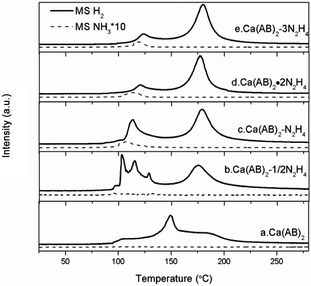image file: c5cp04257g-f3.tif
Fig. 3 TPD-MS results of Ca(NH2BH3)2–nN2H4 complexes. The solid lines represent the signal of H2 and the dotted lines represent the signal of NH3.

Quantitative measurements on hydrogen desorption from the samples were subsequently carried out using a Sievert-type apparatus. It is known that the thermal decomposition pathway of LiBH4·NH3 can be altered by “locking” NH3 in the vicinity of LiBH4 to increase the chance of dehydrogenation rather than deammonization.42 A similar approach was adopted to retain NH3 in this study. As shown in Fig. 4, the pristine Ca(NH2BH3)2 releases 2.6 equiv. H2 (5.2 wt%) at 150 °C, identical to the literature.17 Under the same condition, Ca(NH2BH3)2·2N2H4 can release more than 5.8 equiv. gas, which is composed of hydrogen and ammonia as detected by MS (Fig. S4, ESI†). Approximately 4.6 equiv. of H2 was evolved from both Ca(NH2BH3)2–1/2N2H4 and Ca(NH2BH3)2–N2H4 at 150 °C within 12 hours, equivalent to 7.9 wt% and 7.0 wt% of hydrogen, respectively. Interestingly, no NH3 was detected in the gaseous product (Fig. S4, ESI†). Obviously, under the same condition, more H2 can be released from Ca(NH2BH3)2–nN2H4 than that from Ca(NH2BH3)2, which indicates that the addition of N2H4 enhanced the dehydrogenation properties of Ca(NH2BH3)2. Overall, Ca(NH2BH3)2–1/2N2H4 with an equal amount of Hδ+ and Hδ− produced more hydrogen (7.9 wt%) than other samples, which is worth of further investigation.


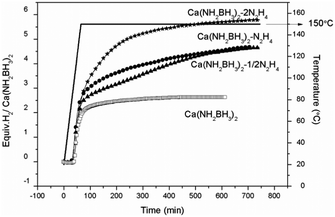image file: c5cp04257g-f4.tif
Fig. 4 Volumetric release measurements of (a) Ca(NH2BH3)2, (b) Ca(NH2BH3)2–1/2N2H4, (c) Ca(NH2BH3)2–N2H4, (d) Ca(NH2BH3)2·2N2H4 at 150 °C.

In order to gain insight into the reaction process, the dehydrogenated products of Ca(NH2BH3)2–1/2N2H4 at different dehydrogenation temperatures, i.e., 80 °C, 100 °C, 150 °C, 250 °C, were collected to be characterized by XRD, FTIR and NMR. Due to the amorphous nature of the intermediates, no structural information can be obtained by XRD. As shown in the FTIR characterization (Fig. S5, ESI†) the B–H and N–H vibrations in the range of 3150 cm−1 to 3400 cm−1 and at 2200 cm−1 are weakened and broadened, respectively, as dehydrogenation progresses. A new vibration centered at 1600 cm−1, which can be assigned to the [N[double bond, length as m-dash]B[double bond, length as m-dash]N] bond (Fig. S5, ESI†),43 gradually emerges upon increasing the temperatures. Agreeing with decreasing intensity of N–H and B–H vibrations, the relative intensity of sp3 hybridized BH3 resonance (−30 to −20 ppm) also decreases as dehydrogenation progressed. On the other hand, the resonances at ∼3 ppm and 20–30 ppm, which can be assigned to sp2-hybridized B species (i.e., N2BH and BN3), become more obvious. This result suggests that the B–N bond is formed concomitantly with the release of H2 (Fig. 5). Therefore, it is clear that B–N formation and the strong combination potential of the oppositely charged hydrogen atoms are the driving forces for the dehydrogenation process.


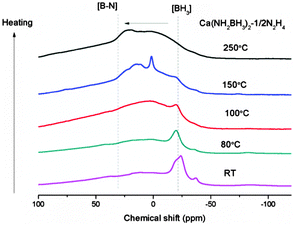image file: c5cp04257g-f5.tif
Fig. 5 11B MAS NMR spectra of Ca(NH2BH3)2–1/2N2H4 and Ca(NH2BH3)2–1/2N2H4 dehydrogenated at different temperatures.

3.3 The kinetics of dehydrogenation

As mentioned above, the addition of N2H4 to Ca(NH2BH3)2 enhanced the dehydrogenation kinetics as compared with pristine Ca(NH2BH3)2. Therefore, the Kissinger method [eqn (1)] was employed to determine the energy barrier in hydrogen desorption from Ca(NH2BH3)2 and Ca(NH2BH3)2·2N2H4.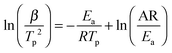
 
image file: c5cp04257g-t1.tif(1)
According to eqn (1), Tp is the peak temperature at which the reaction rate is maximum, β is the heating rate, Ea is the activation energy, A is the pre-exponential factor, and R is the gas constant. The maximum reaction-rate temperatures at different heating rates were collected by means of TPD measurements. The TPD profiles of hydrogen desorption from the Ca(NH2BH3)2·2N2H4 and Ca(NH2BH3)2 samples at different ramping rates are shown in Fig. S6 and S7 (ESI†). It is observed that the peak temperatures shift monotonically to higher values when the ramping rate is increased from 2 to 8 K min−1. The dependence of ln(Ea/Tp2) on 1/Tp is linear (Fig. 6). The slopes of the fitted lines are used to determine the values of Ea. The results of Ea in the first and second dehydrogenation step for Ca(NH2BH3)2·2N2H4 and Ca(NH2BH3)2 are shown in Table 2. The activation energies Ea for hydrogen desorption from Ca(NH2BH3)2·2N2H4 are around 98 ± 5 kJ mol−1 in the first step and 102 ± 4 kJ mol−1 in the second step, respectively. Both of them are lower than those of Ca(NH2BH3)2, ca. 110 ± 5 kJ mol−1 and 139 ± 6 kJ mol−1, suggesting the enhancement in dehydrogenation kinetics of Ca(NH2BH3)2 when coordinates with N2H4.
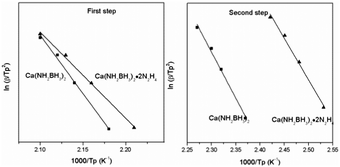image file: c5cp04257g-f6.tif
Fig. 6 Kissinger's plots, which give the activation energy of hydrogen release from the Ca(NH2BH3)2 and Ca(NH2BH3)2·2N2H4 samples.
Table 2 Values of Ea (the first and second step) determined by Kissinger plots
Sample E a (kJ mol−1) 1st step E a (kJ mol−1) 2nd step
Ca(NH2BH3)2 110 ± 5 139 ± 6
Ca(NH2BH3)2·2N2H4 98 ± 5 102 ± 4

3.4 The dehydrogenation mechanism

As mentioned in the Section 3.2, the decomposition of hydrazine follows two competitive ways (R5 and R6). In this study, however, no nitrogen was released during the decomposition of Ca(NH2BH3)2·nN2H4, indicating that hydrogen release is not from the self-decomposition of hydrazine. Furthermore, the onset dehydrogenation temperature of Ca(NH2BH3)2·nN2H4 is lower than that of pristine Ca(NH2BH3)2, which confirms that the hydrogen is released via the interaction of Ca(NH2BH3)2 and N2H4. Considering that the dissociation energy of the N–N bond is lower than that of the N–H bond in hydrazine, the “homogeneous dissociation” of N–N bond forming [˙NH2] radicals may occur.44 The produced [˙NH2] then reacts with Ca(NH2BH3)2 to release H2. In our previous work on LiNH2BH3–nN2H4, two possible dehydrogenation reaction mechanisms were proposed, i.e. the LiN2H3BH3 intermediate pathway and the combination of the protonic hydrogen and hydridic hydrogen (Hδ+ and Hδ−) pathway.32 More specifically, a [˙NH2] from “homogeneous dissociation” of N2H4 may attack the [–NH2] group or the [–BH3] group in Ca(NH2BH3)2 alternatively to evolve H2. However, it is still unable to figure out which group is attacked at the first step. Herein, to confirm the dehydrogenation mechanism, deuterium labeling experiments were conducted. Since three kinds of hydrogen atoms exist in Ca(NH2BH3)2–1/2N2H4, i.e., Hδ+ in [–NH2BH3], Hδ+ in N2H4, and Hδ− in [–NH2BH3], two deuterium substituted complexes Ca(NH2BD3)2·1/2N2H4 and Ca(ND2BH3)2·1/2N2H4 were synthesized and characterized by FTIR and XRD (Fig. S8 and S9, ESI†).

From the TPD-MS of Ca(ND2BH3)2·1/2N2H4 shown in Fig. 7a, although the desorbed gas is a mixture of H2, HD and D2, H2 is the main gaseous product in the first stage. As mentioned above, the formation of H2 should not derive from the self-decomposition of hydrazine, therefore, the combination mechanism of Hδ+ and Hδ− in the amidoborane hydrazinate should have taken place. Due to the fact that Hδ+ on Ca(ND2BH3)2·1/2N2H4 should only come from the N2H4 ligand, the strong H2 signal as compared with HD and D2 (Fig. 7a and inset) suggests that the first step of dehydrogenation should be a result of the combination of Hδ+ on N2H4 and Hδ− on BH3 of Ca(ND2BH3)2. Moreover, the appearance of HD and D2 may be arising from the exchange of H–D at elevated temperature.20 Additionally, the onset temperature of H2 evolution from Ca(ND2BH3)2–1/2N2H4 occurs at 74 °C, which is prior to those of HD and D2 (Fig. 7a inset), further confirming the Hδ+ (NH2NH2) and Hδ− (BH3) combination mechanism.


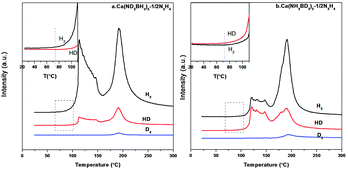image file: c5cp04257g-f7.tif
Fig. 7 TPD-MS curves of Ca(ND2BH3)2–1/2N2H4 and Ca(NH2BD3)2–1/2N2H4. The insets are the enlarged curves of temperature range 20–120 °C.

In addition, the onset temperature of HD evolution from Ca(NH2BD3)2·1/2N2H4 advances 15 °C compared to that of H2, which matches well with the phenomenon of Ca(ND2BH3)2·1/2N2H4 and provides another proof for the protonic hydrogen–hydridic hydrogen (Hδ+ and Hδ−) combination mechanism (Fig. 7b). As reported in the literature, the “metal assisted hydride transfer” path via transferring a hydridic hydrogen atom from [–BH3] to get close to [–NH2] happened in the first-step dehydrogenation of LiNH2BH3 on the basis of gas-phase simulations.45,46 A bridged H could form through the hydride transfer in the form of Li⋯H⋯B,45,47,48 which may be an active H in the transition state. This bridged H may also exist in the other metal amidoboranes and their derivatives during heat treatment, for example, LiNH2BH3·NH3BH3 and Ca(NH2BH3)2·2NH3. Therefore, during the thermal decomposition of these compounds, the combination of a Hδ−(B) atom from the metal amidoborane part and a Hδ+(N) atom from the adjacent molecule (NH3BH3 or NH3) could be observed.18,49 This may also happen in Ca(NH2BH3)2·nN2H4 materials, which is confirmed by our isotopic labelling experiment. Therefore, we propose that the process of dehydrogenation goes through the following steps: 1. the “homogeneous dissociation” of N2H4 to form the [˙NH2] species; 2. [˙NH2] attacks [–BH3] in Ca(NH2BH3)2 with release of H2 by the way of protonic hydrogen–hydridic hydrogen (Hδ+ and Hδ−) combination, excluding the metal hydrazine borane intermediate pathway.27,50 During the dehydrogenation, the H–D exchange will inevitably happen leading to complicated gaseous products. Therefore, we tentatively believe that the protonic hydrogen-hydridic hydrogen (Hδ+ and Hδ−) interaction is the main driving force in the whole dehydrogenation process.

The regeneration of the dehydrogenated products is also a vital important aspect for hydrogen storage materials. However, the dehydrogenation of NH3BH3 and its derivatives are usually exothermic, indicating the irreversibility of those compounds. Recently, it was reported that NH3BH3 or lithium amidoborane can be regenerated by using hydrazine in NH3 solution.28,29,51 Our recent results on the regeneration of lithium amidoborane hydrazinate by employing the same method also realized the partial regeneration of BH3 species, indicating the feasibility of this method for hydrazinate.32 Therefore, it is of great interest to apply the hydrazine reduction method to regenerate calcium amidoborane hydrazinates in the following investigation.

4. Conclusions

The calcium amidoborane hydrazinates with superior dehydrogenation properties were successfully synthesized, among which Ca(NH2BH3)2·2N2H4 crystallizes into the orthorhombic symmetry P212121 space group with the lattice parameters of a = 6.6239(4) Å, b = 13.7932(6) Å, c = 4.7909(2) Å. The isotopic labelling experiment revealed that the protonic hydrogen from NH2NH2 would attack hydridic hydrogen from [–BH3] to form H2 through the combination of Hδ+ and Hδ− at the initial stage of the dehydrogenation of Ca(NH2BH3)2·nN2H4. However, more work is still needed in the future to develop more materials with superior dehydrogenation properties and explore the dehydrogenation mechanism.

Acknowledgements

The authors would like to acknowledge financial support from the project of National Natural Science Funds for Distinguished Young Scholar (51225206), projects of National Natural Science Foundation of China (Grant No. U1232120, 51301161, 21473181 and 51472237) and project from Youth Innovation Promotion Association CAS, and Shanghai Synchrotron Radiation Facility (SSRF BL14B1) for providing the beam time.

References

  1. N. Armaroli and V. Balzani, Energy for a Sustainable World, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2011, pp. I–XXI Search PubMed.
  2. N. Armaroli and V. Balzani, Angew. Chem., Int. Ed., 2007, 46, 52–66 CrossRef CAS PubMed.
  3. N. Cao, J. Su, X. Hong, W. Luo and G. Cheng, Chem. – Asian J., 2014, 9, 562–571 CrossRef CAS PubMed.
  4. F. H. Stephens, V. Pons and R. T. Baker, Dalton Trans., 2007, 2613–2626 RSC.
  5. A. Staubitz, A. P. M. Robertson and I. Manners, Chem. Rev., 2010, 110, 4079–4124 CrossRef CAS PubMed.
  6. T. B. Marder, Angew. Chem., Int. Ed., 2007, 46, 8116–8118 CrossRef CAS PubMed.
  7. A. Gutowska, L. Y. Li, Y. S. Shin, C. M. M. Wang, X. H. S. Li, J. C. Linehan, R. S. Smith, B. D. Kay, B. Schmid, W. Shaw, M. Gutowski and T. Autrey, Angew. Chem., Int. Ed., 2005, 44, 3578–3582 CrossRef CAS PubMed.
  8. F. Baitalow, J. Baumann, G. Wolf, K. Jaenicke-Rossler and G. Leitner, Thermochim. Acta, 2002, 391, 159–168 CrossRef CAS.
  9. Z. Xiong, C. K. Yong, G. Wu, P. Chen, W. Shaw, A. Karkamkar, T. Autrey, M. O. Jones, S. R. Johnson, P. P. Edwards and W. I. F. David, Nat. Mater., 2008, 7, 138–141 CrossRef CAS PubMed.
  10. H. V. K. Diyabalanage, T. Nakagawa, R. P. Shrestha, T. A. Semelsberger, B. L. Davis, B. L. Scott, A. K. Burrell, W. I. F. David, K. R. Ryan, M. O. Jones and P. P. Edwards, J. Am. Chem. Soc., 2010, 132, 11836–11837 CrossRef CAS PubMed.
  11. H. Wu, W. Zhou and T. Yildirim, J. Am. Chem. Soc., 2008, 130, 14834–14839 CrossRef CAS PubMed.
  12. A. E. Carre-Burritt, B. L. Davis, B. D. Rekken, N. Mack and T. A. Semelsberger, Energy Environ. Sci., 2014, 7, 1653–1656 CAS.
  13. S.-K. Kim, S.-A. Hong, H.-J. Son, W.-S. Han, C. W. Yoon, S. W. Nam and S. O. Kang, J. Mater. Chem. A, 2014, 2, 20243–20251 CAS.
  14. H. Li, Q. Yang, X. Chen and S. G. Shore, J. Organomet. Chem., 2014, 751, 60–66 CrossRef CAS.
  15. K. R. Graham, T. Kemmitt and M. E. Bowden, Energy Environ. Sci., 2009, 2, 706–710 CAS.
  16. Z. Xiong, Y. Chua, G. Wu, L. Wang, M. W. Wong, Z. M. Kam, T. Autrey, T. Kemmitt and P. Chen, Dalton Trans., 2010, 39, 720–722 RSC.
  17. Y. S. Chua, G. Wu, Z. Xiong, T. He and P. Chen, Chem. Mater., 2009, 21, 4899–4904 CrossRef CAS.
  18. Y. S. Chua, W. Li, W. J. Shaw, G. Wu, T. Autrey, Z. Xiong, M. W. Wong and P. Chen, ChemSusChem, 2012, 5, 927–931 CrossRef CAS PubMed.
  19. G. Xia, X. Yu, Y. Guo, Z. Wu, C. Yang, H. Liu and S. Dou, Chem. – Eur. J., 2010, 16, 3763–3769 CrossRef CAS PubMed.
  20. T. He, H. Wu, J. Chen, W. Zhou, G. Wu, Z. Xiong, T. Zhang and P. Chen, Phys. Chem. Chem. Phys., 2013, 15, 10487–10493 RSC.
  21. Y. S. Chua, H. Wu, W. Zhou, T. J. Udovic, G. Wu, Z. Xiong, M. W. Wong and P. Chen, Inorg. Chem., 2012, 51, 1599–1603 CrossRef CAS PubMed.
  22. Y. S. Chua, G. Wu, Z. Xiong, A. Karkamkar, J. Guo, M. Jian, M. W. Wong, T. Autrey and P. Chen, Chem. Commun., 2010, 46, 5752–5754 RSC.
  23. L. He, Y. Huang, A. Wang, X. Wang, X. Chen, J. J. Delgado and T. Zhang, Angew. Chem., Int. Ed., 2012, 51, 6191–6194 CrossRef CAS PubMed.
  24. S. K. Singh and Q. Xu, J. Am. Chem. Soc., 2009, 131, 18032–18033 CrossRef CAS PubMed.
  25. Y. S. Chua, Q. Pei, X. Ju, W. Zhou, T. J. Udovic, G. Wu, Z. Xiong, P. Chen and H. Wu, J. Phys. Chem. C, 2014, 118, 11244–11251 CAS.
  26. R. Moury, U. B. Demirci, T. Ichikawa, Y. Filinchuk, R. Chiriac, A. van der Lee and P. Miele, ChemSusChem, 2013, 6, 667–673 CrossRef CAS PubMed.
  27. H. Wu, W. Zhou, F. E. Pinkerton, T. J. Udovic, T. Yildirim and J. J. Rush, Energy Environ. Sci., 2012, 5, 7531–7535 CAS.
  28. A. D. Sutton, A. K. Burrell, D. A. Dixon, E. B. Garner, III, J. C. Gordon, T. Nakagawa, K. C. Ott, P. Robinson and M. Vasiliu, Science, 2011, 331, 1426–1429 CrossRef CAS PubMed.
  29. Z. Tang, Y. Tan, X. Chen and X. Yu, Chem. Commun., 2012, 48, 9296–9298 RSC.
  30. T. He, H. Wu, G. Wu, J. Wang, W. Zhou, Z. Xiong, J. Chen, T. Zhang and P. Chen, Energy Environ. Sci., 2012, 5, 5686–5689 CAS.
  31. L. Zhang, S. Li, Y. Tan, Z. Tang, Z. Guo and X. Yu, J. Mater. Chem. A, 2014, 2, 10682–10687 CAS.
  32. T. He, H. Wu, G. Wu, Z. Li, W. Zhou, X. Ju, D. Xie and P. Chen, J. Mater. Chem. A, 2015, 3, 10100–10106 CAS.
  33. P. V. Ramachandran and P. D. Gagare, Inorg. Chem., 2007, 46, 7810–7817 CrossRef CAS PubMed.
  34. R. Cantelli, A. Paolone, O. Palumbo, F. Leardini, T. Autrey, A. Karkamkar and A. T. Luedtke, J. Alloys Compd., 2013, 580, S63–S66 CrossRef CAS.
  35. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
  36. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
  37. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
  38. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249 CrossRef.
  39. J. Senker, H. Jacobs, M. Müller, W. Press, P. Müller, H. M. Mayer and R. M. Ibberson, J. Phys. Chem. B, 1998, 102, 931–940 CrossRef CAS.
  40. T. Sichla and H. Jacobs, Z. Anorg. Allg. Chem., 1996, 622, 2079–2082 CrossRef CAS.
  41. K. Miwa, M. Aoki, T. Noritake, N. Ohba, Y. Nakamori, S. i. Towata, A. Züttel and S. i. Orimo, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 155122 CrossRef.
  42. X. Zheng, G. Wu, W. Li, Z. Xiong, T. He, J. Guo, H. Chen and P. Chen, Energy Environ. Sci., 2011, 4, 3593–3600 CAS.
  43. S. A. Kulinich, A. N. Zhukov, L. G. Sevast'yanova and K. P. Burdina, Diamond Relat. Mater., 1999, 8, 2152–2158 CrossRef CAS.
  44. J. P. Contour and G. Pannetier, J. Catal., 1972, 24, 434–445 CrossRef CAS.
  45. D. Y. Kim, N. Singh, H. M. Lee and K. S. Kim, Chem. – Eur. J., 2009, 15, 5598–5604 CrossRef CAS PubMed.
  46. W. R. Nutt and M. L. McKee, Inorg. Chem., 2007, 46, 7633–7645 CrossRef CAS PubMed.
  47. T. B. Lee and M. L. McKee, Inorg. Chem., 2009, 48, 7564–7575 CrossRef CAS PubMed.
  48. D. Y. Kim, H. M. Lee, J. Seo, S. K. Shin and K. S. Kim, Phys. Chem. Chem. Phys., 2010, 12, 5446–5453 RSC.
  49. C. Wu, G. Wu, Z. Xiong, X. Han, H. Chu, T. He and P. Chen, Chem. Mater., 2010, 22, 3–5 CrossRef CAS.
  50. R. Moury, U. B. Demirci, V. Ban, Y. Filinchuk, T. Ichikawa, L. Zeng, K. Goshome and P. Miele, Chem. Mater., 2014, 26, 3249–3255 CrossRef CAS.
  51. Z. Tang, H. Chen, X. Chen, L. Wu and X. Yu, J. Am. Chem. Soc., 2012, 134, 5464–5467 CrossRef CAS PubMed.

Footnote

† Electronic supplementary information (ESI) available: XRD, IR and 11B solid state MAS NMR of the prepared samples, MS analyses of the gaseous products and TPD files. CCDC 1412512. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5cp04257g
This journal is © the Owner Societies 2016
Click here to see how this site uses Cookies. View our privacy policy here.