Geometrical and energetical structural changes in organic dyes for dye-sensitized solar cells probed using photoelectron spectroscopy and DFT†
Susanna K.
Eriksson
a,
Ida
Josefsson
b,
Hanna
Ellis
a,
Anna
Amat
c,
Mariachiara
Pastore
c,
Johan
Oscarsson
d,
Rebecka
Lindblad
d,
Anna I. K.
Eriksson
a,
Erik M. J.
Johansson
a,
Gerrit
Boschloo
a,
Anders
Hagfeldt
e,
Simona
Fantacci
c,
Michael
Odelius
*b and
Håkan
Rensmo
*d
aDepartment of Chemistry-Ångström, Uppsala University, Box 523, SE-751 20 Uppsala, Sweden
bDepartment of Physics, Stockholm University, AlbaNova University Center, SE-106 91 Stockholm, Sweden. E-mail: odelius@fysik.su.se
cIstituto CNR di Scienze e Tecnologie Molecolari (CNR-ISTM), Computational Laboratory for Hybrid/Organic Photovoltaics (CLHYO), via Elce di Sotto 8, I-06123 Perugia, Italy
dDepartment of Physics and Astronomy, Uppsala University, Box 516, SE-751 20 Uppsala, Sweden. E-mail: hakan.rensmo@physics.uu.se; Fax: +46 18 471 5999; Tel: +46 18 471 3547
eLaboratory of Photomolecular Science, Institute of Chemical Sciences and Engineering, School of Basic Sciences, Ecole Polytechnique Fédérale de Lausanne (EPFL), CH-1015 Lausanne, Switzerland
First published on 5th November 2015
Abstract
The effects of alkoxy chain length in triarylamine based donor–acceptor organic dyes are investigated with respect to the electronic and molecular surface structures on the performance of solar cells and the electron lifetime. The dyes were investigated when adsorbed on TiO2 in a configuration that can be used for dye-sensitized solar cells (DSCs). Specifically, the two dyes D35 and D45 were compared using photoelectron spectroscopy (PES) and density functional theory (DFT) calculations. The differences in solar cell characteristics when longer alkoxy chains are introduced in the dye donor unit are attributed to geometrical changes in dye packing while only minor differences were observed in the electronic structure. A higher dye load was observed for D45 on TiO2. However, D35 based solar cells result in higher photocurrent although the dye load is lower. This is explained by different geometrical structures of the dyes on the surface.
1 Introduction
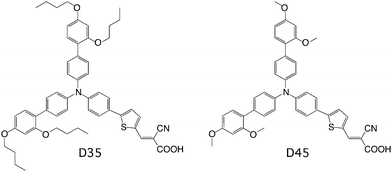
Dye-sensitized solar cells (DSCs) showed a breakthrough with the report in the early 1990s by Grätzel and O'Regan1 and are currently a research area with great potential.2 Their advantage is the possibility of harvesting sunlight for energy production at low cost. Since the earliest publications, a lot of effort has been made to fully understand the complicated nature of these nanostructured solar cells. The basic principle is to use a dye molecule that absorbs sunlight. The dye is attached to a semiconductor (usually TiO2) and a liquid electrolyte, or a solid hole transporter is used to regenerate the dye after electron injection into the semiconductor.During recent years a new family of organic dyes containing the triarylamine unit has been developed and functionalized for different purposes.3–7 When D35 (see Fig. 1) was introduced as a new sensitizer for DSCs together with the new redox couple based on cobalt complexes, steric hindrance for recombination was of great importance.8 In a previous paper,9 we also report on how the linker unit in the dye molecule will affect the performance of solar cells and also the adsorption configurations and coverage. Another recent paper states that steric hindrance will lead to a blocking effect and therefore a longer electron lifetime.10
In the present paper we investigate how the length of the alkoxy groups on the triarylamine unit affects the electron lifetime by comparing two dyes where one contains longer alkane chains (see molecular structures in Fig. 1). While D35 has o,p-dibutoxyphenyl units attached to the triarylamine unit, D4511 has o,p-dimetoxyphenyl units. Both D35 and D45 are organic dyes with a donor–linker–acceptor structure. The donor part consists of the triarylamine unit, including alkoxy chains, where the nitrogen possesses most of the positive charge upon oxidation.12,13 The linker unit in both cases is thiophene, which is conjugated in order to facilitate the electron transfer from the donor to the acceptor. The acceptor is cyanoacrylic acid, which binds to TiO2, and from which the electron is injected into the semiconductor.
These two dyes are investigated by photoelectron spectroscopy (PES) and density functional theory (DFT) both concerning adsorption configurations on the surface and calculations in the gas phase to probe the energy levels. The findings of PES and DFT are also complemented by solar cell data.
2 Methods
2.1 Solar cell preparation and characterization
The solar cells were prepared using a standard method reported before.9 In short the method is as follows. Fluorine doped tin oxide glass substrates (Pilkington, TEC 15) were treated with 40 mM aqueous TiCl4 solution. The TiO2 films were screen printed using one absorption layer (Dyesol DSL 30 NR-D) and one scattering layer (Dyesol WER2-O) to a total thickness of about 7.5 μm. After screen printing the samples were stepwize heat treated up to 500 °C (60 min). After sintering the samples were treated in aqueous TiCl4 solution again and rinsed. The final heating step (500 °C for 60 min) was performed after TiCl4 treatment. The dye baths had a concentration of 0.2 mM D35 or D45 in ethanol. The organic D35 and D45 dyes were synthesized by following the published procedures.4,11 The electrodes were sensitized for 16 hours before the assembly of solar cells. For the counter electrode, TEC8 was used and a platinum catalyst was deposited. The electrolyte contained 0.22 M Co[(bpy)3](PF6)2, 0.05 M Co[(bpy)3](PF)3, 0.2 M 4-tert-butylpyridine (TBP) and 0.1 M LiClO4 in acetonitrile.Current–voltage (IV) measurements were carried out using a Keithley 2400 source and a Newport solar simulator (model 91160). Light intensity was calibrated, using a certified reference solar cell (Fraunhofer ISE), to an intensity of 1000 W m−2 (1 Sun). For the IV-measurements a black mask of 0.4 × 0.4 cm2 was used in order to avoid significant additional contribution from light falling on the device outside the active area (0.5 × 0.5 cm2). Electron lifetime measurements were carried out using a white LED (Luxeon Star 1 W) as a light source. Voltage and current were monitored using a 16-bit resolution digital acquisition board (National Instruments) in combination with a current amplifier (Stanford Research Systems SR570) and a custom made system using electromagnetic switches. The electron lifetimes were determined by monitoring the transient photovoltage at different light intensities when applying a small (10 mV) square wave modulation to the bias of the LED. The resulting photovoltaic transients were fitted using first order kinetics to obtain time constants. IV measurements and electron lifetime measurements were performed on the same day as the assembly of the solar cells.
Incident photon to current conversion efficiency (IPCE) spectra were recorded using a computer controlled setup consisting of a xenon light source (Spectral Products ASB-XE-175), a monochromator (Spectral Products CM110) and a potentiostat (EG&G PAR 273). Calibration was performed using a certified reference solar cell (Fraunhofer ISE). The IPCE measurements were carried out 48 hours after the assembly of solar cells.
2.2 Photoelectron spectroscopy
The samples for photoelectron spectroscopy (PES) measurements were prepared by using similar working electrodes as for the preparation of solar cells, with the difference that the paste used was DSL 18 NR-T (purchased from Dyesol) and the scattering layer and TiCl4 post treatment were excluded. The electrodes were sensitized for 15–16 h and transferred to the vacuum system immediately after sensitization. The PES measurements were performed using synchrotron radiation at BL I411 at the Swedish national laboratory MAX IV in Lund.14 The electron take off angle was 60° and the electron take off direction was collinear with the e-vector of the incident photon beam, i.e. the analyzer was placed orthogonal to the incoming photons. The kinetic energies of the photoelectrons were measured using a Scienta R4000WAL analyzer. The PES spectra were binding energy calibrated by setting the Ti2p3/2 substrate signal to 458.56 eV.15 The techniques are described elsewhere in more detail.15,16 When using PES the inelastic mean free path (IMFP) of the emitted electrons depends on their kinetic energy. Therefore measurements with lower photon energy will be more surface sensitive compared to measurements with higher photon energy.The experimental X-ray absorption spectra (XAS) were also measured at beamline I411. N1s XAS spectra were recorded by the detection of secondary electrons in the partial yield mode and the intensity was normalized versus the number of incident photons. The photon energy calibration was performed by detecting Ti3p from the substrate using first and second order light.
2.3 Theoretical modeling
In the XAS simulations, the half-core hole transition potential approximation37 within DFT was employed, and for an accurate description of the core-excited nitrogen atom we used the IGLO-III basis set.38 Localization of core−hole was ensured by treating the remaining nitrogen atom with an effective core potential in combination with the O-NITROGEN(+5) (211/21) basis set.39,40 The XAS spectrum was generated in a double base set procedure,41 and for comparison to experiment broadened with a Gaussian function of 0.6 eV full-width at half-maximum. The TZVP basis set was used for all other atoms,42 and the DFT functional was approximated by the same correlation functional,34,35 as for the density of states.
For the PDOS and XAS calculations, the auxilary basis sets were generated using the GENA3 option in the StoBe-deMon code,33 except for the nitrogen ECP on which a (5,2;5,2) basis set was employed.
3 Results and discussion
3.1 Solar cell characteristics
In Fig. 2 the IV characteristics of D35 and D45 based solar cells are shown. The values from the IV measurements are summarized in Table 1 and it can be seen that D35 provides higher VOC and JSC compared to D45. Three solar cells of each dye were assembled and master solar cell results are presented.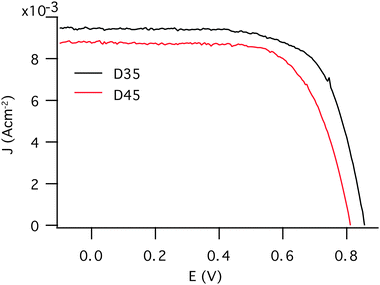 | ||
| Fig. 2 Current–voltage (IV) curves for D35 and D45-sensitized solar cells with a cobalt-based electrolyte under 100 mW cm−2 AM1.5G illumination. | ||
| Dye | V OC (V) | J SC (mA cm−2) | FF | η (%) |
|---|---|---|---|---|
| D35 | 0.86 | 9.43 | 0.69 | 5.6 |
| D45 | 0.81 | 8.8 | 0.68 | 4.8 |
The incident photon to current conversion efficiency (IPCE) curves for the solar cells based on two different dyes are very similar to those shown in Fig. 3. When measuring IPCE, lower light intensities are used compared to the IV-measurements, where 1 sun is used. The lower light intensity used when measuring IPCE causes a difference when comparing the JSC and the integrated current of the IPCE. The integrated currents obtained from the IPCE measurements are slightly lower than the JSC for both dyes, 7.9 mA cm−2 and 7.4 mA cm−2 for D35 and D45, respectively. However, the trend is the same with the integrated currents as with the JSC values; D35 based solar cells show somewhat higher current values.
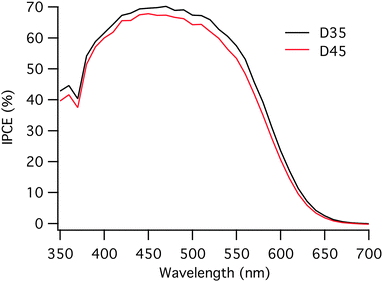 | ||
| Fig. 3 Incident photon to current conversion efficiency (IPCE) for D35 and D45-sensitized solar cells. | ||
The VOC differs for the solar cells assembled with D35 and D45 dye molecules, and D35 based solar cells obtain a higher VOC by 50 mV compared to the D45 equivalents. Moreover, D35 has earlier been shown to work well in cobalt redox mediator systems, partly explained by preventing close contact between the oxidized species in the electrolyte and the TiO2 surface.8 The VOC of a dye-sensitized solar cell generally arises from the difference between the quasi-Fermi level of electrons in TiO2 and the redox potential of the redox mediator. Since the solar cells investigated here are assembled with the same electrolyte, the quasi-Fermi level of TiO2 determines VOC. The quasi-Fermi level is ultimately limited by the position of the conduction band edge of TiO2, which can be assumed to be the same for these two dyes.9,43 The VOC difference for the two dyes may therefore be largely dependent on the electron lifetime, the time the electron stays in the TiO2 before recombining to the oxidized species in the electrolyte or to the oxidized dye. The electron lifetime was measured and the curves are displayed in Fig. 4.
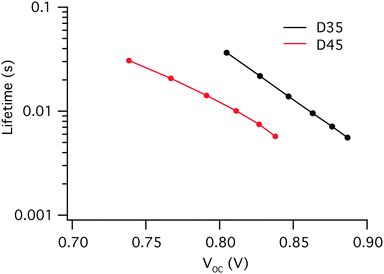 | ||
| Fig. 4 Electron lifetimes in D35 and D45 dye-sensitized solar cell systems where D35 based solar cells clearly render longer electron lifetimes. | ||
By electron lifetime measurements, there is a clear difference seen in the two different dyes. D35 renders much longer electron lifetimes compared to D45. In a recent study it was shown that the recombination rate for D35 was longer also when the surface coverage was taken into account.44 As partly highlighted above, there are two plausible explanations for the differences in the performance of solar cells, geometrical or energetical. PES measurements and DFT calculations were conducted to obtain a detailed understanding of the differences at an atomic level. The results are reported in the following sections.
3.2 Geometrical configurations
To shed some light on the difference in the performance of solar cells and especially the significant difference in electron lifetimes, the geometrical configurations were investigated both experimentally using PES and theoretically by DFT calculations. To investigate the adsorption geometries of the D35 and D45 sensitizers and the chemical bonding to the TiO2 substrate, DFT calculations of an adsorption model, in which the adsorbate and the substrate are explicitly included in DFT calculations and the solvent (ethanol) is implicitly represented, were performed. The calculations also facilitate an interpretation of the spectral data from the PES experiments.According to our calculations in ethanol solution, the most stable adsorption geometry is the one obtained with the dye standing up, by ca. 17 kcal mol−1 (0.7 eV), for both D35 and D45. A stabilization of the “flat” adsorption mode was found in vacuo, likely due to the unscreened interaction with the TiO2 surface. As a matter of fact, in vacuo the “up” geometry is only ca. 3(2) kcal mol−1 more stable than the “flat” one for D35 (D45). In Fig. 5 the “up” and “flat” configurations are reported for D35 and D45 along with the main geometrical parameters related to the interaction between the dye and the TiO2 surface. Noticeably, the longer alkoxy chains do not affect the adsorption geometry, at least in a static picture. In fact, the geometrical parameters are similar for D35 and D45.
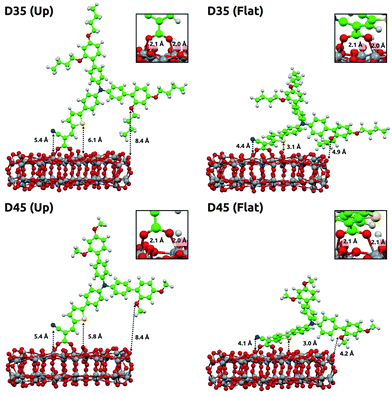 | ||
| Fig. 5 Binding configurations for D35 and D45 with one “up” (standing) and one “flat” (smaller binding angle) mode. | ||
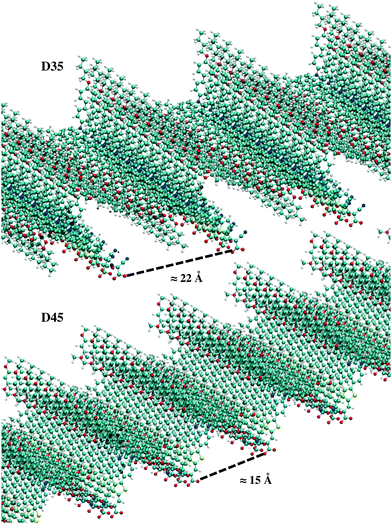
The maximum surface packing of the adsorbed dyes in their most stable “up” configuration (avoiding explicit superposition among the dye atoms) was simulated and is illustrated in Fig. 6. A larger packing density was found for D45 compared to D35, with D45 providing a 47% higher maximum coverage, which can be seen as an upper limit under ideal conditions.
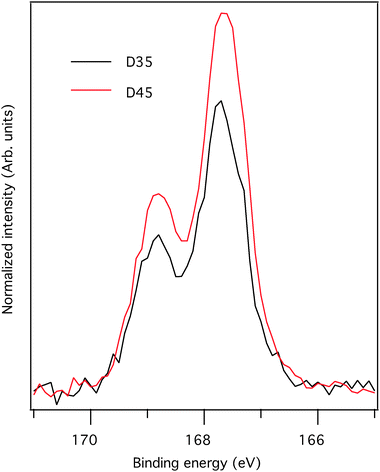
Using PES, the dye coverage can be estimated by a comparison of the intensity of the S2p core-level signals normalized versus the corresponding Ti2p (substrate) signals. As seen in the S2p spectra presented in Fig. 7, the coverage of D45 on the surface is significantly higher in relation to D35. The relative intensities for S2p versus Ti2p are 1 (D35) and 1.3 (D45). A conclusion from the analysis of the S2p core-level spectra is that there are approximately 30% more dye molecules at the surface with D45 as compared to D35. This value is in line with the larger coverage obtained from DFT calculations for D45. The difference in coverage is directly linked to the larger size of D35 due to longer alkoxy chains. However, the larger dye coverage of D45 compared to D35 in combination with lower JSC and lower IPCE could indicate aggregation of D45.45 In order to investigate aggregation, the absorbance spectra of D35 and D45 sensitized TiO2 films were recorded.46 A shift in the absorbance spectrum of D45 compared to D35 would imply aggregation. However, no significant shift was observed (see Fig. S1, ESI†); therefore aggregation should not be the reason for the difference in dye coverage and solar cell characteristics of D35 and D45.
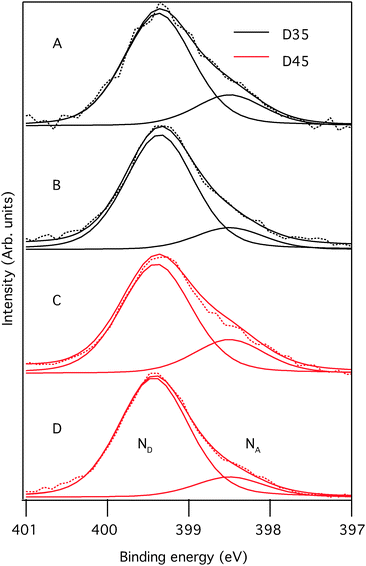
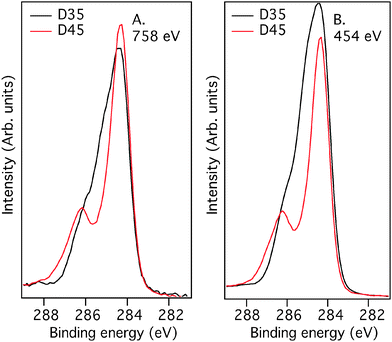
To gain experimental insight into adsorption at the TiO2 surface and orientation of the adsorbed dye molecules, the N1s core-level photoelectron spectra were recorded using different photon energies of ionizing light. D35 and D45 contain two chemically different nitrogen atoms, in a cyano (acceptor) group, from now on denoted as NA, and in a triarylamine group (donor), from now on denoted as ND. Since covalent bonding around these nitrogen atoms is only weakly affected by the elongation of the alkoxy groups, differences in N1s core-level spectra can be assigned predominantly to differences in the adsorption geometry. The core-level peaks originating from these two different nitrogen atoms have different binding energies and can be separated by peak fitting, see Fig. 8. By comparing the intensities for different nitrogen (N1s) contributions a signal ratio can be estimated, i.e. how much of the total signal originates from each nitrogen. Since PES is highly surface sensitive and the intensity is proportional to the inelastic mean free path (IMFP) of the photoelectrons, the average distance (perpendicular to the outermost surface) between the nitrogen atoms in the molecule on the TiO2 surface can be estimated.
A smaller difference in distance to the open surface reflects a smaller binding angle and vice versa. The higher the energy of the photons, the higher the kinetic energy of the electrons and consequently the longer the inelastic mean free path (IMFP). As seen in the spectra, NA-contribution is decreasing with decreasing photon energy which is a consequence of the cyano groups being closer to the TiO2 surface compared to the triarylamine groups. Hence, the dyes are standing on the surface with the triarylamine groups pointing out. By assuming a flat surface and normal emission, a more detailed value representing the molecular organization can be calculated using eqn (1) where I is the ratio between the N1s intensity from NA and the total N1s intensity (NTOT), λ is the inelastic mean free path and d is the average distance between the nitrogen atoms. Here λ = 6 Å for a photon energy of 540 eV and λ = 8 Å for a photon energy of 758 eV were used.9,47,48 Using this procedure, the distance between the two nitrogen atoms projected onto the probing depth vector, i.e. in the probing direction, is 10 Å and 9 Å for D35 and D45, respectively. Considering the crudeness of this analysis, we conclude that the results for the two dyes are similar, hence the binding angle will be similar, a result which also is supported by the DFT calculations.
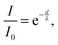 | (1) |
All intensity ratios are presented in Table 2. As a summary from the geometrical discussion we conclude that the introduction of longer alkoxy chains in the D35 dye leads to lower dye coverage but the binding orientation remains unaffected. As indicated by Fig. 9, the alkoxy chains are pointing away from the TiO2 surface and this can prevent the electrons injected into the TiO2 from recombining with the electrolyte. The longer lifetime seen for D35 indicates that the longer alkoxy chains prevent recombination more efficiently.
| Dye | S2p | N1s 758 eV | N1s 540 eV | d (Å) | C1s 758 eV | C1s 454 eV |
|---|---|---|---|---|---|---|
| D35 | 1.0 | 0.23 | 0.15 | 10 | 5.5 | 59.3 |
| D45 | 1.3 | 0.20 | 0.14 | 9 | 5.4 | 42 |
3.3 Energy level matching
Fig. 10 shows the valence level spectra of D35 and D45 adsorbed on a TiO2 surface and recorded with 150 eV photon energy. The larger features between 5 and 25 eV binding energy are mainly from the substrate and the carbon signal (Ti, C, and O) forming molecular orbitals. The small peaks at roughly 1.5 eV are the highest occupied molecular orbitals (HOMO levels) from the dyes. As can be seen, D35 and D45 have a similar binding energy of the HOMO levels, which is in accordance with electrochemical measurements.4,11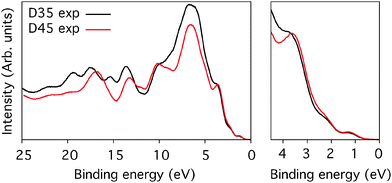 | ||
| Fig. 10 The valence level spectra of D35 and D45. The small features at low binding energy are the HOMO levels of the dyes. The spectra are recorded with a photon energy of 150 eV. | ||
The second set of DFT calculations concern the electronic structure and interpretation of the experimental photoelectron spectra and will be presented in this section. Valence photoelectron spectroscopy can be used to study the valence band and determine the characteristics and density of the highest occupied states in the dyes. In Fig. 11, the experimental valence spectra of D35 and D45 adsorbed on TiO2 (from Fig. 10) are compared to the theoretical spectra of isolated dye molecules, with intact –COOH carboxyl groups. The theoretical spectra reproduce the overall spectral shape very well and can be used to reliably assign the low-binding energy features. However, for agreement with the experimental spectra in the whole energy range shown in Fig. 11, the energy-scale from the calculations would be stretched to account for differential relaxation effects in the ionization process.
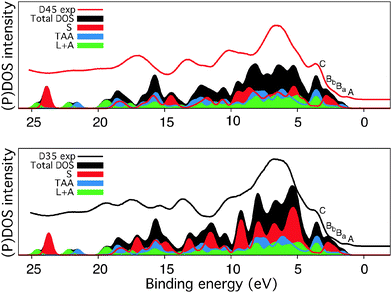 | ||
| Fig. 11 The experimental valence levels (from Fig. 10) compared to calculated density of states for D35 and D45. Partial density of states are shown from the unit including the alkoxy substituents (S), the triarylamine unit (TAA), and linker and anchor units (L + A). The hydrogen atoms were excluded from the calculations. | ||
The states at low binding energy, denoted A–C in the D35 and D45 valence spectra in Fig. 11, are similar for both dyes; the longer alkoxy chains in the D35 molecule thus mainly contribute to the valence orbitals corresponding to binding energies higher than 4 eV. The most important differences between the D35 and D45 valence spectra are observed in the region 4–10 eV, where the D45 intensity is lower, and in the region about 11.5–18 eV (10–15 eV in the theoretical spectrum).
We notice that for the photooxidation of the dye molecules under visible light, the highest occupied molecular orbitals (HOMOs) are important. Hence, in the photoemission spectra in Fig. 11, we focus on the low binding energy peaks which we denote as A, Ba, Bb, and C. The decomposition of the total DOS of the dye molecules into PDOS for the linker and acceptor units (L + A) and for the separate contributions from the triarylamine moiety (TAA), and the part of the donor unit containing the phenyl group with the alkoxy chains (S) shows that the HOMO is mainly localized on the donor (S and TAA units). In comparison to a previous electronic structure study of triarylamine based dyes,49 we observe additional features in the outermost structure of the D35 and D45 valence PES spectra, arising from the π bonding orbitals on the S unit present in these dyes. These two peaks Ba and Bb are separated by 0.5 eV and are characterized by the orientation of the nodal plane of π bonding orbitals on the S unit phenyl group. The orbitals contributing to the peak denoted C are mostly localized on the TAA unit, with a large contribution also from the L and A units.
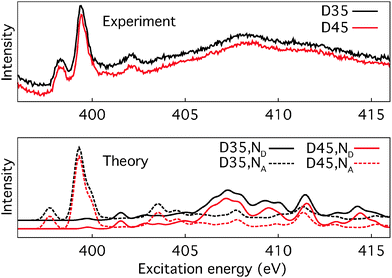
As seen in Fig. 11, the difference in DOS can be attributed to the amount of carbon, but despite the significant change in the molecular structure, we conclude from the experimental PES data and the spectrum calculations that the occupied valence band energy levels of D35 and D45 are similar. To probe also the unoccupied levels N1s, XAS measurements and calculations were performed. For both of the measured samples and also for calculations of the isolated molecules, the XAS of D35 and D45 are very similar as seen in the results presented in Fig. 12. The most distinct difference is the feature at 401 eV only seen in D45, but the assignment against the calculations is not straightforward, since the calculations of D35 and D45 are nearly identical. Further studies on a well-defined experimental model system could determine if the feature at 401 eV contains information about interactions with the cyano group.
4 Conclusions
The surface coverage was found to be significantly higher for D45 than for D35. However, the solar cell performance is higher for solar cells with D35 and the differences in solar cell characteristics when longer alkoxy chains are introduced in the triarylamine unit are attributed to geometrical changes in dye packing. The XPS data show that the butoxy chains are located close to the outermost surface and the longer butoxy chains in D35 therefore effectively protect the surface and suppress recombination with the redox couple and therefore give a longer electron lifetime in a dye-sensitized solar cell. The main conclusion from the theoretical calculations as well as from the PES studies is that the organic dyes D35 and D45 have strikingly similar electronic structure and that introducing the longer alkoxy chains does not affect energy level matching. The differences in electron lifetimes thus cannot be attributed to energy matching changes. Hence, the main conclusion from the present paper is that pure changes in geometrical configurations have vast consequences on the electron lifetime and are therefore responsible for the changes observed in the performance of solar cells. This is of importance for future dye design and hence future striving for higher power conversion efficiencies of DSCs.Acknowledgements
We acknowledge financial support from the Swedish Research Council, the Carl Trygger foundation, the Swedish Energy Agency and STandUP for Energy. The computations were partly performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at the Swedish National Supercomputer Center (NSC) and the High Performance Computer Center North (HPC2N). A. A. and S. F. thank MIUR-PRIN-2010 20104XET32 “DSSCX” for financial support. The kind and helpful staff at the MAX IV laboratory is greatly acknowledged.References
- B. O'Regan and M. Grätzel, Nature, 1991, 353, 737–740 CrossRef
.
- A. Hagfeldt, G. Boschloo, L. Sun, L. Kloo and H. Pettersson, Chem. Rev., 2010, 110, 6595–6663 CrossRef CAS PubMed
.
- D. P. Hagberg, T. Marinado, K. M. Karlsson, K. Nonomura, P. Qin, G. Boschloo, T. Brinck, A. Hagfeldt and L. Sun, J. Org. Chem., 2007, 72, 9550–9556 CrossRef CAS PubMed
.
- D. P. Hagberg, X. Jiang, E. Gabrielsson, M. Linder, T. Marinado, T. Brinck, A. Hagfeldt and L. C. Sun, J. Mater. Chem., 2009, 19, 7232–7238 RSC
.
- A. Mishra, M. Fischer and P. Bäuerle, Angew. Chem., Int. Ed., 2009, 48, 2474–2499 CrossRef CAS PubMed
.
- D. P. Hagberg, T. Edvinsson, T. Marinado, G. Boschloo, A. Hagfeldt and L. Sun, Chem. Commun., 2006, 2245–2247 RSC
.
- L. Kloo, Chem. Commun., 2013, 49, 6580–6583 RSC
.
- S. M. Feldt, E. A. Gibson, E. Gabrielsson, L. Sun, G. Boschloo and A. Hagfeldt, J. Am. Chem. Soc., 2010, 132, 16714–16724 CrossRef CAS PubMed
.
- H. Ellis, S. K. Eriksson, S. M. Feldt, E. Gabrielsson, P. W. Lohse, R. Lindblad, L. C. Sun, H. Rensmo, G. Boschloo and A. Hagfeldt, J. Phys. Chem. C, 2013, 117, 21029–21036 CAS
.
- T. N. Murakami, N. Koumura, M. Kimura and S. Mori, Langmuir, 2014, 30, 2274–2279 CrossRef CAS PubMed
.
- H. Tian, E. Gabrielsson, P. W. Lohse, N. Vlachopoulos, L. Kloo, A. Hagfeldt and L. Sun, Energy Environ. Sci., 2012, 5, 9752–9755 CAS
.
- K. Westermark, S. Tingry, P. Persson, H. Rensmo, S. Lunell, A. Hagfeldt and H. Siegbahn, J. Phys. Chem. B, 2001, 105, 7182–7187 CrossRef CAS
.
- J. Nyhlen, G. Boschloo, A. Hagfeldt, L. Kloo and T. Privalov, ChemPhysChem, 2010, 11, 1858–1862 CAS
.
- M. Bassler, J. O. Forsell, O. Björneholm, R. Feifel, M. Jurvansuu, S. Aksela, S. Sundin, S. L. Sorensen, R. Nyholm, A. Ausmees and S. Svensson, J. Electron. Spectrosc. Relat. Phenom., 1999, 101, 953–957 CrossRef
.
- E. M. J. Johansson, M. Hedlund, H. Siegbahn and H. Rensmo, J. Phys. Chem. C, 2005, 109, 22256–22263 CrossRef CAS PubMed
.
- E. M. J. Johansson, T. Edvinsson, M. Odelius, D. P. Hagberg, L. H. Sun, A. Hagfeldt, H. Siegbahn and H. Rensmo, J. Phys. Chem. C, 2007, 111, 8580–8586 CAS
.
- F. De Angelis, S. Fantacci, A. Selloni, M. K. Nazeeruddin and M. Grätzel, J. Phys. Chem. C, 2010, 114, 6054–6061 CAS
.
- M. Pastore, S. Fantacci and F. De Angelis, J. Phys. Chem. C, 2013, 117, 3685–3700 CAS
.
- C. Anselmi, E. Mosconi, M. Pastore, E. Ronca and F. De Angelis, Phys. Chem. Chem. Phys., 2012, 14, 15963–15974 RSC
.
- M. Pastore and F. De Angelis, J. Phys. Chem. Lett., 2013, 4, 956–974 CrossRef CAS PubMed
.
- M. Pastore and F. De Angelis, Phys. Chem. Chem. Phys., 2012, 14, 920–928 RSC
.
- J. Calbo, M. Pastore, E. Mosconi, E. Orti and F. De Angelis, Phys. Chem. Chem. Phys., 2014, 16, 4709–4719 RSC
.
- M. Pastore and F. De Angelis, Top. Curr. Chem., 2014, 352, 151–236 CAS
.
- G. te Velde, F. Bickelhaupt, E. Baerends, C. Guerra, S. Van Gisbergen, J. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS
.
- C. Guerra, J. Snijders, G. te Velde and E. Baerends, Theor. Chem. Acc., 1998, 99, 391–403 CAS
.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed
.
- E. Van Lenthe and E. Baerends, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed
.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS
.
- A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC
.
- A. Klamt and V. Jonas, J. Chem. Phys., 1996, 105, 9972–9981 CrossRef CAS
.
- C. Pye and T. Ziegler, Theor. Chem. Acc., 1999, 101, 396–408 CrossRef CAS
.
-
K. Hermann, L. G. M. Pettersson, M. E. Casida, C. Daul, A. Goursot, A. Koester, E. Proynov, A. St-Amant, D. R. Salahub, V. Carravetta, H. Duarte, C. Friedrich, N. Godbout, J. Guan, C. Jamorski, M. Leboeuf, M. Leetmaa, M. Nyberg, S. Patchkovskii, L. Pedocchi, F. Sim, L. Triguero and A. Vela, StoBe-deMon version 3.2, 2013 Search PubMed
.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS
.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 7406 CrossRef
.
- N. Godbout, D. R. Salahub, J. Andzelm and E. Wimmer, Can. J. Chem., 1992, 70, 560–571 CrossRef CAS
.
- L. Triguero, L. G. M. Pettersson and H. Ågren, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 8097–8110 CrossRef CAS
.
-
W. Kutzelnigg, U. Fleischer and M. Schindler, The IGLO-Method: Ab Initio Calculation and Interpretation of NMR Chemical Shifts and Magnetic Susceptibilities, NMR-Basic Principles and Progress, Springer Verlag, Heidelberg, 1990, vol. 23, pp. 165–262 Search PubMed
.
- L. G. M. Pettersson, U. Wahlgren and O. Gropen, Chem. Phys., 1983, 80, 7–16 CrossRef CAS
.
- L. G. M. Pettersson, U. Wahlgren and O. Gropen, J. Chem. Phys., 1987, 86, 2176–2184 CrossRef CAS
.
- H. Ågren, V. Carravetta, O. Vahtras and L. G. M. Pettersson, Theor. Chem. Acc., 1997, 97, 14–40 CrossRef
.
- J. Guan, P. Duffy, J. T. Carter, D. P. Chong, K. C. Casida, M. E. Casida and M. Wrinn, J. Chem. Phys., 1993, 98, 4753–4765 CrossRef CAS
.
- E. Ronca, M. Pastore, L. Belpassi, F. Tarantelli and F. De Angelis, Energy Environ. Sci., 2013, 6, 183–193 CAS
.
- H. Ellis, I. Schmidt, A. Hagfeldt, G. Wittstock and G. Boschloo, J. Phys. Chem. C, 2015, 119, 21775–21783 CAS
.
- A. C. Khazraji, S. Hotchandani, S. Das and P. V. Kamat, J. Phys. Chem. B, 1999, 103, 4693–4700 CrossRef CAS
.
- V. Dryza and E. J. Bieske, J. Photochem. Photobiol., A, 2015, 302, 35–41 CrossRef CAS
.
- P. J. Cumpson, Surf. Interface Anal., 2001, 31, 23–34 CrossRef CAS
.
- M. Hahlin, E. M. J. Johansson, S. Plogmaker, M. Odelius, D. P. Hagberg, L. C. Sun, H. Siegbahn and H. Rensmo, Phys. Chem. Chem. Phys., 2010, 12, 1507–1517 RSC
.
- M. Hahlin, M. Odelius, M. Magnuson, E. M. J. Johansson, S. Plogmaker, D. P. Hagberg, L. C. Sun, H. Siegbahn and H. Rensmo, Phys. Chem. Chem. Phys., 2011, 13, 3534–3546 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp04589d |
| This journal is © the Owner Societies 2016 |