Exploring the charging mechanisms in non-aqueous multiphase surfactant solutions, emulsions and colloidal systems via conductivity behaviors predicted with eyring's rate process theory
Received
24th August 2015
, Accepted 17th November 2015
First published on 19th November 2015
Abstract
The common charging agents and charging mechanisms in non-aqueous multiphase systems available in the literature are analyzed, and the conductivity equations derived on the basis of the charging mechanisms with the Eyring's rate process theory are compared with experimental observations. The popular charging mechanisms in non-aqueous systems, such as the ion preferential absorption, ion pair dissociation, and micelle disproportionation/fluctuation models, are found to be incapable of explaining all experimental evidences. Particularly, the ion pair dissociation and micelle disproportionation/fluctuation models apparently suffer a major drawback: how charges are separated and most importantly how charging entities are stabilized in non-aqueous systems, are not adequately addressed; in low dielectric constant non-aqueous media separated ions tend to bind together rather than stay separately. A new charging mechanism incorporating an electric field internally available or externally applied into the charging process is proposed to explain charge separations and stabilizations. The conductivity equations derived on the basis of this new mechanism predict that conductivity should linearly increase with both the electric field and the concentrations of inverse micelles in very low concentration regions, which is consistent with experimental evidences.
I. Introduction
Particles, droplets, and micelles usually carry charges in both aqueous and non-aqueous multiphase surfactant solutions, emulsions, and colloidal systems. The charge properties of those small entities play a critical role in controlling aggregation and agglomeration properties in both dry processes like film coatings and wet processes like electrophoretical motions. These properties are directly related to the physical stability of whole systems and are important in handling and manufacturing powder related products in many industrial areas like inks, paints, foods, pharmaceutics, etc. Understanding charging mechanisms will definitely help us gain insights into why and how charges are generated and attained, and thus desirable charge properties can be smartly controlled.
Dry particulates usually carry charges that are mainly resulted from the triboelectric effect,1–3 which could be explained using the following four mechanisms. (1) Powder particles may be polarized by a nearby weak electric field created by the local charging species; (2) ions could transfer from one particle surface to another due to inter-particle collision; (3) ions from adsorbed water residing on the surfaces of non-ionic insulators could be shared by adjacent particles; (4) electrons could transfer among conductors, semiconductors, and insulators, such as from metallic instrument/container surfaces to particle surfaces.
Once small particles are dispersed into water, particles will continue to carry charges, however, the charging mechanisms are different from that in dry states. In aqueous systems, particle surface charges are generated due to:4–6 (1) different preferences for ions in solid and liquid two phases; (2) direct ionization of surface groups; (3) specific ion adsorptions; (4) defects of specific crystal structures that break down the charge neutralization status.
If dry particles are dispersed into non-aqueous liquids like oil and organic solvents, particle charging mechanisms become more complicated, as the ionization and dissolution in non-aqueous systems typically are very low. The primary reason, as pointed out in the literature,7 is that the Coulombic attractive force is almost 30 times stronger in organic media than that in aqueous systems, since the dielectric constant of organic media is about 2.5, and that of water is 80; ions in non-aqueous systems tend to coalesce together rather than stay apart. For particles to be charged, surfactants or dispersants typically are required for inducing charges or stabilizing charged entities in non-aqueous media; those surfactants or dispersants are called charging agents.
Unlike in aqueous systems, charging agents in non-aqueous systems would create inverse micelle structures with hydrophobic groups extending into oil phases and hydrophilic groups forming center cores; inorganic ions or other hydrophilic species thus stay within those center core places. For this reason, a trace amount of residue water or other water soluble ionic impurities was believed to be critical to charge inverse micelles in non-aqueous systems.8,9 Those inverse micelle structures are soft and easily deformable, but can travel under an external electric field and show measurable zeta-potentials, behaving similarly as solid particles. For this regard, the inverse micelles will be considered as soft “particles” in this article. If solid particles are present in non-aqueous systems, inverse micelles can easily absorb on particle surfaces, travelling together under an external electrical field10,11 and making particles charged in non-aqueous systems.12–14 For emulsions of both oil-in-water15,16 and water-in-oil17 systems, droplets are assumed to be charged very similarly as particles in colloidal systems via micelles or inverse micelles. In this hypothetical physical picture, charged inverse micelles seem critical to the charging mechanisms for both water-in-oil emulsions and colloidal systems, however, how inverse micelles are charged remains a question.
There are many studies and discussions in the literature addressing how inverse micelles are charged in non-aqueous systems,7,10,13,18–23 indeed. Typical experimental methods in revealing charging mechanisms are conductivity and transient current measurements against physical sizes, valencies, and concentrations of charging agents. One of the experimental observations in conductivity studies across many non-aqueous systems is that conductivity linearly increases with the concentrations of charging agents in low concentration regions.21–23 Another interesting phenomenon is that inverse micelles under an electric field behave differently than those intrinsically carrying charges in the absence of an electric field.18 This may indicate that something with inverse micelles under the reaction of an electric field has changed, and the electric field may participate the charging process of inverse micelles.
For unveiling charging mechanisms across all types of non-aqueous systems including both emulsions and colloidal suspensions with the presence of ionic and non-ionic surfactants, conductivity properties are thus focused in this article for easy evaluation with the experimental evidences. Theoretical derivations of conductivity equations on the basis of charging mechanisms with the Eyring's rate process theory are carried out in a generic manner rather than limited to a certain type of non-aqueous systems. Many experimental results indicate that conductivity behaviors of non-aqueous systems could be dramatically different.22 For example, the conductivity of a non-aqueous system containing ionic surfactants shows a very good linear relationship with the concentrations of the surfactant;21 while the conductivity of another non-aqueous system with non-ionic surfactants doesn't show a linear relationship with the concentrations and it levels off at high concentrations of the surfactant.24 A successful charging mechanism in theory should be able to explain rich conductivity phenomena observed so far.
The article is arranged as below. Widely used charging agents and dispersants in non-aqueous systems are briefly reviewed, and the charging mechanisms available in the literature are analyzed afterwards; the corresponding conductivity equations derived on the basis of those mechanisms are examined against the experimental observations, followed by a new charging mechanism proposed to explain currently observed experimental facts. The focuses are placed on theoretical derivations of conductivity equations with the Eyring's rate process theory, which is, however, not the purpose; the goal is by no means to develop an universal conductivity equation for non-aqueous systems nor the conductivity mechanisms in general; instead the conductivity is merely employed as a tool to distinguish which charging mechanisms work.
II. Charging agents and dispersants
The charging agents or dispersants used in non-aqueous systems are surfactants for making particles charged or well dispersed, forming stable emulsions and colloidal suspensions. The charging agents usually form inverse micelle structures, trapping all polar impurities or residues from the non-aqueous oil phase into the center cores. Commonly used charging agents include calcium diisopropylsalicylate,25 tetraisoamylammonium picrate,25 polyisobutylene succinimide, OLOA 1200,26–28 di-(2-ethylhexyl) sodium sulfosuccinate (AOT),29–31 octyl phenol ethoxylate (Triton X-100),32 phosphatidylcholine (lecithin),33 sorbitan oleate (Span 80),34etc. The molecular structures of these charging agents are shown in Fig. 1.
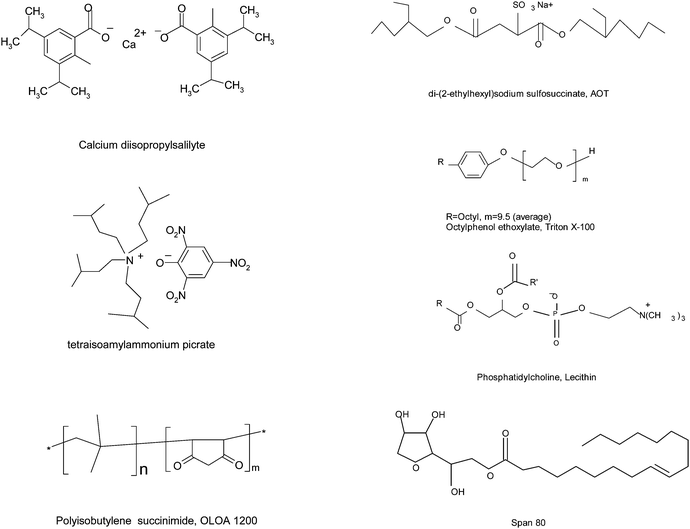 |
| | Fig. 1 Charging agents or dispersants commonly used in non-aqueous systems. | |
As one may notice, all charging agents may contain both positive and negative groups, except Triton X-100 and Span 80. Those two surfactants are more commonly used as dispersants, but also can function as charging agents,24,34 even though they are well considered as non-ionic surfactants. The spatial separation of positive and negative groups in those surfactants creates amphipolar structures that are believed to make particles charged. For example, the negative groups may be hydrophilic and thus can comfortably stay inside the centers of inverse micelles; while the positive groups may be hydrophobic and can only stay outside of the inverse micelle structures. The separated charges may further polarize the neighboring surfactant molecules, driving the charged entities even further away from each other. If solid particles or liquid droplets are available in the systems, charged inverse micelles may preferentially absorb on the surfaces of those entities, making them charged. For non-ionic surfactants, there are no amphipolar centers and thus there should be no such a kind of charge separations occurring in the system. However, they still function as charging agents as indicated in the literature,24,34 indicating that charge separations occur in non-ionic surfactant systems, indeed. Apparently, not only pre-existing charges from charging agents but also later induced or generated charges should be responsible for charging mechanisms in non-aqueous systems. This observation should be a key point for validating the charging mechanisms.
III. Charging mechanisms in non-aqueous systems
In this section, theories or models presented in the literature accounting for charging mechanisms in non-aqueous systems will be briefly reviewed, with the emphasis on the theoretical ideas rather than theoretical details. Readers are encouraged to go through several recent review articles for more detailed information.10,22,23,35
As mentioned previously, a common phenomenon observed for non-aqueous systems is that the conductivity linearly increases with the concentrations of the charging agent.21,36,37 A very good linear relationship was observed for the conductivity of AOT/dodecane solution vs. AOT concentration ranging from 0.8 to 200 mM.21 A similar linear relationship between the conductivity and the charging agent concentrations was observed in OLOA 1200/dodecane,36 AOT/benzene,38 and lecithin/hydrocarbon (Isopar H) systems.37 However, at sufficiently high concentrations, conductivity was found to deviate from this linear relationship.39 This common phenomenon frequently is employed to verify if the proposed charging mechanisms work.
In 1920s, the “ion pairs” or “ion association” concept40,41 was proposed to explain the conductivity properties of weak electrolyte systems like non-aqueous emulsions and colloidal suspensions. The main idea is that in non-aqueous systems ions tend to associate together and form pair structures due to much stronger electrostatic attractive forces in comparison with aqueous systems, almost 30 times stronger than that in aqueous systems due to a much smaller dielectric constant of organic solvents than that of water, as mentioned earlier. The equilibrium between ion dissociation and association determines the conductivity, resulting in a linear relationship between the conductivity and the concentrations of the charging agent. However, at sufficient high concentrations, the conductivity will deviate from the linear relationship,39 and the “ion triplets” concept was even proposed. Since ion pairs or more complex structures are formed in non-aqueous systems, ion dissociations are thus widely regarded as a means for generating free ions carrying charges, which may be expressed as AB ↔ A+ + B−. However, as indicated in the literature,22 ion pairs may dissociate under certain conditions, but the question is where the original ion pairs come from; more importantly, there is no reason for dissociated ions to stay separated in non-aqueous media.
For overcoming the shortcomings of the ion pair dissociation model, the disproportionation model was proposed in the literature,22,42,43 which may be expressed as 2A ↔ A+ + A−. In such a case, no ion pairs are initially needed, and surfactant molecules could attain charges via inverse micelle structures due to charge center separations or charge transfer as discussed earlier.
Nonetheless, in my discretion, the disproportionation model suffers a similar drawback as the dissociation model: the separated two oppositely charged centers tend to pair instead of separate in non-aqueous systems for the same reason, almost 30 times stronger than electrostatic attractive forces in comparison with that in aqueous systems. For microemulsions, a so called fluctuation model44 is proposed to account for the conductivity data, with the argument that droplets may exchange the electrical charges during droplet collisions, as the aqueous droplets contain dissolved ions inside. Essentially, the fluctuation model is similar to the disproportionation model; the only difference is that the former is for water droplets and the latter is for inverse micelles. Again, the same question may come up: after charge separations, how free ions stably remain separated in non-aqueous media? Such a question poses a big challenge to all charging mechanisms proposed in the literature.
IV. Theory
1. Conductivity equations derived with Eyring's rate process theory
In the next few sections, conductivity equations are first derived on a generic base and then extended to non-aqueous systems; the obtained conductivity equations are further modified on the basis of charging mechanisms available in the literature for evaluating if the charging mechanisms work. A new model or mechanism is proposed and the corresponding conductivity equation is examined against the charging phenomena in non-aqueous systems, too.
The conductivity of a pure organic liquid typically is about 10−13 S m−1. Once a charging agent is added in, the conductivity of the whole system can easily reach 10−7 S m−1, an increase of several orders of magnitude. Such a dramatic increase may suggest that a substantial amount of ions is created in systems, though again how the charges are generated and where the charges come from remains a question.
The conductivity of materials in general and liquids containing ions in specific is well understood.45–49 Usually the thermal energy is not strong enough to dissociate the molecules. Suppose that the ionic conductivity may follow the Eyring's rate process theory.48 Due to the collision from neighboring molecules, the molecules may be activated and only the activated molecules may dissociate and contribute to the conductivity; therefore the relative number of the molecules staying in the ground state and the activation state determines the conductivity. Assume that the potential in the ground state is U1, and that in the activation state is U2, and the number of molecules per unit volume is n0, then:
| | 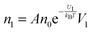 | (1) |
| | 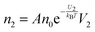 | (2) |
where
V1 and
V2 are the volumes occupied by each state of molecules, and
A is a constant. Assuming
V1 ≈
V2, the dissociation constant
α may be expressed as:
| | 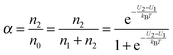 | (3) |
U2 −
U1 =
U0, which is the dissociation energy.
| | 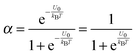 | (4) |
For low dielectric constant liquids like non-aqueous media,
U0 is very large,
U0 ≫
kBT, making
α ≈ 0.
Eqn (1) to (4) clearly show that the thermal motion is unable to make contribution to the conductivity. Without an external electric field, the molecule motions are random and there should be no or extremely low conductivity. Statistically, the number of molecules in one of the three perpendicular axes in a space is
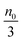
, and the number of molecules in the positive axis is
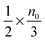
. So in a unit time period the number of molecules overcoming the energy barrier,
U0, is:
| | 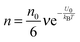 | (5) |
where
ν is the molecule vibration frequency at certain positions, and equals to the hopping time of a molecule trying to overcome the energy barrier,
U0, per unit time. Once an electric field
E is applied, the activation energy in the direction of the applied electric field will be lowered by Δ
U and that in the opposite direction will be increased by the same amount. The excess amount of ions moving along the direction of the electric field thus is expressed as:
| | 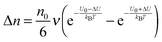 | (6) |
where
| | 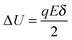 | (7) |
where
q is the charge of ions,
δ is the ion free walking distance in the scale of 10
−9 m. Usually Δ
U ≪
kBT, which can be confirmed by a simple calculation as follows. Suppose Δ
U =
kBT, and at room temperature 300
K,
| | 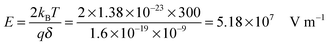 | (8) |
The applied electric field usually is far less than 5.18 × 10
7 V m
−1, making the assumption, Δ
U ≪
kBT, always valid.
Eqn (6) can be approximated by using the equation
ex ≈ 1 +
x(|
x| < 1):
| | 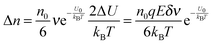 | (9) |
The velocity of the excess amount of ions moving along the electric field is the relative number of the excess amount of ions multiplying the moving distance per second
| | 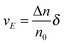 | (10) |
So the mobility of ions is:
| | 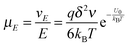 | (11) |
On the basis of
eqn (3), if one activated molecule may generate two ions, then the number of dissociated ions per unit volume may be equal to 2
αn0. According to the generic conductivity equation,
50 the conductivity contributed from ion motions in non-aqueous systems thus can be expressed as:
| | 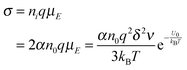 | (12) |
where
ni represents the number of ions per unit volume.
Eqn (12) indicates that the conductivity is dependent on the number of molecules that may dissociate into ions, the charge quantity of ions, the ion free walking distance, the vibration frequency of ions, temperature, and the energy barrier for ions to move away from neighboring ions. The important feature of
eqn (12) is that the conductivity may linearly increase with the number of molecules in non-aqueous systems,
i.e., the concentrations of the charging agent, which has been evidenced in many non-aqueous systems. However, this equation doesn't predict that the conductivity may deviate from the linear relationship in high concentration regions. We may need to extend this equation to non-aqueous systems containing inverse micelles.
2. Conductivity equations extended to non-aqueous systems containing inverse micelles
Note that eqn (12) is derived on a generic basis without being limited to any specific systems. When eqn (12) is applied to non-aqueous systems containing large inverse micelle structures formed by the molecules of the charging agents listed in Fig. 1, one may need to make further assumptions, as the sizes of inverse micelles should be much larger than regular ions and most importantly, they may change with the concentrations of charge agents.34 In addition, many experimental evidences suggest that the charge quantity of inverse micelles is strongly dependent on the concentrations of charging agents.51–53 Those mean that both the parameters q and δ cannot be assumed as an invariable in inverse micelle systems and their relationships with the concentrations of charging agents must be worked out.
Since the Bjerrum length in water at room temperature is about 0.7 nm and would be 28.3 nm in non-aqueous systems,19 one cannot continue to assume that such large inverse micelles can still travel the distance comparable to the diameter of inverse micelle structures. However, one may always assume that inverse micelles can travel the distance between two micelle structures freely available to each inverse micelle. This distance is called the inter-particle spacing (IPS), and Hao provides an approach to calculate:6,54,55
| | 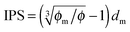 | (13) |
where
ϕm is the maximum packing fraction that the inverse micelles can achieve,
ϕ is the inverse micelle volume fraction, and
dm is the diameter of the inverse micelles. Since an inverse micelle may travel both left and right sides, the free walk distance
δ may be expressed as:
| | 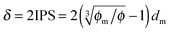 | (14) |
Note the parameter
n0 in
eqn (12) is the number of molecules of the charging agent per unit volume. If one inverse micelle structure contains
nm molecules,
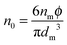
, based on the definition. Therefore,
eqn (12) may be rewritten as:
| | 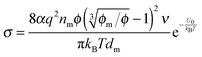 | (15) |
One may certainly anticipate that the diameter of inverse micelles changes with the volume fraction and a relationship must be worked out. According to Hao, the size of inverse micelle could be derived using the Stokes–Einstein equation and Hao's interparticle spacing equation, and it may be expressed as:
6| | 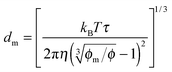 | (16) |
where
τ is the relaxation time related to the parameter
ν, and
η is the viscosity of the medium. Substituting
eqn (16) into
eqn (15) leads to
| | 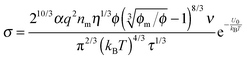 | (17) |
Typically, for ionic systems the parameter
ν has such a relationship with the relaxation time
τ,
45,56,57| | 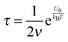 | (18) |
a simple Arrhenius relaxation process. Replacing
τ in
eqn (17) with
eqn (18) leads to:
| | 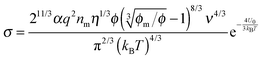 | (19) |
Now, we may need to determine the parameter
q in
eqn (19), as it is not a constant in non-aqueous systems. One may continue to assume that the electrical double layer theory is still valid in non-aqueous inverse micelle systems, the charge quantity on inverse micelles may be expressed as:
4,6,58where
εm and
ε0 are the dielectric constant of the liquid medium and vacuum respectively,
r is the radius of the inverse micelle,
r =
dm/2,
κ−1 is the Debye length, and
ζ is the zeta potential. In non-aqueous systems, the electrical double layer is usually very thick,
κr < 0.1; the Hückel equation,
ζ = 3
ημE/(2
εmε0), can be used and
eqn (20) is re-written as:
under an assumption 1 +
κr ≈ 1. Again,
η is the viscosity of the medium,
μE is the mobility of inverse micelles that can be measured experimentally using the zeta potential instruments. Note that
μE expressed in
eqn (11) cannot be used in
eqn (21), as
eqn (11) is obtained under an assumption that the charge quantity is constant and
μE is a variable, while in
eqn (21) the charge quantity is a variable and
μE is a measurable constant. They are just obtained under different theoretical frameworks for different purposes. Nonetheless,
dm expressed in
eqn (16) can be still used in
eqn (21), as
eqn (16) is purposely derived to estimate the sizes of inverse micelles. If the term 3π
ημE in
eqn (21) is considered as a constant, then the charge quantity is linearly proportional to the size of inverse micelles, which is consistent with both the experimental
58 and theoretical
59,60 results obtained, however, in colloidal suspensions. One may thus assume that, as suggested in the literature,
58eqn (21) may be expressed as:
where
A is a material related constant. Substituting
eqn (22) into
eqn (19) and re-arranging leads to the expression of conductivity of inverse micelle systems:
| | 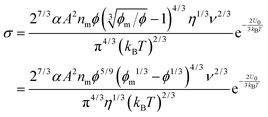 | (23) |
Eqn (23) indicates that the conductivity of non-aqueous systems containing inverse micelles may be dependent on the concentration of the inverse micelle and even the viscosity of the medium, though it has a relatively complicated relationship with the volume fraction of inverse micelles. It would be interesting to evaluate how the conductivity is going to change with the volume fraction.
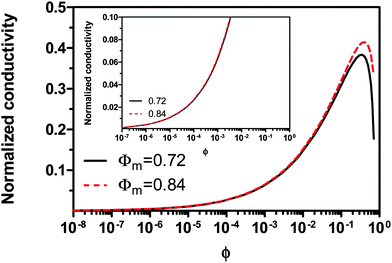
Fig. 2 shows the normalized conductivity
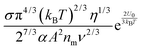
against
ϕ for the illustrative purpose. Since inverse micelle structures are soft and can be deformed easily, two dense packing structures are assumed to occur theoretically:
ϕm = 0.72 and
ϕm = 0.84, which corresponds to non-lattice tetrahedra and Icosahedra,
61,62 respectively. At extremely low volume fractions, the term (
ϕm1/3 −
ϕ1/3)
4/3 in
eqn (23) may be approximated as a constant, (
ϕm1/3 −
ϕ1/3)
4/3 ≈
ϕm4/9, and the conductivity may change with
ϕ5/9. Clearly, the conductivity doesn't have a linear relationship with the volume fraction of the inverse micelles in low concentration regions. Only in the relatively high concentration region, starting at the volume fraction about 2 × 10
−3 and until reaching a concentration of about 5 × 10
−2, there seems to be a linear relationship between the conductivity and the volume fraction. A further volume fraction increase makes the conductivity dramatically increase by obeying a power law and then reach a peak, a very unusual phenomenon. As indicated earlier, the linear dependence of conductivity on the concentrations of the surfactants in low concentration regions has been reported in many articles. However, the drop off in high concentration regions is rarely reported, besides one system with Span 80,
22 showing the surface charge converted from the conductivity drops at relatively higher concentrations, which is qualitatively consistent with
eqn (23). Since the inverse micelles are formed by the surfactant molecules, the high surfactant concentrations could create more charged inverse micelles, resulting in a linear increase of conductivity at the beginning; once more charged micelles are created, those charged micelles will impose electric fields to neighboring inverse micelles, making them charged, too. This chain-reaction like charging process leads to an exponential increase of conductivity at relatively higher concentrations due to the large number of charged inversed micelles. As shown in
eqn (13) and (14), higher concentrations of charging agents will eventually lead to a smaller free walk distance, thus lowering conductivity.
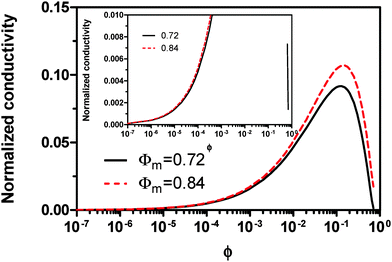 |
| | Fig. 2 The normalized conductivity 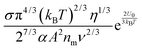 against ϕ based on eqn (23) under the assumptions of ϕm = 0.72 and ϕm = 0.84. The inset is the same data but plotted in a very small normalized conductivity range for clearly demonstrating the linear relationship. against ϕ based on eqn (23) under the assumptions of ϕm = 0.72 and ϕm = 0.84. The inset is the same data but plotted in a very small normalized conductivity range for clearly demonstrating the linear relationship. | |
The parameter ν is assumed to be independent of the volume fraction in deriving eqn (23), which may not be true. The related parameter τ is actually dependent on the volume fraction, according to the Wagner–Maxwell model for diluted suspensions for ϕ < 0.1:6,63
| | 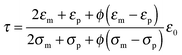 | (24) |
where
ε0,
εm, and
εp are the dielectric constant of vacuum, the dispersing medium, and the dispersed phase, respectively, and
σm and
σp are the conductivity of the dispersing medium and the dispersed phase, respectively. From
eqn (18), the parameter
ν may be written as:
| | 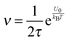 | (25) |
Substituting
eqn (25) into
eqn (23) and replacing
τ with
eqn (24) leads to:
| |  | (26) |
Eqn (26) presents a complicated relationship for conductivity: the conductivity of non-aqueous multiphase systems is a function of many parameters, such as the conductivities and dielectric constants of both the dispersing medium and the dispersed phase, the viscosity of the medium, the volume fraction of the dispersed phase, and temperature. Intuitively, high conductivities of both the dispersing and dispersed phases should lead to high conductivities of the whole system, which is demonstrated in
eqn (26).
Eqn (26) also tells us that the conductivity is independent of the applied electric field strength, which is inconsistent with experimental observation presented in the literature,
53,64,65 where the conductivity was found to linearly increase with the applied electric field strength up to 10
6 V m
−1, a relatively low electric field strength in non-aqueous systems.
3. Evaluating the current charging mechanisms
As briefly stated earlier, there basically are three charging mechanisms proposed for explaining how inverse micelles attain charges in non-aqueous media.26,66–70 Those mechanisms can be roughly classified as: (a) the preferential ion adsorption mechanism. The ions from either impurities or a trace amount of water can be trapped by inverse micelles, making inverse micelles charged; in this mechanism, the charge is uncontrollable as the impurities are hard to control in practice; (b) the ion pair model or dissociation of the weak electrolyte. The inverse micelles behave like a weak electrolyte, dissociating into positively charged or negatively charged parts; (c) disproportionate mechanism due to collision. The inverse micelles become charged by exchange of charges between two uncharged micelles due to collision. However, according to the rate process theory, the probability of charge exchange between micelles is extremely low without an additional driving force. Those three mechanisms are schematically depicted in Fig. 3, and the corresponding conductivity equations are derived below for the evaluation purpose.
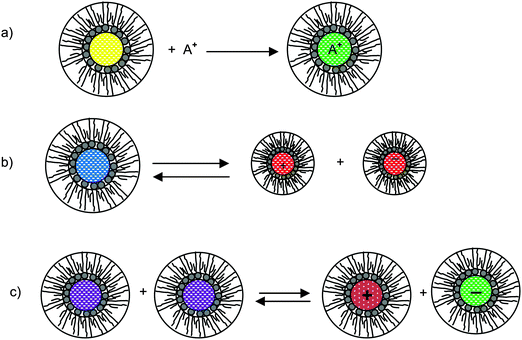 |
| | Fig. 3 Schematic illustration of micelle charging mechanisms proposed in the literature. (a) Preferential ion adsorption: ion A+ is trapped in the center of an inverse micelle structure; (b) ion pair dissociation or called weak-electrolyte-like ionization: a charge neutral inverse micelle containing oppositely charged sites dissociates into two oppositely charged inverse micelles; (c) disproportionation between micelles due to collisions: charge transfer occurred after two inverse micelles collide each other. | |
According to the first ion preferential adsorption mechanism, the concentrations of charged inverse micelles are dependent on the concentrations of impurities and independent of the concentrations of charging agents; apparently, this mechanism is contradictory to the experimental fact that the conductivity linearly increases with the concentrations of the charging agent. The concentration of impurities is a random parameter and the impurities may come from various sources like the container surfaces, the contamination from operators and instruments, the environment conditions, etc. It is hard to imagine that the conductivity may have any predictable patterns with the concentrations of impurities. This mechanism is therefore not discussed further.
According to the second ion pair dissociation mechanism, suppose that the concentration of the original inverse micelles is MAB, and the dissociation equilibrium may be expressed as:
The equilibrium constant of such a process can be expressed:
| | 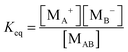 | (28) |
The charged micelle concentrations are:
| | | n+ = n− = Keq1/2(n0/nm)1/2 | (29) |
Again,
n0 is the number of molecules of the charging agent per unit volume and
nm is the number of molecules in a single inverse micelle. Substituting
eqn (29) into
eqn (12) and considering that both positive and negative inverse micelles may contribute to the conductivity leads to:
| | 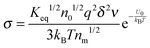 | (30) |
Eqn (30) can be rewritten as below after replacing
δ with
eqn (14) and replacing
n0 with
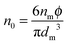
:
| | 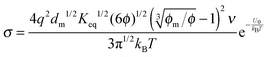 | (31) |
Eqn (31) can be further rewritten below by following the previous methodology,
i.e., replacing
q with
eqn (22),
dm with
eqn (16), and
ν with
eqn (25):
| | 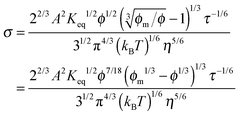 | (32) |
For illustrative purposes, the normalized conductivity
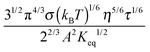
against
ϕ based on
eqn (32) is shown in
Fig. 4. The predicted conductivity doesn't have a linear relationship with the concentrations of the charging agent in any concentration region: it is proportional to
ϕ7/18 even if the term (
ϕm1/3 −
ϕ1/3)
1/3 is considered as a constant in very low concentration regions or a narrow concentration range. This prediction is inconsistent with experimental evidence mentioned earlier. The ion pair dissociation mechanism seemingly answers the question how the charges are generated. However, such a mechanism physically predicts non-linear conductivity dependence on the concentrations of the charging agent. So it may not work for non-aqueous systems.
 |
| | Fig. 4 The normalized conductivity 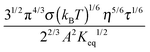 against ϕ based on eqn (32) under the assumptions of ϕm = 0.72 and ϕm = 0.84. The inset is the same data but plotted in a very small normalized conductivity range for clearly demonstrating the linear relationship. This conductivity relationship with the concentration of the inverse micelles is predicted on the basis of the ion pair dissociation charging mechanism. against ϕ based on eqn (32) under the assumptions of ϕm = 0.72 and ϕm = 0.84. The inset is the same data but plotted in a very small normalized conductivity range for clearly demonstrating the linear relationship. This conductivity relationship with the concentration of the inverse micelles is predicted on the basis of the ion pair dissociation charging mechanism. | |
For the third mechanism, the disproportionation model in the literature, the dissociation equilibrium may be expressed as:
The charge exchange may occur between the same types of inverse micelles as expressed earlier, 2A ↔ A
+ + A
−. However, it essentially is the same as expressed in
eqn (33) and thus
eqn (33) will be evaluated. The equilibrium constant can be expressed as:
| | 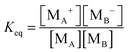 | (34) |
Since there is no difference between the inverse micelles A and B statistically, their concentrations should be the same and equal to:
| | 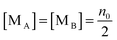 | (35) |
Thus the charged micelle concentration is:
| | 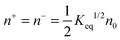 | (36) |
Substituting
eqn (36) into
eqn (12) and considering that both positive and negative inverse micelles may contribute to the conductivity leads to:
| | 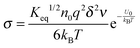 | (37) |
Replacing the parameters
n0,
q,
δ, and
ν with the same methodology used before leads to:
| | 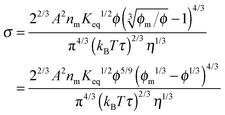 | (38) |
Comparing
eqn (23) with
eqn (38), one may easily tell that
eqn (38) may give a similar normalized conductivity dependence on the volume fraction,
i.e., the conductivity may change with the inverse micelle concentrations at very low concentrations,
σ ∼
ϕ5/9, show a “quasi” linear relationship in the concentration range of 2 × 10
−3 to 5 × 10
−2, and finally reaches a peak at about 0.1. In both equations, the conductivity is inversely proportional to the cubic root of viscosity, which seems to be reasonable; high viscosity usually means low mobility and thus low conductivity intuitively. Although the third mechanism may partially explain the conductivity behavior of the inverse micelles, the charge separation proposed in this mechanism is unlikely to occur, as the Coulombic attraction is so strong in low dielectric constant media, and the probability of charge exchanges is so low based on the rate process theory.
48
In summary, the preferential ion adsorption mechanism leads to the independence of the conductivity to the concentration of the charging agent, which conflicts with the experimental evidence; the ion pair dissociation mechanism looks like a reasonable charging mechanism, but the associated conductivity equation predicts that the conductivity may change with the concentrations of the charging agent as σ ∼ ϕ7/18 most of the time; the disproportionation model predicts that the conductivity could increase with the concentrations of the charging agent in low concentration regions as σ ∼ ϕ5/9. All those equations show that conductivity peaks in relatively high concentration regions, and a further increase of the volume fraction leads to a decrease of the conductivity. Those mechanisms may qualitatively answer the question why non-ionic surfactants could be charged in non-aqueous systems. However, they fail to predict the linear relationship between the conductivity and the concentration of the charging agent, and most importantly, the electric field dependence of conductivity. A new charging mechanism is thus needed.
4. New charging mechanism
As one may know, the Coloumb's law may be expressed as below:| | 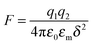 | (39) |
where q1 and q2 are two charge entities, and δ is the distance between them. As mentioned earlier, the dielectric constant of non-aqueous media is about 2.5 and that of water is about 80, the Coloumbic attraction forces in non-aqueous media is almost 30 times stronger than that in aqueous systems. In addition, the electric fields created by charge entities should be almost 30 times stronger in non-aqueous media than that in aqueous media as expressed below:| | 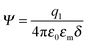 | (40) |
where Ψ is the surface electrical potential created by the charge entity 1 at the distance δ from the center of the charge entity. Such strong electric fields created by many inverse micelles may polarize the neighboring neutral uncharged micelles to disproportionate as shown earlier like 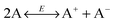 . Under such a scenario, the charge separation may become plausible and non-ionic surfactants could be charged, too.
. Under such a scenario, the charge separation may become plausible and non-ionic surfactants could be charged, too.
We therefore argue that the charges in inverse micelles may most likely be induced by electric fields, especially for non-ionic surfactant systems. The electric fields could be externally applied or generated internally from other charged entities in non-aqueous systems. The primary origin of an electric field could come from many ways: the electrostatic charges from both the containers and the non-aqueous systems themselves, the polar impurities/residues in the non-aqueous systems, the environmental electromagnetic fields, the applied electric field when the conductivity is measured, etc. If a species contains weakly bound charge pairs, the external electric field may induce ion dissociations and create more charged species. Actually, the field-induced charge separation is a generic physical phenomenon widely observed in many other materials.71,72 For non-aqueous systems, this phenomenon was first addressed by Onsager65 who found that the equilibrium constant of such a process is directly proportional to the electric field strength and inversely proportional to the dielectric constant of the medium. In other words, in non-aqueous systems this effect is much more profound than that in aqueous systems.73 Based on the conductivity data, Denat contended38,74 that the inversed micelles may contain a small fraction of the completely ionized (strong electrolytes) component, which may be induced by an external electric field. Lane75 found that the charging process takes place by partitioning ionic species into the inverse micelles. A plausible physical picture for how inverse micelles become charged may be that weakly bound charge pairs on the charging agent or in the inverse micelles may dissociate under an electric field, and the dissociated ions are subsequently stabilized in the polar pool of another neighboring inverse micelle. This charging mechanism is schematically depicted in Fig. 5, and can be simply expressed as:
| | 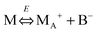 | (41) |
Eqn (41) shows that under an electric field an inverse micelle dissociates into a positively charged inverse micelle and a negative ion. This is an equilibrium process and the equilibrium constant is dependent on the applied electric field; the negative ion is immediately trapped into a polar pool of other neighboring micelles, making this inverse micelle negatively charged. The overall process can be expressed as:
| | 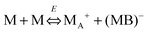 | (43) |
Comparing the processes expressed in
eqn (42) with
eqn (43), one may easily reach the conclusion that
eqn (43) may predict a similar conductivity behavior, as shown in
eqn (38) and (23). However, the equilibrium constant
Keq should be changed, as it is now a function of the applied electric field strength and the resulted conductivity should be different, too. According to Eyring's rate process theory,
48,49 once an electric field is applied, there is a potential gradient that will facilitate the process indicated in
eqn (43), thus generating more separated charge entities. Suppose that in the initial state the free energy is increased by
βw and thus the free energy in the final state will be lowered by (1 −
β)
w, where
β is a fractional operator and
w is the work needed to separate two charge entities to a certain distance. The net rate
k per unit time, representing the “absolute reaction rate” for generating ions, may be expressed as:
48,49| | 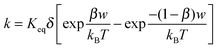 | (44) |
Again,
Keq is the equilibrium constant, and
δ is the distance between two separated charge entities.
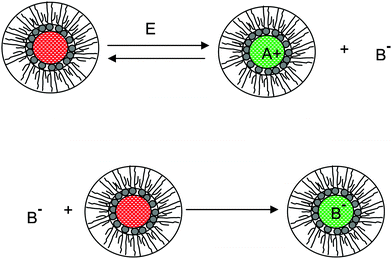 |
| | Fig. 5 The electric-field-induced charging mechanism in inverse micelle systems. A charge neutral inverse micelle becomes charged with the aid of an electric field either from an external or internal sources. The released counterion B− could be further trapped into the center of another charge neutral inverse micelle, making it charged, too. | |
As indicated earlier and shown in eqn (8), αw is usually very small in comparison with kBT. Using the approximation ex ≈ 1 + x, x ≪ 1 leads:
| | 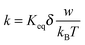 | (45) |
Since
w =
qδE by the definition,
eqn (45) thus can be rewritten as:
| | 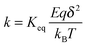 | (46) |
Eqn (46) shows the absolute rate for generating ions under an influence of an electric field. According to Eyring,
48 the concentration of
MA+,
nMA, based on
eqn (43) could be expressed as:
where
nM is the number of inverse micelles per unit volume,
nM =
n0/
nm, by the definition. Therefore,
eqn (47) may be written as:
| | 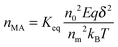 | (48) |
Again, using the generic conductivity equation expressed in
eqn (12) leads to:
| | 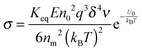 | (49) |
Replacing the parameters,
n0,
q,
δ, and
ν, with the same methodology used before leads to:
| | 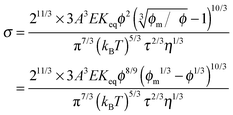 | (50) |
Eqn (50) clearly shows that the conductivity should increase linearly with the applied electric field, which is consistent with experimental results. In most cases, the volume fraction of the charging agent is much smaller than the maximum packing fraction,
ϕ ≪
ϕm, thus (
ϕm−1/3 −
ϕ1/3)
10/3 ≈
ϕm10/9, a constant. Therefore, the conductivity may change with the volume fraction as
σ ∼
ϕ8/9, an almost linear relationship. For illustrating the relationship between the conductivity and the concentrations of inverse micelles, the normalized conductivity
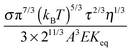
against
ϕ predicted with
eqn (50) is plotted in
Fig. 6. It looks like that the conductivity goes through a maximum at the concentration of inverse micelles of about 5 × 10
−2; in the extremely low concentration region from 10
−9 to 10
−5, the conductivity approximately linearly increases with the concentrations; in the region from 10
−5 to 2 × 10
−3, the conductivity follows a power law with the concentrations; above 2 × 10
−3 and below 5 × 10
−2, the conductivity again linearly increases with the concentrations, before it reaches the maximum point; in the high concentration region above 5 × 10
−2, the conductivity dramatically decreases with the concentrations, which is hard to understand intuitively. The possible reason could be that high concentrations of inverse micelles may impede the movement of charged inverse micelles due to the crowdedness; the competition between different inverse micelles for donating or accepting charges may also slow down the charge exchange rate and then the charge movements. All those factors may lead to a low conductivity resulted from the low mobility of charged inverse micelles.
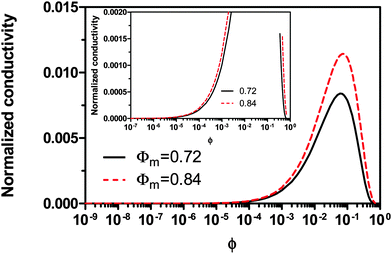 |
| | Fig. 6 The normalized conductivity 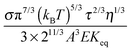 against ϕ based on eqn (50) under the assumptions of ϕm = 0.72 and ϕm = 0.84. The inset is the same data but plotted in a very small normalized conductivity range for clearly demonstrating the linear relationship. This conductivity relationship with the concentrations of the inverse micelles is predicted on the basis of the electric-field-induced charging mechanism. against ϕ based on eqn (50) under the assumptions of ϕm = 0.72 and ϕm = 0.84. The inset is the same data but plotted in a very small normalized conductivity range for clearly demonstrating the linear relationship. This conductivity relationship with the concentrations of the inverse micelles is predicted on the basis of the electric-field-induced charging mechanism. | |
In other words, eqn (50) seems to perfectly catch four major experimental observations: (1) the conductivity linearly increases with the applied electric field; (2) the conductivity may linearly increase with the charge agent concentrations in two concentration regions; (3) the conductivity deviates from the linear relationship in a relatively high concentration region; (4) the conductivity may dramatically drop in very high concentration regions. It also may explain why non-ionic surfactants may get charged; it may be reducible to the disproportionation model in terms of the charging equilibrium process expressed in eqn (43). The electric field induced charging mechanism is therefore considered to correctly reflect how charges are generated in non-aqueous systems. In addition, this mechanism also answers how separated charges are stabilized: it is the electric field that keeps charges separated.
Since the relaxation time τ can be expressed in eqn (24), a function of conductivity and dielectric constants of both phases, eqn (50) may be further written as:
| | 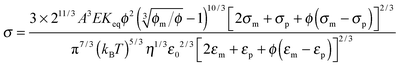 | (51) |
Eqn (51) lists all parameters that may have an impact on conductivity. The conductivity measurement would potentially yield important information like the equilibrium constant
Keq and the material related parameter
A. The major difference between the electric-field-induced charging mechanism and the collision or disproportionation mechanism is that the former shows the conductivity dependence on the electric field strength; while the disproportionation charging mechanism predicts that the conductivity is independent of the electric field. Randriamalala
64 found that the conductivity of AOT solutions indeed increases with an applied electric field as predicted by Onsager's theory up to 5.6 × 10
6 V m
−1 over a wide AOT concentration range. Park
53 showed that the conductivities of both AOT/dodecane and Span 80/dodecane systems are linearly dependent on the applied electric field even as low as 5 × 10
4 V m
−1. The charging mechanisms in non-aqueous systems must take the electric field dependence into account, and the electric-field-induced charging mechanism is thus preferred than other mechanisms like preferential ion absorptions, the ion pair dissociations, and disproportionations.
Note that the relaxation time is assumed to be independent of the applied electric field strength, however, this assumption becomes invalid at high enough electric fields.76,77 Both the dielectric constant and the conductivity have a complicated relationship with strong electric fields45,76–78 due to the nonlinear dielectric effect. The relaxation time therefore becomes dependent on the applied strong electric fields, according to eqn (24). This complication may further make the conductivity deviate from the linear relationship with the concentrations at a very high electric field.
V. Experimental comparisons
For checking the validity of the new mechanism and the associated conductivity equations, eqn (50) and (51), experimental comparisons are made in this section. Fig. 7 shows the experimental conductivity data of Span 80/kerosene solution from the literature52vs. the volume fraction of Span 80. The same data are fitted with eqn (51) and the fitting curve is shown in the same plot. The fitting quality in terms of R2 is 0.952, a very good fitting in the light of that the exact conductivity of kerosene used in the experiment was not specified and is taken from another literature79 for estimation. The deviation from the linear relationship in very low concentration regions could be resulted from the fact that eqn (51) only works for the systems where the inverse micelles have already formed, i.e., above the critical micelle concentration. If the three low concentration data points were removed from the regression, the fitting quality in terms of R2 would become 0.983, a much better fitting. This may imply that eqn (51) may not work for very diluted surfactant systems below the critical micelle concentration. Note that Span 80 is a non-ionic surfactant but frequently used a charging agent. We have to say that eqn (51) fits the experimental conductivity data of Span 80/kerosene solutions pretty well, indicating that charged inverse micelles may form, indeed, in spite of the non-ionic nature of this surfactant.
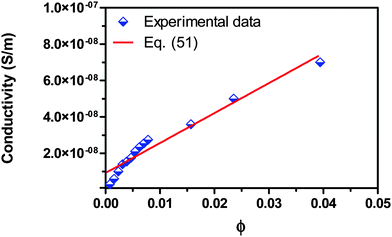 |
| | Fig. 7 Conductivity of Span 80/kerosene solution is plotted against the volume fraction of Span 80 and fitted with eqn (51). The experimental data are taken from Fig. 3 of the literature.52 The conductivities of Span 80 and kerosene are taken as 3.55 × 10−7 S m−1 from the literature52 and 4 × 10−13 S m−1 from the literature,79 and the dielectric constants of Span 80 and kerosene are taken as 4.7 from the literature52 and assumed to be 2.0, respectively. The fitting quality in terms of R2 is 0.952. Note that Span 80 is a non-ionic surfactant. | |
For further validating the new mechanism and the associated conductivity equation for ionic surfactant systems, the conductivity data of AOT/hexadecane solution is taken from the literature80 and plotted against the volume fraction of AOT in Fig. 8. Again, the fitting curve generated from eqn (51) is also shown in Fig. 8. Since there is no experimental data available for the conductivities and dielectric constants of both individual AOT and hexadecane, the conductivities of AOT and hexadecane are assumed to be 6 × 10−8 S m−1 and 3 × 1013 S m−1, and the dielectric constants of AOT and kerosene are assumed to be 5.0 and 2.0, respectively. The fitting quality in terms of R2 is 0.9695, again a pretty good fit with eqn (51). It is noteworthy that the fitting quality is insensitive to what the dielectric constants and conductivities of both AOT and hexadecane are chosen, if they are in a right order of magnitude. Another interesting thing is that eqn (51) may fit the conductivity data very well once the concentration of AOT exceeds the critical micelle concentration, 10−6 according to the literature,80 though the fitting quality in terms of R2, 0.9695, is for the entire dataset. If the two data points at very low concentrations below the critical micelle concentration are taken away, the fitting quality in terms of R2 will increase to 1, a perfect linear fit. This may be inherited from the fact that eqn (51) is derived under the assumption that a large quantity of inverse micelles is formed and the charged inverse micelles solely contribute to the conductivity. Again, this may indicate that eqn (51) is only applicable to the systems where the charging agent concentration is above the critical micelle concentration. Clearly, both Fig. 7 and 8 indicate that eqn (51) works for both non-ionic and ionic surfactant systems, once the charging agent concentration is above the critical micelle concentrations and a large amount of inverse micelle structures form. Those inverse micelle structures would contribute to the conductivity of the whole systems.
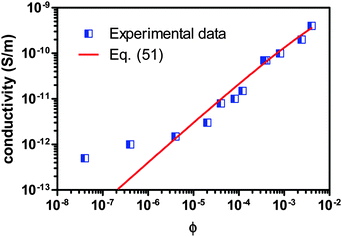 |
| | Fig. 8 Conductivity of AOT/hexadecane solution is plotted against the volume fraction of AOT and fitted with eqn (51). The experimental data are taken from Fig. 3 of the literature80 and the critical micelle concentration is 10−6. The conductivities of AOT and hexadecane are assumed to be 6 × 10−8 S m−1 and 3 × 10−13 S m−1, and the dielectric constants of AOT and hexadecane are assumed to be 5.0 and 2.0, respectively, due to the lack of data from the literature. The fitting quality in terms of R2 is 0.9695 for entire dataset, though eqn (51) may fit the data much better once the concentration is above the critical micelle concentration, 10−5. Note that AOT is an ionic surfactant. | |
We would like to check how eqn (51) is going to fit the electric field dependence of conductivity. Fig. 9 shows the normalized experimental conductivity data of 1 wt% span 85/dodecane against the applied electric field strength from the literature.53 The same data are fitted with eqn (51) and Onsager's equation expressed as σ/![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 1 + γE, where σ/
= 1 + γE, where σ/![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) is the normalized conductivity, γ is a constant
is the normalized conductivity, γ is a constant 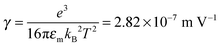 for dodecane. Onsager's theory predicts a linear but relative high conductivity, and eqn (51) again presents a perfect fit with R2 = 0.9953.
for dodecane. Onsager's theory predicts a linear but relative high conductivity, and eqn (51) again presents a perfect fit with R2 = 0.9953.
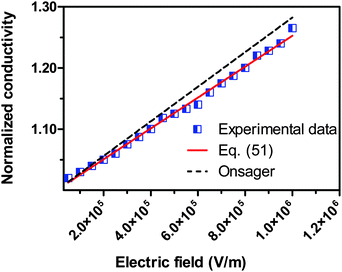 |
| | Fig. 9 The normalized experimental conductivity data of 1 wt% span 85/dodecane against the applied electric field strength from Fig. 4 of the literature.53 The same data are fitted with eqn (51) and Onsager's equation expressed as σ/![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 1 + γE (see literature53), where σ/ = 1 + γE (see literature53), where σ/![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) is the normalized conductivity, and γ is a constant, is the normalized conductivity, and γ is a constant, 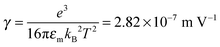 for dodecane. The fitting quality with eqn (51) in terms of R2 is 0.9953, a perfect fit. for dodecane. The fitting quality with eqn (51) in terms of R2 is 0.9953, a perfect fit. | |
From Fig. 7–9, one may easily tell that eqn (51) works for inverse micelle systems and is capable of predicting a correct conductivity dependence on both the charging agent concentrations and the applied electric field.
VI. Discussions
The disproportionation model is relatively favored in the literature,22,34 and is now demonstrated in this article that the corresponding conductivity equation cannot predict the correct relationship between the conductivity and the concentrations of inverse micelles and cannot explain why non-ionic surfactants can be charged in non-aqueous systems. Apparently, one of the major drawbacks of the disproportionation model is that it doesn't lead to a conclusion that the conductivity is also dependent on the applied electric field.
The electric field induced charge mechanism predicts that the conductivity may increase with volume fractions linearly at the beginning, exponentially in the middle, and peak in the relatively high concentrations. A qualitative physical picture could be like this: since the inverse micelles are formed by the surfactant molecules, the high surfactant concentrations could produce more charged inverse micelles, resulting in a linear increase at the beginning; when more charged micelles are created, those charged micelles will impose electric fields to neighboring inverse micelles, making them charged, too. This chain-reaction like charging process leads to an exponential increase of conductivity at relatively higher concentrations due to the large number of charged inversed micelles. In the meanwhile, if the concentrations of the surfactant are too high and too many charged inverse micelles are produced, the collisions between the inverse micelles may slow down the motions of inverse micelles under an electric field, resulting in a lower conductivity and create a conductivity peak against the concentrations. The surprising conductivity decrease at high concentrations of inverse micelles shown in Fig. 2, 4 and 6 is easily understandable. As speculated earlier, the locally concentrated inverse micelles may prevent charged inverse micelles from moving easily due to the spatial crowdedness and reduced free volumes. In addition, the intimate contacts or collisions between neighbored inverse micelles may increase the competitiveness of charge transfers, slowing down the charge movements, too. All those factors may contribute to low mobility of charged inverse micelles, thus resulting in low conductivity.
The electric-field-induced charging mechanism immediately looks awkward to the author, once such a conclusion has to be reached. Intuitively, the charged entities should carry charges intrinsically without relying on external driving forces. On the other hand, since charged entities may generate almost 30 times stronger electric fields locally in non-aqueous systems, they definitely have the capability to polarize the neighboring neutral inverse micelles; the electric-field-induced charge separation thus becomes possible and plausible. The electric fields that either comes from internal neighboring charging entities or from the externally applied sources could be the only reason responsible for polarizing inverse micelles, separating charges, and keeping them apart stably. Both the ion pair dissociation and the disproportionation mechanisms including the fluctuation theory are unable to provide a reasonable explanation on how the separated charges are stabilized in non-aqueous systems; physically, oppositely charged entities in non-aqueous systems tend to preferentially bond together due to almost 30 times stronger Coloumbic attractive forces. Intuitively, the conductivity of inverse micelle systems should be controlled by ionic transportation and those ions likely are the charged inverse micelles.
The conductivity equation derived on the basis of the electric-field-induced charging mechanism shows that the conductivity should linearly increases with the applied electric field strength, and it may increase with the concentrations of inverse micelles as σ ∼ ϕ8/9, an almost linear relationship. Comparison with experimental results obtained by different researchers further demonstrates that the electric-field-induced charging mechanism works for inverse micelle systems, indeed. It even presents a better fit to the conductivity dependence of the applied electric field than Onsager's theory. Although both Park53 and Randriamalala64 confirmed the conductivity dependence on the electric field, they didn't consider the electric field a dominant factor in charging processes; both of those two articles only present a qualitative analysis which may occur in non-aqueous systems and there is no electric-field related conductivity equation proposed.
The relaxation time normally can be considered as a constant, but the relaxation time variation with the electric fields must be taken into account when the applied electric field is high enough. Since the charges of the inverse micelles are induced by electric fields, the dielectric properties of non-aqueous systems may be simply controlled by the electrode polarization process, which is well described in the literature.6 The dielectric investigation together with the conductivity study may provide more insights into the charging mechanisms of non-aqueous systems.
In this article, all surfactants or called charging agents are assumed to fully soluble in non-aqueous media like organic solvents or oils and enough numbers of inverse micelles are already created. This assumption is very true for many non-aqueous systems containing the charging agents listed in Fig. 1. There is no solubility issue in non-aqueous systems, quite different from aqueous systems where surfactant solubility and therefore the Kraft temperature is critical to micelle formation, besides the critical micelle concentrations. The temperatures in my equations are nothing to do with the solubility of surfactants but control the mobility of charged inverse micelles.
VII. Conclusions
The charging mechanisms of non-aqueous multiphase surfactant solutions, emulsions, and colloidal suspensions are addressed in this article, with the focus on inverse micelle charging processes that are commonly involved in all three systems. Three types of charging mechanisms available in the literature, preferential ion absorption, ion pair dissociation, and disproportionation/fluctuation models, are evaluated; the corresponding conductivity equations are derived on the basis of those mechanisms for comparing with the experimental observations. The preferential ion adsorption charging mechanism predicts that the conductivity is dependent on the concentrations of impurities and independent of inverse micelle concentrations, which conflicts with the experimental results; both the ion pair dissociation charging mechanism and the disproportionation mechanism predict that the conductivity may non-linearly increase with the concentrations of inverse micelles, and most importantly the predicted conductivity is independent of the applied electric field strength, which conflicts with experimental observations.
All those three mechanisms are unable to fully explain observed experimental phenomena. Especially, both ion pair dissociation and disproportionation/fluctuation models suffer a big drawback: the charged entities tend to neutrally stay together rather than separate apart due to much stronger Coloumbic attractive forces in non-aqueous systems.
A new electric-field-induced charging mechanism is proposed to explain how inverse micelles are charged and why charges can be separated and stabilized. It clearly answers why non-ionic surfactants can still be charged in non-aqueous systems. The needed electric fields could come from nearby charging species or from the externally applied sources. The obtained conductivity equation under this charging mechanism shows a complicated relationship with the charges, the electric field, the volume fraction of the charging agent, the relaxation time, and the temperature. The conductivity equation derived on this basis of this mechanism correctly captures four major experimental observations: (1) the conductivity linearly increases with the applied electric field; (2) the conductivity almost linearly increases with concentrations, following σ ∼ ϕ8/9; (3) the conductivity deviates from the linear relationship in a relatively high concentration region; (4) the conductivity may dramatically drop in very high concentration regions. It fits the experimental data pretty well for both conductivity vs. the concentration of the charging agent and conductivity vs. the applied electric field. Our work may shed light on many long time puzzles in non-aqueous multiphase systems, and may potentially have a broad impact in many industrial areas.
References
- W. S. Thomas, S. J. Vella, G. K. Kaufman and G. M. Whitesides, Patterns of electrostatic charge and discharge in contact electrification, Angew. Chem., Int. Ed., 2008, 47, 6654–6656 CrossRef PubMed.
- E. D. Lachiver, N. Abatzoglou, L. Cartilier and J. Simard, Insights into the role of electrostatic forces on the behavior of dry pharmaceutical particulate systems, Curr. Pharma Res., 2006, 23(5), 997–1007 CrossRef PubMed.
- L. S. McCarty and G. M. Whitesides, Electrostatic Charging Due to Separation of Ions at Interfaces: Contact Electrification of Ionic Electrets, Angew. Chem., Int. Ed., 2008, 47, 2188–2207 CrossRef CAS PubMed.
-
R. J. Hunter, Zeta Potential In Colloidal Science, Academic Press, 1981 Search PubMed.
-
D. Myers, Surfaces, Interfaces, and Colloids, VCH Publishers, 1991 Search PubMed.
-
T. Hao, Electrotheological Fluids, The non-aqueous suspensions, Elsevier, 2005 Search PubMed.
- I. D. Morrison, Electrical charges in nonaqueous media, Colloids Surf., A, 1993, 71, 1–37 CrossRef CAS.
- L. F. Scatena and G. L. Richmond, Aqueous solvation of charge at hydrophobic liquid surfaces, Chem. Phys. Lett., 2004, 383, 491–495 CrossRef CAS.
- S. Reuter and S. Franks, Models for the Charging of Particles in Liquid Toners: A Summary, J. Imaging Sci. Technol., 2004, 48, 319–323 CAS.
- F. Beunis, F. Strubbe, M. Karvar, O. Drobchak, T. Brans and K. Neyts, Inverse micelles as charge carriers in nonpolar liquids: Characterization with current measurements, Curr. Opin. Colloid Interface Sci., 2013, 18, 129–136 CrossRef CAS.
- F. Strubbe, F. Beunis, T. Brans, M. Karvar, W. Woestenborghs and K. Neyts, Electrophoretic Retardation of Colloidal Particles in Nonpolar Liquids, Phys. Rev. X, 2013, 3, 021001 Search PubMed.
- Y. Huang, F. Lin, S. Wu and P. Yang, Mechanism and Improvement of Charged-Particles Transition in Microcup Electrophoretic Displays, J. Disp. Technol., 2013, 9, 619–625 CrossRef.
- H. Cao, N. Lu, B. Ding and M. Qi, Regulation of charged reverse micelles on particle charging in nonpolar media, Phys. Chem. Chem. Phys., 2013, 15, 12227–12234 RSC.
- S. K. Sainis, V. Germain, C. O. Mejean and E. R. Dufresne, Electrostatic Interactions of Colloidal Particles in Nonpolar Solvents: Role of Surface Chemistry and Charge Control Agents, Langmuir, 2008, 24, 1160–1164 CrossRef CAS PubMed.
- M. E. Leunissen, A. van Blaaderen, A. D. Hollingsworth, M. T. Sullivan and P. M. Chaikin, Electrostatics at the oil–water interface, stability and order in emulsions and colloids, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 2585–2590 CrossRef CAS PubMed.
- L. Moreau, H. Kim, E. A. Decker and D. J. McClements, Production and Characterization of Oil-in-Water Emulsions Containing Droplets Stabilized by beta-Lactoglobulin–Pectin Membranes, J. Agric. Food Chem., 2003, 51(22), 6612–6617 CrossRef CAS PubMed.
- A. Dukhin and P. Goetz, Evolution of water-in-oil emulsion controlled by droplet-bulk ion exchange: acoustic, electroacoustic, conductivity and image analysis, Colloids Surf., A, 2005, 253, 51–64 CrossRef CAS.
- F. Strubbe, M. Prasad and F. Beunis, Characterizing Generated Charged Inverse Micelles with Transient Current Measurements, J. Phys. Chem. B, 2015, 119, 1957–1965 CrossRef CAS PubMed.
- G. S. Roberts, R. Sanchez, R. Kemp, T. Wood and P. Bartlett, Electrostatic Charging of Nonpolar Colloids by Reverse Micelles, Langmuir, 2008, 24, 6530–6541 CrossRef CAS PubMed.
- M. Karvar, F. Strubbe, F. Beunis, R. Kemp, N. Smith, M. Goulding and K. Neyts, Investigation of various types of inverse micelles in nonpolar Using Transient Current Measurements, Langmuir, 2014, 30, 12138–12143 CrossRef CAS PubMed.
- M. F. Hsu, E. R. Dufresne and D. A. Weitz, Charge
Stabilization in Nonpolar Solvents, Langmuir, 2005, 21(11), 4881–4887 CrossRef CAS PubMed.
- A. Dukhin and S. Parlia, Ions, ion pairs and inverse micelles in non-polar media, Curr. Opin. Colloid Interface Sci., 2013, 18, 93–115 CrossRef CAS.
- J. Lyklema, Principles of interactions in non-aqueous electrolyte solutions, Curr. Opin. Colloid Interface Sci., 2013, 18(2), 116–128 CrossRef CAS.
- X. Li, G. He, W. Zheng and G. Xiao, Study on conductivity property and microstructure of TritonX-100/alkanol/n-heptane/water microemulsion, Colloids Surf., A, 2010, 360, 150–158 CrossRef CAS.
- J. L. van der Minne and P. H. J. Hermanie, Electrophoresis measurements in benzene–correlation with stability. II. results of electrophoresis, stability and adsorption, J. Colloid Sci., 1953, 8, 38–52 CrossRef CAS.
- R. J. Pugh, T. Matsunaga and F. M. Fowkes, The dispersibility and stability of carbon black in media of low dielectric constant. 1. Electrostatic and steric contributions to colloidal stability, Colloids Surf., 1983, 7, 183–207 CrossRef CAS.
- R. J. Pugh and F. M. Fowkes, The dispersibility and stability of coal particles in hydrocarbon media with a polyisobutene succinamide dispersing agent, Colloids Surf., 1984, 11, 423–427 CrossRef CAS.
- R. J. Pugh and F. M. Fowkes, The dispersibility and stability of carbon black in media of low dielectric constant. 2. Sedimentation volume of concentrated dispersions, adsorption and surface calorimetry studies, Colloids Surf., 1984, 9, 33–46 CrossRef CAS.
- A. Kitahara, T. Kobayashi and T. Tachibana, Light Scattering Study of Solvent Effect on Micelle Formation of Aerosol OT, J. Phys. Chem., 1962, 66(2), 363–365 Search PubMed.
- H. F. Eicke and H. Christen, Nucleation process of micelle formation in apolar solvents, J. Colloid Interface Sci., 1974, 48, 281–290 CrossRef CAS.
- W. R. Heffiner and M. A. Marcus, Power law behavior of conductivity in the AOT/dichloroethane system, J. Colloid Interface Sci., 1988, 124, 617–623 CrossRef.
- D. M. Zhu, K. I. Feng and Z. A. Schelly, Reverse micelles of Triton X-100 in cyclohexane: effects of temperature, water content and salinity on the aggregation behavior, J. Phys. Chem., 1992, 96(5), 2382–2385 CrossRef CAS.
- P. A. Cirkel, M. Fontana and G. J. M. Koper, Structure and Percolation of Inverted Cylindrical Branched Micelles, J. Dispersion Sci. Technol., 2001, 22, 211–219 CrossRef CAS.
- Q. Guo, V. Singh and S. H. Behrens, Electric Charging in Nonpolar Liquids Because of Nonionizable Surfactants, Langmuir, 2010, 26(5), 3203–3207 CrossRef CAS PubMed.
- G. N. Smith and J. Eastoe, Controlling colloid charge in nonpolar liquids with surfactants, Phys. Chem. Chem. Phys., 2013, 15, 424–439 RSC.
-
I. D. Morrison and S. Ross, Colloidal Dispersion, John Wiley and Sons, Inc., New York, 2002 Search PubMed.
-
T. G. Davis, G. A. Gibson, R. H. Luebbe and K. Yu, Proc. 5th Inter. Cong. Adv. Non-impact Printing Techn., SPSE, Springfield, VA, 1989, pp. 404–416 Search PubMed.
- A. Denat, B. Gosse et and J. P. Gosse, Conductivité électrique de solutions de surfactants dans les hydrocarbures, Rev. Phys. Appl., 1981, 16, 673–678 CrossRef CAS.
- R. M. Fuoss and C. A. Kraus, Properties of electrolytic solutions. IV. The conductance minimum and the formation of triple ions due to the action of columbic forces, J. Am. Chem. Soc., 1933, 55(6), 2387–2399 CrossRef CAS.
- L. Onsager, Report on revision of the conductivity theory, Trans. Faraday Soc., 1927, 23, 341–349 RSC.
- R. M. Fuoss, Ionic association. I. Derivation of constants from conductance data, J. Am. Chem. Soc., 1957, 79(13), 3301–3303 CrossRef CAS.
- S. M. Nelson and R. C. Pink, Solutions of metal soaps in organic solvents. Part IV. Direct current conductivity in solutions of some metal oleates in toluene, J. Chem. Soc., 1954, 4412–4417 RSC.
- A. Kitahara, Zeta potential in non-aqueous media and its effect on dispersion, Prog. Org. Coat., 1973, 2(2), 81–98 CrossRef CAS.
- H. F. Eicke, M. Borkovec and B. Das-Gupta, Conductivity of water-in-oil microemulsions: a quantitative charge fluctuation model, J. Phys. Chem., 1989, 93, 314–317 CrossRef CAS.
-
G. I. Skanavi, Dielectric Physics [in Russian], Gosénergoizdat, Moscow-Leningrad, 1952 Search PubMed.
-
A. R. von Hippel, Dielectric Materials and Applications, Technology Press of MIT and John Wiley, New York, 1954 Search PubMed.
-
S. Smedley, The Interpretation of Ionic Conductivity in Liquids, Springer, 2012 Search PubMed.
-
S. Glasstone, K. Laidler and H. Eyring, The theory of rate process, McGraw-Hill, New York, 1941 Search PubMed.
- T. Hao, Electrical conductivity equations derived with the rate process theory and free volume concept, RSC Adv., 2015, 5, 48133–48146 RSC.
-
C. Kittel, Introduction to Solid State Physics, Wiley, 2004 Search PubMed.
- F. Beunis, F. Strubbe, M. Karvar, O. Drobchak, T. Brans, K. Neyts and A. R. M. Verschueren, Electric charging of inverse micelles in a nonpolar liquid with surfactant, Colloids Surf., A, 2014, 440, 10–19 CrossRef CAS.
- A. S. Dukhin and P. J. Goetz, How non-ionic “electrically neutral” surfactants enhance electrical conductivity and ion stability in non-polar liquids, J. Electroanal. Chem., 2006, 588, 44–50 CrossRef CAS.
- J. K. Park, J. C. Ryu, W. K. Kim and K. H. Kang, Effect of Electric Field on Electrical Conductivity of Dielectric Liquids Mixed with Polar Additives: DC Conductivity, J. Phys. Chem. B, 2009, 113, 12271–12276 CrossRef CAS PubMed.
- T. Hao and R. E. Riman, Calculation of interparticle spacing in colloidal systems, J. Colloid Interface Sci., 2006, 297, 374–377 CrossRef CAS PubMed.
- T. Hao, Tap density equations of granular powders based on the rate process theory and the free volume concept, Soft Matter, 2015, 11, 1554–1561 RSC.
-
H. Fröhlich, Theory of Dielectrics: Dielectric Constant and Dielectric Loss, Clarendon Press, 1949 Search PubMed.
-
E. Iguchi, D. I. Savytskii and M. Kurumada, AC meaurements of high ionic conductivity due to oxygen migrations in doped Lanthanum Gallates, in Diffusion and Reactivity of Solids, ed. J. Y. Murdoch, Nova Publishers, 2007, pp. 115–161 Search PubMed.
- F. Strubbe, F. Beunis and K. Neyts, Determination of the effective charge of individual colloidal particles, J. Colloid Interface Sci., 2006, 301, 302–309 CrossRef CAS PubMed.
- L. Bocquet, E. Trizac and M. Aubouy, Effective charge saturation in colloidal suspensions, J. Chem. Phys., 2002, 117, 8138–8152 CrossRef CAS.
- M. Aubouy, E. Trizac and L. Bocquet, Effective charge versus bare charge: an analytical estimate for colloids in the infinite dilution limit, J. Phys. A: Math. Gen., 2003, 36, 5835–5840 CrossRef CAS.
- J. H. Conway and S. Torquato, Packing, tiling and covering with tetrahedra, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(28), 10612–10617 CrossRef CAS PubMed.
- J. H. Conway, Y. Jiao and S. Torquato, A New Family of Tilings of Three-Dimensional Euclidean Space by Tetrahedra and Octahedra, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(27), 11009–11012 CrossRef CAS PubMed.
- K. W. Wagner, Erklärung der dielektrischen Nachwirkungsvorgänge auf Grund Maxwellscher Vorstellungen, Arch. Elektrotech., 1914, 2(9), 371–387 CrossRef.
- Z. Randriamalala, A. Denat, J. P. Gosse and B. Gosse, Field-Enhanced Dissociation, the Validity of Onsager's Theory in Surfactant Solutions, IEEE Trans. Electr. Insul., 1985, EI–20, 167–176 CrossRef CAS.
- L. Onsager, Deviations from Ohm's Law in Weak Electrolytes, J. Chem. Phys, 1934, 2, 599–615 CrossRef CAS.
-
I. D. Morrison, The influence of electric charges in nonaqueous dispersions, in Dispersion and Aggregation: Fundamentals and applications, ed. B. M. Moudgil and P. Somasundaran, The Eng. Fundation, New York, 1994, pp. 55–73 Search PubMed.
- I. D. Morrison, Electrical charges in nonaqueous media, Colloids Surf., A, 1993, 71, 1–37 CrossRef CAS.
- A. Kitahara, T. Satoh, S. Kawasaki and K. Kon-No, Specific adsorption of surfactants containing Mn or Co on polymer particles revealed by zeta-potential in cyclohexane, J. Colloid Interface Sci., 1982, 86, 105–110 CrossRef CAS.
- F. M. Fowkes, General Discussion, Discuss. Faraday Soc., 1966, 42, 243–247 RSC.
-
M. Kosmulski, Electrical interfacial layer in nonaqueous solvents, in Interfacial Dynamics, ed. N. Kallay, Marcel Dekker, 2000, pp. 273–312 Search PubMed.
- S. Inal, M. Schubert, A. Sellinger and D. Neher, The Relationship between the Electric Field-Induced Dissociation of Charge Transfer Excitons and the Photocurrent in Small Molecular/Polymeric Solar Cells, J. Phys. Chem. Lett., 2010, 1(6), 982–986 CrossRef CAS.
- C. O. Reinhold, S. Yoshida and F. B. Dunning, Field-induced dissociation of Rydberg ion-pair states, J. Phys.: Conf. Ser., 2012, 388, 022064 CrossRef.
- A. Alj, J. P. Gosse, B. Gosse, A. Denat and M. Nemamcha, Influence de la nature du surfactant ionique sur la conduction électrique de ses solutions dans le cyclohexane, Rev. Phys. Appl., 1987, 22, 1043–1053 CrossRef CAS.
- A. Denat, B. Gosse and J. P. Gosse, Electrical conduction of solutions of an ionic surfactant in hydrocarbons, J. Electrost., 1982, 12, 197–205 CrossRef CAS.
-
G. A. Lane, Hard Copy and Printing Materials, Media and Processes, SPIE, 1990, p. 29 Search PubMed.
-
W. F. Schmidt, Liquid State Electronics of Insulated Liquids, CRC Press, 1997 Search PubMed.
-
J. Zioło, S. J. Rzoska and A. Drozd-Rzoska, Medium-Range Ordering in Liquids Appearing in Nonlinear Dielectric Effect Studies, in Nonlinear Dielectric Phenomena in Complex Liquids, ed. S. J. Rzoska and A. V. Zhelezny, Spinger, 2005, vol. 157, pp. 269–273 Search PubMed.
-
D. Andre, Conduction and breakdown initiation in dielectric liquids, IEEE International Conference on Dielectric Liquids (ICDL), Trondheim, 2011, pp. 1–11 Search PubMed.
-
Y. Matsubara, Electrical Conductivity of Kerosene by DC Measurement, Electrical Insulation and Dielectric Phenomena, 2000 Annual Report Conference on, Victoria, BC, 2000, pp. 260–263 Search PubMed.
- S. K. Sainis, J. W. Merrill and E. R. Dufresne, Electrostatic Interactions of Colloidal Particles at Vanishing Ionic Strength, Langmuir, 2008, 24, 13334–13337 CrossRef CAS PubMed.
|
| This journal is © the Owner Societies 2016 |
Click here to see how this site uses Cookies. View our privacy policy here. 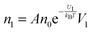
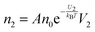
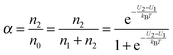
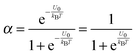
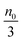 , and the number of molecules in the positive axis is
, and the number of molecules in the positive axis is 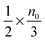 . So in a unit time period the number of molecules overcoming the energy barrier, U0, is:
. So in a unit time period the number of molecules overcoming the energy barrier, U0, is: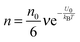
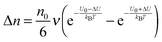
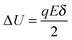
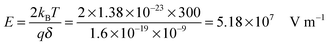
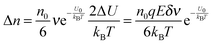
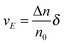
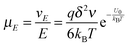
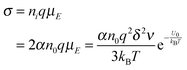
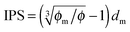
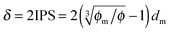
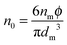 , based on the definition. Therefore, eqn (12) may be rewritten as:
, based on the definition. Therefore, eqn (12) may be rewritten as: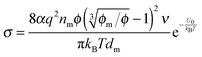
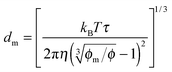
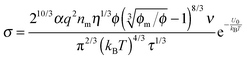
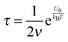
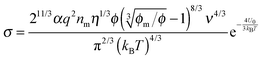
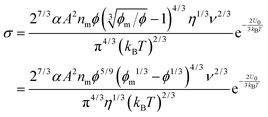
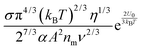 against ϕ for the illustrative purpose. Since inverse micelle structures are soft and can be deformed easily, two dense packing structures are assumed to occur theoretically: ϕm = 0.72 and ϕm = 0.84, which corresponds to non-lattice tetrahedra and Icosahedra,61,62 respectively. At extremely low volume fractions, the term (ϕm1/3 − ϕ1/3)4/3 in eqn (23) may be approximated as a constant, (ϕm1/3 − ϕ1/3)4/3 ≈ ϕm4/9, and the conductivity may change with ϕ5/9. Clearly, the conductivity doesn't have a linear relationship with the volume fraction of the inverse micelles in low concentration regions. Only in the relatively high concentration region, starting at the volume fraction about 2 × 10−3 and until reaching a concentration of about 5 × 10−2, there seems to be a linear relationship between the conductivity and the volume fraction. A further volume fraction increase makes the conductivity dramatically increase by obeying a power law and then reach a peak, a very unusual phenomenon. As indicated earlier, the linear dependence of conductivity on the concentrations of the surfactants in low concentration regions has been reported in many articles. However, the drop off in high concentration regions is rarely reported, besides one system with Span 80,22 showing the surface charge converted from the conductivity drops at relatively higher concentrations, which is qualitatively consistent with eqn (23). Since the inverse micelles are formed by the surfactant molecules, the high surfactant concentrations could create more charged inverse micelles, resulting in a linear increase of conductivity at the beginning; once more charged micelles are created, those charged micelles will impose electric fields to neighboring inverse micelles, making them charged, too. This chain-reaction like charging process leads to an exponential increase of conductivity at relatively higher concentrations due to the large number of charged inversed micelles. As shown in eqn (13) and (14), higher concentrations of charging agents will eventually lead to a smaller free walk distance, thus lowering conductivity.
against ϕ for the illustrative purpose. Since inverse micelle structures are soft and can be deformed easily, two dense packing structures are assumed to occur theoretically: ϕm = 0.72 and ϕm = 0.84, which corresponds to non-lattice tetrahedra and Icosahedra,61,62 respectively. At extremely low volume fractions, the term (ϕm1/3 − ϕ1/3)4/3 in eqn (23) may be approximated as a constant, (ϕm1/3 − ϕ1/3)4/3 ≈ ϕm4/9, and the conductivity may change with ϕ5/9. Clearly, the conductivity doesn't have a linear relationship with the volume fraction of the inverse micelles in low concentration regions. Only in the relatively high concentration region, starting at the volume fraction about 2 × 10−3 and until reaching a concentration of about 5 × 10−2, there seems to be a linear relationship between the conductivity and the volume fraction. A further volume fraction increase makes the conductivity dramatically increase by obeying a power law and then reach a peak, a very unusual phenomenon. As indicated earlier, the linear dependence of conductivity on the concentrations of the surfactants in low concentration regions has been reported in many articles. However, the drop off in high concentration regions is rarely reported, besides one system with Span 80,22 showing the surface charge converted from the conductivity drops at relatively higher concentrations, which is qualitatively consistent with eqn (23). Since the inverse micelles are formed by the surfactant molecules, the high surfactant concentrations could create more charged inverse micelles, resulting in a linear increase of conductivity at the beginning; once more charged micelles are created, those charged micelles will impose electric fields to neighboring inverse micelles, making them charged, too. This chain-reaction like charging process leads to an exponential increase of conductivity at relatively higher concentrations due to the large number of charged inversed micelles. As shown in eqn (13) and (14), higher concentrations of charging agents will eventually lead to a smaller free walk distance, thus lowering conductivity.

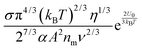 against ϕ based on eqn (23) under the assumptions of ϕm = 0.72 and ϕm = 0.84. The inset is the same data but plotted in a very small normalized conductivity range for clearly demonstrating the linear relationship.
against ϕ based on eqn (23) under the assumptions of ϕm = 0.72 and ϕm = 0.84. The inset is the same data but plotted in a very small normalized conductivity range for clearly demonstrating the linear relationship.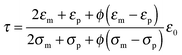
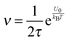

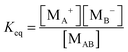
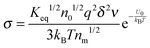
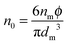 :
: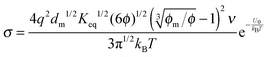
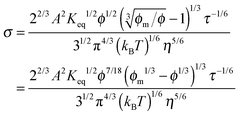
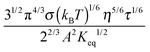 against ϕ based on eqn (32) is shown in Fig. 4. The predicted conductivity doesn't have a linear relationship with the concentrations of the charging agent in any concentration region: it is proportional to ϕ7/18 even if the term (ϕm1/3 − ϕ1/3)1/3 is considered as a constant in very low concentration regions or a narrow concentration range. This prediction is inconsistent with experimental evidence mentioned earlier. The ion pair dissociation mechanism seemingly answers the question how the charges are generated. However, such a mechanism physically predicts non-linear conductivity dependence on the concentrations of the charging agent. So it may not work for non-aqueous systems.
against ϕ based on eqn (32) is shown in Fig. 4. The predicted conductivity doesn't have a linear relationship with the concentrations of the charging agent in any concentration region: it is proportional to ϕ7/18 even if the term (ϕm1/3 − ϕ1/3)1/3 is considered as a constant in very low concentration regions or a narrow concentration range. This prediction is inconsistent with experimental evidence mentioned earlier. The ion pair dissociation mechanism seemingly answers the question how the charges are generated. However, such a mechanism physically predicts non-linear conductivity dependence on the concentrations of the charging agent. So it may not work for non-aqueous systems.

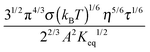 against ϕ based on eqn (32) under the assumptions of ϕm = 0.72 and ϕm = 0.84. The inset is the same data but plotted in a very small normalized conductivity range for clearly demonstrating the linear relationship. This conductivity relationship with the concentration of the inverse micelles is predicted on the basis of the ion pair dissociation charging mechanism.
against ϕ based on eqn (32) under the assumptions of ϕm = 0.72 and ϕm = 0.84. The inset is the same data but plotted in a very small normalized conductivity range for clearly demonstrating the linear relationship. This conductivity relationship with the concentration of the inverse micelles is predicted on the basis of the ion pair dissociation charging mechanism.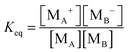
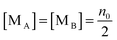
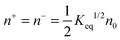
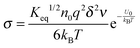
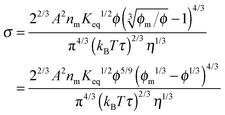
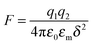
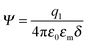
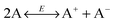 . Under such a scenario, the charge separation may become plausible and non-ionic surfactants could be charged, too.
. Under such a scenario, the charge separation may become plausible and non-ionic surfactants could be charged, too.
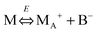
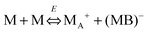
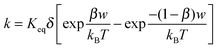
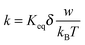
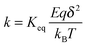
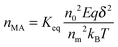
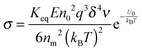
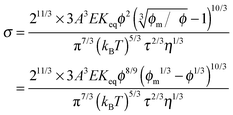
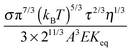 against ϕ predicted with eqn (50) is plotted in Fig. 6. It looks like that the conductivity goes through a maximum at the concentration of inverse micelles of about 5 × 10−2; in the extremely low concentration region from 10−9 to 10−5, the conductivity approximately linearly increases with the concentrations; in the region from 10−5 to 2 × 10−3, the conductivity follows a power law with the concentrations; above 2 × 10−3 and below 5 × 10−2, the conductivity again linearly increases with the concentrations, before it reaches the maximum point; in the high concentration region above 5 × 10−2, the conductivity dramatically decreases with the concentrations, which is hard to understand intuitively. The possible reason could be that high concentrations of inverse micelles may impede the movement of charged inverse micelles due to the crowdedness; the competition between different inverse micelles for donating or accepting charges may also slow down the charge exchange rate and then the charge movements. All those factors may lead to a low conductivity resulted from the low mobility of charged inverse micelles.
against ϕ predicted with eqn (50) is plotted in Fig. 6. It looks like that the conductivity goes through a maximum at the concentration of inverse micelles of about 5 × 10−2; in the extremely low concentration region from 10−9 to 10−5, the conductivity approximately linearly increases with the concentrations; in the region from 10−5 to 2 × 10−3, the conductivity follows a power law with the concentrations; above 2 × 10−3 and below 5 × 10−2, the conductivity again linearly increases with the concentrations, before it reaches the maximum point; in the high concentration region above 5 × 10−2, the conductivity dramatically decreases with the concentrations, which is hard to understand intuitively. The possible reason could be that high concentrations of inverse micelles may impede the movement of charged inverse micelles due to the crowdedness; the competition between different inverse micelles for donating or accepting charges may also slow down the charge exchange rate and then the charge movements. All those factors may lead to a low conductivity resulted from the low mobility of charged inverse micelles.

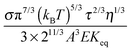 against ϕ based on eqn (50) under the assumptions of ϕm = 0.72 and ϕm = 0.84. The inset is the same data but plotted in a very small normalized conductivity range for clearly demonstrating the linear relationship. This conductivity relationship with the concentrations of the inverse micelles is predicted on the basis of the electric-field-induced charging mechanism.
against ϕ based on eqn (50) under the assumptions of ϕm = 0.72 and ϕm = 0.84. The inset is the same data but plotted in a very small normalized conductivity range for clearly demonstrating the linear relationship. This conductivity relationship with the concentrations of the inverse micelles is predicted on the basis of the electric-field-induced charging mechanism.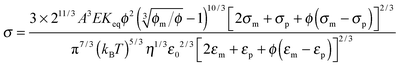


![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 1 + γE, where σ/
= 1 + γE, where σ/![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) is the normalized conductivity, γ is a constant
is the normalized conductivity, γ is a constant 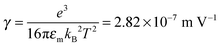 for dodecane. Onsager's theory predicts a linear but relative high conductivity, and eqn (51) again presents a perfect fit with R2 = 0.9953.
for dodecane. Onsager's theory predicts a linear but relative high conductivity, and eqn (51) again presents a perfect fit with R2 = 0.9953.
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 1 + γE (see literature53), where σ/
= 1 + γE (see literature53), where σ/![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) is the normalized conductivity, and γ is a constant,
is the normalized conductivity, and γ is a constant, 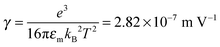 for dodecane. The fitting quality with eqn (51) in terms of R2 is 0.9953, a perfect fit.
for dodecane. The fitting quality with eqn (51) in terms of R2 is 0.9953, a perfect fit.


