Hydrogen-bonded 4H-1-benzopyrane-4-thione–water complexes properties in the S2 excited state: the mechanism and dynamics of deactivation
E.
Krystkowiak
*a,
R. A.
Bachorz
b and
A.
Maciejewski
a
aFaculty of Chemistry, Adam Mickiewicz University in Poznań, Poznań, Poland. E-mail: ewakryst@amu.edu.pl
bInstitute of Medical Biology of the Polish Academy of Sciences, Łódź, Poland
First published on 13th November 2015
Abstract
Unexpected results of spectral emission and photophysical study of S2-excited 4H-1-benzopyrane-4-thione (BPT) in water solution were explained by intermolecular hydrogen bonding. There are at least two types of BPT–water complexes that participate in the S2-fluorescence similarly as in S0 → S2 absorption. They both deactivate with high efficiency in internal conversion S2 → S1 and in intersystem crossing S1 → T1 processes.
Introduction
Aromatic thioketones show many interesting spectral and photophysical properties including direct S0 → T1 absorption, thermally activated S1-fluorescence, well-resolved S0 → S1, S0 → S2 and S0 → S3 absorption bands, fluorescence from the S2 state, and phosphorescence from the T1 state in solution at room temperature.2–5 In perfluorohydrocarbons, the S2(π,π*) state decay is exclusively intramolecular due to weak solute–solvent interactions. In all other solvents, irrespective of polarity and protic character, the S2 state is known to be extremely short-lived because of efficient intermolecular quenching2–8 or intracomplex deactivation as in the hydrogen-bonded thioketone–water complex.9 For illustration, for the xanthione whose S2-state lifetime, τS2, is 152 ps in perfluoro-n-hexane, it is much shortened to τS2 = 38 ps in tetrachloromethane, τS2 = 24 ps in n-hexane, τS2 = 14 ps in acetonitrile and τS2 = 5 ps in toluene.10,11 Similarly, for 4H-1-benzopyrane-4-thione, BPT (Fig. 1), the lifetime τS2 strongly depends on the solvent properties.12 For thiocoumarin, TC, an isomer of BPT, a very short S2-state lifetime, τS2 = 450 fs was found in n-hexane, and only 150 fs in acetonitrile.13 Irrespective of the S2-state lifetime, the observed decays of fluorescence are almost always monoexponential.Unexpectedly, for a few aromatic thioketones and only in perfluorohydrocarbons and aliphatic hydrocarbons, the quantum yields of fluorescence have been determined, ϕF.2,4,7,8,12 Moreover, no information has been published on the influence of the excitation wavelength, λexc, on the position and shape of their emission spectra and ϕF value. Because of a very short τS2, for TC, a strong dependence of the fluorescence spectrum position on λexc is observed. Upon TC excitation to the S2 state with a large excess of vibration energy (Δν ∼ 5000 cm−1) the fluorescence spectrum is strongly hypsochromically shifted.14 It is gradually shifted towards longer wavelengths upon TC excitation to the vibrational levels of the S2 state with decreasing energy excess. For TC, in contrast to BPT, even in perfluoro-n-hexane, the S2-state lifetime is very short, <1 ps, as indicated by a very small ϕF = 5 × 10−5.14 Most probably, the very fast process of conical intersection (intramolecular) is responsible for the very short τS2.
The lifetime in the S2 state determined for BPT in water from emission decay as well as from the transient absorption decay, τS2, is just 1 ps, while in D2O it is close to 2 ps.9 The twice longer τS2 in D2O than in water points directly to a significant role of hydrogen bonds S⋯H(D)–O in deactivation of S2-BPT in water.
The hydrogen bond and nonspecific interaction energies for the BPT–water complexes in the ground state S0 and the excited singlet states S1 and S2 have been determined by us using ab initio computational methods.1 In this paper we have shown that the BPT molecule can form four relatively strong hydrogen bonds with the water molecules in the ground S0 as well as in the excited S1 and S2 electronic states. The energies of the hydrogen bonds formed between BPT and water molecules are predicted to significantly decrease in the S1(n,π*) state and increase in the S2(π,π*) state, when compared to that in the ground state S0. It is worth noting that a similar effect has been found by Zhao and Han15,16 for the BPT–methanol complex. The S0 → S1 and S0 → S2 transition energies calculated for the BPT–(H2O)4 complex, including the nonspecific solute–solvent interactions, are in very good agreement with the experimental absorption maxima of S1 and S2 states, determined for BPT in water.1 Moreover, the changes in the hydrogen bond energies upon electronic excitation to the S1 and S2 states, determined from an experimental solvatochromic study, are in remarkably good agreement with those resulting from the ab initio calculation.1
In the present paper a detailed S2-emission spectral and photophysical study for BPT in water is presented. A computational study of difference in stoichiometry, structure and energy hydrogen-bonded BPT–water complexes in the electronic excited S2 state and their influence on the S2 → S0 transition energies has been also performed. The results of these studies should provide information on the presence and deactivation mechanisms of intermolecular solute–solvent hydrogen-bonded complexes for BPT in their electronic excited S2 state in water solution. They should also permit to conclude if the excess vibrational energy (in the range of 1000–5000 cm−1) in the short-lived S2 state influences the deactivation processes and the position and shape of the emission spectrum.
Computational and experimental methods
Experimental details
BPT was synthesized and purified by the methods described elsewhere.17,18 Compounds 1-chloropropane (99%) (Aldrich), 1-chlorohexane (99%) (Aldrich), 1-chlorodecane (98%) (Aldrich), 1-chlorohexadecane (98%) (Fluka), and propionitrile (PrCN) (Fluka) were additionally dried over molecular sieves (A3, A4). Water was distilled and deionized. The absorption spectra were measured on a spectrophotometer Jasco V-650. Steady-state emission measurements were made on a Jobin Yvon-Spex Fluorolog 3-22 spectrofluorimeter. The emission spectra were corrected for the sensitivity of the detection system. Thioketone concentration was approximately 10−5–10−4 M. All measurements were performed at room-temperature. Fluorescence and phosphorescence quantum yield were measured by a relative method using quinine sulfate in 0.05 M H2SO4 (ϕF = 0.52)19 as a standard.Because of a very low (<10−4) fluorescence quantum yield of BPT in the S2 state, in water,9 to be sure that the weak emission, measured in the range of emission spectra and emission excitation spectra, comes exclusively from BPT and/or BPT complexes with water and not from the emitting impurities, the Ultra-High Performance Liquid Chromatography (UHPLC) was applied with the UV-VIS absorption and emission detection.20 Irrespective of the wavelength of observation in the range of 250–390 nm (40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–25
000–25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 640 cm−1), including all excitation wavelengths, λexc, the absorption chromatograms of BPT in acetonitrile shows only one peak. Similarly, the emission chromatograms measured for all λexc and many emission wavelengths, λem = 400–560 nm (25
640 cm−1), including all excitation wavelengths, λexc, the absorption chromatograms of BPT in acetonitrile shows only one peak. Similarly, the emission chromatograms measured for all λexc and many emission wavelengths, λem = 400–560 nm (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–17
000–17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 860 cm−1), from the range of S2 emission spectra, there is only one peak of BPT of the same retention time as in the chromatogram of absorption. This type of chromatogram means that the sample does not contain absorbing and/or emitting impurities under the conditions of absorption measurements on a spectrophotometer and under the conditions of emission measurements on a spectrofluorimeter.
860 cm−1), from the range of S2 emission spectra, there is only one peak of BPT of the same retention time as in the chromatogram of absorption. This type of chromatogram means that the sample does not contain absorbing and/or emitting impurities under the conditions of absorption measurements on a spectrophotometer and under the conditions of emission measurements on a spectrofluorimeter.
Calculation methods
All quantum-chemical calculations have been carried out using a Turbomole 6.6 quantum chemical software package.21 For all RI-DFT22 and RI-TDDFT23,24 calculations the free-parameter PBE0 hybrid functional has been chosen.25 This functional is constructed in such a way that a fixed fraction (1/4) of the Hartree–Fock exact exchange is added to the PBE exchange–correlation functional.26 For structure preoptimization the double-ζ-quality SV(P) and corresponding auxiliary basis set have been employed.27 Final structure optimization was carried out with a triple-ζ-quality basis set, TZVP28 with analogous auxiliary basis set. The nature of all stationary points (the minima on the electronic potential energy surface) was confirmed by the frequency calculation on top of the optimized geometries. Due to the fact that in Turbomole package analytical second derivatives are not available for the electronic excited states, the excited state hessian matrix has been obtained by numerical differentiation of the excited state electronic energy gradients. All RI-DFT(PBE0) and RI-TDDFT(PBE0) calculations were carried out within the resolution-of-the-identity (RI) approximation which avoids direct evaluation of Coulomb four-center integrals. The structures obtained at the RI-DFT(PBE0)/TZVP and RI-TDDFT(PBE0)/TZVP levels of theory (respectively, for the ground and second excited state) have been subsequently used for the RICC2, CIS(D) and ADC(2)29,30 single-point ab initio calculations. All ab initio calculations have been carried out with the ricc2 program29 with correlation consistent, augmented triple-ζ-quality basis set.31 The Hartree–Fock reference wave functions were obtained within the RIJK approximation32 where direct evaluation of both Coulomb and exchange four-center integrals is avoided. Core orbitals have been frozen during all electronic-correlation ab initio calculations.Results and discussion
Experimental study results
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 220–23
220–23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260 cm−1) and the T1-phosphorescence band with the maximum at about 660 nm (15
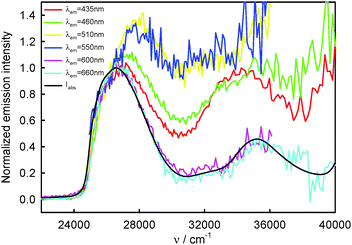
260 cm−1) and the T1-phosphorescence band with the maximum at about 660 nm (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 150 cm−1). It is easy to note that the shape as well as the maximum of the T1-phosphorescence band does not depend on λexc, similarly as for BPT in perfluorohydrocarbons.17,33 In contrast, the excitation wavelength value strongly influences the shape and the maximum of the S2-fluorescence band. The decrease in the λexc value causes a widening of the S2-fluorescence band and a bathochromic shift of this band maximum. In spite of λexc the Stokes shift, ΔνmaxA–F, for BPT in water has smaller value than for BPT in non-specifically interacting solvents. Table 1 lists the S2-fluorescence maxima (νmaxF), FWHM (full width at half maximum) values of the S2-fluorescence spectra (ΔνF1/2) and the Stokes shifts, ΔνmaxA–F = νmaxA − νmaxF, of BPT in water for different λexc. A comparison of the S0 → S2 absorption spectra and S2-fluorescence spectra for BPT in water and in two non-specifically interacting solvents is presented in Fig. 3. The emission excitation spectra measured for BPT in water for different λem differ significantly from one another. These recorded at λem from the range of T1-phosphorescence band are similar to one another and also similar to the S0 → S2 absorption spectrum. In contrast, these recorded at λem from the range of S2-fluorescence band change their shape and intensity depending on λem and their maxima are shifted toward shorter wavelengths for longer λem (Fig. 4).
150 cm−1). It is easy to note that the shape as well as the maximum of the T1-phosphorescence band does not depend on λexc, similarly as for BPT in perfluorohydrocarbons.17,33 In contrast, the excitation wavelength value strongly influences the shape and the maximum of the S2-fluorescence band. The decrease in the λexc value causes a widening of the S2-fluorescence band and a bathochromic shift of this band maximum. In spite of λexc the Stokes shift, ΔνmaxA–F, for BPT in water has smaller value than for BPT in non-specifically interacting solvents. Table 1 lists the S2-fluorescence maxima (νmaxF), FWHM (full width at half maximum) values of the S2-fluorescence spectra (ΔνF1/2) and the Stokes shifts, ΔνmaxA–F = νmaxA − νmaxF, of BPT in water for different λexc. A comparison of the S0 → S2 absorption spectra and S2-fluorescence spectra for BPT in water and in two non-specifically interacting solvents is presented in Fig. 3. The emission excitation spectra measured for BPT in water for different λem differ significantly from one another. These recorded at λem from the range of T1-phosphorescence band are similar to one another and also similar to the S0 → S2 absorption spectrum. In contrast, these recorded at λem from the range of S2-fluorescence band change their shape and intensity depending on λem and their maxima are shifted toward shorter wavelengths for longer λem (Fig. 4).
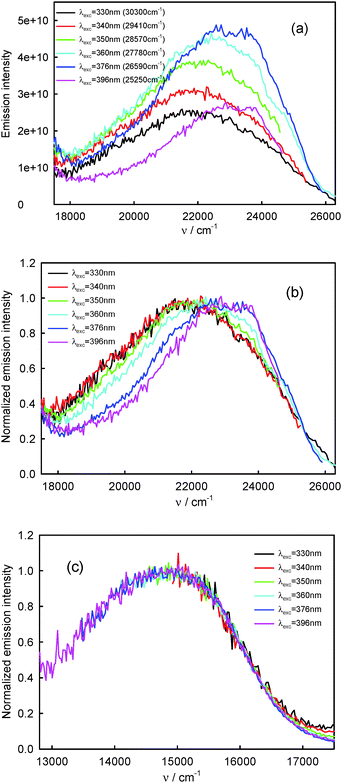 | ||
| Fig. 2 Raw (a) and normalized (b) S2-fluorescence and normalized (c) T1-phosphorescence spectra of BPT in water. | ||
| λ exc [nm/cm−1] | ν maxF [cm−1] | ΔνF1/2 [cm−1] | ΔνmaxA–F [cm−1] |
|---|---|---|---|
ν
maxA = 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1 (from ref. 1) 400 cm−1 (from ref. 1) |
|||
330 (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300) 300) |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 920 920 |
5720 | 4480 |
340 (29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 410) 410) |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 920 920 |
5780 | 4480 |
350 (28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570) 570) |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
5480 | 4400 |
360 (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780) 780) |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 460 460 |
5350 | 3940 |
376 (26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590) 590) |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 040 040 |
4600 | 3360 |
396 (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250) 250) |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 150 150 |
4040 | 3250 |
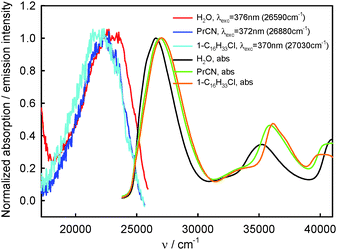 | ||
| Fig. 3 Normalized S0 → S2 and S0 → Sn, n ≥ 3, absorption and S2-fluorescence spectra of BPT in selected non-specifically interacting solvents and in water. | ||
| λ exc [nm/cm−1] | ϕ F | ϕ F/ϕ396F | ϕ P | ϕ P/ϕ396P | (ϕF/ϕ396F)/(ϕP/ϕ396P) |
|---|---|---|---|---|---|
ϕ
396F, ϕ396P – S2-fluorescence and T1-phosphorescence quantum yield determined for λexc = 396 nm (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 cm−1). 250 cm−1). |
|||||
330 (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300) 300) |
0.00053 | 5.3 | 0.00083 | 1.4 | 3.8 |
340 (29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 410) 410) |
0.00038 | 3.8 | 0.00084 | 1.4 | 2.7 |
350 (28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570) 570) |
0.00025 | 2.5 | 0.00079 | 1.4 | 1.8 |
360 (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780) 780) |
0.00016 | 1.6 | 0.00073 | 1.3 | 1.2 |
376 (26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590) 590) |
0.00012 | 1.2 | 0.00066 | 1.1 | 1.1 |
396 (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250) 250) |
0.00010 | 1.0 | 0.00058 | 1.0 | 1.0 |
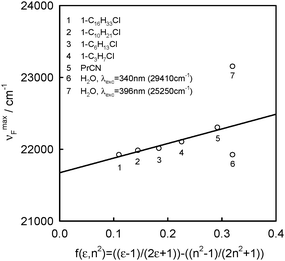
| Solvent |
ν
maxA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a [cm−1] a [cm−1] |
λ exc [nm/cm−1] | ν maxF [cm−1] | ΔνF1/2 [cm−1] | ΔνmaxA–F [cm−1] | f(ε,n2) | ε | n |
|---|---|---|---|---|---|---|---|---|
| a From ref. 1, n – refraction coefficient; ε – relative permittivity; f(ε,n2) = (ε − 1)/(2ε + 1) − (n2 − 1)/(2n2 + 1). | ||||||||
| Propionitrile | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030 030 |
372 (26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 880) 880) |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
4100 | 4730 | 0.292 | 28.26 | 1.363 |
| 1-Chloro-n-propane | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
344 (29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 070) 070) |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030 030 |
4180 | 5070 | 0.226 | 8.59 | 1.388 |
370 (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030) 030) |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
4220 | 5000 | |||||
400 (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030 030 |
4200 | 5070 | |||||
| 1-Chloro-n-hexane | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
370 (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030) 030) |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 010 010 |
4250 | 5090 | 0.184 | 6.10 | 1.419 |
| 1-Chloro-n-decane | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
370 (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030) 030) |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 980 980 |
4220 | 5120 | 0.145 | 4.58 | 1.438 |
| 1-Chloro-n-hexadecane | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
370 (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030) 030) |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 920 920 |
4270 | 5180 | 0.110 | 3.70 | 1.450 |
 | ||
| Fig. 6 Normalized absorption and S2-fluorescence excitation spectra of BPT in selected non-specifically interacting solvents. | ||
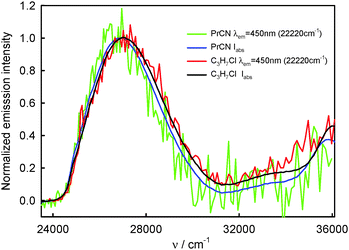
The S2-fluorescence quantum yield values of BPT in 1-chloro-n-alkanes and propionitrile, in contrast to BPT in water, do not depend on the excitation wavelength and do not differ significantly from one another. The results are presented in Table 4.
| Solvent | λ exc [nm/cm−1] | ϕ F | ϕ F/ϕ400F |
|---|---|---|---|
ϕ
400F – S2-fluorescence quantum yield determined for λexc = 400 nm (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1). 000 cm−1). |
|||
| Propionitrile | 344 (29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 070) 070) |
0.00071 | 0.9 |
372 (26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 880) 880) |
0.00071 | 0.9 | |
400 (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
0.00083 | 1.0 | |
| 1-Chloro-n-propane | 370 (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030) 030) |
0.00087 | |
| 1-Chloro-n-hexane | 370 (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030) 030) |
0.00080 | |
| 1-Chloro-n-decane | 370 (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030) 030) |
0.00074 | |
| 1-Chloro-n-hexadecane | 344 (29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 070) 070) |
0.00073 | 0.9 |
370 (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030) 030) |
0.00074 | 0.9 | |
400 (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
0.00082 | 1.0 | |
The similarity in shape of the S2-fluorescence excitation spectra measured for BPT in non-specifically interacting solvents with the absorption S0 → S2 spectrum suggests that after excitation to the S2 state with different excess vibration energy in the range of 0–5000 cm−1, the ϕF value is constant. Slightly lower intensity of emission, IF, than that of absorbed radiation, Iabs, for BPT in propionitrile (see Fig. 6) means – according to the relation IF = ϕF·(10−A(λexc)) – that the deactivation of BPT from higher excited states Sn, n ≥ 3, takes place partly with omission of the emitting S2 state, similarly as for BPT in nonpolar perfluorohydrocarbons and hydrocarbons.
Computational study
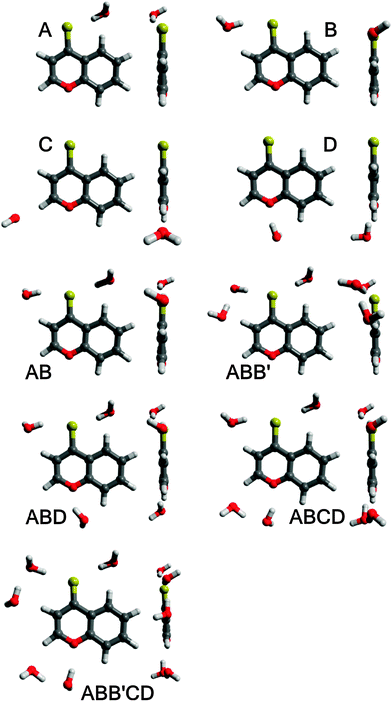
As mentioned above, a detailed computational study of hydrogen-bonded BPT–water complexes in the ground Srel0 state and just after transition to the unrelaxed excited SFC1 and SFC2 states has been presented in ref. 1. The main aim of this study is the analysis of the presence of these complexes in the emitting S2-excited state and their changes upon the Srel2 → SFC0 deactivation process. Therefore, the equilibrium structures of BPT molecules and different BPT–water complexes formed via hydrogen bonds were determined in their relaxed S2-excited state (Srel2) using the RI-TDDFT(PBE0)/TZVP method. For these optimal geometries the energies of the hydrogen bonds in the Srel2 excited state and in the ground unrelaxed SFC0 state were predicted using the RICC2, ADC and CIS(D) methods. The calculations were performed for four different complexes of BPT molecules with a single water molecule, referred henceforth as A, B, C and D, and for the complexes formed by BPT molecules with two, three, four and five water molecules (see Fig. 8). The results presented in the current study as well as in ref. 1 clearly show that, despite the electronic state, the energy of hydrogen bonds formed by the sulphur atom of the thiocarbonyl group of the BPT molecule is significantly higher than that of the hydrogen bonds formed by the oxygen atom of BPT. Therefore, for the computational study and direct comparison with the experiment, we have chosen the complexes formed by the BPT molecule and two, three, four or five water molecules (see Fig. 8). The complex of BPT with two water molecules, dubbed here as AB, is stabilized by the creation of two strong hydrogen bonds between the water molecules and the sulphur atom of the thiocarbonyl group. The ABB′ complex, containing three water molecules, was created by adding the water molecule on the optima location of the C complex to the AB complex. In the course of the geometry optimization the ABB′ molecular system was obtained where three water molecules are located in the surrounding of the sulphur atom. The ABD complex was formed in an analogous way, by supplementing the AB system with additional water molecules placed in the optimal location of the D complex. The ABCD complex contains a BPT molecule and four water molecules. Two water molecules form, in full analogy with the AB complex, the hydrogen bonds with a sulphur atom. The remaining two water molecules are located in the surrounding of the oxygen atom. The largest molecular system considered in the current study, dubbed here as ABB′CD, is formed by a BPT molecule and five water molecules. This system been created by extending the ABCD complex with additional water molecules placed in the neighbourhood of one of the carbon atoms. Further extension of the systems with water molecules has not been reflected in the increase of complex stability. Therefore in the current study we have not considered complexes with more than five water molecules. The geometries of all mentioned molecular complexes were relaxed in their S0 and S2 electronic states.Table 5 gives the predicted hydrogen bond energies, EHB, in the ground states Srel0 and SFC0 and in the excited states SFC2 and Srel2 of the BPT–water complexes. It is worth mentioning that the energies determined in Srel0 and SFC2 taking part in the process of absorption, for A, B, C, D and AB complexes, are in qualitative agreement with the values determined in ref. 1. Very important to notice from Table 5 is that the hydrogen bond stabilization energy for all studied complexes formed by the BPT molecule with more than one water molecule (AB, ABD, ABB′ and especially ABCD and ABB′CD) is very high irrespective of the electronic state. For all BPT–water complexes considered, the total hydrogen bond energy increases as a result of Srel0 → SFC2 excitation, irrespective of the calculation method. As can be noted from Table 5, the hydrogen bond energy changes upon the Srel2 → SFC0 deactivation process are generally small and their sign depends on the calculation method.
| Complex | Optimal geometry | Electronic state | E HB | ||
|---|---|---|---|---|---|
| RICC2 | ADC(2) | CIS(D) | |||
| A | S0 | Srel0 | 2120 | 1980 | 1980 |
| S FC 2 | 2337 | 2252 | 2412 | ||
| S2 | S rel 2 | 2306 | 2091 | 2234 | |
| SFC0 | 2135 | 2047 | 2047 | ||
| B | S0 | Srel0 | 2578 | 2449 | 2449 |
| S FC 2 | 2815 | 2741 | 2949 | ||
| S2 | S rel 2 | 3066 | 2781 | 2954 | |
| SFC0 | 2902 | 2844 | 2844 | ||
| C | S0 | Srel0 | 1256 | 1210 | 1210 |
| S FC 2 | 1202 | 1172 | 1185 | ||
| S2 | S rel 2 | 1471 | 1391 | 1450 | |
| SFC0 | 1262 | 1227 | 1227 | ||
| D | S0 | Srel0 | 1326 | 1298 | 1298 |
| S FC 2 | 1072 | 1020 | 957 | ||
| S2 | S rel 2 | 982 | 988 | 937 | |
| SFC0 | 1214 | 1169 | 1169 | ||
| AB | S0 | Srel0 | 4657 | 4407 | 4407 |
| S FC 2 | 5076 | 4894 | 5253 | ||
| S2 | S rel 2 | 5242 | 4666 | 4946 | |
| SFC0 | 5011 | 4911 | 4911 | ||
| ABB′ | S0 | Srel0 | 6182 | 5892 | 5892 |
| S FC 2 | 6705 | 6480 | 6944 | ||
| S2 | S rel 2 | 6928 | 6153 | 6501 | |
| SFC0 | 6658 | 6577 | 6577 | ||
| ABD | S0 | Srel0 | 5904 | 5620 | 5620 |
| S FC 2 | 6202 | 5977 | 6268 | ||
| S2 | S rel 2 | 6342 | 5765 | 6002 | |
| SFC0 | 6190 | 6044 | 6044 | ||
| ABCD | S0 | Srel0 | 7214 | 6880 | 6880 |
| S FC 2 | 7427 | 7187 | 7535 | ||
| S2 | S rel 2 | 7765 | 7130 | 7421 | |
| SFC0 | 7555 | 7352 | 7352 | ||
| ABB′CD | S0 | Srel0 | 8687 | 8313 | 8313 |
| S FC 2 | 9025 | 8746 | 9193 | ||
| S2 | S rel 2 | 9369 | 8569 | 8928 | |
| SFC0 | 9123 | 8932 | 8932 | ||
To make the calculation conditions closer to the experimental ones, the macroscopic solvent effect was investigated using the COSMO solvation model as implemented in the Turbomole package.21 The predicted energies of nonspecific interactions of BPT–water complexes in Srel0, SFC2, Srel2 and SFC0 states with bulk water molecules are collected in Table 6. As can be seen from these results, the highest stabilization energy due to the nonspecific interactions is observed for ABB′CD and ABCD complexes. In contrast to the results obtained in ref. 1 using the conductor polarisable continuum model (CPCM), no substantial differences in the energies of nonspecific interactions between electronic states were observed. On the basis of the predicted high energies of hydrogen bonds (Table 5) and nonspecific interactions (Table 6), it can be concluded that practically all BPT molecules in Srel0, SFC2, Srel2 and SFC0 states in the water solution formed complexes with five or four water molecules via hydrogen bonds. The highest energies of hydrogen bonds and nonspecific interactions determined for ABB′CD complexes suggest that the concentration of complexes with five water molecules in the surrounding of the BPT molecule is definitely the highest before excitation in Srel0 as well as in the emitting Srel2 state.
| Complex | Srel0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
SFC2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
Srel2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
SFC0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
|---|---|---|---|---|
| a Calculated for the equilibrium structure of the ground state S0. b Calculated for the equilibrium structure of the excited state S2. | ||||
| A | 1293 | 1391 | 1380 | 1232 |
| B | 1044 | 1052 | 758 | 783 |
| C | 1658 | 1649 | 1500 | 1649 |
| D | 1791 | 1920 | 1965 | 1817 |
| AB | 2381 | 2474 | 2190 | 2061 |
| ABB′ | 3080 | 3200 | 2849 | 2706 |
| ABD | 4184 | 4293 | 4131 | 3887 |
| ABCD | 5002 | 5160 | 4721 | 4644 |
| ABB′CD | 5651 | 5820 | 5367 | 5276 |
Further theoretical investigation as well as an in-detail discussion of all relevant issues is the subject of an upcoming article.
Discussion
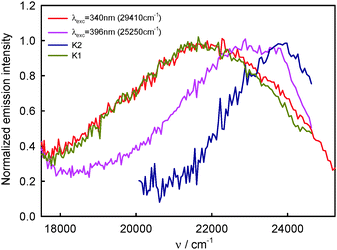
The above-presented results of spectral emission and photophysical study for BPT in water clearly show that the shape and maximum of the S2-fluorescence spectra as well as S2-fluorescence quantum yield strongly depend on λexc. Moreover, the shape of S2-fluorescence excitation spectra depends on λem. The most probable explanation of such results is the presence of at least two different species in the Srel2 emitting state. As mentioned above, on the basis of computational study results, practically all BPT molecules in water solution form with water molecule hydrogen-bonded complexes in the electronic states Srel0, SFC2, Srel2 and SFC0. The calculated energies of the hydrogen bond and nonspecific interaction clearly show that the most stable, irrespective of the electronic state, should be the complexes formed via hydrogen bonds by the BPT molecule with five water molecules (which occur in majority) or with four water molecules. Therefore, we propose that there must be at least two different types of hydrogen-bonded complexes (ABB′CD, referred henceforth as K1 and ABCD, referred henceforth as K2), which are the species responsible for such unexpected S2-fluorescence. We tried to show that the detailed analysis of the experimental study results confirmed this assumption. It is worth noting that the source of fluorescence cannot be the impurities, as explained in the section Experimental details.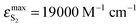 ,35,36 determined for BPT in water is significantly higher than for BPT non-specifically interacting solvents.4,12
,35,36 determined for BPT in water is significantly higher than for BPT non-specifically interacting solvents.4,12
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 920 cm−1 (456 nm) recorded for the shorter excitation wavelength, i.e. λexc = 330–350 nm (30
920 cm−1 (456 nm) recorded for the shorter excitation wavelength, i.e. λexc = 330–350 nm (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300–28
300–28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570 cm−1, see Fig. 2), are similar in shape and are characteristic of complex K1. The S2-fluorescence spectra with the maximum, νmaxF = 23
570 cm−1, see Fig. 2), are similar in shape and are characteristic of complex K1. The S2-fluorescence spectra with the maximum, νmaxF = 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 150 cm−1 (432 nm) recorded for the longest excitation wavelength, i.e. λexc = 396 nm, are characterized for relatively the largest contribution of complex K2.
150 cm−1 (432 nm) recorded for the longest excitation wavelength, i.e. λexc = 396 nm, are characterized for relatively the largest contribution of complex K2.
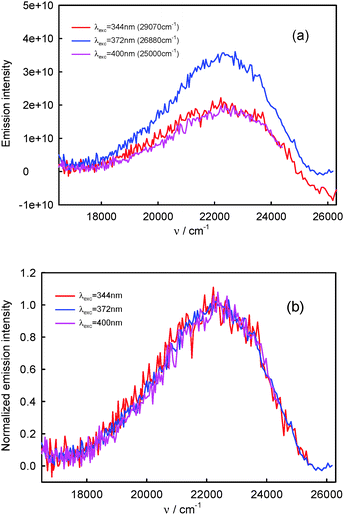
Assuming that the S2-fluorescence spectrum recorded for λexc = 340 nm (29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 410 cm−1) is the most characteristic of complex K1, we determined the spectrum of complex K2 as the difference between the spectrum recorded for λexc = 396 nm (25
410 cm−1) is the most characteristic of complex K1, we determined the spectrum of complex K2 as the difference between the spectrum recorded for λexc = 396 nm (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 cm−1) (at which the contribution of K2 is the highest) and that recorded for λexc = 340 nm (29
250 cm−1) (at which the contribution of K2 is the highest) and that recorded for λexc = 340 nm (29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 410 cm−1). The results are presented in Fig. 9. Than from the spectrum recorded for λexc = 360 nm (27
410 cm−1). The results are presented in Fig. 9. Than from the spectrum recorded for λexc = 360 nm (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780 cm−1), which is the sum of different contributions of K1 and K2 spectra, we subtracted the spectrum of complex K2 (νmaxF = 23
780 cm−1), which is the sum of different contributions of K1 and K2 spectra, we subtracted the spectrum of complex K2 (νmaxF = 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 cm−1), determining the spectrum of complex K1. It is easy to notice that the spectrum of complex K1 is similar to that recorded for λexc = 340 nm (29
740 cm−1), determining the spectrum of complex K1. It is easy to notice that the spectrum of complex K1 is similar to that recorded for λexc = 340 nm (29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 410 cm−1) (and also λexc = 330 nm (30
410 cm−1) (and also λexc = 330 nm (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1) and 350 nm (28
300 cm−1) and 350 nm (28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570 cm−1)), which confirmed our above-mentioned assumption. As the S2-fluorescence spectra recorded for BPT in water for λexc = 330–350 nm (30
570 cm−1)), which confirmed our above-mentioned assumption. As the S2-fluorescence spectra recorded for BPT in water for λexc = 330–350 nm (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300–28
300–28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570 cm−1) are similar, no effect of λexc on the position and shape of S2-fluorescence spectrum of complex K1 is observed, in spite of significant excess of vibrational energy (3000–5000 cm−1) in the short-lived S2 state (τS2 ≤ 1 ps),9 in contrast to the situation for S2-thiocoumarin in perfluorohydrocarbon and hydrocarbon solvents (τS2 = 0.45 ps in n-hexane).13,14 It implies that the process of redistribution of vibrational energy in complex K1 and the solvent cooling of this complex are very fast in water, much faster than for S2-thiocoumarin in n-hexane.14 It is worth noting that the solvent cooling process was found to be very fast also for N-acetyltryptophanamide in water37 and for hot purine derivatives in heavy water.38 The stable shape and position of νmaxF in the experimental S2-fluorescence spectra recorded for λexc = 330–350 nm (30
570 cm−1) are similar, no effect of λexc on the position and shape of S2-fluorescence spectrum of complex K1 is observed, in spite of significant excess of vibrational energy (3000–5000 cm−1) in the short-lived S2 state (τS2 ≤ 1 ps),9 in contrast to the situation for S2-thiocoumarin in perfluorohydrocarbon and hydrocarbon solvents (τS2 = 0.45 ps in n-hexane).13,14 It implies that the process of redistribution of vibrational energy in complex K1 and the solvent cooling of this complex are very fast in water, much faster than for S2-thiocoumarin in n-hexane.14 It is worth noting that the solvent cooling process was found to be very fast also for N-acetyltryptophanamide in water37 and for hot purine derivatives in heavy water.38 The stable shape and position of νmaxF in the experimental S2-fluorescence spectra recorded for λexc = 330–350 nm (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300–28
300–28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570 cm−1), but the quantum yield of S2-fluorescence, ϕF, varying with λexc, indicate the dependence of ϕF of complex K1 on λexc. The significant increase in the width of the band ΔνF1/2, in the experimental S2-fluorescence of BPT in water with increasing excitation energy (decreasing λexc, λexc ≤ 350 nm (28
570 cm−1), but the quantum yield of S2-fluorescence, ϕF, varying with λexc, indicate the dependence of ϕF of complex K1 on λexc. The significant increase in the width of the band ΔνF1/2, in the experimental S2-fluorescence of BPT in water with increasing excitation energy (decreasing λexc, λexc ≤ 350 nm (28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570 cm−1), see Table 1), can be explained by the occurrence of emission from the vibrationally excited S2 state (ν > 0) with a higher quantum yield than from the Srel2 state of complex K1. An indirect confirmation of this interpretation is the lack of influence of λexc on the shape of S2-fluorescence spectra (see Table 3) and ϕF value (see Table 4) for BPT in non-specifically interacting solvents.
570 cm−1), see Table 1), can be explained by the occurrence of emission from the vibrationally excited S2 state (ν > 0) with a higher quantum yield than from the Srel2 state of complex K1. An indirect confirmation of this interpretation is the lack of influence of λexc on the shape of S2-fluorescence spectra (see Table 3) and ϕF value (see Table 4) for BPT in non-specifically interacting solvents.
In order to estimate the contribution of complexes K1 and K2 to the S2-fluorescence as a function of λexc and λem, the relative quantum yields were calculated, defined as ϕF(rel) = IF/Iabs, where IF – S2 is the fluorescence intensity for specific λexc and λem, Iabs is the intensity of absorbed radiation determined for λexc, Iabs = 1–10−A(λexc), where A is the absorbance. The correlations between the values of ϕF(rel)300 determined for λexc = 330 nm (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1) (when practically only complex K1 contributes to S2-fluorescence) and the values of ϕF(rel)396 determined at λexc = 396 nm (25
300 cm−1) (when practically only complex K1 contributes to S2-fluorescence) and the values of ϕF(rel)396 determined at λexc = 396 nm (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 cm−1) (at which the relative contribution of complex K2 to S2-fluorescence is the highest), for selected λem are given in Table 7. The values of λem were chosen to correspond to λem values at which the lifetimes of S2-fluorescence9 and emission excitation spectra were measured. It can be noticed from Table 7 that the highest ratio of ϕF(rel)330/ϕF(rel)396 ≈ 8 was determined for λem = 510–530 nm (19
250 cm−1) (at which the relative contribution of complex K2 to S2-fluorescence is the highest), for selected λem are given in Table 7. The values of λem were chosen to correspond to λem values at which the lifetimes of S2-fluorescence9 and emission excitation spectra were measured. It can be noticed from Table 7 that the highest ratio of ϕF(rel)330/ϕF(rel)396 ≈ 8 was determined for λem = 510–530 nm (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610–18
610–18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 870 cm−1), at which almost exclusively the emission from complex K1 is observed (see Fig. 9). This value is much higher than ϕ330F/ϕ396F = 5.3 obtained for the quantum yields determined on the basis of the areas of the measured S2-fluorescence spectrum which is the sum of the spectra of complexes K1 and K2 (see Table 2). For λem = 410–435 nm (24
870 cm−1), at which almost exclusively the emission from complex K1 is observed (see Fig. 9). This value is much higher than ϕ330F/ϕ396F = 5.3 obtained for the quantum yields determined on the basis of the areas of the measured S2-fluorescence spectrum which is the sum of the spectra of complexes K1 and K2 (see Table 2). For λem = 410–435 nm (24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 390–22
390–22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 990 cm−1), so in the range in which the contribution of complex K2 to the emission is relatively the greatest (see Fig. 9), the ratio of ϕF(rel)330/ϕF(rel)396 ≈ 3 was determined as significantly smaller than ϕ330F/ϕ396F = 5.3. These results confirm the assumption that the experimentally recorded S2-fluorescence spectra must be a sum of the spectra of at least two species. Moreover, the contribution of complex K2 characterised by lower quantum yield is greater in the short-wavelength range 400–450 nm (25
990 cm−1), so in the range in which the contribution of complex K2 to the emission is relatively the greatest (see Fig. 9), the ratio of ϕF(rel)330/ϕF(rel)396 ≈ 3 was determined as significantly smaller than ϕ330F/ϕ396F = 5.3. These results confirm the assumption that the experimentally recorded S2-fluorescence spectra must be a sum of the spectra of at least two species. Moreover, the contribution of complex K2 characterised by lower quantum yield is greater in the short-wavelength range 400–450 nm (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–22
000–22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 220 cm−1), while that of complex K1 characterised by higher quantum yield is greater in the long-wavelength range 500–550 nm (20
220 cm−1), while that of complex K1 characterised by higher quantum yield is greater in the long-wavelength range 500–550 nm (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–18
000–18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180 cm−1). It should be also noted that in the range of emission wavelengths corresponding to T1-phosphorescence, i.e. λem > 600 nm (16
180 cm−1). It should be also noted that in the range of emission wavelengths corresponding to T1-phosphorescence, i.e. λem > 600 nm (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 670 cm−1), the ratio of ϕP(rel)330/ϕP(rel)396 (where ϕP(rel) = IP/Iabs and IP is T1-phosphorescence intensity) is constant and corresponds to ϕ330P/ϕ396P = 1.4 obtained for the quantum yields estimated on the basis of the areas measured under the measured T1-phosphorescence spectrum.
670 cm−1), the ratio of ϕP(rel)330/ϕP(rel)396 (where ϕP(rel) = IP/Iabs and IP is T1-phosphorescence intensity) is constant and corresponds to ϕ330P/ϕ396P = 1.4 obtained for the quantum yields estimated on the basis of the areas measured under the measured T1-phosphorescence spectrum.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1) and 396 nm (25
300 cm−1) and 396 nm (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 cm−1) and for selected values of λem from the range of S2-fluorescence and T1-phosphorescence, for BPT in water
250 cm−1) and for selected values of λem from the range of S2-fluorescence and T1-phosphorescence, for BPT in water
| λ em [nm/cm−1] | I 330F/I396F | ϕ F(rel)330/ϕF(rel)396 |
|---|---|---|
| I 330F, I396F – S2-fluorescence intensity for λexc = 330 and 396 nm; I330P, I396P – T1-phosphorescence intensity for λexc = 330 and 396 nm; ϕF(rel)330, ϕF(rel)396, ϕP(rel)330, ϕP(rel)396 – relative S2-fluorescence and T1-phosphorescence quantum yield determined for λexc = 330 and 396 nm, respectively. | ||
410 (24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 390) 390) |
0.86 | 3.52 |
425 (23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 530) 530) |
0.75 | 3.06 |
435 (22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 990) 990) |
0.89 | 3.65 |
460 (21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740) 740) |
1.18 | 4.84 |
480 (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 830) 830) |
1.47 | 6.02 |
510 (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610) 610) |
2.00 | 8.20 |
520 (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 230) 230) |
1.97 | 8.07 |
530 (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 870) 870) |
1.82 | 7.43 |
| λ em [nm/cm−1] | I 330P/I396P | ϕ P(rel)330/ϕP(rel)396 |
|---|---|---|
600 (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 670) 670) |
0.44 | 1.80 |
620 (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130) 130) |
0.33 | 1.34 |
640 (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 620) 620) |
0.38 | 1.35 |
660 (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 150) 150) |
0.31 | 1.25 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610 cm−1) and 550 nm (18
610 cm−1) and 550 nm (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180 cm−1) are similar and their long-wavelength maximum is shifted hypsochromically with respect to the spectra recorded for other λem and the experimental absorption spectrum of BPT in water. Taking into regard these results, S2-fluorescence spectra determined for complexes K1 and K2 (Fig. 9) and the fact that the highest ratio of ϕF(rel)330/ϕF(rel)396 was determined for λem = 510–530 nm (19
180 cm−1) are similar and their long-wavelength maximum is shifted hypsochromically with respect to the spectra recorded for other λem and the experimental absorption spectrum of BPT in water. Taking into regard these results, S2-fluorescence spectra determined for complexes K1 and K2 (Fig. 9) and the fact that the highest ratio of ϕF(rel)330/ϕF(rel)396 was determined for λem = 510–530 nm (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610–18
610–18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 870 cm−1), it can be assumed that the S2-fluorescence excitation spectrum recorded for λem = 510 nm (19
870 cm−1), it can be assumed that the S2-fluorescence excitation spectrum recorded for λem = 510 nm (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610 cm−1) is characteristic of complex K1 exclusively. A significant difference in the shape and intensity of this S2-fluorescence excitation spectrum and the absorption spectrum is a result of a significant dependence of ϕF of complex K1 on λexc. As follows from Fig. 4 after the normalization of S2-fluorescence excitation spectra of BPT in water at the λexc = 396 nm (25
610 cm−1) is characteristic of complex K1 exclusively. A significant difference in the shape and intensity of this S2-fluorescence excitation spectrum and the absorption spectrum is a result of a significant dependence of ϕF of complex K1 on λexc. As follows from Fig. 4 after the normalization of S2-fluorescence excitation spectra of BPT in water at the λexc = 396 nm (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 cm−1), the emission intensity at λexc = 330 nm (30
250 cm−1), the emission intensity at λexc = 330 nm (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1) is the highest for λem = 510 nm (19
300 cm−1) is the highest for λem = 510 nm (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610 cm−1) and 550 nm (18
610 cm−1) and 550 nm (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180 cm−1) and decreases gradually for λem = 460 nm (21
180 cm−1) and decreases gradually for λem = 460 nm (21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 cm−1) and 435 nm (22
740 cm−1) and 435 nm (22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 990 cm−1). The ratio of emission intensity determined at λexc = 330 nm (30
990 cm−1). The ratio of emission intensity determined at λexc = 330 nm (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1) on the basis of these data for selected λem is equal to I510F/I435F = 2.0 and I460F/I435F = 1.6. These values are consistent with the ratio of (ϕF(rel)330/ϕF(rel)396) = X dependence on the λem determined on the basis of S2-fluorescence spectra (see Table 7), where X510/X435 = 2.2 and X460/X435 = 1.7. These data confirm that ϕF of complex K1 is higher than for complex K2 and it depends on the λexc value.
300 cm−1) on the basis of these data for selected λem is equal to I510F/I435F = 2.0 and I460F/I435F = 1.6. These values are consistent with the ratio of (ϕF(rel)330/ϕF(rel)396) = X dependence on the λem determined on the basis of S2-fluorescence spectra (see Table 7), where X510/X435 = 2.2 and X460/X435 = 1.7. These data confirm that ϕF of complex K1 is higher than for complex K2 and it depends on the λexc value.
The shape and intensity of the emission excitation spectra measured for BPT in water, for λem from the range of T1-phosphorescence spectrum, do not depend on the λem value and are similar to the S0 → S2 absorption spectrum in the wide range of wavelength 260–410 nm (38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 460–24
460–24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 390 cm−1). It implies that both complexes K1 and K2 deactivate to the T1 state in processes S2 → S1 → T1, which differ from the situation for BPT molecules itself (in perfluorohydrocarbons), which deactivate from the S2 state not only to the S1 state, but also directly to S0 with a contribution of ϕS2S0 ∼ 0.10.33
390 cm−1). It implies that both complexes K1 and K2 deactivate to the T1 state in processes S2 → S1 → T1, which differ from the situation for BPT molecules itself (in perfluorohydrocarbons), which deactivate from the S2 state not only to the S1 state, but also directly to S0 with a contribution of ϕS2S0 ∼ 0.10.33
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570 cm−1) and 380 nm (26
570 cm−1) and 380 nm (26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 310 cm−1) excitation wavelength and the analysed fluorescence wavelength from 425 nm (23
310 cm−1) excitation wavelength and the analysed fluorescence wavelength from 425 nm (23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 530 cm−1) to 550 nm (18
530 cm−1) to 550 nm (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180 cm−1), while the fitting analysis was carried out using the single exponential function. It is easy to notice in Fig. 3 in ref. 9 that the τS2 value determined on the basis of the decay obtained upon 380 nm (26
180 cm−1), while the fitting analysis was carried out using the single exponential function. It is easy to notice in Fig. 3 in ref. 9 that the τS2 value determined on the basis of the decay obtained upon 380 nm (26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 310 cm−1) photoexcitation depends on the fluorescence wavelength. Both for BPT in water and in D2O (τS2 = 2.10 ± 0.15 ps) the τS2 value is the longest for the fluorescence wavelength 425 nm (23
310 cm−1) photoexcitation depends on the fluorescence wavelength. Both for BPT in water and in D2O (τS2 = 2.10 ± 0.15 ps) the τS2 value is the longest for the fluorescence wavelength 425 nm (23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 530 cm−1) and the shortest for 550 nm (18
530 cm−1) and the shortest for 550 nm (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180 cm−1). Moreover, the τS2 value determined on the basis of the fluorescence decay for BPT in water, probed at 490 nm (20
180 cm−1). Moreover, the τS2 value determined on the basis of the fluorescence decay for BPT in water, probed at 490 nm (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 410 cm−1) following 350 nm (28
410 cm−1) following 350 nm (28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570 cm−1) photoexcitation, is shorter than following the 380 nm (26
570 cm−1) photoexcitation, is shorter than following the 380 nm (26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 310 cm−1) one. A more extensive analysis39 allows noting that all experimental fluorescence decay curves contain an additional ultrafast component centred at around 750 fs (see Fig. 3 in ref. 9). By a process of elimination, the ultrafast signal was assigned to the BPT–water intermolecular complex quenching process, while the signal observed on the longer time-scale is ascribed to the decay of the S2-BPT molecules.39 The results presented in this study, both experimental and computation ones, allow us to verify that hypothesis. As mentioned above, practically all BPT molecules form in water solution BPT–water complexes in S0 and S2 states. Therefore, the S2-fluorescence decay in water must describe the decay of two types of BPT–water complexes K1 and K2, and not BPT molecules. Their participation in the decay depends on photoexcitation, λexc and fluorescence wavelengths, λem. Taking into regard the S2-fluorescence spectra of complexes K1 and K2 (Fig. 9) and practically the exclusive contribution of complex K1 in the emission for λem = 520 nm (19
310 cm−1) one. A more extensive analysis39 allows noting that all experimental fluorescence decay curves contain an additional ultrafast component centred at around 750 fs (see Fig. 3 in ref. 9). By a process of elimination, the ultrafast signal was assigned to the BPT–water intermolecular complex quenching process, while the signal observed on the longer time-scale is ascribed to the decay of the S2-BPT molecules.39 The results presented in this study, both experimental and computation ones, allow us to verify that hypothesis. As mentioned above, practically all BPT molecules form in water solution BPT–water complexes in S0 and S2 states. Therefore, the S2-fluorescence decay in water must describe the decay of two types of BPT–water complexes K1 and K2, and not BPT molecules. Their participation in the decay depends on photoexcitation, λexc and fluorescence wavelengths, λem. Taking into regard the S2-fluorescence spectra of complexes K1 and K2 (Fig. 9) and practically the exclusive contribution of complex K1 in the emission for λem = 520 nm (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 230 cm−1) and 550 nm (18
230 cm−1) and 550 nm (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180 cm−1), it can be assumed that the S2-fluorescence decay recorded for λexc = 380 nm (26
180 cm−1), it can be assumed that the S2-fluorescence decay recorded for λexc = 380 nm (26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 310 cm−1) and the above λem describe the decay of complex K1. The values of τS2 = 0.97–1.02 ps determined in water solution and τS2 = 1.99–2.06 ps in D2O under these measurement conditions are characteristic of complex K1. Unfortunately, because of a higher concentration of complex K1 than K2, both in the ground S0 as well as the excited S2 state, it is impossible to select such conditions of measurements to make sure that S2-fluorescence would come exclusively from complex K2. The relatively greatest contribution of this complex in S2-fluorescence decays is when this decay is measured following 380 nm (26
310 cm−1) and the above λem describe the decay of complex K1. The values of τS2 = 0.97–1.02 ps determined in water solution and τS2 = 1.99–2.06 ps in D2O under these measurement conditions are characteristic of complex K1. Unfortunately, because of a higher concentration of complex K1 than K2, both in the ground S0 as well as the excited S2 state, it is impossible to select such conditions of measurements to make sure that S2-fluorescence would come exclusively from complex K2. The relatively greatest contribution of this complex in S2-fluorescence decays is when this decay is measured following 380 nm (26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 310 cm−1) photoexcitation and λem = 425 nm (23
310 cm−1) photoexcitation and λem = 425 nm (23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 530 cm−1). Because of the longest τS2 determined under such conditions in both water and D2O solutions, it can be assumed that τS2 of complex K2 must be longer than that of K1, and its value should be longer than 1.03 ps in water solution and longer than 2.20 ps in D2O (see Fig. 3 in ref. 9). The above reasoning is confirmed by a shorter τS2 value determined for the fluorescence wavelength 490 nm (20
530 cm−1). Because of the longest τS2 determined under such conditions in both water and D2O solutions, it can be assumed that τS2 of complex K2 must be longer than that of K1, and its value should be longer than 1.03 ps in water solution and longer than 2.20 ps in D2O (see Fig. 3 in ref. 9). The above reasoning is confirmed by a shorter τS2 value determined for the fluorescence wavelength 490 nm (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 410 cm−1) following 350 nm (28
410 cm−1) following 350 nm (28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570 cm−1) excitation (when the relative contribution of K1 into S2-fluorescence spectra is greater) than 380 nm (26
570 cm−1) excitation (when the relative contribution of K1 into S2-fluorescence spectra is greater) than 380 nm (26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 310 cm−1) photoexcitation.9 Moreover, the transient absorption measurements with photoexcitation at 380 nm give shorter time constant, τ = 0.9 ps, with analysing wavelength at 520 nm (19
310 cm−1) photoexcitation.9 Moreover, the transient absorption measurements with photoexcitation at 380 nm give shorter time constant, τ = 0.9 ps, with analysing wavelength at 520 nm (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 230 cm−1) than at 425 nm (23
230 cm−1) than at 425 nm (23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 530 cm−1), when τ = 1.1 ps.39 The above-mentioned ultrafast component (750 fs) observed as a clear unfit in almost all experimental fluorescence decay curves (see Fig. 3 in ref. 9) cannot come from the emission of complexes K1 and K2, its contribution in the total decay shows a distinctly different dependence on λexc and λem than the decay of these two complexes. This component can come from the processes of vibrational energy redistribution and solvent relaxation. This ultrafast component is responsible for some shortening in τS2 determined for complexes K1 and K2. However, quantitative determination of this effect is impossible.
530 cm−1), when τ = 1.1 ps.39 The above-mentioned ultrafast component (750 fs) observed as a clear unfit in almost all experimental fluorescence decay curves (see Fig. 3 in ref. 9) cannot come from the emission of complexes K1 and K2, its contribution in the total decay shows a distinctly different dependence on λexc and λem than the decay of these two complexes. This component can come from the processes of vibrational energy redistribution and solvent relaxation. This ultrafast component is responsible for some shortening in τS2 determined for complexes K1 and K2. However, quantitative determination of this effect is impossible.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570 cm−1) and λem = 490 nm (20
570 cm−1) and λem = 490 nm (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 410 cm−1) (when the emission of complex K1 is much larger than that of complex K2) and ϕF = 2.5 × 10−4 determined for λexc = 350 nm (28
410 cm−1) (when the emission of complex K1 is much larger than that of complex K2) and ϕF = 2.5 × 10−4 determined for λexc = 350 nm (28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570 cm−1), and kF = 2.5 × 108 s−1 for complex K1.
570 cm−1), and kF = 2.5 × 108 s−1 for complex K1.
As mentioned above, in water solution in the emitting Srel2 state, BPT does not occur in the form of molecules, but exclusively as BPT–water complexes. The energy gap ΔE(Srel2 − SFC1) determined in this study on the basis of theoretical calculations for BPT complexes with five (ABB′CD–K1) and with four (ABCD–K2) water molecules are 4800 and 5400 cm−1 (calculated using the ADC(2) method). These values are by over 3000 cm−1 smaller than ΔE(Srel2 − SFC1) for BPT in perfluorohydrocarbons.4,33 The reason for such a great decrease in the S2 − S1 energy gap is a significant weakening of the energy of hydrogen bonds type A and B (see Fig. 8) formed by the sulfur atom in the thiocarbonyl group of BPT and water molecules in the S1(n,π*) state.1 Because of experimentally determined low values of quantum yields of S2-fluorescence and S2-phosphorescence processes for BPT in water (ϕF = 1–5 × 10−4 and ϕP = 6–8 × 10−4, respectively), no photochemical changes even upon long irradiation of BPT in water (ϕPCH < 10−3), and a decrease in the S2 − S1 energy gap, the dominant process in Srel2 deactivation of complexes K1 and K2 must be the internal conversion to the S1 state. A similar value of S2 − S1 energy gap for both complexes is reflected in a similar value of deactivation constant of S2 → S1, and thus a similar value of their τS2.9
According to the energy gap law for rigid aromatic thioketones in perfluorohydrocarbons, a linear dependence between log knr and ΔE(Srel2 − SFC1) was obtained5 and is presented in Fig. 10. On the basis of this relation, it is possible to find the values of kS2S1 ≈ knr corresponding to the values of ΔE(Srel2 − SFC1) calculated for complexes K1 and K2. These values are 5.6 × 1010 s−1 for complex K1 and 3.8 × 1010 s−1 for complex K2, so τS2 ∼ 1/kS2S1 should be of 17.9 ps and 26.3 ps, respectively. However, the value experimentally determined for BPT in water is τS2 ∼ 1 ps. So, the electronic coupling matrix elements between S2 and S1 states in BPT–water complexes must be 5–6 times greater than for S2 and S1 states of the BPT molecule. The lifetime of S1(n,π*) is τS1 ≪ 1 ps,9 while the radiation rate constant is kF < 105 s−1, so the quantum yield of S1-fluorescence is very small, of ϕF ∼ 10−7. This explains why the S1 state emission is not visible. The S1 state has not been seen in the transient absorption spectra measured for different delay times for BPT in water.39
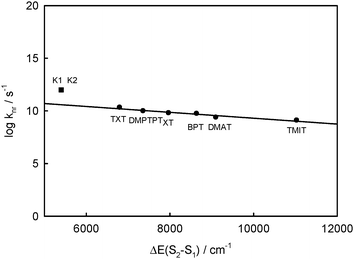 | ||
| Fig. 10 Plot of the logarithm of the rate constant for nonradiative decay processes of the S2 state, knr, vs. Srel2 − SFC1 energy gap, ΔE(S2 − S1), for rigid thioketones in perfluorohydrocarbon solution at room temperature (from ref. 5) together with BPT–water hydrogen bonded complexes with five or four water molecules (K1 = ABB′CD, K2 = ABCD). | ||
As shown above, the phosphorescence spectra and quantum yield, ϕP, do not depend significantly on the excitation wavelength. Moreover, the shape of the phosphorescence excitation spectra does not depend on λem and is similar to that of the absorption intensity spectrum. It means that both types of S1-excited BPT–water complexes (K1 and K2) deactivate to the T1 state with the large and similar yield.
Because of small changes in the energy of hydrogen bonds between BPT and water, as a result of electronic transitions Srel0 → SFC2SFC2 and Srel2 → SFC0, the positions of νmaxA and νmaxF for BPT–water complexes and for the BPT molecule in solvents of similar polarity and polarizability, interacting only non-specifically with it, e.g. propionitrile, do not differ significantly.
BPT–water complexes in water solution show much higher 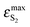 than BPT molecules in solvents with which it interacts only non-specifically,
than BPT molecules in solvents with which it interacts only non-specifically, 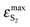 = 16
= 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–17
000–17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 cm−1.4,40 Similarly for BPT–water complexes K1 in water solution the values of kF are significantly higher than for BPT molecules in the exclusively non-specifically interacting solvents.4,35
000 M−1 cm−1.4,40 Similarly for BPT–water complexes K1 in water solution the values of kF are significantly higher than for BPT molecules in the exclusively non-specifically interacting solvents.4,35
It should be emphasised that much (∼25 times) higher kS2S1 ≈ knr for deactivation of the Srel2 state of BPT–water complexes than for BPT molecules4,5 implies that the electron coupling between S2(π,π*) and S1(n,π*) states in BPT–water complexes is about ∼5 times stronger than in the BPT molecule.
Conclusions
The results of the computational study clearly show that in water solution the BPT molecule in its ground S0 and excited S2 electronic states can form solute–solvent complexes via strong hydrogen bonds. As follows from the high values of the hydrogen bond energies, it should be assumed that almost all BPT molecules in the emitting Srel2 state form complexes with four or three water molecules. Therefore, the S2-fluorescence is connected exclusively with BPT–water S2-excited complexes and not with S2-excited BPT molecules, as it was assumed in ref. 9. Detailed spectral and photophysical emission study shows that at least two different types of BPT–water complexes must exist in the Srel2 state and participate in S2-fluorescence process. One of them, with significantly higher concentration in solution, is characterized by longer wavelength S2-fluorescence spectra and higher S2-fluorescence quantum yield which depends on the excitation wavelength value. The hydrogen bonds formed between the BPT molecules and water molecules play a dominant role in the processes of radiationless deactivation from the S2 state. Much lower energy of these bonds in the S1(n,π*) state than in the S2(π,π*) state, similarly as observed for BPT in methanol,15 means that the S2 − S1 energy gap is much smaller. Moreover the electron coupling between these states in the complexes is much greater than in the BPT molecule. As a consequence, both types of S2-excited BPT–water complexes deactivate in very short time (∼1 ps) in a very fast S2 → S1 internal conversion process. Correct interpretation of the BPT properties in water solution in the excited Srel2 state was possible thanks to the analysis of the spectral and photophysical experimental results and on the basis of advanced theoretical calculations of hydrogen bond energies for BPT–water complexes in Srel2, SFC1 and SFC0 states. Similarly as for BPT in water the dual fluorescence of two hydrogen-bonded methyl salicylate–water complexes was recently observed.41Acknowledgements
We thank Julia Józkowiak for technical support and Maria Spychalska for her help in manuscript preparation. Calculations were performed at the Poznań Supercomputer Centre PCSS.Notes and references
- E. Krystkowiak, J. Koput and A. Maciejewski, Phys. Chem. Chem. Phys., 2012, 14, 8842–8851 RSC.
- A. Maciejewski and R. P. Steer, Chem. Rev., 1993, 93, 67–98 CrossRef CAS.
- V. Rammamurthy and R. P. Steer, Acc. Chem. Res., 1988, 21, 380–386 CrossRef.
- A. Maciejewski, D. R. Demmer, D. R. James, A. Safarzadeh-Amiri, R. E. Verrall and R. P. Steer, J. Am. Chem. Soc., 1985, 107, 2831–2837 CrossRef CAS.
- G. Burdziński, J. Kubicki, A. Maciejewski, R. P. Steer, S. Velate and E. K. L. Yeow, in Organic Photochemistry and Photophysics, ed. V. Ramamurthy and K. S. Schanze, Taylor & Francis, Boca Raton, London, New York, 2006, vol. 14, pp. 1–36 Search PubMed.
- C. J. Ho, A. L. Motyka and M. R. Topp, Chem. Phys. Lett., 1989, 158, 51–59 CrossRef CAS.
- A. Maciejewski, J. Photochem. Photobiol., A, 1990, 51, 87–131 CrossRef CAS.
- M. Lorenc, A. Maciejewski, M. Ziółek, R. Naskręcki, J. Karolczak, J. Kubicki and B. Ciesielska, Chem. Phys. Lett., 2001, 346, 224–232 CrossRef CAS.
- G. Burdziński, A. Maciejewski, G. Buntinx, O. Poizat, P. Toele, H. Zhang and M. Glasbeek, Chem. Phys. Lett., 2004, 393, 102–106 CrossRef.
- J. Karolczak, D. Komar, J. Kubicki, T. Wróżowa, K. Dobek, B. Ciesielska and A. Maciejewski, Chem. Phys. Lett., 2001, 344, 154–164 CrossRef CAS.
- T. Wróżowa, B. Ciesielska, D. Komar, J. Karolczak, A. Maciejewski and J. Kubicki, Rev. Sci. Instrum., 2004, 75, 3107–3121 CrossRef.
- J. Kubicki, A. Maciejewski, M. Milewski, T. Wróżowa and R. P. Steer, Phys. Chem. Chem. Phys., 2002, 4, 173–179 RSC.
- G. Burdziński, M. Ziółek, J. Karolczak and A. Maciejewski, J. Phys. Chem. A, 2004, 108, 11160–11164 CrossRef.
- M. Szymański, A. Maciejewski, J. Kozłowski and J. Koput, J. Phys. Chem. A, 1998, 102, 677–683 CrossRef.
- G.-J. Zhao and K.-L. Han, ChemPhysChem, 2008, 9, 1842–1846 CrossRef CAS PubMed.
- G.-J. Zhao and K.-L. Han, Acc. Chem. Res., 2012, 45, 404–413 CrossRef CAS PubMed.
- M. Szymański, A. Maciejewski and R. P. Steer, J. Phys. Chem., 1988, 92, 2485–2489 CrossRef.
- M. Milewski, W. Urjasz, A. Maciejewski and W. Augustyniak, Pol. J. Chem., 1998, 72, 2405–2417 CAS.
- S. R. Meech and D. Phillips, J. Photochem., 1983, 23, 193–217 CrossRef CAS.
- B. Ciesielska, A. Łukaszewicz, L. Celewicz, A. Maciejewski and J. Kubicki, Appl. Spectrosc., 2007, 61, 102–109 CrossRef CAS PubMed.
- TURBOMOLE V6.6 2014, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com.
- M. Von Arnim and R. Ahlrichs, J. Comput. Chem., 1998, 19, 1746–1757 CrossRef CAS.
- R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464 CrossRef CAS.
- R. Bauernschmitt, M. Häser, O. Treutler and R. Ahlrichs, Chem. Phys. Lett., 1997, 264, 573–578 CrossRef CAS.
- M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154–5161 CrossRef.
- C. Hättig, Adv. Quantum Chem., 2005, 50, 37–60 CrossRef.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- F. Weigend, Phys. Chem. Chem. Phys., 2002, 4, 4285–4291 RSC.
- A. Maciejewski, M. Milewski and M. Szymański, J. Chem. Phys., 1999, 111, 8462–8468 CrossRef CAS.
- M. Milewski, PhD thesis, Adam Mickiewicz University in Poznań, 1998.
- M. Milewski, A. Maciejewski and W. Augustyniak, Chem. Phys. Lett., 1997, 272, 225–231 CrossRef CAS.
- A. Maciejewski, A. Safarzadeh-Amiri, R. E. Verrall and R. P. Steer, Chem. Phys., 1984, 87, 295–303 CrossRef CAS.
- F. Messina, A. M. El-Zohry, O. F. Mohammed and M. Chergui, J. Phys. Chem. B, 2012, 116, 10730–10738 CrossRef CAS PubMed.
- Y. Zhang, J. Chen and B. Kohler, J. Phys. Chem. A, 2013, 117, 6771–6780 CrossRef CAS PubMed.
- G. Burdziński, PhD thesis, Adam Mickiewicz University in Poznań, Université des Sciences et Technologies de Lille, 2003.
- M. Milewski, W. Augustyniak and A. Maciejewski, J. Phys. Chem. A, 1998, 102, 7427–7434 CrossRef CAS.
- S. Ghosh, J. Thomas, W. Huang, Y. Xu and W. Jäger, J. Phys. Chem. Lett., 2015, 6, 3126–3131 CrossRef CAS.
| This journal is © the Owner Societies 2016 |