A simple analytical model for signal amplification by reversible exchange (SABRE) process†
Danila A.
Barskiy‡
*a,
Andrey N.
Pravdivtsev
*ab,
Konstantin L.
Ivanov
ab,
Kirill V.
Kovtunov
ab and
Igor V.
Koptyug
ab
aInternational Tomography Center, 3A Institutskaya st., Novosibirsk 630090, Russia. E-mail: danila.barskiy@tomo.nsc.ru; andrey.pravdivtsev@tomo.nsc.ru
bNovosibirsk State University, 2 Pirogova st., Novosibirsk 630090, Russia
First published on 18th November 2015
Abstract
We demonstrate an analytical model for the description of the signal amplification by reversible exchange (SABRE) process. The model relies on a combined analysis of chemical kinetics and the evolution of the nuclear spin system during the hyperpolarization process. The presented model for the first time provides rationale for deciding which system parameters (i.e. J-couplings, relaxation rates, reaction rate constants) have to be optimized in order to achieve higher signal enhancement for a substrate of interest in SABRE experiments.
Nuclear spin hyperpolarization is a rapidly growing field of nuclear magnetic resonance (NMR). Presently, a number of hyperpolarization techniques are able to enhance the NMR sensitivity by several orders of magnitude in solid, liquid and gaseous samples.1–5 One of the most recent hyperpolarization techniques is signal amplification by reversible exchange (SABRE).6–10 In the SABRE effect, signal enhancement is endowed by a reversible association of parahydrogen (nuclear spin isomer of the hydrogen molecule with spin I = 0) and a to-be-polarized substrate with a metal complex, allowing the transfer of nuclear spin order from parahydrogen to the substrate.
SABRE is a physicochemical phenomenon, which depends on both the magnetic resonance properties of the system (J-couplings, spin relaxation and/or decoherence times, etc.) and its chemical parameters (reactant concentrations, reaction rate constants, etc.). The nuclear spin polarization transfer is operative during the quantum-mechanical spin evolution in a coupled multi-spin system, while chemical events are governed by the corresponding reaction rates. So far, only the physical nature of the SABRE phenomenon has been accounted for properly, in particular, to describe the magnetic field dependence of the polarization transfer efficiency.11–13 Herein we present a combined analysis of the chemical kinetics and the polarization transfer process, and derive a formula which describes the dependence of the enhancement factor in a SABRE experiment on the relevant concentrations as well as the exchange and relaxation rates. The derived expression explains well the results of published SABRE studies.
SABRE is typically observed for N-containing heterocycles, such as pyridine and nicotinamide (referred to below as the “substrate”) when a metal complex (referred to below as the “catalyst”) is used to briefly bring hydrogen and a substrate into contact with each other and to facilitate exchange with their free states in solution.
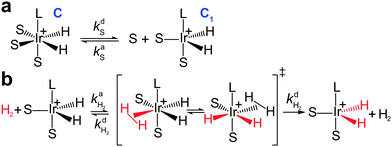
It was found by Cowley et al.7 and Appleby et al.8 that the substrate exchange rate for the [Ir(IMes)S3H2]+ complex (IMes = 1,3-bis(2,4,6-trimethylphenyl)imidazol-2-ylidene, S = pyridine, pyridazine, or phthalazine)—thus far, the best SABRE catalyst—is independent of the substrate and hydrogen concentrations in solution. At the same time, the hydrogen exchange rate was found to be dependent on the solution composition: an increase in hydrogen concentration and a decrease in substrate concentration increase the hydrogen exchange rate.8 These results can be explained by assuming that (i) substrate substitution in the complex is a dissociative process (typically referred to in organic chemistry textbooks as an SN1 reaction), while (ii) hydrogen substitution is an associative process (referred to as an SN2 reaction) which requires the formation of the intermediate species C1 = [Ir(L)S2H2]+ (Fig. 1). Indeed, owing to the chemical equilibrium between C (where C = [Ir(L)S3H2]+), S and C1, the concentration of C1 can be expressed as kdS[C]/kaS[S], where kdS and kaS are the substrate dissociation and association rate constants, respectively. According to the associative substitution mechanism for the hydrogen exchange (Fig. 1b), one can find that the rate of hydrogen exchange (WH2) is indeed inversely proportional to the substrate concentration and is directly proportional to the hydrogen concentration:
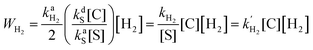 | (1) |
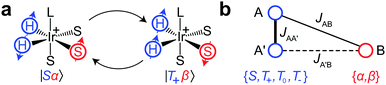
To explain the polarization transfer mechanism in SABRE, we will use as an example the simplest spin system, which is sufficient for the purpose, that is, the AA′B-type three-spin system. The spins AA′ represent the strongly coupled Ir–HH hydride protons of the Ir-complex, while a single proton B of the substrate is coupled either strongly or weakly to the AA′ protons depending on the applied magnetic field (Fig. 2). It has been shown that coherent polarization transfer in SABRE is efficient at low magnetic fields, in the regions of level anti-crossings (LACs).15 In the AA′B-type system all three protons become strongly coupled and the energy levels of the two states |Sα〉 and |T+β〉 approach each other but do not cross (due to the difference in AB and A′B spin–spin couplings, Fig. 2b). The initially overpopulated state |Sα〉 and the initially underpopulated state |T+β〉 are mixed at such a LAC, and the spin order is transferred from Ir–HH to the substrate. However, one should note that at high magnetic fields the SABRE mechanism is different: polarization transfer is incoherent, i.e., it occurs due to cross-relaxation in such a three-spin system.16
Let us introduce quantities [C*] and [S*] as concentrations of hyperpolarized species, for the complex and the free substrate molecule, respectively. These concentrations are determined as an imbalance between concentrations of molecules in the corresponding spin states: 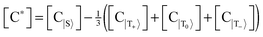 , [S*] = [S|β〉] − [S|α〉], where the subset of states {S,T+,T0,T−} corresponds to the hydride protons and the subset {α,β} corresponds to the substrate protons. That is, [C*] corresponds to the imbalance between the concentrations of the singlet and the triplet states of Ir–HH in the complex; [S*] corresponds to the “concentration” of the net spin polarization of the substrate.
, [S*] = [S|β〉] − [S|α〉], where the subset of states {S,T+,T0,T−} corresponds to the hydride protons and the subset {α,β} corresponds to the substrate protons. That is, [C*] corresponds to the imbalance between the concentrations of the singlet and the triplet states of Ir–HH in the complex; [S*] corresponds to the “concentration” of the net spin polarization of the substrate.
This description is convenient because one can show that the imbalance of the hydrogen isomer concentrations, [H2*] = [H2](4xp − 1)/3 (where xp is the fraction of parahydrogen and [H2] is the hydrogen concentration in solution), is converted directly to the imbalance of complex states [C*] and, subsequently, to the imbalance of substrate states [S*] (see the ESI†).
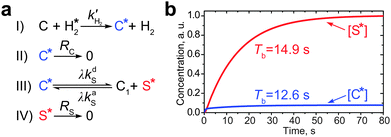
Let us now incorporate the exchange kinetics and polarization transfer into a common set of kinetic equations. In spite of the fact that polarization transfer in low-field SABRE experiments is a coherent process governed by the nuclear spin Hamiltonian, all spin coherences in the ensemble of complexes C are quickly washed out after the start of parahydrogen bubbling because the events of complex formation and dissociation are distributed in time. Consequently, the SABRE-derived polarization build-up is mainly determined by accumulation of populations during the chemical exchange and therefore can be treated using a set of chemical kinetics equations (Fig. 3a).
Thereby, the polarization build-up starts with the formation of hyperpolarized species C* (stage I in Fig. 3a), which decays with the relaxation rate constant RC = 1/TC1 (stage II) or takes part in the exchange process with the substrate with the above mentioned exchange rate constants kdS and kaS (stage III). The hyperpolarized substrate concentration [S*] decays with a rate constant RS = 1/TS1 (stage IV, here we completely neglect the thermal polarization of S and C). The formation of C* is magnetic field independent, while the subsequent processes—the formation of the hyperpolarized substrate—depend on the NMR parameters of the system, e.g., on the magnetic field strength and J-coupling topology. In order to take this dependence into consideration, let us introduce a factor of the polarization transfer efficiency, λ. When polarization transfer is not efficient (i.e., λ is small), S* is not produced in the polarization transfer stage III as shown in Fig. 3a. The analytical expression for the factor λ and its dependence on the magnetic field and rate constants are discussed in the text below.
Using the proposed kinetic model we found that the actual NMR signal enhancement factor, |ε|, provided by SABRE is given by the following formula:
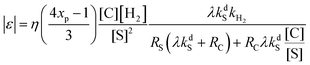 | (2) |
Several important consequences can be derived from analyzing eqn (2). First, the signal enhancement is predicted to be directly proportional to the catalyst concentration for low [C], and to be independent of the catalyst concentration for high [C]/[S] ratios (i.e., when RS(λkdS + RC) ≪ RCλkdS[C]/[S]). The proportionality predicted for low [C] follows from the fact that the complex C is the key molecule, in which polarization transfer takes place: the higher its concentration, the higher is [C*]. However, when [C] is too high it brings about the fast relaxation of the substrate polarization, since generally RC ≫ RS. Second, when [C]/[S] is low (the substrate is present in large excess), the enhancement factor is proportional to the inverse square of the substrate concentration, because the formation of the intermediate C1 responsible for the hydrogen exchange is suppressed and its concentration is low. In this case, polarization depends on the combination of the relaxation rates for the free and bound substrate and the dissociation rate constant. Third, when [C]/[S] is high, the enhancement factor is inversely proportional to the substrate concentration and depends predominantly on the relaxation rate of the bound substrate.
The kinetic scheme shown in Fig. 3a is also useful for analysis of the build-up rate of the SABRE-derived polarization. In general, starting from the same kinetic arguments, it can be shown that the effective substrate relaxation rate is given by Reff = (RS + RC[C]/[S])/(1 + [C]/[S]) (see the ESI†). This relaxation rate governs the substrate polarization build-up rate (Tb = 1/Reff) and thus, we are able to evaluate Tb by substituting specific numbers into the above expression. By running additional measurements, we have found that at a high magnetic field (16.4 T, corresponding to the 700 MHz 1H NMR frequency) the average relaxation time of the protons of free pyridine used as the substrate is ∼27.5 s (hence, RS ∼ 0.036 s−1); for the protons of pyridine bound to the Ir-complex the average T1 is about 3.6 s as measured by the inversion-recovery for protons of the non-exchanging axial pyridine ligand (hence, RC ∼ 0.28 s−1). The T1 time of pyridine is expected not to depend on the magnetic field strength, since conditions of the extreme narrowing regime apply and all protons in the coupled spin network have very similar relaxation rates.17 However, for the pyridine ligand in the complex the relaxation time is expected to decrease when conditions of strong coupling with the hydride protons are fulfilled, i.e., at the LAC region. Hence, it is reasonable to assume that RC ∼ 0.9 s−1 (as for the hydride protons at high field) at 6 mT, which is a typical field for running low-field SABRE experiments. Taking this together, one can calculate the build-up time to be TLFb ∼ 12.2 s for low-field SABRE and THFb ∼ 20.3 s for high-field SABRE. These values correlate well with the results published earlier.16,18 A more accurate analysis for low-field SABRE (based on the numerical simulation of the full kinetic scheme) gives the build-up time of 12.6 s for [C*] and 14.9 s for [S*] (Fig. 3b). It is thus seen that the simplified evaluation for the build-up time is in a good agreement with these values.
We have analyzed the literature data and found that formula (2) explains well the trends observed in other studies (Fig. 4). For example, it is seen that the signal enhancement is higher for lower substrate concentrations for both 1H and 15N nuclei of the substrates;8,9 indeed, polarization as high as 10% was obtained only for low (∼4 mM) substrate concentrations.19 However, the substrate-to-metal ratio cannot be less than 3 because the active catalyst [Ir(L)(S)3(H)2]+ cannot be formed from the precursor (e.g. [IrCl(COD)(IMes)]) until 3 substrate molecules per Ir center are available as ligands. If the initial amount of substrate is low, then during bubbling with hydrogen one would expect the formation of Ir dimers20 or other non-active species21 in solution. Therefore, the expected optimal substrate-to-metal ratio is ∼3. Formula (2) also explains the linear dependence of the SABRE enhancement on the catalyst concentration;7,22 however, [C] values higher than 10 mM are usually limited by precursor solubility. One may anticipate deviations from formula (2) when a strongly binding co-substrate is used along with polarizing substrates in micro- or nanomolar concentrations. In such a case, the concentration of the intermediate species C1 and the hydrogen exchange constant are independent of [S] (see the ESI†); therefore the signal enhancement should be independent of [S], and the NMR signal of the polarized substrate should linearly depend on its concentration. This was indeed observed experimentally.23
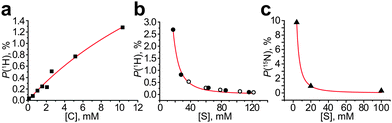 | ||
| Fig. 4 (a) 1H polarization dependence on the catalyst concentration (pyridine concentration is the same for all data points, [S] = 103 mM), data from ref. 7; (b) 1H polarization dependence on the substrate concentration, filled circles show data for pyridazine, empty circles show data for phthalazine (catalyst concentration was the same but was not specified by the authors), data from ref. 8; (c) 15N polarization dependence on the substrate concentration (catalyst concentration [C] = 0.2 mM was the same for all data points); data from ref. 9. The data sets shown were chosen because they provide polarization dependence on [C] or [S] concentration, with other parameters kept constant (see Fig. S7 in the ESI† for fitting details). | ||
It is also seen from our model that the signal enhancement should be directly proportional to the rate of parahydrogen supply (kH2[H2*]). This expectation is confirmed by experiments in which the gas pressure and the parahydrogen flow rate were varied.9,24 This result indicates that much higher enhancements are expected if one could increase the parahydrogen concentration in solution. While this may have seemed intuitive beforehand, we now provide a theoretical basis for why it should be so.
It is important to emphasize that although the parameter λ describing the spin mixing efficiency in SABRE complexes can be granted as an external parameter for our model, we can provide reasonable estimates for it. This can be performed for both models of polarization transfer, which are currently being discussed: (i) coherent polarization transfer and (ii) cross-relaxation. For coherent polarization transfer, we derived the following expression:
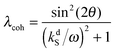 | (3) |
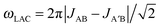 is a LAC angular frequency for a three-spin system and tan(2θ) = ωLAC/(ωA − ωB − 2πJAA′) (for details see the ESI†). At the center of the LAC region sin2(2θ) = 1 and the parameter λcoh has a sharp feature at the magnetic field corresponding to LAC and is close to zero otherwise. In the case of cross-relaxation, λ takes the form
is a LAC angular frequency for a three-spin system and tan(2θ) = ωLAC/(ωA − ωB − 2πJAA′) (for details see the ESI†). At the center of the LAC region sin2(2θ) = 1 and the parameter λcoh has a sharp feature at the magnetic field corresponding to LAC and is close to zero otherwise. In the case of cross-relaxation, λ takes the form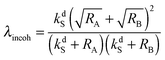 | (4) |
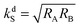 provides the maximal transfer efficiency. However, one should bear in mind that too low kdS values in addition result in lower [S*] concentrations; thus, a compromise has to be found to ensure a high spin mixing efficiency and a sufficiently high dissociation rate.
provides the maximal transfer efficiency. However, one should bear in mind that too low kdS values in addition result in lower [S*] concentrations; thus, a compromise has to be found to ensure a high spin mixing efficiency and a sufficiently high dissociation rate.
Interestingly, the simple expression (3) can account for the so-called “quantum Zeno effect”.25 Frequent substrate association–dissociation events act as quantum-mechanical “measurements” of the nuclear spin system and do not allow the system to evolve from the initial state, |Sα〉, to the other state, |T+β〉, at the LAC. The functional dependence of λ on kdS is such that if we increase both kdS and kaS keeping their ratio (kdS/kaS) constant, the overall enhancement decreases: indeed, repetitive “quantum measurements” on a spin system turn off the spin dynamics. Such an effect is absent in the cross-relaxation case (4), i.e., it is operative only in the case of true coherent quantum-mechanical spin evolution. A more detailed explanation of such behavior is given in the ESI;† a rigorous theoretical analysis based on a quantitative spin dynamics simulation (taking into account the exact nature of spin dynamics and exchange kinetics) can confirm the presence of the quantum Zeno effect in SABRE experiments under multiple exchange events.26 It is interesting to note that our model gives the maximal polarization as 50% (η = 0.5/Pth) for the substrate in low-field SABRE. In the case of incoherent polarization transfer the maximum achievable polarization depends on the cross-relaxation rate and the relaxation rates in the free substrate and the complex.
Summarizing all the results, one can see that the key parameters of the system, which should be optimized, are the relaxation rates (especially, RC) and not the dissociation rate constants. Indeed, kdS is already on the order of 10 s−1,7 while the optimal value derived from the simple analysis as kdS = ωLAC should be ∼4.5 s−1 (for JAB − JA′B = 1 Hz). As it has recently been shown, there is a direct correlation between the substrate exchange rate and the π-accepting ability of NHC ligands.27 This observation together with the results presented here paves the way for prediction of the structure of more efficient catalysts for SABRE. One way to reduce the relaxation rate in the complex is to use deuterated ligands and substrates, which reduces the efficiency of the dipole–dipole relaxation mechanism in solution. It was shown by Fekete et al. that the deuteration of the NHC ligand indeed significantly increases the polarization obtained by SABRE.28 Another strategy is to increase the difference, JAB − JA′B, in J-couplings between the hydride and substrate nuclei: consequently, λ will still be large even at higher kdS. The J-coupling increase along with the prolongation of TC1 and TS1 explains the much higher enhancements observed for 15N nuclei compared to the 1H nuclei of the substrates.19
To conclude, we have derived a formula that describes the dependence of the signal enhancement on the relevant parameters, such as the concentrations of the catalyst, parahydrogen and substrate, the J-couplings, the relaxation rates and the reaction rate constants for SABRE experiments. Although our formula is relatively simple, it is in a good agreement with the data published so far. Furthermore, based on its analysis we can formulate practical recommendations on how to design an optimal chemical system for SABRE: (i) the substrate-to-catalyst ratio should be as low as possible as long as C (e.g., [Ir(L)S3H2]+) remains the main catalyst form in solution, it means that the optimal substrate-to-metal loading is ∼3 (for lower ratios the formation of non-active species is expected); (ii) for low-field SABRE the substrate dissociation rate constant should be on the order of the spin mixing frequency at a LAC, kdS = ωLAC, while for high-field SABRE kdS should be as high as possible; (iii) the relaxation sink in the complex C should be kept low, which can be achieved either by deuteration of the ligands or by using ligands carrying as few magnetic nuclei as possible; (iv) the parahydrogen concentration in solution should be increased, either by using a suitable solvent, high pressure or by an efficient gas–liquid mixing technology. We anticipate that the analysis presented here will be useful for optimization of experimental conditions in SABRE for the development of new NMR and MRI applications.
DAB, KVK and IVK are grateful for RFBR grants (14-03-00374-a, 14-03-31239-mol-a and 14-03-93183 MCXa) for support in conducting NMR experiments. ANP and KLI thank the Russian Science Foundation (grant No. 14-13-01053) for support in spin dynamics calculations.
References
- J. H. Ardenkjær-Larsen, B. Fridlund, A. Gram, G. Hansson, L. Hansson, M. H. Lerche, R. Servin, M. Thaning and K. Golman, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10158–10163 CrossRef PubMed.
- P. Nikolaou, B. M. Goodson and E. Y. Chekmenev, Chem. – Eur. J., 2015, 21, 3156–3166 CrossRef CAS PubMed.
- B. M. Goodson, J. Magn. Reson., 2002, 155, 157–216 CrossRef CAS PubMed.
- J. Natterer and J. Bargon, Prog. Nucl. Magn. Reson. Spectrosc., 1997, 31, 293–315 CrossRef.
- S. B. Duckett and R. E. Mewis, Acc. Chem. Res., 2012, 45, 1247–1257 CrossRef CAS PubMed.
- R. W. Adams, J. A. Aguilar, K. D. Atkinson, M. J. Cowley, P. I. Elliott, S. B. Duckett, G. G. Green, I. G. Khazal, J. Lopez-Serrano and D. C. Williamson, Science, 2009, 323, 1708–1711 CrossRef CAS PubMed.
- M. J. Cowley, R. W. Adams, K. D. Atkinson, M. C. R. Cockett, S. B. Duckett, G. G. R. Green, J. A. B. Lohman, R. Kerssebaum, D. Kilgour and R. E. Mewis, J. Am. Chem. Soc., 2011, 133, 6134–6137 CrossRef CAS PubMed.
- K. M. Appleby, R. E. Mewis, A. M. Olaru, G. G. Green, I. J. Fairlamb and S. B. Duckett, Chem. Sci., 2015, 6, 3981–3993 RSC.
- M. L. Truong, T. Theis, A. M. Coffey, R. V. Shchepin, K. W. Waddell, F. Shi, B. M. Goodson, W. S. Warren and E. Y. Chekmenev, J. Phys. Chem. C, 2015, 119, 8786–8797 CAS.
- V. V. Zhivonitko, I. V. Skovpin and I. V. Koptyug, Chem. Commun., 2015, 51, 2506–2509 RSC.
- R. W. Adams, S. B. Duckett, R. A. Green, D. C. Williamson and G. G. Green, J. Chem. Phys., 2009, 131, 194505 CrossRef PubMed.
- A. N. Pravdivtsev, A. V. Yurkovskaya, H.-M. Vieth, K. L. Ivanov and R. Kaptein, ChemPhysChem, 2013, 14, 3327–3331 CrossRef CAS PubMed.
- A. N. Pravdivtsev, K. L. Ivanov, A. V. Yurkovskaya, P. A. Petrov, H.-H. Limbach, R. Kaptein and H.-M. Vieth, J. Magn. Reson., 2015, 261, 73–82 CrossRef CAS PubMed.
- C. H. Langford and H. B. Gray, Ligand substitution processes, WA Benjamin, Inc., 1966 Search PubMed.
- K. L. Ivanov, A. N. Pravdivtsev, A. V. Yurkovskaya, H.-M. Vieth and R. Kaptein, Prog. Nucl. Magn. Reson. Spectrosc., 2014, 81, 1–36 CrossRef CAS PubMed.
- D. A. Barskiy, K. V. Kovtunov, I. V. Koptyug, P. He, K. A. Groome, Q. A. Best, F. Shi, B. M. Goodson, R. V. Shchepin, A. M. Coffey, K. W. Waddell and E. Y. Chekmenev, J. Am. Chem. Soc., 2014, 136, 3322–3325 CrossRef CAS PubMed.
- K. Ivanov, A. Yurkovskaya and H.-M. Vieth, J. Chem. Phys., 2008, 129, 234513 CrossRef PubMed.
- D. A. Barskiy, K. V. Kovtunov, I. V. Koptyug, P. He, K. A. Groome, Q. A. Best, F. Shi, B. M. Goodson, R. V. Shchepin, M. L. Truong, A. M. Coffey, K. W. Waddell and E. Y. Chekmenev, ChemPhysChem, 2014, 15, 4100–4107 CrossRef CAS PubMed.
- T. Theis, M. L. Truong, A. M. Coffey, R. V. Shchepin, K. W. Waddell, F. Shi, B. M. Goodson, W. S. Warren and E. Y. Chekmenev, J. Am. Chem. Soc., 2015, 137, 1404–1407 CrossRef CAS PubMed.
- M. L. Truong, F. Shi, P. He, B. Yuan, K. N. Plunkett, A. M. Coffey, R. V. Shchepin, D. A. Barskiy, K. V. Kovtunov, I. V. Koptyug, K. W. Waddell, B. M. Goodson and E. Y. Chekmenev, J. Phys. Chem. B, 2014, 118, 13882–13889 CrossRef CAS PubMed.
- B. J. van Weerdenburg, A. H. Engwerda, N. Eshuis, A. Longo, D. Banerjee, M. Tessari, C. F. Guerra, F. P. Rutjes, F. M. Bickelhaupt and M. C. Feiters, Chem. – Eur. J., 2015, 21, 10482–10489 CrossRef CAS PubMed.
- K. D. Atkinson, M. J. Cowley, P. I. Elliott, S. B. Duckett, G. G. Green, J. Lopez-Serrano and A. C. Whitwood, J. Am. Chem. Soc., 2009, 131, 13362–13368 CrossRef CAS PubMed.
- N. Eshuis, B. J. van Weerdenburg, M. C. Feiters, F. P. Rutjes, S. S. Wijmenga and M. Tessari, Angew. Chem., Int. Ed., 2015, 54, 1481–1484 CrossRef CAS PubMed.
- R. V. Shchepin, M. L. Truong, T. Theis, A. M. Coffey, F. Shi, K. W. Waddell, W. S. Warren, B. M. Goodson and E. Y. Chekmenev, J. Phys. Chem. Lett., 2015, 6, 1961–1967 CrossRef CAS PubMed.
- W. M. Itano, D. J. Heinzen, J. Bollinger and D. Wineland, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41, 2295 CrossRef CAS.
- S. Knecht et al., unpublished results.
- B. J. van Weerdenburg, N. Eshuis, M. Tessari, F. P. Rutjes and M. C. Feiters, Dalton Trans., 2015, 44, 15387–15390 RSC.
- M. Fekete, O. Bayfield, S. B. Duckett, S. Hart, R. E. Mewis, N. Pridmore, P. J. Rayner and A. Whitwood, Inorg. Chem., 2013, 52, 13453–13461 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp05134g |
| ‡ Present address: Department of Radiology and Radiological Sciences, Institute of Imaging Science, Vanderbilt University, 1161 21st Avenue South, Medical Center North, AA-1105, Nashville, TN 37232-2310, USA. |
| This journal is © the Owner Societies 2016 |