Unveiling the peculiar hydrogen bonding behavior of solvated N-heterocyclic carbenes†
Oldamur
Hollóczki
ab
aMulliken Center for Theoretical Chemistry, University of Bonn, Beringstr. 4+6, D-53115 Bonn, Germany
bDepartment of Inorganic and Analytical Chemistry, Budapest University of Technology and Economics, Szt. Gellért tér 4, 1111 Budapest, Hungary. E-mail: holloczki@gmail.com
First published on 11th November 2015
Abstract
To investigate the hydrogen bonding and its dynamics of N-heterocyclic carbenes (NHCs) in solution, a molecular mechanical force field was fitted for the homologous series of 1,3-dialkylimidazol-2-ylidenes. During the exploration of the potential energy surface of the water/1,3-dimethylimidazol-2-ylidene system, it was observed for the first time that the carbene is prone to interaction with hydrogen bond donor molecules also from the rather unusual “on top” orientation, where the direction of the interplay is perpendicular to the plane of the NHC's ring. The fitting of the force field parameters for imidazol-2-ylidenes was found to be the best in the case of a two-site model, which reproduces not only the strength, but also the direction dependency of hydrogen bonding. With the aid of this tool, curious, hitherto unknown types of hydrogen bonding could be unveiled for NHCs. In the case of non-hydrogen bonding solvents, carbenes tend to form short lived, but structurally influental hydrogen bonds between each other via ring hydrogen atoms and the divalent carbon atoms. The chemically highly important hydrogen bond dynamics of NHCs was found to be facilitated by three center hydrogen bonding, where two alcohol molecules bind to a carbene, which is allowed only by the aforementioned relatively strong interaction between the NHC and the hydrogen bond donor in the “on top” orientation. The latter finding has significant effects on processes that involve this kind of replacement, such as the selective transesterification reactions, and the mechanism of proton exchange on azolium rings.
1 Introduction
For more than two decades, N-heterocyclic carbenes (NHCs) have been in the focus of academia and industry in many fields of chemistry.1–7 Beside their curious (electronic) structure and stability issues, these species are widely applied, most commonly in catalytic processes either as ligands in organometallic complexes,4,5,8–10 or without metal atoms as organocatalysts.6,11–14 The corresponding catalytic reactions involve many kinds of C–C couplings, and other processes of significant synthetic value, which can be performed with high regio- and stereoselectivity as well. There are also many examples in literature showing the impact of the interactions between carbenes and their closer or longer range environment, which may reach far beyond their mere reactivity. For example they catalyze enzymatic reactions involving thiamine,11,15,16 or they interact with metal17 or oxide18,19 surfaces to form supramolecular structures,17 functionalize the surface,18 or avoid decomposition.19Although in the synthetic application of NHCs the reactivity clearly originates from the characteristic electronic structure of the carbene,20 there are many direct indications showing that the environment has a significant effect on the reactions in terms of selectivity and reaction rates. The choice of the solvent is, for example, one of the reaction conditions that are the most important issues when designing or optimizing a reaction for synthetic purposes. Inoue and co-workers, for example, showed that the NHC-catalyzed cross-benzoin condensations between aliphatic aldehydes and formaldehyde, which can have four different products, can be performed with selectivities up to 100%, and the best results are achieved in alcohols as solvents.21 Similarly, the reaction of α,β-unsaturated aldehydes with other aldehydes catalyzed by carbenes, usually yielding γ-butirolactones could be optimized in a way by changing the temperature, the base and, most remarkably, the polarity of the solvent that an intriguing side product, β-lactone, is produced.22
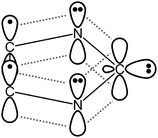
The largest impact of solvents on the reactivity of a free carbene is expected via hydrogen bonding, since the nucleophillicity and the strong hydrogen bond accepting ability23–30 of the carbene are both related to the presence of the lone pair (Fig. 1). Thus, in the presence of hydrogen bond donor molecules, the carbene catalyst should be (at least partly) deactivated. It was reported recently that in 1-butyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide the aforementioned C–C coupling organocatalytic reaction yielding γ-butirolactones is significantly slower than in THF,31 due to the formation of a hydrogen bonded assembly between the carbene and the ring hydrogen atoms of the imidazolium cation, which had been observed before (1, Fig. 2).32 On the other hand, for 1,3-dialkylimidazolium acetate ionic liquids – where the carbene is available from a proton transfer between the solvent cation and anion27,33 – a relatively high activity has been observed experimentally in similar organocatalytic reactions34 and in the chemical absorption of CO2,35,36 despite the very low, spectroscopically untraceable37 amount of carbenes in the corresponding ionic liquids. This interesting discrepancy has been indicated by ab initio molecular dynamics (AIMD) simulations38 and later by experiments as well39 to be due to the high hydrogen bond acceptor affinity of the acetate anion, which – unlike the weakly hydrogen bonding imide anion – occupy the aforementioned ring hydrogen atoms, and the carbene can be relatively free in the solution, retaining its reactivity.
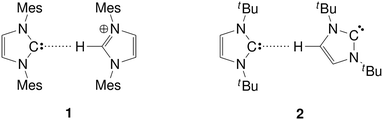 | ||
| Fig. 2 Hydrogen bonding structures of imidazol-2-ylidenes with imidazolium cations (1), and other imidazol-2-ylidenes (2). Mes: 1,2,3-trimethylphenyl group; tBu: tert-butyl group. | ||
All the information above shows that carbenes are present in many different systems either by conscious application, or unintended generation, and while they are closely related to, and affected by the closer or longer range environment, they are in return influencing the behavior of the system they are embedded in. Accordingly, taking into account the interactions – especially hydrogen bonding – between the carbenes and their environment is highly relevant for understanding their chemistry. However, while several theoretical studies have been devoted to understand the electronic structure of carbenes,30,40–43 and the mechanism of their reactions,28,44–49 little is known about their structure in a larger scale from the theoretical perspective, such as their solvation and its effects on the reaction mechanisms. Discussing such behavior requires a multiscalar approach, which takes the environment into account, and would provide, therefore, vital information that can complete the electronic structure resolution calulations to build the full picture on the reactions involving NHCs and related materials, and can be of great help in many ways in their application. This is especially the case for systems that contain hydrogen bond donor solvents or reagents, where the presence and the dynamics of the solute–solvent or solvent–solvent interactions are, as shown above, highly influential on the product, selectivity, and rates of the reaction. The information provided by, for example, molecular dynamics simulations regarding e.g. solvation structures and dynamics, aggregation behavior, hydrogen bonding, π-interactions, interfacial behavior, and polymer–carbene interactions would potentially allow choosing the best solvent for a given process with conscious design; and possibly an increase in the rates and efficiency of (stereo)selective reactions might be achieved with less efforts, if one can select the solvent that can steer the reaction in the desired way by enhancing the required orientation of the reactants.
While the aforementioned studies on the solvation of the carbene in imidazolium acetate ionic liquids,38 and on the fast protonation of imidazol-2-ylidenes in bulk water28 could be performed by using AIMD, in many cases the use of classical molecular dynamics (MD) with force fields is desired, due to the accessible higher time scale and larger sizes. The use of these methods, however, requires the initial establishment of the parameters for the potential. To the best of our knowledge classical MD simulations for free NHCs have not yet been applied, and the corresponding force field parameters have not yet even been established.
The difficulty of the parametrization comes from three issues. First, as mentioned above, carbenes form very strong hydrogen bonds with hydrogen bond donor molecules,25–28 which can be a great challenge for force fields. With water, for instance, the interaction energy of 1,3-dimethylimidazol-2-ylidene is 9.6 kcal mol−1 at the B3LYP/6-311+G** level,27,28 which is by ca. 50% stronger than the interaction between two water molecules (6.4 kcal mol−1 at the B3LYP/6-31+G* level). Secondly, the strength of this hydrogen bond should be highly dependent on the alignment of the hydrogen bonding agent, since the lone pair of the carbon atom is oriented in the plane of the ring, while perpendicular to it the carbon atom possesses a vacant p-orbital, which is involved in aromatic delocalization (Fig. 1).30,40–42 Such anisotropy can also be a difficulty for the generally applied potentials, where the intermolecular interaction energy is described as a function of distances, and not directions. Thirdly, the hydrogen atom in the hydrogen bond can be transferred to the hypovalent carbon atom,27,28,50,51 provided that the hydrogen bond donor is acidic enough, which results in azolium salts. The reactivity of many organic molecules can be reliably reproduced by reactive force fields, e.g. the bond order based ReaxFF.52 This approach holds great potential, but in most classical simulations non-reactive molecular mechanical force fields are applied, and bond breaking/formation is generally avoided or neglected, which still allows us to derive many information on the starting materials in their pre-reaction state, or on the products.
Turning back to the first two points, hydrogen bonds are described in molecular mechanics – if polarizability is not accounted for – generally via non-bonding terms, which include Coulombic and van der Waals interactions. From these two kinds of interplay the Coulombic forces provide the stronger attraction, while the van der Waals potential (often in the form of a Lennard-Jones potential) determines the closest distance between the two atoms that can approach each other. In accordance, in simple force fields mostly the atomic charges determine how strong the interaction is at a certain distance, except for the highly repulsive region of the van der Waals potential. Thus, the simplest way to tune the strength of hydrogen bonding interactions is to alter the charges of the molecules involved, albeit the dipole moment might also become unphysical, which is generally not desirable.
Alternatively, the strength of the hydrogen bonds, together with their directionality, is known to be tunable by placing charges at points other than the atomic nuclei, altering, therefore, the electrostatic distribution around the molecule. In many cases, the charge is completely shifted off the atomic position, separating van der Waals and Coulombic sites of interaction. The most widely known examples for these models are the four-site, and five-site water models, which reproduce many properties of water with impressive accuracy. In the four-site models (e.g. TIP4P53 and its variants, OPC54) the negative charge of the oxygen atom is located in the bisector of the HOH bond angle, and therefore the interaction energy with a hydrogen bond donor molecule can be increased, if the latter molecule is slightly tilted out of the water molecule's plane. This approach, therefore, helps to achieve hydrogen bonding directionalities similar to that in the well-known structure of the water dimer. In the five-site models (e.g. TIP5P,55 ST256), on the other hand, the negative charge of the oxygen atom is distributed between the two of such point charges, which are situated in a fashion that they are directly representing the lone pairs of the oxygen atom. Accordingly, the distance between the positive (hydrogen bond donor) and negative (hydrogen bond acceptor) charge centers becomes shorter, therefore the strength of interplay is altered, while the alignment of the hydrogen bond donor molecules is improved, and becomes similar to those observed in experiments and ab initio calculations.
Accordingly, these many-site models might also make the fitting of a carbene force field possible, allowing the simulations of interest to be performed. In this study this possibility is explored in order to fit a force field that enables the understanding of the solvation, especially the hydrogen bonding behavior of carbenes. The successful development of such potential allows the modeling of imidazol-2-ylidenes in different solutions, uncovering hitherto unknown aspects of their hydrogen bonding behavior, which put the chemistry of carbenes into a new perspective.
2 Applied methods
2.1 Static quantum chemical calculations
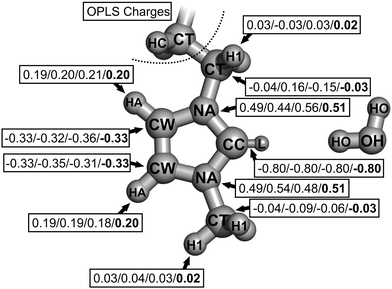
All quantum chemical calculations were performed by the Gaussian 09 program package.57 The geometries of several conformers of 1,3-dimethylimidazol-2-ylidene, 1-ethyl-3-methylimi-dazol-2-ylidene and 1-butyl-3-methylimidazol-2-ylidene were created by the systematic rotation of the alkyl substituents. These structures were then optimized at the HF/6-31G(d) level of theory, following the protocol of Pádua and Canongia Lopes that was used for imidazolium derivatives,58 in order to be compatible with their setup. The default convergence criteria of Gaussian 09 were applied for the SCF cycle and for the geometry optimization as well. The eigenvalues of the Hessian were calculated to confirm if the obtained structures were minima. CHELPG charges59 were calculated on these geometries at the MP2/cc-pVTZ(-f) level (again for the sake of compatibility with the force fields with the imidazolium cation58), and were, thereafter, averaged over the different conformations for each compounds, according to the relative energies. It should be noted here that for the structurally very similar imidazolium cation the CHELPG approach was shown to be not necessarily the best choice of method to calculate atomic partial charges, but it exhibited a consistent behavior in the whole series,60 while the compatibility with the CL&P force field is also required to apply this method. For obtaining the reference potential energy curves, single point DFT calculations were performed at the range separated ωB97-XD/aug-cc-pVTZ level61–65 (including dispersion and long-range correction as well, which are needed for the present systems) on systematically assembled structures (for details see the Results section), consisting of the HF/6-31G(d) optimized 1,3-dimethylimidazol-2-ylidene, and a water molecule. The geometry of the water molecule was identical to that of the SPC/E model,66 since this model was applied for describing the water's non-bonding interactions in the optimization of the non-bonding parameters.2.2 Static potential energy calculations and molecular dynamics simulations by molecular mechanics
All molecular dynamics simulations, and single point energy calculations that were based on molecular mechanics were carried out by using the LAMMPS code.67 For calculating the parameters of the pairwise Lennard-Jones potentials, the Lorentz–Berthelot mixing rules were applied.For the fitting of the non-bonding potentials single point energy calculations were performed on a series of systematically created geometries that consisted of a single carbene, and an SPC/E water molecule. The details of the geometries will be discussed in the Results and discussion section. The cut-off distance was set to be 15 Å, which is much longer than any interatomic distances in any investigated structures. The interaction energies between the water and carbene molecules were compared to the DFT values in the chemically most important HO–CC (Fig. 3) distance range of 1.7–7.0 Å, and the corresponding root mean square deviation (RMSD) values and other descriptors were calculated to quantify the quality of the fit.
After the successful fitting of the parameters, molecular dynamics simulations of solvated 1,3-dimethylimidazol-2-ylidene molecules were performed. For these simulations periodic boundary conditions were applied, and to rationalize the computational demand, a smaller, 10 Å cut-off distance was chosen, which is still almost three times larger than the biggest σij value in the system. For the Coulombic forces between particles being farther apart than the cut-off distance, the particle-particle particle-mesh approach was applied. A time step of 0.5 fs was used. The temperature and pressure were regulated by Nosé–Hoover chain thermostats and barostats, respectively.68–70 The force field parameters for the solvent molecules were taken from the OPLS-AA71,72 and AMBER73 force fields. In the the MD simulations with the two-site model of the carbene's divalent carbon atom, the NA and CC atoms, as well as the L point were treated as a single rigid body within the NHC molecule, to keep L in the desired position in the plane of the ring, exactly at a 0.2 Å distance from the CC atom.
The simulation box was created that it contained about 5–600 solvent molecules, and five NHCs, with the density of the pure solvent. Then 1 ns long NpT simulations were performed (T = 300 K, τT = 100 fs, p = 1 bar, and τp = 1000 fs), in which the volume was averaged over the last half nanosecond. This average volume was taken as a starting point for the production run. The resulting densities of the simulation boxes are listed in Table 1, while a snapshot of each boxes is shown in Fig. 4. After 1 ns of further equilibration in the NVT ensemble (T = 300 K, τT = 100 fs), 10 ns of production run was conducted, along which the atomic coordinates were saved in every 1 ps (used for analyzing structural properties), and during the last 100 ps of the simulation another, separated trajectory was created by saving the atomic coordinates in every 10 fs (used for analyzing dynamic properties).
| System | A | B | C | D | E |
|---|---|---|---|---|---|
| Solvent | Toluene | THF | EtOH/THF | iPrOH/THF | t BuOH/THF |
A snapshots of systems A–E are shown in Fig. 4. Dcarbene: diffusion constant of the carbene; η: viscosity of the solution; ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) Hbond,CC: average hydrogen bond lifetime between the divalent carbon atom and the a Hbond,CC: average hydrogen bond lifetime between the divalent carbon atom and the a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ring hydrogen atoms of the carbene molecule or b ring hydrogen atoms of the carbene molecule or b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hydroxyl hydrogen atom of the alcohol; hydroxyl hydrogen atom of the alcohol; ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) Hbond,HA: average hydrogen bond lifetime between the ring hydrogen atoms of the carbene and the c Hbond,HA: average hydrogen bond lifetime between the ring hydrogen atoms of the carbene and the c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) oxygen atom of the THF or d oxygen atom of the THF or d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) oxygen atom of the alcohol/THF. oxygen atom of the alcohol/THF. |
|||||
| Cell vector/Å | 45.86 | 42.20 | 44.13 | 45.05 | 45.95 |
| ρ/g cm−1 | 0.821 | 0.827 | 0.804 | 0.810 | 0.816 |
| %(n/n) NHC | 1.0 | 1.0 | 0.8 | 0.8 | 0.8 |
| %(n/n) solvent | 99.0 | 99.0 | 33.1/66.2 | 33.1/66.2 | 33.1/66.2 |
| D carbene/10−11 m2 s−1 | 349.5 | 168.1 | 91.7 | 188.8 | 54.2 |
| η/mPa s | 0.2547 | 0.3856 | 0.3687 | 0.4053 | 0.4671 |
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) Hbond,CC/ps
Hbond,CC/ps |
0.8a | 3.8a | 48.3b | 29.5b | 58.5b |
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) Hbond,HA/ps
Hbond,HA/ps |
— | 1.8c | 2.1/1.6d | 2.6/1.7d | 3.3/1.9d |
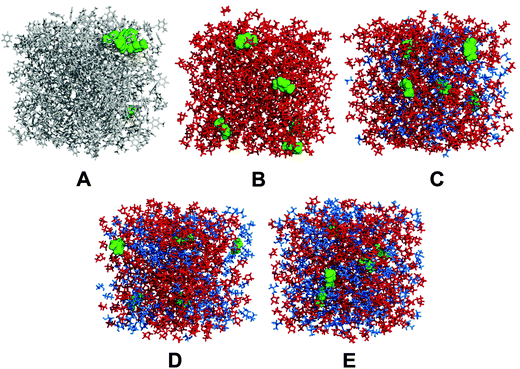 | ||
| Fig. 4 Simulation boxes of systems A–E (for details, see Table 1) investigated by molecular dynamics simulations. Green: 1,3-dimethylimidazol-2-ylidene; grey: toluene; red: tetrahydrofurane; blue: ethanol (in C) or isopropanol (in D) or tert-butanol (in E). | ||
The trajectories were analyzed by the TRAVIS software.74 The lifetime of hydrogen bonds was assessed by the dimer existence autocorrelation function (DACF), as implemented in TRAVIS.74 The DACF is defined as
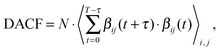 | (1) |
3 Results and discussion
3.1 Force field development
In this work the most fundamental derivatives, 1,3-dialkylimidazol-2-ylidenes were targeted for parametrization. Since there is considerable interest in the carbene content of ionic liquids,33 the development of a force field should be aimed at, which is compatible with the well-known CL&P parameter set of ionic liquids,58,75,76 but also with other, general potentials. The CL&P is the one of the most often applied potential for ionic liquids, which is also compatible77 with the OPLS-AA71,72 and AMBER force fields.73The OPLS potential form
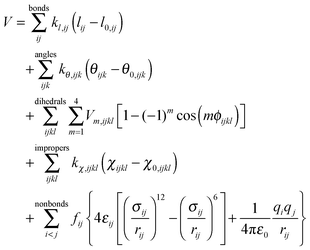 | (2) |
| Bond/angle type | l 0/Θ0 Å/degree | K l /KΘ kcal mol−1 Å−2/kcal mol−1 rad−2 | |
|---|---|---|---|
| Carbene | Imidazolium (CL&P)58 | Carbene | |
| CC–NA/CR–NA | 1.352 | 1.315 | Rigid |
| CC–L | 0.250 | — | Rigid |
| NA–CW | 1.385 | 1.378 | 427.5 |
| NA–CT | 1.443 | 1.466 | 337.0 |
| CW–CW | 1.333 | 1.341 | 520.6 |
| CW–HA | 1.069 | 1.080 | 385.0 |
| NA–CC–NA/NA–CR–NA | 102.50 | 109.80 | Rigid |
| NA–CC–L | 128.75 | — | Rigid |
| CW–NA–CC/CW–NA–CR | 112.46 | 108.00 | 70.0 |
| CW–CW–NA | 106.28 | 107.10 | 70.0 |
| CC–NA–CT/CR–NA–CT | 123.30 | 126.40 | 70.0 |
| CW–NA–CT | 124.24 | 125.60 | 70.0 |
| CW–CW–HA | 130.78 | 130.90 | 35.0 |
| NA–CW–HA | 122.94 | 122.00 | 35.0 |
The force constants for the bonds (kl,ij) and bond angles (kθ,ijk) were taken directly from the CL&P force field,58 which are defined to be identical to the OPLS-AA constants of the also isoelectronic imidazole.78 The reason for the applicability of these force constants stems from the fact that while the three compounds are electronically very similar, the force constants themselves generally do not influence the structure in a significant manner. Similarly, due to the high level of chemical and geometrical analogy between these compounds, the dihedral and improper parameters (Vm,ijkl, χ0,ijkl, kχ,ijkl) were applied directly as they were established for the derivatives of the imidazolium cation.
In the OPLS force field family, the Lennard-Jones parameters are generally optimized by reproducing experimental thermodynamic data, such as heat of vaporization and liquid densities. However, the accessibility of thermodynamic data is limited by the sensitivity of these compounds, while their available denisities correspond to the solid phase. As an alternative approach, probe molecules can be employed for the parametrization, and ab initio or DFT potentials can be used as references, to which the molecular mechanical force field can be fitted. Such an approach has been employed for e.g. alkanes79 or UO22+.80 For the optimization of the non-bonding Lennard-Jones parameters εij and σij, an SPC/E water molecule (dHO = 1 Å, ∢HOH = 109.47°) was employed as a probe for the 1,3-dimethylimidazol-2-ylidene, taking advantage of the Lorentz–Berthelot mixing rules, namely
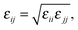 | (3) |
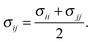 | (4) |
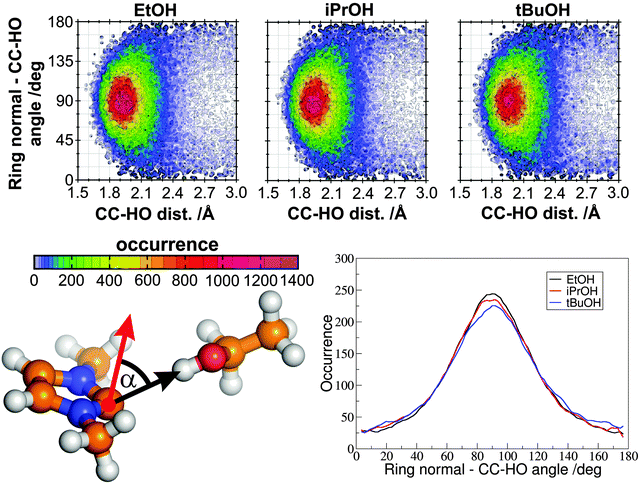
Points along two different potential curves were calculated by the QC methods described in the Applied methods section, as defined in Fig. 5. The first curve “in-plane” was established by moving the water in the plane of the carbene ring between 1.4 and 7.0 Å (measured between the interacting hydrogen atom of the water and the divalent carbon atom), pointing out one of the hydrogen atoms toward the hypovalent carbon atom CC, while in the second case “on-top” the water was moved perpendicular to the plane of the ring between the same HO–CC distances, again pointing a hydrogen atom toward the CC atom (Fig. 5). With these two curves it is possible to measure how good the established force field describes the strong, and direction-dependent hydrogen bonding of the NHC molecule.
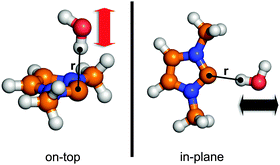 | ||
| Fig. 5 The definition of the two potential curves that are used for the fitting of the non-bonding parameters. The coordinate used to establish the potential curves are indicated by r, and the corresponding black (in-plane) and red (on-top) arrows showing the direction the water molecules were moved. The resulting data points are shown in Fig. 6. | ||
The reference curves from the DFT calculations are shown in Fig. 6 with full circles. Already at first glance it is observable that – in agreement with previous results27,28 – the “in-plane” potential curve has a very deep minimum (−10.3 kcal mol−1) at the 1.95 Å CC–HO distance (Fig. 6, black full circles). This interaction is significantly stronger than that between two water molecules (ca. 6–8 kcal mol−1), while the minimum is also located at a few tenths of Å larger distances. This clearly provides a challenge for the parametrization, since the Coulombic interactions – as a main source of attraction in such models, and which depend on the charge and the distance, see the last term in eqn (2) – will be lower than those between e.g. two SPC/E water molecules66 due to the aforementioned similar charges, but larger distances. Accordingly, in contrast to the “in-plane” potential curve, the interaction between the carbene and the water molecule will be, in fact, weaker in a simple model with the CHELPG charges obtained above.
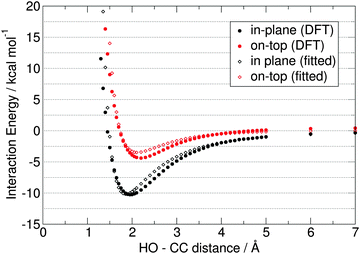 | ||
| Fig. 6 The two reference potential curves from the ωB97-XD/aug-cc-pVTZ single point calculations (full circles), for the systems described in Fig. 5. The fitted parameters are shown for the best fitting two-site model (empty diamonds), with dCC–L distances of 0.20 Å, ε = 0.26 kcal mol−1, and σ = 3.50 Å. | ||
The “on-top” curve is very surprising, since it exhibits a potential well of −4.4 kcal mol−1 at 2.20 Å (Fig. 6 red full circles), although due to the presence of a vacant orbital of the divalent carbon (perpendicular to the ring, see Fig. 1) the interaction should be rather repulsive. The present NHC, however, has an extended delocalized aromatic π-system,40–42 which – together with the π-electron donating nature of the nitrogen atoms – increases the electron density also “on-top” of the CC atom. In fact, hydrogen bonding with aromatic systems are known in literature, and can be represented by the simplest example of water and benzene.81–83 Indeed, the topological analysis of the electron density of the structure at the minimum of the curve (at 2.2 Å) clearly shows a bond critical point between the divalent carbon and the hydrogen atom of the water molecule, with a substantial electron density value (ρBCP = 0.017 at the ωB97-XD/aug-cc-pVTZ level; cf. for the minimum in the “in-plane” structure ρBCP = 0.022 a.u. at the same level), which suggests a certain covalency of this bond. In addition, the hypovalent CC carbon atom possesses the most negative partial charge in the the π-system (cf. the highly positive nitrogen atoms) and even in the whole molecule, therefore the electrostatic contribution to this bond can be substantial. This interesting property will be most likely dependent on the substituents attached to the ring, and on the nature of the heteroatoms connected directly to the divalent carbon atom, and will be, therefore, the subject of a follow-up study.
Starting from an “on-top” orientation, the interaction becomes gradually stronger if the water molecule is shifted toward the “in-plane” structures, hence no minimum on the potential energy surface could be found by a series of geometry optimizations with an “on-top” water molecule, due to the spontaneous rearrangement to an “in-plane”-like geometry. Nevertheless, this feature of the carbene is obviously influencing the dynamics of its solvation, where several hydrogen bond donor molecules are present in the solution, and the system is also exploring many conformations occasionally also farther away from the global potential minimum.
Despite the presence of this interesting attractive force between the water molecule and the carbene also in this unusual orientation, the dependence of the interaction energy on the directionality is clearly observable. Again, this is another difficulty for a pairwise potential, where the intermolecular interaction energies are determined only by the interatomic distances, and not the directions. This is partly taken care of by the different distances between the NA and HO atoms in the two orientations, but the intermolecular potential still has to be very carefully fitted to describe this very important and characteristic directionality with reasonable accuracy. To check how well the CHELPG-derived charges perform without any further tuning, the Lennard-Jones parameters σii and εii were fitted for the CC atom, while the rest of the atoms were assigned to already established atom types (see Fig. 3), with the corresponding Lennard-Jones parameters taken from the OPLS-AA force field (Table 3). The descriptors of the match between the DFT and the force field potential curves were chosen to be the root mean square deviations in the 1.7–7.0 Å range, the displacement of the potential minima, and the maximum deviation (Table 4). Please note when assessing the RMSD data that due to the many points at longer distances, where the fitted and DFT values are both close to zero, the overall RMSD values will be low, thus, the rest of the descriptors have to be considered as well. From the data it is clearly visible that the “on-top” curve can be reproduced well by this model, but it is insufficient to provide even a qualitative description of the strong interaction in the “in-plane” curve Table 4.
| Atom type | ε/kcal mol−1 | σ/Å | Source |
|---|---|---|---|
| CC | 3.500 | 0.210 | This work |
| L | 0.000 | 0.000 | This work |
| NA | 3.250 | 0.170 | OPLS-AA58,72,75,78 |
| CW | 0.070 | 3.550 | OPLS-AA58,72,75,78 |
| CT | 3.500 | 0.066 | OPLS-AA72 |
| HA | 2.420 | 0.030 | OPLS-AA58,72,75,78 |
| HC | 2.500 | 0.030 | OPLS-AA58,72,75 |
| H1 | 2.500 | 0.030 | OPLS-AA58,72,75 |
| OH | 3.166 | 0.155 | SPC/E66 |
| HO | 0.000 | 0.000 | SPC/E66 |
| q, e | d CC–L, Å | ε ii , kcal mol−1 | σ ii , Å | RMSDip, kcal mol−1 | δ maxip, kcal mol−1 | Δ ip, Å | RMSDot, kcal mol−1 | δ maxot, kcal mol−1 | Δ ot, Å | RMSDall, kcal mol−1 |
|---|---|---|---|---|---|---|---|---|---|---|
| −0.8 | 0.00 | 0.30 | 3.50 | 2.24 | 4.4 | 0.05 | 0.31 | 0.6 | 0.10 | 1.28 |
| −1.00 | 0.00 | 0.25 | 3.45 | 0.88 | 3.1 | 0.30 | 0.88 | 5.3 | 0.05 | 0.88 |
| −0.80 | 0.15 | 0.29 | 3.45 | 0.82 | 1.6 | 0.08 | 0.42 | 0.9 | 0.10 | 0.62 |
| −0.80 | 0.20 | 0.26 | 3.50 | 0.56 | 1.2 | 0.10 | 0.50 | 1.0 | 0.10 | 0.53 |
| −0.80 | 0.25 | 0.21 | 3.55 | 0.63 | 2.0 | 0.15 | 0.63 | 1.2 | 0.15 | 0.63 |
| −0.80 | 0.30 | 0.30 | 3.55 | 0.75 | 2.1 | 0.10 | 0.96 | 2.5 | 0.00 | 0.85 |
To tackle the aforementioned issue, two possibilities were considered. In the first model the atomic charges were systematically redistributed, making the CC atom more negatively, and the NA atoms more positively charged. Interestingly, the Coulombic interactions seem to provide insufficient attraction even with partial charges of −1.00e at the CC atom, although by the increase of charge the RMSD data shows a clear decreasing trend (see Table 4 and ESI†). Although the decrease of the RMSD values is prominent, even the best data are not convincing, while the arbitrary increase of polarity and the emprical manipulation of charges seem somewhat questionable, which might induce a large and unrealistic change in the solvation of the NHC when modelled in solution.
The second approach was to slightly displace, rather than increase the CHELPG-derived charges of the CC nucleus into a massless Coulombic site (i.e. point charge L), which is located in the plane of the ring, and figuratively represents the lone pair of the carbon atom (Fig. 3). Defining L allows the positive center of charge of the hydrogen bond donor molecule to be situated closer to the negative charge of the carbene's “lone pair”, resulting in presumably higher interaction energies even at larger distances from the CC atom, which may resemble more the “in-plane” curve in Fig. 5. On the other hand, the HO atoms of the water in the “on-top” orientation are farther from L, therefore they do not benefit from this energy gain, which results in the desired anisotropy. It is visible from the descriptors in Table 4 for the fitted parameters that the quality of the potential improves by applying this model, and the observed minimal RMSD values are well below those achieved by charge modification, while the polarity of the molecule suffered a significantly smaller change.
The most balanced setup was found to be the two-site model with a CC–L distance of 0.20 Å, with εii = 0.26 kcal mol−1, and σii = 3.50 Å, where the quality of the fit is similar for both potential curves, while the total RMSD values, maximal deviations, and the location of the potential energy minimum are all in an acceptable range. The corresponding potential curves calculated with the force field are shown in Fig. 5 with empty diamond symbols. It is also worth mentioning that the optimized σii values closely match those of sp3 and the sp2 carbon atoms of the OPLS-AA force field,71,72 which indicates a certain compatibility as well. In the highly repulsive region of the potential (HO–CC distance <1.5 and <1.6 Å for the “in-plane” and “on top” curves, respectively) the errors are significantly larger. This kind of behavior is not unusual for a Lennard-Jones function, but since the present force field is not intended to reproduce high pressure structures, these errors are acceptable. For other purposes it might be desirable to fit another kind of van der Waals potential to these reference curves, which would not be so steep in the repulsive region, resulting in a possibly better fit there.
3.2 Molecular dynamics simulations of 1,3-dimethylimidazol-2-ylidene in toluene, THF and THF/alcohol mixtures
After fitting the required parameters for imidazol-2-ylidenes, it is now possible to obtain essential information on the solvation structure and dynamics of these compounds, with a special emphasis on their hydrogen bonding behavior. The solvents investigated here were chosen carefully to correspond to realistic systems, which are also related to catalytic processes with carbenes. Toluene and THF are often applied as reaction media for various synthetic approaches, including benzoin condensation, and Stetter–Michael reactions,6,12 which are important C–C couplings. The interaction between alcohols and the NHC in THF was also investigated, where significant details on hydrogen bonding are expected to be found. Carbene catalyzed transesterification reactions – with alcohols as reactants – are often performed in THF,6,84–86 also selectively,6,84,85 and by introducing chiral NHCs as catalysts even stereoselectively6,87,88 for NHC-promoted kinetic resolution of secondary alcohols. The simulation boxes were created to contain each about 5–600 solvent molecules, and five NHCs. The equilibrated densities and compositions of the boxes are found in Table 1, snapshots in Fig. 4.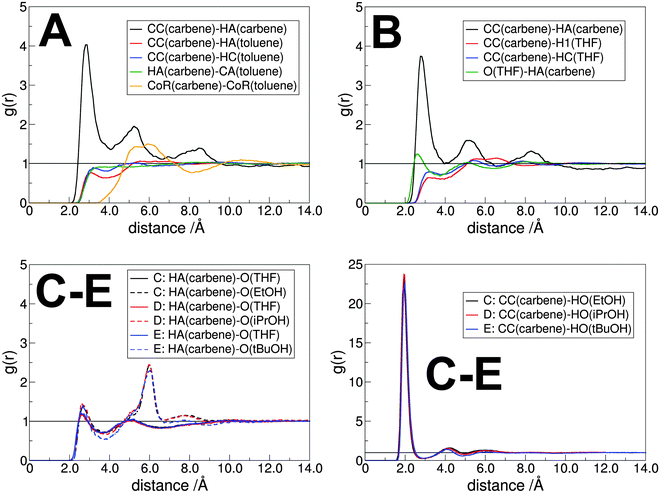 | ||
| Fig. 7 Characteristic radial pair distribution functions in the solution of carbene with toluene (A), THF (B), and THF/alcohol mixtures (C–E) as solvent. The labeling of the atoms is according to the atom types defined in the AMBER73 and OPLS-AA71,72 force fields, for the carbene molecule it is shown in Fig. 3, while for toluene the CA: ring carbon atom, HA: hydrogen atom at the ring, HC: methyl hydrogen atom; for THF the H1 is the α-hydrogen atom, HC is the β-hydrogen atom; for ethanol the HO is the hydrogen atom of the hydroxyl group. | ||
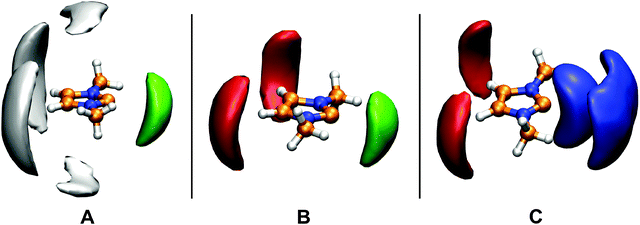
Despite the apparent lack of hydrogen bonds between the toluene and the carbene molecules, they might interact with each other through π-stacking. The RDF between the ring centers of the carbene and the toluene exhibits a broad, but a relatively high (g(r) = 1.5) first peak at distances around 5–6 Å (Fig. 7A). This large distance, and the lack of any preferred orientation (see ESI†) resembling π-stacking indicate that this interplay – in the sense as it is present in e.g. a benzene dimer – is not influential for this system. Interestingly, the spatial distribution function clearly shows the presence of an interaction between the ring hydrogen atoms of the carbene, and the negatively charged toluene ring carbon atoms (Fig. 8A), but the more quantitative RDF shows that this interplay is also of minor importance.
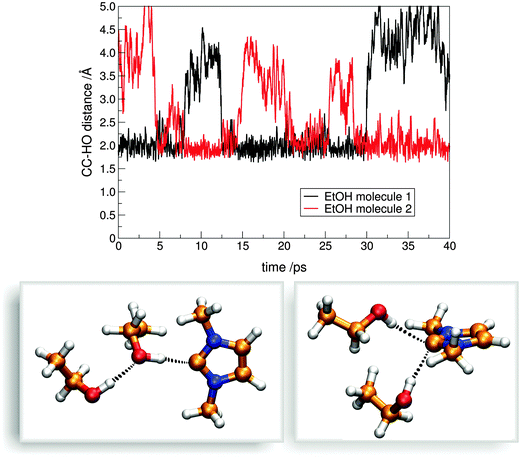
Despite the strength of this hydrogen bond, the contact between the alcohol and carbene molecules is dynamic, and regular exchange can be observed on average for every 48.3 ps for system C. This surprisingly frequent exchange is of great theoretical and practical importance, since beside the fact that it might be relevant for the aforementioned selectivity of transesterification reactions in the presence of multiple alcohol substrates, it is an integrated step of the proton(/deuteron) exchange mechanism11,51 of azolium salts in (deuterated) alcohols or water, where, of course, the reaction involves a deprotonation and a protonation step as well (highlighted with a frame in Fig. 10 below). Similarly, the act of a carbene catalyst generated in situ from azolium salts should be initiated by the exchange of the protonated base being in a hydrogen bond with the carbene to the substrate's electrophillic site in an analogous process (Fig. 10 above). In principle, two mechanisms could be feasible, an associative and a dissociative pathway. In the dissociative mechanism, the new alcohol–carbene hydrogen bond forms after the cleavage of the first one, while in the associative path the second alcohol binds to the NHC as well, which is followed by the departure of the first ethanol molecule. Since the hydrogen bond between the ethanol and the imidazol-2-ylidene is extremely strong (see Fig. 6 and 7), the energy demand of the dissociative mechanism is high. On the other hand, the associative pathway requires the carbene to be able to bind two alcohol molecules at a time, which is an unprecedented interplay for carbenes. However, as discussed above regarding the “on-top” potential curve on Fig. 6 (red full circles), hydrogen bond donor molecules seem to be able to bind to the present type of carbenes also from this rather unusual position with noteable strength, which allows the first alcohol molecule to be slightly tilted away from the “in-plane” arrangement, and provide enough space for the second alcohol molecule for binding to the complex. To reveal which mechanism is dominant, the distribution of coordination numbers was assessed, i.e. the number of alcohol molecules bound – viz. within 3 Å with their hydroxyl hydrogen – to the divalent carbon atom. As expected, the most populated coordination number was found to be one. However, this kind of structure is present only in the ca. 88% of the time, and coordination numbers of zero and two were observed in about 2% and 10%, respectively. This result shows that both mechanisms could occur, although the dissociation of the ethanol from the binding with the NHC – in the absence of a second ethanol molecule – is followed often by the reassociation of these two molecules, avoiding an effective exchange. Thus, in the presence of a second alcohol molecule, where actual exchange can occur, the process follows a predominantly associative mechanism (Fig. 11), through the peculiar, so far unknown, but surprisingly often present hydrogen bonding system containing one carbene and two alcohol molecules (Fig. 11 lower right).
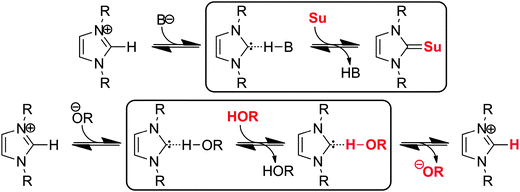 | ||
| Fig. 10 Exchange of the protonated basis in hydrogen bonding with the in situ generated carbene to a substrate (Su) of a catalytic process, as an integral step of the reaction mechanism (above), and the exchange of protons on azolium salts, on the example of imidazolium derivatives in alcohols or in water51 (below). | ||
The exchange mechanism should be dependent on the hydrogen bonding strength of the given carbene, and the steric effects within the hydrogen bonded assemblies of the carbene and one or two alcohol molecules. As visible from the data in Table 1, the lifetime of the hydrogen bonds varies greatly with the alcohol. Interestingly, although one might expect that the lifetimes increase gradually as the alcohol becomes more bulky, the exchange of isopropanol was found to be significantly more frequent than with ethanol. This contraintuitive finding shows that there is a much more complex underlying dynamics that controls this process, and influencing this behavior is more complicated than simply increasing the size of the substituents, at least with the hereby investigated methyl substituted imidazol-2-ylidene. With the tertbutanol, however, the rate of the exchange was found to be the slowest of the three alcohols. The distribution of coordination numbers shows that the mechanism is slowly changing from associative to dissociative, as the ratio of the uncoordinated carbene molecules increase from 2% via 3% to 6% (EtOH, iPrOH, and tBuOH, respectively), while those in twofold coordination occurred in 8% for iPrOH and 7% for tBuOH, compared to the aforementioned 10% for ethanol. Despite these apparent changes, the associative mechanism remains slightly more dominant even for the tBuOH. In a follow-up study, the relation of the carbene's and the alcohol's substituents in terms of hydrogen bond dynamics will be investigated in more detail.
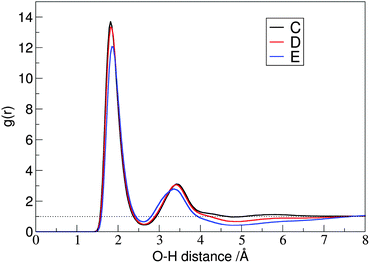
The hydrogen bonded assembly of the carbene and the alcohol is not isolated, but it is incorporated into the extended hydrogen bonded network between the alcohol molecules, which form long linear clusters, or rings in the solution. The RDF of the hydroxyl hydrogen atoms of the ethanol around the CC atoms shows, accordingly, a strong second peak, and a lower third one (Fig. 7C–E right, cf.Fig. 12). Due to the steric hindrance at the side chains, the clusters of iPrOH and tBuOH in the solution are significantly smaller, as shown by the disappearance of the third peak, and the decrease in the height of the second peak in the RDFs between the hydroxyl hydrogen and oxygen atoms of the alcohol molecules (Fig. 12).
Beside the undoubtedly most significant hydrogen bonding between the alcohol and carbene molecules, the oxygen atom of THF and the alcohol both appears to form notable hydrogen bonds with the HA atom of the NHC. These interactions are relatively weak, which can be seen from the large O–HA distances (ca. 2.6 and 2.7 Å for the THF and the alcohols, respectively) at the low first peak of the corresponding RDFs (Fig. 7C–E left). In accordance with their weakness, the lifetime of these interactions is also rather low (Fig. 4), falling in the 1–2 ps range.
Beside the structural data described above, it is also important to observe dynamic properties of the carbene molecules in the present solvents, most importantly the diffusion constants, which have direct effect on reaction rates. Diffusion constants of solutes can be influenced by the temperature, the viscosity of the solvent, and also by the strength of solute–solvent interactions. The diffusion constant and viscosity data can be seen in Table 1. Apparently, the diffusion of the NHCs is the fastest in toluene, where the solute–solvent interactions are the weakest, while the viscosity of the system is the lowest. In the case of systems C, D and E, the diffusion constant of the carbene can be influenced again by the viscosity of the solvent, and by the size and mobility of the alcohol cluster they are attached to. Apparently, these two effects are counteracting, since the size of alcohol clusters decreases in the EtOH → iPrOH → tBuOH order (as discussed above, see Fig. 12), while the viscosity increases. As a result, apparently the iPrOH provides the best environment for fast diffusion, which may also serve as an explanation for the curious fast hydrogen bond dynamics in this solvent.
4 Conclusion and outlook
In this paper the understanding of the hydrogen bonding of imidazol-2-ylidenes in solution was aimed at, which is probably the most influental solute–solvent interaction in the chemistry of NHCs. Due to the lack of available molecular mechanical parameters for carbenes in literature, first a new model had to be developed, which can account for the strength and directionality of hydrogen bonding for these systems. On the basis of the OPLS-AA and the CL&P force fields, a model was established for 1,3-dialkylimidazol-2-ylidenes, where the charge of the hypovalent carbon atom is shifted off the nucleus into a massless point charge, representing figuratively its lone pair. The bonding parameters (bond streching, angle bending, dihedral torsion) of the present force field were determined by geometry optimizations, while the non-bonding parameters (Coulombic and van der Waals) by calculating the atomic partial charges according to the CHELPG model, and by fitting a Lennard-Jones potential to two selected potential curves obtained by DFT calculations for the system consisting of a 1,3-dimethylimidazol-2-ylidene and an SPC/E water molecule as a probe.Exploring the two potential curves – one with the water displaced in the plane of the carbene's ring, the other perpendicular to it – did not only allow to fit the potential for the force field, but also revealed that the carbene can form a hydrogen bond of surprising strength with the water molecule approaching the divalent carbon atom from the direction of the π-system, and not only from the lone pair. This curious, and so far unprecedented finding revealed an unexpected flexibility for the hydrogen bond accepting property of NHCs, which is represented also in the present force field.
After fitting the required parameters for the simulations, the solvation of the carbene, and its dynamics was explored in detail for five synthetically important systems by molecular dynamics simulations. In the non-hydrogen bonding toluene and THF the carbene molecules formed hydrogen bonds with each other, resulting in a short-lived aggregation of these solutes. Given the high number of applications that employ these solvents for processes involving NHCs, it is highly important to be aware of this property that can significantly influence the availability, and distribution of the carbene molecules in solution.
In the hydrogen bonding ethanol/THF, isopropanol/THF, and tertbutanol/THF 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 solutions the CC atoms of the carbenes are interacting predominantly with the hydroxyl hydrogen atom of the alcohols (see RDFs in Fig. 7C–E), which is the most important solute–solvent interplay in these systems. Despite the apparent strength of the interaction between the hydrogen bond donor and acceptor moieties, the alcohol molecules exchanged at the hypovalent carbon atom on average between 20 and 60 ps. From the two conceivable mechanisms, i.e. associative and dissociative, the former was found to be more dominant in all cases, which means that the exchange occurs mostly via a three-centered hydrogen bonded system of a carbene and two alcohol molecules (Fig. 11 lower right). The dissociative mechanism, where the binding of the second alcohol molecule is preceded by the departure of the first one, could be, however, not ruled out in any cases, and was found to become more important with the increasing bulk of the alcohol, hindering sterically the formation of the three-centered hydrogen bonded assembly.
2 solutions the CC atoms of the carbenes are interacting predominantly with the hydroxyl hydrogen atom of the alcohols (see RDFs in Fig. 7C–E), which is the most important solute–solvent interplay in these systems. Despite the apparent strength of the interaction between the hydrogen bond donor and acceptor moieties, the alcohol molecules exchanged at the hypovalent carbon atom on average between 20 and 60 ps. From the two conceivable mechanisms, i.e. associative and dissociative, the former was found to be more dominant in all cases, which means that the exchange occurs mostly via a three-centered hydrogen bonded system of a carbene and two alcohol molecules (Fig. 11 lower right). The dissociative mechanism, where the binding of the second alcohol molecule is preceded by the departure of the first one, could be, however, not ruled out in any cases, and was found to become more important with the increasing bulk of the alcohol, hindering sterically the formation of the three-centered hydrogen bonded assembly.
The results above have interesting consequences on the way how we think of reactions involving NHCs. The very characteristic proton exchange of azolium salts, for example, must follow a deprotonation → exchange → protonation path (Fig. 10 below), where the exchange may occur through the associative mechanism described above. This might be the reason why this reaction can occur at all, since otherwise the very rarely forming carbene in the solution should cleave a very strong hydrogen bond for the reaction to take effect. Similarly to this, when azolium salts are applied as precatalysts, and the corresponding carbene catalyst is produced in situ by an appropriate base, the hydrogen bond between the protonated base and the carbene (see Fig. 10 above) does not need to cleave before the carbene could attack the electrophillic site of the substrate. Instead, via a mechanism that is analogous to the associative exchange of hydrogen bond donor molecules at the carbene, the NHC can access the substrate in a manner that the bond between the catalyst and the substrate can be formed parallel to the cleavage of the hydrogen bond.
Finally, the present force field can be, and will be applied in the close future for many mesoscopic systems of significance, including interactions with cellulose, and at interfaces. The extension of the present approach to provide force fields for a number of carbenes with various heteroatoms and substituents is also planned, which would allow a comprehensive investigation of the influental solute–solvent interactions on the reactions of carbenes.
Acknowledgements
Funding by the OTKA project K 105417, and the inspiring discussion with Prof. Barbara Kirchner, and Prof. László Nyulászi are gratefully acknowledged. O. H. is grateful to Dániel Buzsáki, who performed some of the DFT calculations at the BUTE.References
- F. Hahn and M. Jahnke, Angew. Chem., Int. Ed., 2008, 47, 3122–3172 CrossRef CAS PubMed.
- T. Dröge and F. Glorius, Angew. Chem., Int. Ed., 2010, 49, 6940–6952 CrossRef PubMed.
- D. Martin, M. Melaimi, M. Soleilhavoup and G. Bertrand, Organometallics, 2011, 30, 5304–5313 CrossRef CAS PubMed.
- S. Díez-González, N-Heterocyclic carbenes: from laboratory curiosities to efficient synthetic tools, Royal Society of Chemistry, Cambridge, 2011 Search PubMed.
- P. L. Arnold and S. Pearson, Coord. Chem. Rev., 2007, 251, 596–609 CrossRef CAS.
- D. Enders, O. Niemeier and A. Henseler, Chem. Rev., 2007, 107, 5606–5655 CrossRef CAS PubMed.
- M. N. Hopkinson, C. Richter, M. Schedler and F. Glorius, Nature, 2014, 510, 485–496 CrossRef CAS PubMed.
- G. Frenking, M. Sol and S. F. Vyboishchikov, J. Organomet. Chem., 2005, 690, 6178–6204 CrossRef CAS.
- S. Díez-González, N. Marion and S. P. Nolan, Chem. Rev., 2009, 109, 3612–3676 CrossRef PubMed.
- O. Schuster, L. Yang, H. G. Raubenheimer and M. Albrecht, Chem. Rev., 2009, 109, 3445–3478 CrossRef CAS PubMed.
- R. Breslow, J. Am. Chem. Soc., 1958, 80, 3719–3726 CrossRef CAS.
- D. Enders and T. Balensiefer, Acc. Chem. Res., 2004, 37, 534–541 CrossRef CAS PubMed.
- N. Marion, S. Dez-González and S. Nolan, Angew. Chem., Int. Ed., 2007, 46, 2988–3000 CrossRef CAS PubMed.
- J. L. Moore and T. Rovis, Asymmetric Organocatalysis, Top. Curr. Chem., Springer, Berlin, Heidelberg, 2009, vol. 291, pp. 118–144 Search PubMed.
- L. Stryer, Biochemistry, Freedman and Co., New York, 4th edn, 1995 Search PubMed.
- F. Jordan and M. S. Patel, Thiamine: Catalytic Mechanisms in Normal and Disease States, Marcel Decker Inc., New York, 2004 Search PubMed.
- J. Weidner, J. E. Baio, A. Mundstock, C. Große, S. Karthäuser, C. Bruhn and U. Siemeling, Aust. J. Chem., 2011, 64, 1177–1179 CrossRef PubMed.
- S. Schernich, M. Laurin, Y. Lykhach, H.-P. Steinrück, N. Tsud, T. Skála, K. C. Prince, N. Taccardi, V. Matolín, P. Wasserscheid and J. Libuda, J. Phys. Chem. Lett., 2013, 4, 30–35 CrossRef CAS PubMed.
- F. Bonnette, T. Kato, M. Destarac, G. Mignani, F. Cossío and A. Baceiredo, Angew. Chem., Int. Ed., 2007, 46, 8632–8635 CrossRef CAS PubMed.
- D. Martin, M. Soleilhavoup and G. Bertrand, Chem. Sci., 2011, 2, 389–399 RSC.
- T. Matsumoto, M. Ohishi and S. Inoue, J. Org. Chem., 1985, 50, 603–606 CrossRef CAS.
- C. Burnstein, S. Tschan, X. Xie and F. Glorius, Synthesis, 2006, 2418–2439 Search PubMed.
- I. Alkorta and J. Elguero, J. Phys. Chem., 1996, 100, 19367–19370 CrossRef CAS.
- L. A. Leites, G. I. Magdanurov, S. S. Bukalov and R. West, Mendeleev Commun., 2008, 18, 14–15 CrossRef CAS.
- J. A. Cowan, J. A. C. Clyburne, M. G. Davidson, R. L. W. Harris, J. A. K. Howard, P. Küpper, M. A. Leech and S. P. Richards, Angew. Chem., Int. Ed., 2002, 41, 1432–1434 CrossRef CAS.
- S. D. Sarkar, S. Grimme and A. Studer, J. Am. Chem. Soc., 2010, 132, 1190–1191 CrossRef PubMed.
- O. Hollóczki, D. Gerhard, K. Massone, L. Szarvas, B. Németh, T. Veszprémi and L. Nyulászi, New J. Chem., 2010, 34, 3004–3009 RSC.
- O. Hollóczki, P. Terleczky, D. Szieberth, G. Mourgas, D. Gudat and L. Nyulászi, J. Am. Chem. Soc., 2011, 133, 780–789 CrossRef PubMed.
- O. Hollóczki and L. Nyulászi, Org. Biomol. Chem., 2011, 9, 2634–2640 Search PubMed.
- Z. Kelemen, O. Hollóczki, J. Oláh and L. Nyulászi, RSC Adv., 2013, 3, 7970–7978 RSC.
- M. H. Dunn, M. L. Cole and J. B. Harper, RSC Adv., 2012, 2, 10160–10162 RSC.
- A. J. I. Arduengo, S. F. Gamper, M. Tamm, J. C. Calabrese, F. Davidson and H. A. Craig, J. Am. Chem. Soc., 1995, 117, 572–573 CrossRef CAS.
- O. Hollóczki and L. Nyulászi, Top. Curr. Chem., 2013, 341, 1–24 CrossRef.
- Z. Kelemen, O. Hollóczki, J. Nagy and L. Nyulászi, Org. Biomol. Chem., 2011, 9, 5362–5364 CAS.
- G. Gurau, H. Rodríguez, S. P. Kelley, P. Janiczek, R. S. Kalb and R. D. Rogers, Angew. Chem., Int. Ed., 2011, 50, 12024–12026 CrossRef CAS PubMed.
- Z. Kelemen, B. Péter-Szabó, E. Székely, O. Hollóczki, D. Firaha, B. Kirchner, J. Nagy and L. Nyulászi, Chem. – Eur. J., 2014, 20, 13002–13008 CrossRef CAS PubMed.
- M. Thomas, M. Brehm, O. Hollóczki, Z. Kelemen, L. Nyulászi, T. Pasinszki and B. Kirchner, Chem. – Eur. J., 2014, 20, 1622–1629 CrossRef CAS PubMed.
- M. Thomas, O. Hollóczki and B. Kirchner, Chem. – Eur. J., 2014, 20, 1622–1629 CrossRef CAS PubMed.
- M. Feroci, I. Chiarotto, F. D'Anna, G. Forte, R. Noto and A. Inesi, Electrochim. Acta, 2015, 153, 122–129 CrossRef CAS.
- O. Hollóczki and L. Nyulászi, J. Org. Chem., 2008, 73, 4793–4799 CrossRef PubMed.
- C. Boeme and G. Frenking, J. Am. Chem. Soc., 1996, 118, 2039–2046 CrossRef.
- C. Heinemann, T. Müller, Y. Apeloig and H. Schwartz, J. Am. Chem. Soc., 1996, 118, 2023–2038 CrossRef CAS.
- D. Bourissou, O. Guerret, F. P. Gabba and G. Bertrand, Chem. Rev., 2000, 100, 39–92 CrossRef CAS PubMed.
- J. M. Um, D. A. DiRocco, E. L. Noey, T. Rovis and K. N. Houk, J. Am. Chem. Soc., 2011, 133, 11249–11254 CrossRef CAS PubMed.
- T. Dudding and K. N. Houk, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 5770–5775 CrossRef CAS PubMed.
- O. Hollóczki, Z. Kelemen and L. Nyulászi, J. Org. Chem., 2012, 77, 6014–6022 CrossRef PubMed.
- P. Verma, P. A. Patni and R. B. Sunoj, J. Org. Chem., 2011, 76, 5606–5613 CrossRef CAS PubMed.
- W. Li, D. Huang and Y. Lv, RSC Adv., 2014, 4, 17236–17244 RSC.
- F. Huang, G. Lu, L. Zhao, H. Li and Z.-X. Wang, J. Am. Chem. Soc., 2010, 132, 12388–12396 CrossRef CAS PubMed.
- A. M. Magill, K. J. Cavell and B. F. Yates, J. Am. Chem. Soc., 2004, 126, 8717–8724 CrossRef CAS PubMed.
- T. L. Amyes, S. T. Diver, J. P. Richard, F. M. Rivas and K. Toth, J. Am. Chem. Soc., 2004, 126, 4366–4374 CrossRef CAS PubMed.
- A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- S. Izadi, R. Anandakrishnan and A. V. Onufriev, J. Phys. Chem. Lett., 2014, 5, 3863–3871 CrossRef CAS PubMed.
- M. W. Mahoney and W. L. Jorgensen, J. Chem. Phys., 2000, 112, 8910–8922 CrossRef CAS.
- F. H. Stillinger and A. Rahman, J. Chem. Phys., 1974, 60, 1545–1557 CrossRef CAS.
- M. J. Frisch, et al., Gaussian 09 Revision D.01, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- J. N. Canongia Lopes, J. Deschamps and A. A. H. Pádua, J. Phys. Chem. B, 2004, 108, 2038–2047 CrossRef.
- C. M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11, 361–373 CrossRef CAS.
- J. Rigby and K. Izgorodina, Phys. Chem. Chem. Phys., 2013, 15, 1632–1646 RSC.
- J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- R. A. Kendall, T. H. Dunning, Jr. and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- E. R. Davidson, Chem. Phys. Lett., 1996, 260, 514–518 CrossRef CAS.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- S. Nosé, Mol. Phys., 1984, 52, 255–268 CrossRef.
- G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- W. L. Jorgensen and J. TiradoRives, J. Am. Chem. Soc., 1988, 110, 1657–1666 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. TiradoRives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197 CrossRef CAS.
- M. Brehm and B. Kirchner, J. Chem. Inf. Model., 2011, 51, 2007–2023 CrossRef CAS PubMed.
- J. N. Canongia Lopes and A. A. H. Pádua, J. Phys. Chem. B, 2004, 108, 16893–16898 CrossRef.
- J. N. Canongia Lopes and A. A. H. Pádua, J. Phys. Chem. B, 2006, 110, 19586–19592 CrossRef CAS PubMed.
- B. Kirchner, O. Hollóczki, J. N. Canongia Lopes and A. A. H. Pádua, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 202–214 CrossRef CAS.
- N. A. McDonald and W. L. Jorgensen, J. Phys. Chem. B, 1998, 102, 8049–8059 CrossRef CAS.
- D. Yin and A. D. MacKerell, Jr., J. Comput. Chem., 1998, 19, 334–348 CrossRef CAS.
- N. Rai, S. P. Tiwari and E. J. Maginn, J. Phys. Chem. B, 2012, 116, 10885–10897 CrossRef CAS PubMed.
- S. Suzuki, P. G. Green, R. E. Bumgarner, S. Dasgupta, W. A. Goddard III and G. A. Blake, Science, 1992, 257, 942–945 CAS.
- M. Allesch, E. Schwegler and G. Galli, J. Phys. Chem. B, 2007, 111, 1081–1089 CrossRef CAS PubMed.
- M. S. Mateus, N. Galamba and B. J. Costa Cabral, J. Chem. Phys., 2012, 136, 014507 CrossRef PubMed.
- G. A. Grasa, M. A. Kissling and S. P. Nolan, Org. Lett., 2002, 4, 3583–3586 CrossRef CAS PubMed.
- G. W. Nyce, J. A. Lamboy, E. F. Connor, R. M. Waymouth and J. L. Hedrick, Org. Lett., 2002, 4, 3587–3590 CrossRef CAS PubMed.
- M. Movassaghi and M. A. Schmidt, Org. Lett., 2005, 7, 2453–2456 CrossRef CAS PubMed.
- T. Kano, K. Sasaki and K. Maruoka, Org. Lett., 2005, 7, 1347–1349 CrossRef CAS PubMed.
- Y. Suzuki, K. Yamauchi, K. Muramatsu and M. Sato, Chem. Commun., 2004, 2770–2771 RSC.
- E. Rezabal and G. Frison, J. Comput. Chem., 2015, 36, 564–572 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Extra data and figures. See DOI: 10.1039/c5cp05369b |
| This journal is © the Owner Societies 2016 |