Initial hydration behavior of sodium iodide dimer: photoelectron spectroscopy and ab initio calculations†
Ren-Zhong
Li
abc,
Gao-Lei
Hou
b,
Cheng-Wen
Liu
d,
Hong-Guang
Xu
b,
Xiang
Zhao
*c,
Yi Qin
Gao
*d and
Wei-Jun
Zheng
*b
aCollege of Electronics and Information, Xi'an Polytechnic University, Xi'an 710048, China
bBeijing National Laboratory for Molecular Sciences, State Key Laboratory of Molecular Reaction Dynamics, Institute of Chemistry, Chinese Academy of Sciences, Beijing 100190, China. E-mail: zhengwj@iccas.ac.cn; Fax: +86 10 62563167; Tel: +86 10 62635054
cInstitute for Chemical Physics, School of Science, Xi'an Jiaotong University, Xi'an 710049, China. E-mail: xzhao@mail.xjtu.edu.cn
dBeijing National Laboratory for Molecular Sciences, Institute of Theoretical and Computational Chemistry, College of Chemistry and Molecular Engineering, Peking University, Beijing 100871, China. E-mail: gaoyq@pku.edu.cn
First published on 18th November 2015
Abstract
We investigated (NaI)2−(H2O)n (n = 0–6) clusters to examine the initial solvation process of (NaI)2 in water, using negative ion photoelectron spectroscopy and theoretical calculations. The structures of these clusters and their neutrals were determined by comparing ab initio calculations with experimental results. It is found that bare (NaI)2− is a L-shaped structure and the corresponding neutral is a rhombus. In (NaI)2−(H2O), the water molecule prefers to interact with the middle Na atom of the L-shaped (NaI)2−. For (NaI)2−(H2O)n clusters with n = 2–3, two types of structures are nearly degenerate in energy: one is L-shaped and the other is pyramid-shaped. As for (NaI)2−(H2O)n with n = 4–6, the dominant structures are pyramid-shaped. For the anionic clusters, one of the Na–I distances increases abruptly when n = 2; for the neutral clusters, rapid lengthening of the Na–I distances occurs when n = 4. Additionally, analyses of the reduced density gradient were carried out, and the results reveal that Na+–water interactions dominate in (NaI)2−(H2O)n for n ≤ 4, whereas I−–water and water–water interactions are significantly enhanced when n increases to 5.
1. Introduction
Investigation of the interactions between alkali halide clusters and water molecules can give insights into the dissociation and dissolution processes of salts. The studies can provide useful information for atmospheric and environmental chemistry,1–3 as the dissolution of sea salt particles plays an important role in producing halogen anions, which can destroy ozone (a key species in atmospheric chemistry) via photochemical processes.4 Although salt–water clusters have been investigated previously using both experiments5–9 and theory,10–20 the interactions between water and alkali halide in the gas phase, especially, the interactions of water molecules with clusters containing multiple alkali halide units, have not been studied in detail using experiments.As for the hydration of sodium iodide, the monomer has been investigated by many groups, because of its importance in photodissociation dynamics.21–24 Olleta et al. studied the structures, binding energies and electronic properties of NaI(H2O)1–6 based on ab initio calculations, and found that pentahydrated and hexahydrated clusters show dissociated structures.25 Peslherbe and co-workers23,24,26,27 investigated the structure, dynamics and stability of NaI–water systems using molecular dynamics simulations and found that the ion pair is quite stable with respect to dissociation into free ions, even in large clusters. Grégoire et al.28–30 studied NaI–(H2O)n and NaI–(NH3)n clusters by performing resonance-enhanced two-photon ionization experiments. Their results show a solvent-selective ionization behavior for sodium iodide clustered with various solvents. Raymond et al.31 studied the molecular structure and bonding of the surface of salt solutions of NaX (X: F, Cl, Br, I) using vibrational sum-frequency spectroscopy and the results indicated that the population of the anions at the uppermost layer of the surface diminished significantly. In addition, there also exists studies on the hydration of alkali-rich sodium iodide. Blades et al.32 studied the hydration energies of (MI)mM+ ions in the gas phase, where M+ = Na+, K+, Rb+, Cs+, with up to four water molecules, and their study showed that the sequential hydration bond energies for MIM(H2O)n+ and (MIm)M+ decrease with increasing n and m, respectively. Zhang et al.33 studied the dissolution processes of Na2I+ and Na3I2+ with the association of water molecules, and found that the separation of the Na–I ion pair for Na2I+ occurs when six H2O molecules are added to the salt cluster and only one or two H2O molecules are added to the salt cluster for Na3I2+. Only a limited number of studies on hydrated clusters containing more than one alkali halide unit have been conducted. Woon34 studied (LiF)2 and (LiF)2(H2O) based on MP2 calculations, and suggested that water causes a large distortion of the nearest LiF bond, with a change in (LiF)2(H2O) almost twice as large as that in LiF(H2O). Liu et al.35 studied (NaCl)3(H2O)n (n = 2–7) and found that a water molecule preferentially binds to the Na–Cl edge. Yamabe et al.16 studied the mechanism of ion separation of the NaCl microcrystal via the association of water with (NaCl)m. Fatemi and Bloomfield36 studied (NaI)nH2O− (n = 3, 4, 6) using photoelectron spectroscopy and found that the water molecule attaches to the edge of a NaI particle and orients itself to decrease the NaI particle's electron affinity.
In this work, in order to get a better understanding of how alkali halide clusters interact with water molecules, we conducted a combined experimental/theoretical study of the initial solvation process of (NaI)2 in water using negative ion photoelectron spectroscopy of (NaI)2−(H2O)n (n = 0–6) clusters and ab initio calculations.
2. Experimental and theoretical methods
2.1 Experimental methods
The experiments were conducted using a home-built apparatus consisting of a time-of-flight (TOF) mass spectrometer and a magnetic-bottle photoelectron spectrometer, which has been described previously.37 Various sodium iodide clusters containing water molecules were produced in a laser vaporization source and then analyzed using the TOF mass spectrometer. In the experiment, a rotating and translating NaI disk target was ablated by second harmonic (532 nm) light pulses from a Nd:YAG laser, while helium carrier gas with ∼4 atm backing pressure seeded with water vapor was allowed to expand through a pulsed valve to generate and cool the hydrated sodium iodide clusters. The (NaI)2−(H2O)n (n = 0–6) clusters were each mass-selected and decelerated before being photodetached by 532 nm photons from another Nd:YAG laser. The photodetached electrons were energy-analyzed by the magnetic-bottle photoelectron spectrometer. The photoelectron spectra were calibrated with spectra of Cs− and Bi− taken at similar conditions. The instrumental resolution was approximately 40 meV for electrons with 1 eV of kinetic energy.2.2 Theoretical methods
Theoretical calculations were performed using the GAUSSIAN 09 program package.38 The structures of (NaI)2−(H2O)n and their neutrals were fully optimized with density functional theory (DFT) employing long-range correction in combination with the short-range variant of the Perdew–Burke–Ernzerhof (PBE) exchange functional LC-ωPBE,39–41 which has been previously shown to be suitable to study salt–water clusters.42 The Pople's all-electron basis set 6-311++G(d,p)43 was used for the Na, O, and H atoms. The effective core potential (ECP) basis set LANL2DZdp,44 as obtained from the EMSL basis set library,45 was used for the I atoms. The initial structures of the (NaI)2−(H2O)1–3 clusters were obtained by varying the positions of the water molecules. The large clusters (n > 3) were generated by adding water molecules to the different plausible positions of the smaller ones. Frequencies were calculated to verify that the optimized structures correspond to real minima on the potential energy surfaces. The theoretical vertical detachment energies (VDEs) were calculated as the energy differences between the neutrals and the anions both at the optimized anionic structures. The theoretical adiabatic detachment energies (ADEs) were calculated as the energy differences between the neutrals and the anions with the neutrals relaxed to the nearest local minima using the geometries of the anions as initial structures. We further performed single-point energy calculations at high-level ab initio CCSD(T) (couple-cluster with single and double and perturbative triple excitations)46,47 for (NaI)2−/0(H2O)0–4 clusters with the same basis set to get more accurate energetic information. All the relative energies and theoretical ADEs have been corrected by zero-point vibrational energies (ZPEs) obtained at the LC-ωPBE/6-311++G(d,p) level of theory. To evaluate the uncertainty of the DFT method, the structures of (NaI)2−(H2O)1–3 clusters were also optimized using the MP248–50 method, which gave essentially the same results as the LC-ωPBE method (see ESI†). Additionally, a visual study of cation–anion, cation–water, anion–water, and water–water interactions was performed by calculating the reduced density gradient (RDG) proposed by the Yang group,51 based on electron density (ρ(r)) and its first derivative (s = 1/(2(3π2)1/3)|∇ρ|/ρ4/3), and the second largest eigenvalue (λ2) of the Hessian matrix of electron density functions, by using the Multiwfn program.52 The RDG can be used to describe the deviation from a homogeneous electron distribution within density functional theory. As a fundamental dimensionless variable, the reduced gradient is found to be the ratio of density and gradient values and noncovalent interactions can be clearly isolated in real space. The regions of noncovalent interactions are marked with the gradient approaching zero and equal to zero at the critical point. The different noncovalent interaction types can be distinguished by the values of sign(λ2)(ρ).51 Thus, the RDG can be used to analyse noncovalent interactions in cluster systems.3. Experimental results
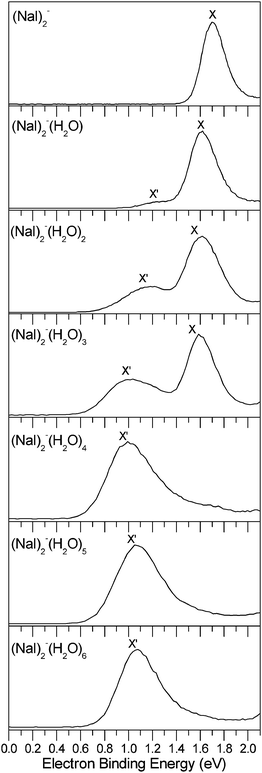
The photoelectron spectra of the (NaI)2−(H2O)n (n = 0–6) clusters measured with 532 nm photons are shown in Fig. 1. The VDEs and ADEs of these clusters estimated from their spectra are summarized in Table 1.| Isomer | X′ | X | ||
|---|---|---|---|---|
| ADE (eV) | VDE (eV) | ADE (eV) | VDE (eV) | |
| (NaI)2− | 1.56 ± 0.08 | 1.70 ± 0.08 | ||
| (NaI)2−(H2O) | 1.03 ± 0.10 | 1.24 ± 0.10 | 1.46 ± 0.08 | 1.62 ± 0.08 |
| (NaI)2−(H2O)2 | 0.83 ± 0.10 | 1.18 ± 0.10 | 1.37 ± 0.10 | 1.62 ± 0.08 |
| (NaI)2−(H2O)3 | 0.74 ± 0.08 | 1.04 ± 0.10 | 1.37 ± 0.10 | 1.59 ± 0.08 |
| (NaI)2−(H2O)4 | 0.75 ± 0.08 | 1.00 ± 0.08 | ||
| (NaI)2−(H2O)5 | 0.79 ± 0.08 | 1.07 ± 0.08 | ||
| (NaI)2−(H2O)6 | 0.84 ± 0.08 | 1.08 ± 0.08 | ||
The photoelectron spectrum of bare (NaI)2− at 532 nm shows an unresolved broad band feature centered at about 1.70 eV. The ADE of (NaI)2− is estimated to be 1.56 ± 0.08 eV. The spectrum shows a large change with a new band X′ showing up at the lower binding energy side when the first water molecule is adsorbed on (NaI)2−. The measured spectrum in the experiment shows that the major band feature X has a VDE of 1.62 eV and the weak new band X′ has a lower VDE of 1.24 eV. Similar to (NaI)2−(H2O), the double-peak spectral pattern in the threshold region is also observed in the spectra of (NaI)2−(H2O)n (n = 2–3), except that the peaks shift to a lower binding energy and the relative intensities of the X′ versus X band increases when n increases from 1 to 3. The peaks (X′ and X) of (NaI)2−(H2O)2 are centered at ∼1.18 and 1.62 eV, respectively, and those of (NaI)2−(H2O)3 are centered at ∼1.04 and 1.59 eV, respectively. These observations indicate that two kinds of isomers may coexist in the spectra of (NaI)2−(H2O)n (n = 1–3), corresponding to the X′ and X spectral features. The photoelectron spectra of (NaI)2−(H2O)n with n = 4–6 each has only a major broad feature X′, and the band X at the higher binding energy side disappears, suggesting that there is only one kind of dominant structure. The VDE of (NaI)2−(H2O)4 is measured to be about 1.00 eV; those of (NaI)2−(H2O)5 and (NaI)2−(H2O)6 shift to higher electron binding energies of 1.07 and 1.08 eV, respectively.
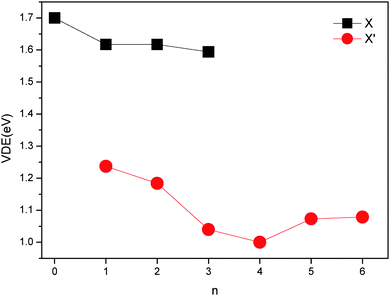
The changes of VDEs with the number of water molecules in the (NaI)2−(H2O)n (n = 0–6) clusters are shown in Fig. 2. It can be seen that the VDE of X of (NaI)2−(H2O)n first decreases when n changes from 0 to 1, stays nearly unchanged from 1 to 2, and then decreases again as n increases to 3. As for the VDE of X′ of (NaI)2−(H2O)n, the value first decreases when n changes from 1 to 4, and then increases when n increases from 4 to 6. These observations suggest that the Na–water interactions are very strong for (NaI)2−(H2O)n from n = 0 to 4, and the I−–water and water–water interactions are dominant when the fifth and sixth water molecules are adsorbed, as it has been analyzed previously that the alkali metal–water interactions reduce VDEs while anion–water and water–water interactions increase VDEs.42 These inferences will be confirmed by the analysis of interactions in Section 4.
4. Theoretical results and discussion
4.1 The structures of (NaI)2−(H2O)n and (NaI)2(H2O)n (n = 0–6)
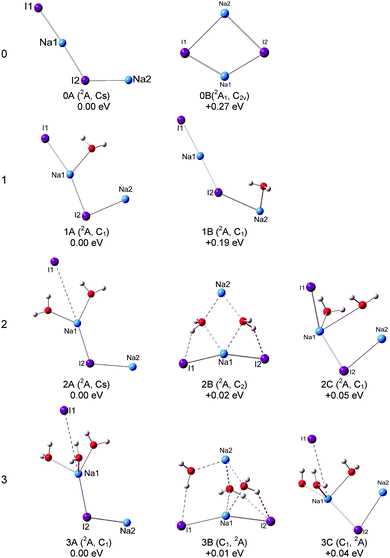
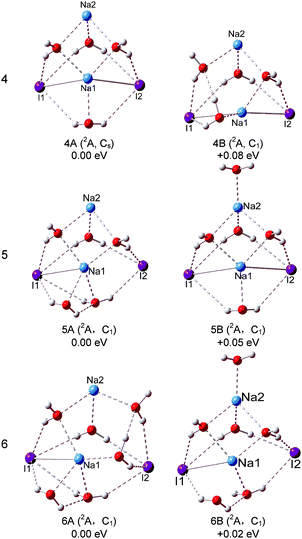
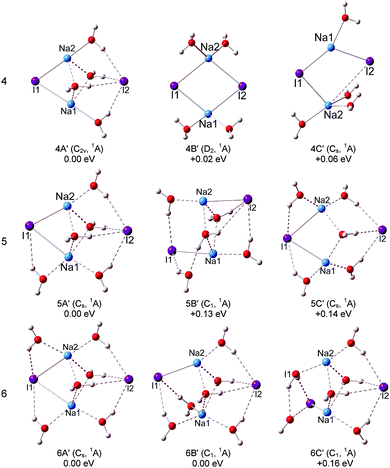
The optimized structures of the typical low-lying isomers of (NaI)2−(H2O)n are presented in Fig. 3 and 4, while the neutral structures are shown in Fig. 5 and 6. The theoretical relative energies and VDEs of these low-lying isomers are listed in Table 2 and compared with the experimental values.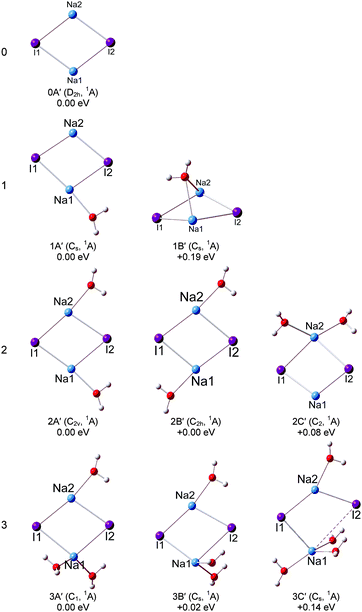 | ||
| Fig. 5 Optimized geometries of the low-lying isomers of the neutral (NaI)2(H2O)n (n = 0–3) clusters. | ||
 | ||
| Fig. 6 Optimized geometries of the low-lying isomers of the neutral (NaI)2(H2O)n (n = 4–6) clusters. | ||
| Isomer | ΔEa (eV) | Sym. | State | Theo. | Expt. | ||
|---|---|---|---|---|---|---|---|
| VDE (eV) | VDE (eV) | ||||||
| LC-ωPBE | CCSD(T) | ||||||
| a The ΔE values are from the LC-ωPBE functional. | |||||||
| (NaI)2− | 0A | 0.00 | C s | 2A | 1.83 | 1.62 | 1.70 |
| 0B | 0.27 | C 2v | 2A1 | 0.80 | 0.62 | ||
| (NaI)2−(H2O) | 1A | 0.00 | C 1 | 2A | 1.77 | 1.58 | 1.62 |
| 1B | 0.19 | C 1 | 2A | 1.55 | 1.37 | 1.24 | |
| (NaI)2−(H2O)2 | 2A | 0.00 | C s | 2A | 1.85 | 1.65 | 1.62 |
| 2B | 0.02 | C 2 | 2A | 1.56 | 1.39 | 1.18 | |
| 2C | 0.05 | C 1 | 2A | 1.30 | 1.13 | ||
| (NaI)2−(H2O)3 | 3A | 0.00 | C 1 | 2A | 1.70 | 1.50 | 1.59 |
| 3B | 0.01 | C 1 | 2A | 1.16 | 1.04 | 1.04 | |
| 3C | 0.04 | C 1 | 2A | 1.26 | 1.10 | ||
| (NaI)2−(H2O)4 | 4A | 0.00 | C s | 2A | 1.28 | 1.16 | 1.00 |
| 4B | 0.08 | C s | 2A | 1.19 | 1.07 | ||
| (NaI)2−(H2O)5 | 5A | 0.00 | C 1 | 2A | 1.29 | 1.07 | |
| 5B | 0.05 | C 1 | 2A | 1.08 | |||
| (NaI)2−(H2O)6 | 6A | 0.00 | C 1 | 2A | 1.25 | 1.08 | |
| 6B | 0.02 | C 1 | 2A | 1.08 | |||
Our calculations show that the global minimum of (NaI)2− is 0A in the 2A state with a L-shaped structure and Cs symmetry, and the angle ∠Na–I–Na is 122.5°. The theoretical VDE of (NaI)2− is 1.62 eV with the CCSD(T) method, close to the experimental value of 1.70 eV measured in this work. Isomer 0B is higher than 0A by 0.27 eV and it is a ring structure with C2v symmetry and a 2A1 state. The calculated VDE of 0B is 0.62 eV, which largely deviates from the experimental measurement. Therefore, we conclude that the L-shaped structure makes a main contribution to the photoelectron spectrum. For the (NaI)2 neutral, the most stable structure 0A′ is a rhombus with C2v symmetry, different from the square structure suggested by previous theoretical calculations.53 The significant deformations between the most stable structures of (NaI)2− and the corresponding neutral one indicate that the excess electron induces a significant change to the (NaI)2 framework.
We can see that the typical minimal energy structures of (NaI)2−(H2O) are formed by attaching a water molecule to the L-shaped (NaI)2−. In the most stable structure 1A, the water molecule interacts with the nearest Na1–I1 unit with its oxygen atom connecting to the middle Na atom (Na1) and with one H atom pointing to the terminal I atom (I1), and the Na1–I1 distance is longer than that in bare (NaI)2− by 0.12 Å. The theoretical VDE of 1.77 eV is in agreement with the experimental VDE (1.62 eV) of the second peak (X) in the photoelectron spectrum of (NaI)2−(H2O). In isomer 1A, the Na1–O bond length of 2.32 Å is shorter than the I1–H length of 2.72 Å, indicating that the Na–water interaction is stronger than the I–water interaction. This observation indicates that the negative end of the permanent dipole of water molecules prefers to point toward the Na1–I1 portion of (NaI)2−(H2O) and weakens the electron's attachment. Such a result is consistent with the spectrum of (NaI)2−(H2O) being shifted to a lower binding energy compared with that of bare (NaI)2−. A similar result can be found in the previous work on (NaI)n−(H2O) (n = 3, 4, 6) by Fatemi and Bloomfield.36 They reported that water could orient itself to decrease the electron affinity of the alkali halide. In isomer 1B, the water molecule interacts with the terminal Na atom (Na2) via its O atom and has one of its H atoms forming a hydrogen bond with I2. The water does not significantly distort the bare (NaI)2−, except that the Na2–I2 distance is increased by only 0.29 Å. The calculated VDE of 1B at the CCSD(T) level is 1.37 eV, close to the measurement of the VDE(X′) of 1.24 eV in our experiment. So the weak band X′ is most likely due to the contribution from isomer 1B. The most stable isomer of neutral (NaI)2(H2O) can be considered to be derived from 0A′, with an extra water molecule added via Na–O and I–H interactions.
For (NaI)2−(H2O)2, 2A, 2B, and 2C are almost degenerate in energy. In isomer 2A, the (NaI)2− unit remains a L framework with two water molecules inserted between Na1 and I1. It is noteworthy that the distance between Na1 and I1 abruptly increases to 4.59 Å, which is significantly longer than in bare (NaI)2−. The theoretical VDE of 2A calculated with the CCSD(T) method is 1.65 eV, in good agreement with the experimental VDE of the higher binding energy peak of 1.62 eV. In isomer 2B, (NaI)2− forms a pyramid-shaped unit with Na2 sitting at the apex site. The distances between Na2 and two adjacent O atoms are both 2.39 Å, shorter than those between Na1 and O atoms (2.53 Å), and I1 or I2 and its adjacent H atoms (2.49 Å). This result thus suggests that the Na2–O interaction is dominant in isomer 2B. The distances between Na2 and the two I atoms are both elongated to 5.12 Å, indicating that the Na2 atom would leave the (NaI)2− unit. The theoretical VDE of isomer 2B with CCSD(T) is 1.39 eV, close to the VDE of the lower binding peak. Isomer 2C is derived from 1A with the H atom of the second water interacting with an I atom and its O atom interacting with a Na atom. The calculated VDE of 2C is 1.13 eV with the CCSD(T) method, consistent with the experimental value of 1.18 eV of the first peak X′. Thus it is likely that both isomers 2B and 2C make contributions to the first peak at a lower binding energy and 2A contributes to the second peak at a higher binding energy. From Fig. S1 (ESI†), the relative energies between 2A and 2B changed slightly for the LC-ωPBE and MP2 methods. But the changes of the relative energies are under the uncertainties of the theoretical calculations. Thus both the LC-ωPBE and MP2 methods give reasonable results. From Fig. 5, we can see that all neutral isomers are derived from 1A′. Isomers 2A′ and 2B′ are degenerate, and 2C′ is higher than the global minimum by 0.08 eV in energy. Isomer 2A′ has a C2v symmetry, the second water interacts with another Na atom via its O atom and connects to the same I atom that interacts with the first water; 2B′ with a C2h symmetry has a similar structure except one water prefers to form a hydrogen bond with the other I atom. In 2C′, the two water molecules interact with the same Na atom.
For (NaI)2−(H2O)3, three low-lying isomers nearly degenerate in energy are found, as presented in Fig. 3. Isomer 3A is derived from 2A, with the third water molecule interacting with the Na1 atom via its O atom, and interacting with the I1 atom via one of its H atoms. The length between Na1 and I1 is 4.36 Å, longer than that in bare (NaI)2− by 1.53 Å. The calculated VDE of 3A is 1.50 eV at the CCSD(T) level of theory, in good agreement with the experimental VDE(X) of 1.59 eV. So we conclude that isomer 3A yields the VDE of the second peak X at a higher binding energy. Isomer 3B is derived from 2B, with the H atom of water interacting with the nearest I atom and the O atoms of water connecting with the adjacent Na atoms, and its calculated VDE is 1.04 eV with the CCSD(T) method. Isomer 3C is derived from 2C with the additional water sitting between Na1 and I1 and the Na1–I1 distance increases to 4.16 Å. The calculated VDE is 1.10 eV at the CCSD(T) level of theory. It is noteworthy that the calculated VDEs of 3B and 3C are both consistent with the experimental VDE (X′, 1.04 eV) of the lower binding energy peak. Therefore we conclude that isomers 3B and 3C make contributions to the lower binding energy peak. Similar to (NaI)2−(H2O)2, the relative energies between 3A and 3B also changed slightly for the LC-ωPBE and MP2 methods, and these changes are under the uncertainties of theoretical calculations (Fig. S1, ESI†). As for the neutrals, the most stable isomer 3A′ can be considered as 2A′ attaching a third water to interact with one Na atom via its O atom and to form a hydrogen bond with an I atom via one of its H atoms. Isomer 3B′ has a Cs symmetry, and is derived from isomer 2A′ with the additional water molecule interacting with one Na atom via its O atom and with the same I atom through one of its H atoms.
For (NaI)2−(H2O)4, the global minimum isomers are shown in Fig. 4 and they differ in energy by only 0.08 eV at the LC-ωPBE level. Isomers 4A and 4B can be considered as pyramid-shaped structures based on the framework (NaI)2−. Isomer 4A has a Cs symmetry, each I atom of the (NaI)2− unit interacts with three H atoms of three water molecules and the Na atoms interact with the adjacent oxygen atoms. In isomer 4B, there are three H atoms of three water molecules pointing to I1, and two H atoms of two water molecules pointing to I2. The calculated VDEs of 4A and 4B with the CCSD(T) method are 1.16 and 1.07 eV, respectively, close to the experimental VDE of 1.00 eV. So we suggest that the band features of the experiment are contributed collectively by isomers 4A and 4B. For the neutral isomers, the (NaI)2 unit of the most stable 4A′ has a C2v symmetry with four water molecules sitting around one side of the quadrilateral unit (NaI)2. The distances of both Na1⋯I2 and Na2⋯I2 abruptly increase to 4.36 Å, whereas the Na1⋯I1 and Na2⋯I1 distances are 2.96 Å, only slightly different from those in the bare (NaI)2 unit. This indicates that the water molecules' interferences induced a significant change in the (NaI)2 unit. 4B′ is derived from 3A′, just 0.02 eV higher than 4A′, the further calculated energy difference is 0.18 eV with the CCSD(T) method, and each Na atom interacts with two water molecules.
For (NaI)2−(H2O)5, two low-lying isomers derived from 4A are found. In the most stable isomer 5A, the fifth water molecule interacts with a Na atom via its O atom and interacts with the adjacent I via one of its H atoms, and the other H atom points to the O atom of the nearest water to form a water–water H-bond. The VDE of 5A is calculated to be 1.29 eV with the LC-ωPBE method. The experimental photoelectron peak is very broad and extends in the range of 0.76–1.47 eV. Thus, isomer 5A may contribute to the high EBE part of the photoelectron peak. Isomer 5B is higher in energy than 5A by only 0.05 eV, with the additional water molecule interacting with Na2 via its O atom. The calculated VDE of 5B is 1.08 eV with the LC-ωPBE method, in agreement with the experimental VDE of 1.07 eV. Considering the calculation error limit, we conclude that both 5A and 5B exist in the experiment. As for the neutral isomer, the most stable isomer 5A′ is built by attaching an additional water molecule to 4A′ by interacting with Na1 via its O atom and forming a hydrogen bond with I2. For (NaI)2−(H2O)6, two typical low-lying isomers with water–water H-bonds are found. The most stable structure 6A is derived from 5A, and the sixth water molecule interacts with I2 via one H atom and interacts with the O atom of the adjacent water to form water–water H-bonding via another H atom. The theoretical VDE of 6A (1.25 eV) calculated at the LC-ωPBE level of theory is close to the experimental VDE of 1.08 eV. As for isomer 6B, it can considered to be derived from 5B with an additional water molecule interacting with I1 and Na1 via one H atom and O atom respectively. The other H atom of the additional water interacts with the adjacent water to form a water–water H-bond. The calculated VDE of 6B (1.08 eV) is in excellent agreement with the experimental VDE. Therefore, both isomers 6A and 6B make contributions to the spectrum of the experiment. As for the neutrals of (NaI)2(H2O)6, two isomers degenerate in energy (6A′ and 6B′) are found. Isomer 6A′ is a Cs symmetry structure derived from 5A′, with a sixth water molecule sitting between Na2 and I2. The distances between I2 and the two Na atoms are both 4.41 Å, and the Na1–I1 and Na2–I1 distances are both 3.17 Å. In isomer 6B′, four water molecules sit around one side of the quadrilateral (NaI)2 unit and the other two water molecules sit between Na1 and I4. The I2–Na2, I2–Na1, I1–Na1, and I1–Na2 distances are 4.28, 4.40, 3.77, and 2.98 Å respectively. From this, we can see that the Na–I distances are significantly affected by the water molecules.
4.2 The ion separation in (NaI)2−(H2O)n and (NaI)2(H2O)n (n = 0–6)
The structures mentioned above and the Na–I distances listed in Tables S1 and S2 (see ESI†) reflect very interesting properties. For the anion clusters, the distance between the middle Na atom and the terminal I atom in the L-shaped structures, and the distances between the Na atom at the apex and the two I atoms in the pyramid-shaped structures, increase abruptly when the number of water molecules is equal to two. This reveals that the terminal I− ion is separated from the L-shaped (NaI)2− unit, and the apex Na atom is firstly separated from the pyramid-shaped (NaI)2− unit. However, for the neutrals, the abrupt elongation of distances between an I atom and the two Na atoms occurs when the number of water molecules increases to 4 (isomer 4A′ in Fig. 6). It is interesting to note that it is an I− ion that is first separated from the neutral (NaI)2 by the water molecules instead of a Na+ ion.In order to understand the structural variation mechanism of the (NaI)2−(H2O)n (n = 0–6) anions versus their corresponding neutrals, we carried out a natural population analysis (NPA)54 and calculated NPA charges. The NPA charge distributions (see ESI†) show that Na2 in neutral (NaI)2(H2O)n is positively charged, 0.72 to 0.87 e, whereas the charge of Na2 in the corresponding anion (NaI)2−(H2O)n is −0.04 to −0.07 e, that is, the charge of Na2 is reduced by 0.72 to 0.91 e while the charges on the other Na and I atoms are almost unchanged, therefore the excess electron of the anions (NaI)2−(H2O)n is mainly localized on Na2. The addition of the excess electron weakens the Coulomb attraction between Na2 and the adjacent I ions compared with that in the corresponding neutral, so the (NaI)2− unit can form a L-shaped or pyramid-shaped structure rather than a ring structure like that of the neutrals. The Na2 atom can be more easily separated from the (NaI)2− unit in the pyramid-shaped structures of the anion clusters because of the weak interaction between Na2 and the two I atoms.
In addition, from the analysis of the structures, we can see that both in the anionic and the neutral isomers, water molecules prefer to stay near the Na rather than I, and I always stays out at the surface; this is similar to MI(H2O)n−(M = Li, Cs).42 Some previous work8,17,28 reported that the polarizable iodide anion is poorly solvated and presents itself at the surface of a water cluster. Our results are consistent with the previous work.
4.3 Interaction analyses
Fig. 7 shows the calculated electron localization function (ELF)55 of (NaI)2−. It can be seen that there is nearly no electron pairing density between the Na and I atoms, indicating that the chemical bonds in (NaI)2− are mainly ionic instead of covalent.To investigate and visualize the cation–anion, cation–water, anion–water, and water–water interactions in the (NaI)2−(H2O)n clusters, we carried out a reduced density gradient (RDG) analysis. Reduced density gradient, coming from the density and its first derivative, is a very useful method to explore noncovalent interactions. Fig. 8 displays the gradient isosurfaces of the (NaI)2−(H2O)n (n = 1–6) cluster anions. From Fig. 8, we can see that the green areas localize near the terminal Na atom (Na2) in the (NaI)2−(H2O)n clusters. This indicates that the excess electron of a (NaI)2−(H2O)n cluster is mainly localized on its terminal Na atom, consistent with the result of the NPA analysis mentioned in the previous section.
As can be seen in Fig. 8, for (NaI)2−(H2O), the region between Na and I atoms, as well as that between one H atom of water and the terminal I atom, are dominated by a light green color, indicating that there are mainly weak attractive interactions in these regions; while the region between the O atom of water and its adjacent Na atom shows a blue color, indicating a strong electrostatic attraction. This is consistent with the results in the previous sections, that is, the bond length of Na–O is shorter than that of I–H. The strong Na+–water interaction would reduce the VDE of (NaI)2−(H2O) by stabilizing the product state of photodetachment, the corresponding neutral. This is responsible for the shift of VDE to a lower binding energy for (NaI)2−(H2O) compared to that of bare (NaI)2−.
For (NaI)2−(H2O)n with n = 2–4, the RDG isosurfaces of the L-shaped structures show blue color disks between the middle Na atom and the adjacent O atoms of water, revealing that Na+–water interactions are still dominant. Additionally, the regions between the terminal I atom and the neighboring H atoms of water are light blue accompanied by green, indicating that the interactions are enhanced compared with those in (NaI)2−(H2O). For the pyramid-shaped structures at n = 2–4, the isosurfaces between Na atoms and the adjacent O atoms of water show a blue color, indicating very strong electrostatic attraction between Na and water; while the regions between I atoms and the adjacent H atoms have a light-blue color accompanied by green, showing the characteristics of weak H-bonding.
As for the most stable isomers of (NaI)2−(H2O)5 and (NaI)2−(H2O)6, we can see that the interaction regions of two I atoms and their adjacent H atoms are blue accompanied by green and the interaction regions of water–water are blue; while the interaction regions of the Na atoms and their neighboring O atoms of water show a light green color. These results indicate that the I−–water and water–water interactions are considerably enhanced and are dominant in (NaI)2−(H2O)5 and (NaI)2−(H2O)6. This may explain why the VDEs of (NaI)2−(H2O)n shift toward higher EBE at n = 5–6.
5. Conclusions
The VDEs and ADEs of (NaI)2−(H2O)n (n = 0–6) clusters are determined from their photoelectron spectra, and the most probable structures of each cluster are determined by comparing the theoretical VDEs with the experimental results. It is shown that the bare (NaI)2− is a L-shaped structure. The first water molecule prefers to interact with the middle Na atom of the L-shaped (NaI)2− unit. Two types of structures are found when two/three water molecules are attached to the salt cluster: one type is derived from the L-shaped structure of bare (NaI)2− and the other one is considered to be a pyramid-shaped structure. More interestingly, the L-shaped structures disappear while the pyramid-shaped structures start to be dominant when n is equal to or larger than 4. For the anionic clusters, one of the Na–I distances (the distance between the terminal I atom and the middle Na atom) in the L-shaped structures increases abruptly when n = 2 and the distances between the apex Na atom and the two I atoms in the pyramid-shaped structures also increase abruptly when n = 2. An I− ion is separated from the L-shaped (NaI)2− unit while a Na atom is firstly separated from the pyramid-shaped (NaI)2− unit. However, for the neutrals, the distances between one I atom and two Na atoms are elongated abruptly at n = 4 with the I− ion firstly separated from the (NaI)2 cluster. From the structures and the reduced density gradient (RDG) analyses, it can be found that the Na+–water interactions are dominant until the number of water molecules is increased to four, and then the I−–water and water–water interactions are considerably enhanced.Acknowledgements
WJZ and YQG acknowledge the Beijing National Laboratory for Molecular Sciences for financial support. RZL thanks the National Natural Science Foundation of China (NSFC, Grant No. 21301134), and the Open Fund of Beijing National Laboratory for Molecular Sciences (No. 2013003) for support, and the Scientific Research Program Funded by Shanxi Provincial Education Department (No. 2013JK0655) and Postdoctoral Science Foundation of China (No. 2015M572545). Part of the theoretical calculations were conducted using the ScGrid and DeepComp 7000 of the Supercomputing Center, Computer Network Information Center of Chinese Academy of Sciences.References
- K. W. Oum, M. J. Lakin, D. O. DeHaan, T. Brauers and B. J. Finlayson-Pitts, Science, 1998, 279, 74 CrossRef CAS PubMed.
- F. Schweitzer, L. Magi, P. Mirabel and C. George, J. Phys. Chem. A, 1998, 102, 593 CrossRef CAS.
- E. M. Knipping, M. J. Lakin, K. L. Foster, P. Jungwirth, D. J. Tobias, R. B. Gerber, D. Dabdub and B. J. Finlayson-Pitts, Science, 2000, 288, 301 CrossRef CAS PubMed.
- S. W. Hunt, M. Roeselová, W. Wang, L. M. Wingen, E. M. Knipping, D. J. Tobias, D. Dabdub and B. J. Finlayson-Pitts, J. Phys. Chem. A, 2004, 108, 11559 CrossRef CAS.
- B. S. Ault, J. Am. Chem. Soc., 1978, 100, 2426 CrossRef CAS.
- A. Mizoguchi, Y. Ohshima and Y. Endo, J. Am. Chem. Soc., 2003, 125, 1716 CrossRef CAS PubMed.
- D. Liu, G. Ma, L. M. Levering and H. C. Allen, J. Phys. Chem. B, 2004, 108, 2252 CrossRef CAS.
- S. Ghosal, J. C. Hemminger, H. Bluhm, B. S. Mun, E. L. Hebenstreit, G. Ketteler, D. F. Ogletree, F. G. Requejo and M. Salmeron, Science, 2005, 307, 563 CrossRef CAS PubMed.
- J. C. H. Sutapa Ghosal, H. Bluhm, B. S. Mun, E. L. D. Hebenstreit, G. Ketteler, D. Frank Ogletree, F. G. Requejo and M. Salmeron, Science, 2005, 307, 563 CrossRef PubMed.
- D. E. Smith and L. X. Dang, J. Chem. Phys., 1994, 100, 3757 CrossRef CAS.
- T. Asada and K. Nishimoto, Chem. Phys. Lett., 1995, 232, 518 CrossRef CAS.
- D. E. Woon and T. H. Dunning, Jr., J. Am. Chem. Soc., 1995, 117, 1090 CrossRef CAS.
- T. Asada and K. Nishimoto, Mol. Simul., 1996, 16, 307 CrossRef CAS.
- C. P. Petersen and M. S. Gordon, J. Phys. Chem. A, 1999, 103, 4162 CrossRef CAS.
- P. Jungwirth and D. J. Tobias, J. Phys. Chem. B, 2000, 104, 7702 CrossRef CAS.
- S. Yamabe, H. Kouno and K. Matsumura, J. Phys. Chem. B, 2000, 104, 10242 CrossRef CAS.
- P. Jungwirth and D. J. Tobias, J. Phys. Chem. B, 2001, 105, 10468 CrossRef CAS.
- S. Godinho, P. C. do Couto and B. C. Cabral, Chem. Phys. Lett., 2004, 399, 200 CrossRef CAS.
- C. Krekeler, B. Hess and L. D. Site, J. Chem. Phys., 2006, 125, 054305 CrossRef PubMed.
- A. C. Olleta, H. M. Lee and K. S. Kim, J. Chem. Phys., 2007, 126, 144311 CrossRef PubMed.
- T. J. Martinez and R. D. Levine, J. Chem. Phys., 1996, 105, 6334 CrossRef CAS.
- T. J. Martinez and R. D. Levine, Chem. Phys. Lett., 1996, 259, 252 CrossRef CAS.
- G. H. Peslherbe, B. M. Ladanyi and J. T. Hynes, J. Phys. Chem. A, 2000, 104, 4533 CrossRef CAS.
- D. M. Koch, Q. K. Timerghazin, G. H. Peslherbe, B. M. Ladanyi and J. T. Hynes, J. Phys. Chem. A, 2006, 110, 1438 CrossRef CAS PubMed.
- A. C. Olleta, H. M. Lee and K. S. Kim, J. Chem. Phys., 2006, 124, 024321 CrossRef PubMed.
- G. H. Peslherbe, B. M. Ladanyi and J. T. Hynes, Chem. Phys., 2000, 258, 201 CrossRef CAS.
- G. H. Peslherbe, B. M. Ladanyi and J. T. Hynes, J. Phys. Chem. A, 1998, 102, 4100 CrossRef CAS.
- G. Grégoire, M. Mons, I. Dimicoli, C. Dedonder-Lardeux, C. Jouvet, S. Martrenchard and D. Solgadi, J. Chem. Phys., 2000, 112, 8794 CrossRef.
- G. Grégoire, M. Mons, C. Dedonder-Lardeux and C. Jouvet, Eur. Phys. J. D, 1998, 1, 5 CrossRef.
- G. Grégoire, M. Mons, I. Dimicoli, F. Piuzzi, E. Charron, C. Dedonder-Lardeux, C. Jouvet, S. Martrenchard, D. Solgadi and A. Suzor-Weiner, Eur. Phys. J. D, 1998, 1, 187 CrossRef.
- E. A. Raymond and G. L. Richmond, J. Phys. Chem. B, 2004, 108, 5051 CrossRef CAS.
- A. T. Blades, M. Peschke, U. H. Verkerk and P. Kebarle, J. Am. Chem. Soc., 2004, 126, 11995 CrossRef CAS PubMed.
- Q. Zhang, C. J. Carpenter, P. R. Kemper and M. T. Bowers, J. Am. Chem. Soc., 2003, 125, 3341 CrossRef CAS PubMed.
- D. E. Woon, J. Phys. Chem., 1994, 98, 8831 CrossRef CAS.
- C.-W. Liu, G.-L. Hou, W.-J. Zheng and Y. Q. Gao, Theor. Chem. Acc., 2014, 133, 1 CrossRef.
- D. J. Fatemi and L. A. Bloomfield, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 66, 013202 CrossRef.
- H.-G. Xu, Z.-G. Zhang, Y. Feng, J. Y. Yuan, Y. C. Zhao and W. J. Zheng, Chem. Phys. Lett., 2010, 487, 204 CrossRef CAS.
- M. J. Frisch, et al., Gaussian 09, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 234109 CrossRef PubMed.
- O. A. Vydrov, J. Heyd, A. V. Krukau and G. E. Scuseria, J. Chem. Phys., 2006, 125, 074106 CrossRef PubMed.
- O. A. Vydrov, G. E. Scuseria and J. P. Perdew, J. Chem. Phys., 2007, 126, 154109 CrossRef PubMed.
- R.-Z. Li, C.-W. Liu, Y. Q. Gao, H. Jiang, H.-G. Xu and W.-J. Zheng, J. Am. Chem. Soc., 2013, 135, 5190 CrossRef CAS PubMed.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650 CrossRef CAS.
- W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284 CrossRef CAS.
- K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045 CrossRef CAS PubMed.
- G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910 CrossRef CAS.
- G. E. Scuseria, C. L. Janssen and H. F. Schaefer, J. Chem. Phys., 1988, 89, 7382 CrossRef CAS.
- M. Head-Gordon, J. A. Pople and M. J. Frisch, Chem. Phys. Lett., 1988, 153, 503 CrossRef CAS.
- S. Sæbø and J. Almlöf, Chem. Phys. Lett., 1989, 154, 83 CrossRef.
- M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166, 275 CrossRef CAS.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580 CrossRef CAS PubMed.
- A. Aguado, A. Ayuela, J. López and J. Alonso, J. Phys. Chem. B, 1997, 101, 5944 CrossRef CAS.
- E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO Version 3.1, 1988.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp05550d |
| This journal is © the Owner Societies 2016 |