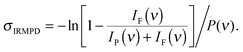Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Probing the microsolvation of a quaternary ion complex: gas phase vibrational spectroscopy of (NaSO4−)2(H2O)n=0–6,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h2_char_2009.gif) 8†
8†
Torsten
Wende‡
a,
Nadja
Heine§
a,
Tara I.
Yacovitch¶
b,
Knut R.
Asmis
*acd,
Daniel M.
Neumark
*be and
Ling
Jiang
*ad
aFritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, 14195 Berlin, Germany
bDepartment of Chemistry, University of California, Berkeley, California 94720, USA. E-mail: dneumark@berkeley.edu
cWilhelm-Ostwald-Institut für Physikalische und Theoretische Chemie, Universität Leipzig, Linnéstrasse 2, D-04103 Leipzig, Germany. E-mail: knut.asmis@uni-leipzig.de
dState Key Laboratory of Molecular Reaction Dynamics, Collaborative Innovation Center of Chemistry for Energy and Materials, Dalian Institute of Chemical Physics, Chinese Academy of Sciences, Dalian 116023, Liaoning, P. R. China. E-mail: ljiang@dicp.ac.cn
eChemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
First published on 18th November 2015
Abstract
We report infrared multiple photon dissociation spectra of cryogenically-cooled (NaSO4−)2(H2O)n dianions (n = 0–6, 8) in the spectral range of the sulfate stretching and bending modes (580–1750 cm−1). Characteristic absorption bands and structural trends are identified based on a comparison to harmonic spectra of minimum-energy structures. The bare quarternary complex (NaSO4−)2 exhibits a C2h structure containing two fourfold-coordinated sodium cations in-between the two chelating sulfate dianions. Its stepwise solvation is driven by an interplay of SO42−–H2O and Na+–H2O interactions. The first water binds in a tridentate intersulfate-bridging fashion. The second and third water molecules bind to the sulfate groups at either end of the complex, which is followed by the onset of water hydrogen-bond network formation. In contrast to the binary ion pair, NaSO4−, no clear evidence for the disruption of the quaternary ion complex upon microhydration is found up to n = 8, underlining its remarkable stability and suggesting that the formation of quaternary ion complexes plays a central role in the initial stages of prenucleation in aqueous Na2SO4 solutions.
Introduction
Since the original concept of electrolytic dissociation was put forth by Arrhenius1 more than a century ago, scientists have been intrigued by how acids, bases and salts are solvated in solution, but a molecular level understanding of ion solvation is still far from complete. How salts are solvated in aqueous solution is fundamental for understanding chemical, biological, geophysical and atmospheric processes.2 With increasing salt concentrations, ion association becomes progressively more important and this is usually discussed in the context of free ions (FI), as well as the formation of contact (CIP), solvent-shared (SIP), and solvent separated ion pairs (SSIP).3,4 At higher concentrations, the formation of triple ions and larger complexes needs to be considered, e.g. in explaining the dielectric relaxation as well as Raman spectra of concentrated salt solutions.5,6 While condensed phase measurements often lack the specificity to differentiate between different types of ion aggregates, measurements on mass-selected microhydrated clusters in the gas phase have provided valuable insight into the stepwise formation of hydration shells of ions.7,8 However, this work has focused mainly on microhydrated clusters containing single ions or binary ion pairs. The formation of ion aggregates or complexes containing more than two ions is particularly intriguing in identifying precursors to prenucleation clusters,9 but has been much less studied in the cluster regime.10–14 Here, we characterize the vibrational spectroscopy of the microhydrated dimer of the sodium sulfate anion, (NaSO4−)2(H2O)n=0–6,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8, in order to gain an understanding on how the stepwise addition of up to eight water molecules influences the structure, binding and spectroscopic infrared (IR)-fingerprint of this prototypical doubly-negatively charged quaternary ion complex.
8, in order to gain an understanding on how the stepwise addition of up to eight water molecules influences the structure, binding and spectroscopic infrared (IR)-fingerprint of this prototypical doubly-negatively charged quaternary ion complex.
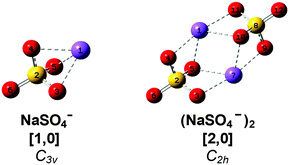
Sodium sulfate is ubiquitous in nature and an important constituent of sea salt aerosols.15 Ion pairs as well as larger ion aggregates are known to be formed in supersaturated droplets16 as well as in aqueous Na2SO4 solutions with increasing temperature and decreasing pressure prior to precipitation.17 Gas phase studies on sodium sulfate clusters have focused on their anion photoelectron spectroscopy (APES).18,19 Wang et al. have determined adiabatic electron affinities (ADEs) for NaSO4− (3.5 eV) and (NaSO4−)2 (1.6 eV). The latter is significantly lower due to the additional electron–electron repulsion. Density functional theory (DFT) as well as higher level calculations recover the reported ADEs and predict C3v and C2h ground state geometries for the monomer anion and dimer dianion (see Scheme 1), respectively.18 In the dimer, the two fourfold-coordinated sodium cations are equally shared by the sulfate moieties and the Na–S distance is 8% longer than in the monomer. Addition of up to four water molecules to the monomer anion was also studied by APES in combination with DFT calculations.19 The first three water molecules strongly interact with both Na+ and SO42−, manifesting the initial steps of dissolution. Microhydrated dimer dianions were not probed in this latter study. More recently, the IR and Raman signatures of microhydrated sodium sulfate ion pairs as well as triple ions were studied computationally, predicting that gas phase vibrational spectroscopy should provide abundant structural information on the early stages of microsolvation in this prototypical system.20,21
IR photodissociation (IRPD) spectroscopy is a powerful tool to study the structure of microhydrated ions in the gas phase,22–25especially when combined with a cryogenic ion trap26–28 to produce cold clusters. The gas phase vibrational spectroscopy of microhydrated CIPs was studied by Schröder and coworkers, who characterized [MgNO3]+(H2O)3 and [Ni2SO4]2+(H2O)5 near room temperature.12,29 Subsequent studies on [MgNO3]+(H2O)0–4, [MgOH]+(H2O)1–4,[CaOH+](H2O)1–5, and [Mg2SO4]2+(H2O)4–11 were performed at cryogenic temperatures, yielding substantially better resolved IR spectra.14,30,31 These studies show that the strong M2+⋯OH2 electrostatic interaction dictates the geometry of the observed structures; anion–water hydrogen bonding is only observed in the larger hydrated clusters (n > 3). On the other hand, electronic structure calculations on [Ni(SO4)2]2−(H2O)n dianions predict that the metal dication acts as a fourfold coordinated bridging unit between the sulfate groups.12 This effectively shields the metal center, and the first water molecules exclusively form hydrogen bonds with the O-atoms of the sulfate groups. However, microhydrated ternary dianion clusters were not experimentally observed (at room temperature), which was attributed to the roughly factor of three weaker hydration energies in the dianions vs. the dications.12
Here, we combine IR multiple photon dissociation (IRMPD) spectroscopy of cryogenically cooled (NaSO4−)2(H2O)n=0–8 dianions in the fingerprint region of the IR spectral range with electronic structure calculations in order to characterize the structure of the bare dianion and its stability with regard to microhydration with up to eight water molecules.
Methods
Experimental setup
IRMPD experiments are carried out on a previously described ion-trap/tandem mass spectrometer,32,33 which was temporarily installed at the “Free Electron Laser for Infrared eXperiments” (FELIX) user facility in the FOM institute Rijnhuizen (Nieuwegein, The Netherlands).34 Briefly, microhydrated sodium sulfate anion dimers, (NaSO4−)2(H2O)n, are continuously produced in a Z-spray source from a 10 mM solution of Na2SO4 in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 water/acetonitrile solvent. The beam of ions passes through a 4 mm diameter skimmer and is then collimated in a radio frequency (RF) decapole ion-guide. Parent ions are mass-selected in a quadrupole mass-filter and focused into a cryogenically-cooled RF ring-electrode ion-trap. To allow for continuous ion accumulation and ion thermalization, the trap is continuously filled with helium buffer gas at an ion-trap temperature of 15 K. After loading the trap for 98 ms, all ions are extracted and focused both temporally and spatially into the center of the extraction region of an orthogonally-mounted linear time-of-flight (TOF) mass spectrometer. Here, the ion packet is irradiated with a single FELIX macropulse (ca. 5 μs temporal width) and high-voltage TOF extraction pulses are applied for recording a TOF mass spectrum. FELIX operates in the spectral region from 600–1800 cm−1 and the spectral bandwidth amounts to ca. 0.2% RMS of the central wavelength. The repetition rate is 10 Hz and pulse energies of up to 30 mJ are typically obtained. IRMPD measurements are carried out using attenuated radiation pulses, such that the loss of a single water molecule becomes the dominant fragmentation channel (further details will be given below). The dissociation limit of the clusters lies above the IR photon energy used to measure the IRMPD spectra, so absorption of multiple photons is required to induce fragmentation.
1 water/acetonitrile solvent. The beam of ions passes through a 4 mm diameter skimmer and is then collimated in a radio frequency (RF) decapole ion-guide. Parent ions are mass-selected in a quadrupole mass-filter and focused into a cryogenically-cooled RF ring-electrode ion-trap. To allow for continuous ion accumulation and ion thermalization, the trap is continuously filled with helium buffer gas at an ion-trap temperature of 15 K. After loading the trap for 98 ms, all ions are extracted and focused both temporally and spatially into the center of the extraction region of an orthogonally-mounted linear time-of-flight (TOF) mass spectrometer. Here, the ion packet is irradiated with a single FELIX macropulse (ca. 5 μs temporal width) and high-voltage TOF extraction pulses are applied for recording a TOF mass spectrum. FELIX operates in the spectral region from 600–1800 cm−1 and the spectral bandwidth amounts to ca. 0.2% RMS of the central wavelength. The repetition rate is 10 Hz and pulse energies of up to 30 mJ are typically obtained. IRMPD measurements are carried out using attenuated radiation pulses, such that the loss of a single water molecule becomes the dominant fragmentation channel (further details will be given below). The dissociation limit of the clusters lies above the IR photon energy used to measure the IRMPD spectra, so absorption of multiple photons is required to induce fragmentation.
IRMPD spectra are recorded by monitoring all ion intensities simultaneously as the laser frequency ν is scanned. The photodissociation cross section σIRMPD is determined from the relative abundances of the parent and photofragment ions, IP(ν) and IF(ν), and the frequency-dependent laser power P(ν) using35
Note, σIRMPD reflects the fragment ion yield from a multiple photon process and is different from σIRPD for IRPD spectra of messenger-tagged species.35,36
Computational details
Electronic structure calculations are performed using both the Gaussian03 and the TURBOMOLE V6.2 program.37,38 Geometry optimizations and harmonic frequency calculations are carried out for different isomers of (NaSO4−)2(H2O)n complexes (n = 0–5). The initial geometries of the bare complex are constructed based on previously published results.18 Initial structures of the solvated complexes (n = 1–5) are constructed based on chemical intuition. Using Gaussian03, full optimization of cluster geometry is employed using the B3LYP hybrid exchange–correlation functional39 and the 6-311+G(D,P) basis set in order to determine preliminary energetic ordering. Harmonic frequency calculations are performed for all converged structures to test for local minima and to obtain zero-point corrected energies (ZPEs). The lowest-energy structures are then further optimized employing B3LYP in combination with the def2-TZVP basis set, using TURBOMOLE V6.2. To allow for comparison of different single determinant methods, structure optimization is additionally performed employing MP2/def2-TZVP for complexes n ≤ 3. Simulated IR spectra are derived from B3LYP/def2-TZVP harmonic frequencies and IR intensities. The resulting stick spectra are convoluted using a Gaussian line shape function with a full width at half maximum linewidth of 10 cm−1, in order to account for line-broadening effects. We refrain from using a specific scaling factor, in accordance with our previous study on hydrated bisulfate clusters.40Labeling
For convenience, we refer to the (NaSO4−)m(H2O)n cluster as [m,n], where [1,0] and [2,0] refer to the monomer anion and the dimer dianion, respectively (see Scheme 1). As the number of water molecules n in the dianion cluster increases, a larger number of energetically close-lying isomers with similar solvation motifs are predicted. In order to simplify the subsequent discussion, calculated minimum-energy structures are classified into groups and labeled with n-bx, where b refers to the number of water molecules donating a hydrogen bond to each of the sulfate moieties, i.e. the number of intersulfate bridging water molecules, and x represents a small letter (a, b, c, …) indicating the energetic ordering of the isomers according to the calculated relative energies including zero-point energy corrections.Results
The first part of this section discusses the photofragmentation behavior of the [2,n] vs. the [1,n] clusters and introduces the strategy for the IRMPD measurements. We then present an overview of all experimental spectra, which covers the observed trends in the IRMPD features with increasing degree of microhydration. In the second part, structural candidates obtained from DFT calculations are introduced and their simulated linear absorption spectra are compared to the IRMPD spectra.Mass spectrometry
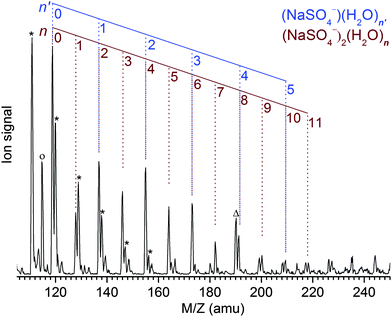
The Z-spray source conditions were optimized for the formation of the dianionic [2,n] clusters. However, the formation of singly charged [1,n′] clusters could not be fully suppressed and hence the resulting progressions in the mass spectrum (see Fig. 1) overlap for n′ = n/2. The peak at the mass-to-charge ratio m/z of 119 amu corresponds to the bare dimer dianion [2,0] as well as the bare monomer anion [1,0] and represents the origin of the [2,n] and [1,n′] peak progressions with Δm/z = +9 amu and Δm/z = +18 amu, respectively. Note that monomeric counterparts do not exist for the [2,n] clusters with odd n and hence these peaks appear less intense, indicating a [2,n]/[1,n′] abundance ratio of ∼1–2. The previously reported mass spectrum shows similar peak progressions, although the [2,n] mass peaks are less intense and only appear as shoulders in the members of the neighboring SO42−(H2O)n progression.19Photodissociation channels
The lowest accessible dissociation channel for [2,0] is the formation of two singly-charged [1,0] monomer anions, | (1) |
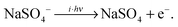 | (2) |
Hence, the IRMPD spectrum of the [2,0] complex can indeed be measured by monitoring the signal depletion at the center as well as the signal enhancement in the wings of the TOF distribution. Depletion of [1,0], on the other hand, is not observed in the experiment, even when the highest laser pulse energy of 30 mJ is applied. We attribute this to the high electron detachment threshold for [1,0] combined with a lower multiple photon absorption cross section, as a result of the lower density of states and thus less efficient intramolecular vibrational energy (IVR) transfer in [1,0] vs. [2,0].
IRMPD of the hydrated clusters proceeds via loss of one or more water molecules:
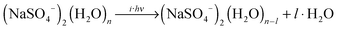 | (3) |
 | (4) |
For [2,n] clusters with odd n, such as [2,1], [2,3] and [2,5] studied here, monomeric counterparts with identical mass-to-charge ratio do not exist. Hence, the observed parent ion depletion and fragment ion formation signals are exclusively due to dissociation of dimer dianion complexes. For [2,n] clusters with even n, on the other hand, dissociation of [1,n′] complexes with n′ = n/2 contribute to the depletion of the parent ion signal as well as to the formation of every other fragment ion signal, i.e., loss of l water molecules from [1,n/2] coincides with loss of 2l water molecules from [2,n]. This hampers assignment of the characteristic absorption frequencies. Fortunately, the [2,n] clusters exhibit lower dissociation energies (and presumably higher photodissociation efficiencies) compared to the [1,n/2] clusters. By sufficiently attenuating the IR laser pulse energy, the monomeric contribution to the IRMPD signal can be significantly (but not completely) reduced (see Fig. S2 in the ESI,† for more details).
IRMPD spectra
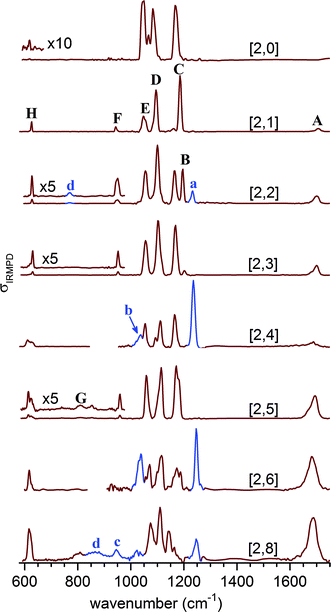
Fig. 3 shows the experimental IRMPD spectra of the [2,n] clusters up to n = 8. Peaks are labeled with capital letters (A–H) and their positions are summarized in Table S1 (see ESI†). Absorption signals attributed to the monomer anions [1,n/2] are labeled with small letters and peak positions are listed in Table S2 (see ESI†).We observe four absorption regions and assign them based on the previous IRMPD study on hydrated sulfate clusters.27 These correspond, from highest to lowest energy, to regions covering the water bending (1750–1600 cm−1, band A), the sulfate stretching (1215–925 cm−1, B–F), the water librational (∼900–650 cm−1, G), and the sulfate bending modes (650–600 cm−1, H).
Bands B–F, due to the strongly IR-active stretching modes of the two sulfate moieties, dominate the IRMPD spectra of the smaller clusters and represent sensitive probes for the local solvation environment.27 The observation of three intense peaks in the [2,0] spectrum agrees with the predicted structure shown in Scheme 1, in which the tetrahedral symmetry of each of the two equivalent sulfate cores is significantly perturbed by the highly asymmetric charge distribution induced by the chelated Na+ atoms, lifting the degeneracy of the antisymmetric stretching modes within each sulfate group. Upon microhydration with up to eight water molecules, the overall spectral signature remains similar, indicating that the binding motif remains intact. A small blue shift (≤+30 cm−1) of bands D and E over the cluster size range shown in Fig. 3 indicates that water is hydrogen bonding to the O-atoms of the sulfate cores, caging the stretching motions. Splitting of bands C and D into two more or less resolved components for n > 1 signals an asymmetry with respect to the solvation of the two sulfate groups and lifting of the remaining degeneracy in-between the corresponding sulfate stretches of each group. Finally, the separation between the dominant absorptions in this region (B–E) decreases from ∼140 cm−1 at n = 2 to ∼90 cm−1 at n = 8, indicating a reduction of the asymmetry in the charge distribution in the cluster as a result of more charge transfer to the solvent molecules with increasing microhydration. These characteristic changes in the band pattern of the sulfate stretching modes with cluster size will prove valuable for identifying characteristic hydration motifs.
The position of the water bending modes (band A) is only weakly affected by the degree of hydration with a slight red-shift (1706 cm−1 → 1689 cm−1) between n = 1 and n = 8. While band A initially appears weak, its relative intensity grows substantially for n > 4. Similar observations were reported in our previous results on microhydrated sulfate,27 bicarbonate,44 bisulfate40 and dihydrogen phosphate45,46 anions. The positions of the sulfate bending modes (band H) also stay relatively constant. Band H initially appears rather weak at 619 cm−1 for [2,0], blue-shifts to 631 cm−1 for [2,3], and then red-shifts again to 616 cm−1 for [2,8]. Its relative intensity increases substantially in the spectra with n > 5. Furthermore, for [2,5], a broad feature (labeled G) starts to appear around 810 cm−1 which slightly grows in intensity. Based on IRMPD studies on related systems we assign it to the water libration modes.27,40,44,47
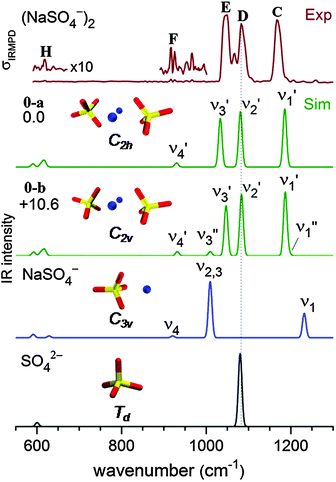
Bare dianion geometry
The B3LYP/def2-TZVP global minimum-energy structure for [2,0] is the C2h conformation 0-a shown in Fig. 4, in which the two sulfate cores share the two central sodium cations, in agreement with previous results.18 A C2v variant of this motif (0-b) is predicted +11 kJ mol−1 higher in energy. Natural charges and Wiberg bond orders48 of the C2h isomer are summarized in Table 1. These show that the interaction between the four ionic moieties is mainly of electrostatic nature. Effective shielding by the sulfate groups as well as substantial negative charge transfer (−0.2 e) from each of the sulfate dianions to the sodium cations results in an exceptionally short Na–Na interatomic distance of 2.91 Å in 0-a compared to 3.17 Å in solid Na2SO4.49| Atom | Natural charge | Bond | Wiberg bond order |
|---|---|---|---|
| Na1 | +0.81 | Na1–O5 | 0.0923 |
| S3 | +2.56 | Na1–O6 | 0.0711 |
| O5 | −1.10 | Na1–O9 | 0.0711 |
| O6 | −1.12 | Na1–O11 | 0.0923 |
| O7 | −1.10 | ||
| O8 | −1.05 |
Bare dianion: simulated IR spectra
In order to obtain a detailed assignment of the bands observed in the experimental IRMPD spectrum of [2,0], it is compared to simulated IR spectra of the C2h and C2v minimum-energy structures of [2,0], as well as of the C3v ground state structure of [1,0] and the Td structure of SO42− in Fig. 4.In SO42−, the four S–O bonds are symmetry equivalent and hence the totally symmetric stretching mode is IR inactive. The triply degenerate antisymmetric stretches, predicted at 1080 cm−1, contribute a single, intense peak to the IR spectrum (bottom panel, Fig. 4). The presence of the sodium cation in [1,0] reduces the symmetry from Td to C3v and partially lifts this degeneracy. Consequently, the four sulfate stretching modes of [1,0] (see Fig. S3 in the ESI†) are best viewed as a nearly pure IR-active symmetric S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch (ν1, 1232 cm−1) at highest energy and involving motion of the uncoordinated O-atom, an intense doubly degenerate antisymmetric SO3 stretch (ν2,3, 1009 cm−1), and a weakly IR-active symmetric SO3 stretch (ν4, 921 cm−1). Finally, the ground state geometry of the dimer dianion [2,0] exhibits only twofold symmetry. The nature of the sulfate stretches remains similar to those in [1,0], but the remaining degeneracy is lifted and three similarly intense peaks are predicted at 1186 (ν1′), 1081 (ν2′) and 1033 cm−1 (ν3′). Note, the two sets of four sulfate stretching modes of the individual sulfate groups in [2,0] weakly couple (10–20 cm−1) producing a set of four symmetric (νi′′) and four antisymmetric (νi′) linear combinations. Due to the inversion symmetry of the C2h isomer, only excitation of the νi′ fundamentals is IR-allowed, in contrast to the C2v isomer (see Fig. 4).
O stretch (ν1, 1232 cm−1) at highest energy and involving motion of the uncoordinated O-atom, an intense doubly degenerate antisymmetric SO3 stretch (ν2,3, 1009 cm−1), and a weakly IR-active symmetric SO3 stretch (ν4, 921 cm−1). Finally, the ground state geometry of the dimer dianion [2,0] exhibits only twofold symmetry. The nature of the sulfate stretches remains similar to those in [1,0], but the remaining degeneracy is lifted and three similarly intense peaks are predicted at 1186 (ν1′), 1081 (ν2′) and 1033 cm−1 (ν3′). Note, the two sets of four sulfate stretching modes of the individual sulfate groups in [2,0] weakly couple (10–20 cm−1) producing a set of four symmetric (νi′′) and four antisymmetric (νi′) linear combinations. Due to the inversion symmetry of the C2h isomer, only excitation of the νi′ fundamentals is IR-allowed, in contrast to the C2v isomer (see Fig. 4).
The experimental IRMPD spectrum of [2,0] (top panel in Fig. 4) is characterized by three strong absorption peaks of similar intensity in the sulfate stretching region at 1167, 1083 and 1050 cm−1 (labeled C–E) and two weaker features at 1067 (band F) and 619 cm−1 (band H). The simulated IR spectrum of the ground state C2h isomer (0-a in Fig. 4) recovers all these features, supporting the previous assignment based on the APES data in combination with DFT calculations.18 The origin of the absorption peak at 1067 cm−1 in-between bands D and E (see Fig. 4) remains unclear. It could be assigned to the ν3′ mode (1040 cm−1) of the energetically higher-lying C2v isomer (see Fig. 4). Compared to the C2h isomer, its ν3′ mode is blue-shifted by 14 cm−1, while all other IR-active modes of the two isomers are predicted at similar energies. The C2v isomer may either be present from the start or, if the two strong peaks D and E overlap sufficiently to warrant sufficient absorption probability for the first few photons by the C2h isomer, then it is also feasible that the C2v isomer is populated during this early stage of the multiple photon absorption process45 and subsequently enhances the IRMPD cross section.
Microhydrated structures
An overview of low-lying B3LYP/def2-TZVP minimum-energy structures for microhydrated anion–dimer clusters with up to five water molecules is shown in Fig. 5. Only structures with unique solvation motifs are shown. See Table S4 (in the ESI†) for a complete list of structures and relative B3LYP and MP2 energies of all low energy isomers considered.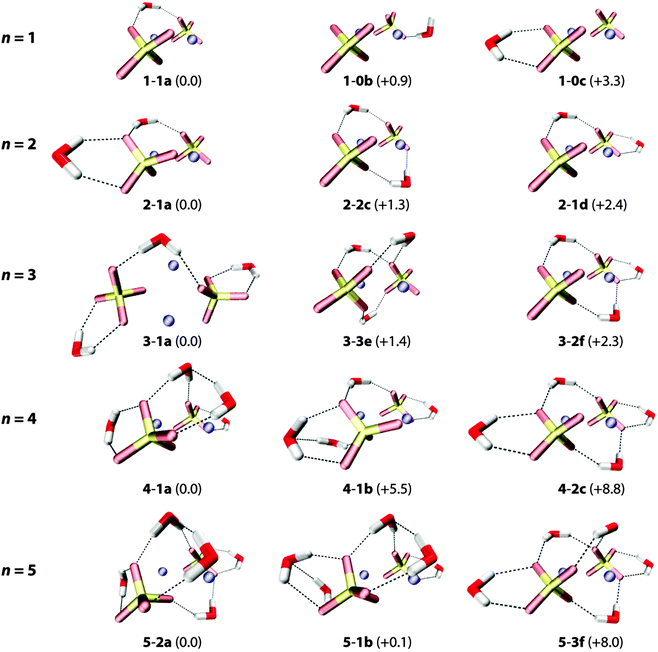 | ||
| Fig. 5 B3LYP/def2-TZVP minimum-energy structures of the (NaSO4−)2(H2O)n complexes with n = 1–5. Relative energies (with ZPE correction) are given in kJ mol−1. | ||
The first water molecule can bind to [2,0] in three different ways (see top row in Fig. 5). The lowest energy structure 1-1a exhibits a triply-coordinated water as part of an intersulfate bridging motif. (Note, in the following the term bridging exclusively refers to water molecules hydrogen bonding to both sulfate groups simultaneously.) In 1-1a the water molecule binds to one of the Na+ ions (dO–Na = 2.54 Å) and donates two hydrogen bonds (DD motif), one to each sulfate group (dH–O = 1.87 Å, 1.91 Å). Structures 1-0b (B3LYP: +0.9 kJ mol−1, MP2: +4.6 kJ mol−1) and 1-0c (B3LYP: +3.3 kJ mol−1, MP2: +7.1 kJ mol−1) exhibit bidentate binding motifs involving either an acceptor–donor (AD) water (2.41 Å, 1.59 Å,) with a dangling O–H bond or a DD water (2.00 Å, 2.03 Å) that binds rather symmetrically to a single sulfate group.
Addition of the second and third water molecules leads to structures that exhibit a combination of these motifs, as water–water hydrogen bond formation is not energetically competitive for these smaller clusters. Starting from the bridged 1-1a structure, the second water binds to one sulfate group in a DD fashion and the third does likewise to the other sulfate group, favoring the more asymmetrically solvated 2-1a (vs.2-2c) structure and the more symmetrically solvated 3-1a (vs.3-2f). Structures containing more than one intersulfate bridging DD water, e.g.2-2c (+1.3 kJ mol−1), 3-3e (+1.4 kJ mol−1) and 3-2f (+2.3 kJ mol−1) in Fig. 5, are predicted slightly higher in energy using B3LYP, while the MP2 calculations indeed energetically favor the multiple bridging motifs in the small clusters (see ESI†). As the IRMPD spectra are particularly sensitive to differences in the hydration environment of the two sulfate groups, it is possible to determine which of these different binding motifs is probed in the experiment.
The onset of water–water hydrogen bonding is predicted for n ≥ 4 and is concomitant with the hydration of the second Na+ ion. The lowest energy n = 4 structure 4-1a includes an intersulfate bridging ADD water that accepts a hydrogen bond from one of the two DD water molecules bound to the same sulfate ion. These two DD waters also each solvate a Na+ ion (dO–Na = 2.37 Å and 2.52 Å). Water–water hydrogen bonding involving a non-bridging DD water is less favorable (4-1b, +5.5 kJ mol−1). Isomers containing no or multiple intersulfate bridging water molecules are less stable (>8 kJ mol−1).
For n = 5, structures containing one (5-1b) or two (5-2a) intersulfate bridging water molecules are predicted to be nearly isoenergetic. The fifth water adds to structure 4-1a in one of two ways (5-2a and 5-2b in Fig. 5) selectively filling the hydration shell around one of the two sulfate groups. The more symmetrically-solvated triply bridged structure 5-3f (+8.0 kJ mol−1) is predicted substantially higher in energy.
Summarizing, all lowest energy structures for n = 2–5 contain less than the maximum possible number of intersulfate bridging water molecules, which has important implications for onset of the formation of SIPs in this cluster size regime.
Experimental vs. harmonic spectra
For comparison of the experimental with the simulated IR spectra, we mainly focus on the vibrations in the sulfate stretching region, which are particularly sensitive to changes in the hydration environment. Fig. 6 shows a comparison between the experimental IRMPD spectra (left column) and simulated linear IR absorption spectra of lowest energy isomers of up to three characteristic microhydration motifs for the [2,n] dianions with n = 0–5. A more complete comparison is provided in Fig. S4–S8 (see ESI†).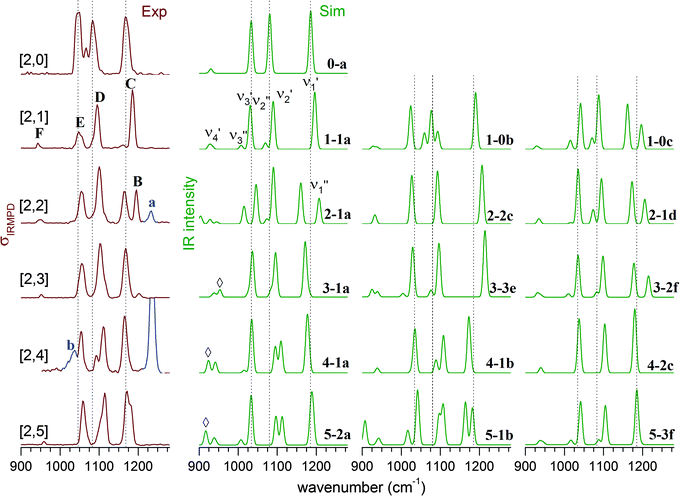 | ||
| Fig. 6 Experimental IRMPD (left) and simulated B3LYP/def2-TZVP harmonic vibrational spectra (right) in the sulfate stretching region of (NaSO4−)2(H2O)n complexes with n = 0–5 (denoted as [2,n]). The corresponding structures are illustrated in Fig. 5. Contributions of the monomer species to the IRMPD spectra are highlighted (blue trace) and labelled with small letters. | ||
The experimental IRMPD spectrum of [2,1] shows three intense bands (C–E), similar to the spectrum of [2,0], but all three bands are slightly blue-shifted and band E is significantly less intense. The simulated spectrum of the intersulfate bridging motif 1-1a shows best agreement with the experimental spectrum. Note that the symmetric combinations (νi′′) are still quite weak in intensity, which indicates that the C2h symmetry of the anionic core is largely retained. The spectra of 1-0b and 1-0c show additional bands corresponding to the νi′′ modes as a result of more asymmetric solvation; these are not observed in the experimental spectrum.
Upon addition of the second water, an additional band (band B in Fig. 6) appears in the spectrum at higher energies. The spectra of the singly bridged isomers 2-1a and 2-1d both recover this characteristic spectral pattern, while that of the more symmetrically solvated doubly bridged motif 2-2c does not. For 2-1a an additional band (ν3′′) is predicted at lower energies, which is not observed experimentally, so 2-1d exhibits slightly better agreement. The second water thus binds to one of the sulfate groups, effectively decoupling three (of the four) sulfate stretching modes of one sulfate group from those of the other. Peaks B and C now correspond to the S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretches ν1′′ and ν1′ (see Fig. S3 in the ESI†), predominantly localized on the singly (B) and the triply hydrogen-bonded (C) sulfate group, respectively.
O stretches ν1′′ and ν1′ (see Fig. S3 in the ESI†), predominantly localized on the singly (B) and the triply hydrogen-bonded (C) sulfate group, respectively.
Addition of the third water molecule leaves the positions of bands C–E unchanged, but leads to a reduction of the intensity of peak B, suggesting that this water now adds to the other sulfate group leading back to a more symmetric solvation motif. Only the spectrum of isomer 3-1a reproduces the band pattern and band positions satisfactorily, confirming this assumption and ruling out the presence of multiple intersulfate bridging water molecules in [2,3], e.g. as in isomers 3-3e and 3-2f.
The IRMPD spectrum of [2,4] looks similar to that of [2,3] suggesting that its structure is obtained by adding the fourth water to 3-1a. The peak positions remain nearly unchanged, but the ν2′′ and ν2′ modes (band D) are now resolved. The simulated spectra for 4-1a and 4-1b both capture the observed spectral pattern with the latter reproducing the relative intensities better, while that of the doubly-bridged isomer 4-2c predicts an IR-inactive ν2′′ mode due to the inversion symmetry of this isomer.
Addition of the fifth water in [2,5] leads to a broadening of band B, but leaves the rest of the spectrum nearly unchanged. An increase in the relative intensity of the ν1′′ peak is predicted for both of the nearly isoenergetic structures 5-2a and 5-1b but not for 5-3f, indicating that the solvation of the sulfate groups proceeds asymmetrically. On the other hand the spectra of all three isomers exhibit a weakly IR-active ν3′′ mode, which is not resolved in the experimental spectrum. Indeed, all three spectra reproduce certain features particularly well, but none of the three captures all of the observed peak positions and band patterns significantly better than the other ones. Note, the spectrum of [2,5] is the first to show IR-activity in the spectral region of the water librations (band G in Fig. 3). This may be seen as an indication for the onset of water–water hydrogen bond network formation as well as an increase in the importance of dynamic effects in this size range.45,46
Discussion
The following picture for the stepwise microhydration of the quaternary ion complex [2,0] evolves from the present result. In contrast to binary and tertiary ions, the initial solvation of [2,0] is not driven by the dominant cation–water interaction but by a more complex interplay involving also the sulfate–water and water–water interactions as the two chelating sulfate groups shield the two Na+ centers rather well. The first water bridges the two sulfate groups by donating two hydrogen bonds and also binds to one of the Na+ ions, breaking the C2h symmetry of the bare dianion. The formation of additional intersulfate bridges could recover the more symmetric arrangement, but this is not observed and up to n = 5, single bridging motifs are found to be dominant (n < 5) or at least to contribute significantly (n = 5). The second and third water molecules bind to the sulfate groups at either end of the cluster and weaken the electrostatic interaction dominant at the center of the complex by charge delocalization. The addition of the fourth and fifth waters then begins the formation of a hydrogen bonded network, which initially forms preferentially around one of the sulfate cores.At n = 5, the effect of microhydration on the separation of the monomers remains small, underlining the particular inherent stability of the quaternary ion complex. Note, the Na–S interatomic distances (see Table S5 in the ESI†) in [2,0] are predicted to be longer than in [1,0], 2.86 Å vs. 2.42 Å, due to the bidentate vs. tridentate binding motifs. However, while this distance increases upon hydration by +0.43 Å in [1,5] it only increases by +0.19 Å on average in [2,5] and the shortest Na–S distance actually remains nearly constant (2.88 Å). A more pronounced effect is observed for the Na–Na interatomic distance upon microhydration of [2,0], which increases by 11% to 3.31 Å in [2,5], while the S–S distance only increases by 4%. Hence, isomers with less than three bridging waters favor a more asymmetric solvation of the two sodium ions (see Table S5 in the ESI†), selectively weakening one of the Na–S electrostatic interactions. However, in contrast to microsolvation of the monomer anion,19 considerably more than five water molecules are necessary for observing a pronounced onset of SIP and SSIP formation in the dimer dianion.
The present results have implications for the interpretation of the vibrational spectra of aqueous sodium sulfate solutions. The IR-active antisymmetric stretches ν3 of free sulfate ions are observed at ∼1100 cm−1 in the FTIR-spectra of dilute solutions. With increasing concentration, the corresponding feature broadens substantially and red-shifts to 1085 cm−1 for a 2 M Na2SO4 solution.50 Ion complexes will contribute to the broadening with (binary) CIPs absorbing around 1025 cm−1 and 1250 cm−1 and the quaternary ion complexes in-between 1050 cm−1 and 1200 cm−1 (bands B–E in Fig. 2). The Raman-active sulfate symmetric stretching mode ν1 is observed at 982 cm−1 in dilute solutions17 and at 994 cm−1 in crystalline Na2SO4.51 The corresponding feature (band F in Fig. 3) is observed at lower energies in the IRMPD spectra, in-between 943–959 cm−1 for the quaternary ion complex and 941–945 cm−1 for the ion pair (see ESI†), confirming the previously predicted red-shift of this mode upon ion pair formation, although further solvation of the ion complexes will presumably reduce the red-shift.20
Recent ab initio molecular dynamics (AIMD) simulations combined with IRMPD spectra of microhydrated H2PO4− anions show that dynamic and entropic effects have a profound effect on the spectral fingerprints observed in IRMPD spectra even when the ions are precooled to cryogenic temperatures.45,46 Moreover, an assignment of these spectra based on 0 K harmonic spectra of minimum-energy structures may be problematic and misleading. Performing computational demanding AIMD simulations goes beyond the scope of this work, but we have taken care in not trying to over-interpret the present results. The situation in the quaternary ion studied here may, however, be less problematic, as the ion–water binding energies are substantially larger in this case and hence we expect the barriers to interconversion between different isomers to be larger too.
Conclusions
The quaternary ion complex (NaSO4−)2 exhibits a markedly different microsolvation behavior than the binary ion pair NaSO4− due to the efficient shielding of the Na+ centers by the chelating sulfate groups in the complex. This leads to an enhanced relative stability of the CIP configuration and a shift to larger n for the onset of SIP and SSIP formation in (NaSO4−)2(H2O)nvs. (NaSO4−)(H2O)n clusters. Consequently, the formation of quaternary ion complexes may play a central role in the initial stages of prenucleation in aqueous Na2SO4 solutions and this needs to be considered in kinetic models aimed at simulating this process.The present data may also help in the spectroscopic characterization of quaternary ion complexes in solution. Both, the fundamentals of the IR-active sulfate antisymmetric stretching modes as well as the Raman-active symmetric stretching modes, are predicted to lie energetically in-between those of the free sulfate ions and those of the binary CIP in solution.
Finally, additional and possibly more detailed information regarding the degree of dissolution of the quaternary ion complex in microhydrated clusters may be gained from measurements in the far-IR spectral region (<300 cm−1), the region where the IR-active modes involving the interion Na+–SO42− stretching modes are predicted with appreciable intensity.
Acknowledgements
We would like to thank the Stichting voor Fundamenteel Onderzoek der Materie (FOM) for beam time at FELIX and the FELIX-staff for excellent support and assistance. K. R. A. acknowledges a professorship under the Chinese Academy of Sciences (CAS) President's International Fellowship Initiative (PIFI) for Visiting Scientists (Grant No. 2015VMA068). L. J. thanks the Alexander von Humboldt Foundation for a postdoctoral scholarship, the National Natural Science Foundation of China (Grant No. 21273232), and Hundred Talents Program of Chinese Academy of Sciences. D. M. N. and T. Y. acknowledge support from the Air Force Office of Scientific Research under Grant No. FA9550-12-1-0160. We thank Harald Knorke for providing the kinetic energy release simulations.Notes and references
- S. Arrhenius, Z. Phys. Chem., 1887, 1, 631–649 Search PubMed.
- P. Jungwirth and D. J. Tobias, Chem. Rev., 2006, 106, 1259–1281 CrossRef CAS PubMed.
- M. Eigen and K. Tamm, Zeitschrift Fur Elektrochemie, 1962, 66, 107–121 CAS.
- Y. Marcus, Ions in Water and Biophysical Implications: From Chaos to Cosmos, Springer Science+Business Media, Dordrecht, 2012 Search PubMed.
- Y. Marcus and G. Hefter, Chem. Rev., 2006, 106, 4585–4621 CrossRef CAS PubMed.
- R. Buchner, T. Chen and G. Hefter, J. Phys. Chem. B, 2004, 108, 2365–2375 CrossRef CAS.
- C. Dedonder-Lardeux, G. Gregoire, C. Jouvet, S. Martrenchard and D. Solgadi, Chem. Rev., 2000, 100, 4023–4037 CrossRef CAS PubMed.
- V. E. Bondybey and M. K. Beyer, Int. Rev. Phys. Chem., 2002, 21, 277–306 CrossRef CAS.
- D. Gebauer and H. Coelfen, Nano Today, 2011, 6, 564–584 CrossRef CAS.
- Q. Zhang, C. J. Carpenter, P. R. Kemper and M. T. Bowers, J. Am. Chem. Soc., 2003, 125, 3341–3352 CrossRef CAS PubMed.
- A. T. Blades, M. Peschke, U. H. Verkerk and P. Kebarle, J. Am. Chem. Soc., 2004, 126, 11995–12003 CrossRef CAS PubMed.
- D. Schröder, L. Ducháčková, J. Tarábek, M. Karwowska, K. J. Fijalkowski, M. Ončák and P. Slavíček, J. Am. Chem. Soc., 2011, 133, 2444–2451 CrossRef PubMed.
- C. J. Johnson and M. A. Johnson, J. Phys. Chem. A, 2013, 117, 13265–13274 CrossRef CAS PubMed.
- J. W. DePalma, P. J. Kelleher, C. J. Johnson, J. A. Fournier and M. A. Johnson, J. Phys. Chem. A, 2015, 119, 8294–8302 CrossRef CAS PubMed.
- K. A. Prather, C. D. Hatch and V. H. Grassian, Annu. Rev. Anal. Chem., 2008, 1, 485–514 CrossRef CAS PubMed.
- Y. H. Zhang and C. K. Chan, J. Phys. Chem. A, 2002, 106, 285–292 CrossRef CAS.
- J. Reimer, M. Steele-MacInnis, J. M. Wambach and F. Vogel, J. Phys. Chem. B, 2015, 119, 9847–9857 CrossRef CAS PubMed.
- X. B. Wang, C. F. Ding, J. B. Nicholas, D. A. Dixon and L. S. Wang, J. Phys. Chem. A, 1999, 103, 3423–3429 CrossRef CAS.
- X. B. Wang, H. K. Woo, B. Jagoda-Cwiklik, P. Jungwirth and L. S. Wang, Phys. Chem. Chem. Phys., 2006, 8, 4294–4296 RSC.
- H. Zhang, S. Wang and C.-C. Sun, J. Chem. Phys., 2011, 135, 084309 CrossRef PubMed.
- T. Jin, B. Zhang, J. Song, L. Jiang, Y. Qiu and W. Zhuang, J. Phys. Chem. A, 2014, 118, 9157–9162 CrossRef CAS PubMed.
- M. Okumura, L. I. Yeh and Y. T. Lee, J. Chem. Phys., 1985, 83, 3705–3706 CrossRef CAS.
- J. M. Lisy, Int. Rev. Phys. Chem., 1997, 16, 267–289 CrossRef CAS.
- M. A. Duncan, Int. J. Mass Spectrom., 2000, 200, 545–569 CrossRef CAS.
- W. H. Robertson and M. A. Johnson, Annu. Rev. Phys. Chem., 2003, 54, 173–213 CrossRef CAS PubMed.
- K. R. Asmis, N. L. Pivonka, G. Santambrogio, M. Brümmer, C. Kaposta, D. M. Neumark and L. Wöste, Science, 2003, 299, 1375–1377 CrossRef CAS PubMed.
- J. Zhou, G. Santambrogio, M. Brümmer, D. T. Moore, G. Meijer, D. M. Neumark and K. R. Asmis, J. Chem. Phys., 2006, 125, 111102 CrossRef PubMed.
- K. R. Asmis and D. M. Neumark, Acc. Chem. Res., 2012, 45, 43–52 CrossRef CAS PubMed.
- B. Jagoda-Cwiklik, P. Jungwirth, L. Rulisek, P. Milko, J. Roithova, J. Lemaire, P. Maitre, J. M. Ortega and D. Schroder, ChemPhysChem, 2007, 8, 1629–1639 CrossRef CAS PubMed.
- L. Jiang, T. Wende, R. Bergmann, G. Meijer and K. R. Asmis, J. Am. Chem. Soc., 2010, 132, 7398–7404 CrossRef CAS PubMed.
- C. J. Johnson, L. C. Dzugan, A. B. Wolk, C. M. Leavitt, J. A. Fournier, A. B. McCoy and M. A. Johnson, J. Phys. Chem. A, 2014, 118, 7590–7597 CrossRef CAS PubMed.
- D. J. Goebbert, G. Meijer and K. R. Asmis, AIP Conf. Proc., 2009, 1104, 22–29 CrossRef CAS.
- D. J. Goebbert, T. Wende, R. Bergmann, G. Meijer and K. R. Asmis, J. Phys. Chem. A, 2009, 113, 5874–5880 CrossRef CAS PubMed.
- D. Oepts, A. F. G. van der Meer and P. W. van Amersfoort, Infrared Phys. Technol., 1995, 36, 297–308 CAS.
- N. Heine and K. R. Asmis, Int. Rev. Phys. Chem., 2015, 34, 1–34 CrossRef CAS.
- J. Oomens, G. Meijer and G. von Helden, J. Phys. Chem. A, 2001, 105, 8302–8309 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. J. A. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian, Inc., Wallingford CT, 2004.
- TURBOMOLE V 6.2, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com, 2010.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- T. I. Yacovitch, T. Wende, L. Jiang, N. Heine, G. Meijer, D. M. Neumark and K. R. Asmis, J. Phys. Chem. Lett., 2011, 2, 2135–2140 CrossRef CAS.
- H. G. Weikert, L. S. Cederbaum, F. Tarantelli and A. I. Boldyrev, Z. Phys. D, 1991, 18, 299–305 CrossRef CAS.
- D. Schröder and H. Schwarz, J. Phys. Chem. A, 1999, 103, 7385–7394 CrossRef.
- M. Beyer, E. R. Williams and V. E. Bondybey, J. Am. Chem. Soc., 1999, 121, 1565–1573 CrossRef CAS PubMed.
- E. Garand, T. Wende, D. J. Goebbert, R. Bergmann, G. Meijer, D. M. Neumark and K. R. Asmis, J. Am. Chem. Soc., 2010, 132, 849–856 CrossRef CAS PubMed.
- L. Jiang, S.-T. Sun, N. Heine, J.-W. Liu, T. I. Yacovitch, T. Wende, Z.-F. Liu, D. M. Neumark and K. R. Asmis, Phys. Chem. Chem. Phys., 2014, 16, 1314–1318 RSC.
- S.-T. Sun, L. Jiang, J. W. Liu, N. Heine, T. I. Yacovitch, T. Wende, K. R. Asmis, D. M. Neumark and Z.-F. Liu, Phys. Chem. Chem. Phys., 2015, 17, 25714–25724 RSC.
- D. J. Goebbert, E. Garand, T. Wende, R. Bergmann, G. Meijer, K. R. Asmis and D. M. Neumark, J. Phys. Chem. A, 2009, 113, 7584–7592 CrossRef CAS PubMed.
- K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096 CrossRef CAS.
- A. G. Nord, Acta Chem. Scand., 1973, 27, 814–822 CrossRef CAS.
- Z. F. Wei, Y. H. Zhang, L. J. Zhao, J. H. Liu and X. H. Li, J. Phys. Chem. A, 2005, 109, 1337–1342 CrossRef CAS PubMed.
- B. K. Choi and D. J. Lockwood, Solid State Commun., 1990, 76, 863–866 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Assignments (Table S1), experimental absorption frequencies for microhydrated NaSO4− (Table S2), calculated sulfate stretching frequencies and relative energies of representative low-lying isomers (Table S3), B3LYP/def2-TZVP and MP2/def2-TZVP relative energies of several low-lying isomers (Table S4), Na–Na, S–S, Na–S, and S–O distances of low-lying isomers (Table S5), simulation of arrival time distributions as a function of kinetic energy release (Fig. S1), photofragment ion yield for m/z = 137 amu e−1 corresponding to [2,2] and [1,1] as a function of the wavenumber for two laser pulse energies (Fig. S2), fundamental sulfate stretching modes of the C3v isomer of NaSO4− (Fig. S3), harmonic spectra for (NaSO4−)2(H2O)1–5 (Fig. S4–S8), Cartesian coordinates for all isomers. See DOI: 10.1039/c5cp05762k |
| ‡ Current address: Physical and Theoretical Chemistry Laboratory, University of Oxford, South Parks Road, Oxford OX1 3QZ, UK. |
| § Current address: Chemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA. |
| ¶ Current address: Aerodyne Research, Inc., Billlerica, MA 01821, USA. |
| This journal is © the Owner Societies 2016 |