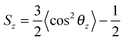Interaction of C₆₀ fullerenes with asymmetric and curved lipid membranes: a molecular dynamics study

Abstract

Interaction of fullerenes with asymmetric and curved DOPC/DOPS bicelles is studied by means of coarse-grained molecular dynamics simulations. The effects caused by asymmetric lipid composition of the membrane leaflets and the curvature of the membrane are analyzed. It is shown that the aggregates of fullerenes prefer to penetrate into the membrane in the regions of the moderately positive mean curvature. Upon penetration into the hydrophobic core of the membrane fullerenes avoid the regions of the extreme positive or the negative curvature. Fullerenes increase the ordering of lipid tails, which are in direct contact with them, but do not influence other lipids significantly. Our data suggest that the effects of the membrane curvature should be taken into account in the studies concerning permeability of the membranes to fullerenes and fullerene-based drug delivery systems.

---

Introduction

Discovery of fullerenes in 1985 manifested the beginning of the era of carbon nanomaterials which revolutionized the areas of materials science and biomedical research. Although other forms of carbon, such as nanotubes and graphene, are argued to be more promising for practical applications nowadays, C₆₀ fullerenes remain the most extensively studied carbon nanoparticles. Their nanometer size and unusual physical and chemical properties¹ make them suitable for numerous biomedical applications. The solubility and charge of fullerenes can be routinely modified by chemical functionalization.^2,3 Changes in the surface chemistry make them usable as anti-HIV, antitumor and antimicrobial agents as well as enzyme inhibitors,^4–8 antibiotics^4,6,9,10 and antioxidants.¹¹ The most promising application of fullerenes is, however, their usage as drug delivery vectors.¹² The hydrophobic nature of fullerenes and their very high affinity for the lipid membranes make them promising drug carriers, which can transport polar or charged compounds into cells.^13,14 Fullerenes are known to be toxic, which often limits their application in medicine. However, pure C₆₀ molecules are more toxic than water-soluble functionalized forms.¹⁵

The exact mechanisms of biological activity and toxicity of C₆₀ fullerenes are still subject to debate, which stimulated numerous computational studies of their interaction with biological membranes and macromolecules.¹⁶ Early computational studies of fullerenes were mainly focused on their aggregation in water¹⁷ or behavior of individual fullerenes inside the lipid bilayer.¹⁸ Recent studies of the translocation of fullerenes through lipid membranes^19,20 showed that pristine C₆₀ fullerenes are trapped inside the hydrophobic core of the membrane which may cause toxicity by means of the membrane disruption.²¹

Despite obvious practical interest, no dedicated studies focusing on the interaction of fullerenes with realistic models of eukaryotic cell membranes were performed to date. To our knowledge all computational studies done so far on fullerenes in lipid membranes deal with planar symmetric lipid bilayers. Such a simulation setup ignores two major properties of real cell membranes – their asymmetry and curvature.^22,23 Indeed, living cells exhibit various membrane shapes ranging from random undulations to highly curved protrusions and invaginations.²⁴ There are well-known experimental and theoretical studies of the membrane curvature^25–27 and bending elasticity,²⁸ however only a few dedicated simulations of the curved membranes are available. Most of them are related to membrane fusion^29–31 and the functioning of mechanosensitive ion channels³² thus the curvature itself and its influence on the properties of the bilayer are usually not analyzed in detail.

The lipid composition of the membrane leaflets also differs dramatically. It is well known that phosphatidylcholine and sphingomyelin are located mostly in the outer leaflet of the plasma membranes, while phosphatidylethanolamine, phosphatidylserine and phosphoinositides are abundant in the inner leaflet.^33,34 The distribution of sterols, which are the most abundant molecules in eukaryotic membranes after the lipids, is also remarkably uneven.^35–37 Many important cellular phenomena such as the formation of synaptic vesicles²⁷ and apoptotic bodies,^38,39 membrane fusion,^40,41 budding of enveloped viruses from the plasma membrane,^42,43 the formation of blebs during apoptosis,^38,39 blood cell maturing⁴⁴ and mitosis⁴⁵ are known to be influenced by the lipid asymmetry and the membrane curvature.⁴⁶ Thus, it is expected that the interaction of fullerenes with membranes is also dependent on the membrane curvature and asymmetry of their lipid composition.

In the present study we focus on the interaction of C₆₀ fullerenes with curved and asymmetric DOPC/DOPS membranes. We constructed asymmetric bicelles with the leaflets containing DOPC and DOPS lipids, respectively. The middle of such bicelles possesses a moderate spontaneous curvature caused by the lipid asymmetry, while the caps show an extremely positive curvature. This allows us to sample regions with very different curvatures and lipid packing in a single simulation. Pure DOPC bicelles without a spontaneous curvature were used as a reference in order to distinguish the curvature and lipid composition effects. We used coarse-grained molecular dynamics simulations to simulate the spontaneous penetration of fullerenes from the water phase to the bicelle and their distribution inside the hydrophobic core of the membrane at the time scale of tens of microseconds. To our knowledge, this work is the first systematic study of the interaction of fullerenes with asymmetric non-planar membranes.

Methods

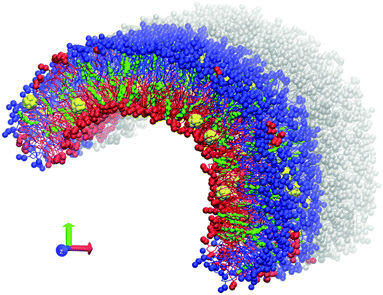
Coarse-grained MARTINI force field version 2.1⁴⁷ was used for all computations. C₆₀ fullerene molecules were modeled according to the previous work of Monticelli et al.⁴⁸ The GROMACS software package, versions 4.6.5 and 5.0.4,^49–51 was used. All simulations were performed at a temperature of 320 K with recommended simulation parameters for the MARTINI force field.⁴⁷ A Berendsen barostat with a relaxation constant of 5 ps was used for semi-isotropic pressure coupling. Pressure of 1 atm was maintained in the Z direction while the size of the box in the XY plane was fixed to prevent uncontrollable deformation of the simulation box.

An asymmetric bicelle consisting of neutral DOPC (dioleoylphosphatidylcholine), charged DOPS (dioleoylphosphatidylserine) lipids and cholesterol was constructed. Each monolayer of the bicelle was built from either DOPC or DOPS lipids (Fig. 1). The bicelle is periodic in the Z direction and has semi-cylindrical caps in the XY plane. It is important to mention that the distribution of cholesterol molecules between the lipid monolayers can be significantly affected by the initial setup, due to a very large flip-flop transition time (up to a few hundreds of ns) between the two leaflets in comparison with the total simulation time²² (micro second time scale). Unbiased distribution of cholesterol molecules between the monolayers was obtained by following the method already used in our previous work.²³ C₆₀ molecules were initially placed between the membrane leaflets and were allowed to freely diffuse into the monolayers during the simulation.

Fig. 1 Equilibrated asymmetric DOPC/DOPS bicelles. DOPC lipids are blue, DOPS lipids are red, cholesterol molecules are green, individual fullerenes are yellow. Water is not shown for clarity. One of the periodic images of the system in the Z dimension is shown in grey to emphasize that the bicelle is infinite in this direction.

Fig. 2 Average size of the fullerene clusters as a function of time. Presented curve is an average over five independent trajectories with different starting velocities. The curve is smoothed by moving window average (window size 50 ns) for clarity.

The tails of DOPC and DOPS lipids are identical which leads to their spontaneous mixing both in experiments and in simulations with MARTINI force field. In our setup such mixing, which may occur by lateral diffusion through the caps of the bicelle, should be prevented in order to maintain the asymmetry between the monolayers. This is accomplished by introducing artificial repulsive potential between the coarse-grained phosphate groups of DOPC and DOPS lipids. This repulsive potential was implemented in the form of Lennard–Jones interactions with the interaction constants C₆ = 0, C₁₂ = 2.581 (GROMACS force field units). These parameters were already tested in our previous studies.²² They ensure that individual lipids almost never cross the boundary between the DOPC and DOPS domains. Small compact clusters of lipids of one type could sometimes diffuse into the domain of the other lipid type (several such clusters are visible in Fig. 1) but their number remains small at the time scale of tens of microseconds and they never distort the overall shape of the curved bicelle. Such clusters were excluded from analysis by considering only the lipids, which are surrounded by the nearest neighbors of the same type.

The bicelle was equilibrated for 10 μs. During equilibration, it developed a significant curvature in the XY plain due to different intrinsic curvatures of DOPC and DOPS lipids.

After initial equilibration, 32 C₆₀ fullerene molecules were randomly distributed in the water phase around the bicelle. The final system was composed of 504 DOPC lipids, 504 DOPS lipids, 196 cholesterol molecules, 32 C₆₀ molecules, ∼64 000 coarse-grained water particles and 504 coarse-grained Na⁺ ions to compensate the negative charges of DOPS lipid heads.

Five independent production simulations of the system with fullerenes were done. Each trajectory was 4 μs long (effective time). It is proved that the effective time of simulations with the coarse-grained MARTINI model is 4 times longer than the real simulation time.⁴⁷ In addition, the following reference trajectories were produced: (1) the 4 μs trajectory of DOPC/DOPS bicelles without fullerenes; (2) five independent trajectories of symmetric DOPC bicelles with fullerenes (1.5 μs each).

To compute local curvatures and instantaneous areas per lipid, the compiled C++ plug-in implemented in the Pteros molecular modeling library⁵² developed in our previous work⁵³ was used. The plug-in was modified in order to work with fullerene molecules. Its functionality was enhanced by adding ability to compute order parameters of the lipid tails taking into account the local normal of the membrane.

The distributions of means and Gaussian curvatures shown in Fig. 3–5 are computed by weighing the local curvature at the position of particular lipid by the instantaneous areas occupied by this lipid at the given simulation frame (see ref. 53 for details).

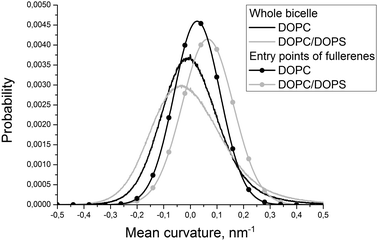Fig. 3 Distributions of the mean curvature for individual DOPC and DOPS monolayers and for the points of the first entry of fullerenes into these monolayers.

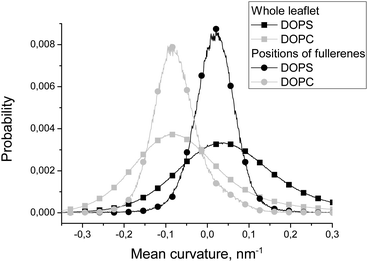Fig. 4 Distributions of the local mean curvature in the whole DOPC and DOPS leaflets and in the positions of fullerenes in these leaflets.

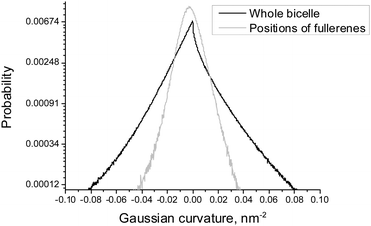Fig. 5 Distributions of the local Gaussian curvature in the whole bicelle and in the positions of fullerenes for asymmetric DOPC/DOPS bicelles.

Aggregation of fullerenes was monitored by performing simple agglomerative clustering. Fullerene is considered to belong to a given cluster if the distance between its center of masses and the center of masses of any fullerene in the cluster is less than 2R + d, where R = 0.6 nm is the fullerene effective radius, d = 0.01 nm. The mean cluster size was computed by averaging the size of all distinct clusters formed for each particular simulation frame.

To estimate the influence of fullerenes on the packing of lipids in asymmetric bicelles, the order parameter for the lipid tails with respect to the local normal of the bicelle was computed as:

where angle brackets denote time averaging over the trajectory; θ_z is the angle between the local membrane normal and the vector between two consecutive carbons in the tail. Order parameters can vary from 1 (full ordering along the interface normal) to −1/2 (full ordering in the tangent plane). The zero value corresponds to the case of isotropic orientation.

Results

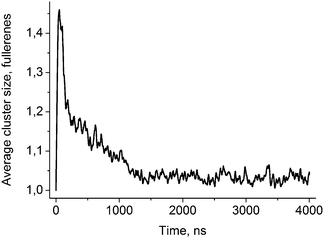
Fig. 2 shows the evolution of the average size of the fullerene clusters in the course of simulations. The size of the clusters is one in the starting configuration because all fullerenes are added as single molecules. During the first ∼50 ns, the average size of clusters increases rapidly due to very fast aggregation of fullerenes in the water phase. After this initial period, the clusters start penetrating into the bicelle. Then the clusters dissociate upon penetration which is clearly visible by the rapid decrease of their mean size. After the first ∼700–1000 ns (depending on the trajectory), all fullerene clusters are absorbed by the bicelle and after ∼1400 ns all clusters fall apart into individual molecules.

Fig. 3 shows distributions of the mean curvature for four different cases: (1) for the points of the first entry of fullerenes into the asymmetric DOPC/DOPS bicelle; (2) for the whole DOPC/DOPS bicelle; (3) for the points of the first entry into the symmetric DOPC bicelle and (4) for the whole symmetric DOPC bicelle. The number of distinct first entry events is only 160 (32 fullerenes in 5 independent trajectories) for each system thus we computed first and second statistical moments of the distribution (mean value and dispersion) and plotted corresponding approximated Gaussian distribution in Fig. 3.

The maximum of distribution for the symmetric DOPC bicelle is centered at zero, while the distribution for DOPC/DOPS is shifted slightly to positive curvatures. This is explained by the larger surface area of the convex DOPC monolayer and the presence of the caps with a positive mean curvature (the curvatures are weighted by the instantaneous area per lipid as explained in the Methods section). The distributions in the points of the first entry are shifted substantially to positive curvatures in comparison with the corresponding distributions for the whole bicelles in both systems. The magnitude of this shift is very similar in asymmetric and symmetric bicelles which means that this effect is systematic and not caused by the presence of artificial repulsive potential in the asymmetric bicelle.

Fig. 4 compares distributions of the mean curvature in the points where fullerenes are located in equilibrium with the distributions for the whole DOPC and DOPS monolayers. The maxima of the distributions for fullerenes and for the whole monolayers almost coincide for both DOPC and DOPS lipids. However, the half-widths of the distributions for fullerenes are much smaller in comparison with the distributions for corresponding monolayers. This clearly shows that fullerenes concentrate in the regions which have the curvature close to the average curvature of the particular monolayer and avoid the regions with an unusually large or an unusually small curvature.

Fullerenes are distributed almost uniformly between different monolayers in equilibrium (51% in the DOPC monolayer and 49% in the DOPS monolayer) despite the fact that the convex DOPC monolayer has larger surface area.

Fig. 5 shows the distribution of the Gaussian curvature in the equilibrium positions of fullerenes and for the whole bicelle. The distributions are not subdivided into DOPC and DOPS monolayers because they are essentially identical for both of them (data not shown). The maxima of both distributions coincide and equal to zero while their widths show the same behavior as the distributions of the mean curvature in Fig. 4. The distribution for fullerenes is significantly narrower which means that fullerenes avoid the regions of a very large or a very small Gaussian curvature in the same way as they do this in the case of the mean curvature.

Fig. 6 shows the distribution of the distance from the bicelle's surface to the fullerene molecules. There are two peaks on this distribution but only one of them (the one close to the surface of the membrane) is significant while the other one is an artifact caused by the coarse-grained force field (see Discussion for details). This distribution is essentially the same for DOPC and DOPS monolayers of the asymmetric bicelle and for the symmetric DOPC bicelle (data not shown).

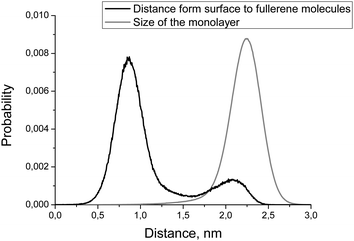Fig. 6 Distributions of the distance from membrane's surface to the fullerene molecules (black line) and monolayer size (gray line).

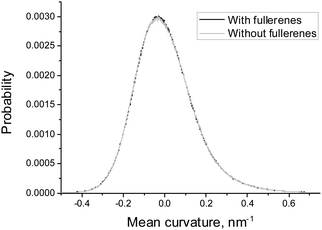
In order to estimate the influence of fullerenes on the shape of the asymmetric DOPC/DOPS bicelle, we compared the distributions of mean and Gaussian curvatures for the systems with and without fullerenes (Fig. 7 and 8). It is clearly seen that addition of fullerenes does not lead to any significant change of these distributions which means that fullerenes do not change the overall shape and the curvature of the bicelle.

Fig. 7 Distributions of the mean curvature of the DOPC/DOPS bicelle with and without fullerenes.

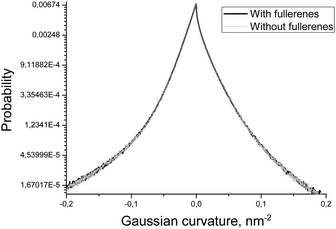Fig. 8 Distributions of the Gaussian curvature of the DOPC/DOPS bicelle with and without fullerenes.

Despite the fact that fullerenes do not change the curvature of the bicelle, they influence the packing of individual lipid chains. Fig. 9 shows the orientational order parameter for the lipid tails which are in direct contact (within 0.6 nm) with fullerenes and those which are far from them. Tails of the DOPC and DOPS lipids are represented by six coarse-grained beads in the MARTINI force field. Every point on the plot represents an order parameter of the vector, which connects two neighboring coarse-grained particles counting from the lipid head. It is clearly seen from Fig. 9 that ordering of the first particles of the lipid tails increases for the lipids, which are in contact with fullerenes.

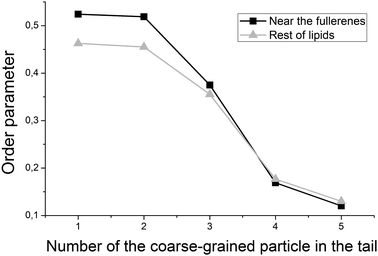Fig. 9 Order parameter of the lipid tails, computed for the lipids near (black line) and far (gray line) from fullerenes inside of the bicelle.

Discussion

Aggregation of fullerenes

Fullerene molecules are hydrophobic by nature and tend to aggregate in aqueous solution. In our simulations, 32 individual fullerene molecules were initially placed at random positions in the water phase. In the course of simulations, there is a competition between the aggregation of fullerenes in water and their incorporation into the bicelle. Aggregation dominates in the first ∼50 ns of simulations when the average size of clusters increases rapidly. After this initial period, the clusters start colliding with the bicelle and penetrating into its hydrophobic core. Visual inspection shows that the clusters of fullerenes penetrate into the bicelle without dissociation. Rather big clusters of up to 5–7 fullerenes can enter the bicelle. Upon penetration into the lipid bilayer, the clusters start dissociating into individual molecules. This process finishes completely after ∼1400 ns. The equilibrium size of the clusters is slightly larger than one due to random collisions of fullerenes inside the hydrophobic core of the bicelle. Such collisions are transient and do not lead to aggregation.

Curvature-dependent penetration of fullerenes

In order to study the role of the mean curvature in the process of penetration of fullerenes into the lipid bilayer, we analyzed the points of their first entry into the bicelle. The data obtained from five independent simulations of asymmetric DOPC/DOPS and symmetric DOPC bicelles were collected to account for the role of asymmetric lipid distribution.

The fact that the distribution of the mean curvature of the pure DOPC bicelle is centered at zero (Fig. 3) is expected since the symmetric bicelle does not develop any significant curvature except random undulations. The only regions of a large positive mean curvature are cylindrical caps of the bicelle. In the case of asymmetric DOPC/DOPS bicelles the peak of the mean curvature distribution is shifted towards positive curvatures due to the fact that the asymmetric bicelle is significantly curved as a whole and the convex DOPC monolayer has larger surface area.

The distributions of the mean curvature in the points of the first entry of fullerenes are shifted significantly to more positive values for both symmetric and asymmetric bicelles (Fig. 3). This clearly indicates that fullerenes prefer to penetrate through the convex membrane surface with a positive mean curvature where the distances between the lipid head groups are larger than in the concave surface with a negative mean curvature.

Visual inspection of trajectories shows that the majority of entry events occur far from the bicelle caps in the regions of the moderately positive mean curvature. In the case of the asymmetric bicelle the number of entries through the caps is significantly higher. This could be attributed to the repulsion between DOPC and DOPS lipids which prevents their spontaneous mixing in the caps of the bicelle but increases the distance between their head groups. If one excludes extra penetration events through the bicelle caps caused by this artifact then both symmetric and asymmetric bicelles show very similar behavior.

It is possible to conclude that fullerenes prefer to penetrate into the membrane displaying regions with a positive local mean curvature. In contrast, preferred positions of penetration into the bicelle are not sensitive to the local Gaussian curvature (data not shown).

Equilibrium distribution of fullerenes inside the bicelle

According to Fig. 4, equilibrium distribution of fullerenes inside the bicelle is not significantly influenced by the mean curvature except the slight preference for negative mean curvatures (concave surfaces) in the DOPS monolayer. However, it is clearly seen that only a negligible amount of fullerenes is located in the regions with extreme values (either positive or negative) of the mean curvature. Thus, we can conclude that fullerenes are distributed almost evenly in the regions with a moderate curvature and avoid the regions with an extreme curvature (including the bicelle caps).

Fig. 5 shows that the equilibrium distribution of fullerenes is independent of the local Gaussian curvature. The sharp peak obtained in the distribution of the Gaussian curvature near zero confirms that most of the membrane has cylinder-like topology imposed by the system setup (the membrane is infinite in Z dimension).

Another important characteristic of equilibrium fullerene distribution inside the bicelle is its distance from the membrane surface (Fig. 6). Two distinct populations of fullerenes exist: the major one at ∼0.9 nm from the surface, and the minor one at approximately 2.1 nm. The major population is located at the beginning of the lipid tails just underneath the head groups. The minor population is located at the center of the bilayer but it is proved to be an artifact of the coarse-grained MARTINI force field for fullerenes.⁴⁸ Indeed, the potentials of mean force (PMF) for transferring fullerenes across the membrane in all-atom simulations show a single energy well, which coincides with our major population.⁴⁸ However, coarse-grained PMF with MARTINI force field shows very small additional energy well in the center of the bilayer which leads to the appearance of minor population.⁴⁸ The minor population in the center of the bilayer is ignored in our analysis. The appearance of such small artifacts in energy profiles is a usual trade-off of the coarse grained force fields which is almost impossible to avoid during parameterization. In the case of our system small additional population of fullerenes in the center of bilayer is harmless since fullerenes in general do not influence the overall shape and curvature of the bicelle, which is apparent from Fig. 7 and 8.

Ordering of the lipid tails

It is expected that the presence of large fullerene molecules in the membrane should affect the ordering of the lipid tails significantly. However, in the previous studies which utilized the MARTINI force field,¹⁹ the authors did not observe any significant changes in the average order parameter of the lipid tails in the presence of fullerenes. Detectable changes in the order parameter were only observed for very high concentrations of the fullerene molecules (∼11% molar concentration). In this work, we studied ordering of the lipid tails in more details by computing an order parameter for the lipid tails, which are in direct contact with fullerenes and for the rest of the lipid tails separately. Fig. 9 shows that the tails of the lipids, which are in direct contact with fullerenes, are significantly more ordered in the region close to the head groups. This is in perfect agreement with the average location of fullerenes in the bilayer in this region (Fig. 6) and suggests that fullerenes induce additional ordering of the lipid tails in their local vicinity but do not influence remote lipids significantly.

Conclusions

In this work, we studied interaction of asymmetric DOPC/DOPS bicelles with C₆₀ fullerenes using coarse-grained molecular dynamics simulations. We performed a series of simulations of DOPC/DOPS bicelles with fullerenes in water and compared the results with the simulations of symmetric DOPC bicelles in order to distinguish the effects of the membrane asymmetry and the curvature.

It is shown that fullerenes form stable aggregates in water which penetrate into the membrane as a whole. However, such clusters dissociate quickly into separate molecules inside the membrane.

Our data show that fullerenes prefer to penetrate into the membrane in the regions with a positive mean curvature. This preference is observed in symmetric and asymmetric bicelles alike.

Fullerenes are distributed almost evenly in the regions with a moderate curvature inside the membrane. However, they strongly avoid the regions with extreme positive or negative curvatures. Also neither mean nor Gaussian curvature of the bicelle itself is changed significantly in the presence of fullerenes at ∼3.2% molar concentration.

The fullerene molecules significantly increase the order parameter of the lipid tails which are in direct contact with them. At the same time, the ordering of the lipids which are not in contact with fullerenes is not affected.

Our data clearly show that behavior of fullerenes in asymmetric and curved membranes is non-trivial. The effects of the curvature are more pronounced in comparison with the effects of lipid composition of the membrane leaflets. Penetration of fullerenes into the membranes and their distribution in the hydrophobic part of the bilayer are curvature-dependent and should be taken into account in the studies concerning permeability of the membranes to fullerene-based drug delivery systems.

Acknowledgements

S. Y. and Y. C. thank the Université de Bourgogne Franche-Comté for financial support. The authors thank the Mésocentre de calcul de Franche-Comté for providing computational resources for this work.

Notes and references

1. T. Da Ros and M. Prato, Chem. Commun., 1999, 663–669.
2. M. Brettreich and A. Hirsch, Tetrahedron Lett., 1998, 39, 2731–2734.
3. A. Hirsch, Nat. Mater., 2010, 9, 868–871.
4. S. Bosi, T. Da Ros, G. Spalluto and M. Prato, Eur. J. Med. Chem., 2003, 38, 913–923.
5. R. Bakry, R. M. Vallant, M. Najam-ul-Haq, M. Rainer, Z. Szabo, C. W. Huck and G. K. Bonn, Int. J. Nanomed., 2007, 2, 639–649.
6. S. Nakamura and T. Mashino, J. Phys.: Conf. Ser., 2009, 159, 012003.
7. G. D. Nielsen, M. Roursgaard, K. A. Jensen, S. S. Poulsen and S. T. Larsen, Basic Clin. Pharmacol. Toxicol., 2008, 103, 197–208.
8. R. Partha and J. L. Conyers, Int. J. Nanomed., 2009, 4, 261–275.
9. T. Mashino, K. Okuda, T. Hirota and M. Hirobe, Bioorg. Med. Chem. Lett., 1991, 9, 2959–2962.
10. H. Aoshima, K. Kokubo, S. Shirakawa, M. Ito, S. Yamana and T. Oshima, Biocontrol Sci., 2009, 14, 69–72.
11. I. C. Wang, L. A. Tai, D. D. Lee, P. P. Kanakamma, C. K. F. Shen, T.-Y. Luh, C. H. Cheng and K. C. Hwang, J. Med. Chem., 1999, 42, 4614–4620.
12. R. Partha and J. L. Conyers, Int. J. Nanomed., 2009, 4, 261–275.
13. R. Partha, L. R. Mitchell, J. L. Lyon, P. P. Joshi and J. L. Conyers, ACS Nano, 2008, 2, 1950–1958.
14. L. L. Dugan, D. M. Turetsky, C. Du, D. Lobner, M. Wheeler, C. R. Almli, C. K. F. Shen, T. Y. Luh, D. W. Choi and T. S. Lin, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 9434–9439.
15. C. M. Sayes, J. D. Fortner, W. Guo, D. Lyon, A. M. Boyd, K. D. Ausman, Y. J. Tao, B. Sitharaman, L. J. Wilson, J. B. Hughes, J. L. West and V. L. Colvin, Nano Lett., 2004, 4, 1881–1887.
16. D. Bedrov, G. D. Smith, H. Davande and L. Li, J. Phys. Chem. B, 2008, 112, 2078–2084.
17. N. Choudhury, J. Chem. Phys., 2006, 125, 034502.
18. L. Li, H. Davande, D. Bedrov and G. D. Smith, J. Phys. Chem. B, 2007, 111, 4067–4072.
19. J. Wong-Ekkabut, S. Baoukina, W. Triampo, I. M. Tang, D. P. Tieleman and L. Monticelli, Nat. Nanotechnol., 2008, 3, 363–368.
20. S. O. Yesylevskyy, S. Kraszewski, F. Picaud and C. Ramseyer, Mol. Membr. Biol., 2013, 30, 338–345.
21. C. Cusan, T. Da Ros, G. Spalluto, S. Foley, J. M. Janto, P. Seta, C. Larroque, M. C. Tomasini, T. Antonelli, L. Ferraro and M. Prato, Eur. J. Org. Chem., 2002, 2928–2934.
22. S. Yesylevskyy and A. Demchenko, Eur. Biophys. J., 2012, 41, 1043–1054.
23. S. O. Yesylevskyy, A. P. Demchenko, S. Kraszewski and C. Ramseyer, Sci. World J., 2013, 2013, 10.
24. H. T. McMahon and J. L. Gallop, Nature, 2005, 438, 590–596.
25. D. Marsh, Biophys. J., 1996, 70, 2248–2255.
26. Y. Shibata, J. Hu, M. M. Kozlov and T. A. Rapoport, Annu. Rev. Cell Dev. Biol., 2009, 25, 329–354.
27. H. T. McMahon, M. M. Kozlov and S. Martens, Cell, 2010, 140, 601–605.
28. D. Marsh, Chem. Phys. Lipids, 2006, 144, 146–159.
29. S. Martens and H. T. McMahon, Nat. Rev. Mol. Cell Biol., 2008, 9, 543–556.
30. V. Knecht and S.-J. Marrink, Biophys. J., 2007, 92, 4254–4261.
31. S. Marrink and A. Mark, J. Am. Chem. Soc., 2003, 125, 11144–11145.
32. G. R. Meyer, J. Gullingsrud, K. Schulten and B. Martinac, Biophys. J., 2006, 91, 1630–1637.
33. V. Kiessling, C. Wan and L. K. Tamm, Biochim. Biophys. Acta, 2009, 1788, 64–71.
34. A. P. Demchenko and S. O. Yesylevskyy, Chem. Phys. Lipids, 2009, 160, 63–84.
35. M. R. Ali, K. H. Cheng and J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 5372–5377.
36. A. Radhakrishnan and H. McConnell, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 12662–12666.
37. H. Ohvo-Rekila, B. Ramstedt, P. Leppimaki and J. P. Slotte, Prog. Lipid Res., 2002, 41, 66–97.
38. G. J. Gores, B. Herman and J. J. Lemasters, Hepatology, 2005, 11, 690–698.
39. R. C. Taylor, S. P. Cullen and S. J. Martin, Nat. Rev. Mol. Cell Biol., 2008, 9, 231–241.
40. R. Jahn, T. Lang and T. C. Südhof, Cell, 2003, 112, 519–533.
41. M. A. Churchward, T. Rogasevskaia, J. Höfgen, J. Bau and J. R. Coorssen, J. Cell Sci., 2005, 118, 4833–4848.
42. T. L. Cadd, U. Skoging and P. Liljeström, BioEssays, 2005, 19, 993–1000.
43. M. Lorizate and H.-G. Kräusslich, Cold Spring Harbor Perspect. Biol., 2011, 3, a004820.
44. R. E. Griffiths, S. Kupzig, N. Cogan, T. J. Mankelow, V. M. S. Betin, K. Trakarnsanga, E. J. Massey, J. D. Lane, S. F. Parsons and D. J. Anstee, Blood, 2012, 119, 6296–6306.
45. C. Roubinet, B. Decelle, G. Chicanne, J. F. Dorn, B. Payrastre, F. Payre and S. Carreno, J. Cell Biol., 2011, 195, 99–112.
46. W. B. Huttner and J. Zimmerberg, Curr. Opin. Cell Biol., 2001, 13, 478–484.
47. S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812–7824.
48. L. Monticelli, J. Chem. Theory Comput., 2012, 8, 1370–1378.
49. B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447.
50. S. Páll, M. Abraham, C. Kutzner, B. Hess and E. Lindahl, in Solving Software Challenges for Exascale, ed. S. Markidis and E. Laure, Springer International Publishing, 2015, vol. 8759, ch. 1, pp. 3–27.
51. S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854.
52. S. O. Yesylevskyy, J. Comput. Chem., 2015, 36, 1480–1488.
53. S. O. Yesylevskyy and C. Ramseyer, Phys. Chem. Chem. Phys., 2014, 16, 17052–17061.

---